Lung texture in serial thoracic CT scans: Registration-based methods to compare anatomically matched regions

Abstract

Purpose: The aim of this study was to compare three demons registration-based methods to identify spatially matched regions in serial computed tomography (CT) scans for use in texture analysis.

Methods: Two thoracic CT scans containing no lung abnormalities and acquired during serial examinations separated by at least one week were retrospectively collected from 27 patients. Over 1000 regions of interest (ROIs) were randomly placed in the lungs of each baseline scan. Anatomically matched ROIs in the corresponding follow-up scan were placed by mapping the baseline scan ROI center pixel to (1) the original follow-up scan, (2) the follow-up scan resampled to match the baseline scan voxel size, and (3) the follow-up scan aligned to the baseline scan through affine registration. Mappings used the vector field obtained through demons deformable registration of each follow-up scan variant to the baseline scan. 140 texture features distributed among five feature classes were calculated in all ROIs. Feature value differences between paired ROIs were evaluated using Bland-Altman 95% limits of agreement. For each feature, (1) the mean feature value change and (2) the difference between the upper and lower limits of agreement were normalized to the mean feature value to obtain, respectively, the normalized bias and normalized range of agreement (nRoA). Nonparametric tests were used to evaluate differences in normalized bias and nRoA across the three methods.

Results: Because patient CT scans contained no pathology, minimal changes in feature values were expected (i.e., low nRoA and normalized bias). Seventy-five features with very large feature value variability (nRoA ≥ 100%) were excluded from further analysis. Across the remaining 65 features, significant differences in normalized bias were observed among the three methods. The lowest normalized bias (median: 0.06%) was achieved when feature values were calculated on original follow-up scans. The affine registration method achieved the lowest nRoA, though nRoA was not significantly increased using original follow-up scans. Features with low nRoA values also had low normalized bias, though the converse was not necessarily true. Using nRoA as a metric, a set of 20 features having both low nRoA and normalized bias were identified.

Conclusions: Three methods to facilitate texture analysis of serial CT scans using demons registration for ROI placement were evaluated. The bias in feature value change between matched ROIs was minimized when feature values were calculated on original baseline and follow-up scans. A set of features that had both low bias and variability (nRoA) in feature value change using this method were identified. This texture analysis approach could facilitate future measurement of pathologic changes between CT scans without necessitating calculation of feature values on deformed scans.

INTRODUCTION

Texture analysis of thoracic computed tomography (CT) images can allow for identification of various disease patterns and/or aid in the diagnosis of lung disease. Several groups have used CT image texture analysis to identify various patterns of diffuse lung disease, including emphysema, ground-glass opacification, and honeycombing.^{1, 2, 3} Yao et al.⁴ showed that a set of first-order, gray-level co-occurrence matrix (GLCM), and gray-level run-length matrix texture features could distinguish H1N1 influenza from fibrosis, noninfluenza infections, and normal lung tissue. Ganeshan et al.⁵ found that lung cancer tumor metabolism and stage correlated with a set of first-order texture features calculated using CT scans that had been filtered to emphasize certain morphology. These researchers have demonstrated that, using texture analysis, CT scans can provide valuable information about a patient's disease status at a single point in time.

For patients with progressive lung disease, CT scans at multiple time points may be acquired to assess disease progression or treatment response. Coregistration of these serial CT scans facilitates assessment of disease changes in spatially matched locations over time. A number of algorithms based on control point matching (splines deformable registration) (Refs. ⁶ and ⁷) or optical flow (demons deformable registration) (Refs. ⁸ and ⁹) have been applied for thoracic CT scan registration. These deformable registration techniques correct for differences both in patient positioning and respiratory phase between serial scans. Changes between serial scans that are not due to positioning differences can thus be identified.

Texture analysis of coregistered serial CT scans would allow for measurement of texture changes between anatomically matched regions over time, providing objective measurement of disease progression or treatment response. Several groups have performed quantitative analysis using coregistered CT scans. Palma et al.¹⁰ measured pixel value changes between thoracic CT scans acquired before and after lung radiation therapy that had been registered using B-splines deformable registration; no higher-order features were investigated. Arzhaeva et al.¹¹ used B-splines registration to align CT scan pairs acquired from patients with interstitial lung disease, then quantified changes between scans using a set of first-order, dissimilarity, and filter-based texture features. They did not determine, however, whether the registration process itself may have also altered CT scan texture, potentially confounding changes due to disease. In a previous publication, we evaluated the registration accuracy achieved using four image registration algorithms and examined their effects on lung CT image texture features.¹² While demons deformable registration achieved the highest registration accuracy among the four methods, this registration method introduced nonzero bias in feature values due to the altered lung parenchymal texture in deformed CT scans. This study demonstrated that although texture analysis of coregistered CT scans appears a straightforward method for measuring temporal changes, this approach may not be reliable due to the registration-induced changes in the deformed scans. Alternatively, methods that facilitate texture comparisons using CT scans that have not been deformed should be investigated.

In the current work, several approaches to measure changes in image texture between serial CT scans are presented and evaluated. These methods use the registration accuracy achieved by demons deformable registration to identify matched regions in CT scan pairs. Texture features are then calculated directly on CT scans that have not been deformed, thus eliminating the possibility that deformation itself had altered texture. The bias and variability in feature value change introduced by these methods are calculated and compared. The goal is to identify a method that minimizes bias across features in the absence of disease change and to identify a set of texture features with low variability using this approach.

METHODS

Patient database

The patient database has been described previously.¹² Healthy thoracic CT scan pairs acquired between one week and two years apart (mean: 126 days) for 27 patients were retrospectively collected under Institutional Review Board (IRB) approval. For each patient, CT scan pairs were acquired either with (n = 24) or without (n = 3) intravenous contrast injection. All scans were determined to have no lung abnormalities, defined by the absence of acute disease or nodules exceeding 4 mm, by an experienced radiologist. Scans were acquired after patients were instructed to inspire and hold their breath using multislice Philips Brilliance CT scanners (Brilliance 16, Brilliance 16P, Brilliance 64, or Brilliance iCT256) and reconstructed at submillimeter pixel spacing and 1 mm slice thickness using identical high-resolution lung reconstruction and smoothing kernels. The peak kilovoltage was 120 kVp for all scans, and the exposure ranged from 144 to 351 mAs. The median difference in exposure between scan pairs was 20 mAs (range: 0–156 mAs).

Region of interest (ROI) identification and mapping

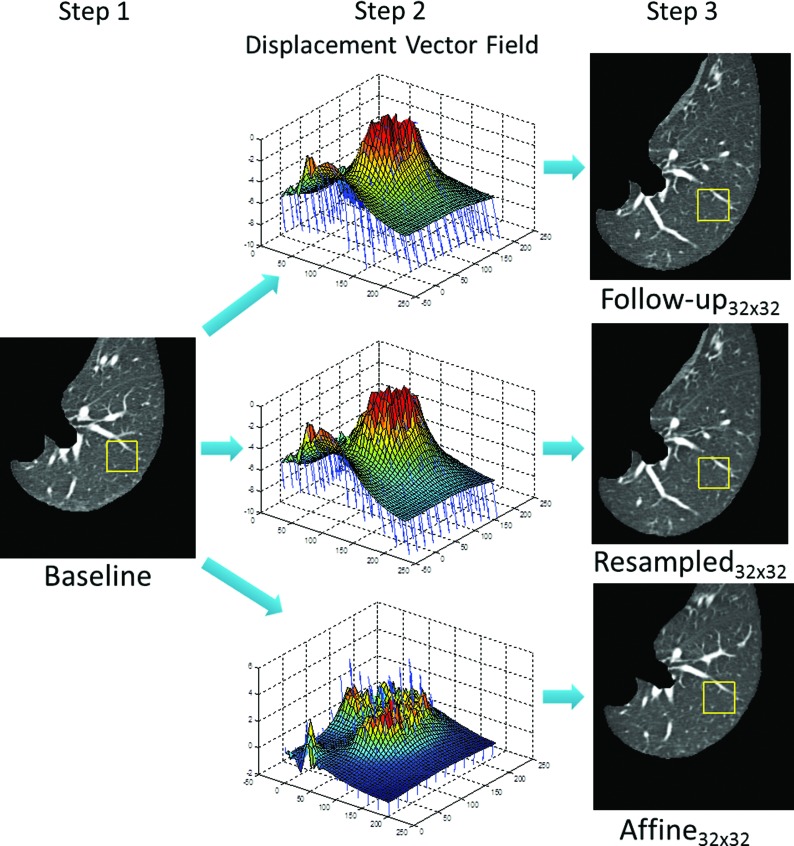
The method used to identify ROIs in a baseline scan CT and map them to their corresponding locations in a follow-up scan is shown in Fig. 1. Following automated lung segmentation,¹³ randomly placed 32 × 32-pixel ROIs were automatically identified in each patient's baseline scan (Step 1). Only ROIs lying entirely within the lung borders while not overlapping previously selected ROIs were retained. A maximum of ten ROIs were identified in each axial CT section, resulting in 1435–2413 (mean: 1898) ROIs per patient.

Figure 1.

Steps for ROI (yellow box) mapping from a baseline scan to a follow-up scan and two follow-up scan transformations using the displacement vector fields displayed in column 2.

Identification of ROIs in follow-up scans relied on application of fully automated demons deformable registration using the open-source software package Plastimatch (version 1.5.12-beta).⁸ First, the follow-up scan was deformed to match the baseline scan, outputting a displacement vector field (Step 2) that mapped each pixel in the baseline scan to a corresponding location in the follow-up scan. The center of a baseline scan ROI was mapped to the original (i.e., not deformed) follow-up scan using the vector field, with the remainder of the ROI placed in the same axial section (Step 3). Follow-up scan ROIs with the same size in pixels as the baseline scan ROIs (i.e., 32 × 32 pixels) and with the same physical size in millimeters (i.e., n × n pixels) as the baseline scan ROIs were both considered, otherwise referred to as “follow-up_32×32” and “follow-up_n×n” ROIs, respectively. This distinction results from the fact that baseline and follow-up scans generally do not possess the same pixel size.

In addition, follow-up CT scans were transformed using two distinct techniques that could potentially improve ROI alignment between baseline and follow-up scans. For the first alternative approach, the patient's follow-up CT scan was resampled to match the voxel size of the baseline scan, with bilinear interpolation used to assign the corresponding gray-level values. 32 × 32-pixel ROIs in the baseline scans and resampled follow-up scans (“resampled_32×32” ROIs) were therefore the same physical size, removing the possibility that differences in the pixel size between CT scans in a pair could affect texture feature value comparisons. For the second approach, the follow-up CT scan was globally registered to the baseline scan using affine registration. While previously presented methods ensured only that the center of a baseline scan ROI was well-matched in the follow-up scan, this alternative approach increases the likelihood that an entire inplane 32 × 32-pixel ROI in the globally registered follow-up scan (“affine_32×32” ROI) contains similar anatomy to the ROI in the baseline scan. The transformed follow-up scans were then registered to the baseline scan using demons registration to achieve a mapping between ROIs in the baseline and transformed follow-up scans as previously described (see Fig. 1).

CT scan texture analysis

A set of 140 texture features distributed among first-order, fractal, Fourier, GLCM, and Laws’ filter classes were calculated. These features are presented in more detail in Sec. 2D. Feature values in matched ROIs in baseline and follow-up scans were compared using Bland-Altman limits of agreement for the case of multiple measurements per patient.¹⁴ The difference between the upper and lower 95% limits of agreement was calculated and normalized to the mean feature value across all baseline scan ROIs to obtain the normalized range of agreement (nRoA). The bias was also calculated as the mean difference between baseline and follow-up scan ROI feature values and normalized to the mean ROI feature value in the baseline scan to obtain the normalized bias (nBias)

$$\begin{array}{ccc}\hfill \mathrm{nRoA}& =& \frac{(95\%\mathrm{limit}\mathrm{upper}\mathrm{bound}-95\%\mathrm{limit}\mathrm{lower}\mathrm{bound})}{\left|\mathrm{Mean}\mathrm{feature}\mathrm{value}\right|}\hfill \\ & & \times 100\%,\hfill \end{array}$$ (1)

$$\mathrm{nBias}=\frac{\mathrm{Bias}}{\left|\mathrm{Mean}\mathrm{feature}\mathrm{value}\right|}\times 100\%,$$ (2)

$$\begin{array}{c}\hfill \mathrm{Mean}\mathrm{feature}\mathrm{value}=\frac{1}{\mathrm{nROIs}}\sum _{\mathrm{all}\mathrm{ROIs}}\mathrm{Feature}{\mathrm{value}}_{\mathrm{baseline}},\end{array}$$ (3)

where nROIs is the total number of baseline scan ROIs across all patients. Because patient CT scans contained no pathology, minimal changes in feature values were expected between scans in a pair, with the expectation of narrow limits of agreement (low nRoA) and low bias.

To separate bias introduced during the mapping technique from bias introduced due to intrinsic CT scan differences, analysis was repeated in the reverse order as detailed in a previous publication.¹² ROIs were first identified in follow-up CT scans, then ROI center pixels were mapped to their corresponding locations in all of the variants of the baseline CT scans. The normalized bias was again calculated and averaged with the bias achieved using the forward registration method. For bias introduced by differences between scans in a pair, the magnitude of bias was expected to be similar using both forward and reverse methods, though the direction of bias (i.e., the sign) would be reversed. Bias introduced by scan resampling or registration, however, was expected to have the same sign and similar magnitude irrespective of the registration direction. Thus, the average normalized bias (nBias_avg) represented the bias introduced during the registration/mapping method rather than by differences between the CT scans themselves.

Values of nRoA and nBias_avg were calculated for all features and compared among the approaches. Friedman rank sum tests were used to determine if significant (p < 0.05) differences in nRoA and nBias_avg existed among the three methods. nRoA and nBias_avg values were then compared between each pair of approaches using Wilcoxon signed rank tests (paired, two-tailed). To maintain model significance at α = 0.05, significance levels for individual tests were modified according to the Bonferroni method. Results were also compared with our previous study in which texture feature differences had been calculated between baseline scans and demons-deformed follow-up scans directly, after renormalizing values of nRoA and nBias_avg to the average baseline scan feature values.¹² nRoA and nBias_avg values for GLCM features reported in our previous study were adjusted for consistency with the methods reported by Haralick et al.¹⁵

Texture features

Texture features were derived from five feature classes.

First-order histogram features

First-order histogram features^{16, 17, 18} characterize the gray-level histogram of an image or region. The 19 first-order features calculated were: mean, median, maximum, minimum, mean absolute deviation, range, interquartile range (IQR), standard deviation, skewness, kurtosis, energy, entropy, binned entropy (calculated after sorting data into 256 histogram bins), 5%, 30%, 60%, and 95% histogram quantiles, and balance of the inner 40% and inner 90% of the gray-level histogram.

Fractal features

These features characterize region self-similarity at different scales and indicate image detail. Fractal dimension was calculated using three methods: the blanket method,¹⁹ the Brownian motion method,²⁰ and the box-counting method^{18, 21, 22} (including total, coarse, and fine aspects of the box-counting dimension).

Fourier features

Fourier-based features characterize the spatial frequency components of a region. Fourier features calculated include the first moment of the power spectrum,²³ the root-mean-squared variation,²³ and the energy of the Fourier-transformed region and of several subspaces representing different frequency components. These subspaces were the high- and low-frequency rings when the region was subdivided into two sections; the low, moderately low, moderately high, and high frequency rings when the region was subdivided into four sections; and the eight sectors formed when the region was divided into 45° sectors.¹⁶

Laws’ filter features

These features emphasize five aspects of region microstructure: spot, wave, ripple, edge, and level surfaces.²⁴ Regions were first convolved with a particular filter, then a set of features (mean, energy, binned entropy, maximum, minimum, and standard deviation) were calculated on rotationally invariant filtered regions.

Gray-level co-occurrence matrix features

GLCM features^{15, 16, 17} quantify the spatial relationships of gray-level values in a region. For each region, a GLCM was first constructed to count all gray-level pairs separated by 1 pixel and at angle θ. Fourteen features were calculated from the GLCM: correlation, inertia, absolute value, inverse difference, energy, entropy, contrast, sum of squares variance, sum average, sum variance, sum entropy, difference average, difference variance, and difference entropy. Four directions were examined (θ = {0°, 45°, 90°, and 135°}), and each feature was calculated by taking the average over the four directions.

RESULTS

For 75 of 140 features, nRoA values were greater than 100% using all approaches, indicating that the variability exceeded the mean feature value across baseline scan ROIs [see Eq. 1]. These findings were similar to our previous study, in which 52 features had nRoA values that exceeded 100%.¹² For the remaining 65 features with nRoA < 100%, follow-up_32×32 ROI and follow-up_nxn ROI texture feature values were compared to determine if it was necessary to change ROI size to accommodate differences in pixel dimension in the follow-up scan. Boxplots (Fig. 2) display the nBias_avg and nRoA for these two approaches. nBias_avg appeared slightly higher when ROI size was altered (median: 0.14% versus 0.06%), though this difference was not significant. Furthermore, several outlier values of nBias_avg existed using the follow-up_nxn ROIs. There was no significant difference in nRoA between the two approaches (median: 67.32% versus 67.44%). Due to the similarities between the two approaches, only the measurements obtained with 32 × 32-pixel ROIs (follow-up_32×32) were considered for the remainder of the analysis.

Figure 2.

Boxplot compare nBias_avg (left) and nRoA (right) values when follow-up scan ROI size was fixed at 32 × 32 pixels versus when size was adjusted to match the physical ROI size in the baseline scan.

For the 65 features with nRoA < 100%, Friedman rank sum tests indicated that significant differences in nBias_avg existed among the follow-up_32×32, resampled_32×32, and affine_32×32 ROI approaches (p = 3 × 10⁻⁹). Wilcoxon signed rank tests showed that the differences in nBias_avg between each pairwise comparison of the three methods were significant (p < α/3 = 0.017 for all three tests). The lowest median value of nBias_avg across features occurred for follow-up_32×32 ROIs, while affine_32×32 ROIs yielded the highest median value of nBias_avg (Table 1). Significant difference in nRoA among the three methods were also observed (p = 1 × 10⁻⁹). Using Wilcoxon signed ranks tests for pairwise comparisons, no significant differences in nRoA were observed between the follow-up_32×32 and the affine_32×32 ROIs (p = 0.30); however, these two mapping methods achieved significantly lower nRoA than the resampled_32×32 ROIs (p < 0.017), indicating lower variability in feature value change. Figure 3 depicts histograms of nBias_avg and nRoA values across the 65 features for each ROI mapping technique. For features calculated from resampled_32×32 and affine_32×32 ROIs, values of nBias_avg were more widely distributed about zero than for follow-up_32×32 ROIs, indicating that feature values were consistently altered from baseline using these methods.

Table 1.

Median normalized bias, median nRoA, and the respective IQR for the three methods using the 65 features with nRoA < 100% for at least one method.

Mapping	Median nBiasavg [IQR] (%)	Median nRoA [IQR] (%)
Follow-up32×32	0.1 [0.0, 0.2]	67.4 [17.3, 91.1]
Resampled32×32	−5.2 [−12.7, −0.8]	72.3 [18.6, 97.1]
Affine32×32	−5.9 [−14.2, −0.9]	64.6 [16.2, 86.6]

Figure 3.

Histograms of nBias_avg (top) and nRoA (bottom) values obtained for 65 features using the three mapping methods. For visualization purposes, the range of nBias_avg values displayed on the x-axis for the follow-up scan mapping (top left) is smaller than for the two transformed scan mappings (top middle and top right).

The relationship between nRoA and nBias_avg across features was investigated. For all three mapping methods, the variability in nBias_avg increased with increasing nRoA, as indicated in Fig. 4. Although the features with the lowest nRoA values also had low nBias_avg values, many of the features with low nBias_avg had large values of nRoA.

Figure 4.

Scatterplot of nBias_avg versus nRoA when features were calculated directly on follow-up scans. Each of the 65 features with nRoA < 100% for at least one method is included. Although not shown, plots generated using the two alternative methods (resampled_32×32 and affine_32×32) were similar.

Table 2 compares nRoA and nBias_avg values obtained using the three presented mapping methods with the values obtained previously when feature values were calculated on demons-deformed follow-up scans directly (demons_32×32).¹² The 20 features displayed in the table are those that yielded nRoA ≤ 20% for at least one of the three currently presented approaches.

Table 2.

Values of nRoA and nBias_avg for the 20 features with nRoA ≤ 20% for at least one of the three methods.

	Follow-up32×32		Resampled32×32		Affine32×32		Demons32×32
	nRoA (%)	nBiasavg (%)	nRoA (%)	nBiasavg (%)	nRoA (%)	nBiasavg (%)	nRoA (%)	nBiasavg (%)
First-order features
Minimum	5.82	−0.02	7.77	1.35	8.09	1.57	9.79	3.39
Mean	13.79	0.00	13.56	0.03	12.94	−0.02	7.58	0.24
Median	10.95	−0.03	10.83	0.13	10.74	0.14	7.30	0.19
Binned entropy	16.79	0.01	16.96	−1.20	16.15	−1.43	14.42	−4.03
Unbinned entropy	11.53	0.01	12.00	−1.66	11.52	−2.02	10.13	−4.66
5% quantile	10.11	−0.05	11.32	2.93	10.86	3.26	10.84	4.83
30% quantile	9.67	−0.04	9.65	1.15	9.56	1.28	7.46	1.85
70% quantile	16.77	−0.01	16.45	−0.82	15.88	−0.92	9.19	−1.45
Fractal features
Box counting dim.	15.13	−0.05	15.65	−3.92	13.53	−4.29	11.51	−5.91
Fine dimension	17.33	−0.04	21.03	−6.58	19.16	−7.08	16.27	−8.46
Brownian dimension	7.16	−0.01	6.85	−0.83	5.70	−0.91	4.48	−1.28
Laws’ filter features
E5L5 entropy	17.21	0.06	16.79	−1.46	14.05	−1.76	10.68	−2.54
R5L5 entropy	19.00	0.01	19.82	−5.23	17.66	−5.75	14.17	−4.01
S5L5 entropy	19.22	0.07	18.57	−2.67	15.65	−3.12	11.52	−3.67
W5L5 entropy	19.11	0.05	18.87	−4.04	16.31	−4.55	12.45	−4.36
GLCM features
Difference entropy	13.26	0.02	15.20	−4.93	13.54	−5.53	12.84	−9.48
Entropy	3.55	0.00	2.88	0.02	2.88	−0.03	3.04	−0.50
Sum of squares var.	15.48	0.03	15.75	−1.77	14.59	−2.12	12.94	−3.95
Sum average	7.12	0.01	7.32	−0.78	6.91	−0.94	6.36	−1.86
Sum entropy	8.38	0.01	8.78	−1.68	8.34	−1.94	7.23	−3.63
Mean across all features	12.87	0.00	13.30	−1.60	12.20	−1.81	10.01	−2.46

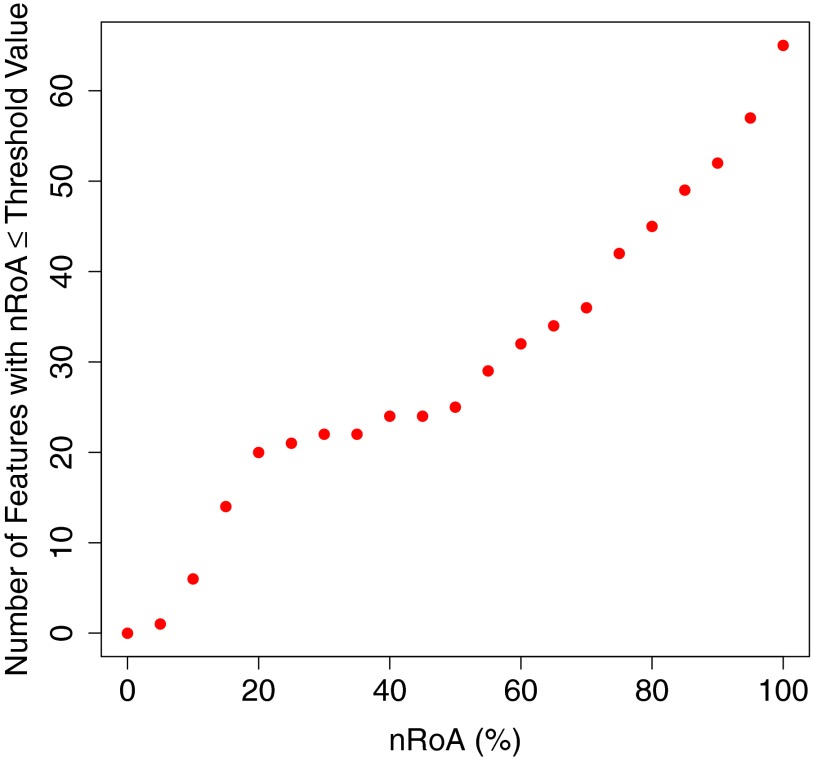
Beyond nRoA = 20%, the number of features per nRoA increment decreased, indicated by the changing slope in Fig. 5. For the 20 features presented, nRoA was significantly smaller using the demons_32×32 method than the follow-up_32×32 method (p = 4 × 10⁻⁴), while nBias_avg was significantly smaller for follow-up_32×32 ROIs (p = 0.008).

Figure 5.

The cumulative number of features with at most a given nRoA value for at least one of the methods. Plots generated using each of the methods individually (not shown) were similar. nRoA values ranged from 0% to 100% in 5% increments.

DISCUSSION

This study investigated the effects on texture feature values of mapping ROIs between serial CT scans. Compared to resampled_32×32 and affine_32×32 ROIs, follow-up_32×32 ROIs were found to yield the lowest values of nBias_avg without significantly increasing nRoA. This mapping method may therefore be the most appropriate technique for texture analysis of serial CT scans, as minimal bias in feature values was introduced. With this method, low values of nRoA also had low values of normalized bias (Fig. 4), though low normalized bias did not imply low values of nRoA. As the variability in feature value change increased (nRoA increased), it is possible that the accuracy with which bias could be measured decreased, resulting in increasing variability in nBias_avg with increasing nRoA. Thus, the use of nRoA is more selective of features than nBias_avg. Table 2 displays features that had low nRoA and nBias_avg when feature values were calculated on follow-up scans and compares the results with a previous study.¹² Although mean nRoA was lower using the previously reported methods that directly deformed scans, nBias_avg was an order of magnitude larger, indicating that feature values were consistently altered using these methods. In the previous study, feature values were also calculated on scans that were deformed through B-splines registration. For 19 of the 20 features, values of nRoA and nBias_avg calculated using follow-up_32×32 ROIs remained less than or equal to the values calculated previously using B-splines-deformed follow-up ROIs, indicating that localizations of ROI center pixels using demons registration remained more accurate than B-splines. The previous study demonstrated that deformable registration of CT scans introduced bias in texture feature values, potentially restricting the utility of this approach in future texture analysis applications. The techniques presented in this study, however, provide an avenue for texture analysis of serial scans that utilizes demons for coregistration of ROIs but not for scan deformation, thereby reducing the effects of image distortion.

The 20 features displayed in Table 2 had the lowest values of nRoA (nRoA < 20%) using follow-up_32×32 ROIs. Above nRoA = 20%, the number of features per nRoA increment declined so that approximately one feature was added per 5% increase in nRoA (Fig. 5). Because increasing the nRoA threshold (and thus increasing feature value variability) would include few additional features, nRoA = 20% seemed an appropriate cutoff for this study. The choice of features to select for future texture analysis applications, however, will ultimately depend on the disease change itself. If, for example, the appearance of a particular disease pattern results only in small changes in feature values from baseline, features with low variability (i.e., small nRoA) relative to the disease change should be selected. In general, the nRoA of features used for the detection task should be smaller than the change introduced by disease to achieve sufficiently high sensitivity. Thus, higher-nRoA features could be included in analysis, particularly if they measure independent aspects of image texture. Steps should be taken, however, to minimize nBias_avg, as nonzero bias indicates that the image (and thus the disease pattern itself) is being distorted due to CT scan manipulation. As demonstrated in our previous work, deformable registration had similar effects on nBias_avg as the transformations presented here (resampling and affine registration).¹²

It is possible that some of the features identified may be insensitive to changes in lung parenchymal texture, resulting in similar feature values (thus, low nRoA and nBias_avg) irrespective of actual differences between CT scans in a pair. In our previous work,¹² we observed that two of the features presented in Table 2 (minimum and 5% quantile) remained similar between CT scans in a pair even when registration accuracy was low, suggesting that these features may be ill-equipped to detect true changes between scans. In future studies, features that are insensitive to lung parenchymal changes will be identified using a database of patients with lung disease.

Only small changes in nRoA and nBias_avg were introduced when follow-up scan ROI size was adjusted. The reason for the generally small differences using the two techniques may be due to the similarities between matched ROIs in CT scan pairs. Differences in pixel size between scans in a pair did not exceed 0.18 mm, resulting in small differences in the extent of anatomy included in 32 × 32-pixel ROIs in the baseline and follow-up scans. ROI size adjustment was therefore not necessary to correct for differences in pixel size between scans. Instead, changing the ROI size may have affected the values of features, resulting in slightly larger values of nBias_avg. As an alternative to changing ROI size, follow-up scans were resampled to match voxel sizes in the corresponding baseline scans prior to texture analysis in 32 × 32-pixel ROIs (resampled_32×32). Resampling the scans, however, introduced consistent changes in feature values, indicated by an increased nBias_avg. We therefore concluded that changing ROI size to match a baseline scan ROI introduced considerably smaller bias than transforming the CT scan itself. In applications where pixel size differences between scan pairs are larger than those observed here, the effects of ROI size on feature values will need to be reevaluated.

While all CT scans in this study scans were acquired using Philips Brilliance CT scanners, CT scan pairs were not necessarily acquired using the same scanner model (n = 12 with the same model for both scans versus n = 15 with different models). To determine the effects of scanner differences on nRoA and nBias_avg, the results for patients with scans acquired using different scanners were compared with those of the patients who had both scans acquired using the same scanner model. Across the 20 features displayed in Table 2, the mean difference in nRoA between the two groups did not exceed 2% using the three methods (resampled_32×32, affine_32×32, and follow-up_32×32), while the mean difference in nBias_avg remained below 0.1%. Wilcoxon signed rank tests (paired, one-sided) showed that, across the 20 features, nRoA and nBias_avg were not significantly increased for any of the methods when scans were acquired using different scanner models. One limitation of this study is that it only considers CT scans acquired with Philips scanners and reconstructed using a single high-resolution lung reconstruction algorithm. The utility of the features identified here remains to be tested using other CT scanner models and reconstruction techniques. Furthermore, the results of this study should be validated using a database of patients with progressive disease. Differences between CT scan pairs resulting from disease changes may complicate the registration process, leading to inferior anatomic matching between baseline and follow-up scan ROIs. Future studies will evaluate the differences in anatomic alignment achieved when registering diseased patient CT scans and examine the effects on nRoA and nBias_avg.

To our knowledge, this is the first investigation that quantifies the effects of lung CT scan transformations on a variety of texture features. A study by Palma et al.²⁵ concluded that the registration algorithm used (B-splines) did not introduce notable changes in mean pixel value between CT scans. These results remain consistent with our study, in which minimal changes in mean pixel value due to CT scan transformation were observed with all of the approaches studied, resulting in low values of nRoA and nBias_avg (Table 2). For the majority of the features investigated, however, nonzero bias was introduced when scans underwent transformation. Further studies that use these higher-order features to detect disease changes should consider the effects of scan transformation on the values of these features.

CONCLUSIONS

Three methods for mapping ROIs between anatomically matched regions of serial CT scans were evaluated based on their effects on texture feature values. For each approach, the anatomic alignment accuracy achieved through demons registration was used to map ROI centers from baseline to follow-up scans. Feature values were calculated, however, on scans that had not been deformed, thus eliminating the possibility for CT scan deformation to alter image texture. One method (follow-up_32×32) achieved significantly lower nBias_avg than the other approaches, indicating that feature values were minimally perturbed. nBias_avg for this method was also smaller than in a previous study where features were calculated directly on demons-deformed scans. Compared with the method that achieved lowest variability (affine_32×32), nRoA values for follow-up_32×32 ROIs were not significantly higher, indicating low variability in feature value differences between scans with this approach. Twenty features with both low nRoA and nBias_avg were identified for use with the follow-up_32×32 method. In future studies of patients with lung disease, this method may facilitate quantitative measurement of differences between serial CT scans due to disease progression or response to treatment, allowing for improved detection and characterization of pathologic change.