Asymmetry of the cross-sectional area of paravertebral and psoas muscle in patients with degenerative scoliosis

Abstract

Purpose

This study was undertaken to assess the change of psoas and paravertebral muscles in patients with degenerative scoliosis.

Methods

Eighty-five patients with degenerative scoliosis were evaluated with simple radiography for the location and direction of the apex of scoliosis, coronal Cobb’s angle, rotational deformity and lumbar lordosis, and with magnetic resonance imaging scan at the apex level of each patient, the cross-sectional area (CSA) and the fatty infiltration rate (FI) of bilateral paravertebral and psoas muscles were measured and the values of convex and concave side were compared.

Results

Fifty-three patients had apex of curves on the left side and thirty-two patients on the right. The mean Cobb’s angle was 17.9°. The difference index of CSA (CDI) of psoas and multifidus muscle at apex of curvature level was significantly larger in convex side rather than that in concave side (by 6.3 and 8.4 % with P = 0.019 and 0.000, respectively). FI of each muscle showed no significant difference.

Conclusions

Hypertrophy of the muscles on the convex side is suggested as the explanation of this asymmetry rather than atrophy of the muscles on the concave side as muscle atrophy is known to be associated with increased fatty infiltration.

Introduction

Degenerative scoliosis has been thought to develop as a result of asymmetry in degeneration of discs [1] and facet joints [2] and/or osteoporosis and compression fractures of vertebral bodies [3], although it has not yet been determined whether the asymmetric changes of these structures come first before or after deformation of the spine. In order to assess the relationship of these various factors and the possible mechanism of how degenerative scoliosis develops, a hypothesis of a vicious cycle in which the deformity is perpetuated by the asymmetric loading and degeneration and vice versa was proposed by Aebi [4]. It is a reasonable explanation, though it ignores the role of the neuromuscular system, the function of which is essential to the stability of the spine as is seen in other parts of the musculoskeletal system [5, 6]. As to the low back pain or the degenerative flat-back, a deformity in the sagittal plane, there are also many reports describing the changes in the paraspinal musculature [7]. Nevertheless, regarding degenerative scoliosis there are few works which elucidate the changes of the paravertebral musculature. Authors have postulated that the paraspinal musculature would show a significant difference on each side in patients with degenerative scoliosis and we investigated the patterns and extent of change of paraspinal and psoas muscles by measuring the cross-sectional area (CSA) and the intramuscular fatty infiltration rate (FI).

Materials and methods

Based on the electronic medical records, a retrospective cohort of patients with de novo degenerative scoliosis or presumed de novo scoliosis was constructed from the population seen in the outpatient clinic of the Department of Orthopaedic Surgery of our hospital during the period from January 2007 to December 2008 after approval from our institutional review board (IRB). De novo degenerative scoliosis was diagnosed when a new curve, in the coronal plane, was identified with a Cobb’s angle of more than 10° compared to that seen on older films, and was presumed when curvature showed the characteristic of de novo degenerative scoliosis which is a relatively short curvature confined to the level between the T12 and S1 vertebra and with Cobb’s angle more than 10° in a standing simple radiograph in patients more than 50 years of age. Patients who had previously undergone spinal surgery and who had multiple fractures or other systemic disease, such as muscular dystrophy or Parkinson disease, etc. which can affect the spinal alignment, were excluded from the review.

The Cobb’s angle of scoliosis, the degree of rotational deformity according to Nash and Moe’s method [8], lumbar lordosis (from upper the end-plate of L1 to upper end-plate of S1) were measured using the simple upright radiograph with anteroposterior and lateral projection. From the digitalized magnetic resonance image in the picture archiving and communication system (PACS), the CSA and the fatty infiltration rate (FI) of the bilateral psoas major and paravertebral muscles were measured using the technique described in the following paragraph.

Magnetic resonance imaging (MRI) protocol

The MR images were acquired on the 1.5T scanner (Genesis Sigma; GE Milwaukee, WI, USA) using a spine or body-array coil. The patients were placed in the supine position with the spine in a neutral position and a pillow under their knees. A sagittal sequence was performed with the following sequences: T1-weighted turbo spin echo (SE; TR 550 ms, TE 12 ms) and T2-weighted turbo SE (TR 4,000 ms, TE 120 ms). With same sequences, transverse images were acquired at the level of disc space, parallel to the disc being corrected for lordosis, from T12–L1 to L5–S1 with four slices of 4 mm section thickness, a 180 × 180 mm field of view, a 512 × 512 matrix per level.

Measurement of the cross-sectional area and fatty infiltration rate of muscles as seen on MRI

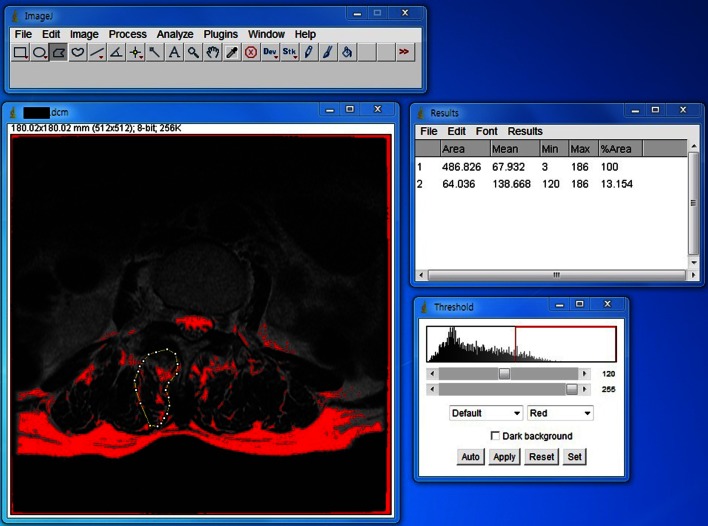
In order to minimize the effect of the deformity of the spinal column itself on the morphometry of the paraspinal and psoas muscle, the axial image obtained at the level of the apex of the curvature, and which is horizontal, was used as a reference for comparison. Within slices at the same level, the most distal slice of the transverse images at each level, and cutting the upper endplate of the lower vertebra, was used as the bony structure of vertebral body showed more distinct contrast to muscle than the disc with a dark signal. Images with T2 sequence were chosen to refer to the results of previous studies [9, 10]. The regions of interest (ROI) were defined by manual tracing of the fascial boundary of the following muscles at both sides around the spinal column: psoas major, multifidus (also including rotatores lumborum), spinal erectors (encompassing both longissimus and iliocostalis), and quadratus lumborum muscle. The ROIs were analyzed for the areas and histograms of the signal intensity using digitalized image processing software (Image J from National Institutes of Health, Bethesda, MD, USA).

And to facilitate comparison of the CSA on the concave and convex sides, thus obviating the individual differences of muscle size and obesity, the difference index of CSA (CDI) was calculated as follows and it was evaluated using a one-sample t test with a test value of zero:

CDI (Cross-sectional area difference index) = {1 − (CSA_concave/CSA_convex)} × 100 (%).

CSA_concave: cross-sectional area of interested muscle in concave side, CSA_convex: cross-sectional area of interested muscle in convex side.

Pixels of intramuscular fatty tissue were distinguished using the threshold gray-scale value of 120 [10]. The FI was calculated as a percentage of the number of pixels representing fat among the total numbers of pixels in each ROI (Fig. 1).

Fig. 1.

Measurement of the cross-sectional area and fatty infiltration rate

Results

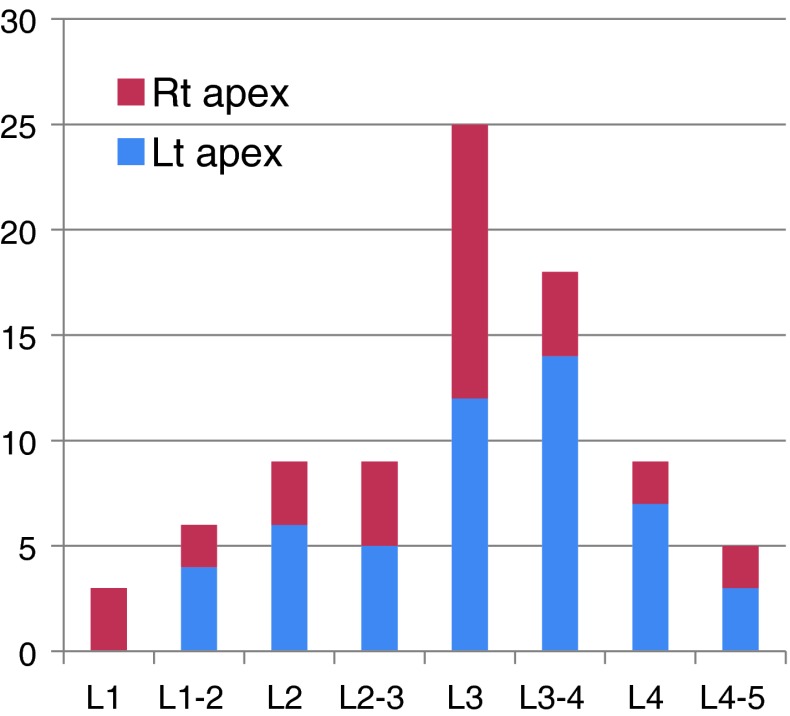
A total of 85 patients (68 women and 17 men) with an average age of 67.8 (47–88) years were included. Fifty-three patients had the apex of the curve on the left side and 32 patients had it on the right side. The most common apex levels were L3 and L3–4 (51.4 % of all) (Fig. 2). The mean of the coronal Cobb’s angle was 17.9° (range from 10.0 to 43.6°), and it did not differ according to patient age, gender, or the side of the apex (P = 0.572, 0.187, and 0.641, respectively). The one-way ANOVA test of the Cobb’s angle with an independent variable of the level of the apex showed a P value of 0.048, though the post hoc analysis using Scheffe’s method proved that it was just derived from multiple comparison and did not indicate a significant difference. The average degree of apical vertebra rotation according to Nash and Moe’s grade was 2, it was also similar regardless of age, gender and the side and level of the apex (Table 1).

Fig. 2.

Distribution of the level and side of the apex

Table 1.

Demographic data (n = 85) with subgroup analysis of Cobb’s angle and the degree of apical vertebra rotation

Subgroup by	Number	Cobb’s angle of scoliosis Mean ± SD (range)	Significance (P)	Apical vertebra rotation	Significance (P)
Overall	85	17.92 ± 6.34 (10.0–43.6)	0.572**	2.00 ± 0.83	0.706**
Sex			0.187*		0.094*
Male	17	16.09 ± 4.22 (10.0–23.1)		1.69 ± 0.79
Female	68	18.38 ± 6.72 (10.2–43.6)		2.07 ± 0.83
Side of apex			0.641*		0.278*
Left	53	18.12 ± 6.8 (10.0–43.6)		1.92 ± 0.80
Right	32	17.46 ± 5.5 (10.2–31.0)		2.12 ± 0.87
Level of apex			0.048a		0.334†
L1	3	21.62 ± 9.25 (12.16–30.64)		2.67 ± 0.58
L1–2 disc	7	23.35 ± 11.21 (12.13–43.64)		2.14 ± 1.07
L2	10	19.99 ± 6.87 (11.97–31.88)		2.00 ± 0.67
L2–3 disc	9	12.73 ± 6.37 (10.15–28.68)		1.78 ± 0.67
L3	22	15.40 ± 3.52 (10.45–22.68)		1.95 ± 0.76
L3–4 disc	19	18.80 ± 5.31 (12.90–36.66)		2.26 ± 1.00
L4	10	16.72 ± 5.74 (10.48–26.10)		1.80 ± 0.79
L4–5 disc	5	13.70 ± 4.17 (10.07–19.73)		1.40 ± 0.55

* Significance of difference by t test, ^† Significance of difference by one-way ANOVA

** P value from ANOVA between subgroup by age

^a Due to multiple comparisons, verified to be insignificant on post hoc analysis using the Scheffe test

The difference index of CSA (CDI) of psoas and multifidus muscle at the apex of the curvature level was significantly larger in 6.3 and 8.4 % on the convex side rather than that on the concave side (P = 0.019 and 0.000). However, the erector spine muscle at the apical level did not show a significant difference, and the CDI of the quadratus lumborum muscle was significantly smaller in the convex side. The patients were divided into three subgroups according to Cobb’s angle. There were 62 patients in group with Cobb’s angle of 10–20°, 18 patients with Cobb’s angle of 20–30°, and 5 patients with Cobb’s angle larger than 30°. Within subgroups with the Cobb’s angle of 10–20°, the pattern of asymmetry in CDI of psoas and multifidus muscles was similar with that of total group, however, in the subgroups with Cobb’s angle of 20–30° the asymmetry was not significant statistically (Table 2).

Table 2.

Cross-sectional difference index of psoas and paraspinal muscles at the apical level

Subgroup			Mean of CDI (%)	Standard deviation	Test value = 0
					P value†
Total	n = 85	Psoas major	6.32	24.33	0.019
		Multifidus	8.94	20.56	0.000
		Erector spinae	−10.27	111.57	0.399
		Quadratus lumborum	−19.20	45.18	0.000
Cobb’s angle	10–20°	Psoas major	5.26	19.83	0.041
	n = 62	Multifidus	9.65	18.70	0.000
		Erector spinae	0.14	15.92	0.944
		Quadratus lumborum	−22.63	46.05	0.001
	20–30°	Psoas major	5.49	33.07	0.491
	n = 18	Multifidus	11.40	23.50	0.055
		Erector spinae	−49.72	241.83	0.395
		Quadratus lumborum	−12.13	46.52	0.284
	>30°	Psoas major	22.53	37.94	0.255
	n = 5	Multifidus	−8.64	27.81	0.526
		Erector spinae	2.63	11.47	0.635
		Quadratus lumborum	−6.25	29.16	0.657

CSA_concave: cross-sectional area of each muscle on the concave side

CSA_convex: cross-sectional area of each muscle on the convex side

CDI (cross-sectional area difference index) = {1 − (CSA_concave/CSA_convex)} × 100 (%)

^†P value from t test with test value of 0

The fatty infiltration rate of each muscle was similar on both sides in total group and within subgroups according to Cobb’s angle (Table 3). The comparison to find differences in degrees of CDIs or FI rates between three subgroups according to Cobb’s angle revealed no statistically significant difference by any of parametric and non-parametric tests. Additional subgroup analysis did not find any difference in the CDI or FI at the apex level according to patient age, sex, the side and level of the apex, and the degree of rotation by ANOVA test (Table 4). The CDI and FI at the apex level were not correlated with the Cobb’s angle, degree of rotation, or with the lumbar lordosis (Table 5).

Table 3.

Fatty infiltration rate (FI) of psoas and paraspinal muscles at the apical level

			Mean of FIconcave (%)	Mean of FIconvex (%)	Paired differences of FI between concave and convex side
					95 % confidence interval of the difference
					Mean	Lower	Upper	P value
Total	n = 85	Psoas major	15.86	28.73	−12.88	−36.14	10.38	0.274
		Multifidus	45.02	44.10	0.93	−0.62	2.47	0.237
		Erector spinae	44.83	44.51	0.32	−1.51	2.16	0.729
		Quadratus lumborum	31.48	30.11	1.37	−1.40	4.14	0.330
Cobb’s angle	10–20°	Psoas major	16.74	33.04	−16.29	16.04	−48.37	0.314
	n = 62	Multifidus	42.99	42.14	0.84	0.93	−1.01	0.365
		Erector spinae	43.85	43.08	0.77	1.03	−1.29	0.459
		Quadratus lumborum	31.95	29.36	2.59	1.41	−.234	0.072
	20–30°	Psoas major	12.16	15.99	−3.83	1.88	−7.79	0.057
	n = 18	Multifidus	49.88	47.29	2.58	1.54	−0.66	0.111
		Erector spinae	46.94	46.68	0.252	1.99	−3.94	0.900
		Quadratus lumborum	27.53	31.56	−4.03	3.58	−11.66	0.277
	>30°	Psoas major	18.16	21.20	−3.04	3.01	−11.39	0.369
	n = 5	Multifidus	52.82	56.83	−4.01	3.08	−12.55	0.263
		Erector spinae	49.50	54.45	−4.96	6.00	−21.62	0.455
		Quadratus lumborum	38.34	34.62	3.72	9.94	−23.89	0.727

Table 4.

Difference of cross-sectional area difference index (CDI) and fatty infiltration rate (FI) of paravertebral and psoas muscles at the apex level by subgroups

Subgroups by	Sex	Side of apex	Level of apex	Rotation	Age	Cobb’s angle
Parameters	P value*	P value*	P value†	P value†	P value†	P value†	P value**	P value†‡
CDI
Psoas major	0.403	0.088	0.021‡	0.581	0.787	0.311	0.604	0.328
Multifidus	0.358	0.080	0.460	0.178	0.882	0.136	0.212	0.095
Erector spinae	0.533	0.208	0.347	0.711	0.000‡	0.242	0.699	0.924
Quadratus lumborum	0.105	0.402	0.929	0.804	0.383	0.562	0.238	0.357
FI
Psoas major	0.474	0.302	0.649	0.181	0.984	0.4	0.65	0.404
Multifidus	0.055	0.393	0.648	0.718	0.999	0.431	0.201	0.98
Erector spinae	0.052	0.539	0.587	0.602	0.907	0.386	0.173	0.189
Quadratus lumborum	0.042‡	0.048	0.064	0.926	0.211	0.624	0.829	0.775

* Significance of difference according to the t test, ^† Significance of difference using one-way ANOVA

^‡From multiple comparisons, verified to be insignificant on post hoc analysis using the Scheffe test

** Significance of difference using Kruskal–Wallis test between three groups according to Cobb’s angle

^†‡Significance of difference using Kruskal–Wallis test between groups with Cobb’s angle <20° and more than 30°

Table 5.

Correlation test of CDI, FI with Cobb’s angle, the degree of rotation and lumbar lordosis

		Fatty infiltration rate				CSA difference index
		Psoas major	Multifidus	Erector spinae	Quadratus lumborum	Psoas major	Multifidus	Erector spinae	Quadratus lumborum
Cobb’s	Coefficient*	−0.194	−0.131	0.025	−0.030	0.044	−0.080	−0.118	0.151
	Significance†	0.076	0.238	0.818	0.786	0.688	0.467	0.283	0.185
Rotation	Coefficient*	−0.213	−0.087	0.014	−0.057	0.024	−0.205	0.022	0.081
	Significance†	0.053	0.440	0.902	0.613	0.828	0.063	0.841	0.482
Lordosis	Coefficient*	0.174	−0.192	0.054	−0.138	−0.067	0.052	−0.113	0.054
	Significance†	0.112	0.082	0.622	0.212	0.541	0.636	0.304	0.638

* Pearson correlation coefficient, ^† 2-tailed significance

Discussion

The pattern of asymmetry was consistent in that muscles on the convex side showed larger CSA than those on the concave side, irrespective of age, sex, and the direction and the level of apex or the magnitude of the deformity supporting our aforementioned hypothesis that adult degenerative scoliosis might be associated with the asymmetry of muscle changes. Considering the fact that the curvature of the spinal column in the coronal plane causes the asymmetry of the length of the arc of the convex and concave sides, the muscles on the convex side may be stretched, elongated and thinned, while those on the concave side then become shortened and stout. Therefore, the CSA of the muscles on the concave side is expected to be larger than that of the opposite side. Our study results showed that the CSA of the quadratus lumborum muscle on the convex side was smaller than that on the concave side as is expected by this positional change of muscles around the curved and rotated spinal column. However, the CSA of the psoas major and multifidus muscles was larger on the convex side, and the CSA of the erector spinae muscle did not show a significant difference, this does not correspond to the prediction according to the aforementioned positional change. The positional change of the morphometry of muscles around the spinal column will be affected by the difference in the length of the arc in the convex and concave sides, and which is proportional to the radius of the arc, or to their distance from the center of the axis or the spinal column. The discordant pattern of difference in the CSA of the quadratus lumborum and other muscles can be explained by the fact that the muscles far from the axis of the spinal column, such as the quadratus lumborum, will show the conspicuous effect of the positional change more so than other paraspinal muscles which are closer to the center of the spine. However, the opposite result in the psoas and multifidus muscles regarding the expectation of the positional change is thought to result from the change in the muscle itself, in terms of the atrophy on the concave side or hypertrophy on the convex side.

Based on the Nachemson’s [12] and Panjabi’s [5, 6] point of view that psoas and paravertebral muscles are dynamic stabilizers of the spinal column, authors suggest that the increased CSA of the psoas and multifidus muscle in the convex side could be a result of hypertrophy to compensate and maintain the coronal balance as otherwise the spinal column would incline to the concave side. In addition, the erector spinae muscle, located between the multifidus and the quadratus lumborum muscles, did not show a significant difference in CSA as it was affected by the opposing influence of both positional change and the effect of compensatory hypertrophy. The result of the similar intramuscular fatty infiltration rate of all paraspinal muscles on both sides of a curved spine also supports this interpretation as muscle atrophy is known to be related to increased fatty infiltration [13]. Most recently, Shafaq et al. [14] reported the higher fatty degeneration rate and smaller CSA of multifidus muscles on concave side which were related with foraminal stenosis of ipsilateral side in patients with degenerative scoliosis. They used preoperative data of patients who went through operative treatment for the lumbar spinal stenosis with degenerative scoliosis. Possibly, foraminal stenosis might precede and contribute to the development of deformity, as they interpreted. However, there was a significant selection bias of including patients who needed decompression for the foraminal stenosis and their conclusion cannot be true in every patient with degenerative scoliosis. This bias is thought to be one of the major sources of difference from our data in result and its interpretation of fatty degeneration rate.

Another limitation in the interpretation of the results of this study is that the CSA itself is not proved to represent the physiologic cross-sectional area (pCSA) of muscles which represent the functional status of muscle. However, the pCSA is difficult to measure in each muscle due to the complexity of anatomy regarding shape, insertion and origin [11]; we used the CSA to crudely represent pCSA. In addition, further study with volumetric measurement of the musculature will provide a way to avoid bias from the positional change of the CSA. Although the interpretation of this retrospective cross-sectional study is inconclusive, the existence of asymmetric muscle changes of the CSA at the apical level of curvature was verified quantitatively. This study gives degenerative scoliosis researchers a new point of view regarding the pathomechanism of the deformity to be considered in the context of the neuromuscular structure stabilizing the spinal column. Understanding the pathomechanism and the natural history of this disorder will provide a basis for clinical decisions regarding the application of recent advances in surgical techniques, perioperative management, and rehabilitation regarding how to develop ideal treatment and to satisfy older patients by providing them with a higher expectation regarding their potential physical activity and less of a need to accept pain and physical limitation.

Hypertrophy of the muscles on the convex side is suggested as the explanation of this asymmetry rather than atrophy of the muscles on the concave side as muscle atrophy is known to be associated with increased fatty infiltration. However, at this time, it is difficult to judge whether hypertrophy is a possible cause of scoliosis or a secondary change following deformity resulting from degeneration or compensation in order to maintain balance. Future study with long-term follow-up data of consecutive series of 85 patients selected without bias of clinical decision in treatment, who were studied in our study, will offer better clue for the pathophysiology of degenerative scoliosis.