Comparison of scoliosis measurements based on three-dimensional vertebra vectors and conventional two-dimensional measurements: advantages in evaluation of prognosis and surgical results

Abstract

Purpose

A new concept of vertebra vectors based on spinal three-dimensional (3D) reconstructions of images from the EOS system, a new low-dose X-ray imaging device, was recently proposed to facilitate interpretation of EOS 3D data, especially with regard to horizontal plane images. This retrospective study was aimed at the evaluation of the spinal layout visualized by EOS 3D and vertebra vectors before and after surgical correction, the comparison of scoliotic spine measurement values based on 3D vertebra vectors with measurements using conventional two-dimensional (2D) methods, and an evaluation of horizontal plane vector parameters for their relationship with the magnitude of scoliotic deformity.

Methods

95 patients with adolescent idiopathic scoliosis operated according to the Cotrel-Dubousset principle were subjected to EOS X-ray examinations pre- and postoperatively, followed by 3D reconstructions and generation of vertebra vectors in a calibrated coordinate system to calculate vector coordinates and parameters, as published earlier. Differences in values of conventional 2D Cobb methods and methods based on vertebra vectors were evaluated by means comparison T test and relationship of corresponding parameters was analysed by bivariate correlation. Relationship of horizontal plane vector parameters with the magnitude of scoliotic deformities and results of surgical correction were analysed by Pearson correlation and linear regression.

Results

In comparison to manual 2D methods, a very close relationship was detectable in vertebra vector-based curvature data for coronal curves (preop r 0.950, postop r 0.935) and thoracic kyphosis (preop r 0.893, postop r 0.896), while the found small difference in L1–L5 lordosis values (preop r 0.763, postop r 0.809) was shown to be strongly related to the magnitude of corresponding L5 wedge. The correlation analysis results revealed strong correlation between the magnitude of scoliosis and the lateral translation of apical vertebra in horizontal plane. The horizontal plane coordinates of the terminal and initial points of apical vertebra vectors represent this (r 0.701; r 0.667). Less strong correlation was detected in the axial rotation of apical vertebras and the magnitudes of the frontal curves (r 0.459).

Conclusions

Vertebra vectors provide a key opportunity to visualize spinal deformities in all three planes simultaneously. Measurement methods based on vertebral vectors proved to be just as accurate and reliable as conventional measurement methods for coronal and sagittal plane parameters. In addition, the horizontal plane display of the curves can be studied using the same vertebra vectors. Based on the vertebra vectors data, during the surgical treatment of spinal deformities, the diminution of the lateral translation of the vertebras seems to be more important in the results of the surgical correction than the correction of the axial rotation.

Introduction

In spite of evidence that scoliosis is a three-dimensional (3D) spinal deformity, routine analysis is limited to measurements of frontal and sagittal curves. Various methods for measuring frontal curvature have been developed like the Greenspan index [1], Diab method [2] or Centroid method [3]. On Ferguson’s proposal, the earliest measuring technique evaluated the angle formed by the lines connecting the central points of the upper and lower end-vertebrae of the curve with the central point of the apical vertebra [4]. For quantitative analysis of scoliosis, Cobb [5] suggested using the value of the complementary angle by perpendiculars to the upper and lower endplates of the upper and lower end-vertebrae. The Cobb angle, in reality, reflects the inclination of the vertebrae and not the real curvature of the spine, because it ignores lateral translation of the apical vertebra, a very common feature in spinal deformities. Although lateral translation is taken into account by the Ferguson method, the Cobb method became the most widely used, partly because it is easier to perform and has a higher reproducibility while its value appears to be closely related to the magnitude of the curvature.

Since recognition by the Scoliosis Research Society (SRS) in 1966, the Cobb method became the standard method for quantitative analysis of spinal deformities.

Given the relatively wide variability in values of physiological sagittal curvature, quantitative analysis of sagittal curves accompanying scoliosis remained a challenging task. Although the Cobb method was first modified for the purpose of analyzing frontal side-bending radiographs, it quickly became a preferred method for the analysis of sagittal curves, as well [6]. The modified Cobb method as used for sagittal plane measurements, in essence, depicts the slope of upper and lower endplates and cannot supply consistent information on deformations of the curvature [7]. As a routine method, it is valuable in the analysis of thoracic kyphosis [8] and lumbar lordosis [9], when uniform measurements are used.

Variations in thoracic kyphosis and lumbar lordosis accompanying structural scoliosis are significantly related to coronal curve size and pelvic tilt [10].

The search for a precise analysis of vertebral rotation associated with scoliosis is hardly new: various methods have been described by Cobb [5], Nash and Moe [11], Perdriolle [12] or Mehta [13], all of which are based on evaluation of the relative position of posterior vertebral elements. Although Perdriolle’s torsiometer became the most widely used in clinical practice, its reproducibility and accuracy are very limited [14].

Computer tomography (CT) permits a potentially more precise analysis of vertebral rotation in horizontal plane, but it is limited to short spinal segments and requires a prohibitively high radiation dose [15]. Expert opinion is divided on the accuracy and reproducibility of CT scans for such measurements [16, 17].

Despite the assertion in 1994 by the SRS that it was desirable to develop a new method for three-dimensional diagnosis and analysis of scoliotic deformities, the aspiration mostly remained theoretical because no routinely applicable clinical procedure existed for simultaneous measurement of sagittal and frontal curvatures with vertebral rotation in horizontal plane [18].

Georges Charpak won the Nobel Prize in Physics in 1992 for his research in particle detection and development of gaseous detectors [19–21]. A radiological device based on his detector enabled obtaining good-quality radiographs at significantly lower radiation doses [22].

This technology leads to the commercial availability of a new low-dose medical imaging system called EOS 2D/3D. This system is based on a double innovation: it allows obtaining high quality two-dimensional (2D) perpendicular images in an upright position [23, 24], as well as providing 3D visualization of the entire skeleton from head to toe, by parametric surface 3D models created with new 3D reconstruction techniques [25, 26]. Using an EOS 2D/3D system, the radiation dose required to obtain good-quality 2D images of the skeletal system was reduced by 80–90 %, and to generate a 3D reconstruction from a CT scan dramatically decreased to a level of 800–1,000 times less [22, 24].

3D models offer very realistic view of the spine, which, in many cases, proved difficult to be further analyzed due to the complexity of vertebral morphology. This was particularly true for the new top view image presenting the whole spine in 3D from above.

To help understanding top view images, to simplify the complex visualization and to create a possibility for mathematical quantification, replacement of vertebrae with vectors furnishing all vertebral features (size, position, orientation and rotation) was proposed recently [27].

The aims of this study were examination of the actual spinal layout provided by EOS 3D in adolescent idiopathic scoliotic (AIS) patients undergoing surgical correction, simplifying the visualization of the spine using vertebra vectors, calculating scoliotic spine measurement values based on vertebra vectors and comparing them with measurements using conventional 2D methods. A main goal was to test horizontal plane vector parameters for correlation with the magnitude of scoliotic deformity and quantitative results of surgical correction.

Methods

The EOS 2D/3D system with its sterEOS 3D software for surface 3D reconstruction (EOS Imaging, France) has been used in our Department since September 2007. Presented data are of 95AIS patients [87:8 female/male ratio, aged 18.6 years (SD = ± 7.41)] who have been operated on in 2009. The curve types were type 1: 30; type 2: 1; type 3: 36; type 4: 2; type 5: 14; type 6: 12; using Lenke classification. Average follow-up was 2.4 years (SD = ±0.22). The instrumentation of the spine was performed according to the Cotrel-Dubousset principle, using hybrid constructions (hooks on thoracic region and screws on lumbar region) of SCS implants (Scient’x, France). The correction was obtained with a derotation maneuver, which was always finished with in situ contouring of the corrective rod required for the sagittal curves to create harmonious sagittal balance.

Preoperative EOS 2D images were taken 2–7 days before surgery, and postoperative images were produced 4–5 days after operation. For quantitative analysis of coronal and sagittal plane curves, conventional Cobb measurements were performed by the senior author using native EOS 2D AP/LAT images on high-resolution medical grade computer screens and an appropriate software. Thoracic kyphosis was measured between vertebrae T₄ and T₁₂ and was indicated by positive values, while lumbar lordosis was measured between vertebrae L₁ and L₅ and recorded as negative values. Horizontal plane vertebral axial rotation was automatically calculated by sterEOS 3D.

3D reconstructions were made with sterEOS 3D software version 1.3.4.3740 performing the full 3D procedure, using pre- and postoperative EOS 2D images.

For comparative 3D analysis, the concept of vertebra vectors was employed, with adaption to all three planes. A vertebra vector is a simplified representation of a vertebra and it is based on known vertebral landmarks. The vertebra vector appears as a line starting at the midpoint of the straight connecting the two pedicular centroids, parallel to the upper endplate at the level of pedicles, terminating at the ventral surface of the vertebra body. So, the vertebra vector forms the axis of the vertebra body in the sagittal median axis of the vertebra.

The vectors were placed in a coordinate system, which was created utilizing principles described by SRS Working Group on the 3D Terminology of Spinal Deformity [18]. A line connecting the two acetabular centers forms the x axis of the coordinate system. The y axis is perpendicular to the coronal, the z axis is a perpendicular to the horizontal plane crossed each other and the x axis in the midpoint of the interacetabular straight.

Calibration scale of the coordinate system is based on the interacetabular distance. A value of 100 is assigned to the distance between the origin and either of the acetabular centers (Fig. 1).

Fig. 1.

Horizontal plane visualization in calibrated coordinate system of a vertebra and the vertebra vector. The coordinate system was created in which the x axis is the interacetabular axis, line connecting the two acetabular centers. The y axis is the sagittal median axis, which is perpendicular to x axis in the midpoint of interacetabular distance The z axis is perpendicular to both x and y axes in the midpoint of interacetabular distance. The scale of this coordinate system is individual, since regardless of the real length of the interacetabular distance, it has been divided always into 200 units. Thus, the scale is 100 = 50 % interacetabular distance (100 = d_IAC50). In this coordinate system, it is possible to determine the each vector point in all three planes using basic vector algebra. Coordinates of initial point A and terminal point B of a vector AB in the horizontal plane are A (A_x; A_y), B (B_x; B_y). These coordinates are used directly to determine lateral translation B_x from the y axis, while the vector angle α relative to the y axis is calculated using tangent function

After vertebra vectors are placed inside this calibrated coordinate system, the coordinates of each vector point can be determined in all three planes using basic vector algebra. Coordinates of initial point A and terminal point B of a vector AB in the horizontal plane are A(A_x; A_y), B(B_x; B_y). Coordinates of vector AB are, therefore,

These coordinates are used directly to determine lateral translation B_x from the y axis, while the vector angle α relative to the y axis is calculated using a tangent function

The detailed definition of a vertebra vector and the description of methods for creation of a patient-specific individually calibrated 3D coordinate system, recording vector coordinates and calculation of 3D vector parameters as well as frontal, sagittal and horizontal plane spinal curvature data were published earlier [27].

Means comparison T test was used for analysis of differences in values for coronal and sagittal spinal curvature data obtained by traditional methods and methods based on vertebra vectors. Differences in values for vertebral axial rotation as calculated by sterEOS 3D and as indicated by horizontal plane vector angles were also analysed by T test. Relationship between horizontal plane vertebra vector parameters of apical vertebrae and Cobb angle values was evaluated by Pearson bivariate correlation and linear regression. Both pre- and postoperative data and pairwise changes as delta (Δ) values in corresponding pre- and postoperative parameters were evaluated. Statistical analysis was performed using SPSS version 19.0 (IBM Corp., USA).

Results

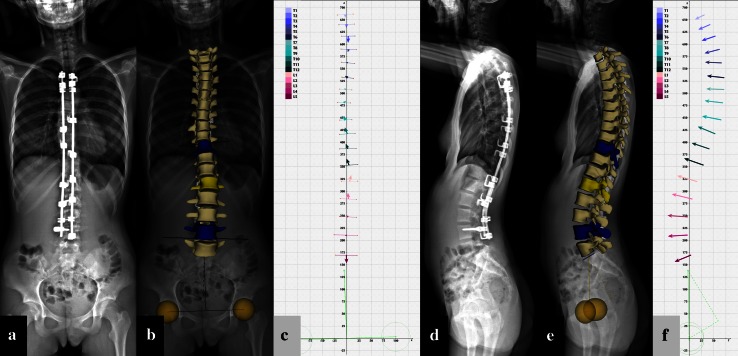
Frontal and lateral EOS 2D images were captured for each patient pre- and postoperatively as shown for a representative case with a Lenke type 5 curve (Figs. 2a, d, 3a, d). Three-dimensional surface reconstructions (Figs. 2b, e, 3b, e) and vertebra vector generation for calculation of vector parameters were carried out (Figs. 2c, f, 3c, f). Top views of preoperative (Fig. 4a) and postoperative 3D models (Fig. 4b) were then presented followed by replacement of vertebrae by corresponding vectors (Fig. 4c, d).

Fig. 2.

Coronal (a–c) and sagittal plane (d–f) visualizations of a representative adolescent idiopathic scoliotic case before surgical correction. Preoperative EOS 2D X-ray images (a, d); corresponding preoperative sterEOS 3D reconstructions (b, e); and corresponding preoperative full spine vertebra vectors (c, f)

Fig. 3.

Postoperative coronal (a–c) and sagittal plane (d–f) visualizations of a representative adolescent idiopathic scoliotic case (same case as shown in Fig. 2). Postoperative EOS 2D X-ray images (a, d); corresponding postoperative sterEOS 3D reconstructions (b, e); and corresponding postoperative full spine vertebra vectors (c, f)

Fig. 4.

Preoperative (a, c) and postoperative (b, d) horizontal plane visualizations of a representative adolescent idiopathic scoliotic case (same case as shown in Fig. 2). Topview sterEOS 3D reconstructions of the spine before (a) and after (b) correction. The pelvis (semi-transparent), acetabulums (yellow spheres) and interacetabular axis (yellow line) are also visible. Horizontal plane projections of full spine vertebra vectors before (b) and after (d) correction. See legends for color-coded identification of individual vertebrae. Axial rotation of apical vertebra L₂ (yellow in a, b) was decreased from 21° to 5° as calculated by sterEOS 3D software and from 21.9° to 4.3° as measured by angle α_H of vertebra vector L₂. Lateral ejection of apical vertebra L₂ was decreased from 70.2 to 2.5 as indicated by coordinate B_x values of vertebra vector L₂

The average Cobb angle value was 50.9° preoperatively, while postoperative curves were reduced to 16.6°, as measured by conventional Cobb method. Measurements based on vertebra vectors showed values of 49.4° and 16.8°, respectively, indicating only small, non-significant pairwise differences. Pearson correlation of corresponding Cobb angle values was strong and statistically significant both for preoperative and postoperative data (Table 1, rows 1–2). Similarly, a strong and significant correlation was detected for preoperative T₄–T₁₂ kyphosis values obtained with conventional measurements and based on vertebra vectors (25.7° and 28.4°, respectively). Kyphosis values slightly increased after correction (29.2° and 31.2°, respectively) with identical correlation between them (Table 1, rows 3–4).

Table 1.

Descriptive statistics, comparison and correlation of frontal and sagittal plane spinal curves and apical vertebra (APV) axial rotation of pre- and postoperative scoliotic cases—values obtained by conventional and vertebra vector-based measurement methods

		Preop			Postop
		Mean ± SD	Paired samples T test	Pearson correlation	Mean ± SD	Paired samples T test	Pearson correlation
1.	Cobb (°)	50.9 ± 18.5	−1.56*	0.95**	16.6 ± 12.1	0.21†	0.94**
2.	VV-Cobb (°)	49.4 ± 20.4			16.8 ± 12.8
3.	Kyphosis (°)	25.7 ± 17.4	2.61**	0.89**	29.2 ± 9.8	2.04**	0.90**
4.	VV-kyphosis (°)	28.4 ± 16.1			31.2 ± 9.9
5.	Lordosis (°)	43.7 ± 13.4	−8.55**	0.76**	45.3 ± 9.9	−7.04**	0.81**
6.	VV-lordosis (°)	35.1 ± 12.2			38.2 ± 9.4
7.	AVR (°)	19.2 ± 11.4	0.65*	0.96**	12.2 ± 8.9	0.16†	0.97**
8.	APV-αH (°)	18.5 ± 12.5			12.0 ± 9.0

mean statistical mean value, SD standard deviation, kyphosis T₄–T₁₂ kyphosis, lordosis L_I–L_V lordosis, VV measurement method based on vertebra vectors, AVR axial vertebral rotation, α_H horizontal plane vertebra vector angle relative to the y axis, A_x vertebra vector initial point A coordinate x, B_x vertebra vector terminal point B coordinate x

* p < 0.05; ** p < 0.01; ^†p value not significant

Average preoperative lumbar lordosis was −43.7° as measured conventionally, while the method based on vertebra vectors showed a value significantly lower by 8.5°, with good correlation. After surgery, average lumbar lordosis slightly increased for both measurement methods with good correlation but still a significant 7.0° difference in between (Table 1, rows 5–6).

Horizontal plane axial vertebral rotation (AVR) of the apical vertebra was automatically calculated by sterEOS 3D software based on reconstructed 3D models. Average AVR was 19.2° preoperatively and 12.2° postoperatively. Axial rotation of the apical vertebra (APV) as calculated by the method based on vertebra vectors was 18.5° before surgery and 12.0° after surgery. The corresponding values showed very small, non-significant differences and very strong correlations both pre- and postoperatively (Table 1, rows 7–8).

Further evaluation of correlation analysis results revealed the strongest correlation between the magnitude of scoliosis and coordinate value x of the terminal (APV-B_x) and initial point (APV-A_x) of apical vertebra vectors. Medium–strong correlations (r = 0.46) were observed between the Cobb angle and AVR of apical vertebrae by APV-α_H (Table 2, row 1). A similar correlation was shown between the value of average surgical correction achieved (ΔCobb) and change in values for coordinate x of terminal (ΔAPV-B_x; r = 0.48) and initial point (ΔAPV-A_x; r = 0.49) of apical vertebra vectors. Only weak, non-significant correlations were found between the extent of surgical correction (ΔCobb) and decrease in axial rotation of apical vertebrae (ΔAPV-α_H; r = 0.12) (Table 2, row 2).

Table 2.

Pearson correlation analysis of (1) pre- and postoperative apical vertebra (APV) vector parameters with the Cobb angle value of the main scoliotic curve; (2) preop–postop change in APV vector parameters with change in Cobb angle value of the main scoliotic curve after correction

	Positive correlations	APV-αH		APV-Ax		APV-Bx
		Preop	Postop	Preop	Postop	Preop	Postop
1	Cobb	0.46**	0.31*	0.68**	0.35**	0.70**	0.43**
		ΔAPV-αH (°)		ΔAPV-Ax		ΔAPV-Bx
2	ΔCobb	0.12†		0.45**		0.48**

α_H horizontal plane vertebra vector angle relative to the y axis, A_x vertebra vector initial point A coordinate x, B_x vertebra vector terminal point B coordinate x, Δ delta value of corresponding parameter change

* p < 0.05; ** p < 0.01; ^†p value not significant

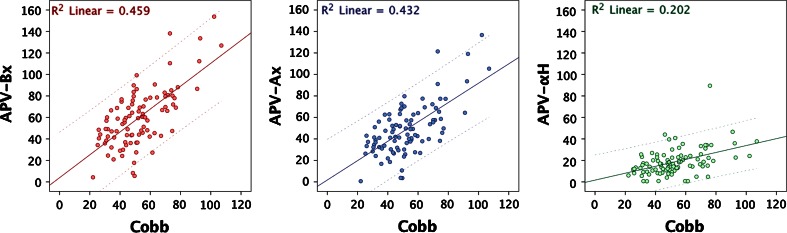
Linear regression analysis of corresponding parameters with strong correlation further elucidated the relationship between horizontal plane vertebra vector parameters and the magnitude of scoliotic deformity. Preoperative coordinate x values of terminal and initial APV vector points and horizontal plane axial rotation angle of the apical vertebra (APV B_x, A_x and α_H, respectively) were plotted against the Cobb angle value of the scoliotic curve, and linear regression curves showing linear regression coefficients of 0.46, 0.43 and 0.20, respectively, were obtained (Fig. 5). On this basis, the magnitude of scoliosis in frontal plane is much more dependent on the horizontal plane lateral translation of the apical vertebra rather than on the axial rotation of the apical vertebra in the same plane.

Fig. 5.

Scatterplot and linear regression of apical vertebra (APV) vector parameters APV-B_x (left), APV-A_x (middle) and APV-α_H (right) with the Cobb angle of the scoliotic curve. APV-B_x vertebra vector terminal point B coordinate x; APV-A_x vertebra vector initial point A coordinate x; APV-α_H horizontal plane vertebra vector angle relative to the y axis; R² linear square of the linear regression coefficient

Discussion

In idiopathic scoliosis, either the origin and nature of the structural deformity or the course of progression is unknown. The first step is believed to be related to vertebral rotation, which causes sagittal plane instability and a modest frontal plane imbalance. The study scoliosis showed that there is a direct non-linear relationship among elemental components of 3D deformities, while details of this correlation are unknown [28]. After the initial onset, deformation progresses with a self-supporting biomechanical process.

Clinical diagnosis is established using frontal and lateral X-ray images [5, 11, 12]. The horizontal plane alterations are difficult to visualize and analyze in spite of that numerous methods using these 2D images exist for evaluation of axial rotation [29]. All of these methods are indirect estimations of vertebral axial rotations, based on visible coronal projections of vertebral pedicles. Its reproducibility has been shown very limited and cannot be quantified precisely [14, 30].

The most accurate assessment of axial rotation is thought to be achieved by CT [15, 31]; however, it is limited in routine scoliosis diagnosis due to high radiation doses and the effect of supine position during imaging that may lead to significant alterations of coronal and sagittal curves relative to an upright position [32]. Another important factor to consider is the vertical level of rotation measurement within vertebral bodies since values—and even direction—of rotation may be different at levels of upper and lower endplates of the same vertebral body [33]. For a standardized and reasonably accurate visualization of vertebrae in horizontal plane, measurement of axial rotation is required to be performed in a segment that is either at an equal vertical distance from both endplates, or, where the difference in variable rotational values of lower and upper endplates can be offset.

There is evidence that vertebral rotation measurement based on 3D reconstruction of conventional bidirectional X-ray images gives more accurate results as compared with all other methods [34]. On the other hand, segmental intervertebral rotation could also be evaluated based on 3D reconstructions [35]. Nevertheless, for obtaining a highly accurate 3D reconstruction, the precisely perpendicular placement of frontal and lateral X-ray detectors and proper patient positioning during imaging are essential.

The EOS device and sterEOS 3D reconstruction software brought a strikingly new possibility in visualization of the scoliotic spine. Due to simultaneous capture of full-body, upright perpendicular images at considerably lower radiation doses in a spatially calibrated way, positioning problems that can distort a proper 3D reconstruction could be avoided. Using the EOS system, the anatomical and positional pelvic parameters (pelvic incidence, sacral slope, sacral tilt) in sagittal plane could be easily measured in upright position. The determination of the relationships between the pelvic parameters and the thoracic kyphosis and the lumbar lordosis in each case had become a daily routine. This enables accurate determination of the sagittal balance in function of pelvic incidence pre-op and post-op and follow-up. Image quality is optimized, providing clear anatomical landmarks that are required for 3D surface reconstruction, resulting in a complete 3D model of the spine, ready to be inspected in horizontal plane. Currently, this is the only routinely available tool approved for clinical use radioimaging solution in scoliosis that provides simultaneous representation of spinal deformities in all three planes, in an upright load-bearing position.

Basis for the concept of vertebra vectors involves long-established, well-defined and widely accepted entities that are either defined by the SRS Working Group on 3D Terminology of Spinal Deformity [18] (pedicular centroid, vertebral body upper endplate), or represent basic elements of trigonometry (midpoint of a distance, parallel line) and vector algebra (initial and terminal points of a vector, vector angle).

A vertebra vector originates at the center of the interpedicular line connecting the pedicular centroids, extends parallel to the upper endplate, and terminates at the intersection with the vertebral ventral surface. In the horizontal plane, the orientation of the vector always corresponds to the symmetry axis of the vertebra. Variance in axial rotation due to vertebral body torsion is neutralized by the positioning of the vector inside the vertebra because the relative distance of the vector from the upper endplate is constant for each vertebra. A vertebra vector defined in this way is least prone to be affected by scoliotic vertebral shape changes. By its definition, a vertebra vector furnishes all information related to the actual size, position, and orientation of the corresponding vertebra.

In a suitably calibrated coordinate system, evaluation of all vertebra vector coordinates is possible, allowing a mathematical description of vertebral position and rotation for each vertebra. For characterization of scoliosis in frontal and sagittal plane, measurement methods based on vertebral vectors proved to be just as accurate and reliable as conventional measurement methods. This seems to be confirmed by only small, non-significant differences and strong correlational values found between corresponding measurements of the two methods. Although L₁–L₅ lumbar lordosis values showed significant differences compared to values obtained with the Cobb method, the discrepancy of 7–8.5° is, in one hand, well within reported values of interobserver variations for lumbar lordosis measurements [9], on the other hand, this discrepancy could be explained by an important difference between the two methods. The Cobb method measures the angle formed by the L₁ upper and L₅ lower endplates, while vertebra vector-based sagittal measurements refer to angles between parallels to upper endplates of corresponding vertebrae. Since upper and lower endplates of L₅ are reportedly not parallel due to L₅ wedges [36], lordosis measurements by vertebra vectors will consequently yield lower values, equal to the magnitude of corresponding L₅ wedges.

As a representation of the third dimension of spinal deformities, assessable in horizontal plane views of the spine with vertebra vectors, axial rotation of apical vertebra vectors was found to perfectly agree with AVR values calculated by sterEOS 3D. Given the strong correlation observed in three-dimensional measurements between conventional and vertebra vector-based methods, it could be concluded that vertebra vectors provide a key opportunity to examine spinal deformities in all three planes. Therefore, most important feature of the vertebra vector system is its ability of visualization of the scoliotic spine in the horizontal plane from above (“Topview”), providing a unique insight into spinal deformities in the “third” dimension. Until now, this possibility has been missing from the routine clinical diagnostic tools of orthopedic surgeons.

The moderate correlation and the low linear regression coefficient between coronal Cobb angle values and vertebral axial rotation in the horizontal plane may indicate that despite a critical role of axial rotation [37], other factors co-exist in the complex mechanism of development and progression of scoliotic curves. Analysis of preoperative top view images with vertebra vectors revealed an interesting feature, namely, vertebrae—while displaced laterally—rearrange along the interacetabular line (x axis) with a relatively small axial rotation (Fig. 2c). Based on these findings, the relationship between the magnitude of the curvature and distance to y axis (represented by vector coordinate B_x) of apical vertebrae was evaluated. Results showed that correlation of coronal curve magnitude is significantly stronger with lateral displacement (or lateral translation) than with axial rotation of apical vertebrae of the curves.

The distance of vertebral translation measured from the median sagittal axis of the body is called lateral translation, represented by vertebra vector coordinate B_x. On postoperative top view images, vertebrae are repositioned along y axis, with diminishing lateral translation values. Surgical correction of coronal curves was undoubtedly more strongly correlated with the displacement of vertebrae towards the midline of the body; change in axial rotation of vertebrae did not show a similarly close correlation. This conclusion seems to be supported by the observation of an increased lateral bending under gravity without an increment of axial rotation [38].

In conclusion, vertebra vector analysis in spinal deformities simplifies and facilitates the understanding of the complex visual information provided by EOS 2D/3D. The method of vertebra vectors is the only way with which it is possible to visualize, analyze and characterize the spinal deformity simultaneously in all three planes. Its parametric calculations furnish simple and intelligible visual and mathematical information of spine deformities, especially in the horizontal plane. Based on horizontal plane view data, it became possible to analyze the relationship of various elements of spine deformities, like vertebral rotation or lateral translation. In our opinion, the possibility of a precise and sensitive evaluation of changes in the horizontal plane allows us to follow-up the evolution of mild scoliotic curves or to clarify curve progression mechanisms during longitudinal studies.

According to results from analysis of presented data obtained from the routinely used vertebra vector visualization, the primary goal of corrective intervention may be the minimization of lateral translation rather than the elimination of axial rotation, which appears to be relatively less important. Of course the all-spinal surgical correction should be carried out with preserving or restoring a good sagittal balance that is defined by the sagittal spinopelvic parameters. This represents a new philosophical approach in surgical treatment of spinal deformities, an exciting idea that needs further exploration.