Skip to main content
PMC home page
Clinical Orthopaedics and Related Research logoLink to Clinical Orthopaedics and Related Research
. 2013 Mar 28;471(7):2278–2283. doi: 10.1007/s11999-013-2864-3

Cylindrical Axis, Not Epicondyles, Approximates Perpendicular to Knee Axes

Clifton W Hancock 1,2,✉, Mark J Winston 3, Joel M Bach 4, Bradley S Davidson 5, Donald G Eckhoff 6
PMCID: PMC3676579  PMID: 23536175

Abstract

Background

The transepicondylar axis (TEA) is often used as a surrogate for the flexion-extension axis, ie, the axis around which the tibia moves in space, because of a belief that both axes lie perpendicular to the mechanical axis. However, studies suggest the cylindrical axis (CA), defined as a line equidistant from contact points on the medial and lateral condylar surfaces from 10o to 120o flexion, more closely approximates the axis around which the tibia moves in space.

Questions/purposes

We examined the TEA and CA angles relative to mechanical axes to determine whether one more consistently and closely approximates the surgical goal of orthogonality to the mechanical axis.

Methods

Three-dimensional (3-D) models were reconstructed from CT scans of five cadaver limbs. Three observers repeated three measurement sets to locate the TEA, CA, and femoral mechanical and tibial mechanical axes. Angles of the TEA and CA relative to the mechanical axes were calculated in two-dimensions (2-D) and as 3-D projections and compared for differences in magnitude and variance.

Results

Angles between CA and the mechanical axes were closer to 90° than the TEA in 2-D (92° versus 94° for the femur, 93° versus 94° for the tibia) and 3-D (88° versus 87° for the femur, 88° versus 86° for the tibia). Variance of the TEA was higher than the CA in 2-D.

Conclusions

The CA forms angles more orthogonal to the mechanical axes of the thigh and leg than the TEA.

Clinical Relevance

Although we found a consistently greater deviation of the TEA from the mechanical axis than the CA with small differences, future studies will need to determine whether these differences are biomechanically or clinically important.

Introduction

Although the concept of a single flexion axis for the knee is becoming more widely recognized [1, 6, 9–12, 17, 21, 26, 28], how best to find this axis intraoperatively has become a matter of dispute among orthopaedic surgeons. This single axis around which the tibia rotates in space is not captured in any of the traditional coronal, sagittal, or transverse planes and attempts to project it onto these planes gives rise to an artifact. Therefore the use of a surrogate axis passing through identifiable landmarks has been proposed as a solution [1, 2, 4–7, 30]. Churchill et al. [6] suggested a line passing through the most medial and lateral portions of the epicondyles, the transepicondylar axis (TEA), best approximates the actual flexion-extension axis (FEA) of the knee. Using this TEA as a surrogate for the actual axis of flexion is attractive because these landmarks can be palpated by a surgeon intraoperatively and are not altered by joint surface degeneration [1, 4, 23, 24, 27]. With their two-dimensional (2-D) analysis, Churchill et al. [6] concluded there was a statistically insignificant difference of 3° ± 1° between the TEA and the true FEA. However, recent work by Eckhoff et al. [9] suggested the TEA may be an unsatisfactory surrogate of the FEA because the TEA lies anterior and superior to the actual FEA (Fig. 1). Using three-dimensional (3-D) CT, Eckhoff et al. reported an angle considered statistically insignificant by Churchill et al. in 2-D can be statistically significant when measured in 3-D using the dot product to assign an angle between nonintersecting lines projected onto a plane. Eckhoff et al. found 2-D angles were small, with an average 2° difference and a range of 0.1° to 4° in the coronal plane and 2° with a range of 0.2° to 5° in the transverse plane, but they doubled to an average 5° difference with a range of 2° to 11° measured in 3-D with the TEA more superior and anterior.

Fig. 1.

Fig. 1

Open in a new tab

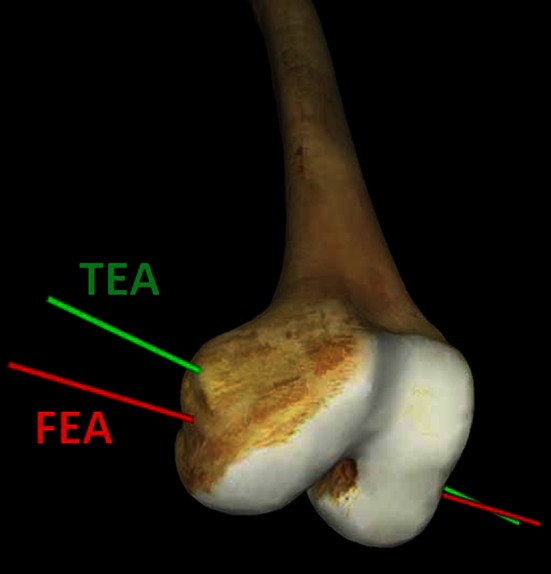
The TEA is anterior and superior to the FEA [9].

This 5° average difference appeared important in a biomechanical and clinical study by Hsu et al. [19], where a 5° variation in either varus or valgus produced a 7% change in the distribution of load under the tibial component. Further, a 10° misalignment, consistent with the 11° maximum varus outlier reported by Eckhoff, et al. [9], showed a 62% change in load distribution in the biomechanical study by Hsu et al. [19]. Although it is difficult to say what is clinically significant based on a biomechanical study, in a concurrent clinical radiographic review published in the same paper, Hsu, et al. [19] found a disturbing clinical correlation between increased implant malalignment and increasing lucent lines around the tibial components of otherwise successful implants at average 6 years followup. Other studies [15, 20] confirm this clinical relationship between orthogonal positioning of an implant and implant longevity, and there have been no papers challenging this concept of orthogonal positioning, biomechanical or clinical, for two decades.

Although previous work suggests the cylindrical axis (CA) is a better surrogate for the FEA [2, 3, 8–12], there is no documentation in the literature regarding the relationship of either the TEA or CA to the femoral mechanical axis or the tibial mechanical axis. Because the goal of a contemporary TKA is to position the tibial component at a right angle to the tibial axis and the femoral component at a right angle to the femoral mechanical axis [15, 19, 20], it may be useful to know whether either axis being used as a surrogate is perpendicular to these longitudinal axes.

Therefore, we addressed the following two questions: (1) does the CA angle relative to the mechanical axes of the femur and tibia consistently differ from the TEA angle relative to these mechanical axes in either 2-D or 3-D, and (2) does the CA angle relative to the mechanical axis better approximate perpendicular than the TEA angle relative to the mechanical axis, ie, closer to orthogonal?

Materials and Methods

We imaged five cadaver limbs using a nonhelical CT scanner. CT scans were obtained for each of these limbs from the pelvis to the ankle in 0.5-mm increments. All knees were determined to be normal anatomically and nonpathologic; ie, they showed no observable or radiographic sign of varus, valgus, or rotational malalignment of congenital, developmental, or traumatic origin and there was no demonstrable arthritis or other articular abnormality. The ages of the cadaveric specimens used for this study ranged from 61 to 87 years. Three of the limbs were obtained from white male cadavers and two from white female cadavers.

CT images were reconstructed into 3-D models using Mimics® software (Materialise, Leuven, Belgium). This program automatically assigns weights to the radiodensity of each voxel (3-D equivalent of 2-D pixel) in each plane of the study, which then is compared with the weight of an observer-selected pixel lying within bone. The voxel thickness corresponds to the 0.5-mm thickness of the CT cuts through the limb. The program constructs a 3-D image of the bone in the absence of soft tissue attachments but remaining within proper 3-D alignment and relation to the other bones of the limb. In most of the reconstructions, the bone near the articular surface of the femur and tibia was less radiopaque than the dense cortical bone of the diaphysis. Occasionally, this caused the articular surface of the bone in 3-D reconstruction to be rough or caused some soft tissue artifact to be included on the articular surface of the 3-D model. In such cases, an observer reviewed the frames of the CT that included the joint surface and manually selected voxels that corresponded to the bone surface to produce smoothing of the articular surface.

Once completed and reviewed, the 3-D models were imported and viewed with Rapidform® 2006 software (Inus Technology, Inc, Seoul, South Korea). Using this software, axes were generated for the TEA, CA, femoral mechanical axis, and tibial mechanical axis consistent with previous studies [5–14, 16, 18, 21, 23–25, 31]. The femoral mechanical axis was defined as a line connecting the center of the hip to the middle of the knee. This line runs medial to the shaft of the femur and then between the condyles of the distal femur through the posterior aspect of the femoral sulcus meeting with the tibial mechanical axis between the tibial intercondylar tubercles. To generate this axis, a sphere was fit to the surface of the femoral head and the geometric center point of this sphere was extrapolated. A point judged by the observer to be equidistant between the tibial intercondylar tubercles was chosen to represent the distal pole of the femoral mechanical axis and a line was generated connecting the center at the hip to the middle of the knee. The tibial mechanical axis was defined as a line starting at the midpoint between the tibial intercondylar tubercles and extending to the midpoint between the cortical surface of the medial and lateral malleoli of the ankle. The CA was generated by selecting points on the articular surface of each posterior condyle and using least-squares regression to fit a cone to the posterior condyles. The center axis of this cone lying equidistant from all points on the condyle was extrapolated to be the CA. The TEA was defined by selecting the most prominent points of the medial and lateral epicondyles, according to the method of Churchill et al. [6]. These medial and lateral points were connected to create the TEA. Three separate observers (CWH, MJW, HCE) repeated each of these described measurements in triplicate, resulting in nine serial measurements for each limb.

Four angles in 2-D and 3-D were generated from these measurements for analysis: TEA relative to tibial mechanical axis, CA relative to tibial mechanical axis, CA relative to femoral mechanical axis, and TEA relative to femoral mechanical axis. The lines and the 2-D angles between them were calculated by Rapidform®. Dot products, the angle between the lines that do not intersect in a plane, were used to generate the 3-D angle [29]. Angles calculated from each of the three replications for each angle were averaged to obtain one dependent variable from each rater for each angle. Consistency of location of the TEA and CA was examined with Levene’s test for equality of variance, which is not susceptible to conditions of nonnormality. Interobserver reliability of the measurements was assessed using an intraclass correlation coefficient model (2,k). Differences between the TEA and CA were examined with a paired t-test and compared with the goal of orthogonality to the mechanical axes.

Results

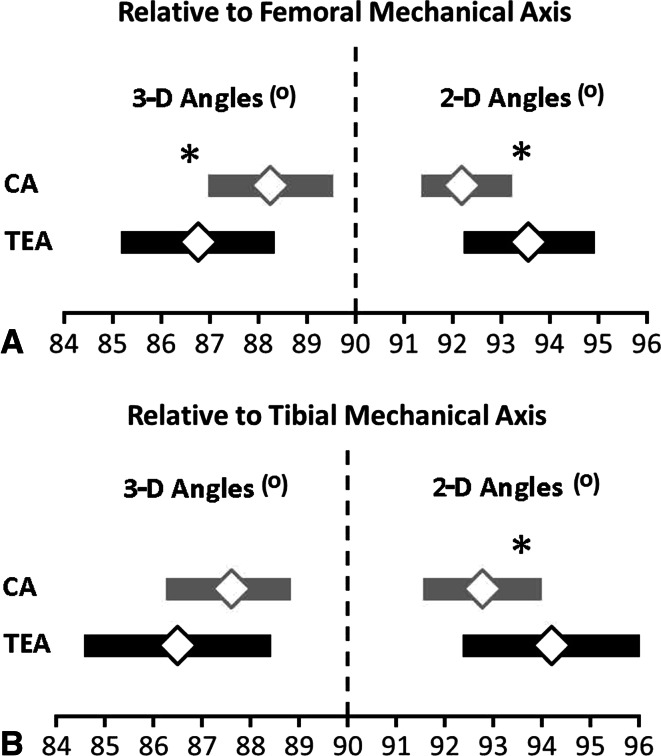
We found the angles formed by the TEA consistently further from perpendicular than angles formed by the CA relative to the mechanical axes of the femur and tibia in 2-D and 3-D measurements. In 2-D, all angles were greater than 90° for the TEA and CA (Fig. 2). The CA was 1.3° (95% CI, 0.0°, 2.6°; p = 0.04) closer to orthogonal than the TEA relative to the femoral mechanical axis and 1.4° (95% CI, 0.1°, 3.0°; p = 0.04) closer to orthogonal than the TEA relative to the tibial mechanical axis (Table 1). In 3-D projections, all angles to the mechanical axes were less than 90° for the TEA and CA. The CA was 1.4° (95% CI, 0.1°, 3.1°; p = 0.04) closer to orthogonal than the TEA relative to the femoral mechanical axis and 1.1° (95% CI, 0.7°, 3.2.8°; p = 0.24) closer to orthogonal than the TEA relative to the tibial mechanical axis (Table 1).

Fig. 2A–B.

Fig. 2A–B

Open in a new tab

The 95% CIs of the CA and TEA relative to the mechanical axis of the (A) femur and (B) tibia calculated in 2-D and 3-D projections are shown.

Table 1.

TEA and CA angles relative to femoral and tibial mechanical axes

Axis Two-dimensional angles (°) Three-dimensional angles (°)
TEA CA p value TEA CA p value
Femoral mechanical axis 93.6 ± 2.0 92.3 ± 1.3 0.04 86.8 ± 2.4 88.2 ± 1.9 0.04
Tibial mechanical axis 94.2 ± 2.5 92.8 ± 1.6 0.04 86.5 ± 3.1 87.6 ± 1.9 0.24
Open in a new tab

Values are expressed as mean ± SD; * paired t-tests used to compare axes; TEA = transepicondylar axis; CA = cylindrical axis.

The positions of the 95% CIs suggest the measured CA more closely approximates an orthogonal angle than the TEA (Fig. 2). For the TEA, the 95% CIs showed the mean angle could range from 85.4° to 94.6° and 84.8° to 95.8° across 2-D and 3-D measurements relative to the femoral and tibial mechanical axes, respectively (Fig. 2). For the CA, the 95% CIs showed the mean angle could range from 87.2° to 93.0° and 87.6° to 93.8° across 2-D and 3-D measurements relative to the femoral and tibial mechanical axes, respectively (Fig. 2).

Corresponding with the differing widths of CIs between the axes (Fig. 2), the measured variances of the TEA generally were larger than measured variances of the CA. For 2-D, the variance of the TEA trended 60% greater (p = 0.07) than the CA relative to the femoral mechanical axis and the variance was 91% greater (p = 0.05) than the CA relative to the tibial mechanical axis (Table 2; compare widths of 95% CIs in Fig. 2). For 3-D, the variances of the TEA and CA were similar (p > 0.05) relative to the femoral and tibial mechanical axes.

Table 2.

Variance of axis location and interobserver reliability

Axis Mean absolute difference from mean measurement (°)
Two-dimensional angles Three-dimensional angles
TEA CA p value* TEA CA p value*
Femoral mechanical axis 1.6
ICC = 0.83		 1.0
ICC = 0.56		 0.07 2.4
ICC = 0.83		 1.9
ICC = 0.56		 0.23
Tibial mechanical axis 2.1
ICC = 0.86		 1.1
ICC = 0.70		 0.05 2.4
ICC = 0.83		 1.5
ICC = 0.72		 0.15
Open in a new tab

* Levene’s tests used to compare variances; TEA = transepicondylar axis; CA = cylindrical axis; ICC = intraclass correlation coefficient.

Interobserver reliability ranged from 0.56 to 0.86 for the CA and TEA measurements (Table 2).

Discussion

The common practice of using the TEA as a surrogate for the FEA when implanting artificial joints in TKA may not be ideal, as the CA more closely corresponds to the actual FEA of the knee. We therefore addressed the following two questions: (1) Is the CA angle relative to the mechanical axes of the femur and tibia consistently different from the TEA angle relative to these mechanical axes in either 2-D or 3-D? (2) Does the CA angle relative to the mechanical axis better approximate perpendicular than the TEA angle relative to the mechanical axis, ie, closer to orthogonal?

The limitations of this study are (1) sampling from a single population, (2) modeling with a truncated cone, and (3) small relative/absolute differences. First, the observations are confined to a single population of white cadavers. A survey of the literature suggests there is morphologic variation in the femur and tibia between subpopulations based on race. For example, there appears to be a difference between white, black, and Asian populations in the degree of femoral anteversion [12]. Although our data show a difference between the CA and TEA for whites, we do not suggest the observation of a difference between the CA and TEA, or their relative orientation to mechanical axes, extends across all populations. Such an assertion is left for future investigation.

Second, we used a truncated cone as a model for the distal femur. Eckhoff et al. [9] used cylinder centers and Churchill et al. [6] used the center of spheres fit to the condyles to find the axis equidistant from the condylar surface. Cone axis and cylinder axis are the same, ie, collinear, by virtue of the fact that both lie equidistant from the condylar surface of the femur, but the cone is a better geometry to describe the distal femur. The cone model used here allows for the use of a single-fitting over double-fitting algorithm, ie, a single cone versus two cylinders or two spheres, which simplifies the algorithm to extrapolate an axis. The validity of this simplified algorithm is borne out in the consistency of our repeated observations by single and multiple observers (Table 2). This analysis, however, does not confirm the axis of the cone is the exact match of the true FEA. Confirmation of the proximity of the cone axis to the FEA is left to future biomechanical studies.

Third, the measured differences between the two angles averaging 1° are small. The absolute difference of each line from the perpendicular is greater with 2° deviation of the CA versus 3° deviation of the TEA from the femoral mechanical axis and 3° deviation of the CA versus 4° deviation of the TEA from the tibial mechanical axis, but is this small deviation clinically important? Although there is no literature establishing the absolute limit of tolerable malalignment in contemporary TKA, there is a long tradition in TKA to minimize the potential for malalignment, and this tradition extends back to the work of Lotke and Ecker [22] who “… noted that there is a statistically significant positive correlation between a good clinical result and a well-positioned prosthesis. In addition, it was appreciated [in their study] that perfect positioning of the device was difficult to obtain. [They] believe that the long-term clinical results, wear resistance, and resistance to prosthetic failure depend on correct positioning of the devices.” Despite studies [15, 20] published since that of Lotke and Ecker, what constitutes “correct component positioning” remains elusive, but subsequent work [19] does show the small tolerance, biomechanically and clinically, for off-axis alignment in TKA.

Our study documents the previously unreported relationship between two reference axes, FEA and CA, and their relationship to the mechanical axes of the femur and tibia. It is not within the scope of this paper to say the 1° average difference, 2° to 3° paired difference, or the even larger difference between outliers, are biomechanically or clinically important. We further do not assert that one axis is superior, but rather to show there is a consistent difference between the two axes and a consistently greater deviation of the TEA from the mechanical axis than the CA. It is left to future biomechanical testing and long-term outcome studies to validate if this difference between axes is clinically relevant.

Acknowledgments

We thank Heidi C. Eckhoff, laboratory technician, for data collection.

Footnotes

Each author certifies that he or she, or a member of his or her immediate family, has no commercial associations (eg, consultancies, stock ownership, equity interest, or patent/licensing arrangements) that might pose a conflict of interest in connection with the submitted article.

All ICMJE Conflict of Interest Forms for authors and Clinical Orthopaedics and Related Research editors and board members are on file with the publication and can be viewed on request.

Each author certifies that his or her institution approved or waived approval for the human protocol for this investigation and that all investigations were conducted in conformity with ethical principles of research.

This work was performed at University of Colorado–Denver/Anschutz Medical Campus, Aurora, CO, USA.

References

  • 1.Asano T, Akagi M, Nakamura T. The functional flexion-extension axis of the knee corresponds to the surgical epicondylar axis: in vivo analysis using a biplanar image-matching technique. J Arthroplasty. 2005;20:1060–1067. doi: 10.1016/j.arth.2004.08.005. [DOI] [PubMed] [Google Scholar]
  • 2.Bargren JH, Blaha JD, Freeman MA. Alignment in total knee arthroplasty: correlated biomechanical and clinical observations. Clin Orthop Relat Res. 1983;173:178–183. [PubMed] [Google Scholar]
  • 3.Bäthis H, Perlick L, Tingart M, Lüring C, Zurakowski D, Grifka J. Alignment in total knee arthroplasty: a comparison of computer assisted surgery with the conventional technique. J Bone Joint Surg Br. 2004;86:682–687. doi: 10.1302/0301-620X.86B5.14927. [DOI] [PubMed] [Google Scholar]
  • 4.Berger RA, Rubash HE, Seel MJ, Thompson WH, Crossett LS. Determining the rotational alignment of the femoral component in total knee arthroplasty using the epicondylar axis. Clin Orthop Relat Res. 1993;286:40–47. [PubMed] [Google Scholar]
  • 5.Blaha JD, Mancinelli CA, Simons WH. Using the transepicondylar axis to define the sagittal morphology of the distal part of the femur. J Bone Joint Surg Am. 2002;84(suppl 2):48–55. doi: 10.2106/00004623-200200002-00006. [DOI] [PubMed] [Google Scholar]
  • 6.Churchill DL, Incavo SJ, Johnson CC, Beynnon BD. The transepicondylar axis approximates the optimal flexion axis of the knee. Clin Orthop Relat Res. 1998;356:111–118. doi: 10.1097/00003086-199811000-00016. [DOI] [PubMed] [Google Scholar]
  • 7.Coughlin KM, Incavo SJ, Churchill DL, Beynnon BD. Tibial axis and patellar position relative to the femoral epicondylar axis during squatting. J Arthroplasty. 2003;18:1048–1055. doi: 10.1016/S0883-5403(03)00449-2. [DOI] [PubMed] [Google Scholar]
  • 8.Doro LC, Hughes RE, Miller JD, Schultz KF, Hallstrom B, Urquhart AG. The reproducibility of a kinematically-derived axis of the knee versus digitized anatomical landmarks using a knee navigation system. Open Biomed Eng J. 2008;2:52–56. doi: 10.2174/1874120700802010052. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Eckhoff D, Hogan C, DiMatteo L, Robinson M, Bach J. Difference between the epicondylar and cylindrical axis of the knee. Clin Orthop Relat Res. 2007;461:238–244. doi: 10.1097/BLO.0b013e318112416b. [DOI] [PubMed] [Google Scholar]
  • 10.Eckhoff DG, Bach JM, Spitzer VM, Reinig KD, Bagur MM, Baldini TH, Flannery NM. Three-dimensional mechanics, kinematics, and morphology of the knee viewed in virtual reality. J Bone Joint Surg Am. 2005;87(suppl 2):71–80. doi: 10.2106/JBJS.E.00440. [DOI] [PubMed] [Google Scholar]
  • 11.Eckhoff DG, Bach JM, Spitzer VM, Reinig KD, Bagur MM, Baldini TH, Rubinstein D, Humphries S. Three-dimensional morphology and kinematics of the distal part of the femur viewed in virtual reality. Part II. J Bone Joint Surg Am. 2003;85(suppl 4):97–104. doi: 10.2106/00004623-200300004-00012. [DOI] [PubMed] [Google Scholar]
  • 12.Eckhoff DG, Dwyer TF, Bach JM, Spitzer VM, Reinig KD. Three-dimensional morphology of the distal part of the femur viewed in virtual reality. J Bone Joint Surg Am. 2001;83(suppl 2, pt 1):43–50. doi: 10.2106/00004623-200100021-00010. [DOI] [PubMed] [Google Scholar]
  • 13.Eckhoff DG, Kramer RC, Watkins JJ, Alongi CA, Van Gerven DP. Variation in femoral anteversion. Clin Anat. 1994;7:72–75. doi: 10.1002/ca.980070203. [DOI] [Google Scholar]
  • 14.Elias SG, Freeman MA, Gokcay EI. A correlative study of the geometry and anatomy of the distal femur. Clin Orthop Relat Res. 1990;260:98–103. [PubMed] [Google Scholar]
  • 15.Ewald FC, Jacobs MA, Miegel RE, Walker PS, Poss R, Sledge CB. Kinematic total knee replacement. J Bone Joint Surg Am. 1984;66:1032–1040. [PubMed] [Google Scholar]
  • 16.Freeman MA, Pinskerova V. The movement of the normal tibio-femoral joint. J Biomech. 2005;38:197–208. doi: 10.1016/j.jbiomech.2004.02.006. [DOI] [PubMed] [Google Scholar]
  • 17.Hollister AM, Jatana S, Singh AK, Sullivan WW, Lupichuk AG. The axes of rotation of the knee. Clin Orthop Relat Res. 1993;290:259–268. [PubMed] [Google Scholar]
  • 18.Howell SM, Kuznik K, Hull ML, Siston RA. Longitudinal shapes of the tibia and femur are unrelated and variable. Clin Orthop Relat Res. 2010;468:1142–1148. doi: 10.1007/s11999-009-0984-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Hsu HP, Garg A, Walker PS, Spector M, Ewald FC. Effect of knee component alignment on tibial load distribution with clinical correlation. Clin Orthop Relat Res. 1989;248:135–144. [PubMed] [Google Scholar]
  • 20.Insall JN, Binazzi R, Soudry M, Mestriner LA. Total knee arthroplasty. Clin Orthop Relat Res. 1985;192:13–22. [PubMed] [Google Scholar]
  • 21.Iwaki H, Pinskerova V, Freeman MA. Tibiofemoral movement 1: the shapes and relative movements of the femur and tibia in the unloaded cadaver knee. J Bone Joint Surg Br. 2000;82:1189–1195. doi: 10.1302/0301-620X.82B8.10717. [DOI] [PubMed] [Google Scholar]
  • 22.Lotke PA, Ecker ML. Influence of positioning of prosthesis in total knee replacement. J Bone Joint Surg Am. 1977;59:77–79. [PubMed] [Google Scholar]
  • 23.Luo CF. Reference axes for reconstruction of the knee. Knee. 2004;11:251–257. doi: 10.1016/j.knee.2004.03.003. [DOI] [PubMed] [Google Scholar]
  • 24.Luo CF, Zeng BF, Koshino T. Transepicondylar line and condylar line as parameters for axial alignment in knee arthroplasty. Knee. 2004;11:213–217. doi: 10.1016/j.knee.2003.08.003. [DOI] [PubMed] [Google Scholar]
  • 25.Martelli S, Pinskerova V. The shapes of the tibial and femoral articular surfaces in relation to tibiofemoral movement. J Bone Joint Surg Br. 2002;84:607–613. doi: 10.1302/0301-620X.84B4.12149. [DOI] [PubMed] [Google Scholar]
  • 26.Pinskerova V, Johal P, Nakagawa S, Sosna A, Williams A, Gedroyc W, Freeman MA. Does the femur roll-back with flexion? J Bone Joint Surg Br. 2004;86:925–931. doi: 10.1302/0301-620X.86B6.14589. [DOI] [PubMed] [Google Scholar]
  • 27.Uehara K, Kadoya Y, Kobayashi A, Ohashi H, Yamano Y. Bone anatomy and rotational alignment in total knee arthroplasty. Clin Orthop Relat Res. 2002;402:196–201. doi: 10.1097/00003086-200209000-00018. [DOI] [PubMed] [Google Scholar]
  • 28.Williams A, Logan M. Understanding tibio-femoral motion. Knee. 2004;11:81–88. doi: 10.1016/j.knee.2003.12.004. [DOI] [PubMed] [Google Scholar]
  • 29.Wolfram Research, Inc. Wolfram MathWorld™. Available at: http://mathworld.wolfram.com/search/?q=Dot+Product. Accessed November 20, 2012.
  • 30.Yamada K, Imaizumi T. Assessment of relative rotational alignment in total knee arthroplasty: usefulness of the modified Eckhoff method. J Orthop Sci. 2000;5:100–103. doi: 10.1007/s007760050135. [DOI] [PubMed] [Google Scholar]
  • 31.Yoshioka Y, Siu D, Cooke TD. The anatomy of functional axes of the femur. J Bone Joint Surg Am. 1987;69:873–880. [PubMed] [Google Scholar]

Articles from Clinical Orthopaedics and Related Research are provided here courtesy of The Association of Bone and Joint Surgeons

RESOURCES