Abstract
Most models of nucleotide or amino acid substitution used in phylogenetic studies assume that the evolutionary process has been homogeneous across lineages and that composition of nucleotides or amino acids has remained the same throughout the tree. These oversimplified assumptions are refuted by the observation that compositional variability characterizes extant biological sequences. Branch-heterogeneous models of protein evolution that account for compositional variability have been developed, but are not yet in common use because of the large number of parameters required, leading to high computational costs and potential overparameterization. Here, we present a new branch-nonhomogeneous and nonstationary model of protein evolution that captures more accurately the high complexity of sequence evolution. This model, henceforth called Correspondence and likelihood analysis (COaLA), makes use of a correspondence analysis to reduce the number of parameters to be optimized through maximum likelihood, focusing on most of the compositional variation observed in the data. The model was thoroughly tested on both simulated and biological data sets to show its high performance in terms of data fitting and CPU time. COaLA efficiently estimates ancestral amino acid frequencies and sequences, making it relevant for studies aiming at reconstructing and resurrecting ancestral amino acid sequences. Finally, we applied COaLA on a concatenate of universal amino acid sequences to confirm previous results obtained with a nonhomogeneous Bayesian model regarding the early pattern of adaptation to optimal growth temperature, supporting the mesophilic nature of the Last Universal Common Ancestor. [Ancestral sequence reconstruction; nonhomogeneous model; optimal growth temperature; phylogenomics; phylogeny.]
Many evolutionary studies use genomic sequences to infer a phylogenetic tree depicting the relationships between species. To reconstruct such trees, substitution models that describe the stochastic process of evolution acting on sequences are preferred. The use of complex models of evolution has provided insights into early events of evolution such as the origin of major groups of organisms (Cox et al. 2008; Philippe et al. 2011), the absolute or relative chronological appearance of major clades or important phenotypic characters (Douzery et al. 2004; Delsuc et al. 2006), and ancestral conditions of life (Boussau and Gouy 2012). Over recent years, many authors have proposed to perform ancestral sequence reconstruction to tackle such problems, either at the scale of a single gene alignment (Gaucher et al. 2008; Finnigan et al. 2012) or at the scale of concatenates of genes (Boussau et al. 2008; Groussin and Gouy 2011). To infer the characteristics of ancestral molecules from the analysis of extant genomes, accurate and biologically relevant models of evolution must be utilized.
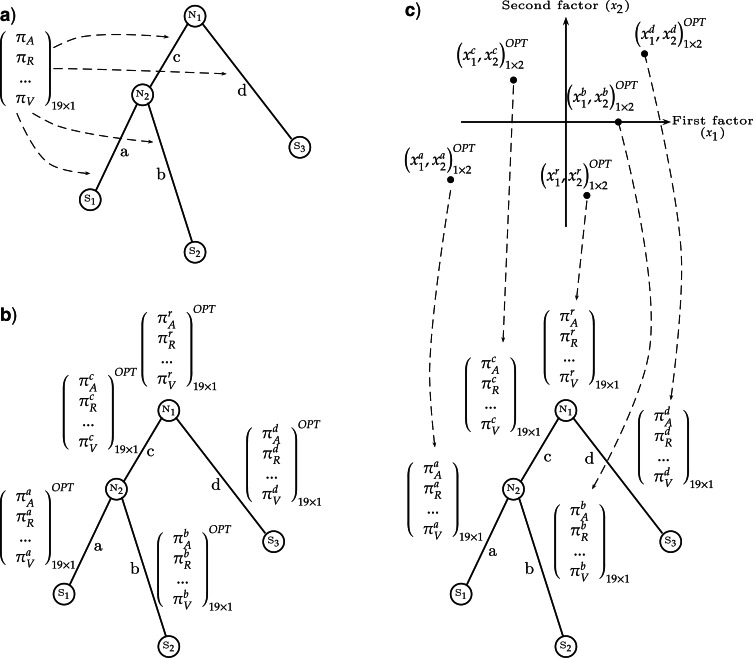
However, standard models are usually designed with the simplifying assumptions that the evolutionary process was globally stationary, reversible, and homogeneous (Yang 2006; Jermiin et al. 2008; Jayaswal et al. 2011a) (Fig. 1a). It has been shown that homologous sequences can diverge widely in their base or amino acid compositions (Hasegawa and Hashimoto 1993; Galtier and Lobry 1997; Zeldovich et al. 2007). Consequently, the assumption that the composition of nucleotides or amino acids in the sequences has remained unchanged from the root of the tree to its leaves (stationarity hypothesis), and that all branches of a phylogenetic tree share the same relative amino acid substitution rates (homogeneity hypothesis), is not appropriate for compositionally heterogeneous sequences. Compositional heterogeneity across sets of homologous sequences may lead to erroneous reconstructions of phylogenetic trees or ancestral frequencies (Ho and Jermiin 2004; Jermiin et al. 2004; Blanquart and Lartillot 2006, 2008; Boussau and Gouy 2006; Boussau et al. 2008). A natural approach to avoid these erroneous reconstructions is to use a model that represents in a more realistic fashion the evolutionary process.
Figure 1.
The COaLA model substantially decreases the dimension of the space of equilibrium frequency parameters. a) In homogeneous and stationary models, only one vector of amino acid frequencies represents the equilibrium state of sequences and is used for likelihood computation. This vector may be optimized by ML (LG+Fopt model) or not (LG or LG + Fobs models). b) With a standard nonhomogeneous approach, the homogeneity and stationarity hypotheses are relaxed by assigning independent vectors of 19 equilibrium frequencies per branch to model the variations of overall composition through time. c) With the COaLA model, small dimension vectors of coordinates along the first axes of the COA are optimized per branch. In this example, a two-dimension vector corresponding to the first two axes is associated to each branch and is optimized by ML (OPT). Reversing the COA (dashed arrows), from a vector of coordinates in the low-dimension space, one can compute the corresponding vector of 20 frequencies that is used to compute transition probabilities along the branch.
Several models that relax the homogeneity and stationarity hypotheses have been developed, either in the distance-based framework (Lake 1994; Lockhart et al. 1994; Galtier and Gouy 1995; Tamura and Kumar 2002) or in the likelihood or Bayesian frameworks (Yang and Roberts 1995; Galtier and Gouy 1998; Foster 2004; Jayaswal et al. 2005, 2007, 2011b; Blanquart and Lartillot 2006; Dutheil and Boussau 2008; Zou et al. 2012). In each of these methodological contexts, the branch-heterogeneous models require several substitution matrices to be used for a given phylogenetic tree (Fig. 1b) whereas the branch-homogeneous models only require one such matrix (Fig. 1a). Therefore, more parameters need to be estimated for branch-heterogeneous models than for branch-homogeneous models. The purpose of branch-heterogeneous models is to decrease the bias in the estimation of model parameters, but their drawback may be an increase in variance. This tradeoff between bias and variance should be a matter of concern when employing parameter-rich models (Wertheim et al. 2010). It is necessary to make sure that the parameters that capture the time variability of global compositions increase the fit of the model to the data enough to compensate for the increased number of parameters. Objective criteria such as Akaike Information Criterion (AIC) or Bayesian Information Criterion (BIC) can be used to determine the optimal choice for the trade-off between the fit of the model to the data and the number of parameters in the model (Steel 2005). Thus, it was observed that branch-heterogeneous models of sequence evolution may be preferred or rejected over branch-homogeneous models, depending on the choice of parameters or the amount of heterogeneity in the data (Dutheil and Boussau 2008; Groussin and Gouy 2011). Finally, the issue of computational cost has hampered the use of branch-heterogeneous models at a broad scale, especially for proteins, making the development of statistically and computationally efficient branch-heterogeneous models necessary. Note that for convenience the terms “branch-heterogeneous” and “nonhomogeneous” are used interchangeably in the rest of the article, excepted in cases where “nonhomogeneous” is used to describe other types of heterogeneities (e.g., site-specific process-heterogeneity).
Several studies have presented approaches to reduce the number of parameters to be estimated with branch-heterogeneous models. For instance, some methods do not estimate one matrix per branch, but use groups of branches that share substitution matrices (Yang 1998; Foster 2004; Dutheil and Boussau 2008). These groups can be defined a priori (Dutheil and Boussau 2008), or estimated during the course of the computation (Jayaswal et al. 2011a; Dutheil et al. 2012). Similarly, Bayesian approaches have been developed that place breakpoints along the branches of the phylogeny: substitution models are shared by all branches between breakpoints, but change at breakpoints (Blanquart and Lartillot 2006, 2008). Another approach to further reduce the number of parameters has been to share some parameters of the substitution matrices among all branches and have only a subset of them estimated separately for each branch or group of branches. Using such an approach, Galtier and Gouy (1998) were able to propose a branch-heterogeneous model of nucleotide sequence evolution with only one extra parameter per branch of the phylogenetic tree, namely branch-wise equilibrium G+C contents. The resulting model has a good fit to the data because some nucleotide sequences vary extensively in their G+C content. For amino acid sequences, however, it is unclear how variations among homologous sequences could be efficiently summarized by a single or even a small number of variables for any data set.
An efficient model of protein evolution would be useful in studies aimed at protein resurrection. Ancestral sequence reconstruction and resurrection is a powerful approach to characterize ancient molecular properties, to highlight the complex relationship between sequence, structure, and function, or to infer past lifestyle conditions (Harms and Thornton 2010; Boussau and Gouy 2012). The widely applied protocol for ancestral sequence reconstruction starts with the choice of one of the time-reversible Markov models that ModelTest (Posada and Crandall 1998; Posada 2008) considers. Then, this model is used in the PAML package (Yang 2007) to compute the most likely ancestral sequence at each internal node of a maximum-likelihood (ML) tree for the gene under consideration. However, the variation of the substitution process through time or among sites is not accounted for, even when billions of years separate all sequences from their common ancestor (Gaucher et al. 2008; Hobbs et al. 2011). Using a model that can take into account a higher proportion of the complexity of evolutionary processes without excess of variance should help inferring better ancestral sequences.
We do not know of any statistically and computationally efficient branch-heterogeneous substitution model for proteins in the ML framework. Here, we present the correspondence and likelihood analysis (COaLA) model, a new branch-heterogeneous model of amino acid sequence evolution for ML. This model achieves computational efficiency through the same means as Galtier and Gouy (1998), reducing the number of variables that need to be estimated per branch of a phylogenetic tree; it focuses only on a few directions explaining most of the compositional variance observed in the data (Fig. 1c). These variables correspond to linear combinations of observed amino acid frequencies in the data set according to a correspondence analysis (COA) (Greenacre 1984). COA constructs linear combinations of amino acid frequencies ranked by decreasing contribution to the explained variance (these linear combinations are also called axes or factors in the statistical literature; here, we refer to them as axes). Consequently, exploring different values along the first axes amounts to exploring a high proportion of the compositional variability encountered in the data set. In addition, as COA has been previously used to characterize the determinants of compositional heterogeneity among protein sequences (Boussau et al. 2008), estimated branch-wise values along the axes of the COA may be used to directly gain information about the evolution of biological or physical properties affecting compositions over time.
In this article, we describe the COaLA model and how it is applied to the data. The model has been tested on both simulated and biological data sets and we show results focusing on its ability to efficiently fit the data, estimate ancestral frequencies as well as ancestral sequences in comparison with standard homogeneous models. Finally, we apply the model on a previously published data set to confirm the phylogenetic signal explaining the early pattern of adaptation to environmental temperature before the emergence of the three domains of life.
Materials and Methods
Branch-Homogeneous and Branch-Heterogeneous Markovian Substitution Processes
We consider a tree, T, rooted at node r, along which amino acid sequences evolve. Sequence evolution proceeds from the root to the leaves of the tree, where sequences are observed. At the root, a vector πr specifies the amino acid frequencies of the (unobserved) ancestral sequence. Along the branches of the tree, we assume that substitutions occur according to a Markov process. In the context of molecular evolution, the kernel of the Markov process is called the substitution matrix and is denoted as Q. If the kernel is time-reversible, then Q can be decomposed into two matrices, ρ and Π, where ρ = ρyz is a matrix of exchangeabilities (or relative exchange rates) and Π= diag(πy) is the diagonal matrix of stationary or equilibrium frequencies (Whelan and Goldman 2001), with y,z = 1,. . .,20 (where 20 is the number of amino acids). The general term of Q is computed as follows:
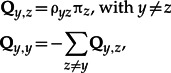 |
with ρyz = ρzy for y > z.
The transition probabilities py→z(t), defined as the probability of change from state y to state z along an edge of length t time units, are calculated as follows:
Common models of sequence evolution assume a constant substitution rate matrix over the tree (Jermiin et al. 2008). Such models are said to be globally homogeneous. In addition, it is often assumed that the evolutionary process is at equilibrium, in which case the process is also said to be stationary with πr = π. Reversibility implies that the flux from one amino acid y to another z is equal to the flux from z to y:
These assumptions have two major consequences: (i) such models (i.e., the commonly used models of sequence evolution) cannot infer a direction of evolution, so the root can be placed anywhere on the tree without affecting the likelihood value (Felsenstein 1981; Yang 2006) and (ii) as previously noted (Galtier and Gouy 1998; Boussau and Gouy 2006), these models assume that all sequences in a tree share similar base or amino acid frequencies.
As illustrated in Jermiin et al. (2008), the evolutionary process can be defined as one of the six (out of eight) possible permutations of homogeneous/nonhomogeneous condition, reversible/nonre-versible condition, and stationary/nonstationary condition. These conditions may be applied globally (e.g., to every branch in the tree) or locally (e.g., to a particular branch of the tree). The model presented here is designed to work on amino acid data and to relax the assumptions of global homogeneity, reversibility, and stationarity; in other words, it allows different lineages to diverge toward different amino acid compositions, starting from another set of amino acid frequencies at the root (πr). Therefore, the model is nonreversible, and the position of the root affects the likelihood value. COaLA is inspired from the N2 model initially proposed by (Yang and Roberts 1995), designed for DNA, in which a single exchangeability matrix is shared by all branches of T, and a distinct vector of equilibrium nucleotide frequencies is associated with each branch of T. The model also uses the vector πr of amino acid frequencies at the root.
Mathematical Model
COA is a standard multivariate statistical technique that decomposes the χ2 statistic associated with a contingency table into orthogonal factors that represent most of the variance (Thioulouse et al. 1997). Here, the contingency table is the matrix of observed amino acid frequencies in protein sequences. In essence, COA summarizes the original data variability using a reduced number k < 20 of variables (the factors or axes), which are linear combinations of the 20 original frequencies (see Appendix). Thus, COA reveals the principal axes of a high-dimensional space, enabling at the end the projection of amino acid frequencies into a subspace of lower dimension. In that sense, COA is similar to principal component analysis (PCA). However, PCA uses the Euclidean distance between vectors of frequencies, whereas COA uses the χ2 distance, which makes COA equally sensitive to deviations in rare amino acids as it is to deviations in frequent amino acids.
The compositional variation among all compared protein sequences is thus summarized in a subspace capturing most of this variation. This subspace allows us to reduce the dimension of the above-mentioned branch-heterogeneous model of protein evolution along a tree by working in the subspace of k principal axes instead of the complete space of 20 parameters. The dimension of the evolutionary model with branch-specific equilibrium frequencies is thus reduced from 19 free parameters per branch to k per branch. From a set of coordinates on a chosen number k of principal axes, it is possible to reverse the COA in order to compute a 20-dimensional vector of amino acid frequencies for which the COA would give these coordinates as factor values (see Appendix). The reduced evolutionary model works by optimizing k coordinates on each branch of T, which are transformed into branch-specific vectors of equilibrium amino acid frequencies, which in turn define branch-specific substitution matrices. To illustrate this, consider a rooted phylogenetic tree of 30 species, containing 58 branches and imagine a full branch-heterogeneous LG+Fopt model, where 19 free frequencies are optimized per branch and on the root, with a common LG exchangeability matrix (Le and Gascuel 2008) for all branches. It can be compared with a branch-heterogeneous COaLA model where only k free parameters (k ∈[1 : 19]) representing axis positions are estimated per branch and on the root. In the first case, the number of parameters (m) involved in the model is m = 19×58+19 = 1121, whereas in the second case, the number of parameters is m = k ×58+k. As most of the COA performed on real alignments show that a large majority of the variance is explained by the first two or three axes, the improvement in terms of number of parameters can be huge. Thus, if k = 2, m = 118, a number of parameters 10-fold smaller than with the full approach.
Model Availability
The COaLA model is implemented in the Bio++ libraries (Dutheil et al. 2006), which are a set of freely available C++ libraries dedicated, among other things, to evolutionary biology. The model can be employed with the BppML program, available in the bppSuite series of programs (Dutheil and Boussau 2008). BppML is a general program to optimize a large set of homogeneous/stationary or nonhomogeneous/nonstationary models in the ML framework for several types of data sets (e.g., DNA, codons, and proteins). Information on the model and on how to download and install the libraries can be found at http://pbil.univ-lyon1.fr/software/COaLA/.
Models Used in This Study
In the following, homogeneous and stationary, homogeneous and nonstationary, and nonhomogeneous and nonstationary approaches will be referred by HS, H–NS and NH–NS approaches, respectively. For all phylogenetic experiments, the LG exchangeability matrix (Le and Gascuel 2008) is used, but every empirical exchangeability matrix may be employed (e.g., JTT [Jones et al. 1992]; WAG [Whelan and Goldman 2001]). When the vector of equilibrium frequencies specific to the LG model is employed, we will refer to the model as LG. If the vector of equilibrium frequencies is fixed to the observed frequencies computed from the alignment under study (the so-called “+F” model [Adachi and Hasegawa 1996]), the model is referred as LG+Fobs. When stationary frequencies are optimized by ML, LG+Fopt is used. COaLA can also be used as an H–S model. If so, LG+COaLA[k] means that the equilibrium frequencies of the single substitution matrix in use by all branches are optimized through k axis positions. With an H-NS approach, a second and independent set of axis positions is optimized on the root. With an NH approach, LG+COaLA[k] means that k independent axis positions per branch and on the root are optimized. In this study, the number of axis positions k is set a priori and is equal for all branches of the tree. This number is not optimized during the run of the program. Rather, the method is run with all integer values between 1 and k, and the optimal number of axes is then determined according to model selection statistical criteria (AIC or BIC, see below). Note that the method could be generalized so that k is optimized to obtain variable numbers of axis positions per branch.
Simulations
Sequence Simulations
All simulations of amino acid sequences with nonhomogeneous models were performed with BppSeqGen, from the bppSuite series of programs (Dutheil and Boussau 2008).
To simulate these nonhomogeneous amino acid sequences, we considered the 5000 trees used by Guindon and Gascuel (2003) to test the performance of PhyML and which are available at http://www.atgc-montpellier.fr/phyml/datasets.php. These trees contain 40 species. We randomly removed 20 of these 40 species for each of the 5000 trees. Branch lengths were increased to allow different parts of the tree to have sufficient time to diverge in terms of compositions. Thus, the height of the tree, defined as the maximum distance between a leaf and the root, was set to a minimum of 0.8 substitutions/site and all other branches were scaled up accordingly. The resulting branch lengths are still realistic since the overall mean is 0.13 substitutions/site/edge and the overall median is 0.08 substitutions/site/edge, showing that many small branches remain in the trees. We simulated alignments of 5000 amino acids, with rate heterogeneity across sites modeled by a discretized 3 distribution with four rate categories (Yang 1994). To specify the nonhomogeneity and nonstationarity, we assigned different independent sets of amino acid equilibrium frequencies to different parts of the tree as well as one for the root; these sets of frequencies were drawn from a Dirichlet distribution. To do so, we determined the means and standard deviations of each amino acid frequency from a protein sequence alignment containing 3336 sites from 115 species spanning the tree of life (Boussau et al. 2008). These means and standard deviations were used to define the marginal densities employed to randomly draw the sets of equilibrium frequencies from the Dirichlet distribution. For each amino acid, we multiplied the observed standard deviations by 3 to increase the nonhomogeneity of simulated sequences in terms of composition. Only two or four different parts of the tree are specified to have different equilibrium compositions (see below), all branches belonging to one of these parts being compositionally homogeneous. This procedure was adopted in order to generate alignments with sizeable levels of compositional heterogeneity. In addition, we randomly drew a set of frequencies that was assigned to the root. We then randomly chose an integer number w (1 or 2). If w = 1, independent sets of frequencies were assigned on the first two branches around the root. If w = 2 and if the root has four descendant nodes, the first six branches were assigned different equilibrium compositions. Finally, all branches below one of the nodes of the w-th generation were assigned the set of frequencies of the preceding branch leading to that given node.
For each of these 5000 simulated alignments, we computed all pairwise Bowker tests (Bowker 1948) to assess the global heterogeneity of the alignment. The Bowker test relies on a pairwise comparison and on a test of symmetry between two aligned sequences (Ababneh et al. 2006). If the test statistic from the Bowker test is significant, then it is unlikely that the pair of diverging sequences being considered have evolved under the same process. As Dutheil and Boussau (2008) proposed, we defined the global heterogeneity of the alignment as the number of tests that are statistically significant at the 5% level that we corrected with a Holm–Bonferroni correction (Holm 1979) for multiple test comparisons.
Many among the 5000 alignments were moderately heterogeneous according to the Bowker test (half of all the alignments had less than 37% significant pairwise tests). To globally assess the ability of NH–NS COaLA to estimate ancestral frequencies and branch lengths regardless of the data heterogeneity, the 1000 (out of 5000) first trees were selected and their corresponding alignments were analyzed. Moreover, to compare the fit to the data between COaLA and H–S approaches, we retrieved the alignments having the top 5% highest heterogeneity among the 5000 alignments. The mean heterogeneity of the resulting 272 alignments was in accordance with what is observed on empirical data (about 64% of the tests were significant, which is comparable with the heterogeneity of the biological data sets used in this study [see below] and many other concatenated protein data sets [data not shown]).
Assessing the Performance of COaLA on Simulated Sequences
To globally assess the performance of NH–NS COaLA, we first focused on (i) its ability to estimate ancestral frequencies and (ii) to fit data.
We evaluated the capacity of different models to reconstruct sequence evolution from simulated alignments by two means. First, we investigated the accuracy of the reconstructed amino acid frequencies at the root. Second, we evaluated the capacity of the models to reproduce the composition of simulated alignments, in a manner akin to parametric bootstrapping or posterior predictive simulations (Huelsenbeck et al. 2001; Bollback 2002; Lartillot and Philippe 2004). We ran each model on each simulated alignment, and recorded the estimated parameters. Then, we used these parameters to simulate new alignments using BppSeqGen. Finally, we compared these newly simulated alignments with the original alignments: for each of the 20 sequences per alignment, the amino acid frequencies were computed and compared with the amino acid frequencies observed in the original alignments.
We also investigated the influence of the alignment size on the estimation of equilibrium frequencies (see Supplementary Fig. S2 that can be found in the Dryad data repository [doi:10.5061/dryad.7h66k]). We simulated 1000 alignments containing either 100 or 200 amino acids, with the same trees and sets of parameters as previously. This approach was motivated by two main reasons. First, it is not obvious whether NH–NS COaLA is able to generate accurate parameter estimates for short single-gene alignments. Second, in short alignments, some amino acids, especially rare amino acids such as tryptophan or cystein, may never be observed in any sequences. In such a case, the standard COA algorithm cannot be applied, since all elements of a column (here, the counts of a particular amino acid) are divided by its marginal sum. We devised a procedure to deal with such cases (see “Results” section and Supplementary Information). This procedure has proved to be efficient to avoid optimization problems.
To estimate the best model in terms of fitting data, either homogeneous or nonhomogeneous, BIC values (Schwarz 1978) were computed for each model (Felsenstein 2004; Ripplinger and Sullivan 2008) to penalize the number of parameters influencing the likelihood. A rooted tree is characterized by 2s–2 internal branches, s being the number of species. In the case of the NH–NS COaLA model, we count k axis positions optimized per branch and at the root, and add the α parameter of the Γ distribution, which results in the total number K of parameters
The BIC value is computed as:
where lnL is the optimal log-likelihood and n is the alignment length. In this study, the LG (Le and Gascuel 2008) empirical exchangeability matrix does not add free parameters to the model. However, if a general time reversible (GTR) matrix is considered, 190 free exchangeabilities have to be taken into account in the total number of parameters. Moreover, it is worth noting that other statistical criteria for model selection may be employed. AIC (Akaike 1974) is one such criterion, which penalizes complex models less than does BIC (AIC = −2×lnL+2×K). We chose to employ BIC because it was observed that AIC tends to favor models that are too parameterized with phylogenomic data sets (see “Results” section). We thus recommend the use of this criterion for model selection on large alignments. However, the situation is rather different on single-gene alignments, where BIC may penalize too strongly the more complex models in comparison with AIC (see “Results” section).
We note here that the NH–NS COaLA model used to estimate evolutionary parameters on simulated data sets is more parameter rich than the model used to simulate sequences, as in the latter several branches share the same substitution matrix (See “Materials and Methods” section). Although these simulation experiments therefore are a clear example of overparameterization, we believe they can provide valuable information regarding the accuracy of the COaLA model. One way to avoid overparameterization in this simulation setting would be to use the algorithms presented in Dutheil et al. (2012), which select the best branch-heterogeneous model on a fixed tree by finding the optimal partition of branches according to statistical criteria such as AIC or BIC. As the work of both Dutheil et al. (2012) and ours are based on the Bio++ libraries, the COaLA model can be easily incorporated to these programs to select the best configurations of axis position assignments over the tree.
Biological Data Sets
Phylogenomic Alignments
The COaLA model was tested on four previously published phylogenomic data sets (see below). For each data set, rate heterogeneity across sites was modeled with a discretized Γ distribution with four categories (Yang 1994).
Yeast data set.—This data set is a concatenation of 106 genes belonging to eight yeast species (Rokas et al. 2003). This alignment contains 42 342 amino acids and the species tree presented in Figure 4 of the corresponding paper is used to estimate evolutionary parameters and compute the likelihood. The G+C content of third codon positions is heterogeneous among the eight species, ranging from 0.28 in Candida albicans to 0.45 in Saccharomyces kluyveri, possibly influencing the composition at the amino acid level. In line with this, 46% of the pairwise Bowker tests performed on the protein concatenate are statistically significant (according to Holm correction for multiple comparisons).
Figure 4.
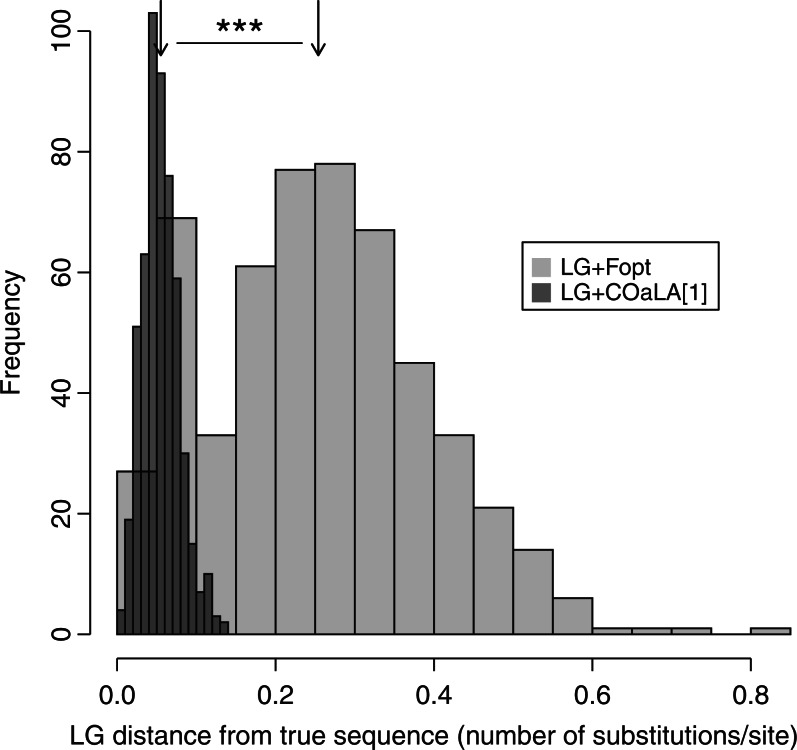
Accuracy of the ancestral sequence reconstruction. With the 535 simulations of single-gene alignments (see “Materials and Methods” section), ancestral sequence reconstruction was performed with a H–S model (LG+Fopt) and with a NH–NS model (LG + COaLA[1]). For all ancestral sequences, a LG distance was computed between the inferred and the true sequences recorded during the simulation procedure. For each of the 535 cases, the mean LG distance was calculated and the distribution of means is represented in light and dark gray for the LG+Fobs and LG + COaLA[1] models, respectively. The mean of the distributions (black arrows) are 0.25 and 0.06, respectively (P < 0.001).
Archaea data set.—These data are a concatenation of 72 protein-coding genes sampled in 35 archaeal species and 10 bacterial species (Groussin and Gouy 2011). We removed bacteria from the alignment, as well as the two uncultured thaumarchaeal species, for which only one protein sequence was present in the alignment. The final alignment of 9387 amino acids contains 33 archaeal species. We used the topology presented in figure 3 of Groussin and Gouy (2011) to determine the best evolutionary model with BppML. These sequences are compositionally highly heterogeneous since 86% (after correction for multiple tests) of the pairwise Bowker tests significantly rejected the stationarity or homogeneity hypotheses.
Figure 3.
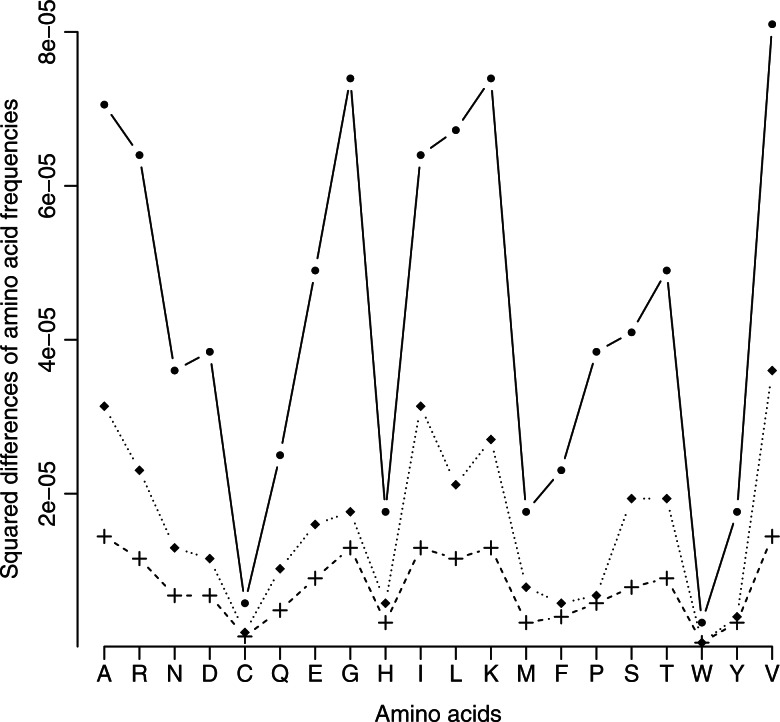
Accuracy of the phylogenetic signal capture. The H, H–NS, and NH–NS approaches are compared. For each of the original 1000 simulated alignments, parameters estimates were obtained with each one of the three approaches. From these estimates, new alignments were simulated with BppSeqGen. For each of the 20 sequences per alignment, the amino acid frequencies were computed and compared with the amino acid frequencies observed in the original alignments. The medians of squared differences for each amino acid frequency are represented. Solid line: H–S model. Dotted line: H–NS model. Dashed line: NH–NS model. The NH–NS approach is the best approach regarding the modeling of evolutionary processes and the capture of the phylogenetic signal present in the data.
Eocyte data set.—Cox et al. (2008) used 45 genes to build a universal alignment of 5521 sites and 40 species. Using a nonhomogeneous model that allowed them to explore the space of tree topologies in the Bayesian framework, they obtained a topology called “eocyte” where Crenarchaea is the sister group of Eukaryotes. This topology was used in our analysis of their alignment. The compositional heterogeneity present in the data is strong, with 77% significant pairwise Bowker tests (after multiple tests correction).
Three domains data set.—Boussau et al. (2008) used 56 unicopy genes to build a universal alignment of 30 species. Because of a drastic selection of sites allowing only sites with less than 5% of gaps to remain in the final alignment, the total number of sites is rather small (3336 sites). We increased the size of the final alignment by using a less drastic site selection. Each individual gene alignment was realigned with Muscle v3.7 (Edgar 2004), internally used by Guidance v1.1 (Penn et al. 2010) with its default parameters. Guidance is a program allowing users to evaluate the reliability of alignments by taking into account the uncertainty of the guide tree used to align sequence positions with a bootstrap procedure. The resulting alignments were then treated by Gblocks (Castresana 2000) to eliminate ambiguous regions (default parameters with the authorization to conserve gap sites were used). The final gene alignments were concatenated and the sites with more than 50% of gaps were removed to eventually obtain an alignment of amino acids with 6269 sites.
Single Gene Alignments
To evaluate both the ability to fit the data and the accuracy of ancestral sequence reconstruction on single-gene alignments with NH–NS COaLA in comparison with a homogeneous model, gene alignments were constructed from 24 methanogenic archaeal genomes (15 Methanococcales, 8 Methanobacteriales, and 1 Methanopyrale, see Supplementary Table S2). This data set presents two advantages: these species do not have extreme rates of evolution (Brochier-Armanet et al. 2011) and are adapted to different optimal growth temperatures (OGTs), leading to compositional variability (Groussin and Gouy 2011). All genome sequences were retrieved from GenBank. The software package SiLiX (Miele et al. 2011) was employed to cluster amino acid sequences into homologous gene families. Unicopy gene families containing at least 80% of the 24 species were conserved, leading to 535 gene families. Each family was further aligned with PRANK (Löytynoja and Goldman 2008) internally used by Guidance. The resulting alignments were then trimmed by Gblocks (Castresana 2000) with default parameters and the authorization to conserve gap sites. Phylogenetic trees were computed with PhyML (Guindon and Gascuel 2003) with a WAG+Γ(4) model (Yang 1994; Whelan and Goldman 2001). The trees were subsequently mid-point rooted and used with their corresponding alignments to run COaLA in a NH–NS fashion with a LG+COaLA[1]+Γ(4) model. From the ML estimates (model parameters and branch lengths), 535 alignments were simulated (one per set of ML estimates) with BppSeqGen (Dutheil and Boussau 2008). During simulations, ancestral sequences for each internal node were conserved and are henceforth referred to as “true” sequences. For each of the 535 simulated alignments, a model comparison was performed with the H–S LG+Fopt and NH–NS LG+ COaLA[1] models. With the ML estimates obtained with each model, ancestral sequences were computed with BppAncestor (Dutheil and Boussau 2008), with a marginal reconstruction (see Appendix). For each internal node, the ML pairwise distances between the homogeneously inferred sequence and the true sequence and between the nonhomogeneously inferred sequence and the true sequence were computed with the LG model (Le and Gascuel 2008).
Results
Simulations
NH–COaLA accurately estimates ancestral amino acid frequencies.—We verified that the compositional variance encountered in the simulated alignments was distributed as in biological data. For the first 1000 simulated alignments (out of 5000; see “Materials and Methods” section “Sequence simulations”), Supplementary Figure S1a shows that on average, the first three axes represent 53%, 23%, and 11% of the total variance, which is very similar to what can be observed in real sequences (Supplementary Fig. S1b–e and see below). This suggests that our simulated alignments have properties that are routinely encountered in biological data sets. When COaLA models were employed on these simulated data sets, two axis positions per branch were estimated, allowing to take into account, on average, about 75% of the variance (Supplementary Fig. S1a). Note that the NH–NS model with 19 free parameters per branch was not used in simulations as it generally takes too much time to converge. A comparison with the NH–NS COaLA model for calculation time and fit to data is provided with the analysis of real data (see below).
Figure 2 shows that for the first 1000 alignments, both the NH–NS and H–NS LG+COaLA[2] models outperform the H–S LG+F model when it comes to estimating ancestral root frequencies. The sums of the squared differences between true and inferred amino acid frequencies are equal to 4.38, 1.15, and 0.98 for the H–S, H–NS, and NH–NS models, respectively, with the NH–NS model exhibiting slightly better performances than the H–NS approach (Wilcoxon paired test, P < 0.001). Furthermore, we observed that for both rare (such as cysteine or tryptophan) or frequent amino acids (such as alanine), the NH–NS COaLA model remains the best (P < 0.001) at estimating ancestral frequencies at the root (the sums of the squared differences are, in the same order as before, 0.018, 0.0025, and 0.0022 for tryptophan and 0.398, 0.112, and 0.098 for alanine). This might be explained by the fact that COA is equally sensitive to deviations in rare amino acids as it is to deviations in frequent amino acids.
Figure 2.
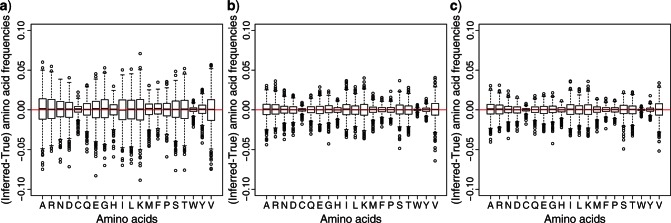
Accuracy of estimation of ancestral root amino acid frequencies. On the y-axes, the differences between inferred amino acids frequencies by ML and true amino acid frequencies used to simulate sequences are represented. a) Results obtained with the H–S LG+Fopt model. b) Results obtained with the H–NS LG+COaLA[2] model. c) Results obtained with the NH–NS LG+COaLA[2] model.
For the H–S, H–NS, and NH–NS approaches, we resimulated alignments from the parameters estimated by BppML to compare the ability of the different approaches to capture the evolutionary signal within the tree. We reasoned that if the model is able to correctly extract the signal from the data, sequences simulated from the ML parameter estimates should be close to the original sequences regarding their amino acid compositions. Thus, the amino acid frequencies of each simulated sequence were then computed and compared with the amino acid frequencies of the corresponding sequence from the original simulated alignment. Medians of squared differences of amino acid frequencies are presented in Figure 3. This figure highlights that the NH–NS approach better captures the evolution of compositional heterogeneities through time, as attested by the low-squared differences between simulated and expected amino acid frequencies.
Influence of the size of the alignment on the estimation of ancestral amino acid frequencies.—For short alignments, the standard NH–NS COaLA model might experience optimization problems for rare amino acids that may be totally absent in the alignment. We implemented a special procedure to deal with such cases (see “Materials and Methods” section and Supplementary Information for a full description) to avoid optimization issues.
The branch-wise NH–NS models can be expected to perform poorly with short alignments, because a large amount of data is needed to accurately optimize the equilibrium frequencies. Accordingly, Supplementary Figure S2 shows that the optimization of ancestral root frequencies for amino acid aligments with 100 sites is less accurate than what can be obtained with a H–S model: the sums of squared differences between the estimated frequencies and the true frequencies are equal to 7.64 and 6.72, respectively (P < 0.001). However, for amino acid aligments with 200 sites, NH–NS COaLA becomes better than a homogeneous model (4.55 and 5.27, respectively [P < 0.001], data not shown).
NH–COaLA accurately estimates branch lengths.—The ability of NH–NS COaLA to accurately estimate branch lengths was assessed (See Supplementary Information). Supplementary Figure S3 shows that NH–NS COaLA has similar performances to an H–S LG+Fobs model without any bias.
NH–COaLA efficiently fits data.—The H–S, H–NS, and NH–NS sequence evolution models were compared using the BIC, which aims at identifying the best compromise between fit of the model to the data (likelihood) and small number of parameters. We used the 272 most heterogeneous alignments (out of 5000 simulations), whose compositional heterogeneity, measured by the fraction of statistically significant Bowker tests, is comparable with what can be observed in real data (See “Materials and Methods” section).
The NH–NS LG+COaLA model with one or two parameters per branch outperforms, according to the BIC, the H–S LG+Fopt model in 53% and 70% of the 272 cases, respectively. Furthermore, the H–NS model is better than the H–S model only in 10% of the cases and is better than the NH–NS LG+COaLA model with one and two parameters per branch only in 11% and 5% of the cases, respectively. These results illustrate the excellent fit of nonhomogeneous evolutionary models to compositionally heterogeneous sequences.
Model misspecifications.—If one considers two Markovian transition probability matrices, P1 = eQ1l1 and P2 = eQ2l2, modeling the evolutionary process along two neighboring branches of length l1 and l2, the transition probability matrix P′ modeling evolution along the combined branch can be expressed as P′ = P1P2. In a recent article, Sumner et al. (2012b) demonstrated that the GTR model (Yang 2006), as well as several other substitution models in the context of DNA sequences, lacks closure under matrix multiplication. More precisely, if P1 and P2 are two GTR transition probability matrices with different exchangeabilities and/or equilibrium frequencies, their product P′ is not a GTR transition probability matrix, but belongs to a different model class. However, if P1 and P2 have identical exchangeabilities and equilibrium frequencies but differ by their branch lengths only, their product P′ is a GTR probability matrix.
These considerations have a direct bearing on our ability to infer evolutionary parameters. If one assumes that the data have been generated through a succession of GTR matrices that differ in their exchangeabilities and/or equilibrium frequencies along branches of the phylogeny, then a GTR-based model is bound to make some error, and a proper model to perform inference would be a model that has the closure property. In contrast, if one assumes that the data have been generated through a succession of GTR matrices that differ in their branch lengths only, then the closure property ensures that a H–S GTR-based model can correctly estimate the parameters of the model provided there is enough data.
It is of interest to determine whether the model considered here, a single empirical exchangeability matrix of the GTR-based LG model (Le and Gascuel 2008) with branch-wise equilibrium frequencies lacks closure under multiplication and is, as a result, affected by the type of misspecification studied in Sumner et al. (2012b).
To verify this point, and to quantify the amount of misspecification affecting our approach, we performed an experiment similar to Sumner et al. (2012a). These authors measured how much the nonclosure of the GTR model affects the estimation of transition probabilities for DNA sequences. In our case, two LG substitution matrices P1 and P2 were employed, with the equilibrium frequencies π1 and π2 of Q1 and Q2 drawn from the same Dirichlet distribution as presented above, modeling the succession of two independent substitution models along two successive branches. We then computed the product P′ = P1P2, with both l1 and l2 equal to 0.5 substitutions/site. Finally, we computed the equilibrium frequencies of another substitution matrix 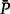 with the same LG exchangeability matrix that minimized its distance to P′ using the Euclidean distance between matrices:
with the same LG exchangeability matrix that minimized its distance to P′ using the Euclidean distance between matrices:
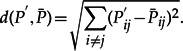 |
This distance measures the amount of misspecification caused by the nonclosure property of the model. If the minimization procedure finds equilibrium frequencies so that this distance is zero, the model has the desired closure property. If not, the model is nonclosed under multiplication and the distance reflects the amount of errors in the estimation of transition probabilities due to the nonclosure property. We ran 1000 simulations and, for each simulation, we measured both the average percentage error and the average absolute difference between corresponding transition probabilities of P′ and  . We observed that the mean distance
. We observed that the mean distance 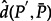 is 0.02. Furthermore, the mean percentage error in transition probabilities is 5.0% and the mean absolute difference is 7 ×10−4. These results show that, like the GTR model for nucleotide sequence evolution (Sumner et al. 2012a), our model of amino acid sequence evolution based on a fixed LG exchangeability matrix with optimized equilibrium frequencies lacks closure under multiplication. In both cases, it remains to be seen to what extent this creates a problem for evolutionary inference of parameters, phylogenetic trees, and ancestral sequences. It will be further interesting to study how H–S versus NH–NS models cope with such model misspecifications. Nonetheless, despite the nonclosure property of the model employed here, NH–NS COaLA brings strong benefit in terms of data fitting or inference of ancestral frequencies and sequences in comparison with the H–S model.
is 0.02. Furthermore, the mean percentage error in transition probabilities is 5.0% and the mean absolute difference is 7 ×10−4. These results show that, like the GTR model for nucleotide sequence evolution (Sumner et al. 2012a), our model of amino acid sequence evolution based on a fixed LG exchangeability matrix with optimized equilibrium frequencies lacks closure under multiplication. In both cases, it remains to be seen to what extent this creates a problem for evolutionary inference of parameters, phylogenetic trees, and ancestral sequences. It will be further interesting to study how H–S versus NH–NS models cope with such model misspecifications. Nonetheless, despite the nonclosure property of the model employed here, NH–NS COaLA brings strong benefit in terms of data fitting or inference of ancestral frequencies and sequences in comparison with the H–S model.
Tests on Phylogenomic Data Sets
COA of the observed frequencies.—The concatenated alignments of yeast, archaea, and eocyte sequences are studied here (the fourth “Three domains” alignment is analyzed later). For each of these alignments, a matrix of observed amino acid frequencies was computed and used to compute a COA. For the yeast data set, the first and second axes account, respectively, for 63% and 32% of the total variance initially present in the data, meaning that the plane defined by the first two factors of the COA reflect 95% of the total compositional variance in the data (Supplementary Fig. S1b). In the eocyte data set, the first three axes account, respectively, for 46%, 24%, and 9% (Supplementary Fig. S1c), while their contribution is 43%, 28%, and 10% (Supplementary Fig. S1d), respectively, in the archaea data set. These variation axes are strongly linked to biological properties that influence the global amino acid composition of proteomes. We observed that the first axis of the COA highly correlates with the G+C content of third codon positions (GC3) of each yeast species (r = −0.89). In the eocyte data set, the first factor discriminates eukaryotic from archaeal/bacterial species. The second factor highly correlates with the genomic G+C content (r = 0.9) and the third factor is strongly linked to OGT (r = 0.88). Finally, in the archaeal data set, the first and second axes highly correlate with the genomic G+C content (r = 0.74) and the OGT (r = 0.83), as previously reported (Groussin and Gouy 2011).
NH–COaLA fits the data better than homogeneous models.— We applied the COaLA model to these biological data sets to estimate the ML values of branch lengths and evolutionary parameters. Table 1 summarizes the results. In all cases, according to the BIC, the NS COaLA model fits the sequence data better than the best homogeneous and stationary model (LG+Fopt). For the yeast data set, the H–NS model is the best model in terms of BIC values. It is interesting to note that the COaLA model, used in the homogeneous case with fewer parameters, provides a better fit than the classic LG+Fopt model. Concerning archaea, the best model is the NH–NS LG+COaLA[3] model. However, only two axis positions per branch were necessary to best fit the eocyte data set. It is surprising to observe that in this case the LG+Fobs model fits the data less well than the LG model, where the vector of equilibrium frequencies is the one empirically estimated by (Le and Gascuel 2008), on several biological data sets. The exact same final likelihood was also obtained using PhyML, which indicates that this unexpected result is not a problem specifically found by BppML. We hypothesize that this is because the observed frequencies are not ML estimates and potentially lead to worse likelihood scores. Finally, we found that using AIC instead of BIC for model selection (see “Materials and Methods” section) systematically leads to the choice of overparameterized models, illustrating the property of BIC to more heavily penalize parameter-rich models. For instance, with the archaea data set, AIC selects the NH–NS LG+COaLA[7] model, where the seventh axis of the COA only represents 1.4% of the total compositional variance of the data.
Table 1.
Assessing the fit to the data between several evolutionary models
| Data set | Process | Model | lnL | nbr Param | BIC |
|---|---|---|---|---|---|
| Yeast |
H–S |
LG | −299506.1 | 1 | 599022.9 |
| LG+Fobs | −298702.5 | 1 | 597415.7 | ||
| LG+Fopt | −298575.3 | 20 | 597363.7 | ||
| LG+COaLA[1] |
−298667.9 |
2 |
597357.1 |
||
|
H–NS |
LG+COaLA[1]
|
−298 595.4 |
3 |
597 222.8 |
|
| NH–NS |
LG+F | −297621.7 | 286 | 598290.3 | |
| LG+COaLA[1] | −298543.5 | 16 | 597257.5 | ||
| LG+COaLA[2] | −298505.3 | 31 | 597340.9 | ||
| LG+COaLA[3] | −298500.6 | 46 | 597491.3 | ||
| LG+COaLA[4] | −298491.7 | 61 | 597633.3 | ||
| LG+COaLA[5] |
−298486.4 |
76 |
597782.5 |
||
| Eocyte |
H–S | LG | −277967.3 | 1 | 555943.2 |
| LG+Fobs | −278064.5 | 1 | 556137.6 | ||
| LG+Fopt | −277444.0 | 20 | 555060.3 | ||
| LG+COaLA[1] | −277877.0 | 2 | 555771.2 | ||
| H–NS | LG+COaLA[1] | −277695.3 | 3 | 555416.4 | |
|
NH–NS |
LG+F | −274279.4 | 1502 | 561501 | |
| LG+COaLA[1] | −277263.8 | 80 | 555216.9 | ||
| LG+COaLA[2] | −276 483.0 | 159 | 554 336 | ||
| LG+COaLA[3] | −276253.3 | 238 | 554557.3 | ||
| LG+COaLA[4] |
−276090.3 |
317 |
554912 |
||
| LG+COaLA[5] |
−275946.5 |
396 |
555305.1 |
||
| Archaea | H–S | LG | −340369.1 | 1 | 680747.3 |
| LG+Fobs | −340047.3 | 1 | 680103.7 | ||
| LG+Fopt | −339217.9 | 20 | 678618.7 | ||
| LG+COaLA[1] | −339887.8 | 2 | 679793.9 | ||
| H–NS | LG+COaLA[1] | −339865.7 | 3 | 679758.8 | |
| NH–NS | LG+F | — | 1236 | — | |
| LG+COaLA[1] | −338985.4 | 66 | 678574.5 | ||
| LG+COaLA[2] | −338237.7 | 131 | 677673.7 | ||
| LG+COaLA[3] | −337 932.3 | 196 | 677 657.4 | ||
| LG+COaLA[4] | −337721.0 | 261 | 677829.4 | ||
| LG+COaLA[5] | −337541.1 | 326 | 678064.1 |
Bold lines highlight the best model according to the BIC.
With respect to the number of parameters involved, the COaLA model strongly reduces the dimension of the evolutionary model. Consequently, COaLA is fast and saves a large amount of computing time: with the yeast data set containing eight species, 5 h 32 min were necessary to compute the likelihood with 19 equilibrium frequencies per branch in comparison with 2 h 38 m for the NH–NS COaLA[1] model and with 16 min 14 s for the H–NS COaLA[1] model. Concerning the eocyte data set, the model with 19 equilibrium frequencies per branch required about 522 h of calculation to converge to the ML optimum. Comparatively, the best COaLA model only required about 40 h of calculation. For the two other data sets (archaea and three domains), we cannot provide a precise comparison as the 19 equilibrium frequencies per branch model was stopped after 1 month of calculation before reaching the ML optimum. The best COaLA models used about 26 and 18 h of calculation, respectively, with a very stringent threshold of 10−6 below which convergence is accepted.
Tests on Single Gene Data Sets
NH–COaLA is overparameterized for single-gene alignments.—From the 24 methanogenic archaeal genomes, we built all homologous gene families (see “Materials and Methods” section) and conserved the unicopy and nearly universal families, leading to 535 genes. For each of these gene families and their corresponding ML phylogenetic trees (see “Materials and Methods” section), we compared the performance of the NH–NS LG+COaLA model with the best H–S model (LG+Fopt) regarding the fit to the data. Only in 19 cases did the NH–NS LG+COaLA[1] model with the optimization of one axis position per branch outperform the homogeneous model, according to the BIC criterion. However, the NH–NS LG+COaLA[1] model outperformed the homogeneous model in 172 cases according to AIC. Overall, these results indicate that with small single-gene alignments, COaLA may model the evolutionary process more accurately than homogeneous models but is generally overparameterized, calling for future improvements (see “Discussion” section). However, in all estimations, we did not observe unconventional frequencies for rare amino acids, showing that the way COaLA copes with the problem of completely absent amino acids (see “Materials and Methods” section and Supplementary Information) is robust.
NH–COaLA reconstructs ancestral sequences more accurately.—In studies using ancestral sequence reconstruction and resurrection, major biological conclusions can sometimes rely on one or few amino acid differences between ancient or between extant and ancient proteins (Finnigan et al. 2012; Huang et al. 2012). However, these substitutions may differ depending on the model employed. Here, we attempt to test whether the NH–NS COaLA model can lead to better ancestral sequence reconstruction, at the single gene level, in comparison with the H–S LG+Fopt model.
We simulated the evolution of 535 gene families using the parameter values (sequence length, tree shape, branch lengths, and amino acid equilibrium frequencies) given by the 535 alignments of methanogenic archaea described above. We ran NH–NS COaLA[1] and H–S LG+Fopt on these 535 alignments simulated in a nonhomogeneous fashion and then reconstructed the ancestral sequences with BppAncestor for all internal nodes (see Appendix). These inferred sequences were then compared with a LG distance (computed by ML) to their true corresponding sequences recorded during the simulation procedure. For each of the 535 simulations, we computed the average distance for all nodes. Figure 4 shows the distribution of the 535 mean LG distances for the two models. First, the NH–NS COaLA model outperforms the best H–S model (LG+Fopt) regarding the accuracy of ancestral sequence reconstruction. Second, the mean of the distribution of the LG+Fopt model is 0.25 substitution/site, meaning that every four sites on average, an amino acid difference exists between the inferred and the true sequence with the H–S approach. In contrast, the mean distance is reduced to 0.06 with the NH–NS approach of ancestral sequence reconstruction.
NH–COaLA Confirms the Mesophilic State of the Last Universal Common Ancestor
This section is focused on the three-domains data set used by Boussau et al. (2008) to study the early pattern of adaptation to temperature. Given the results presented above concerning the performances of COaLA, we used the NH–NS approach to infer the ancestral environmental temperatures over the universal Tree of Life. We first demonstrate that COaLA accurately fits the data with the concatenate alignment. Finally, we confirm the results regarding the early adaptation to environmental temperature obtained by Boussau et al. (2008) with a different NH–NS model.
Capturing the nonhomogeneity of the data.—We first determined the best model. Supplementary Table S1 shows that the NH–NS LG+COaLA[2] model better fits the data than the other models according to BIC. Given the ML estimates of the evolutionary parameters obtained with this model, 200 simulated alignments of similar size as the original alignment were produced to check the capability of COaLA to capture the heterogeneity present in the data. On average, 35% of the Bowker pairwise tests were significant after the Holm–Bonferroni correction, in comparison with 38% significant tests observed on the original alignment. Consequently, according to this measure, 92% of the original compositional heterogeneity is captured by the model, even though only two parameters per branch are used. When the NH–NS LG+COaLA[3] model is used, thereby optimizing three axis positions per branch instead of two, simulated alignments have on average a higher level of heterogeneity than the original data (41% vs. 38%, respectively). The BIC criterion is therefore conservative and favors a model with fewer parameters, even if it does not capture all the heterogeneity in the data.
The COaLA model confirms the early pattern of adaptation to temperature.—Boussau et al. (2008) proposed that the Last Universal Common Ancestor (LUCA) lived in a mesophilic environment in opposition to its two descendants, inferred as being thermophilic organisms. They used the strong relationship that exists between either the G+C content in rRNAs or the amino acid contents in proteins and the OGT of bacteria and archaea. This relation allows constructing molecular thermometers (Galtier and Lobry 1997; Boussau et al. 2008; Groussin and Gouy 2011) that give estimates of environmental temperatures from ancestral amino acid or nucleotide compositions. With nonhomogeneous models of evolution, Boussau et al. (2008) inferred the ancestral compositions for all nodes of a universal tree and estimated the corresponding OGTs with the molecular thermometers. For proteins, these inferences were realized with the NH–NS CAT-BP model (Blanquart and Lartillot 2008) in the Bayesian framework. Since COaLA and CAT-BP are implemented in different frameworks and model differently the nonhomogeneity of the evolutionary process, it is interesting to determine whether they give similar estimations of ancestral equilibrium frequencies and OGTs. With CAT-BP, Boussau et al. (2008) inferred that LUCA lived at 20°C [0–37°C] and the ancestors of bacteria and archaea+eukarya at 69°C [64–75°C], and 55°C [45–65°C], respectively. NH–NS COaLA also recovered a signal for a parallel adaptation to high temperatures from LUCA to its two descendants (Wilcoxon test, P < 0.001), with estimates that are very close to the ones obtained with CAT-BP. Thus, the ancestral OGTs are 34°C [24–44°C], 69°C [64–76°C], and 57°C [46–70°C] for LUCA, the ancestor of bacteria and the ancestor of archaea+eukarya, respectively. The 95% confidence intervals were computed with a nonparameteric bootstrap procedure. It is interesting to observe that with two different approaches, the COaLA and CAT-BP models converge toward a similar phylogenetic signal for the evolution of amino acid frequencies during early life and quantitatively similar estimates of ancestral compositions and temperatures.
Discussion
When phylogenetic data are consistent with the assumption of compositional homogeneity, homogeneous models are often more suited for model-based phylogenetic analyses than nonhomogeneous models. In these cases, it is advisable to use a HS model where the 20 equilibrium frequencies are fitted to the data by likelihood optimization (i.e., use the “+Fopt” model). Indeed, for all biological data sets investigated here, the gains of likelihood were significant when the 19 free equilibrium frequencies were estimated by ML. To our knowledge, BppML is the only phylogenetic program capable of generating ML estimates of the equilibrium amino acid frequencies (most other phylogenetic programs that we have checked appear to assume that the equilibrium amino acid frequencies are either equal to the equilibrium frequencies of the empirical model or to the observed amino acid frequencies).
Following Galtier and Gouy (1998), Galtier et al. (1999), Foster (2004), Jermiin et al. (2004), Gowri-Shankar and Rattray (2007), Blanquart and Lartillot (2008), and Boussau et al. (2008), we confirm the importance of using a nonhomogeneous and nonstationary model to estimate evolutionary parameters when compositional heterogeneity is present in the data. The COaLA model appears to be very efficient for the estimation of ancestral frequencies and to better fit heterogeneous data than classic NH or H models.
COaLA is flexible in the sense that it may be employed either as an H–S, H–NS, or NH–NS model. In the NH–NS approach, COaLA is a branch-wise heterogeneous model that assumes that (i) each branch is characterized by its own set of equilibrium frequencies and (ii) all branches share a common exchangeability matrix. Contrarily to Galtier and Gouy (1998) who used G+C equilibrium content as branch-wise variable irrespective of the nucleotide sequence data set under study, for each protein data set, the COaLA model constructs the branch-wise variables that summarize most of the variance in the data set under study. Therefore, the nature of the branch-wise variables differs among data sets. Previous authors mentioned the possibility that such branch-wise models may be overparameterized (Foster 2004; Blanquart and Lartillot 2006), as they assume that, at each speciation node, equilibrium frequencies evolve toward different positions in the space of frequencies. COaLA performs an efficient reduction of the parameter space used to optimize branch stationary frequencies. In all phylogenomic experiments, we showed that the model is very efficient at estimating evolutionary parameters such as ancestral frequencies or branch lengths. Even with rather small (5000 sites) phylogenomic data sets in the simulation experiments, and when the heterogeneity is similar to what one can observe with real data, the model is on average better than a homogeneous model. Overparameterization by the branch-wise approach in comparison with a homogeneous approach was detected in only 30% of the cases according to BIC with simulation experiments of sequence alignments having levels of compositional heterogeneity comparable with empirical data. With real data, three out of the four phylogenomic data sets were more efficiently fitted by the NH–NS branch-wise model than by other models. With more and more biological data coming from many and diverse sequencing projects, the data set sizes should increase as well. We observed that large, concatenated data sets are less frequently overparameterized by NH–NS models than single-gene data sets. This suggests that overparameterization may become less of an issue for data sets of increasing size.
Besides, we also demonstrated that the use of branch-heterogeneous models is crucial to infer accurate ancestral sequences. This result may be especially relevant for protein resurrection experiments where the accuracy of ancestral sequence reconstruction is crucial. Consequently, we strongly recommend the use of nonhomogeneous models for such studies when homologous sequences are observed to be composition-ally different.
In many studies, NH–NS models were proved to better capture the evolutionary signal and to improve our knowledge concerning various biological questions (Herbeck et al. 2005; Nabholz et al. 2011; Boussau and Gouy 2012). Using NH–NS protein models in the Bayesian framework, Boussau et al. (2008) proposed that LUCA was a mesophilic organism and that its two descendants independently adapted to higher temperatures. This nonparsimonious scenario raised questions about possible biases in the models used to infer ancestral compositions. In their study, Boussau et al. (2008) extensively tested that their prediction was not the result of a bias in the model employed. They showed that this parallel adaptation to high temperatures was also recovered with different universal topologies and in the presence or absence of Eukaryotes. In this study, we confirmed this evolutionary pattern of adaptation to OGT with NH–NS COaLA using a ML rather than a Bayesian approach.
The COaLA model presented here is implemented in the ML framework but could be easily defined in a Bayesian context. Further theoretical work might improve the fit of the COaLA model to protein sequences. First, to further reduce the number of free parameters, a discretized version of the model could be developed. As already shown in Boussau and Gouy (2006) for nucleotide sequences, the model could propose a subset of fixed or optimized axis positions per branch, making it less flexible. For each branch, the best of the possible axis positions would be retained and could be used to compute the likelihood. This procedure could be especially relevant for single-gene alignments, where overparameterization was detected in this study. Second, the time-wise nonhomogeneity of the model could be extended with site-wise nonhomogeneity. Currently, the CAT-BP model (Blanquart and Lartillot 2008), in the Bayesian context, is able to combine the modeling of compositional variations both over time and over sites. However, the major drawback of this model is its huge computational cost, underlining the need for a more efficient model. To model the variation of evolutionary processes among sites, several approaches are already available, such as the mixture models implemented by Le et al. (2008b), or the empirical profile mixture models developed by Le et al. (2008a) (analogous to the CAT model [Lartillot and Philippe 2004] available in the Bayesian framework). Therefore, COaLA could be extended to the use of mixture models for which the equilibrium frequencies of each category would be modulated by the equilibrium frequencies of the branch under consideration. With such site and branch heterogeneity, COaLA would better take into account the variation of substitution processes depending on the localization of the residue in the protein 3D structure or depending on amino acid biochemical properties.
Supplementary Material
Supplementary information can be found in the Dryad data repository at http://datadryad.org, doi:10.5061/dryad.7h66k.
Funding
This work is a contribution to the project Ancestrome supported by the Agence Nationale de la Recherche (ANR-10-BINF-01-01).
Acknowledgments
Sincere thanks to Lars Jermiin, Greg Fournier, and two anonymous reviewers for their suggestions and comments which greatly improved this article. The authors are also particularly thankful to Julien Dutheil, Anne-Béatrice Dufour, Jean Thioulouse, and all other members of the Bioinformatics and Evolutionary Genomics team for suggestions and fruitful discussions.
Appendix
Correspondence Analysis
We summarize here the principles used to compute a COA, which is necessary in order to understand the COaLA model. For more details about the specific properties of a COA, see (Greenacre 1984).
Let I and J be the number of rows and columns, respectively, of the matrix NI×J with elements nij, where nij corresponds to the observed frequency of amino acid j in sequence i, I corresponds to the number of sequences in the alignment (i = 1,...,I), and J corresponds to the number of different amino acids in the alignment (j = 1 ,...,J). Let ni• and n•j be the sum of the ith row and jth column, respectively, and n denotes the total sum of NI×J:
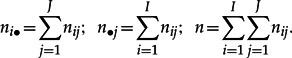 |
The matrix PI×J of relative frequencies pij is then derived, so that:
where pi• and p•j represent the row and column weights, respectively.
Let DI×I and DJ×J be the following diagonal matrices:
The matrix ZI×J is then computed:
with:
The general term of ZI×J is
ZI×J is the table analyzed by the COA and represents the distance between expected under independence and observed frequencies.
To obtain the eigen elements of the COA, the matrix H containing the χ2 distances is computed:
with
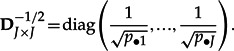 |
Next, HJ×J is diagonalized to determine its eigenvalues and eigenvectors. The k first eigenvalues in decreasing order are conserved and stored in Λk. The k first associated eigenvectors, which are orthonormal, are stored as columns in UJ×k. UJ×k possesses J rows, k columns, and verifies Uk×JT UJ×k = Ik×k.
The row coordinates are computed with:
The columns of RI×k are the row coordinates. The columns' coordinates may also be computed:
The columns of CJ×k represent the column coordinates.
Once the COA is computed from a particular set of species, it may be useful to add a new row containing a set of values, where observed amino acid frequencies coming from another species. Thus, this vector of frequencies (F1×J) defines a point in the space of the row profiles and it is possible to represent that point in the new space by projecting the point onto the space. To do so, the coordinates of the new vector in the new space can be calculated:
Conversely, from a set of row coordinates LF′′, one can calculate a corresponding set of absolute frequencies F1×J′ in the original space using the matrix of column coordinates and accounting for the column weights (row weights are always equal to 1):
Using this relation, from any set of coordinates in the new space, one can generate its corresponding set of frequencies in the original space of species profiles. It is worthwhile to note that one coordinate along the first axis of most variance is enough to propose a set of corresponding frequencies.
Ancestral Sequence Reconstruction
We describe here how ancestral sequences are computed with a marginal reconstruction (Yang et al. 1995), either with a homogeneous or branch-heterogeneous model. In the following, we refer to the notations of figure 1 of Boussau and Gouy (2006). The BppAncestor program was used to compute for each site and each inner node the posterior probabilities of each amino acid. The amino acid having the highest posterior probability is then retained in the ancestral sequence.
Consider the inner node C in figure 1 of (Boussau and Gouy 2006). The marginal posterior probability of the state v is
where P(Data) is the total likelihood L of the site. Using the upper conditional likelihoods introduced by Boussau and Gouy (2006), the joint probability of the data and having the state v at node C is
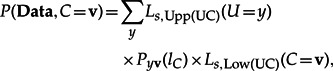 |
where
Ls,Low(UC)(C = v) is the lower conditional probability of having v at node C.
Pyv(lC) is the transition probability for a state y to be substituted to v along a branch of length lC
Ls,Upp(UC)(U = y) is the upper conditional likelihood of having the state y at the parent node U.
Ls,Upp(UC)(U = y) can be seen as the joint probability of the data excluding the part under node C and having state y at node U. It is recursively defined (Boussau and Gouy 2006) by
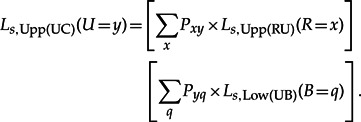 |
Thus, as mentionned in the “Materials and Methods” section of Boussau et al. (2008):
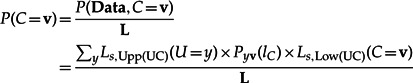 |
References
- Ababneh F., Jermiin L.S., Ma C., Robinson J. Matched-pairs tests of homogeneity with applications to homologous nucleotide sequences. Bioinformatics. 2006;22:1225–1231. doi: 10.1093/bioinformatics/btl064. [DOI] [PubMed] [Google Scholar]
- Adachi J., Hasegawa M. MOLPHY version 2.3: programs for molecular phylogenetics based on maximum likelihood. Comput. Sci. Monogr. 1996;28:1–150. [Google Scholar]
- Akaike H. A new look at the statistical model identification. IEEE Trans. Autom. Contr. ACM. 1974;19:716–723. [Google Scholar]
- Blanquart S., Lartillot N. A Bayesian compound stochastic process for modeling nonstationary and nonhomogeneous sequence evolution. Mol. Biol. Evol. 2006;23:2058–2071. doi: 10.1093/molbev/msl091. [DOI] [PubMed] [Google Scholar]
- Blanquart S., Lartillot N. A site- and time-heterogeneous model of amino acid replacement. Mol. Biol. Evol. 2008;25:842–858. doi: 10.1093/molbev/msn018. [DOI] [PubMed] [Google Scholar]
- Bollback J.P. Bayesian model adequacy and choice in phylogenetics. Mol. Biol. Evol. 2002;19:1171–1180. doi: 10.1093/oxfordjournals.molbev.a004175. [DOI] [PubMed] [Google Scholar]
- Boussau B., Blanquart S., Necsulea A., Lartillot N., Gouy M. Parallel adaptation to high temperature in the archaean eon. Nature. 2008;456:942–945. doi: 10.1038/nature07393. [DOI] [PubMed] [Google Scholar]
- Boussau B., Gouy M. Efficient likelihood computations with nonreversible models of evolution. Syst. Biol. 2006;55:756–768. doi: 10.1080/10635150600975218. [DOI] [PubMed] [Google Scholar]
- Boussau B., Gouy M. What genomes have to say about the evolution of the Earth. Gondwana Res. 2012;21:483–494. [Google Scholar]
- Bowker A.H. A test for symmetry in contingency tables. J. Am. Stat. Assoc. 1948;43:572–574. doi: 10.1080/01621459.1948.10483284. [DOI] [PubMed] [Google Scholar]
- Brochier-Armanet C., Forterre P., Gribaldo S. Phylogeny and evolution of the Archaea: one hundred genomes later. Curr. Opion. Microbiol. 2011;14:274–281. doi: 10.1016/j.mib.2011.04.015. [DOI] [PubMed] [Google Scholar]
- Castresana J. Selection of conserved blocks from multiple alignments for their use in phylogenetic analysis. Mol. Biol. Evol. 2000;17:540–552. doi: 10.1093/oxfordjournals.molbev.a026334. [DOI] [PubMed] [Google Scholar]
- Cox C.J., Foster P.G., Hirt R.P., Harris S.R., Embley T.M. The archaebacterial origin of eukaryotes. Proc. Natl Acad. Sci. U. S. A. 2008;105:20356–20361. doi: 10.1073/pnas.0810647105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delsuc F., Brinkmann H., Chourrout D., Philippe H. Tunicates and not cephalochordates are the closest living relatives of vertebrates. Nature. 2006;439:965–968. doi: 10.1038/nature04336. [DOI] [PubMed] [Google Scholar]
- Douzery E.J.P., Snell E.A., Bapteste E., Delsuc F., Philippe H. The timing of eukaryotic evolution: does a relaxed molecular clock reconcile proteins and fossils? Proc. Natl Acad. Sci. U. S. A. 2004;101:15386–15391. doi: 10.1073/pnas.0403984101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dutheil J., Boussau B. Non-homogeneous models of sequence evolution in the Bio++ suite of libraries and programs. BMC Evol. Biol. 2008;8:255. doi: 10.1186/1471-2148-8-255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dutheil J., Gaillard S., Bazin E., Glémin S., Ranwez V., Galtier N., Belkhir K. Bio++: a set of C++ libraries for sequence analysis, phylogenetics, molecular evolution and population genetics. BMC Bioinform. 2006;7:188. doi: 10.1186/1471-2105-7-188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dutheil J.Y., Galtier N., Romiguier J., Douzery E.J.P., Ranwez V., Boussau B. Efficient selection of branch-specific models of sequence evolution. Mol. Biol. Evol. 2012;29:1861–1874. doi: 10.1093/molbev/mss059. [DOI] [PubMed] [Google Scholar]
- Edgar R.C. MUSCLE: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 2004;32:1792–1797. doi: 10.1093/nar/gkh340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J. Evolutionary trees from DNA sequences: a maximum likelihood approach. J. Mol. Evol. 1981;17:368–376. doi: 10.1007/BF01734359. [DOI] [PubMed] [Google Scholar]
- Felsenstein J., editor. Inferring phylogenies. Sunderland (MA): Sinauer Associates; 2004. [Google Scholar]
- Finnigan G.C., Hanson-Smith V., Stevens T.H., Thornton J.W. Evolution of increased complexity in a molecular machine. Nature. 2012;481:360–364. doi: 10.1038/nature10724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foster P.G. Modeling compositional heterogeneity. Syst. Biol. 2004;53:485–495. doi: 10.1080/10635150490445779. [DOI] [PubMed] [Google Scholar]
- Galtier N., Gouy M. Inferring phylogenies from DNA sequences of unequal base compositions. Proc. Natl Acad. Sci. U. S. A. 1995;92:11317–11321. doi: 10.1073/pnas.92.24.11317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galtier N., Gouy M. Inferring pattern and process: maximum-likelihood implementation of a nonhomogeneous model of DNA sequence evolution for phylogenetic analysis. Mol. Biol. Evol. 1998;15:871–879. doi: 10.1093/oxfordjournals.molbev.a025991. [DOI] [PubMed] [Google Scholar]
- Galtier N., Lobry J.R. Relationships between genomic G+C content, RNA secondary structures, and optimal growth temperature in prokaryotes. J. Mol. Evol. 1997;44:632–636. doi: 10.1007/pl00006186. [DOI] [PubMed] [Google Scholar]
- Galtier N., Tourasse N., Gouy M. A nonhyperthermophilic common ancestor to extant life forms. Science. 1999;283:220–221. doi: 10.1126/science.283.5399.220. [DOI] [PubMed] [Google Scholar]
- Gaucher E.A., Govindarajan S., Ganesh O.K. Palaeotemperature trend for Precambrian life inferred from resurrected proteins. Nature. 2008;451:704–708. doi: 10.1038/nature06510. [DOI] [PubMed] [Google Scholar]
- Gowri-Shankar V., Rattray M. A reversible jump method for Bayesian phylogenetic inference with a nonhomogeneous substitution model. Mol. Biol. Evol. 2007;24:1286–1299. doi: 10.1093/molbev/msm046. [DOI] [PubMed] [Google Scholar]
- Greenacre M. Theory and applications of correspondence analysis. London: Academic Press; 1984. [Google Scholar]
- Groussin M., Gouy M. Adaptation to environmental temperature is a major determinant of molecular evolutionary rates in Archaea. Mol. Biol. Evol. 2011;28:2661–2674. doi: 10.1093/molbev/msr098. [DOI] [PubMed] [Google Scholar]
- Guindon S., Gascuel O. A simple, fast, and accurate algorithm to estimate large phylogenies by maximum likelihood. Syst. Biol. 2003;52:696–704. doi: 10.1080/10635150390235520. [DOI] [PubMed] [Google Scholar]
- Harms M.J., Thornton J.W. Analyzing protein structure and function using ancestral gene reconstruction. Curr. Opin. Struct. Biol. 2010;20:360–366. doi: 10.1016/j.sbi.2010.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasegawa M., Hashimoto T. Ribosomal RNA trees misleading? Nature. 1993;361:23. doi: 10.1038/361023b0. [DOI] [PubMed] [Google Scholar]
- Herbeck J.T., Degnan P.H., Wernegreen J.J. Nonhomogeneous model of sequence evolution indicates independent origins of primary endosymbionts within the Enterobacteriales (Gamma-Proteobacteria) Mol. Biol. Evol. 2005;22:520–532. doi: 10.1093/molbev/msi036. [DOI] [PubMed] [Google Scholar]
- Ho S.Y.W., Jermiin L.S. Tracing the decay of the historical signal in biological sequence data. Syst. Biol. 2004;53:623–637. doi: 10.1080/10635150490503035. [DOI] [PubMed] [Google Scholar]
- Hobbs J.K., Shepherd C., Saul D.J., Demetras N.J., Haaning S., Monk C.R., Daniel R.M., Arcus V.L. On the origin and evolution of thermophily: reconstruction of functional precambrian enzymes from ancestors of Bacillus. Mol. Biol. Evol. 2011;29:825–835. doi: 10.1093/molbev/msr253. [DOI] [PubMed] [Google Scholar]
- Holm S. A simple sequentially rejective multiple test procedure. Scand. J. Stat. 1979;6:65–70. [Google Scholar]
- Huang R., Hippauf F., Rohrbeck D., Haustein M., Wenke K., Feike J., Sorrelle N., Piechulla B., Barkman T.J. Enzyme functional evolution through improved catalysis of ancestrally nonpreferred substrates. Proc. Natl Acad. Sci. U. S. A. 2012;109:2966–2971. doi: 10.1073/pnas.1019605109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huelsenbeck J.P., Ronquist F., Nielsen R., Bollback J.P. Bayesian inference of phylogeny and its impact on evolutionary biology. Science. 2001;294:2310–2314. doi: 10.1126/science.1065889. [DOI] [PubMed] [Google Scholar]
- Jayaswal V., Ababneh F., Jermiin L.S., Robinson J. Reducing model complexity of the general Markov model of evolution. Mol. Biol. Evol. 2011a;28:3045–3059. doi: 10.1093/molbev/msr128. [DOI] [PubMed] [Google Scholar]
- Jayaswal V., Jermiin L.S., Poladian L., Robinson J. Two stationary nonhomogeneous Markov models of nucleotide sequence evolution. Syst. Biol. 2011b;60:74–86. doi: 10.1093/sysbio/syq076. [DOI] [PubMed] [Google Scholar]
- Jayaswal V., Jermiin L.S., Robinson J. Estimation of phylogeny using a general Markov model. Evol. Bioinform. Online. 2005;1:62–80. [PMC free article] [PubMed] [Google Scholar]
- Jayaswal V., Robinson J., Jermiin L. Estimation of phylogeny and invariant sites under the general Markov model of nucleotide sequence evolution. Syst. Biol. 2007;56:155–162. doi: 10.1080/10635150701247921. [DOI] [PubMed] [Google Scholar]
- Jermiin L.S., Ho S.Y.W., Ababneh F., Robinson J., Larkum A.W.D. The biasing effect of compositional heterogeneity on phylogenetic estimates may be underestimated. Syst. Biol. 2004;53:638–643. doi: 10.1080/10635150490468648. [DOI] [PubMed] [Google Scholar]
- Jermiin L.S., Jayaswal V., Ababneh F., Robinson J. Phylogenetic model evaluation. In: Keith J., editor. Bioinformatics—Volume I: data, sequences analysis and evolution. Totowa (NJ): Humana Press; 2008. pp. 331–363. [Google Scholar]
- Jones D.T., Taylor W.R., Thornton J.M. The rapid generation of mutation data matrices from protein sequences. Comput. Appl. Biosci. 1992;8:275–282. doi: 10.1093/bioinformatics/8.3.275. [DOI] [PubMed] [Google Scholar]
- Lake J.A. Reconstructing evolutionary trees from DNA and protein sequences: paralinear distances. Proc. Natl Acad. Sci. U. S. A. 1994;91:1455–1459. doi: 10.1073/pnas.91.4.1455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lartillot N., Philippe H. A Bayesian mixture model for across-site heterogeneities in the amino acid replacement process. Mol. Biol. Evol. 2004;21:1095–2004. doi: 10.1093/molbev/msh112. [DOI] [PubMed] [Google Scholar]
- Le S.Q., Gascuel O. An improved general amino acid replacement matrix. Mol. Biol. Evol. 2008;25:1307–1320. doi: 10.1093/molbev/msn067. [DOI] [PubMed] [Google Scholar]
- Le S.Q., Gascuel O., Lartillot N. Empirical profile mixture models for phylogenetic reconstruction. Bioinformatics. 2008a;24:2317–2323. doi: 10.1093/bioinformatics/btn445. [DOI] [PubMed] [Google Scholar]
- Le S.Q., Lartillot N., Gascuel O. Phylogenetic mixture models for proteins. Phil. Trans. R. Soc. Lond. B. 2008b;363:3965–3976. doi: 10.1098/rstb.2008.0180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lockhart P.J., Steel M.A., Hendy M.D., Penny D. Recovering evolutionary trees under a more realistic model of sequence evolution. Mol. Biol. Evol. 1994;11:605–612. doi: 10.1093/oxfordjournals.molbev.a040136. [DOI] [PubMed] [Google Scholar]
- Löytynoja A., Goldman N. Phylogeny-aware gap placement prevents errors in sequence alignment and evolutionary analysis. Science. 2008;320:1632–1635. doi: 10.1126/science.1158395. [DOI] [PubMed] [Google Scholar]
- Miele V., Penel S., Duret L. Ultra-fast sequence clustering from similarity networks with SiLiX. BMC Bioinform. 2011;12:116. doi: 10.1186/1471-2105-12-116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nabholz B., Künstner A., Wang R., Jarvis E.D., Ellegren H. Dynamic evolution of base composition: causes and consequences in avian phylogenomics. Mol. Biol. Evol. 2011;28:2197–2210. doi: 10.1093/molbev/msr047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penn O., Privman E., Landan G., Graur D., Pupko T. An alignment confidence score capturing robustness to guide-tree uncertainty. Mol. Biol. Evol. 2010;27:1759–1767. doi: 10.1093/molbev/msq066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Philippe H., Brinkmann H., Lavrov D.V., Littlewood D.T.J., Manuel M., Wörheide G., Baurain D. Resolving difficult phylogenetic questions: why more sequences are not enough. PLoS Biol. 2011;9:e1000602. doi: 10.1371/journal.pbio.1000602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Posada D. jModelTest: phylogenetic model averaging. Mol. Biol. Evol. 2008;25:1253–1256. doi: 10.1093/molbev/msn083. [DOI] [PubMed] [Google Scholar]
- Posada D., Crandall K.A. MODELTEST: testing the model of DNA substitution. Bioinformatics. 1998;14:817–818. doi: 10.1093/bioinformatics/14.9.817. [DOI] [PubMed] [Google Scholar]
- Ripplinger J., Sullivan J. Does choice in model selection affect maximum likelihood analysis? Syst. Biol. 2008;57:76–85. doi: 10.1080/10635150801898920. [DOI] [PubMed] [Google Scholar]
- Rokas A., Williams B.L., King N., Carroll S.B. Genome-scale approaches to resolving incongruence in molecular phylogenies. Nature. 2003;425:798–804. doi: 10.1038/nature02053. [DOI] [PubMed] [Google Scholar]
- Schwarz G. Estimating the dimension of a model. Ann. Statist. 1978;6:461–464. [Google Scholar]
- Steel M. Should phylogenetic models be trying to “fit an elephant”? Trends Genet. 2005;21:307–309. doi: 10.1016/j.tig.2005.04.001. [DOI] [PubMed] [Google Scholar]
- Sumner J., Jarvis P., Fernandez-Sanchez J., Kaine B., Woodhams M., Holland B. Is the general time-reversible model bad for molecular phylogenetics? Syst. Biol. 2012a;61:1069–1074. doi: 10.1093/sysbio/sys042. [DOI] [PubMed] [Google Scholar]
- Sumner J.G., Fernández-Sánchez J., Jarvis P. Lie Markov models. J. Theor. Biol. 2012b;298:16–31. doi: 10.1016/j.jtbi.2011.12.017. [DOI] [PubMed] [Google Scholar]
- Tamura K., Kumar S. Evolutionary distance estimation under heterogeneous substitution pattern among lineages. Mol. Biol. Evol. 2002;19:1727–1736. doi: 10.1093/oxfordjournals.molbev.a003995. [DOI] [PubMed] [Google Scholar]
- Thioulouse J., Chessel D., Dolédec S., Olivier J.-M.. ADE-4: a multivariate analysis and graphical display software. Statist. Comput. 1997;7:75–83. [Google Scholar]
- Wertheim J.O., Sanderson M.J., Worobey M., Bjork A. Relaxed molecular clocks, the bias–variance trade-off, and the quality of phylogenetic inference. Syst. Biol. 2010;59:1–8. doi: 10.1093/sysbio/syp072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whelan S., Goldman N. A general empirical model of protein evolution derived from multiple protein families using a maximum-likelihood approach. Mol. Biol. Evol. 2001;18:691–699. doi: 10.1093/oxfordjournals.molbev.a003851. [DOI] [PubMed] [Google Scholar]
- Yang Z. Maximum likelihood phylogenetic estimation from DNA sequences with variable rates over sites: approximate methods. J. Mol. Evol. 1994;39:306–314. doi: 10.1007/BF00160154. [DOI] [PubMed] [Google Scholar]
- Yang Z. Likelihood ratio tests for detecting positive selection and application to Primate Lysozyme evolution. Mol. Biol. Evol. 1998;15:568–573. doi: 10.1093/oxfordjournals.molbev.a025957. [DOI] [PubMed] [Google Scholar]
- Yang Z., editor. Computational molecular evolution. New York: Oxford University Press; 2006. [Google Scholar]
- Yang Z. PAML 4: phylogenetic analysis by maximum likelihood. Mol. Biol. Evol. 2007;24:1586–1591. doi: 10.1093/molbev/msm088. [DOI] [PubMed] [Google Scholar]
- Yang Z., Kumar S., Nei M. A new method of inference of ancestral nucleotide and amino acid sequences. Genetics. 1995;141:1641–1650. doi: 10.1093/genetics/141.4.1641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z., Roberts D. On the use of nucleic acid sequences to infer early branchings in the Tree of Life. Mol. Biol. Evol. 1995;12:451–458. doi: 10.1093/oxfordjournals.molbev.a040220. [DOI] [PubMed] [Google Scholar]
- Zeldovich K.B., Berezovsky I.N., Shakhnovich E.I. Protein and DNA sequence determinants of thermophilic adaptation. PLoS Comput. Biol. 2007;3:e5. doi: 10.1371/journal.pcbi.0030005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou L., Susko E., Field C., Roger A.J. Fitting nonstationary general-time-reversible models to obtain edge-lengths and frequencies for the Barry–Hartigan model. Syst. Biol. 2012;61:927–940. doi: 10.1093/sysbio/sys046. [DOI] [PMC free article] [PubMed] [Google Scholar]