Evaluation of Fiber Tracking from Subsampled q-Space Data in Diffusion Spectrum Imaging

Abstract

Diffusion spectrum imaging (DSI) is capable of resolving crossing and touching fiber bundles in a given voxel. Acquisition of DSI data involves sampling large number of points in the q-space which significantly increases scan times. The scan times can be reduced by exploiting the symmetry of the q-space. In this study the fiber pathways for five (fornix, cingulum, superior longitudinal fasciculus, corticospinal tract, and crossing fibers in the centrum semiovale region) fiber bundles derived using three subsampled data sets of different sizes derived from the 257 samples in the q-space are compared. The coefficient of variation of the ratio of the number of fiber pathways for each subsample data set to the original data points, averaged over all the 10 subjects, was used for quantitatively investigating the effect of subsampling on the tractography. The effect of threshold angles on tractography is also investigated. The effect of subsampling on the orientation distribution function (ODF) was quantitatively evaluated using both scalar and vector measures derived from the ODF. A streamline tractography method that improves the curvature problem and reduces the local truncation error to further improve the mapping of fiber pathways is adapted. Analysis of the fiber pathways in ten normal subjects, based on qualitative and quantitative methods, shows that the 129 and 198 q-space points provide very similar result with angle of threshold between 41° and 45°. Based on the scan time advantage, 129 subsampled points appear to be adequate for tractography.

Introduction

Diffusion tensor magnetic resonance imaging (DT–MRI) is a noninvasive method that is most commonly used for in vivo fiber tracking in the human brain. Conventional diffusion tensor imaging (DTI) has the ability to reconstruct fiber pathways but cannot fully resolve touching and crossing fibers [1, 2]. High-angular resolution diffusion imaging (HARDI) is proposed to overcome these limitations. In HARDI the number of diffusion gradient directions is typically between 30 and 100 [3]. In HARDI the orientation distribution function (ODF) is used to describe the probability of fiber direction [4, 5]. The method of deriving ODF from the q-space data is analytical and the linear transformation is based on spherical harmonics [5]. HARDI allows exploration of complex white matter microstructure. However, HARDI methods still require parameterization of the diffusion probability [6-8].

Diffusion spectrum imaging (DSI) [6, 9-10] is a model free technique that considers diffusion pattern in each voxel using the ODF. In DSI, diffusion weighted images are acquired along different directions that are organized in the q-space (integral points of a cubic lattice) within a sphere. Diffusion in each voxel is described by the probability density function (PDF) which specifies the 3D distribution of microscopic displacement of water molecules [6]. DSI requires sampling large number of points in the q-space that results in long acquisition times. As a balance between scan time, hardware limitations, and accuracy of tractography, based on tract similarity, 515 encoding gradient directions with b_max of 6000s/mm² was proposed for DSI, suitable in a clinical setting [11]. However, this is still a large number of encoding gradient directions. It is possible to reduce the scan time by multiplexed echo sampling [12, 13], but this method is not commonly available. Another way to reduce the scan time is to limit the number of q-space points sampled and fill the q-space by exploiting its symmetry. By exploiting the geometric symmetry of diffusion anisotropy and diffusion cross-term correlation, Lin et al [14] sampled 319 q-space points to create 515 diffusion encoding directions. Cho et al [15], based on phantom studies, showed the preservation of the fiber orientations by using half the spherical encoding points in DSI. Reese et al [16] have presented a highly efficient multiplexing method, simultaneous image refocusing, for reducing the total DSI scan time by half. Yeh et al [17] have shortened the acquisition times using reduced-encoding DSI with a bi-Gaussian diffusion model. These authors used a crossing phantom model and manganese-enhanced rat model as standards for assessing the effect of reduced-encoding in DSI.

Nezamzadeh et al [8] have segmented the cingulum fiber bundle in humans by optimizing the DSI parameters, especially spatial resolution and diffusion encoding bandwidth, for tract level diffusion measurements. It was also suggested that 257 q space points, and perhaps even as small as 129 points, may be adequate to generate the PDF in DSI [7]. Majority of these studies have investigated the effect of subsampling on the ODF using a single metric in a phantom or on a single tract in brain. However, the smallest number of q-space points needed to generate nearly artifact free tractography of multiple white matter tracts is yet to be systematically investigated in the human brain.

A mathematical framework for fiber tract trajectory as a 3D space curve parameterized by the arc length of the trajectory was introduced by Basser et al [18]. These authors indicated that the Euler's numerical integration method for reconstructing the fiber pathways is prone to truncation errors. Using this framework, the fiber assignment by continuous tracking (FACT) algorithm was formulated [1, 19]. In the FACT algorithm variable step sizes are used which depend on the length of the trajectory that is needed to pass through a voxel. This method is a special case of Euler's numerical integration method for reconstructing the fiber pathways and is also prone to truncation errors. DSI-based fiber tracking was adapted from the Euler's integration tracking that is used in DTI and its limitation in reconstructing the fiber pathways with high curvature was pointed out [20].

In this study we compared the fiber pathways generated in five fiber bundles using three subsampled data sets of different sizes derived from sampling of 257 points in q-space. The effect of subsampling was quantitatively evaluated using both vector and scalar measures derived from the ODFs. A streamline tractography method was adapted to avoid premature stoppage of the tracks and smooth the fiber pathways. The tracking results obtained with our proposed method with fixed and variable step lengths were compared with the commonly used Euler method for a number of fiber bundles (cingulum, superior longitudinal fasciculus (SLF), fornix and corticospinal tract (CST) and crossing fibers at the centrum semiovale (CS) region). In addition, the ratio of the fiber pathways was used for quantitative assessment of the effects of subsampling and threshold angles on the tractography.

Materials and Methods

Data acquisition

DSI data on brain was acquired on 10 normal subjects (7 men, 3 women mean age 31.4 ± 8.34 years; age range 26-49 years). These controls did not have any history of neurological disorders. Their conventional MRIs were read as normal by a board certified neuroradiologist. The MRI and DSI data were acquired on a 3T MRI scanner (Achieva, Philips Medical Systems, Best, Netherlands) with a maximum gradient amplitude and slew rate of 80 mT/m and 200 mT/m/ms, respectively. The subjects were positioned in the scanner with their heads secured by a soft Velcro to minimize head motion. An 8 channel head coil with a SENSE factor 1.5 was used for data acquisition. Multi-slice, diffusion-weighted images were acquired with a single shot spin echo planar imaging (EPI) sequence with 257 diffusion encodings. The sampled q-space points were located on a cubic lattice within a sphere of 4 lattice units in radius, i.e, q = mq_x + nq_y + lq_z where m, n, and l are integers such that m²+ n² + l² ≤ 16 and q_x, q_y, and q_z are the unit diffusion sensitizing gradient vectors along the X, Y, and Z directions. The sequence parameters were: FOV= 240×240 mm², 256×256 image matrix, and slice thickness = 4mm, total number of slices =28, TR/TE = 11400ms/95ms, b_max= 9700 s/mm², corresponding to a diffusion resolution of 1/|q_max|=12 μm. The total DSI data acquisition time was 48 min per subject. Because of the long acquisition time, data with larger gradient encoding directions (>257) was not acquired.

DSI Data Analysis

A diffusion gradient can be represented by a 3D vector, q, whose direction is along the diffusion gradient and length proportional to the gradient strength. The signal is sampled at each point by varying the direction and strength of the diffusion gradient. The spin displacement is encoded by the bipolar gradient pulses whose sensitivity is given by the vector q = γδg, where g is the diffusion-encoding gradient, δ is the time duration of the gradient, and γ is the gyro magnetic ratio [21].

The angular resolution θ in radians is given by $\theta =\sqrt{\frac{4\pi }{S}}$, where S is the number of linearly independent sample points [6]. Out of the 256 sampled points, 226 points (on the unit sphere) are linearly independent in the q-space. Thus the 226 samples can provide an angular resolution of 13.5°.

Three different sets of reduced sampling were investigated in this study. The datasets were generated by sub sampling the original 257 data sets based on the symmetry of the q-space. The first set of 129 subsampled points was from the lower half of the q-space i.e, {(m, n, l); n < 0 or (n = 0 and m < 0) or (n = 0 and m = 0 and l ≤ 0)}. The second subsampled dataset consisted of 153 points {(m, n, l) / n ≤ 0)} (the lower half with the boundary). The third dataset consisted of 198 points {(m, n, l)/ n ≤ 1)}.

The most fundamental relationship between the diffusion MRI signal, E(q), and the diffusion propagator, P(r), is given by the Fourier transformation [6]:

$$P\left(r\right)=\int E\left(q\right)\text{exp}(-2\pi iq\cdot r)dq$$ (1)

The 3D diffusion function or PDF at each spatial location was reconstructed by taking the discrete 3D Fourier transform of the modulus of the sampled signal [9]. Hanning window was applied to E(q) prior to discrete 3D Fourier transformation [10]. The PDF was normalized by dividing it with the sum of the PDFs at every voxel [10]. The ODF, Ψ, was obtained from the PDF by taking the radial summation of the 3D PDF, P(r) [9]:

$$\Psi \left(u\right)={\int }_0^{4}P\left(\rho u\right){\rho }^{2}d\rho$$ (2)

where ρ and u represent the radius and the vertex of the tessellated unit sphere, respectively. The tessellated unit sphere, centered at the origin, was obtained using the function “vtkSphereSource” from the VTK open sources (http://www.vtk.org/). The tessellated surface of the sphere has 362 vertices and 720 triangles. From Eq. (2), it can be seen that the ODF in the direction of u can be obtained by integrating the PDF weighted by the square of the position from the center. The radius of the tessellated sphere in the direction of u is Ψ (u). For anisotropic voxels, the sphere will deform and this deformation is proportional to the sum of values of the diffusion PDF in that direction. Unlike DTI, where the principal eigenvector is obtained from the tensor, in DSI the vectors which indicate the highest possible diffusion directions are obtained from the ODF using the local maximum method [10]. Each vector has either 5 or 6 neighboring vectors; the maximum ODF value among all the neighbors is considered to be the local maximum, i.e. the local maximum at u_i occurs if and only if Ψ(u_i) ≥ Ψ(u_j) for all neighbors u_j of u_i.

The generalized fractional anisotropy, GFA, is given by $GFA\left(\Psi \right)=\frac{STD\left(\Psi \right)}{RMS\left(\Psi \right)}$, where STD and RMS are the standard deviation and the root mean square of the ODF, respectively [22]. Kuo et al [23] defined the diffusion anisotropy (DA) as the standard deviation of the radial mean squared lengths of the normalized PDF.

Tracking Method

Tractography utilizes the diffusion-weighted data to reconstruct 3D curves of the fiber pathways which are estimates of the white matter axonal bundle trajectories [24, 25]. In DTI, the most popular streamline tracking method uses the principal eigenvector as the direction of the local fiber orientation [18]. The mathematical formulation is given by

$$\frac{dr\left(s\right)}{ds}=V\left(r\left(s\right)\right)$$ (3)

where V is the principal eigenvector and r(s) is the arc length parameterization of the curve which represents the fiber pathways. The solution to the above equation using the Euler's integration method with step length, h, is given by

$$r_{n+1}=r_n+hV\left(r_n\right)$$ (4)

Euler's integration method is obtained using the first order approximation of the Taylor series, with the truncation error at each step proportional to h² (0<h<1). In Euler's integration method the reconstructed pathways tend to deviate more from the actual pathways as we move away from the seed point than in other numerical integration methods. In DSI, the direction of fiber orientations in a number of voxels is more than one, say m. These vectors can be denoted by V_n⁽¹⁾, V_n⁽²⁾, ..., V_n^(m) at the n^th voxel. Hagmann et al [20] adapted the DTI Euler's integration tracking method to the DSI data as

$$r_{n+1}=r_n+h{V}_n^k\left(r_n\right)$$ (5)

where V_n^(k) is most collinear to the previous vector V_n-1^(j). Our modified tracking method is based on Eq. (5) and Euler-trapezoidal (predictor-corrector) numerical integration method. The predictor-corrector tracking procedure was used in previous studies based on the Kalman filter method [26, 27]. The same procedure was also used to trace the filaments through scalar volume data sets that are robust to both noisy and under sampled data [28]. Our predictor-corrector method uses the Euler-trapezoidal numerical integration method, which is simpler to apply than the Kalman filter methods. In this approach, the “predictor” uses the previous fiber pathways direction while the “corrector” uses the average of the previous and the current fiber pathway directions. Using this method, the solution to Eq. (3) can be written as

$$r_{n+1}=r_n+\frac{h}{2}\left[V_{n+1}^{\left(k\right)}\left(r_{n+1}^p\right)+V_n^j\left(r_n\right)\right]$$ (6)

where

$$r_{n+1}^p=r_n+h{V}_n^j\left(r_n\right)$$ (7)

is the predictor and the variable step length h depends on the maximum norm of the vector $V_n^j\left(r_n\right)$. The truncation error in the Euler-trapezoidal method is proportional to h³. At each step in the tracking we consider the direction vector with the largest inner product with the incoming vector. The most commonly used numerical integration method is the fourth-order Runge-Kutta method, where the total truncation error is proportional to h⁴. Most of the time, this method is more powerful than the Euler and Euler-trapezoid methods but not always [29]. At each voxel, three direction vectors (if they exist) were chosen using the local maximum method. Tracking was initiated along the three directions from each voxel in the region of interest (ROI). There are 27 seed points for each voxel (one at the center of the voxel and others at 0.1 from the midpoints of the boundary of the 26 neighboring voxels). As an example, the placement of seeds for cingulum and CST bundles is shown in Figs. 1. For tracking the fornix, two ROI's were placed around the mammillary body and hippocampus in order to separate it from other bundles with the same seed points shown in Fig. 2. The seed region for CST was placed on the internal capsule with the destination ROI close to the cortex. The seed regions with the specified target regions (ROI) are adequate to discriminate each of these bundles from others [30]. The crossing fiber bundles in the CS region were generated from the intersection of the bundles shown in Fig. 3 by following the three principal direction vectors.

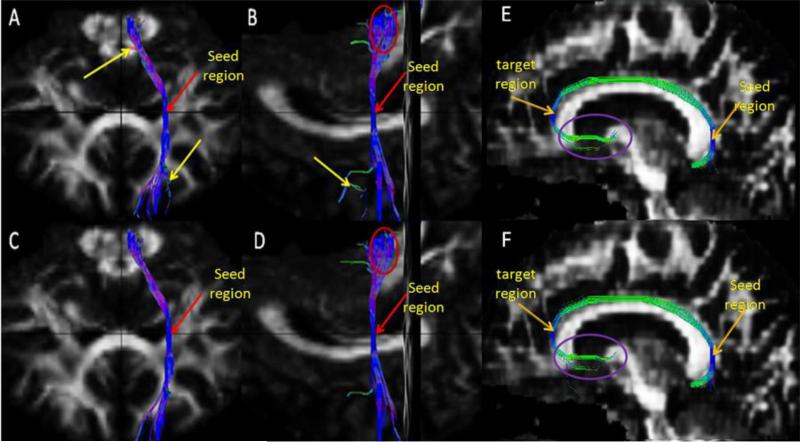
Fig. 1.

Euler vs predictor-corrector (tracking methods) for CST and cingulum fiber bundles. Coronal view (A) and sagittal view (B, F) of Euler's method, Coronal view (C) and sagittal view (D, E) of predictor-corrector method.

Fig. 2.

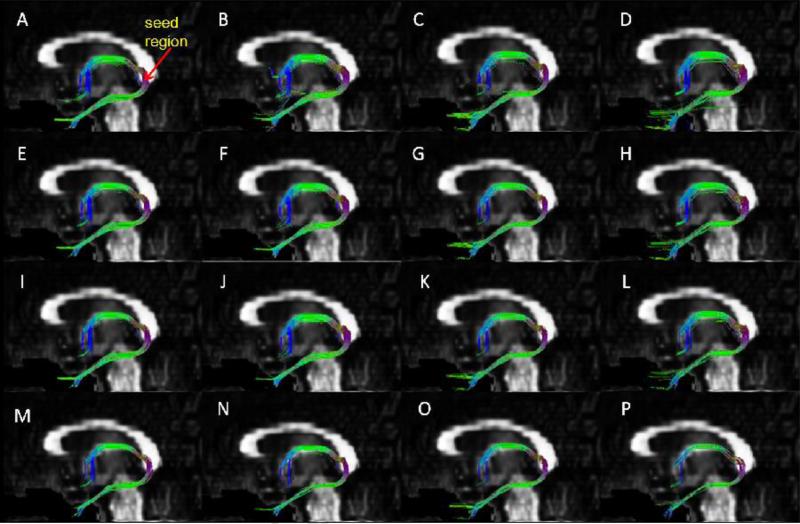
Fiber bundle of fornix reconstructed with 257 (A, E, I, M), 198 (B, F, J, N), 153 (C, G, K, O), and 129 (D, H, L, P) q-space encoding samples using tracking angle thresholds of 60° (A, B, C, D), 45° (E, F, G, H), 41° (I, J, K, L) and 35° (M, N, O, P).

Fig.3.

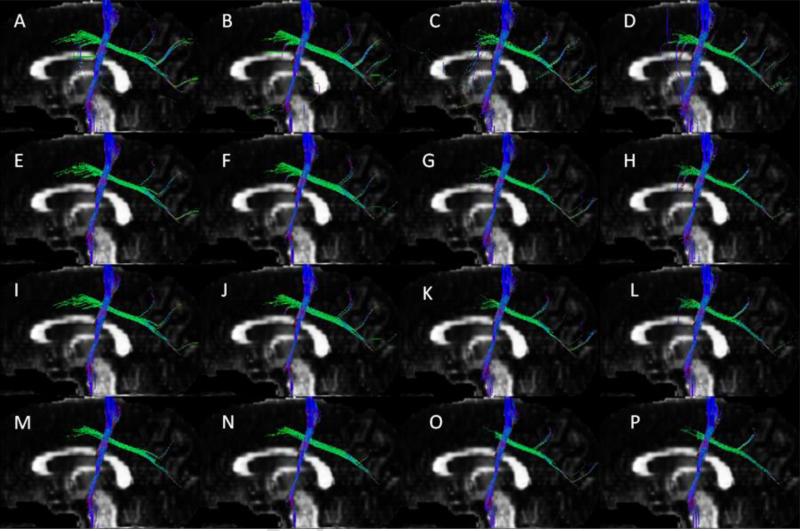
Crossing fiber bundles of partial CST and partial SLF reconstructed with 257 (A, E, I, M), 198 (B, F, J, N), 153 (C, G, K, O), and 129 (D, H, L, P) q-space encoding samples using tracking angle thresholds of 60° (A, B, C, D), 45° (E, F, G, H), 41° (I, J, K, L) and 35° (M, N, O, P).

The threshold angle is an important variable in generating the tractography. Most previously published tracking procedures used threshold angles between 30° [31] and 70° [19]. In this work we have chosen, somewhat arbitrarily, four threshold angles, 35°, 41°, 45°, and 60°, to identify the optimum threshold angle. For each data set and subject, tracking was performed using these four threshold angles.

Let A, B, and C be three successive points on a curve (fiber path), and let a=||A-B||, b=||B-C||, and c = ||A-C||. Assuming the step length to be small, i.e. a and b are small, the curvature of the fiber path at B, κ(B), can be approximated as [32]

$$\kappa \left(B\right)=\frac{\sqrt{(a+b+c)(b+c-a)(a+c-b)(a+b-c)}}{abc}$$ (8)

Smaller curvature implies smoother fiber pathways. We have calculated the curvature for four fiber bundles: fornix, SLF, cingulum, and CST. For demonstrating the improvement in tracking with our procedure, we have compared the curvature for each of the fiber bundles using both the Euler's and the predictor-corrector methods. Curvature was calculated using the fully sampled data and compared with the results obtained with the Euler's integration method. A threshold angle of 45° that was found to be optimal (see below) was used.

We assessed the agreement between subsampled and fully sampled data using the vectors that represent the fiber orientation directions and the scalar measures DA, GFA and RMS, derived from the ODFs. Specifically the scalar and vector measures were compared for two volumes of interest (genu of the corpus callosum (CC) with single fiber and the CS where corona radiata, superior longitudinal fasciculus, and callosal fibers cross. The fiber orientation deviation with subsampled data was assessed using the inner product of fiber orientation obtained with subsampled and fully sampled data. For scalar measures, the agreement between the subsampled and fully sampled data was assessed using the correlation and variability of the scalar measures within the volumes of interest.

In order to quantify the closeness of the fiber tracts generated with subsampled q-space points to those obtained with the fully sampled data; we used the ratio of the number of pathways obtained with the subsampled data to that obtained from the full data set.

Results

As an example, Fig. 1 shows the CST and cingulum fiber tracts generated using the Euler and the predictor-corrector methods. The Euler method resulted in divergence of the fiber pathways away from the seed point as shown for part of the CST. The red arrow in this figure shows the seed region where tracking was initiated and displayed in the coronal and sagittal planes. The yellow arrow indicates the regions where some of the fiber pathways begin to deviate from the main pathways due to the accumulation error in the Euler's method. The two congruent red ellipses show that far from the seed point the fiber pathways deviated more in the Euler method than in the predictor-corrector method. Table 1 summarizes results of the quantitative comparison of Euler and Euler-trapezoidal (predictor-corrector) based tracking procedures for the fornix, SLF, cingulum, and CST bundles.

Table 1.

Comparison of Euler and Euler-trapezoidal (predictor-corrector) based tracking procedures using the mean of maximum curvature of fornix, SLF, cingulum and CST fiber bundles. The values are expressed as mean±sd)

Methods/ Bundles	Fornix	SLF	Cingulum	CST
Euler fixed	0.102±0.023	0.076±0.023	0.075±0.030	0.069±0.025
Predictor Corr. fixed	0.057±0.020	0.051±0.029	0.046±0.026	0.035±0.014
Euler variable	0.079±0.017	0.060±0.023	0.061±0.015	0.056±0.020
Predictor Corr. Variable	0.041±0.010	0.034±0.014	0.032±0.009	0.029±0.011

SLF = superior longitudinal fasciculus; CST = cortico spinal tract

Sixty tractograpghs were generated from the subsampled data points for each of the ten subjects with four threshold angles. Tractography from the original 257 and subsampled q-space encoding data sets are shown, as an example, for fornix (Fig. 2) and crossing fiber bundles in the CS region (Fig. 3). From the reconstructed fiber bundles we compared qualitatively how each subsampled data reproduced the corresponding bundles with the fully sampled data consisting of 257 q-space points. For quantitative comparison we have used the coefficient of variation [8] of the ratio of the number of pathways for each subsample data set to the original 257 encoding data points, averaged over all the 10 subjects. The results are summarized in Table 2. A ratio of unity implies perfect agreement with the fully sampled data. For the cingulum, CST, SLF, and crossing fiber bundles the coefficient of variation is smaller than for fornix for all the three subsamples. For angles 41° and 45° the ratio for all fiber bundles is close to unity with minimum coefficient of variation in the 198 q-space encoding samples. The ratio for the 129 samples is also close to unity, but the coefficient of variation is relatively high for fornix. Qualitatively we also observed that for the pathways reconstructed from 129 subsamples the tracts do not appear to be part of the bundles as can be seen in the lower part of the fornix in Fig. 3 (D, H, L and P).

Table 2.

Mean ± SD of the ratio of fiber pathways for three q-space encoding samples with four angles of thresholds of fornix, cingulum, CST, SLF and crossing fiber bundles.

		Fornix	Cingulum	CST	SLF	Crossing
Sa	An	Mean± SD	Mean± SD	Mean± SD	Mean± SD	Mean± SD
198	60	1.34±0.61	0.966±0.08	1.02±0.30	1.01±0.296	0.98±0.048
	45	1.31±0.80	1.021±0.07	1.03±0.31	1.02±0.056	1.01±0.019
	41	1.28±0.82	1.007±0.08	1.01±0.32	1.03±0.057	1.01±0.016
	35	0.93±0.58	1.005±0.10	0.91±0.23	1.03±0.085	1.00±0.014
153	60	0.68±0.49	0.860±0.08	1.07±0.30	1.07±0.302	0.99±0.027
	45	0.61±0.36	0.886±0.13	1.05±0.40	1.01±0.086	0.99±0.055
	41	0.53±0.30	0.884±0.12	1.00±0.40	1.02±0.087	0.98±0.062
	35	0.50±0.24	0.898±0.08	0.88±0.53	1.03±0.094	0.96±0.062
129	60	0.74±0.45	0.872±0.09	1.09±0.32	1.08±0.316	0.99±0.027
	45	1.07±1.25	1.0 22±0.15	1.03±0.34	0.96±0.072	0.99±0.073
	41	1.05±1.18	1.005±0.16	0.93±0.48	0.97±0.072	0.98±0.068
	35	1.52±1.30	1.002±0.16	1.09±0.99	0.95±0.082	0.96±0.063

SLF= superior longitudinal fasciculus; CST= corticospinal tract; An = Angle; Sa = number of q-space points

Table 3 summarizes the average values, correlations, and magnitude difference in the scalar measures (DA, GFA, RMS) derived from the ODFs of the subsampled and fully sampled data for two regions (CC and CS). A decrease in correlation along with an increase in the absolute variation was observed as the number of subsampled points decreased. For all the subsampled data the absolute variation in DA is minimum and absolute variation of GFA is maximum among the three scalar measures.

Table 3.

Summary of values, correlation and absolute difference of three scalar measures (DA, GFA, and RMS; expressed as mean ± sd) derived from the ODF of subsamples and reference of fiber bundles (genu of CC and centrum semiovale) in 10 subjects.

	Samples	257		198		153		129
	bundles	CS	CC	CS	CC	CS	CC	CS	CC
Values	DA	0.22±0.005	0.24±0.003	0.22±0.005	0.24±0.003	0.22±0.004	0.24±0.003	0.22±0.003	0.24±0.004
	GFA	0.54±0.01	0.75±0.008	0.54±0.01	0.75±0.006	0.54±0.02	0.74±0. 012	0.54±0.02	0.74±0.011
	RMS	0.41±0.01	0.32±0.005	0.41±0.01	0.32±0.004	0.42±0.02	0.32±0.005	0.42±0.02	0.32±0.005
Correlation	DA	-	-	0.96±0.01	0.93±0.05	0.89±0.03	0.85±0.10	0.88±0.03	0.83±0.11
	GFA	-	-	0.93±0.03	0.85±0.11	0.83±0.08	0.71±0.19	0.81±0.07	0.71±0.18
	RMS	-	-	0.98±0.01	0.85±0.19	0.93±0.03	0.76±0.23	0.93±0.02	0.76±0.22
Absolute Difference	DA	-	-	0.004±0.001	0.002±0.001	0.005±0.001	0.003±0.001	0.006±0.001	0.004±0.001
	GFA	-	-	0.012±0.003	0.013±0.002	0.022±0.004	0.019±0.007	0.023±0.004	0.022±0.007
	RMS	-	-	0.007±0.002	0.004±0.002	0.014±0.002	0.006±0.002	0.015±0.003	0.006+0.003

DA= Diffusion Anisotropy; GFA= Generalized Anisotropy; RMS = Root-Mean-Square CS = Centrum Semiovale; CC= Corpus Callosum

The maximum observed variation in the principal fiber orientation for both CC and CS was around 12° which is less than the angular resolution (13.5°) for the 256 sampled data. In the CS region that has three crossing fibers, the number of voxels where the second and third fiber orientations directions varied by more than 12° was about 0.2% and 0.6% (for 198 subsample), 0.4% and 1.6% (for 153 subsample), and 0.5% and 1.9% (for 129 subsample), respectively.

Discussion and Conclusions

This study focused on two major points. First we used the predictor-corrector with variable step length stream line tracking procedure that is an improvement over the Euler's tracking method to reconstruct the fiber pathways. Second, we quantitatively evaluated, based on a number of metrics, the effect of q-space sample size on ODF and tractogarphy relative to the fully sampled data. Tracking procedure using Euler's numerical integration method has two drawbacks: (1) the truncation error in Euler's method is relatively high, which leads to a poor reconstruction of fiber pathways and (2) if the inner product of two consecutive direction vectors of the pathways is beyond the threshold, tracking stops. That is, if the curvature of the fiber pathways is high, Euler's method might fail to reconstruct the fiber pathways. The total truncation error in the Euler's method is proportional to h while that of the predictor-corrector method is proportional to h². For example, for h = 0.5, the truncation error with Euler's method is four times higher than with the predictor-corrector method. We have shown that the mean maximum curvature is lower for all the fiber bundles that we have considered with the predictor-corrector method with variable step length (Table 1). Therefore, the predictor-corrector method also addresses the curvature problem associated with the Euler's method that was reported earlier [20]. That is, the predictor-corrector method improves the coherence of two consecutive direction vectors on the same pathway. Therefore, premature stoppage of the reconstruction will be reduced by this method. As can be seen from Fig. 1 some pathways deviated from the normal path for the CST fiber bundle due to error accumulation in the Euler's, but not in the predictor-corrector method. Qualitative comparison of the Euler's and predictor-corrector methods has shown that the later produces a better reconstruction of the fiber pathways (Fig. 1). While the fiber pathways reconstructed using the Euler method deviate as we move farther from the seed region, for shorter distances from the seed region and coherent fiber bundles both methods yield the same pathways (Fig. 1). Quantitatively, we have shown that the proposed method produces smoother fiber pathways (Table 1). The predictor-corrector method, as can be seen from Eqs. (6) and (7), has to evaluate an additional function at each step of tracking. Therefore, the computational cost for the predictor-corrector method is slightly higher than that of the Euler's method. The fourth order Runge-Kutta method requires evaluation of four functions per step h (one at the initial point, twice at the trial mid points and once at the trial endpoint). Runge-Kutta method is of higher order than the predictor-corrector method but does not always mean higher accuracy [26]. The principal direction vector information per voxel is the same; whether we calculate the direction of the pathways one or four times it does not change the result. Therefore, the order of tracking does not matter so long as we are in the same voxel. The order is important when the pathways cross one voxel and enters the other where they may have different direction. Therefore, fourth order Runge-Kutta method does not yield better tracking pathways and needs more computations.

The concept of reducing the scan times by subsampling only part of the q-space is not new. As pointed out in the Introduction, a number of publications have addressed this issue. We believe that our studies differ from other published studies at least in three ways. We have used multiple metrics, both scalar and vector, to compare the effect of subsampling on the ODF as well as fiber tracts. Unlike the previously published studies [8] that have used only the cingulum fiber bundle for evaluation, we have used five bundles to demonstrate the ability of subsampled data to reproduce fiber bundles. In addition, we have also investigated the effect of threshold angle on tractography. Overall our results show that there is no significant difference in any of the metrics between the 198 and fully sampled data. In the genu of CC, the DA, GFA, and RMS values for 129 and 153 subsamples are significantly different (p < 0.05) compared to the values obtained with the fully sampled data. In the CS region the values of GFA and RMS, but not DA, obtained with 129 and 153 samples differed significantly (P<0.05) from the fully sampled data. For all the scalar measures the 153 and 129 subsamples have yielded identical average values. The analysis of the vector metric yielded results that are consistent with those based on the scalar metrics. For example, the percentage of the number of voxels in CC where the principal diffusion direction (first vector) deviated about 12° is less than that of the CS region. In the CS region the three crossing fiber directions deviates about 12° from the corresponding diffusion directions of the full sample starting from 9% up to 36%. This angular deviation does not affect the tracking significantly as it is much smaller than the threshold angle for tracking.

For all the bundles investigated in this study (fornix, cingulum, CST, SLF, and crossing fiber bundles) qualitatively and quantitatively the 198 q-space encoding samples with angles of threshold between 41° and 45° have yielded results that are closest to the 257 q-space encoding samples. This sub sampling translates into a reduction in the scan time by 11 minutes. While the 129 data also produced fiber tracts close to the full data set, in some instances we have observed extraneous fibers with this subsample set as it can be seen in the crus of fornix (temporal lobe part of the fornix) in Fig. 3 (D, H, L, and P). This subsampled set reduces the scan time by 24 minutes.

Even for 129 q-space sampling points, the scan times are still too long for routine clinical use of DSI. The scan times could be further reduced by combining the partial q-space sampling with simultaneous acquisition of more than one slice, as was reported by Reese et al [16]. It is also possible to exploit techniques such as compressed sensing to further reduce the sampling density and shorten the acquisition times. Other time efficient techniques such as hybrid diffusion imaging (HYDI) [33], CHARMED [34] and multi-shell sampling [35]. Each of these techniques has its own advantages and disadvantages relative to DSI and a detailed comparison among these techniques is beyond the scope of this study.

As is the case with all tracking methods, the DSI-based tractography is affected by the partial volume averaging and noise. For example, in the case of fornix which is adjacent to the CSF spaces, the delineation of the bundle and its absolute diffusion parameters may be adversely affected by the partial volume [36]. This perhaps explains the larger variability in the reconstruction of the fornix in the 10 subjects compared to other bundles as summarized in Table 2. We also observed that the reconstruction of the fornix fiber bundle is poor with 35° angle of threshold. This is perhaps expected since this bundle exhibits high curvature.

Tractography, whether based on DTI or HARDI techniques, is affected by the signal-to-noise ratio (SNR). Investigation of the effect of SNR on tractography would require acquisition of the DSI data at different SNR levels. Because of the long acquisition times we have not investigated the effect of SNR on the DSI-derived tractography. In order to improve the SNR we used in this study slice thickness that is larger than the in-plane pixel size. However, the final analysis was done on interpolated images with isotropic voxel dimensions.

This study is not without its limitations. A major limitation is that the fully sampled q-space contained only 257 points. All the results with subsampled space were compared with those obtained for the 257 points. It would have been desirable to include more points (like 515) in the fully sampled q-space. However, this was not possible because of excessively long scan times. In this study we exploited the geometric symmetry of the q-space to reduce the scan time. There may be other clever strategies, including compressed sensing, for further reducing the scan times. In this study we have not investigated these other strategies. However, this is beyond the scope of the current study. We plan to pursue these strategies in future.