Abstract
Permeability images derived from magnetic resonance (MR) perfusion images are sensitive to blood-brain barrier derangement of the brain tissue and have been shown to correlate with subsequent development of hemorrhagic transformation (HT) in acute ischemic stroke. This paper presents a multi-center retrospective study that evaluates the predictive power in terms of HT of six permeability MRI measures including contrast slope (CS), final contrast (FC), maximum peak bolus concentration (MPB), peak bolus area (PB), relative recirculation (rR), and percentage recovery (%R). Dynamic T2*-weighted perfusion MR images were collected from 263 acute ischemic stroke patients from four medical centers. An essential aspect of this study is to exploit a classifier-based framework to automatically identify predictive patterns in the overall intensity distribution of the permeability maps. The model is based on normalized intensity histograms that are used as input features to the predictive model. Linear and nonlinear predictive models are evaluated using a crossvalidation to measure generalization power on new patients and a comparative analysis is provided for the different types of parameters. Results demonstrate that perfusion imaging in acute ischemic stroke can predict HT with an average accuracy of more than 85% using a predictive model based on a nonlinear regression model. Results also indicate that the permeability feature based on the percentage of recovery performs significantly better than the other features. This novel model may be used to refine treatment decisions in acute stroke.
Keywords: brain ischemia, hemorrhagic transformation, prediction, acute stroke diagnostic, stroke, permeability
1. Introduction
At present, acute ischemic stroke is treated with mechanical clot-retrieval devices and/or pharmaceutical re-canalization therapies with the ultimate goal of restoring blood perfusion in the affected area and saving the endangered tissue. While a successful recanalization of the vessel improves the chances of recovery, critical complications such as intracerebral hemorrhage may result. A general guideline to reduce those risks is to limit the administration of thrombolytic therapy with recombinant tissue plasminogen activator (tPA) to patients admitted within 4.5h of symptoms onset. This restrictive time-window aims primarily at reducing the risk of hemorrhagic transformation (HT) due to disruption of the blood-brain barrier (BBB) which is known to increase over time. HT, and intracranial hemorrhage in general, causes blood to accumulate within the brain, and may lead to devastating consequences as they may trigger potentially deadly increase of intracranial pressure (ICP).
This study focuses on the automatic prediction of HT in acute ischemic stroke from MRI images acquired at day 0. The administration of tPA constitutes a major cause of HT as it has been reported [1] that there is a 5.9% risk of HT associated with patients treated with tPA compared to 1.1% for controls. But the relationship is complex, other factors also come into play; previous studies [2] have identified clinical variables that may be linked to HT after tPA treatment. In addition, imaging studies based on multi-modal MRI are also promising as they provide unique insights regarding tissue status and potential risks for HT. For example, it has been shown that the volume of diffusion and perfusion abnormality is linked to an increased risk of HT after re-canalization therapy [3, 4, 5]. Other imaging studies have found a variety of features correlated with an increased risk of HT, such as: low mean apparent diffusion coefficient (ADC) [3], reduced cerebral blood volume (CBV) or flow (CBF) [6, 7], leukoaraiosis [8], prior microbleeds [9], early parenchymal enhancement [5], large vessel circle of Willis occlusion [10], poor collateral vessels on CT angiography [11], and early colony-stimulating factor hyperintensity [12].
It has been suggested [13] that HT may result from reperfusion into a large volume of ischemic tissue. It is possible to identify certain BBB permeability derangements in patients with acute ischemic stroke using dedicated MRI acquisitions. More recently, however, specific permeability parameters [14] derived from perfusion-weighted images (PWI) were computed before treatment and were shown to identify patients at risk for HT. The identification of BBB compromise relies on the fact that, during a PWI scan, the intensity of T2* signal decreases with bolus passage through the cerebrovasculature followed by a return to baseline intensity. In some areas, signal intensity may demonstrate a later decline at the terminal phase of scan acquisition; a synonym of continued increase in the concentration of the contrast agent. Late signal intensity changes at the terminal phase of scan acquisition may indicate accumulation of contrast within a region, rather than the expected return to baseline signal intensity after contrast clearance. Such an accumulation may be produced by slow leakage of contrast. In patients with BBB compromise, the contrast agent will leak out of the vasculature into surrounding tissue, which will result in persisting or even falling T2* intensity. In recent years, several permeability imaging features [15, 16, 17, 18, 19, 14] extracted from T2* PWI images and reflecting this phenomenon have been introduced and have been shown to provide distinctive markers to identify patients with an increased risk of HT.
This study relies on these findings and evaluates six previously introduced T2* permeability imaging features (relative recirculation rℝ, percentage recovery %ℝ, post-bolus area (PB), mean post-bolus intensity (MPB), contrast slope (CS), final contrast
 ) on a large set of 263 patients treated for acute ischemic stroke in four different ischemic centers. To the best of our knowledge, this is the first multicenter study that evaluates the significance of these six permeability maps in predicting HT. It uses a large set of patients to more precisely assess the possibility of predicting HT from onset PWI images. A key technical contribution of the proposed statistical framework is to train classifier-based predictive model that uses histogram-based descriptor to summarize the distribution of the parameter intensity across the two hemispheres. The interventional decision-making process may benefit from a predictive model of HT by supplementing standard diffusion and perfusion MRI imaging parameters with predicted maps of HT based on permeability imaging.
) on a large set of 263 patients treated for acute ischemic stroke in four different ischemic centers. To the best of our knowledge, this is the first multicenter study that evaluates the significance of these six permeability maps in predicting HT. It uses a large set of patients to more precisely assess the possibility of predicting HT from onset PWI images. A key technical contribution of the proposed statistical framework is to train classifier-based predictive model that uses histogram-based descriptor to summarize the distribution of the parameter intensity across the two hemispheres. The interventional decision-making process may benefit from a predictive model of HT by supplementing standard diffusion and perfusion MRI imaging parameters with predicted maps of HT based on permeability imaging.
2. Methods
2.1. Patients and MRI Data Acquisition
The multi-center collaborative imaging study presented in this paper was conducted on 277 patients admitted to an intensive care unit (ICU) for acute is-chemic stroke. The four following centers were involved in the study: Stroke Diagnostics and Therapeutics, NIH, Bethesda, MD (95 patients); University of Calgary Medicine, Calgary, AB, Canada (79 patients); University of California Los Angeles (UCLA) Stroke Center, Los Angeles, CA (78 patients); Institute of Neurosciences and Psychology, University of Glasgow, Glasgow, United Kingdom (25 patients). The use of this data was approved by the local Institutional Review Board (IRB).
Inclusion criteria for this retrospective study were: (1) diagnosis of acute ischemic stroke, (2) PWI of the brain performed at day 0, (3) HT assessed 24h after intervention. A stroke neurologist (D.S.L.) from UCLA retrospectively examined gradient-recalled echo (GRE) (and any other images available) for signs of HT. The expert was blinded to PWI permeability images and asked to subdivide HT into 4 types according to previously described definitions [20]: HI1, HI2 (Petechiae within the infarcted area), PH1 or PH2 (parenchymal hematoma with extensive hemorrhage). Among the 277 patients considered, 14 were discarded due to either short scan acquisition times, artifact due to patient movement, or failed image processing. The demographics of the 263 selected patients who satisfied the above-mentioned criteria are summarized in Table 1. They had a mean age of 69 ± 15 years, 153 were women, and baseline median NIHSS was 10 (range, 0 – 40). All patients underwent MRI before possible recanalization therapy. T2*-MRI sequences were acquired as part of routine imaging evaluation at a median of 214 minutes from symptom onset. Treatments included IV tPA alone (129), endovascular recanalization alone (55), and both in 27 cases. Overall, HT on gradient-echo (GRE) images at 24 hours was observed in 84 (31.9%), including 34 HI1, 30 HI2, 9 PH1 and 11 PH2.
Table 1.
Demographic information from 263 patients with Acute Is-chemic Stroke.
| Patient Demographics
| |
|---|---|
| Characteristic | Value |
| Gender | 110 men, 153 women |
| Age | 69 ± 15 |
| NIHSS | 10 (0 – 40) |
| Imaging time | 258 min (33 – 1620 min) |
| Treatment | IV tPA (129), endovascular recanalization (55), both (27) |
| Number of HT | 84 (31.9%) |
| Type of HT | HI1 (34), HI2 (30), PH1 (9), and PH2 (11) |
Because of the multicentric origin of the data, image acquisition parameters vary across subjects. The MRI protocol (at 1.5 or 3 Tesla) included T2* perfusion-weighted imaging (PWI) sequences at onset. PWI was performed with a timed contrast bolus passage technique (0.1mg/kg contrast administered into an antecubital vein with a power injector at a rate of 5 cm3/sec). The PWI parameters were as follows (median, minimum, maximum): repetition time, 2000 ms (from 1400 to 4000 ms); TE, 45 ms (from 21.6 to 65 ms); slice thickness, 5 mm (from 4 to 7 mm); no gap; matrix size, 128 × 96 to 256 × 256; and field of view, 240 mm. Post-intervention gradient-recalled echo (GRE) was acquired with repetition time, 800 ms; TE, 15 ms. The analysis was confined to cases with sufficient scan acquisition times (> 60 sec) to permit BBB leakage to be discerned from analysis of late transit phases of gadolinium passage associated with contrast bolus.
2.2. Permeability Features From Perfusion MRI (PWI)
PWI source images are processed retrospectively to extract specific permeability imaging features used as surrogate for risks of HT using previously introduced image processing algorithms [19, 14]. A total of six T 2*-based permeability feature maps are extracted from the contrast concentration-versus-time curve using the Stroke Cerebral Analysis (SCAN) software developed in our imaging laboratory. The features included in this study were selected because they demonstrated significant correlation with development of HT in previous works; they are relative recirculation rℝ, percentage recovery %ℝ, post-bolus area (PB), mean post-bolus intensity (MPB), terminal slope of concentration curve (CS), final contrast (FC).
Features are estimated for each voxel of the brain volume using the concentration-time curve ΔR2* [21] (an illustrative example from simulated data is shown in Fig. 1) derived from the measured image intensity I,
Figure 1.
Illustrative example of a concentration versus time curve ΔR2* (orange), as well as its γ-variate fit (blue). The peak ( ) corresponds to the maximum value on the fitted curve. tA and tN define the dynamic phase comprised between the onset of the recirculation phase measured at half height of the descending curve and the end of measurements. The PB area corresponds to the difference between the actual ΔR2* and the fitted curve . From this area, it is possible to derive rℝ (Eq. (2)) and %ℝ (Eq. (4)). In addition to those ratios, the contrast slope (CS) and the final contrast (FC) are also used as permeability features.
| (1) |
where I(0) is the baseline image intensity of a voxel before injection, I(t) is the image intensity at time t (with contrast agent present), and TE is the echo time. Once the concentration curve ΔR2* has been calculated (as depicted by the orange curve in Fig. 1), it is fitted using a γ-variate function to produce a theoretical curve (see blue curve in Fig. 1).
The relative recirculation rℝ [17] corresponds to the difference between the measured ΔR2* and theoretical curve relative to the maximum of the theoretical curve . It is formalized as follows,
| (2) |
| (3) |
where α is the weighted maximum of the fitted contrast curve, tA is the dynamic phase corresponding to the on-set of the recirculation phase measured at half height of the descending aspect of the curve, and tN is the final dynamic phase.
The total area difference in Eq (2) is denoted PB (for post-bolus area) and the mean post-bolus intensity (MPB) is computed as follows, MPB = PB/(tN − tA).
The percentage of recovery %ℝ was computed by determining the difference between the maximum of the fitted curve and mean post-bolus intensity (MPB),
| (4) |
The contrast slope (CS) of late signal intensity change was calculated using linear regression from signal intensities at the terminal 10 seconds (between 50 and 60 seconds after contrast injection) of the PWI sequence. It was shown in a recent study that the permeability images obtained at this time interval provided more sensitive BBB leakage than earlier scan images. The remaining permeability feature corresponds to the final contrast value (FC) at time tN projected from the linear model.
2.3. Description of Permeability Map Distribution
In order to evaluate the predictive power of the six types of permeability images presented in the previous section, the images need to be transformed into vectors x that can be input to the classifier to predict HT. The proposed approach computes histograms h1, h2 of the permeability feature intensity distribution across each hemisphere and combines them (by concatenating their values and their difference) to create a descriptor x = {h1, h2, | h1 − h2|} that characterizes the volume, as detailed in this section and illustrated in Figure 2.
Figure 2.

Illustration of the framework used to predict hemorrhagic transformation (HT) on ischemic stroke patients. A permeability feature map is first extracted from source perfusion weighted images (PWI). Intensity histograms are then computed from each hemisphere and used as input features to a classifier trained to discriminate between HT and control patients.
Before computation of the histograms however, the framework requires segmentation of the two cerebral hemispheres. The skull and non-brain tissue that could interfere with the process is stripped using the FSL Brain Extraction Tool (BET) [22] that is integrated into a pipeline software developed by the Laboratory of Neuro Imaging (LONI) at UCLA (http://www.loni.ucla.edu/). BET estimates an intensity threshold to discriminate between brain/non-brain voxels based on the average intensity of the PWI over the entire run. Then, it determines the center of gravity of the head, defines a sphere based on the center of gravity of the volume, and finally deforms it towards the brain surface.
Once the brain volume has been segmented, the next step is to identify the two cerebral hemispheres. The approach chosen in this study is similar in spirit to the one presented by Maes et al [23] and successfully applied on several problems. The brain volume is registered to the high-resolution single-subject template of the ICBM (International Consortium for Brain Mapping) [24] available freely at http://www.loni.ucla.edu/Atlases/. The template is aligned within the stereotaxic space of the ICBM average template derived from Montreal Neurological Institute database [25]. Cortical gyri, subcortical structures and the cerebellum have been delineated from the structural brain template and are used to derive the labels of the two cerebral hemispheres. Registration is applied to each volume by inferring an affine transformation. The registration parameters are then applied to deform a labeled mask of the cerebral hemispheres to the current study; thus obtaining the hemisphere labels for each voxel by overlaying the projected mask.
The description of the intensity distribution across the hemisphere is challenging for three main reasons: first, it is high-dimensional as an hemisphere is made of thousands of voxels, second the number of voxels is different for each case, and finally, image abnormalities may occur at different locations. Therefore, direct voxel-to-voxel matching of images between patients is not feasible. To overcome these issues, the hemisphere of each permeability image is represented as a normalized histogram. Histograms are one of the simplest non-parametric way to characterize a distribution. Each of the two histograms h1, h2 ∈ R40 contains 40 bins distributed equally between the minimum and maximum value computed using the 10th and 90th percentile of the data. Because the total number of voxels N is different for each hemisphere, each histogram is hi is normalized according to N, hi = hi/N. The final descriptor x = {h1, h2, |h1 − h2|} is constructed by concatenating the values of the two histograms as well as their bin-to-bin difference. The difference between the two histograms |h1 − h2| allows to detect asymmetrical changes in the permeability image; a possible indicator of future HT. It also become makes the descriptor invariant to baseline shift of the permeability value.
Finally, each bin x( j), j ∈ [1,120] is normalized individually using the minimum and maximum value observed across the training set. This is a very common pre-processing procedure in machine learning that helps to account for the possible differences in the range between the different bins. If such a normalization was not performed, the bins that tend to have a larger number of observations might have been favored during the training of the regression models. Each descriptor is labelled y ∈ {0,1} as HT (1) or not (0), depending if an hemorrhagic transformation occurred and could be observed for the patient at followup by examining GRE images.
2.4. Prediction Model
The framework developed in this study aims at representing the possible relation between the proposed descriptor using a classifier which is learned in a supervised way from a set of training images with known outcome (HT or not). The use of a machine learning model, unlike correlation studies, has the advantage that it may be able to capture nonlinearity and later be used to predict the likelihood of HT on new cases.
The model takes the form a classification model y = f (x) that maps the 120-dimensional normalized histogram x ∈ X computed over the two hemispheres to the outcome y ∈ Y, described in terms of hemorrhagic transform observed in the followup GRE image. A comparative analysis is provided between Spectral Regression (SR-DA) [26], Kernel Spectral Regression (SR-KDA) [26] and Support Vector Machine (SVM) [27]. Note that these models are well established in the machine learning community and have been successfully applied to a wide variety of imaging prediction applications. In addition to these classification techniques, we also evaluate a k-nearest neighbor classifier (k-NN) [28] as baseline predictive model. k-NN is a method for classifying samples based on the closest training samples in the feature space (measured using Euclidean distance). The output of any new sample is chosen as the most common outcome among those associated to its k closest neighbors.
2.4.1. SR-DA algorithm
SR-DA algorithm [26] is a recently proposed method to solve discriminant analysis (DA) as a regularized regression problem,
| (5) |
where xi is the input vector (i.e. histogram), yi the corresponding HT outcome, α is the eigenvector, and β is the regularization parameter.
To solve this problem (Eq. (5)), the main idea behind SR-DA is to find vectors α that map the input features x to the output y so that samples that are close also produce similar outputs. SR-DA formulates the regularization as follows,
| (6) |
where I is the identity matrix, α is the eigenvector, and δ > 0 the regularization parameter. Interestingly, this formulation can be solved efficiently using a Cholesky decomposition,
| (7) |
| (8) |
2.4.2. SR-KDA algorithm
SR-KDA [26] generalizes SR-DA to utilize a kernel projection of the data and obtain nonlinearity. Input data samples x ∈ X are projected onto a high-dimensional space via a Gaussian kernel K,
| (9) |
where σ is the standard deviation of the kernel.
Similarly to SR-DA, SR-KDA uses a Cholesky decomposition from the regularized positive definite matrix K and class labels y to obtain vectors α,
| (10) |
| (11) |
When a new input feature vector, xnew, is extracted from a new patient, the likelihood for HT, ŷnew, is computed using
| (12) |
| (13) |
where k is the vector resulting from the kernel projection of xnew into the kernel space using training data X.
2.4.3. Support Vector Machine
A Support Vector Machine (SVM) [27] is a supervised machine learning technique for classification problems where each sample xi ∈ X is labelled as yi ∈ {1, −1}. SVM aims at finding the optimal separating hyperplane that minimizes the misclassification rate on the training set, while maximizing the sum of distances of the training samples from this hyperplane. Formally, this problem amounts to finding the parameter α, such that:
| (14) |
where C is a constant that controls the amount of penalty on the error term during the minimization process, e is the vector of all ones, and Q is a matrix defined as:
| (15) |
This minimization provides a solution for the following function:
| (16) |
where x is a new input vector.
2.5. Experimental Setup
The experiments proposed in this study first aim at evaluating if the proposed methodology that uses machine learning models of permeability-based histograms can be used to predict HT in a reliable fashion. The second purpose is to provide a comparative analysis between six previously introduced permeability imaging features (section 2.2) used a surrogate markers for risk of HT. Finally, the performance of three state-of-the-art machine learning techniques (SR-DA, SR-KDA, SVM) are compared to a standard k-nearest neighbor (k-NN) classifier used as baseline method.
Using the dataset of 263 patients (section 2.1), a 10-fold cross-validation (CV) is performed to compare the different permeability maps and the predictive models; SR-DA, SR-KDA, SVM, and k-NN. The cross-validation process is repeated for five independent runs such that the distribution among the different folds is randomized at each run. The parameters of each model (δ for SR-DA, δ,σ for SR-KDA, C,σ for SVM, k for k-NN) are optimized at each iteration of the crossvalidation by applying an inner 10-fold cross-validation that excludes the patients to be tested at the current iteration. Such practice is highly recommended to avoid model overfitting. Once the cross-validation is completed, the area under the curve (AUC) is computed from the relative operating characteristic (ROC) curve and used as measure of performance. The ROC curve is a plot created by considering the true positive rate (TPR = TP/(TP+FN)) versus the false positive rate (FPR = FP/(FP+TN)), at various threshold settings. Intuitively, the AUC represents the probability of correct classification for a randomly chosen pair of positive and negative samples.
The comparison of the different single permeability parameters should indicate which maps perform better. It can also be hypothesized that these features may hold complementary information about development of HT. To test this hypothesis, we evaluate the predictive power of the combination of the six feature maps for each patient using the same crossvalidation protocol described in the previous paragraph. For each volume, a combined input descriptor xc is constructed by concatenating the input features of the six different permeability features into a single vector xc = [x1 x2 x3 x4 x5 x6].
Differences observed in AUCs can be used to rank different models, however, they may not be statistically significant. To verify if the differences between images and regression models are statistically significant on our dataset, the 95% confidence interval associated with each AUC is computed using DeLong et al [29] method and significance tests are performed using a binomial exact test between AUCs obtained for the different models.
In addition to these tests, we compute the average histogram of each permeability feature to examine if obvious differences could be observed between HT and non-HT patients at the population level.
3. Results
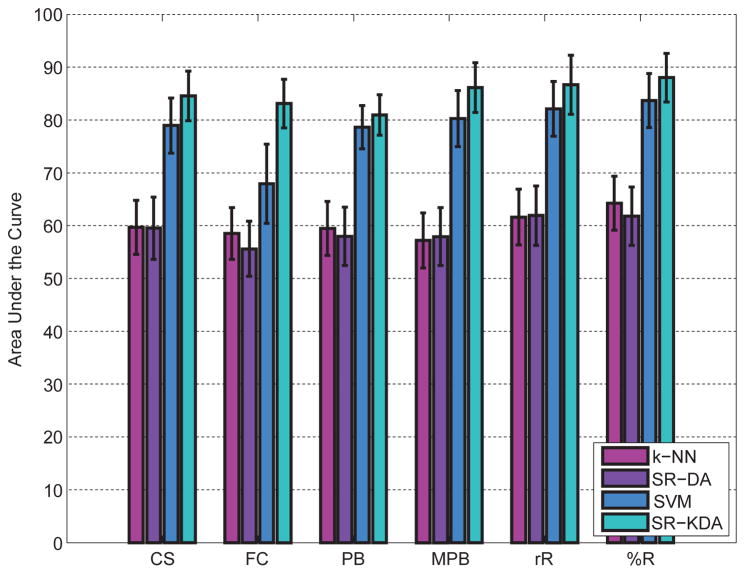
Results in terms of AUC after a 10-fold crossvalidation are depicted in Figure 3 for each permeability feature. SR-KDA and SVM offer significantly (p < 0.01) better results than SR-DA and k-NN for each permeability feature map. Performance for SR-KDA is as follows, 84.53% (CS), 83.12% (FC), 80.96% (PB), 86.11% (MPB), 86.66% (rℝ), 88.03% (%ℝ). For SVM, results are 78.95% (CS), 67.9% (SC), 78.61% (PB), 80.25% (MPB), 82.12% (rℝ), 83.67% (%ℝ), respectively. For linear regression, results are significantly lower 59.51% (CS), 55.61% (FC), 57.98% (PB), 57.92% (MPB), 61.90% (rℝ), 61.79% (%ℝ). Similarly, the baseline method based on k-NN does not predict HT reliably 59.69% (CS), 58.50% (FC), 57.21% 59.48% (MPB), 61.62% (rℝ), 64.26% (%ℝ). NIHSS at onset (r = 0.25, p < 0.01) was correlated with HT at 24 hours.
Figure 3.
Area under the cuve (AUC) computed for each permeability parameter after a 10-fold crossvalidation. 95% confidence intervals were estimated using DeLong’s method and reported as error bars.
For SR-KDA and SVM, the percentage recovery feature %ℝ was found significantly better than CS, FC, and PB features.
Results obtained by combining the six permeability maps reached 88.21% for SR-KDA but were not found significantly better (p > 0.01) than %ℝ (88.03%). This might be explained by the fact that each permeability features may require a different optimal parameter (e.g. regularization parameter for SR-KDA) and therefore may not be optimal when all the features are combined within a single input vector. A possible solution to solve this problem would be to consider hierarchical models that would have several layers and may therefore exploit the respective optimal parameters of each feature map.
Figure 4 illustrates an example of typical permeability abnormalities that may occur for five patients that underwent hemorrhagic transformation. For each patient, the six permeability maps are shown side by side. GRE and FLAIR images acquired 24 hours after intervention are also shown. GRE was used by the expert to identify possible bleeding. It can be seen that for HT cases, local changes in the area with BBB disruption and HT can be observed in the permeability imaging features and are predictive of HT as observed in post-treatment GRE.
Figure 4.
Illustration of the six permeability parameters (percentage recovery %,ℝ, relative recovery rℝ, post-bolus area (PB), mean post-bolus area (MPB), final contrast (FC), contrast slope (CS)) used in this study on five acute ischemic stroke patients with subsequent hemorrhagic transform.
The average normalized histogram of each feature is reported in Figure 5. It can be observed that each feature has a specific average distribution. The peak observed in each graph corresponds to the permeability value that was the most frequent and can be thought to originate from the brain area that was not affected by permeability abnormalities. Values located away from the peak are more likely to correspond to disrupted permeability areas. Note that the peaks are not centered at 0 because the range is defined using a normalization procedure based on the 10th and 90th percentiles. Although, they were not statistically significant, differences can observed between HT and non-HT patients by looking at the average over the population. For example, rℝ and %ℝ for HT average both exhibit an increase in the non-peak area. PB, which is thought to be larger for HT patients in the affected area, also indicates an increase. However, we could not observe any specific patterns in the average distribution of the final contrast (FC) and contrast slope (CS). It is likely that their distribution is multi-modal and therefore not clearly separated when the average value is used to summarize the population. This observation reinforces the need of nonlinear models such as the ones used in this study (SR-KDA, SVM).
Figure 5.
Illustration of the normalized histograms corresponding to each permeability imaging feature: FC, CS, PB, MPB, rℝ, %ℝ. The average distribution is reported for the two populations; with subsequent development of hemorrhagic transform (HT, blue) or not (controls, red).
We did not observe a significant correlation between the accuracy of the model and the time from symptom onset. However, this does not imply that the timing information may not be useful to improve the accuracy of the predictive model when used jointly with imaging features.
4. Discussion
The prediction of hemorrhagic transformation in acute ischemic stroke is a challenging problem that could potentially improve the clinical decision making process and make safe treatment available to victims of stroke who are excluded by current standards. Ultimately, automatic predictive models could also help us improve our understanding of the underlying mechanisms of HT through images acquired during routine acquisition protocol. While these mechanisms rely on complex, inter-related factors (time-to-onset, age, medical history), permeability disruption can be observed by extracting parameters from perfusion images in the acute phase. Integrating all these elements within a unified predictive model is the long-term goal of our research.
Several works [15, 16, 17, 18, 14] have reported the correlation existing between the permeability features extracted from PWI and the development of HT. However, the use of these features within a predictive model remained to be done. Inspired by recent works [19] that successfully tackled this problem, we have described in this paper a generic predictive model of HT in acute ischemic stroke. Our multi-center study of HT prediction (263 patients) ranks among the largest to date and provides a comparative analysis between six permeability imaging features. A particularity of the model is to be based on normalized intensity histograms to represent the overall distribution of each hemisphere to characterize possible assymetrical permeability abnormalities. Therefore, the proposed model does not require the direct identification of abnormal voxels (or infarct core [19]).
Our experimental results have validated the method by reaching accuracy levels of over 85%. Note that such a level of accuracy apply for a patient population with similar treatment methods (IV tPA (129), endovascular recanalization (55)) as the type of treatment is likely to have influenced HT for those patients. Nonlinear predictive models based on SR-KDA and SVM significantly improve results obtained by linear and k-NN approaches. The good performance demonstrated by the system may be explained by the three main following factors. First, as it has been demonstrated in several studies, all the six permeability maps tested within the framework are strong predictors of subsequent HT for patients with acute ischemic stroke. Second, the histogram descriptor used in this study is able to describe the intensity distribution of the parameters in a compact fashion and obtain invariance to the location of the potential abnormality. Third, the use of nonlinear mapping (through the classifier) can capture specific precursory patterns within the normalized histograms.
There is a margin for improvement in several aspects of this research direction. A major limitation of these permeability parameters is that their use is confined to areas where the contrast agent can be measured. It would be interesting to study the relationship between the permeability maps with the size of the region at risk, as well as other perfusion imaging parameters routinely acquired during the imaging protocol such as cerebral blood volume (CBV), cerebral blood flow (CBF), mean transit time (MTT), and Tmax. Although the descriptors used in this work were sensitive to global changes of the intensity distribution and produces a single score of likelihood of HT as output, it would be of great interest to extend the model so that it can produce risk maps of HT across the entire brain volume. Visual interpretation of current permeability maps is not trivial and often require specific windowing of the intensity. A possible approach to standardize the predicted maps would be to use a regional predictive model, similar to what we have recently utilized for tissue fate prediction [30, 31]. The model would then become sensitive to regional changes in the permeability maps. In addition to predicting the likelihood of HT across the brain volume, it may be interesting to predict the type of HT. We should also acknowledge that there is currently no gold standard for the characterization of HT from images and the use of GRE using visual review may also hold some limitations.
While the six permeability maps have been shown to correlate with HT among stroke patients in various studies, it is still not clear which one would be the most beneficial in practice and provide the best information to the clinician. With the multiplication of imaging parameters derived from PWI and DWI, there is a danger that clinicians may soon become overwhelmed with abundant and possibly contradicting information. Therefore, the selection or the combination of these parameters into summarized images may be a topic of interest. Another possible line of research would be to use raw PWI directly to a machine learning algorithm that would automatically learn the most useful features to predict HT; thus avoiding the choice of a specific permeability map. We are currently exploring this idea for our future studies.
Permeability imaging features have demonstrated to be good predictors of HT. However, additional variables may also be helpful in improving the development of HT, such as type of intervention, clinical parameter, degree of success of arterial recanalization intervention, time-to-symptom onset, quality of collateral, etc. Integrating all these factors within a single multi-modal predictive is likely to provide even more accurate predictions.
5. Conclusion
In summary, we have demonstrated that the distribution of the intensity of previously introduced permeability maps can be used to predict future hemorrhagic transformation in acute ischemic stroke patients treated with t-PA or recanalization therapy. The generalization of such a predictive model to produce continuous risk maps would bring additional information during the clinical decision making process. Specifically, it would help to identify patient with no BBB abnormalities which may be a criterion to extend the time window to administer t-PA for acute ischemic stroke patients who would currently be excluded by the current fixed time window.
Acknowledgments
This work was supported by the National Institute of Neurological Disorders and Stroke (NINDS), grants from the National Institutes of Health K23-NS054084, P50-NS044378, R01-NS066008, and the Canadian Institutes for Health Research (CIHR MOP-118096) and Heart and Stroke Foundation (HSF) of Alberta, NWT and Nunavut. STIR and VISTA Imaging steering committee: Steven Warach (co-chair), Gregory Albers, Stephen Davis, Geoffrey Donnan, Marc Fisher, Tony Furlan, James Grotta, Werner Hacke, Dong-Wha Kang, Chelsea Kidwell, Walter Koroshetz, Kennedy R. Lees, Michael Lev, David Liebeskind, A. Gregory Sorensen, Vincent Thijs, Götz Thomalla, Joanna Wardlaw, Max Wintermark (co-chair).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Hacke W, Donnan G, Fieschi C, Kaste M, von Kummer R, Broderick JP, Brott T, Frankel M, Grotta JC, Haley EC, Kwiatkowski T, Levine SR, Lewandowski C, Lu M, Lyden P, Marler JR, Patel S, Tilley BC, Albers G, Bluhmki E, Wilhelm M, Hamilton S. Association of outcome with early stroke treatment: pooled analysis of ATLANTIS, ECASS, and NINDS rt-PA stroke trials. Lancet. 2004;363:768–774. doi: 10.1016/S0140-6736(04)15692-4. [DOI] [PubMed] [Google Scholar]
- 2.Jaillard A, Cornu C, Durieux A, Moulin T, Boutitie F, Lees KR, Hommel M. Hemorrhagic transformation in acute is-chemic stroke. The MAST-E study. MAST-E Group. Stroke. 1999;30:1326–1332. doi: 10.1161/01.str.30.7.1326. [DOI] [PubMed] [Google Scholar]
- 3.Selim M, Fink JN, Kumar S, Caplan LR, Horkan C, Chen Y, Linfante I, Schlaug G. Predictors of hemorrhagic transformation after intravenous recombinant tissue plasminogen activator: prognostic value of the initial apparent diffusion coefficient and diffusion-weighted lesion volume. Stroke. 2002;33:2047–2052. doi: 10.1161/01.str.0000023577.65990.4e. [DOI] [PubMed] [Google Scholar]
- 4.Fiehler J, Remmele C, Kucinski T, Rosenkranz M, Thomalla G, Weiller C, Zeumer H, Rother J. Reperfusion after severe local perfusion deficit precedes hemorrhagic transformation: an MRI study in acute stroke patients. Cerebrovasc Dis. 2005;19:117–124. doi: 10.1159/000083180. [DOI] [PubMed] [Google Scholar]
- 5.Kim EY, Na DG, Kim SS, Lee KH, Ryoo JW, Kim HK. Prediction of hemorrhagic transformation in acute is-chemic stroke: role of diffusion-weighted imaging and early parenchymal enhancement. AJNR Am J Neuroradiol. 2005;26:1050–1055. [PMC free article] [PubMed] [Google Scholar]
- 6.Campbell BC, Christensen S, Butcher KS, Gordon I, Parsons MW, Desmond PM, Barber PA, Levi CR, Bladin CF, De Silva DA, Donnan GA, Davis SM. Regional very low cerebral blood volume predicts hemorrhagic transformation better than diffusion-weighted imaging volume and thresholded apparent diffusion coefficient in acute ischemic stroke. Stroke. 2010;41:82–88. doi: 10.1161/STROKEAHA.109.562116. [DOI] [PubMed] [Google Scholar]
- 7.Gupta R, Yonas H, Gebel J, Goldstein S, Horowitz M, Grahovac SZ, Wechsler LR, Hammer MD, Uchino K, Jovin TG. Reduced pretreatment ipsilateral middle cerebral artery cerebral blood flow is predictive of symptomatic hemorrhage post-intra-arterial thrombolysis in patients with middle cerebral artery occlusion. Stroke. 2006;37:2526–2530. doi: 10.1161/01.STR.0000240687.14265.b4. [DOI] [PubMed] [Google Scholar]
- 8.Neumann-Haefelin T, Hoelig S, Berkefeld J, Fiehler J, Gass A, Humpich M, Kastrup A, Kucinski T, Lecei O, Liebeskind DS, Rother J, Rosso C, Samson Y, Saver JL, Yan B. Leukoaraiosis is a risk factor for symptomatic intracerebral hemorrhage after thrombolysis for acute stroke. Stroke. 2006;37:2463–2466. doi: 10.1161/01.STR.0000239321.53203.ea. [DOI] [PubMed] [Google Scholar]
- 9.Kidwell C, Alger J, Saver J, Mattiello J, Woods R, Starkman S, Liebeskind D, Vespa P, Jahan R, Gobin Y, Sayre J, Duckwiler G, Vinuela F. Mr signatures of infarction vs salvageable penumbra in acute human stroke: a preliminary model. Stroke. 2000;31:285. [Google Scholar]
- 10.Puetz V, Dzialowski I, Hill MD, Subramaniam S, Sylaja PN, Krol A, O’Reilly C, Hudon ME, Hu WY, Coutts SB, Barber PA, Watson T, Roy J, Demchuk AM. Intracranial thrombus extent predicts clinical outcome, final infarct size and hemorrhagic transformation in ischemic stroke: the clot burden score. Int J Stroke. 2008;3:230–236. doi: 10.1111/j.1747-4949.2008.00221.x. [DOI] [PubMed] [Google Scholar]
- 11.Kassner A, Roberts TP, Moran B, Silver FL, Mikulis DJ. Recombinant tissue plasminogen activator increases blood-brain barrier disruption in acute ischemic stroke: an MR imaging permeability study. AJNR Am J Neuroradiol. 2009;30:1864–1869. doi: 10.3174/ajnr.A1774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Latour LL, Kang DW, Ezzeddine MA, Chalela JA, Warach S. Early blood-brain barrier disruption in human focal brain ischemia. Ann Neurol. 2004;56:468–477. doi: 10.1002/ana.20199. [DOI] [PubMed] [Google Scholar]
- 13.Schaefer PW, Copen WA, Lev MH, Gonzalez RG. Diffusion-weighted imaging in acute stroke. Neuroimaging Clin N Am. 2005;15:503–530. doi: 10.1016/j.nic.2005.08.011. [DOI] [PubMed] [Google Scholar]
- 14.Bang OY, Saver JL, Alger JR, Shah SH, Buck BH, Starkman S, Ovbiagele B, Liebeskind DS, Bang OY, Saver JL, Buck BH, Alger JR, Starkman S, Ovbiagele B, Kim D, Ali LK, Shah SH, Panagotacos J, Ohanian A, Yoon SR, Jahan R, Salamon N, Duckwiler GR, Villablanca JP, Vinuela F, Liebeskind DS. Patterns and predictors of blood-brain barrier permeability derangements in acute is-chemic stroke. Stroke. 2009;40:454–461. doi: 10.1161/STROKEAHA.108.522847. [DOI] [PubMed] [Google Scholar]
- 15.Lupo JM, Cha S, Chang SM, Nelson SJ. Dynamic susceptibility-weighted perfusion imaging of high-grade gliomas: characterization of spatial heterogeneity. AJNR Am J Neuroradiol. 2005;26:1446–1454. [PMC free article] [PubMed] [Google Scholar]
- 16.Bang OY, Buck BH, Saver JL, Alger JR, Yoon SR, Starkman S, Ovbiagele B, Kim D, Ali LK, Sanossian N, Jahan R, Duckwiler GR, Vinuela F, Salamon N, Villablanca JP, Liebeskind DS. Prediction of hemorrhagic transformation after recanalization therapy using T2*-permeability magnetic resonance imaging. Ann Neurol. 2007;62:170–176. doi: 10.1002/ana.21174. [DOI] [PubMed] [Google Scholar]
- 17.Wu S, Thornhill RE, Chen S, Rammo W, Mikulis DJ, Kassner A. Relative recirculation: a fast, model-free surrogate for the measurement of blood-brain barrier permeability and the prediction of hemorrhagic transformation in acute is-chemic stroke. Invest Radiol. 2009;44:662–668. doi: 10.1097/RLI.0b013e3181ae9c40. [DOI] [PubMed] [Google Scholar]
- 18.Thornhill RE, Chen S, Rammo W, Mikulis DJ, Kassner A. Contrast-enhanced MR imaging in acute ischemic stroke: T2* measures of blood-brain barrier permeability and their relationship to T1 estimates and hemorrhagic transformation. AJNR Am J Neuroradiol. 2010;31:1015–1022. doi: 10.3174/ajnr.A2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kassner A, Liu F, Thornhill RE, Tomlinson G, Mikulis DJ. Prediction of hemorrhagic transformation in acute ischemic stroke using texture analysis of postcontrast T1-weighted MR images. J Magn Reson Imaging. 2009;30:933–941. doi: 10.1002/jmri.21940. [DOI] [PubMed] [Google Scholar]
- 20.Berger C, Fiorelli M, Steiner T, Schabitz WR, Bozzao L, Bluhmki E, Hacke W, von Kummer R. Hemorrhagic transformation of ischemic brain tissue: asymptomatic or symptomatic? Stroke. 2001;32:1330–1335. doi: 10.1161/01.str.32.6.1330. [DOI] [PubMed] [Google Scholar]
- 21.Rosen BR, Belliveau JW, Vevea JM, Brady TJ. Perfusion imaging with NMR contrast agents. Magn Reson Med. 1990;14:249–265. doi: 10.1002/mrm.1910140211. [DOI] [PubMed] [Google Scholar]
- 22.Smith S. Fast robust automated brain extraction. Human Brain Mapping. 2002;17:143–155. doi: 10.1002/hbm.10062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Maes F, Leemput K, DeLisi L, Vandermeulen D, Suetens P. Quantification of cerebral grey and white matter asymmetry from mri. In: Taylor C, Colchester A, editors. MICCAI 99, volume 1679 of Lecture Notes in Computer Science. Springer; Berlin Heidelberg: 1999. pp. 348–357. [Google Scholar]
- 24.Mazziotta JC, Toga AW, Evans A, Fox P, Lancaster J. A probabilistic atlas of the human brain: theory and rationale for its development. The International Consortium for Brain Mapping (ICBM) Neuroimage. 1995;2:89–101. doi: 10.1006/nimg.1995.1012. [DOI] [PubMed] [Google Scholar]
- 25.Talairach J, Tournoux P. A co-planar stereotaxic atlas of a human brain. Thieme; Stuttgart: 1988. [Google Scholar]
- 26.Cai D, He X, Han J. Spectral Regression for Efficient Regularized Subspace Learning. ICCV; [Google Scholar]
- 27.Chang C-C, Lin C-J. LIBSVM: a library for support vector machines. 2001 Software available at http://www.csie.ntu.edu.tw/~cjlin/libsvm.
- 28.Cover T, Hart P. Nearest neighbor pattern classification, Information Theory. IEEE Transactions on. 1967;13:21–27. [Google Scholar]
- 29.DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics. 1988;44:837–845. [PubMed] [Google Scholar]
- 30.Scalzo F, Hao Q, Alger JR, Hu X, Liebeskind DS. Regional prediction of tissue fate in acute ischemic stroke. Ann Biomed Eng. 2012;40:2177–2187. doi: 10.1007/s10439-012-0591-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Scalzo F, Hao Q, Alger J, Hu X, Liebeskind D. Advances in Visual Computing, volume 6454 of Lecture Notes in Computer Science. Springer; Berlin/Heidelberg: 2010. Tissue fate prediction in acute ischemic stroke using cuboid models; pp. 292–301. [Google Scholar]