Quantitative Assessment of in vivo Breast Masses using Ultrasound Attenuation and Backscatter

Abstract

Clinical analysis of breast ultrasound imaging is done qualitatively, facilitated with the ultrasound breast imaging-reporting and data system (US BIRADS) lexicon which helps to standardize imaging assessments. Two descriptors in that lexicon, “posterior acoustic features” and the “echo pattern” within a mass, are directly related to quantitative ultrasound parameters, namely ultrasound attenuation and the average backscatter coefficient. The purpose of this study was to quantify ultrasound attenuation and backscatter in breast masses and to investigate these quantitative ultrasound (QUS) properties as potential differential diagnostic markers.

RF echo signals were from patients with breast masses during a special ultrasound imaging session prior to core biopsy. Data were also obtained from a well characterized phantom using identical system settings. Masses include 14 fibroadenomas and 10 carcinomas. Attenuation for the acoustic path lying proximal to the tumor was estimated offline using a Least Squares Method with constraints. Backscatter coefficients (BSC) were estimated using a Reference Phantom Method. The attenuation coefficient within each mass was assessed using both the Reference Phantom Method and a hybrid method, and effective scatterer diameters (ESD) were estimated using a Gaussian form factor model.

Attenuation estimates obtained with the reference phantom method were consistent with estimates done using the hybrid method in all cases except for two masses. The mean slope of the attenuation coefficient vs. frequency for carcinomas was 20% greater than the mean slope value for the fibroadenomas. The product of the attenuation coefficient and anteroposterior dimension of the mass was computed to estimate the total attenuation for each mass. That value correlated well with the BI-RADS assessment of “posterior acoustic features” judged qualitatively from gray scale images. Nearly all masses were described as “hypoechoic”, so no strong statements could be made about the correlation of echo pattern findings in BI-RADS with the averaged BSC values. However, most carcinomas exhibited lower values for the frequency average BSC than fibroadenomas. The mean ESD alone did not differentiate the mass type but fibroadenomas had greater variability in ESDs within the ROI than that found for invasive ductal carcinomas. This study demonstrates the potential to utilize attenuation and QUS parameters associated with the backscatter coefficient as quantitative descriptors.

INTRODUCTION

Ultrasound is a valuable tool to use in conjunction with X-ray mammography for diagnosing breast masses. A common use of ultrasound in breast imaging is to distinguish between cystic and solid masses. However ultrasound can also assist in differentiating among different solid masses. Clinically, the modality is most useful in assessing very dense breasts because the sensitivity of mammography for dense breast conditions is low (35–48%).¹

Considerable progress has been made to establish ultrasound criteria for differentiating benign from malignant breast tumors.^2–6 Various sonographic features, including a lesion’s margin, its shape, and its internal echo texture are evaluated.^3,7,8 Malignant masses are often characterized by poorly defined margins on ultrasound B-mode images, irregular and sometimes spiculated boundaries, micro-lobulations, hypo-echogenicity, and shadowing. They sometimes are associated with duct extension, and tissue architectural distortion. Benign masses, on the other hand, more often have well-defined and circumscribed boundaries, and round or oval shapes with gentle bi- or tri-lobulations.⁹ Several studies^10,11 evaluated the inter-observer variability in judging these features. Rahbar et al.¹¹ agreed that although such features help differentiate benign from malignant breast masses, there was a need to investigate their practice and interpreter variability. Arger et al.¹⁰ found that the interpretations made by four different readers were comparable when standardized descriptors of breast masses were applied.

In 2003, the American College of Radiology (ACR) developed the first edition of a lexicon, the Ultrasound Breast Imaging Reporting And Data System (US BI-RADS), to standardize the interpretation and reporting of breast masses in ultrasound.¹² Hong et al.¹³ demonstrated that the US BI-RADS descriptors involving lesion margin, shape, orientation, lesion boundary, and internal echo pattern, as well as acoustic features posterior to a mass can be used in differentiating benign from malignant conditions. After applying ultrasound BI-RADS criteria they reported a positive predictive value (PPV) for malignancy of 62–86%.¹³ The PPVs reported by Hong et al. were comparable to PPV values obtained (68–81%) when applying the BI-RADS descriptors for X-ray mammography as reported by Liberman et al.¹⁴

Conventional B-mode ultrasound imaging itself is a qualitative modality because image brightness and other features of displayed echo signals depend on operator settings and on system- and tissue-dependent factors. The subjective interpretation and only moderate specificity result in most solid masses viewed on ultrasound also undergoing a core biopsy to provide a definitive diagnosis. This in turn leads to a high rate of biopsies of benign tumors, resulting in increased stress and burden to patients and high costs to the healthcare system.⁹

Quantitative Ultrasound (QUS) is being studied as a means of aiding in this diagnosis. QUS methods extract estimates of attenuation and backscatter on absolute scales, as well as other features that depend on acoustic wave-tissue interactions. QUS has shown potential for detecting diffuse disease and for diagnosing focal lesions in a number of clinical tasks. For example, estimates of ultrasound attenuation from backscattered echo signals were used to differentiate fatty liver from normal liver.^15,16 Other researchers have demonstrated that ultrasound attenuation has diagnostic value in trabecular bone,¹⁷ cortical bone,¹⁸ and in the breast.^19,20 In addition spectral analysis of backscattered echo signals has been used successfully to differentiate benign from malignant masses in the eyes²¹ and in lymph nodes,^22,23 and to outline high-risk regions to guide prostate biopsies.²⁴ A “scatterer size” descriptor was successfully applied to estimate glomerular and arteriole sizes in kidneys.²⁵ Also preliminary data have been obtained to evaluate the role of QUS in areas such as identifying malignant thyroid nodules²⁶ and liver masses.²⁷ Finally, estimation of the effective scatter diameter differentiated rat mammary fibroadenomas from 4T1 mouse carcinomas.²⁸

The focus of this study is in quantifying attenuation and backscatter properties of breast masses and comparing results with related features reported clinically when applying US BI-RADS descriptors. Within US BI-RADS, echo patterns of breast masses are categorized as anechoic, hypoechoic, isoechoic, hyperechoic or complex. Similarly, posterior acoustic features are described as none, enhancement, shadowing, and combined. Although these descriptors are closely related to the backscatter and the attenuation properties of breast masses, current clinical practice evaluates these features qualitatively and subjectively. This work is the next step in assessing these acoustic features quantitatively using local attenuation values and backscatter coefficients (beyond the work of D’Astous and Foster²⁹) and extends that work by comparing the quantitative estimates to the subjectively assessed BI-RADS descriptors. This study also investigates acoustic attenuation, averaged backscatter coefficients (ABSCs), and effective scatterer diameters (ESDs) as QUS parameters for differentiating benign from malignant breast masses.

METHODS

Data collection

Human subject protocols were University of Wisconsin Health Sciences Institutional Review Board approved and HIPAA compliant. Fifty subjects who were scheduled for an ultrasound-guided breast core biopsy of a suspicious mass were recruited. Subjects were scanned with a Siemens S2000 (Siemens Medical Solutions USA, Inc., Malvern, PA) using an 18L6 linear array transducer operated at a center frequency of 15MHz. Using the Axius Direct ultrasound research interface (URI),³⁰ we obtained RF echo data from longitudinal and transverse planes of the mass and surrounding tissues.

Reference phantom data were also obtained immediately after scanning the breast using the same transducer and equipment settings. The acoustic properties of the reference phantom had been estimated previously using a narrow-band substitution technique³¹ applied to test samples manufactured at the same time as the reference phantom. The sound speed was 1492m/s, measured at 2.5MHz. Attenuation coefficients in the reference phantom, determined at frequencies from 2–10MHz were fit to a linear function of frequency, yielding α(f) (dB · cm⁻¹) = 0.54f, where f is the frequency in MHz. The scanning window of the reference phantom was a 25μm-thick Saran^™ film (Dow Chemical, Midland MI, USA). The backscatter coefficients were measured using a broadband reference reflector method with focused single element transducers.³²

For this report, we restricted the analysis to masses diagnosed by core biopsy to be either fibroadenomas or carcinomas and whose size was larger than 7mm axially. This lesion size restriction was imposed to reduce bias and variance in parameter estimates³³ and resulted in retaining 17 of the total of 54 data sets. This group included 9 fibroadenomas, 5 invasive ductal carcinomas, and one each of invasive lobular carcinoma, intracystic papillary carcinoma, and adenocarcinoma.

We also included in this analysis data from 7 patients scanned using an earlier protocol designed to evaluate breast elasticity imaging,³⁴ where RF echo data had also been acquired. These patients were scanned using a Siemens Antares (Siemens Medical Solutions USA, Inc., Malvern, PA) equipped with a VFX13-5 linear array transducer operated at a center frequency of 10MHz. RF echo data were recorded while the sonographer applied small deformations using the transducer, with an inter-frame strain of less than 1%. Each frame consisted of either 256 or 312 acoustic scan lines. Among the masses present in these 7 patients, there were 5 fibroadenomas, one invasive ductal carcinoma, and one invasive lobular carcinoma. As in the previous data set, echo signals also were recorded from a reference phantom using the same transducer and system settings. In this case the reference phantom consisted of an emulsion containing 70% safflower oil,³⁵ covered with a plastic-coated aluminum foil (Gammex Inc., Middleton, WI, USA). Properties of this reference phantom³¹ were a speed of sound of 1492m/s and an attenuation coefficient vs. frequency slope of 0.54dB·cm⁻¹ MHz⁻¹. Similar to the reference described above, backscatter coefficients were measured using a broadband reference reflector method.³²

Attenuation coefficient estimations

Two methods were used to estimate the local attenuation within the masses: a reference phantom method (RPM)³⁶ and a “hybrid method.”³⁷ Both methods are based on computations of the echo signal power spectral density from a region, and both apply data from the reference phantom to account for system-dependent factors on the echo data.³⁸ For a uniform region in the tissue, referred to as a “parameter estimation region” (PER), the ratio of the echo signal power spectrum at depth z, S_sam(f, z) to S_ref(f, z), the echo signal power spectrum from the same depth in the reference medium, can be written as,³⁶

$$\frac{S_{\mathit{sam}}(f,z)}{S_{\mathit{ref}}(f,z)}=\frac{B_{\mathit{sam}}(f)exp\{-4{\alpha }_{\mathit{sam}}(f)z\}}{B_{\mathit{ref}}(f)exp\{-4{\alpha }_{\mathit{ref}}(f)z\}}$$ (1)

where B(f)’s are backscatter coefficients at frequency f, the α(f) values represent attenuation coefficients, and the subscripts sam and ref designate the sample and the reference phantom, respectively. Assuming B_sam(f) is constant over the PER, the attenuation coefficient within that region may be computed using

$${\alpha }_{\mathit{sam}}(f)=-\frac{{ln\left(\frac{S_{\mathit{sam}}(f,z)}{S_{\mathit{ref}}(f,z)}\right)|}_{z2}-{ln\left(\frac{S_{\mathit{sam}}(f,z)}{S_{\mathit{ref}}(f,z)}\right)|}_{z1}}{4(z_2-z_1)}+{\alpha }_{\mathit{ref}}(f),$$ (2)

where z₁ and z₂ are different depths within the PER in the mass, with z₂>z₁.

A “hybrid” technique, shown to be less prone to artifacts from backscatter variations than the RPM,³⁶ was also applied. It evaluates changes in the center frequency of the sample-to-reference power spectra ratio with depth after applying a Gaussian frequency filter to this ratio. Kim and Varghese³⁷ assumed a linear frequency dependence of the attenuation and modeled the backscatter coefficient B(f) with a simple power law. Then, the relationship between α₀, the attenuation coefficient in dB·cm⁻¹MHz⁻¹, and the slope of the downshifted center frequency vs. depth, df_c(z)/dz, is given by³⁷

$${\alpha }_{0,\mathit{sam}}=-\frac{8.686}{4{\sigma }^2}·\frac{{df}_c(z)}{dz}+{\alpha }_{0,\mathit{ref}}$$ (3)

where σ² is the bandwidth of the transmit pulse.

During breast scanning the sonographer marked the limits of the mass that was to be biopsied, placing fiducial marks near the tumor margins as viewed on B-mode, color flow, and elasticity images. These served as guides during offline analysis. She also measured the dimensions in the acoustic scan line direction using digital calipers. For either attenuation estimation technique, we defined a PER within the mass that was judged to be homogeneous, avoiding distinct boundary echoes, specular reflectors and specular highlights. The power spectrum analysis window size was 3mm (axially, 8 pulse lengths) by 3mm (laterally, 6 uncorrelated acoustic scan lines). Analysis windows overlapped axially and laterally by 90% over the PER, and power spectra were calculated using Welch’s periodogram³⁹ with a 2mm Hann window and the Chirp Z Transform (CZT).⁴⁰ The analysis bandwidth was chosen independently for each mass to select a frequency range where the signal was at least 10dB above the noise floor. In all cases, the lower limit of the bandwidth was between 3MHz and 4MHz, whereas the upper limit ranged from 8MHz to 13MHz for different patients, depending on the depth of the PER. Ratios of the power spectra from the mass to those from the reference were calculated over the PER, and the slope of the attenuation coefficient vs. frequency was determined using the entire axial length of the parameter estimation region, applying either Eq. (2) or Eq. (3). When multiple PERs could be identified within a mass, attenuation coefficient estimates for the different PERs were averaged to obtain a final result using each method.

BI-RADS descriptor “posterior acoustic features”

The BI-RADS descriptor “posterior acoustic features” mainly expresses the degree of attenuation within a mass. To investigate further, the region distal to each mass was assessed on B-mode images by one radiologist and two physicists who are familiar with the BI-RADS criteria and how ultrasound-tissue interactions contribute to B-mode image features. The physicists also reviewed BI-RADS sonographic criteria through discussions with breast radiologists, including reviewing images containing different examples of features. Each observer conducted the assessment independently by subjectively comparing the B-mode image brightness distal to the mass with the brightness of the adjacent tissue (at the same depth). Due to inter-observer variability, the final assessment of the posterior acoustic feature was determined based on the majority opinion from the three observers. When there was no majority opinion, the posterior acoustic feature was rated as “competing interpretation.”

Backscatter coefficient determinations

Echogenicities of masses were quantified by computing the backscatter coefficient applying the reference phantom technique as in Eq. (1).³⁶ For backscatter coefficient estimation, it is necessary to compute the total ultrasound attenuation from the skin surface to the PER.

We define an “effective attenuation coefficient,” α_eff(f) to represent attenuation for the entire tissue path above each backscatter coefficient PER. A least squares method (LSM) has been shown to provide accurate assessments of attenuation when this path is inhomogeneous, such as many cases in the breast scanned here.³⁸ The LSM approximates the total attenuation in Eq. (1) as having a linear frequency dependence so the total attenuation losses are modeled as exp(−α_eff fz), where z is the depth to the midpoint of the backscatter PER. Similarly, the backscatter coefficient B(f) within the PER is modeled using a power law, B(f)=b fⁿ. From Eq. (1), the ratio of the echo signal power spectrum from the sample to that from the reference phantom at the same depth can be expressed as

$$\frac{S_{\mathit{sam}}(f,z)}{S_{\mathit{ref}}(f,z)}=\frac{b_{\mathit{sam}}{f}^{n_{\mathit{sam}}}}{b_{\mathit{ref}}{f}^{n_{\mathit{ref}}}}\mathit{exp}\{-4({\alpha }_{\mathit{eff},\mathit{sam}}-{\alpha }_{\mathit{eff},\mathit{ref}})f·z\}.$$ (4)

To solve for the b_sam(f), n_sam, and α_eff,sam in Eq (4), a least squares fitting process is applied over the band of frequencies contained in the backscattered signal.³⁸ To keep the solutions within realistic ranges, the following constraints were imparted during the LSM:

$${10}^{-7}\le b_{\mathit{sam}}\le {10}^{-1},0\le n_{\mathit{sam}}\le 5,0.2\le {\alpha }_{\mathit{eff},\mathit{sam}}(dB·{cm}^{-1}·{\mathit{MHz}}^{-1})\le 2).$$ (5)

The total attenuation over the path above a backscatter PER was accounted for from the estimated effective attenuation coefficient at the depth of the PER. Then the estimated BSCs for PERs within the mass were averaged to obtain the final result.

One use of these data was to compare with subjective descriptors of the echo level according to the BI-RADS lexicon. To do this, the B(f) values computed for the mass were averaged^41,42 over the central frequency range of the echo signal power spectrum (from ~5–8MHz for our cases). The echo pattern of each mass was subjectively evaluated on B-mode images by comparing the echo level within the mass with the echo level of fat surrounding the mass. Just as with the attenuation and posterior feature data, the final determination of the echo pattern was based on a majority opinion. When there was no majority opinion, the echo pattern of the mass was rated as “competing interpretation.” The echo pattern of each mass was also compared with its “average backscatter coefficient” (ABSC) results.

Effective scatterer diameter estimation

The effective scatter diameter (ESD) was estimated from the BSCs over the central frequency range (5–8MHz) using a Gaussian form factor, a model used by many researchers for describing scattering from biological tissues,^43–47 In the case of a Gaussian form factor model, the ESD can be estimated by a minimax approach⁴⁸ and is given as:

$${\widehat{a}}^2=-\frac{-{d_1}^2{c}^2}{80}\frac{{\displaystyle \sum _{f_i=f_{\mathit{min}}}^{f_{\mathit{max}}}}(y(f_i)f_i^2-\overline{y(f)}\overline{f^2})}{{\displaystyle \sum _{f_i=f_{\mathit{min}}}^{f_{\mathit{max}}}}{(f_i^2-\overline{f^2})}^2},$$ (6)

where f is the frequency, y(f) =10ln(B(f)/f⁴), $d_1={(12\sqrt{2\pi })}^{1/3}$, and c is the speed of sound. B(f) is the backscatter coefficient at frequency f. Also, $\overline{y(f)}=\frac{1}{N}{\displaystyle \sum _{f_i=f_{\mathit{min}}}^{f_{\mathit{max}}}}\overline{y(f_i)},\overline{f^2}=\frac{1}{N}{\displaystyle \sum _{f_i=f_{\mathit{min}}}^{f_{\mathit{max}}}}{f}_i^2$, where N is the number of discrete frequencies between f_min and f_max. The form factor approach uses a model to describe frequency-dependent deviations in the backscatter coefficient from that from Rayleigh (point-like) scatterers which have an f⁴ frequency dependence. A Gaussian model for the form factor is a common and convenient choice when there is little known about the sources of scattering in the tissue being studied.

RESULTS

Comparison of attenuation coefficient estimates

The estimated slope of the attenuation coefficient vs. frequency for each mass is listed in Table 1. The patient number was assigned here to group similar pathology results so that the attenuation variation among different mass types can be easily noted. Inspection of the data in columns 3 and 4 reveals that the reference phantom method and the hybrid method provided comparable results. That is, the difference in the estimates using the hybrid method and the RPM ranged from 0.7–43.9%, and the mean difference was 12.0%. The results using the two methods were consistent, with the exception of two of the fibroadenoma cases, patients 12 and 14.

Table 1.

Estimated slope of the attenuation coefficient vs. frequency from 24 masses using the RPM and hybrid method. Column 5 gives the percent difference between the attenuation coefficient estimated with the reference phantom method from that determined using the hybrid method.

Patient number	Biopsy result	RPM result (dBcm−1MHz−1)	Hybrid result (dBcm−1MHz−1)	% difference in estimates
1	Fibroadenoma	1.06	0.90	−15.1
2	Fibroadenoma	0.44	0.47	+6.8
3	Fibroadenoma	0.97	1.12	+17.5
4	Fibroadenoma	1.29	1.30	+0.8
5	Fibroadenoma	1.12	1.05	−6.2
6	Fibroadenoma	1.02	1.17	+14.7
7	Fibroadenoma	1.01	0.91	−9.9
8	Fibroadenoma	1.63	1.72	+5.5
9	Fibroadenoma	0.51	0.58	+13.7
10	Fibroadenoma	1.42	1.41	−0.7
11	Fibroadenoma	0.57	0.58	+1.8
12	Fibroadenoma	0.41	0.59	+43.9
13	Fibroadenoma	1.37	1.69	+23.4
14	Fibroadenoma	0.37	0.51	+37.8
15	invasive ductal carcinoma	0.72	0.85	+18.1
16	invasive ductal carcinoma	1.03	0.96	−6.8
17	invasive ductal carcinoma	1.71	1.62	−5.3
18	invasive ductal carcinoma	1.77	1.64	−7.3
19	invasive ductal carcinoma	1.13	1.12	−0.9
20	invasive ductal carcinoma	1.52	1.84	+21.1
21	invasive lobular carcinoma	0.80	0.82	+2.5
22	invasive lobular carcinoma	1.37	1.69	+23.4
23	intracystic papillary carcinoma	0.51	0.52	+2.0
24	Adenocarcinoma	1.02	0.98	−3.9

To assess possible attenuation changes among different types of masses, the attenuation coefficient vs. frequency slope estimates from the 14 fibroadenomas were averaged, as were those for the 10 carcinomas. The mean values for both tumor types are shown in Fig. 1. The error bars indicate one standard deviation. The mean attenuation value of the carcinomas (1.16dB·cm⁻¹MHz⁻¹ and 1.20 dB·cm⁻¹MHz⁻¹ for the RPM and the hybrid method, respectively) was somewhat greater than the mean attenuation value of the fibroadenomas (0.94dB·cm⁻¹MHz⁻¹ and 1.00dB·cm⁻¹MHz⁻¹ for the RPM and the hybrid method, respectively), and the standard deviation of these estimates for the two mass types are similar. The range of attenuation values for carcinomas overlaps the range of values found for fibroadenomas.

Figure 1.

Average and standard deviation of the slopes of the attenuation coefficient vs. frequency estimated using the RPM and hybrid method for fibroadenomas and carcinomas.

D’Astous and Foster²⁹ reported mean attenuation coefficient vs. frequency slopes for five excised invasive ductal carcinomas as 0.86dB·cm⁻¹MHz⁻¹ at 7MHz while our results for six invasive ductal carcinomas were 1.32dB·cm⁻¹MHz⁻¹ and 1.33dB·cm⁻¹MHz⁻¹ from the RPM and hybrid method, respectively. In our study, the attenuation estimates were from in vivo breast masses and the analyses utilized broader bandwidths.

Attenuation coefficients and BI-RADS “posterior acoustic features”

In relating attenuation coefficients to “posterior acoustic features”, the attenuation estimates from the RPM were chosen (since the estimates from the two methods were in agreement, so evidently, tissue inhomogeneities within the ROI did not compromise RPM determinations). Furthermore, in our experience the RPM exhibits a lower variance for attenuation estimates in homogeneous phantoms.

The slopes of the attenuation coefficient vs. frequency estimated using the RPM are listed again in Table 2 (column 4), along with each mass’s stated posterior acoustic feature (column 3). The mean ± 1 standard deviation of the estimated attenuation coefficients was (0.75 ± 0.31) dB·cm⁻¹MHz⁻¹ for masses that exhibited “enhancement”; values were (1.07 ± 0.38) dB·cm⁻¹MHz⁻¹ for masses whose posterior acoustic features were said to be “none” and (1.56 ± 0.18) dB·cm⁻¹MHz⁻¹ for masses judged to be “shadowing.” Also presented in this table are the sonographer measured lesion dimensions (in the direction of beam propagation - column 5) as well as the products of the attenuation coefficient vs. frequency slope and lesion diameter (“total attenuation,” column6).

Table 2.

Estimated slopes of the attenuation coefficient vs. frequency using the RPM, lesion dimensions along the acoustic beam, and posterior acoustic feature descriptors for 24 breast tumors. Total attenuation was calculated as a product of the slope of the attenuation coefficient vs. frequency and lesion dimension.

Patient number	Biopsy result	Posterior acoustic feature	RPM result (dBcm−1MHz−1)	Lesion dimension (cm)	Total attenuation (dB MHz−1)
1	Fibroadenoma	None	1.06	0.9	0.954
2	Fibroadenoma	Enhancement	0.44	1.2	0.528
3	Fibroadenoma	Combined	0.97	1.4	1.358
4	Fibroadenoma	None	1.29	1.2	1.548
5	Fibroadenoma	Enhancement	1.12	0.8	0.896
6	Fibroadenoma	Combined	1.02	0.6	0.612
7	Fibroadenoma	Enhancement	1.01	0.7	0.707
8	Fibroadenoma	None	1.63	0.8	1.304
9	Fibroadenoma	Enhancement	0.51	1.2	0.612
10	Fibroadenoma	Shadowing	1.42	1.7	2.414
11	Fibroadenoma	None	0.57	0.7	0.399
12	Fibroadenoma	Enhancement	0.41	1.4	0.574
13	Fibroadenoma	Combined	1.37	0.8	1.096
14	Fibroadenoma	Combined	0.37	1.2	0.444
15	invasive ductal carcinoma	None	0.72	1.1	0.792
16	invasive ductal carcinoma	Enhancement	1.03	0.8	0.824
17	invasive ductal carcinoma	Shadowing	1.71	1.4	2.394
18	invasive ductal carcinoma	Shadowing	1.77	0.5	0.885
19	invasive ductal carcinoma	None	1.13	1.3	1.469
20	invasive ductal carcinoma	Shadowing	1.52	1.7	2.584
21	invasive lobular carcinoma	Combined	0.80	1.8	1.44
22	invasive lobular carcinoma	Shadowing	1.37	1.0	1.37
23	Intracystic papillary carcinoma	Enhancement	0.51	1.4	0.714
24	Adenocarcinoma	Enhancement	1.02	0.7	0.714

The total attenuation estimate is plotted for each mass, along with its corresponding posterior acoustic feature in Fig. 2. The mean ± 1 standard deviation of the estimated attenuation value times the lesion dimension along the acoustic beam was (0.70 ± 0.12) dB·MHz⁻¹ for masses that exhibited “enhancement”; values were (1.08 ± 0.44) dB·MHz⁻¹ for masses whose posterior acoustic features were said to be “none” and (1.93 ± 0.76) dB·MHz⁻¹ for masses judged to be “shadowing.” As can be seen, there is potential to quantify parameters directly related to “posterior acoustic features.” Relatively low values for the computed attenuation within the mass correspond to cases where echo enhancement was seen by the 3 readers; computed high attenuation values correspond to cases of “shadowing.” QUS has an advantage of assessing the characteristics of the mass itself without subjective comparison with the surrounding tissues.

Figure 2.

Total attenuation (product of the slope of the attenuation coefficient vs. frequency and lesion dimension) in each mass, categorized according to its BI-RADS descriptor, “posterior acoustic features.”

Backscatter coefficients and BI-RADS “echo pattern”

For each mass, BSCs were averaged over the 5–8MHz range. The resultant “average backscatter coefficient” (ABSC) for each mass is presented along with its corresponding echo pattern in Fig. 3. No strong statements can be made about the utility of the echo pattern for lesion differentiation, nor of the degree of correlation of echo pattern findings with ABSC values, since nearly all tumors in this data set had “hypo-echoic” findings. However, most tumors with ABSC values below 0.04 cm⁻¹sr⁻¹ were described as “hypo-echoic”. Another interesting finding is that most of the carcinomas exhibited very low ABSC.

Figure 3.

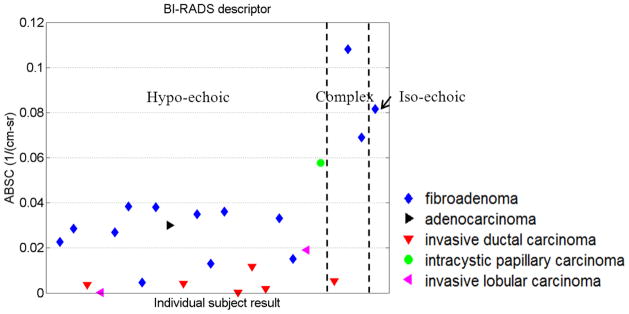
Averaged BSC for each mass, categorized according its BIRADS “echo pattern.”

The approximate mean backscatter coefficient from five excised invasive ductal carcinomas measured by D’Astous and Foster²⁹ was 0.0008cm⁻¹sr⁻¹ over 3–7MHz. Our result for six in vivo invasive ductal carcinomas was 0.005cm⁻¹sr⁻¹ over 5–8MHz.

Averaged backscatter coefficients vs. attenuation coefficient

We also investigated whether combining attenuation and backscatter results might improve the ability to differentiate malignant from benign masses. The ABSCs vs. attenuation coefficients (slope of attenuation coefficient vs. frequency) are plotted in Fig. 4. This is analogous to the plots by D’Astous and Foster²⁹ although their work involved excised tissue.

Figure 4.

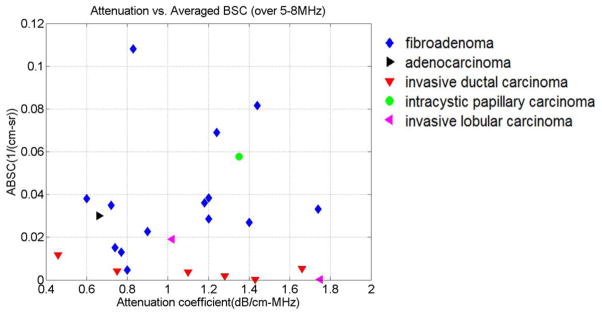
Averaged BSC vs. attenuation coefficient (slope of attenuation coefficient vs. frequency) for individual masses.

Effective scatterer diameter estimation

The estimated ESDs over the ROI were averaged for each breast mass. The mean and “heterogeneity index” (HI) of the ESD values are presented in Fig. 5. A heterogeneity index here is defined as a square root of the ESD variances (ignoring parameter estimate correlations from overlapping regions) within the PER. Though the mean ESD alone did not differentiate the mass type, most of the fibroadenomas had more variation in ESD within the ROI than did carcinomas in this study.

Figure 5.

ESDs (calculated from 5–8MHz) over the ROI were averaged and the mean and heterogeneity index are plotted for each mass.

DISCUSSION

The intent of the work reported here was to determine whether quantitative measures of attenuation and backscatter were consistent with subjectively assessed BI-RADS parameters that describe these phenomena. The hypothesis was that quantitative assessments of these parameters add more information by conveying information such as “How much does it shadow?” and “How hypo-echoic is it?”. Since these parameters are assessed computationally, there is great potential for them to be assessed automatically in a computer-aided diagnosis algorithm.

Estimates of ultrasound attenuation within breast masses done using a reference phantom method and a hybrid frequency shift technique were in agreement, except for two fibroadenoma cases. In one of these, Patient 12 in Table II, there is evidence of specular reflection within the ROI as seen in Fig. 6(a). Backscatter changes affect the reference phantom method to a much greater degree than they do the hybrid method, and this likely is the reason for this discrepancy.⁴⁹ The accuracy of RPM attenuation estimates might be improved if methods to account for these backscatter changes were available. One approach that holds promise is to test for the presence of a significant coherent component in the echo signals⁵⁰ and use that information to avoid ROIs that violate the assumption of incoherent scattering.⁴⁹ This will be a topic for future studies.

Figure 6.

B-mode images of a breast mass; (a) Patient 12; (b) Patient 14.

Another case where disagreement exists between values obtained with the two attenuation estimation methods is patient 14 (Fig. 6(b)). Here a B-mode image of the mass exhibits a “complex” echo pattern. Such a feature would be difficult to characterize by a single backscatter coefficient or a single attenuation coefficient. Note, however, in the present study the QUS representation for each mass was simplified because the study was focused on relating BI-RADS descriptors to attenuation and backscattering. It may prove useful to generate attenuation and ABSC maps within an ROI to more thoroughly describe spatial variations within breast masses.

Nevertheless, the consistency between attenuation estimates using the hybrid method and the reference phantom method is encouraging. The results motivate continued investigation into quantitative in vivo breast mass attenuation estimation since at the moment there is little published data on quantitative acoustical properties, including the degree of variability among specific types of masses.

In general there was good correspondence between posterior acoustic features and measured attenuation for each mass. There were some masses, however, that did not follow the expected trend. A “total attenuation” for each mass was calculated by multiplying the attenuation coefficient by the lesion dimension along the acoustic scan line. As pointed out above, breast masses (especially ones with “complex” echo patterns or “combined” posterior acoustic feature) likely possess complexity that a single attenuation estimate would not capture. We believe further refinement in attenuation estimations, including computing attenuation coefficient maps, is worth pursuing in order to continue to study this property.

The BI-RADS expressed “echo patterns” within masses agreed well with the ABSC values. Since all but 3 masses in the study were judged to be “hypo-echoic”, more data will be needed to draw conclusions regarding this preliminary result. In Figure 3, most of carcinomas had relatively low ABSCs suggesting quantitative backscatter levels could also provide additional diagnostic information. For example, the study by Hong et al.¹³ showed that among 403 masses, masses judged “iso-echoic” and “hypo-echoic” had 12% prevalence and 80% prevalence, respectively. Thus, most breast masses viewed on clinical ultrasound scans are characterized with one of these two descriptions, so it is hard to classify masses based on echo patterns. On the other hand, there is no gradation within the term “hypo-echoic” (how hypo-echoic is it?) and the results in Fig. 3 suggest that characterizing tumors with an absolute quantity might improve differentiation. Although some cancers have relatively high ABSC values, most exhibit low values compared to ABSCs from benign tumors. ABSC and attenuation values were evaluated together for differentiating fibroadenomas from carcinomas and demonstrated modest performance.

The effective scatterer diameter was calculated to assess the variability of the frequency dependence of BSCs among masses. As seen in Fig. 5, the mean and heterogeneity index (HI) of ESD estimates fell into a narrow range of values for our patient data. However, the ESD and HI pair could be combined to separate most fibroadenomas from carcinomas. It should be noted that the bandwidth used for effective scatterer diameter estimation (5–8MHz) was quite narrow and thus the estimated ESD likely have relatively high uncertainty. Relatively broadband data are needed for accurate ESD estimations.⁵¹ In the future, the comparison of ESD estimates using all available bandwidths should be tested. A more robust differentiator would likely include these and other features, such as the mass shape, margin, and orientation that could be quantized and used with other factors, such as patient demographics for improved risk stratification.

One limitation in this study was a possible sound speed mismatch between reference phantoms and tissues during data collection. The sound speed of the reference phantom was 1490m/s. To minimize any effects related to a mismatch in the speed of sound we have begun collecting data with the transducer transmit focus set distal to the lesion being scanned. Nam, et al.⁵² found this is the most optimal configuration for reducing errors in the estimated attenuation coefficient. However, further effort to match all sound speeds will be needed in the future to reduce any possible error in estimation of QUS parameters.

CONCLUSIONS

Except for two complex masses, attenuation coefficients of breast tumors estimated using the RPM were consistent with those estimated using a hybrid method. This demonstrates the potential for quantitative attenuation estimates in breasts. The product of the slope of the attenuation coefficient vs. frequency and the lesion dimension was used to compute the total attenuation in breast masses. That value correlated with the subjectively assessed “posterior acoustic feature” and has potential as a quantitative measure to supplement that BI-RADS descriptor. ABSC values correlated with the subjectively determined “echogenicity” within breast masses. The combination of ABSC and attenuation coefficient showed limited utility in differentiating fibroadenomas and carcinomas. Finally, most fibroadenomas exhibited relatively high variation in ESD estimates within the mass compared to that of carcinomas.