Recorded Scan Times Can Limit the Accuracy of Sedimentation Coefficients in Analytical Ultracentrifugation

Abstract

We report systematic and large inaccuracies in the recorded elapsed time in data files from the analytical ultracentrifuge, leading to overestimates of the sedimentation coefficients of up to 10%. This far exceeds previously considered factors contributing to the uncertainty in this parameter, and has significant ramifications for derived parameters, such as hydrodynamic shape and molar mass estimates. The source of this error is at present unknown, but we found it to be quantitatively consistent across different instruments, increasing with rotor speed. Furthermore, its occurrence appears to correlate with the use of the latest data acquisition software from the manufacturer, in use in some of our laboratories for nearly two years. Many of the recently published sedimentation coefficients may need to be re-examined. The problem can be easily recognized by comparing the file time-stamps provided by the operating system with the elapsed scan times recorded within the data files. We therefore implemented a routine in SEDFIT that can automatically examine the data files, alert the user to significant discrepancies, and correct the scan times accordingly. This eliminates errors in the recorded scan times.

Introduction

Analytical ultracentrifugation (AUC) is a biophysical technique based on first-principles that, throughout the 20^th century, has been intimately involved in the development of cell biology, biochemistry, and molecular biology [1–6]. It is widely applied and has contributed to the study of macromolecular interactions, and the study of membrane proteins, among others [7, 8], and is also used commercially for the characterization of protein pharmaceuticals [9] and polymers [10].

Sedimentation velocity analytical ultracentrifugation studies the spatial redistribution of particles in solution after application of a high centrifugal field. Radial concentration profiles are measured as a function of time, using absorbance or Rayleigh interferometry optical detection systems. The sedimentation boundaries typically observed, and their displacement as a function of time, reports on macromolecular parameters related to size, shape, and buoyancy, chiefly in the form of translational diffusion and sedimentation coefficients (s-values). Sedimentation coefficient distributions obtained by modern data analysis methods achieve high hydrodynamic resolution of co-sedimenting species, and the accuracy of s-values is typically considered to be on the order of one or a few percent [11]. This makes these data highly suitable for the interpretation of macromolecular shapes, by either creating shape information de novo in models of equivalent ellipsoids [12], or extracting more detailed information in the context of available structures or domain structures [13,14], or small angle X-ray or neutron scattering data [15]. Equally widespread is the use of sedimentation coefficients to obtain molar mass estimates, either from Stokes’ law as a minimum mass of a particle of given density that can achieve a measured s-value, or as a molar mass on the basis of assumptions of shape models or common shape asymmetry.

With the rapid advance in both computational modeling of hydrodynamics and the ultracentrifugal data analysis, we have embarked on an extensive study to ascertain which experimental factors limit the precision of analytical ultracentrifugation (R. Ghirlando et al., manuscript in preparation), in order to reduce their impact through improved calibration procedures. In the course of this study, after removing other confounding factors, we noticed unexpected irregularities on the order of 10% in the recorded elapsed times after the start of centrifugation as reported in the raw data files. Obviously, any errors in the time intervals ascribed to the observed movements of the sedimentation boundary position will translate proportionally into errors in the calculated s-value. This error appeared to occur only in instruments running the latest data acquisition software provided by the manufacturer, but not those running previous versions. Since we believe this finding to be of significant importance for the interpretation of sedimentation coefficients in the recently published literature, as well as for current studies in many ultracentrifugation laboratories, we formally communicate and establish a record of this problem. Furthermore, we describe in detail a simple approach to detect the presence of this error and to repair affected data files for subsequent analysis.

Materials and Methods

Sedimentation velocity (SV) experiments were carried out on Beckman Coulter analytical ultracentrifuges (Indianapolis, IN) running the manufacturer’s data acquisition software ProteomeLab™ XL-I Graphical User Interface Version 5.8 (firmware 4.21) in instrument A and the ProteomeLab™ XL-A/XL-I Graphical User Interface Version 6.0 (0419111340) (firmware 5.06) in instrument B. Samples of bovine serum albumin (BSA) were prepared by reconstituting lyophilized powder (catalog #7030, Sigma-Aldrich, St. Louis, MO) in phosphate buffered saline to a final concentration of 0.5 mg/ml. SV experiments were conducted following the standard protocol [16, 17]. Briefly, after loading 400 µl BSA samples and buffer into the sample and reference sectors, respectively, of the Epon double-sector centerpiece, cell assemblies were inserted the rotor. The rotor was subsequently temperature-equilibrated in the centrifuge to a nominal temperature of 20 °C, and then evenly accelerated to 50,000 rpm. Both Rayleigh interference and UV absorbance data were acquired, the latter in the continuous mode with a nominal radial increment of 0.003 cm and a single acquisition per scan. The same AUC cell with BSA sample and PBS buffer was used in all the experiments without disassembly. After each SV experiment, the sample was remixed by gently reversing the cell. The reproducibility of the experimental results was confirmed from multiple replicate experiments (data not shown). Data were analyzed in SEDFIT (sedfitsedphat.nibib.nih.gov/software) using the c(s) sedimentation coefficient distribution approach [18], and graphs were prepared in GUSSI (biophysics.swmed.edu/MBR/software.html).

Results

Over the last two years, we have carried out an extensive comparison of sedimentation velocity data among a group of approximately 11 instruments in our joint laboratories. As will be described elsewhere in detail (R. Ghirlando et al., manuscript in preparation), we have found that BSA is a suitable and stable standard for SV. A typical SV data set is shown in Figure 1, from which it can be discerned that a c(s) sedimentation coefficient analysis provides excellent fits. The BSA monomer species is baseline-resolved from the oligomers, thereby providing a highly reproducible marker for sedimentation velocity measurements. In the course of that study, we also developed novel methods to control for both temperature and radial calibration, which will be described in a forthcoming communication (R. Ghirlando et al., manuscript in preparation). However, even after removal of these confounding factors, we were still unable to reconcile a ~10% difference in the measured s-value of the BSA monomer from certain instruments independent of the optical system used.

Figure 1.

Top: Absorbance scans of the sedimentation velocity data of BSA centrifuged in instrument A (symbols, showing only every 3^rd data point of every 3^rd scan), and best-fit boundary model from the c(s) analysis (solid lines). Middle: Residuals of the fit, with a root-mean-square deviation of 0.0054 OD. Bottom: Best-fit sedimentation coefficient distribution c(s).

We therefore questioned basic assumptions regarding data acquisition and inspected the time-stamps created by the Windows operating system upon modification of the data files, which has an accuracy of seconds. Despite the small, fairly constant delay between actual acquisition and creation of the corresponding data file, the difference in these timestamps from pairs of scans, Δt_OS, is an independent measure of the time-interval between scans. This can be compared to the elapsed times after start of centrifugation as stated in the header of the actual data file contents, and their difference between pairs of scans, Δt_AUC. For example, in the case of instrument A we found the ratio τ = Δt_OS/Δt_AUC to be 1.0029, and approximately constant throughout the data acquisition process. The differences ΔΔt = Δt_OS − Δt_AUC were within less than 10 sec within the first hour of data acquisition, steadily growing to a difference of 57 sec after 5.4 hours (Supplementary Table T1). The origin of this small difference is unknown at present. A slightly different τ-value of 1.0027 was obtained from the analysis of the interference data. However, the resulting uncertainty in s-values of 0.3% is within the uncertainties from other instrumental factors, such as radial calibration errors [19].

In contrast, we were surprised to find that for instrument B, Δt_OS and Δt_AUC exhibit significant discrepancies, with ΔΔt being ~350 sec after one hour, and steadily growing to a lag of ~ 1.9 hours after a runtime of 21 hours (Supplementary Table T2), with an approximately constant ratio throughout the run of τ = 1.0994 (varying by approximately ±0.001 dependent on scan selection). Importantly, we found similar discrepancies in all instruments of our set that were running version 6.0 of the manufacturer’s data acquisition software ProteomeLab™ XL-A/XL-I Graphical User Interface, but not on others. We subsequently timed the scanning operations manually and confirmed that the time-stamp assigned by the operating systems correctly reflected the time-interval between scans, and that the reported elapsed time in the header of the scan files was erroneous. Interestingly, we observed that the elapsed time was correctly displayed in the centrifuge console window. In fact, the scanning log-file created by the data acquisition software reports accurate system times for the start and stop of the scan sequence, consistent within 1 – 2 sec with the timestamp given by the operating system to the created files. Thus, the file timestamps correctly reflect the time intervals between scans.

We therefore used the dilation factor τ as a correction for the elapsed time entries and generated a new set of corrected scan data files. The s-values derived for the BSA monomer from the original raw data of instrument A was 4.317 S, whereas the value obtained from instrument B was 7.7% higher, or 4.680 S (Supplementary Figure 1). We examined, independently of the manufacturer’ calibration procedures, the temperature and radial calibration (R. Ghirlando et al., manuscript in preparation), and found small errors between the two instruments (0.44% stemming from rotor temperatures of 19.66 °C for A and 19.48 °C for B) and differences in radial calibration amounting to errors of 1.05% (Supplementary Table T3), yielding corrected s-values of 4.328 S for A and 4.762 S for B, or a 10.03% difference (Figure 2). After application of the time dilation correction factor τ, the value for instrument B reduces to 4.332 S (Figure 2). This observed remaining difference of 0.09% corresponds to the level of accuracy to be expected from s-values measured for the same sample analyzed side-by-side in the same run [11]. These s-value data are further evidence for the errors in the elapsed time values in the file headers, and validate the use of time dilation corrections from the operating system timestamps.

Figure 2.

Overlay of the sedimentation coefficient distributions for the same BSA sample from centrifuges A and B. The cyan bold solid line is the c(s) distributions for instrument A running data acquisition software version 5.8. The c(s) distributions from instrument B using data acquisition software version 6.0 is shown in purple. After scan time corrections, the sedimentation coefficient distribution of instrument B is shown as blue line, virtually overlapping that of instrument A. Shown are the distributions after temperature and radius calibration; for an analogous plot of c(s) distributions uncorrected for radius and temperature calibration errors, see Supplementary Figure 1.

Similar values for ΔΔt and τ were found in the interference and absorbance data, ruling out errors from the finite time required to perform a single absorbance scan. Such a small factor, that itself is s-value dependent [19], can be computationally accounted for in SEDFIT. An additional parameter stored in the data files related to the passage of time is the value for the integral ∫ω²dt. As the migration from sedimentation is dependent only on the value of this integral, this parameter has been traditionally used to account for varying rotor speeds, and more importantly the obligatory initial acceleration phase, which takes a few minutes for a final rotor speed of 50,000 rpm. Unfortunately, apparent times based on ∫ω²dt values are incorrect for the description of diffusion. Direct Lamm equation modeling with a time-varying rotor speed was introduced more than a decade ago, and this allows for the computational simulation of the precise rotor acceleration, resulting in a more accurate modeling of both sedimentation and diffusion [20]. Nevertheless, ∫ω²dt values have been exploited in SEDFIT as a convenient source of information about the duration of the rotor acceleration phase [20]. Therefore, it was of interest to examine the accuracy of the ∫ω²dt entries in the scan files. We found this parameter to be equally affected by the time dilation error: Scan time differences based on differences of ∫ω²dt entries were within numerical precision consistent with those from elapsed seconds entries and equally erroneous. Thus, other analysis software utilizing the older approach of effective sedimentation times based on ∫ω²dt entries will benefit from the same corrections as applied in SEDFIT.

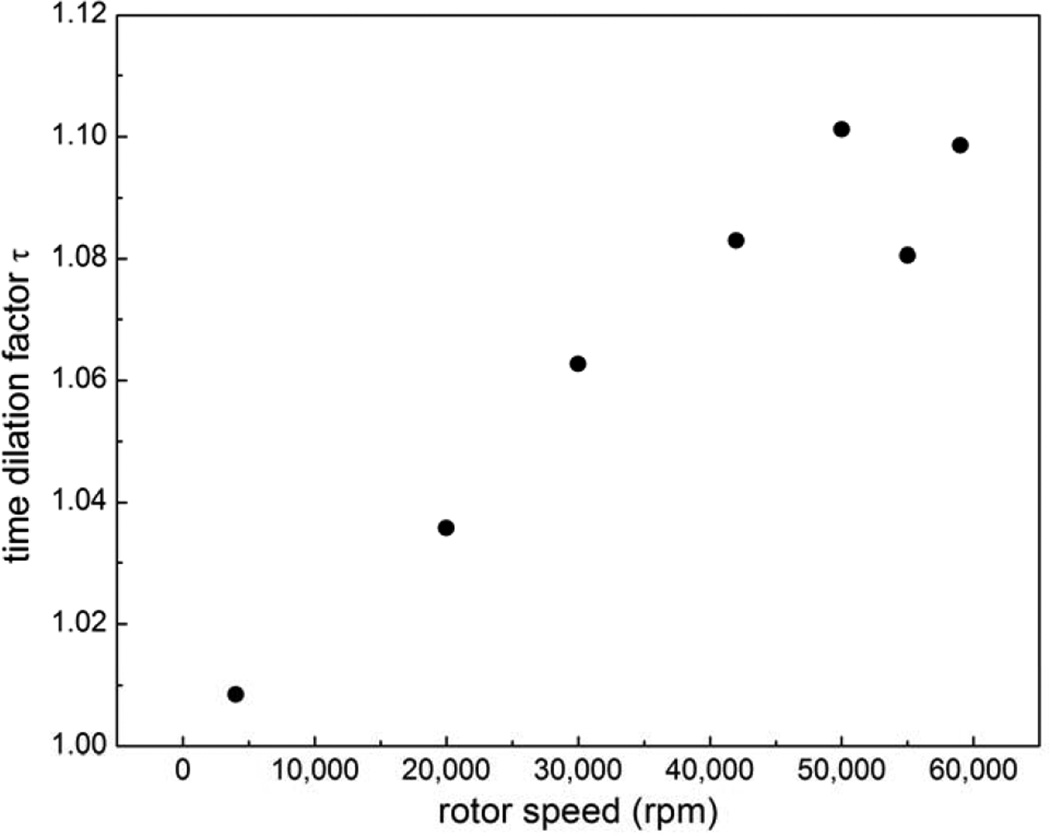
Next, we systematically examined the time discrepancy for SV data acquired at different rotor speeds. As shown in Figure 3, there is a strong rotor-speed dependence, with approximately a linear increase up to 50,000 rpm where the maximum error of ~ 10% is observed. The same rotor-speed-dependent behavior was found on other instruments from our set that were running version 6.0 of the manufacturer’s data acquisition software ProteomeLab™ XL-A/XL-I Graphical User Interface.

Figure 3.

Dependence of the scan time dilation factor τ as a function of rotor speed, for an instrument using data acquisition software version 6.0.

Finally, in order to facilitate recognition of this error, an automatic timestamp check was implemented in the software SEDFIT version 14.0c and later (available from sedfitsedphat.nibib.nih.gov/software) that compares Δt_OS with Δt_AUC and alerts the user to the presence of this error. Because we are not certain of the origin of the comparatively small ΔΔt for data from previous data acquisition software versions, we implemented a user-defined threshold for τ, by default initially equal to 1.005 for this alert. If τ exceeds the threshold, SEDFIT creates a report file and prompts the user regarding whether to write new data files with time-corrected time and ∫ω²dt entries, through multiplication of both existing numbers with τ, in new scan data files for further analysis.

Discussion

The unexpected and systematic error we discovered in the reported passage of time from the start of centrifugation causes a systematic over-estimate of sedimentation coefficients by typically ~10% at commonly used high rotor speeds. It appears to be associated with the manufacturer’s data acquisition software version 6.0 and∕or related firmware, which was installed on the affected instruments in the Spring and Summer of 2011. We believe it is installed in a significant fraction of ultracentrifuge laboratories throughout the world. The systematic error is significantly larger, approximately 10-fold, than the accuracy commonly attributed to experimental s-values, and about 100-fold larger than the statistical precision of s-values measured in the same run [11]. We have shown that it can be virtually eliminated through the use of operating system data file timestamps.

While the present version of the SEDFIT data analysis software allows one to detect this problem, the possibility for large hidden errors occurring previously raises questions about the integrity of sedimentation velocity data published over the past two years (including some of our own), some of which may have to be critically reexamined in light of the present discovery. Certainly, 10% errors in s-values could cause significant quantitative and qualitative misinterpretation on many levels. For example, if we were to consider the 30S subunit of the 70S ribosome of prokaryotes [21], under the present conditions it could appear to run at 33S, which would have to be interpreted as a significant additional mass or conformational change. The application of SV to determine consistency of protein preparations, for example, in protein pharmaceuticals, would give misleading results for batches studied with different data acquisition software versions. Furthermore, the calculation of 10% too high s-values could significantly bias the conclusions from hydrodynamic modeling. For example, a typical 65 kDa protein sedimenting at 4.1 S has frictional ratio of 1.39, corresponding to a hydrodynamically equivalent prolate ellipsoid of axial ratio 4.82, but with a 10% higher s-value the apparent frictional value would be 1.27, corresponding to a prolate ellipsoid with axial ratio 3.22, i.e. it would appear to be 30% too short. Generally, if shapes are assumed known but not molar masses, the 10% over-estimate in sedimentation coefficient would, based on a hydrodynamic power law of compact particles, suggest a 15% overestimate in molar mass.

Fortunately, for many applications the systematic error in s-values will be of less consequence. First, any conclusions from sedimentation equilibrium experiments will be invariant. Likewise, when using Lamm equation modeling to determine the molar mass from the combination of sedimentation and the diffusion coefficient (or frictional ratio, respectively, as in the c(s) method [22]), as long as both are extracted from the same data of the evolution of boundary shape, the error in the recorded time will cancel out (as can be seen from inspection of the Lamm and Svedberg equations (R. Ghirlando et al., manuscript in preparation)). Similarly, binding constants derived from isotherms of signal-weighted s-values (either integrated over species populations, over the entire sedimenting system [23], or over reaction boundaries [24]) will be unaffected, although the species s-values will still be inaccurate. Errors in kinetic rate constants from explicit Lamm equation modeling [25–27] will be insignificant compared to the inherent precision in this approach. Conclusions from the use of SV to qualitatively detect conformational changes, based on relative sedimentation coefficients [28], will similarly be invariant. Finally, conclusions on complex stoichiometries drawn from the application of multi-signal sedimentation coefficient distributions [29,30] will be unaffected since they are only dependent on signal amplitudes.

Lastly, the fact that the error was discovered in a larger set of experiments using BSA as a stable sample to study instrument accuracy and consistency (R. Ghirlando et al. manuscript in preparation) highlights the need for periodically running control experiments in analytical ultracentrifugation with a well-characterized sample, despite the fact that analytical ultracentrifugation is a first-principle technique. As will be described elsewhere, in that study we have also observed a large, previously unrecognized temperature calibration error, although only adventitiously in one of the 11 instruments examined. We believe that, in conjunction with diffusion-deconvoluted c(s) analysis, BSA is well-suited for such a study, as it is readily available, sufficiently stable over long time, and produces sharp peaks in the sedimentation coefficient distributions, as will be described in a forthcoming communication (R. Ghirlando et al. manuscript in preparation).