A General Method for Constructing Atomic-Resolution RNA Ensembles using NMR Residual Dipolar Couplings: The Basis for Inter-helical Motions Revealed

Abstract

The ability to modulate alignment and measure multiple independent sets of NMR residual dipolar couplings (RDCs) has made it possible to characterize internal motions in proteins at atomic resolution and with timescale sensitivity ranging from picoseconds up to milliseconds. The application of such methods to the study of RNA dynamics, however, remains fundamentally limited by the inability to modulate alignment and by strong couplings between internal and overall motions that complicate the quantitative interpretation of RDCs. Here, we address this problem by showing that RNA alignment can be generally modulated, in a controlled manner, by variable elongation of A-form helices, and that the information contained within the measured RDCs can be extracted even in the presence of strong couplings between motions and overall alignment via structure-based prediction of alignment. Using this approach, four RDC data sets, and a broad conformational pool obtained from a 8.2µs molecular dynamics simulation, we successfully construct and validate an atomic resolution ensemble of HIV-1 TAR RNA. This ensemble reveals local motions in and around the bulge involving changes in stacking and hydrogen bonding interactions, which are undetectable by traditional spin relaxation and that drive global changes in inter-helical orientation. This new approach broadens the scope of using RDCs in characterizing the dynamics of nucleic acids.

Introduction

The growing importance of RNA conformational changes in gene expression and regulation has spurred great interest in moving beyond static structures of RNA and toward dynamic ensembles describing RNA flexibility at atomic resolution^1–5. A major challenge in determining structural ensembles is that the number of experimental measurements that can be made typically pales in comparison to the number of parameters needed to specify the structure and population weights of all conformers populating the free-energy landscape. The ability to modulate partial alignment of proteins^{6, 7} in solution Nuclear Magnetic Resonance (NMR) spectroscopy studies through dissolution into different ordering media^7–11 has made it possible to measure up to five independent sets of Residual Dipolar Couplings (RDCs), providing a rich source of information for guiding the construction and validation of atomic resolution ensembles^{10, 12–16}. RDCs provide information regarding the orientational distribution of bond vectors relative to the overall alignment frame, and are particularly attractive measurements for constructing dynamic ensembles, given their broad sensitivity to motions occurring on sub-millisecond timescales^{17, 18}. In contrast to proteins, the uniform charge distribution in nucleic acids results in similar electrostatic and steric alignment forces, making it difficult if not impossible to modulate alignment by simply changing the ordering medium^19–21. This, combined with the coupling between an RNA’s inter-helical motions and its overall alignment ^22–24 limits the applicability of RDCs in studies of nucleic acid dynamics.

We previously introduced an approach for both decoupling internal and overall motions in RNA and modulating alignment that relies on extensive elongation of target helices by ~22 base-pairs ^{23, 25}. The resulting overall alignment of elongated RNAs is nearly axially symmetric and to a good approximation, independent of other motions takes place in other parts of the molecule. Using two sets of RDCs measured in such elongated RNA samples, we previously reported an ensemble of the transactivation response element (TAR) RNA (Figure 1A) from the human immunodeficiency virus type I (HIV-1)^{26, 27}. Internal motions in TAR have previously been shown to play important roles in adaptive protein recognition^{28, 29}. TAR is also an excellent model system for exploring the basic dynamic properties of RNA and has been extensively characterized using a wide variety of techniques^{23, 25, 30–33}. The TAR ensemble was constructed by using the RDCs to guide selection³⁴ of conformers form a pool generated using an 80 ns molecular dynamics (MD) trajectory of TAR. Although this provides a powerful approach for constructing RNA ensembles, the requirement for extensive elongation in order to decouple internal and overall motions generally limits the number of independent alignments that can be attained typically to no more than two. This not only severely limits the achievable spatial resolution with which the ensemble can be constructed, it also makes it impossible to rigorously assess the validity of the ensemble using cross-validation. Moreover, many RNA systems cannot tolerate extensive elongation either because this can affect structural properties or because it can lead to prohibitively poor relaxation properties.

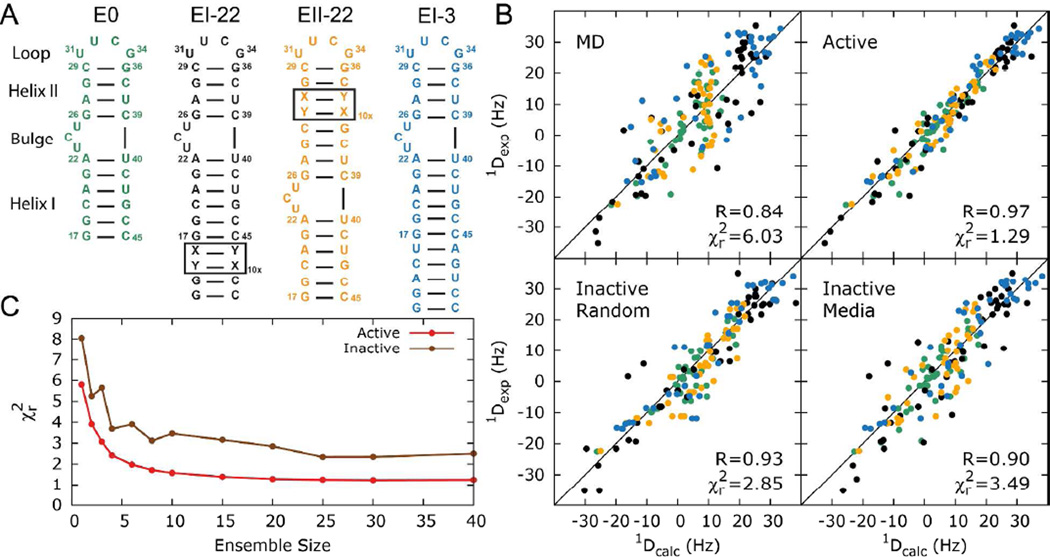
Figure 1. Constructing HIV-1 TAR ensemble using variable elongation RDCs and structure based prediction of alignment.

(A) Secondary structures of the four differentially elongated TAR constructs used to measure multiple sets of RDCs. (B) Comparison of RDCs measured in the four TAR constructs (color coded according to Figure 1A) and those predicted for the MD trajectory (MD) and an ensemble of 20 conformers in which all RDCs are used in the selection process (Active). Also shown is how well the RDC-selected ensembles reproduce a subset of RDCs that were not used in the selection process including randomly omitted RDCs (Inactive Random) and when omitting each of the four RDC data sets (Inactive Media). (C) Comparison of measured and predicted RDCs in terms of reduced χ² as a function of the size of the selected ensembles (N) when using all the RDCs in the ensemble selection (red) and for a sub-set of randomly chosen RDCs that are excluded from the selection process (brown).

We previously showed that variable elongation of a RNA terminal helix by as little as three base-pairs provides a convenient approach for controllably modulating overall alignment of the molecule without affecting the intrinsic structural and dynamic properties of the RNA target^{23, 35} and that incremental elongation of a target helix leads to an overall alignment that progressively approaches axial symmetry with its principal direction oriented along the elongated helix^{23, 35}. While variable helix elongation provides a practical, general, and robust route for modulating RNA alignment, the quantitative interpretation of RDCs measured in partially elongated RNAs proves difficult owing to couplings between internal and overall motions^{23, 35}. Here, we introduce a new strategy that enables the use of RDCs measured in variably elongated RNAs for constructing ensembles. In this approach, we predict RDCs for a given RNA conformer based on its overall shape using the program PALES^{36, 37}. Prior studies have shown that PALES^{23, 35, 38–40} and other structure-based approaches⁴¹ can accurately reproduce the overall orientation and asymmetry of the alignment of nucleic acids dissolved in Pf1 phage when assuming a simple steric model. With this approach, we have successfully constructed and validated an atomic-resolution ensemble of HIV-1 TAR, based on four sets of RDCs.

Results and Discussion

Constructing HIV-1 TAR Ensemble

We analyzed four different sets of directly bounded C-H, C-C and N-H RDCs spanning bulge and helical residues measured on four variably elongated HIV-1 TAR constructs; a native non-elongated construct²⁴ (E0), two constructs in which either helix I (EI-22) or helix II (EII-22) is elongated by twenty-two base-pairs²³ and one construct (EI-3) in which helix I is elongated by only three base-pairs³⁵ (Figure 1A). Previous analysis³⁵ of the RDC data sets measured on these four constructs using Pf1 phage^{42, 43} strongly suggests that they carry independent information (Supporting Information, Figure S1). To more quantitatively evaluate the independence of RDC datasets, we determined the alignment tensor for helix I by fitting RDCs measured in non-terminal base-pairs to a canonical idealized A-form helix, as described previously³⁵ (Table S1). We then computed the normalized scalar product between pairs of alignment tensors⁴⁴, which varies between 0 and 1 from coaxial to orthogonal alignment tensors. The six scalar products (0.092, 0.351, 0.586, 0.795, 0.823 and 0.840, Table S2) suggest the presence of independent information in the different datasets, with the short constructs E0 and EI-3 providing less independent information than the elongated constructs EI-22 and EII-22.

To construct an HIV-1 TAR ensemble, we obtained a broad conformational pool for non-elongated HIV-1 TAR by computing a 8.2µs MD trajectory computed on the Anton supercomputer⁴⁵ using the CHARMM36 force field^46–48. We first examined the ability of the MD trajectory to reproduce the RDC data. To compute RDCs for each of the four TAR constructs, each of the 10,000 non-elongated TAR snapshots in the MD pool were variably elongated in silico as needed (Methods) and submitted to PALES for structure-based predication of alignment and RDCs. The predicted RDCs were then averaged over all snapshots and their value uniformly scaled for a given type of TAR construct to optimize the agreement with the measured RDCs⁴⁹ (Methods). Note that the MD simulation was carried out on a TAR construct containing a CUGGGA hexanucleotide apical loop that differs form the UUCG tetra-loop used to measure the RDCs (Figure 1A). However, we previously showed that this apical loop substitution has little to no effect on the structural and dynamic properties of the TAR helices and the bulge⁵⁰. Furthemore, simulations show that the two different loops affected the PALES predicted RDCs by an amount smaller than the measurement uncertainty (<4Hz), as expected given their similar size and overall shape. Interestingly, the agreement between the measured RDCs and values predicted for the long MD trajectory (${\chi }_r^2=6.03$, RMSD = 8.6Hz, Pearson’s correlation coefficient R=0.84) has improved significantly as compared to the agreement observed for a shorter 80ns trajectory⁵¹ (${\chi }_r^2=10.11$, RMSD = 11.3Hzk, R= 0.73) employing the CHARMM27 force field. However the RMSD remains significantly larger than the RDC measurement uncertainty, estimated to range between 2–4Hz for the different TAR constructs⁵¹ (Figure 1B).

The inability of the MD simulation to accurately reproduce the measured RDCs may arise from improper weighting of the different conformers rather than incomplete sampling of the conformational space. We therefore examined if the RDCs could be used to guide selection of sub-ensembles from the MD conformational pool. Here, the SAS Monte-Carlo selection scheme was used to minimize a reduced χ² function assessing the agreement between measured and predicted RDCs for a given selected ensemble^{23, 51}. Sub-ensembles with increasing size (N) were then constructed to find the smallest ensemble satisfying all of the measured RDCs.

As shown in Figure 1C, the agreement between measured and predicted RDCs improves significantly with increasing ensemble size and reaches a plateau at N~20 (${\chi }_r^2=1.29$, RMSD=4.0Hz, R=0.97). A similar trend is observed when comparing the agreement with RDCs that are left out and not actively used in the ensemble selection (Figure 1C). Importantly, the quality of the RDC fits deteriorated considerably (${\chi }_r^2=2.55$, RMSD=5.8Hz, R=0.93) when constructing ensembles using a conformational pool obtained from a shorter 80ns MD trajectory (data not shown), underscoring the importance of having broad conformational sampling for highly flexible RNAs.

Using this SAS approach, we were able to construct ensembles that simultaneously satisfy RDCs measured in all four TAR constructs close to experimental precision (Figure 1C), as evaluated by direct comparison of the measured and predicted RDCs and by cross-validation and comparison of how well the selected ensembles predict RDC data that was not used in the selection, including very demanding validations in which each of the four RDC data sets (~25% of the data) was removed entirely. The agreement observed for the cross-validations (${\chi }_r^2=2.85$, RMSD=5.9Hz, R=0.93 for randomly removed RDCs and ${\chi }_r^2=3.49$, RMSD=6.7Hz, R=0.90 for the successive removal of each dataset) represents a significant improvement compared to a randomly selected ensemble of the same size (${\chi }_r^2=6.47$, RMSD=8.8Hz, R=0.83). This self-consistency suggests that PALES accurately reproduces the overall alignment of the RNA and provides additional support that variable elongation does not significantly affect the properties of TAR, as also inferred independently based on comparison of chemical shifts ^{25, 50}.

While the ensemble is able to back-predict correctly unused RDC data, this could arise in part due to partial correlations between experimental dataset (Supporting Information). Therefore, we further quantitatively tested the accuracy of the ensemble by examining its ability to reproduce data of other physical nature that were completely ignored in the ensemble construction, namely magnetic field induced RDCs and ¹H chemical shifts. First, the ensemble reproduces small magnetic field induced RDCs (ranging in size between −2.1 to 2.6Hz) measured in a non-elongated TAR at 18.8T (800MHz ¹H Larmor frequency) in the absence of ordering media to within almost experimental precision (reproduction of the experimental data with RMSD = 0.59Hz compared to experimental error ~0.50Hz) ^{22, 52} (Figure S2). Much poorer agreement is observed for the MD starting pool (RMSD=0.90Hz). As a second independent test, we examined how well the ensemble reproduces ¹H experimental chemical shifts measured at the bulge using the program NUCHEMICS^{53, 54} to compute ¹H chemical shifts based on structure. The RDC ensemble reproduces the ¹H chemical shifts with RMSD of 0.17ppm as compared to 0.20ppm for the entire MD trajectory (Methods). While this improvement is small, it does bring the agreement closer to the reported NUCHEMICS ¹H chemical shift error prediction (~0.16ppm). As we discuss in subsequent sections, the RDC TAR ensemble agrees with other independent information available on this RNA.

To further evaluate how well the RDC constructed ensemble actually reproduces key conformational features of HIV-1 TAR we preformed extensive simulations employing synthetic RDCs and a variety of target ensembles (Supporting Information). These simulations establish the ability to extract accurate information regarding the orientation distribution of base-pair and inter-helical parameters using the four RDC datasets measured in TAR (Table S3, Figure S3–S5). These well-defined angular distributions will be the focus of further analysis in the following sections.

Inter-helical Motions

A general and functionally important motion in RNA involves collective changes in the orientation of A-form helices across bulges and junctions. Such motions have been shown to play important roles in adaptive protein and ligand recognition, in the catalytic cycles of ribozymes and in the assembly of ribonucleoprotein machines^{1, 55}. TAR provides an excellent model system to explore inter-helical motional modes across its three-residue bulge. The relative reorientation of two helices (Figure 2A) can be defined using three inter-helical Euler angles (α_h,β_h,γ_h)^{56, 57} that specify the twist angles about the two helices (α_h and γ_h) and an inter-helical bend angle (β_h).

Figure 2. Inter-helical dynamics.

(A) Definition of the inter-helical Euler angles (α_h,β_h,γ_h) used to specify the relative orientation of two A-form RNA helices. The inter-helical Euler angle distribution for HIV-1 TAR observed in (B) 8.2µs MD trajectory and (C) RDC-selected ensemble obtained from combining 100 rounds of N=20 selections. The population of a given inter-helical orientation is color-coded, increasing from blue to red. Black circles correspond to seven distinct ligand-bound HIV-1 TAR structures (pdb codes: 1QD3, 1UUI, 1UTS, 1UUD, 1ARJ, 1LVJ and 397D).

Figure 2 compares the RDC-selected inter-helical ensemble with that of the MD generated pool. Interestingly, we find that many of the RDC-selected conformers fall in low populated regions of the MD trajectory. This includes conformers with large bend angles (β_h >50°) and relatively small twist angles (|α_h|<30° and |γ_h|<30°). These conformers also tend to have a distorted geometry for the junction A22-U40 base-pair, which is known to be locally flexible⁵⁸. Overall the RDC-selected ensemble features both a larger mean bend angle and larger variations about this mean (|β_h|= 52±27° for the selected ensemble compared to 32±18° in the MD simulation). The twist angles around the two helices for the RDC-selected ensemble are more similar to the starting MD pool but feature on average ~30° shift in γ_h (α_h and γ_h = −15±47° and −28±44° respectively for the selected ensemble compared to −22±42° and −57±40° for MD), leading to a smaller degree of inter-helical over-twisting as compared to the MD pool⁵⁶ (inter-helical twist ζ_h=α_h+γ_h being −43±36° and −79±23° for the selected ensemble and the starting pool respectively). Thus improper weighting of the MD trajectory in the (α_h,β_h,γ_h) can partly explain its inability to reproduce experimental RDCs. This could be due to a lack of convergence, given that the MD trajectory remains much shorter than the RDC timescale sensitivity (< milliseconds), improper parameterization of the force fields or inadequate modeling of interactions with monovalent ions since it is known that increasing the concentration of monovalent or divalent ions simultaneously decreases the average bend angle and the amplitude of bending motions in TAR⁵⁹. In the MD simulation, ions were simply placed to ensure electroneutrality, which may not necessarily reflect experimental conditions.

The RDC-selected ensemble reproduces many salient features of TAR inter-helical dynamics that have been characterized previously^{23, 51} (Figure S6 and S7) including the presence of very large amplitude bending and twisting motions (|β_h| varies over the range of 3° to 91°, and the twist angles α_h and γ_h vary between −123° and 101° and −127° and 64°, respectively). The ensemble also shows strong correlations between the inter-helical twist angles α_h and γ_h which have been attributed to steric and connectivity constraints imposed by the TAR bulge^{57, 60}. Interestingly, the selected ensemble comes closer to the sampling of known ligand bound structures of TAR as compared to a previous ensemble constructed using only RDCs measured in EI-22 and EII-22 TAR (Figure S8), reinforcing the idea that adaptive recognition could in principle occur via conformational selection ^{23, 51}.

Local Motions

The validated multi-alignment RDC ensemble of TAR afforded a unique opportunity to examine with exquisite detail local motions that are more challenging to characterize given that they involve many more degrees of freedom. Specifically, we investigated the angles defining the intra- and inter-base-pair geometry⁶¹ (buckle, propeller twist and base opening and tilt, roll and twist) and sugar torsion angles (ν₀, ν₁, ν₂, ν₃ and ν₄). The distribution of those quantities for the base-pairs G18-C44, C19-G43, A20-U42, G21-C41, A27-U38 and G28-C37 indicate that the central base-pairs of the two helices remains statistically very close to an idealized A-form helix and exhibit variations usually comparable or slightly bigger to those expected based on a statistical survey of X-ray structures (Tables S4–S6). This is consistent with other studies showing excellent agreement between measured RDCs and those predicted using an idealized A-form geometry containing Watson-Crick base-pairs¹⁹ and recent chemical shift based analysis of A-form helices⁶². This also validates a posteriori use of idealized A-form helices to elongate conformers during the PALES analysis (Methods).

Interestingly, the two base-pairs around the bulge show asymmetric behavior with G26-C39 adopting an A-from like conformation and A22-U40 adopting a much broader conformational distribution, deviating from a classical Watson-Crick base-pairing (Figure 3 and S9). This is consistent with prior NMR studies employing trans-hydrogen bonding scalar coupling, ¹³C and ¹⁵N spin relaxation and RDC measurements^{51, 58, 63}. The observed conformational flexibility in the A22-U40 base-pair is not limited to the two bases but also includes the sugars, which sample both C2’-endo and C3’-endo conformations. An high degree of flexibility is also observed for bulge residues, particularly C24 and U25 and to a lesser extent U23, which frequently stacks on A22, consistent with previous Nuclear Overhauser Effect (NOE), spin relaxation, RDC and MD studies of TAR^{51, 63, 64}.

Figure 3. Local dynamics within A-form helices.

For the RDC-selected ensemble: (A) distribution of intra- and inter-base pair (buckle, propeller twist and opening and tilt, roll and twist) angular parameters for the junction A22-U40 (red) and central A20-U42 (blue) base-pairs and (B) five sugar torsion angles (ν₀–ν₄) for the same nucleotides (top) A22 (red) and A20 (blue), (bottom) U40 (red) and U42 (blue).

To gain further insights into the local dynamics at the bulge linker, we examined the stacking interactions between bulge and neighboring residues. Previous studies showed that the inter-helical hinge is primarily defined by bulge residue U23 and the lower residue A22, which forms a flexible base-pair with U40^{51, 63}. In free TAR, U23 stacks on A22 and promotes inter-helical bending. However, in coaxial TAR structures observed under high ionic strength conditions, or when bound to ligands, U23 is flipped out^{59, 65, 66}. We observe a unique multi-modal A22-U23 distance distribution in the RDC-selected ensemble (Figure 4A), whereas others distances exhibit significantly flatter distributions (Figure S10), a trend clearly emphasized by the selection procedure. Relative to MD, the RDC-selected ensemble significantly increases the population of unstacked C24-U25 and U25-G26 conformations, indicating a potential bias in the force field towards stacked conformations at these sites. The observation of an higher population of nearby conformations for A22-U23 is consistent with the observation of NOEs between these two bases⁶⁴.

Figure 4. Relationship between local and inter-helical dynamics.

(A) Clustering of the selected ensemble. Distribution of the A22-U23 distance (top) and its correlation between the |β_h| inter-helical angle (bottom). Results are shown for the MD trajectory (grey), full selected ensemble, obtained from combining 100 rounds of N=20 selections (red). Shown are clusters 1 (green), 2 (orange) and 3 (blue) along with their population weighted averages and standard deviations (B) Conformational properties of the three clusters presented using a sub-ensemble of the selected conformers. Cluster 1 (left), 2 (right) and 3 (middle). (C) Schematic representation of the three clusters and a proposed ordering for transitioning between conformations with different bend angles. Curved arrows indicate local dynamics. Interactions with helix II are indicated with a dashed line.

Interplay between Local and Collective Motions

Despite many studies on inter-helical motions in RNA, the local hinge motions at inter-helical junction that activate these dynamics remain poorly understood. To gain insights into the interplay between the TAR bulge local conformation and inter-helical orientation, we examined how the A22-U23 distance distribution correlates with the inter-helical bend angle |β_h| (Figure 4A). This analysis revealed three distinct clusters. Cluster 1 (population 66%) features highly bent conformations in which A22 and U23 are in close proximity and adopt a looped in stacked conformation; cluster 2 (population 19%) features smaller bend angles and conformers in which A22 and U23 are far apart with U23 adopting a flipped out conformational and finally cluster 3 (population 15%) features intermediate bend angles and distorted bulge conformations, where A22 may interact with the upper helix or where the deformation may propagate down to the G21-C41 base pair (Figure 4A,B). In this cluster U40 tends to form an unusual base-pair with U25 rather than A22, whereas U23 and C24 remain unpaired and flexible. Interestingly, this alternative secondary structure is predicted to be the second most energetically favorable bulge secondary structure for HIV-1 TAR using the structure prediction program MC-fold^{67, 68}.

Together, the above observations suggest a mechanism for inter-helical bending that is tightly coupled to the local conformation of the bulge and specifically the conformation of U23, which may serve to modulate the steric constraints imposed on certain inter-helical orientations, with linear co-axial structures becoming sterically more accessible when U23 is flipped out (Figure 4C). Cluster 3 suggests that the transition between those two sub-states might proceed through the breaking of the flexible A22-U40 base pair, possibly accompanied by local changes in secondary structure around the bulge, including formation of a non-canonical U25-U40 base pair and possibly other interactions between A22 or U23 and the upper helix, as previously documented in ligand bound states of TAR, e.g. in the TAR argininamide complex, where U23 forms a base-triple with A27-U38 in the upper helix⁵⁸. Strong support for such a pathway for inter-helical motions comes from previous studies showing that both the average inter-helical bend angle and amplitude of inter-helical motions decrease dramatically when replacing A22-U40 with a stronger G22-C40 base-pair⁶⁹.

Timescale of Motions: Reconciling RDC and Spin Relaxation Data

Previous studies showed that the amplitude of inter-helical motions determined by RDCs²³ (ϑ_int = 0.45±0.05, where ϑ_int, ranges between 0 and 1 for maximum to minimum amplitude inter-helical motions) greatly exceed those derived by spin relaxation²⁵ (S_s = 0.86±0.02). This was attributed to slower micro-to-millisecond motions occurring at timescales longer than overall rotational diffusion of the molecule²⁵ (~19ns for EI-22-TAR) which are sensed by RDCs but not spin relaxation. Though RDCs provide valuable information about the amplitude and direction of motions, they do not provide direct information regarding motional timescales. Therefore the comparison with spin relaxation data provides a simple way to classify dynamics into fast and slow motion compared to the molecular rotational diffusion time, as documented previously in studies of protein dynamics^{6, 10, 13–15, 70–74}. However, the nature of the slower motions sensed by RDCs and not spin relaxation has remained elusive for nucleic acids. To gain further insights into the nature of these slower motions, we used the RDC-ensemble to compute site-specific order parameters^75–77 describing the amplitude of motions at C-H and N-H bonds and compared values with order parameters determined by ¹³C and ¹⁵N spin relaxation data^{63, 78} (Figure 5 and Methods).

Figure 5. Resolving motional modes occurring at different timescales.

Comparison of order parameters (S²) describing motions of individual bond vectors in TAR obtained from the RDC-selected ensemble (bars) and based on analysis of ¹³C and ¹⁵N spin relaxation data (circles) measured in EI-22 HIV1-TAR. RDC based order parameters (bars) are obtained by aligning all the conformers of the selected ensemble on an idealized helix I. Error bars represent experimental uncertainty. Color coding (A) N1H1 (blue) and N3H3 (grey), (B) C2H2 (orange) and C8H8 (red), (C) C5H5 (brown) and C6H6 (green) and (D) C1H1 (black).

Similar RDC and spin relaxation order parameters are observed for residues in the reference elongated helix I, as well as for the highly flexible bulge residues C24 and U25. Thus, these sites appear to experience insignificant motions at micro-to-millisecond timescales. By contrast, the RDC-derived order parameters are significantly smaller than their spin relaxation counterparts in the upper helix, as well as for bulge residue U23, and the junction A22-U40 base-pair, suggesting the presence of significant micro-to-millisecond dynamics at these sites. The lower RDC-derived order parameters for the upper helix can be attributed to excess micro-to-millisecond inter-helical motions that yield a net ϑ_int = 0.46±0.04 (Methods), in good agreement with values obtained previously using an order tensor analysis of RDCs²³. Interestingly, the much lower RDC-derived order parameters for U23 and the adjacent A22-U40 base-pair, coincides with lower order parameters for inter-helical motions, and may reflect slower local motions at the junction that lead to the breaking of the A22-U40 base-pair or loss of A22-U23 stacking interactions, which results in transitions between bent and coaxial inter-helical conformations. The need to break favorable base-paring and stacking interactions can explain why such motions occur at slower timescales inaccessible by spin relaxation. The absence of µs-ms exchange broadening at these sites using R_1ρ relaxation-dispersion experiments⁵⁰ suggests that the motions occurs on the ns to µs timescales, a window which is invisible to spin relaxation methods.

The picture that emerges is one in which the helices ‘rattle’ about a predefined bulge conformation at picosecond-to-nanosecond timescales but that transitions between different conformational sub-states involving highly bent or linear inter-helical conformations occurs at slower ns to µs timescales through pathways that require disruption of favorable stacking and hydrogen bonding interactions in and around the bulge. This is consistent with recent NMR relaxation dispersion data showing that even stable Watson-Crick base-pairs in and around bulges, internal loops, and apical loops can undergo slow changes in stacking and hydrogen bonding interactions^{50, 68}.

Conclusion

In conclusion we have developed a new method for constructing, at high resolution, dynamic ensembles of nucleic acids. The combination of long MD simulations with elongation modulated RDCs allowed us to probe elusive nucleic acid motions at atomic resolution and to explore the interplay between local and global motions. Our results expose complex local motions occurring at different timescales, including picosecond-to-nanosecond motions of bulged-out residues and slower ns to µs motions involving the disruption of stacking and hydrogen bonding and the flipping in and out of residues, all concentrated within the bulge two way junction and the immediately neighboring base-pairs. These local motions provide the molecular basis for larger-amplitude collective motions of juxtaposed helices. The ability of the approach to bypass the coupling between internal dynamics and global reorientation and to accommodate any level of elongation makes it readily applicable to a large variety of nucleic acid systems, providing a basis for exploring the dynamic properties of diverse structural motifs in nucleic acids at atomic resolution. The approach can easily be extended to accommodate other sources of experimental information regarding the ensemble⁵⁵, including Small Angle X-ray Scattering (SAXS)^{79, 80}, which can provide complementary distance-based information and chemical shifts^{53, 54, 81} reporting on local conformational environment.

Methods

RDC Data

The TAR ensemble was constructed using four phage-induced RDC data sets previously measured on four variably elongated HIV-1 TAR constructs in which the wild-type apical loop is replaced by a UUCG apical loop; E0²⁴, EI-22²³, EII-22²³ and EI-3³⁵ (Figure 1A). All RDCs were measured at 298K using identical buffer conditions (15mM sodium phosphate, 25mM sodium chloride, 0.1mM EDTA, and pH~6.4). The TAR concentration ranged between ~0.6–1.2mM and that of Pf1 phage between 6 and 22 mg/mL depending on the level of elongation of the construct). Previous studies have shown that this apical loop mutation has little to no effect on the bulge and inter-helical dynamics⁵⁰. The data included sugar (C1’-H1’, C2’-H2’, C3’-H3’ and C4’-H4’) and base (C2-H2, C5-H5, C6-H6 C8-H8, C5-C6, N1-H1 and N3-H3) one-bond RDCs measured in the two helices and the bulge. A total of 44, 45, 36, and 38 RDCs were measured in E0, EI-22, EII-22 and EI-3 TAR respectively.

Molecular Dynamics Simulations

The starting pool for selection consisted of 10,000 snapshots obtained by regular sampling of a 8.2 microsecond MD simulation run on the supercomputer Anton; a special-purpose machine built specifically for highly efficient computation of accurate molecular dynamics trajectories⁴⁵. Computational hours were obtained on Anton through the National Resource for Biomedical Supercomputing (NRBSC) and the Pittsburgh Supercomputing Center donated by D.E. Shaw Research. Initial coordinates for HIV-1 TAR were obtained from the Protein Data Bank (Access Code 1ANR). The system was solvated in VMD⁸² with TIP3 water and 27 Na⁺ ions to neutralize the overall electrical charge in a 64×64×64 Angstrom cube for initial heating, which was carried out using the CHARMM Molecular Dynamics package^{83, 84}. CHARMM36 force field parameters for ribonucleic acids were used, which included recent changes made in 2011 by Mackerell et al. to the 2’ hydroxyl dihedral parameters^46–48. The system was heated to 300K with harmonic constraints on backbone atoms for 100ps, at which point restraints were gradually released over another 100ps and the system was equilibrated for 5ns.

Velocities, coordinates, system, and force field parameters were then all transferred from the initial heating run to Anton style formats and the simulation was extended on Anton for 8.2µs. The Nose-Hoover NVT integrator with a time step of 2fs was used and coordinates were saved every 820ps, yielding 10,000 conformational snapshots. According to the standard Reference System Propagator Algorithm (RESPA) near bonded and non-bonded forces were computed every time step while far non-bonded forces were computed every third time step. Standard periodic boundary conditions were applied, with long range interactions calculated according to the Particle Mesh Ewald summation⁸⁵ with cut-off parameter 12.99A. In addition to convergence of RMSD and energy, the trajectory was found to be predominantly in A-form by pucker angles and inter-helical distances (data not shown).

RDC Calculation

Since the MD simulation was preformed on non-elongated E0-TAR, an elongation procedure was used to elongate – as needed – each snapshot prior to PALES structure-based calculation of alignment and RDCs. For each snapshot, the elongated helix was aligned onto an idealized elongated A-form helix that contains the sequences of the TAR helices by superimposing heavy atoms of the RNA backbone⁷⁸ (base-pairs G18-C44 to G21-C41 for helix I and base-pairs G26-C39 to G28-C37 for helix II). The required number of base-pairs for elongation were then added to the MD snapshot. In the case of EII-22, the apical loop from the MD snapshot was translated to the end of helix II to conserve its global structural features. As the experimental RDCs were measured on a UUCG mutant of HIV-1 TAR, the wild-type loop of the snapshots could have been substitute by a structural model of the UUCG loop⁸⁶. However, due to the absence of good dynamical description of this loop, the small effect expected from previous studies⁵⁰ and the absence of improvement in the RDC reproduction after such substitution, the wild type loop was kept to avoid unnecessary complication of the protocol. RDCs were then calculated for each conformer using PALES^{36, 37}, using a pure steric description according to the cylindrical wall model with a low effective concentration (0.022g/mL).

The averaging over an ensemble assumes equi-probable conformations and that a given conformation cannot be selected more than once. As the magnitude of alignment is dependent on experimental conditions, including the concentration of Pf1 phage and nature of elongation, an overall scaling factor is allowed to float for each of the four RDC sets as described previously⁴⁹. Therefore the RDCs are expressed as:

$$D_{i,j}^{\mathit{\text{calc}}}=\frac{{\lambda }_j}{N}\sum _{k=1}^N{D}_{i,j}^k$$ (1)

where k runs over the N conformers in the selected ensemble, λ_j represents an overall scaling factor for j^th TAR construct and D_i,j is the i^th coupling in the j^th construct.

Sample and Select

TAR conformations were selected in generating ensembles using the standard Monte-Carlo based selection approach that minimizes a χ² function representing the quality of the data reproduction³⁴:

$${\chi }^2=\sum _{i,j}\frac{{\left(D_{i,j}^{\mathit{\text{calc}}}-D_{i,j}^{\mathit{\text{exp}}}\right)}^2}{{\delta }_{i,j}^2}$$ (2)

where i runs over all the RDCs measured for the different constructs j and δ is the weight used to normalize different RDCs (C-H, C-C and N-H), and was fixed for each medium at one tenth of the range of RDCs clustered in ¹D_NH, ¹D_CC, aromatic and non-aromatic ¹D_CH RDCs.

The process of selection starts with the generation of a random ensemble of size N from the conformational pool of 10,000 snapshots. At each evolution step a new ensemble is created by randomly replacing one conformer by another in the pool. If the fitness of the new ensemble is lower than the old ensemble the newest ensemble is kept, otherwise it is accepted only with a probability:

$$P=\text{exp}\left(\frac{{\chi }_{\mathit{\text{old}}}^2-{\chi }_{\mathit{\text{new}}}^2}{T}\right)$$ (3)

where T is an effective temperature that starts at 100 and decreasing by a factor of 0.9 every 500,000 steps. Each selection is composed in total of 50,000,000 steps.

The selection procedure was repeated 10 times and the ensemble that best fits the experimental data among the 10 trials is kept and presented in terms of reduced χ²:

$${\chi }_r^2=\frac{1}{K}{\chi }^2$$ (4)

where K is the total number of RDCs involved in the selection process.

Cross-Validation

New RDC datasets were generated by randomly removing four RDCs per TAR construct. The reduced RDC dataset was then used in the Monte-Carlo selection and the determined optimized ensemble was used to predict RDCs that are left out of the selection. As for direct analysis, this procedure was repeated 10 times, and the ensemble with the best active χ² is kept and used to back-calculate experimental data. A similar procedure was used for the cross-validation where each of the four datasets measured on each TAR construct was independently removed. The calculations of field-induced RDCs were carried out using a previously described protocol^{22, 52}.

Chemical Shift Calculation

Chemical shifts for H1’, H2, H5, H6 or H8 (total of 48) were computed using NUCHEMICS ^53,54 for the TAR helices and bulge (excluding terminal base-pairs G17-C45 C29-G36 which are near sites of elongation and apical loop, respectively).

Ensemble Analysis

Inter-helical angles (α_h,β_h,γ_h) describing the relative orientation of two A-form helices were computed using in-house software (http://hashimi.biop.lsa.umich.edu/resources) following a previously described procedure⁵⁶. Owing to the high flexibility of the A22-U40 base-pair, the lower helix is defined using central base-pairs C19-G43, A20-U42 and G21-C41 and the inter-helical Euler angles relate the upper helix defined by base-pairs G26-C39, A27-U38 and G28-C37 to the lower reference helix. Previous studies used an identical procedure except the three base-pairs used for the lower helix were A20-U42, G21-C41 and A222-U40. Note that because the Euler angles used here are defined relative to a reference A-form helix lacking the locally flexible A22-U40 base-pair, the α_h and γ_h inter-helical Euler angles reported here are each systematically shifted by ~17° as compared to previously reported TAR inter-helical Euler angles^{23, 51, 56}. This systematic shift of a constant value δ in Euler angles (α_h+δ,β_h,γ_h-δ) is due to the fact that identical reference helices were used compared to previous studies, but that the set of base-pairs used for the calculation was shifted by one. This induces a shift in the inter-helical twist of 2δ=34° simply corresponding to the twist between two successive base-pairs in an idealized A-form helix (twist between G21-C41 and A22-U40). This referencing does not affect any local parameters and is used to ensure maximal accuracy in the description of the relative orientation of the two helices. Parameters defining local geometry of the bases were determined using Curves+⁶¹ and the calculation of sugar dihedral angles were preformed using in-house programs available from the authors upon request. The distance between two bases was calculated by measuring the distance between the center of mass of each base. All order parameters where calculated using the following equation^{76, 77}:

$$S^2=\frac{1}{2}(3\sum _{i=1}^3\sum _{j=1}^3<{\mu }_i{\mu }_j{>}^2-1)$$ (5)

where µ_i represent the Cartesian coordinates of the normalized inter-nuclear vector, after alignment of the conformers by superimposing heavy of the RNA backbone in the central base-pairs C19-G43, A20-U42 and G21-C41 to an idealized A-form helix containing the same sequence. Error bars were obtained through Monte Carlo analysis (vide infra). The internal degree of order, ϑ_int, was calculated using helix I as reference according to a previously described procedure²³ and the associated uncertainties were derived from Monte Carlo analysis (vide infra).

Monte-Carlo Analysis

A Monte-Carlo based approach was used to obtain error bars in the presented parameters. 250 independently noise corrupted pseudo-experimental RDC dataset were generated using the RDCs predicted from the ensemble selected during the direct analysis of the experimental data (with 20 conformers). For each set of data, a selection of an ensemble of 20 conformers is done and the presented errors bars correspond to the standard deviation obtained from this distribution of results.

Testing the Approach on Simulated Data

Target conformational ensembles were generated by selecting 2,000 conformers from the conformational pool using as probability of acceptance, a Gaussian distribution with predefined width and center for each of the three Euler angles. The set of 2,000 conformers were then used to generate noise corrupted synthetic RDCs for the 4 different TAR constructs. The noise level used for the calculations were set to the weights used in the selection procedure. The synthetic RDCs were then inputted in the selection procedure. For each synthetic dataset, 100 ensembles of 20 conformers were selected and combined for increased resolution and the ability of the procedure to reproduce an introduced sampling is characterized for both (α_h,β_h,γ_h) angles and local geometry.