Subthreshold outward currents enhance temporal integration in auditory neurons

Abstract

Many auditory neurons possess low-threshold potassium currents (I_KLT ) that enhance their responsiveness to rapid and coincident inputs. We present recordings from gerbil medial superior olivary (MSO) neurons in vitro and modeling results that illustrate how I_KLT improves the detection of brief signals, of weak signals in noise, and of the coincidence of signals (as needed for sound localization). We quantify the enhancing effect of I_KLT on temporal processing with several measures: signal-to-noise ratio (SNR), reverse correlation or spike-triggered averaging of input currents, and inter-aural time difference (ITD) tuning curves. To characterize how I_KLT, which activates below spike threshold, influences a neuron’s voltage rise toward threshold, i.e., how it filters the inputs, we focus first on the response to weak and noisy signals. Cells and models were stimulated with a computer-generated steady barrage of random inputs, mimicking weak synaptic conductance transients (the “noise”), together with a larger but still subthreshold postsynaptic conductance, EPSG (the “signal”). Reduction of I_KLT decreased the SNR, mainly due to an increase in spontaneous firing (more “false positive”). The spike-triggered reverse correlation indicated that I_KLT shortened the integration time for spike generation. I_KLT also heightened the model’s timing selectivity for coincidence detection of simulated binaural inputs. Further, ITD tuning is shifted in favor of a slope code rather than a place code by precise and rapid inhibition onto MSO cells (Brand et al. 2002). In several ways, low-threshold outward currents are seen to shape integration of weak and strong signals in auditory neurons.

1 Introduction

Due to the temporal cues present in sound signals, the auditory nervous system provides a good opportunity to explore how multiple membrane currents (intrinsic and synaptic) influence signal integration (Trussell 1999). The preservation of precise temporal information is crucial for coding and decoding, especially below about 2 kHz in mammals. Correspondingly, brainstem auditory neurons have very fast decaying synaptic currents (Raman and Trussell 1992; Gardner et al. 1999) and fast low-threshold potassium (I_KLT ) currents (Manis and Marx 1991; Reyes et al. 1994; Rathouz and Trussell 1998). They typically fire phasically, not tonically, for step current stimuli, presumably because of I_KLT (Manis and Marx 1991; Reyes et al. 1994; Smith 1995; Svirskis et al. 2002). Experimental and modeling studies suggest that such biophysical properties enhance the ability of auditory neurons to synchronize (phase lock) to strong (Oertel 1983; Rothman and Young 1996; Reyes et al. 1996) as well as to weak (Svirskis et al. 2002) sinusoidal stimuli and thus to transmit more precisely the signal’s temporal information. Medial superior olivary (MSO) neurons and their avian analogs are implicated as coincidence detectors for sound localization (Jeffress 1948; Goldberg and Brown 1969; Carr and Konishi 1990) and provide an opportunity to relate membrane properties to neuronal function (Reyes et al. 1996).

A common feature of afferent input to brainstem auditory nuclei is a high level of spontaneous activity. In the absence of a sound stimulus, this random firing can reach rates of 100 Hz (Liberman 1978, 1982). Fibers with different spontaneous rate have different projections in the cochlear nucleus (Liberman 1991, 1993), suggesting a specific role of the spontaneous random activity. It is well known that noise can facilitate the detection of weak signals in diverse natural and artificial systems (Wiesenfeld and Moss 1995; Bezrukov and Vodyanoy 1995). It is possible that neuronal spontaneous activity could serve a similar function since it increases in lower auditory brainstem centers during performance (Ryan et al. 1984). Notably, some MSO cells are spontaneously active in vivo, reflecting a significant amount of random spontaneous input (Goldberg and Brown 1969; Carr and Konishi 1990; Young and Rubel 1986).

Since I_KLT activates below the threshold for spike generation, it is expected to play an important role in the integration of subthreshold signals. To gain more insight on this role, we studied the responsiveness of MSO neurons (gerbil, in vitro) and Hodgkin-Huxley-like models (that included currents for spike generation and I_KLT ) to computer-generated currents that mimic transient random weak synaptic conductances. We found that blocking I_KLT in MSO neurons decreased the SNR when a brief subthreshold excitatory postsynaptic conductance (EPSG) “signal” was injected together with weak random excitatory and inhibitory PSGs. This input protocol also enabled us to determine, by using the reverse correlation method, the net synaptic input that leads on average to spike generation. We further saw that, in order to spike, the cell and the model with I_KLT selects for faster inward current transients, i.e., that its temporal integration window is narrowed. These results demonstrate benefits from I_KLT for detecting weak signals with increased SNR and shortening the integration time.

The neural computation for localizing low-frequency sounds involves coincidence detection of binaural inputs, as occurs in MSO. We show that a model’s ITD window for spiking in response to well-timed excitatory inputs (that are individually subthreshold) narrows with increasing I_KLT (over a certain range). In actuality, the computation is carried out in the presence of noise and inhibition (Grothe and Sanes 1994; Brand et al. 2002). For a pure tone, say, while the auditory nerve inputs are well phase-locked (with some jitter), the probability of an auditory nerve spike per cycle is less than 1 (cycle-skipping) and decreases strongly with frequency, so stochastic factors are involved here as well. Interestingly, it was recently found in gerbils (Brand et al. 2002) that precisely timed inhibition shifts the ITD tuning curve so that it is steeply sloped around ITD = 0. Moreover, as had been seen previously (see McAlpine et al. 2001 and references therein), many ITD-sensitive cells do not have their peak locations spanning or lying within the physiological range. These results call into question (McAlpine et al. 2001) whether the classical hypothesis of a place code (Jeffress 1948) applies to small mammals even while it is widely accepted for the avian system (Carr and Konishi 1990). The model shows a similar effect from brief and time-locked inhibition, and we see that I_KLT contributes to the effect of inhibition on coincidence detection, at least for individually subthreshold inputs.

2 Methods

2.1 Experimental

Recordings were done at room temperature in slices from gerbils (Meriones unguiculatus) aged postnatal days 8–17 (P8–17) as described in (Svirskis et al. 2002). In brief, the artificial cerebrospinal fluid contained (in mM) 125 NaCl, 4 KCl, 1.2 KH₂PO₄, 1.3 MgSO₄, 26 NaHCO₃, 15 glucose, 2.4 CaCl₂, and 0.4 L-ascorbic acid (pH 7.3 when bubbled with 95% O₂-5% CO₂). The internal patch solution contained (in mM) 127.5 potassium gluconate, 0.6 EGTA, 10 HEPES, 2 MgCl₂, 5 KCl, 2 ATP, and 0.3 GTP (pH 7.2). Recording electrodes were fabricated from borosilicate glass microcapillaries (1.5 mm outer diameter), and their resistance ranged from 7 to 12 MΩ. We used the dynamic clamp method for stimulus generation (Reyes et al. 1996; Sharp et al. 1993). The program determined in real time the time-varying current that was injected into the neuron according to the calculated conductance value and the measured instantaneous membrane potential. The time course of injected current was kept in the computer memory buffer and used to calculate spike-triggered reverse correlation (Bryant and Segundo 1976; Mainen and Sejnowski 1995). Several thousand events were used for computing average spike-triggering currents and poststimulus time histograms (PSTHs). To study the integration of weak transient signals in the presence of noise, a single subthreshold “signal” synaptic conductance, EPSG, was generated as a simple exponential decay from a step onset and time constant of 1 ms. Two trains of random smaller (on average) transient EPSGs and IPSGs (1-ms decay time constants) were delivered as random trains continuously representing the “noise”. For random excitation the reversal potential was 0 mV, and for inhibition it was −70 mV.

2.2 Theoretical

We used two different single-compartment (lumped neuron) models with Hodgkin-Huxley-type Na⁺ and K⁺ conductances for spike generation and a low-threshold potassium conductance (Brand et al. 2002; Svirskis et al. 2002; Rothman et al. 1993). For results in Figs. 1–3 the weak stimuli for the computational neuron (Svirskis et al. 2002) were the same as in experiments, except for the conductance amplitudes of the PSGs. For the simulations of coincidence detection described in Figs. 4–6 we used a different MSO model (Brand et al. 2002; Rothman et al. 1993) that incorporates similar intrinsic currents and an auditory nerve model for pure-tone input generation (Rothman et al. 1993). See the Appendix for more complete descriptions of these two models.

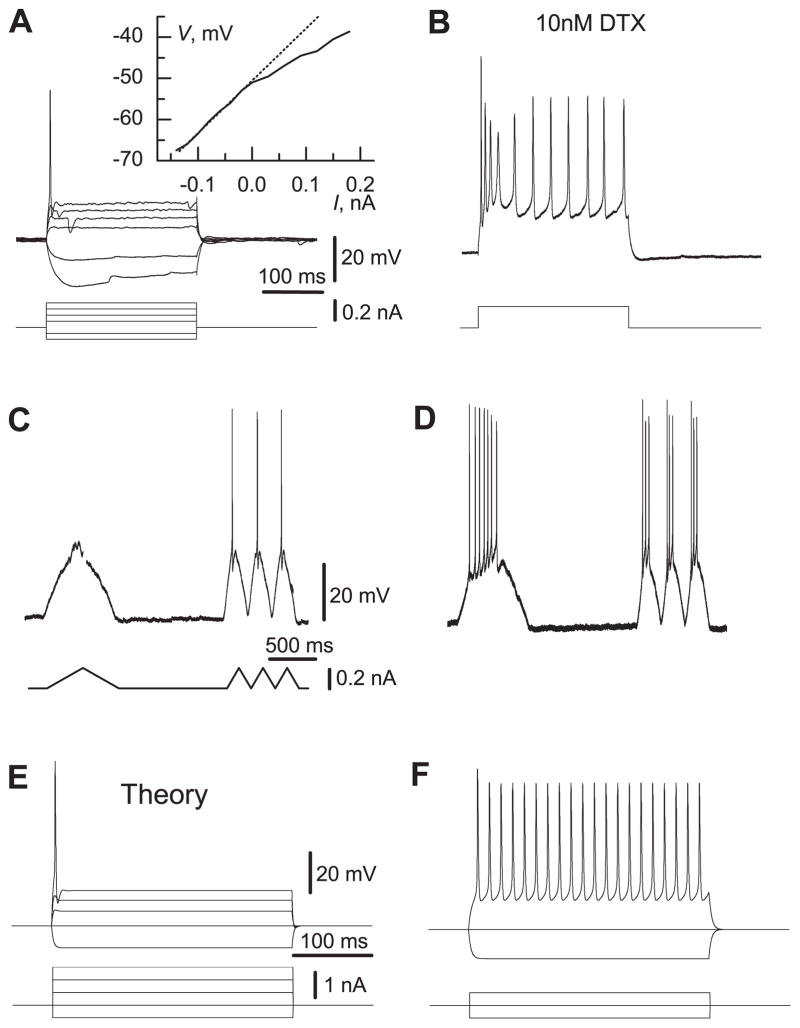
Fig. 1.

Fig. 1A–F. The firing properties of MSO neurons and models. A In response to a step current injection, MSO neurons showed outward rectification and only a single spike when the stimulus exceeded the threshold (phasic firing). The steady state current–voltage curve (inset) generated from the responses to step current stimuli showed that low-threshold outward rectification appeared near the resting membrane potential. The same properties suppressed firing in response to a slow triangular current ramp stimulus while faster stimuli evoked single spikes (C). B After an application of DTX the cells fired tonically and responded with spikes to a slow current ramp stimulus (D). E The model neuron showed similar response and firing properties. F The model without I_KLT responded with tonic firing to the current injection, which was three times weaker. The scales in B, D, and F are the same as in A, C, and E, respectively. A and B are from the same P14 neuron. C and D are from the same P12 neuron

Fig. 3.

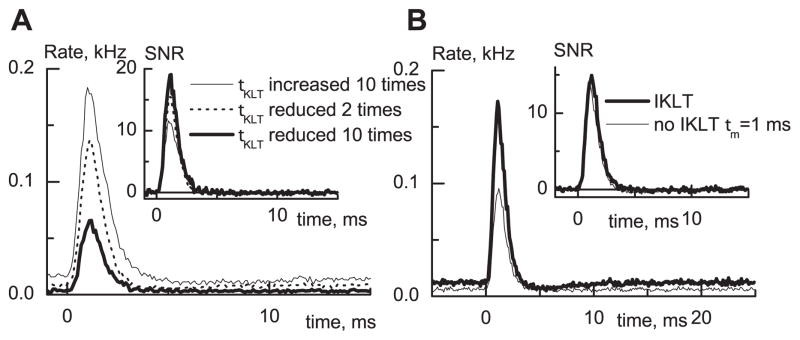
Fig. 3A,B. Influence of I_KLT properties on small signal integration in the model. A Very slow I_KLT activation increases spontaneous activity, while very fast activation strongly suppresses both the response to the signal and spontaneous activity. Parameters A₀ and B₀ were changed to speed up or slow down the activation of I_KLT. B When I_KLT is replaced by an increased leak conductance in the model, the SNR is little changed, although suppression of the response was stronger without I_KLT

Fig. 4.

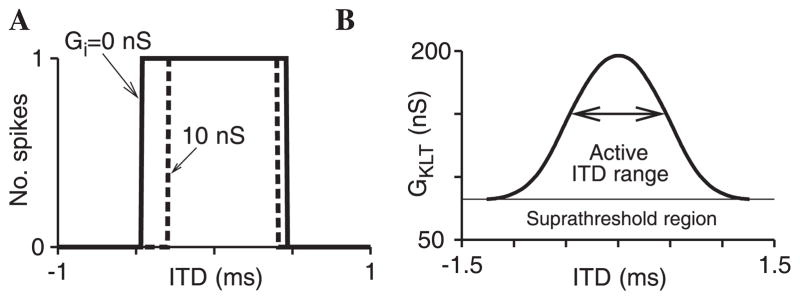
Fig. 4A,B. Effect of inhibition and I_KLT on coincidence detection for individual input pairs. A Response vs. ITD for single subthreshold contralateral and ipsilateral excitatory synaptic events, with G_e = 8.2 nS and contralateral inhibition that leads the contralataral excitation by 0.4 ms at G_KLT = 150 nS. The solid curve is for G_i = 0 nS, and the dashed curve is for 10 nS. Positive ITD indicates contralateral leading. The response range is depressed more on the ipsileading side than on the contraleading side. B The subthreshold contra- and ipsilateral synapses with G_e = 8.2 nS evoke a spike for a range of ITD values. This ITD window is shown as a function of G_KLT, G_i = 0; the arrow corresponds to the ITD curve shown in A. For smaller values of G_KLT, a single synapse would itself evoke action potential exhibiting suprathreshold behaviour

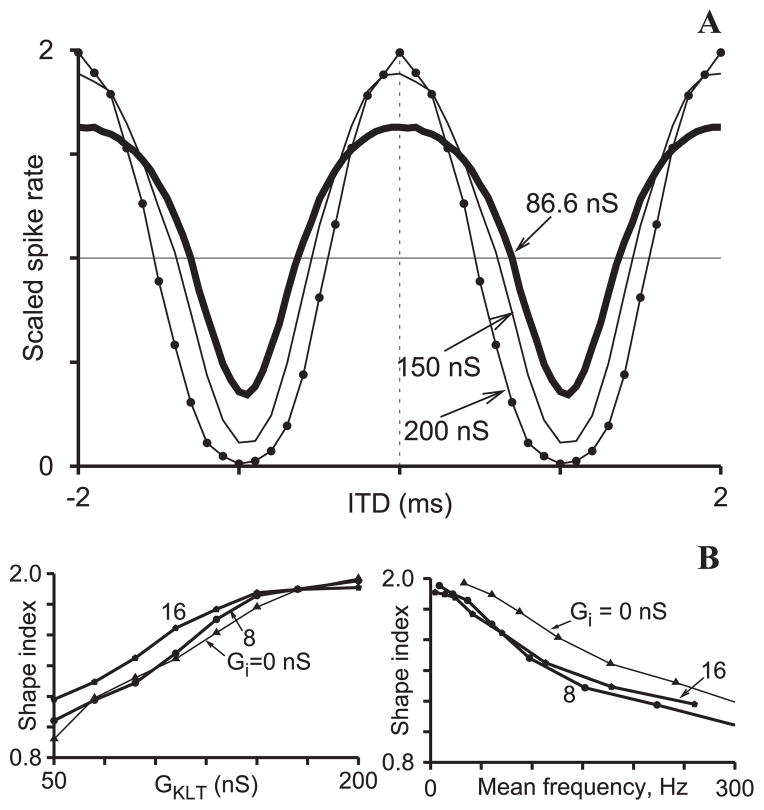
Fig. 6.

Fig. 6A,B. Dependence of ITD tuning sensitivity on I_KLT; G_e = 3 nS. A Effect of G_KLT on ITD curves (with G_i = 0) shown for three values of G_KLT: 86.6 nS (thick solid curve), 150 nS (thin curve), and 200 nS (thin curve with dots). Each curve is scaled by dividing spiking rate by the average of maximum and minimum responses for that curve. B Shape index, defined as the ratio of the difference and the mean of the maximum and minimum of the ITD response curves, shown as a function of G_KLT (left). As G_KLT increases, the ITD sensitivity (shape index) increases, but the corresponding response frequency (mean of maximum and minimum on a tuning curve) decreases (right). Curves are plotted for three values of G_i = 0, 8, and 16 nS

3 Results

3.1 I_KLT contributes to phasic behavior

In the majority of MSO neurons, a step stimulus would not evoke more than a single spike (Fig. 1A). Such a phasic firing pattern and the outward rectification (Fig. 1A, inset) that appears near the resting membrane potential, V_rest, suggest the presence of an I_KLT in these MSO cells. This fast and strong outward current prevented spike generation in response to slowly rising current ramps (n = 3), although faster ramps of the same amplitude could evoke single spikes (Fig. 1C).

The application of 10 nM dendrotoxin (DTX), which is known to block some Kv1 family potassium channel subtypes (Hopkins et al. 1994; Robertson et al. 1996), converted the phasic firing pattern of P12–14 MSO neurons into tonic firing in 9 out of 11 cases (Fig. 1B), and the cells could fire action potentials in response to slow ramps (Fig. 1D).

To confirm that the low-threshold potassium current (I_KLT ) could account for these observed changes in response to current steps and ramps and for the integration of weak noisy signals (see below), we carried out a modeling study. Our Hodgkin-Huxley-like model (see Methods) contains sodium and potassium currents for spike generation and a model for I_KLT that is based on voltage-clamp data (Rathouz and Trussell 1998). It exhibits phasic firing (Fig. 1E) and tonic firing when I_KLT is eliminated (Fig. 1F).

3.2 Detection of weak inputs in noise

To explore how the low-threshold outward current influenced the integration of small and random signals, we applied computer-generated dynamic clamp stimuli. For small signal detection in particular, we considered how effectively the occurrence of a subthreshold “signal” EPSG changed the firing rate in the presence of smaller random excitatory and inhibitory transients, the “noise” (Fig. 2A). For auditory neurons, this signal EPSG could represent the synchronized arrival of unitary inputs in the case of a very weak auditory stimulus.

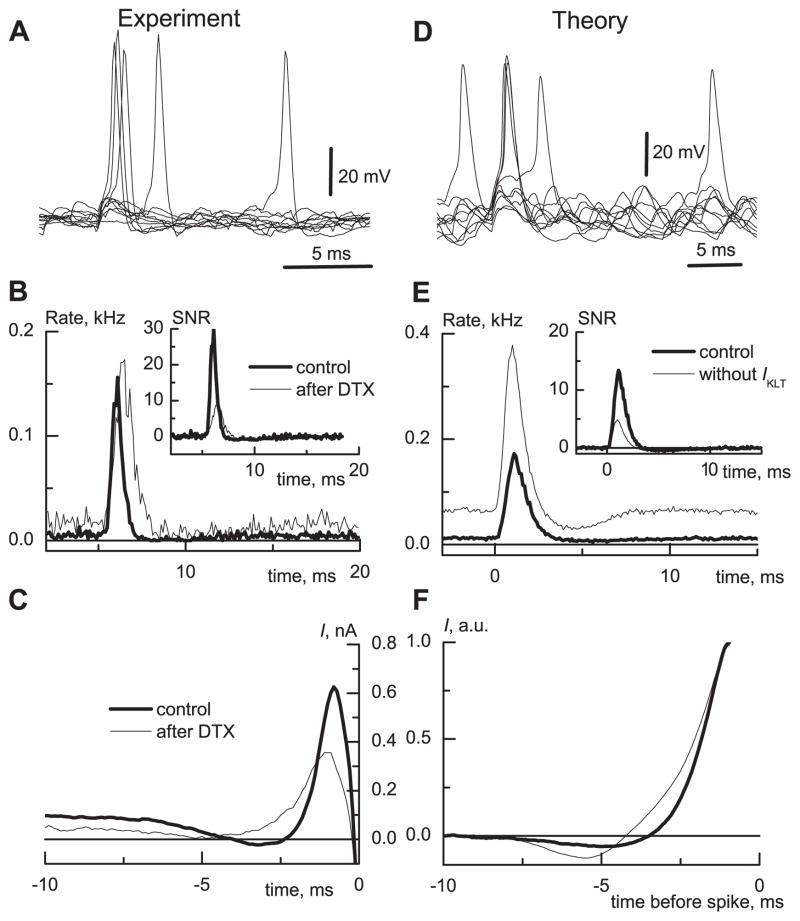
Fig. 2.

Fig. 2A–F. The firing statistics of MSO neuron and model in response to weak and noisy stimuli. A Traces of membrane potential illustrating random and “signal”-evoked firing. B The PSTH for the response to a subthreshold EPSP “signal” in the presence of smaller random excitatory and inhibitory input transients. The EPSG, generated by dynamic clamp, in addition to the random input caused a sharp increase in the probability to fire. DTX increased the spontaneous firing rate and thereby reduced the signal-to-noise ratio (SNR) several times (inset labeled SNR shows difference of PSTH probability from baseline, then divided by baseline). C A spike-triggered reverse correlation exhibited a hyperpolarizing component followed by excitation in control conditions. In the presence of DTX, an average spike-evoking current developed slower. The baselines were not subtracted. D Traces of membrane potential of a model with Hodgkin-Huxley type conductances. E The PSTH for a subthreshold EPSP in the presence of random input. The low-threshold outward current reduced the spontaneous firing rate to 2 Hz but increased the SNR (inset). F The spike-triggered reverse correlation had the same shape as for the recorded neurons, with a hyperpolarizing component and faster dynamics for the spike-evoking current in the model with I_KLT. The traces were normalized and baselines subtracted to compare the time course shapes more easily

The signal EPSG could not evoke a spike in the absence of random input. However, as seen in the computed PSTH, when the signal EPSG occurred together with noise, there was a sharp increase in firing probability over the spontaneous firing levels (Fig. 2B). To measure the efficiency of signal detection, we defined and computed the SNR as the ratio of the increased firing rate in response to the “signal” EPSG (deviation of PSTH value from its baseline) and the spontaneous firing rate in response to “noise” (Fig. 2B, inset). The application of I_KLT blockers lowered spike threshold and increased the spontaneous rate significantly, thus reducing the SNR (n = 11). That is, in the control case, I_KLT prevents some of the temporally summated random inputs from generating spikes while the larger-amplitude (but subthreshold) and faster signal can ride on the noise and “break through” before the transient outward rectification is fully recruited.

Our model shows these same basic response properties as MSO neurons when presented with the same (but amplitude-adjusted) stimuli as in our experiments (see Methods and Fig. 2D). The presence of I_KLT in the model makes the spontaneous firing rate much lower than in the model without I_KLT (Fig. 2E). The presence of I_KLT reduces the response to the signal EPSG as well, but not as much as for the spontaneous firing probability. Consequently, I_KLT increases the SNR (Fig. 2E, inset).

3.3 I_KLT narrows the temporal integration window

To observe the transient net input current that develops before an MSO neuron generates a spike, we performed a reverse correlation analysis to compute the average spike-triggering dynamic clamp “synaptic” current (Fig. 2C). As could be expected, the average spike-triggering current was predominantly an inward (depolarizing) current that developed on a time scale of 2–3 ms (Fig. 2C). The application of DTX or DTXK changed the time course of the mean spike-triggering input current: it developed more slowly (Fig. 2C). The maximal rate of mean injected current calculated for a 0.5-ms time window was significantly slower after a block of I_KLT (n = 7, P < 0.05 paired t-Student test) and decreased from 0.8 ± 0.38 nA/ms to 0.5 ± 0.3 nA/ms. The faster dynamics of the spike-triggering current as mediated by I_KLT further implicated I_KLT ’s role in enhancing the precision of temporal processing.

For the model, the mean input current that precedes spike generation has the same shape as in MSO neurons (Fig. 2F), and it has a faster mean time course with I_KLT compared to when I_KLT is eliminated. Notice further that, in both the experimental and computational records, the mean spike-triggering current has a hyperpolarizing undershoot before its strong depolarizing rise. We interpret this hyperpolarizing “dip” as evidence of input combinations that favor spike generation by first deactivating some I_KLT and then providing properly timed depolarizing input. The dip is reduced when I_KLT is blocked (the effect is seen more clearly in the unscaled case of Fig. 2C).

Next, we illustrate more directly the significance of I_KLT’s dynamic and voltage dependence specifically by comparing the model neuron’s behavior as adjustments are made in the parameters of I_KLT that alter the activation rate τ_KLT of the I_KLT conductance or that eliminate its voltage dependence. As τ_KLT is decreased, the probability of firing generally decreases (Fig. 3A); the speeded up conductance acts to filter out more of the spikes coming from slower summated noisy inputs (with or without signal riding on top). But the net effect is an increase in the SNR (Fig. 3A, inset). The relative advantage of faster I_KLT depends on the compromise between the SNR and the strength of the response. It is tempting to view I_KLT ’s influence as an additional conductance in the subthreshold regime that effectively shortens the membrane time constant. To examine this notion, we eliminated I_KLT and increased by threefold the model’s leak conductance. In comparison with the control case, the SNR of these two realizations of the model were almost the same (Fig. 3B, inset); however, the response amplitude for the model with I_KLT was almost two times larger (Fig. 3A). Again, supposing that not only the SNR but also the strength of the response is important leads us to conclude that the subthreshold voltage-dependent outward current is important for enhancing small signal integration. Moreover, it is not adequate to view the net improvement as due only to a change in the membrane time constant.

3.4 Coincidence detection, inhibition, and subthreshold outward currents

For localizing low-frequency sounds, the detection of ITDs between binaural inputs is important (Jeffress 1948; Goldberg and Brown 1969; Carr and Konishi 1990). We address this issue here using the model in two protocols. How does I_KLT influence the ITD window for the neuron model to respond to two subthreshold inputs or to, in a more in vivo-like caricature, an ensemble of periodically Poisson-modulated input trains as might be delivered from phase-locked but cycle-skipping firings of auditory nerve fibers from ipsilateral and contralateral sides? In each case, motivated by recent in vivo experimental and computational findings (Brand et al. 2002), we allow for the effects of brief transient inhibitory inputs that might be time locked to excitatory inputs (from the contralateral side). We adopt the same model as was used in (Brand et al. 2002) (see Methods).

When two identical but individually subthreshold inputs are presented to the noise-free model, a spike is elicited if the inputs occur within a critical ITD window around perfect coincidence (provided, of course, that a doubled-amplitude input is superthreshold) (Fig. 4A). As one expects, this window for detection of the pair narrows as I_KLT is strengthened (by increasing G_KLT ), i.e., timing selectivity is enhanced (Fig. 4B). But again one sees that there is a compromise between this enhanced temporal filtering and signal throughput. If G_KLT is made too large, the cell cannot respond to even a perfectly coincidental presentation of inputs at this amplitude. In Figs. 4–6, ITD < 0 corresponds to the “ipsilateral” input leading.

The effect of a brief inhibitory input that is time locked to just precede (by 0.4 ms) the contralateral input is to narrow the ITD window for detection (Fig. 4A, dashed). The ipsilateral leading side is affected more, i.e., when the inhibitory input occurs between the two excitatory inputs. The conditions for firing are disfavored if the preceding excitatory input has created a larger transient of I_KLT (or, more accurately, of I_KLT ’s conductance). This occurs here when the ipsilateral excitatory (full strength) input precedes the composite input, the combination of contralateral inhibition followed shortly by the contralateral excitation.

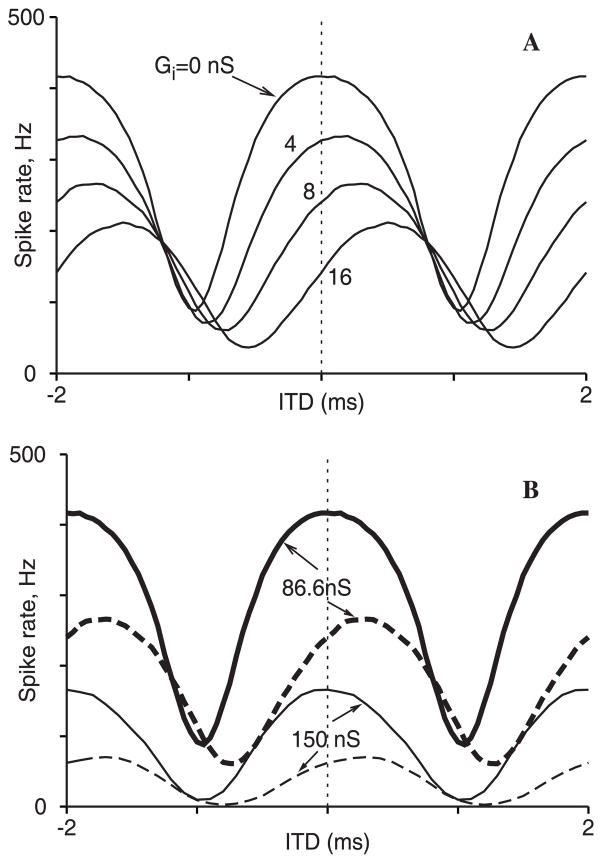
When multiple ipsilateral and contralateral input lines are incorporated into the model (see Methods and Appendix) with stochastic but phase-locked EPSG events that idealize auditory nerve responses, ITD tuning to a pure tone is seen (Fig. 5A). Here the sculpting out of the ITD window on the ipsilateral-leading side with increasing inhibition (as in Fig. 4A) is also apparent. The effective rightward shift, with the tuning curve’s peak not at ITD = 0, is presented (Brand et al. 2002) as evidence of inhibition’s involvement in the hypothesis that the coding of sound localization may not involve the location of the peak (as in the classical Jeffress model (Jeffress 1948)) but rather involves the region around ITD = 0 where the response is most sensitive to ITD variation – i.e., a slope code rather than a place code. This relates to our general notion (as above in Fig. 4) that subthreshold outward currents (in this case, also synaptic) can influence temporal processing in MSO neurons. However, our main points in this paper are the effects of I_KLT, not I_syn, on tuning and temporal processing.

Fig. 5.

Fig. 5A,B. Dependence of ITD tuning curves on brief inhibition and I_KLT. (See Appendix for model description.) Maximum excitatory synaptic strength is 3 nS, and stimulus frequency is 500 Hz. A ITD responses as the maximum inhibitory synaptic strength is increased from 0 to 16 nS. B Effect of G_KLT on ITD tuning properties, shown for two values of G_i: 0 nS (solid) and 8 nS (dashed) as in A. The thick and thin curves are, respectively, for G_KLT = 86.6 nS and 150 nS. Increasing G_KLT reduces the response at each ITD and level of inhibition

As G_KLT is increased, we see that the firing rate decreases at all ITDs shown here – and irrespective of whether inhibition is included (Fig. 5B). Both the peaks and the troughs of the tuning curves are considerably affected. To compare the shape changes in these curves and possibly detect some relative narrowing as G_KLT is increased, we first rescale the curves (divide the ordinate values by the mean of the peak and trough rates) to bring them into the same response range (Fig. 6A). In this representation, it seems to the naked eye as though increasing G_KLT leads to a steeper sloped tuning curve between the peak and trough – sharper tuning. By defining a shape index parameter as the difference between the peak and trough in this scaled representation we see that tuning sharpens (shape index increases) as G_KLT is increased (Fig. 6B, left). On the other hand, the response decreases (Fig. 6B, right) – meaning again a tradeoff between enhancement of coincidence detection and signal throughput. The shape index curves are affected somewhat by inhibition, but these curves do not reveal the inhibition-induced rightward shift (which is actually reduced slightly for increasing G_KLT, not shown). In contrast to our considerations in previous sections of how I_KLT affects the integration of weak signals in noise, here the signals are not weak and I_KLT acts, through its conductance, more via a shunting mechanism than through a dynamic selective filtering mechanism.

4 Discussion

Low-threshold potassium currents enhance temporal processing and sensitivity to spike timing in the auditory system, and we have seen these effects in several ways. In gerbil MSO neurons, the DTX-sensitive I_KLT increased the SNR for a subthreshold signal in the presence of weak random input. A computational model with Hodgkin-Huxley-type conductances for spike generation and I_KLT had the same qualitative integration properties for noisy signals as did MSO neurons in vitro. By using the reverse correlation method we can see that I_KLT shortens the integration time window for the neurons and the model. Both the voltage and time dependence of the subthreshold outward current contribute to enhancing weak signal integration. If I_KLT activates more rapidly, the phasic filtering properties are enhanced but at some cost of lower throughput. If it is too slow, then G_KLT acts to effectively increase the leakage conductance. The resulting SNR could match that of the model with I_KLT, but the response to the signal is significantly reduced; the benefits of dynamic voltage-gated filtering are not realized. Increasing the strength of I_KLT tightens the model’s critical temporal window for coincidence detection of weak signals. For stronger signals, I_KLT ’s effect is more like a shunt and perhaps less selective. Again, the enhancements must be weighed against reduction of overall response. Brief inhibition contributes to shaping the ITD tuning curve.

The ability of neuronal properties to influence signal integration in the presence of noise was extensively investigated previously. For example, such studies suggested that an interaction between noisy signals and voltage-dependent currents could bring about increased temporal precision (Gauck and Jaeger 2000), improved coincidence detection (Softky and Koch 1993; Softky 1994), increased information transfer (Manwani and Koch 1999), and spike-timing reliability (Mainen and Sejnowski 1995; Hunter et al. 1998). Our studies concentrated on the effects of a particular current, I_KLT, and tried to elucidate the mechanisms by which neurons could improve small or strong signal integration.

In a separate computational study (Svirskis and Rinzel 2003), we have shown that an integrate-and-fire-type model without an I_KLT but with an idealized sub-threshold inward current can behave phasically if the inward current inactivates with an appropriate time scale and in a voltage range below its activation threshold; the model also shows improved SNR as compared with the case with no subthreshold inactivation. Thus, multiple forms of subthreshold fast, but not necessarily instantaneous, negative feedback can contribute to enhancing temporal processing.

We have emphasized that the dynamic aspects (i.e., the time scale of the gating kinetics) of I_KLT activation are important for understanding how I_KLT affects signal throughput (Fig. 3). Fast just-suprathreshold depolarizing inputs can squeeze through to spike threshold before I_KLT is activated, while slower ones that would be suprathreshold, if the membrane conductance remained at its resting level, will now be rendered subthreshold because there will be adequate time for reducing the membrane resistance by activating the conductance of I_KLT. In this sense, I_KLT effectively acts to implement a dynamic threshold or filter. Here we have considered a spontaneous state of noisy fast weak inputs. A few nearly coincident ones provide fast depolarization that can lead to a spontaneous firing. Occasionally, some of these, not so nearly coincident, will summate temporally to create a slower transient that would be suprathreshold if it were not falling into the temporal window for recruiting I_KLT. Therefore, I_KLT can eliminate false positives.

We have shown with a model that detection of nearly coincident “binaural” inputs is improved by I_KLT. For subthreshold inputs, I_KLT exerts its dynamic filtering property (Fig. 4). It also interacts with brief inhibition (timed to just precede contralateral excitation) to shape the ITD tuning properties, narrowing and shifting the tuning range’s center toward the contralateral-leading direction (Fig. 4, dashed). For strong inputs, I_KLT acts more like a shunt lowering the overall firing rates while sharpening ITD tuning (Fig. 6). Inhibition shifts the peak of the ITD tuning curve, suggesting a slope code ((Brand et al. 2002), and Figs. 4–6 here). A better understanding of I_KLT ’s effect on the inhibition-induced reshaping and shifting in the strong input case (Fig. 6b) will be sought in future studies.

Various investigators have proposed that low-threshold potassium currents help to suppress weak subthreshold inputs while improving the temporal precision of integration of strong suprathreshold inputs (Brew and Forsythe 1995; Oertel 1983; Manis and Marx 1991; Rathouz and Trussell 1998; Reyes et al. 1994; Rothman and Young 1996). It is important to stress that, in the case of weak subthreshold inputs, the noise is necessary so that the neuron can detect a potentially meaningful subthreshold signal. On the other hand, if the signal is absent, noise creates false positives. The low-threshold potassium current in such circumstances plays two roles: it allows the noise to aid in signal detection, while it suppresses false positives if the signal is absent.

Appendix A: Model used for Figs. 1–3

The currents were calculated by using the general equation I = gA_cellm^ph^q(V − E), where g is specific conductance, A_cell is membrane area, p and q represent the numbers of gating subunits, V is membrane potential, and E is reversal potential for the current. Activation and inactivation gating variables, m and h respectively, were governed by equations of the form du/dt = (u_∞ − u)/τ_u. The “steady state” value for the gating variable, u, was u_∞ = α/(α + β) and time constant τ_u = 1/(α + β); both u_∞ and τ_u were voltage dependent: α = A₀ exp{−0.0393zγ(V_0.5 − V )}, β = B₀ exp{0.0393z(1 − γ)(V_0.5 − V )}, where z is the effective gating charge. The fast-activating sodium current had a reversal potential of E = 50 mV; its activation was described by the parameters p = 3, z = 3.3, γ = 0.7, A₀ = 4.2 ms⁻¹, B₀ = 4.2 ms⁻¹, V_0.5 = −29.5 mV; inactivation had the following parameters: q = 1, z = −3.0, γ = 0.27, A₀ = 0.09 ms⁻¹, B₀ = 0.09 ms⁻¹, V_0.5 = −40 mV. The time constants for activation and inactivation had limits to their minimal values set to 0.05 and 0.25 ms, respectively, to avoid exponents from occasional overflowing. The delayed rectifier conductance had only an activation gating variable, described by the parameters: E = −90 mV, p = 4, z = 3, γ = 0.8, A₀ = 0.3 ms⁻¹, B₀ = 0.3 ms⁻¹, V_0.5 = −30 mV, and the minimal time constant for activation of 1 ms. The conductance of the low-threshold potassium current, I_KLT, was described by the parameters: E = −90 mV, p = 1, z = 2.88, γ = 0.39, A₀ = 0.2 ms⁻¹, B₀ = 0.17 ms⁻¹, V_0.5 = −45 mV. This current did not inactivate.

The specific conductances, g, were 0.1 nS/μm², 0.01 nS/μm², and 0.005 nS/μm² for Na⁺, K⁺, and I_KLT conductances, respectively. The area of the compartment, A_cell, was 104 μm²; specific conductance for membrane leakage was 3.333 × 10⁻³ nS/μm²; specific capacitance was 10⁻⁵ nF/μm² with the resulting time constant τ_m of 3 ms. The model’s rest potential was about −60 mV, and the spike threshold was about 20 mV above rest.

Appendix B: Model used for Figs. 4–6

A single-compartment model described by Hodgkin-Huxley-type equations that incorporate Na⁺, K⁺, and low-threshold potassium conductances is used. The model is identical to the one used earlier in modeling bushy cells of antroventral cochlear nucleus by Roth-man et al. (Rothman and Young 1996), as well as simulating MSO neurons to study ITD shifts caused by contralateral inhibition (Brand et al. 2002). Our parameters, voltage dependences of the rate constants and a Poisson spike generation mechanism including the refractory function, are the same as those of Rothman et al. In simulating 2 × 25 excitatory and 25 inhibitory inputs the parameters we used for Poisson spike generation are R_ss = 90, R_r = R_st = 0. The membrane evolution equation is C_totdV/dt = −G_L(V − E_L) − G_Nam²h(V − E_Na) − G_K n(V − E_K ) − G_KLT w(V − E_K ) − G_e(V − E_E) − G_i(V − E_I ). The membrane conductance is C_tot = 23 pF. The activation variables m, n, and w and the inactivation variable h evolve according to dη/dt = α_η(1 − η) − β_ηη, for η = m, n, w, and h. The voltage dependences of α_η and β_η are identical to those listed in the Appendix of Rothman et al. (Rothman et al. 1993) at temperature T = 38°C. The absolute conductance values are G_L = 5.2 nS, G_Na = 985.2 nS, G_K = 173.3 nS. The reversal potentials are E_Na = 55 mV, E_L = 2.8 mV, E_K = −77 mV, E_E = −10 mV, E_I = −66.5 mV. The value of G_KLT is fixed at 86.6 nS for Fig. 5A but varied for other figures as indicated in the figure captions. The time constants of excitation and inhibition for Fig. 4 are 0.3 ms for each but 0.1 ms for Fig. 5 and Fig. 6. Figure 4 uses single deterministic alpha-function synapses. Figures 5 and 6 use 2 × 25 excitatory and 25 inhibitory presynaptic inputs given as alpha functions generated at intervals specified by independent Poisson spike trains whose rate is modulated with a stimulus frequency of 500 Hz. The inhibitory synapses precede the contralateral excitation by 0.2 ms as in Brand et al. (Brand et al. 2002).