Enhanced neuronal response induced by fast inhibition

Abstract

We report a facilitatory role of inhibitory synaptic input that can enhance a neuron’s firing rate, in contrast to the conventional belief that inhibition suppresses firing. We study this phenomenon using the Hodgkin-Huxley model of spike generation with random Poisson trains of subthreshold excitatory and inhibitory inputs. Enhancement occurs when, by chance, brief inhibition leads excitation with a favorable timing and counterintuitively induces a reduction of the spike threshold. The basic mechanism is also illustrated with the phase-plane analysis of a two variable model.

Inhibitory synaptic inputs play an important role in generating collective neuronal mechanisms of synchronization [1–3], wave propagation [4], chaos [5,6], asynchronous behavior [7], persistent states [8,9], neural oscillations [10], and a formation of cluster states [11]. At the single neuron level, inhibition is also effective in gain control of neuronal signals [12] and temporal sensitivity to coincident inputs [13]. In the classical view, an inhibitory input hyperpolarizes the membrane away from its spike threshold resulting in a reduction of the spike probability. Thus inhibition has conventionally been viewed as a suppressor of neuronal response [14–17], and, in particular, causing either divisive or subtractive effect on the output firing rate [14]. But inhibition playing a facilitatory role was recognized about 50 years ago [18,19], to the best of our knowledge, in the form of postinhibitory rebound [PIR] and is thought to play a major role in central pattern generator networks [20]. In PIR a neuron fires after being released from a long-lasting hyperpolarizing input. Here we report a facilitatory mechanism by which brief inhibitory inputs can, in contrast to the conventional belief, enhance firing probability during ongoing stimulation by trains of brief excitatory inputs. Unlike PIR, this mechanism does not require that an inhibitory input by itself leads to a rebound spike. In our case both the excitatory and inhibitory single inputs are subthreshold in magnitude.

We study this phenomenon using a Hodgkin-Huxley model neuron [21] with external excitatory and inhibitory input conductances. The inputs are subthreshold α functions timed at random independent Poisson intervals. For pure excitatory driving, the neuron responds with a finite output rate due to temporal summation of nearly coincident inputs. When inhibitory inputs are included some spikes are lost but other ones are added. With respect to the onset time of these evoked spikes, inhibitory events form a temporally localized distribution leading ahead of a similar distribution of excitatory events. The leading inhibition can transiently reduce the spike threshold, and a well timed brief subthreshold excitation can utilize this to evoke a spike. We term this phenomenon as the postinhibitory facilitation (PIF) [22]. The enhanced output response could also consist of inhibitory events that are paired with another set of inhibitory events displaying PIR for temporally brief inputs. Our result stresses the importance of the timing of the prespike input events rather than postspike [23,24] or the diffusion process response [25] of the membrane. Experimentally, some neurons’ firing probability and precision in response to excitatory synaptic input is enhanced by a preceding fast inhibition [26].

The membrane potential of the Hodgkin-Huxley model evolves according to the following equation [21,36]: C_mV̇ =−I_Na − I_K − I_L − I_syn, where I_Na[=G_Nam³h(V −E_Na)], I_K[= G_Kⁿ⁴(V − E_K)], and I_L[= G_L (V − E_l)] are, respectively, sodium, potassium, and leakage currents through the membrane. The gating variables, activation m, and inactivation h of the sodium current and activation n of the potassium current, evolve according to ẋ = α_x(1−x)− β_xx, where x = m, h, and n. h and n are feedback variables. The rates α_x and β_x are voltage dependent, and are expressed via standard formulation [21,27]. The total synaptic current I_syn(=I_ex + I_inh) is the sum [Σ_ji_ex(t −t_j) + Σ_ji_inh(t −t_j)] of individual events of excitatory [i_ex(t)=G_ex(t/τ_ex)exp(1−t/τ_ex)(V −E_ex)H(t)] and inhibitory [i_inh(t)=G_inh(t/τ_inh)exp(1−t/τ_inh)(V −E_inh)H(t)] α-function synaptic currents, that are generated at times t_j determined by independent random Poisson processes each with a rate λ. G_ex and G_inh (measured in mS/cm²) are the peak conductances, and τ_ex and τ_inh (measured in ms) are the time constants of excitatory and inhibitory synaptic currents. For finding reverse correlations and input arrival distributions about 250 000 action potentials per integration were generated in a typical run. The model’s response is described by the average firing rate, i.e., the number of evoked action potentials per second. For our long integration times, this quantity relaxes to a steady state and the errors in the mean firing rate can be neglected.

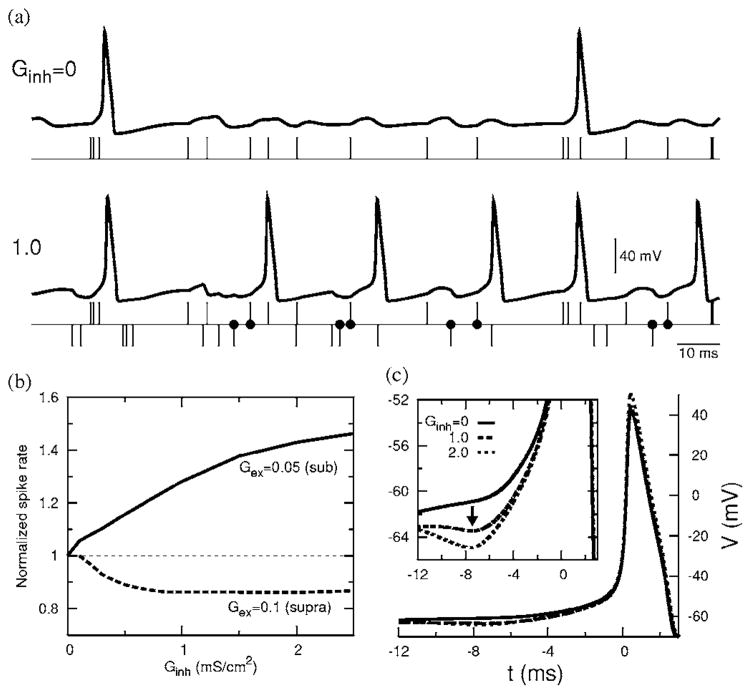
An individual input i_ex(t −t_j) is subthreshold. However, spikes are evoked during trains of inputs, e.g., when two or more inputs are nearly coincident if their arrival times fall within a window t_w whose width depends on the strength of the input. For an input strength of G_ex =0.05 and τ_ex =1 ms, the window’s width is t_w =2.24 ms. An excitatory input train with λ=100 Hz produces a firing pattern with a mean firing rate of 19.3 Hz. When a train of inhibitory synaptic inputs is added to this, however, more spikes occur [Fig. 1(a)] than before. For G_inh =0.5, the spike rate is enhanced by 15% (22.3 Hz) and for G_inh =1.0, it is further enhanced by a total of 28% (24.7 Hz). For further increments in G_inh, the mean firing rate plateaus (explained later). In contrast, a suppression of the spike rate with G_inh would occur if the membrane received a suprathreshold excitatory signal [shown in Fig. 1(b)]. The inhibition-induced enhancement of a firing rate for subthreshold excitatory inputs is the major result of our paper. The voltage reverse correlations, in the presence of inhibition, show a noticeable depression several milliseconds before the spike onset [Fig. 1(c)]. For example, for G_inh =1 and τ_inh =1 ms this depression occurs at a spike-preceding time of t_d =7.4 ms and increases in depth with G_inh. This is indicative of the effect of inhibition either before or around t_d. As we will see for the present membrane whose effective membrane time constant is 0.86 ms, inhibition is indeed distributed with a finite width around t_d. Thus the enhanced firing is evidenced by the role of inhibition in the voltage reverse correlations. In the rest of the paper we describe the mechanisms that contribute to such an enhancement. From Fig. 1(a) we see that each output spike in the absence of inhibition is preceded by a sequence of excitatory arrivals with a leading ee pair. Some of these ee-caused spikes are eliminated in the presence of inhibition, and thus their contribution to the total spike rate is reduced. Also in the presence of inhibition, many of the spikes are preceded by a sequence of e and i combinations led by an ie pair. That is, these spikes are generated by an excitatory arrival (e) with a leading and well timed inhibitory arrival (i). This is an important observation. Some spikes are also caused by a leading ii pair and a very small fraction could also appear to have come from leading ei pairs. For the time windows of relevance for our input, the first two arrivals preceding a spike would be more effective to either induce or inhibit a spike. We present in Fig. 2(a) the relative contributions of these spike-causing pairs to the total spike rate. The effect of the ee contribution has decreased as expected in the presence of inhibition, but a prominent contribution is coming from ie pairs. As the strength of inhibition is increased, more and more ie pairs that were previously too far apart now become capable of causing spikes and the resultant contribution to the total spike rate increases. However, the number of such pairs is limited by the input arrival rate. Thus an increasing G_inh recruits these pairs up to the maximum available number resulting in a saturation of the spike rate.

FIG. 1.

Enhancement due to inhibition. (a) Membrane response without and with inhibitory input. The excitatory (e) and inhibitory (i) input arrival times are marked, respectively, by upward and downward vertical lines. Well timed ie pairs marked with dots induce additional spikes (G_ex =0.050. (b) The normalized spike rate as a function of G_inh showing enhancement of the firing rate for a subthreshold excitation (G_ex =0.05) and suppression for a suprathreshold excitation (G_ex =0.1). (c) Reverse correlations of V showing a depression with increasing inhibition (G_ex =0.05). (For all figures τ_ex =1 ms, τ_inh =1 ms, and when applicable λ =100 Hz.)

FIG. 2.

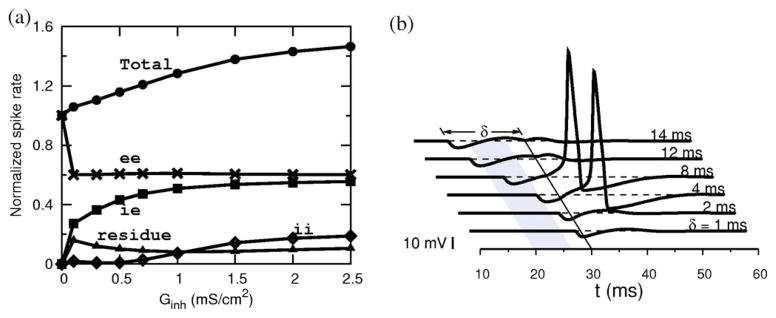
(a) Breakdown of the total spike rate (normalized to control, 19.3Hz) into four contributors. The ie pairs contribute to most of the enhancement overcoming the ee losses. (b) A precisely timed ie pair can evoke a spike in a resting membrane: an excitatory input is given at t =30 ms, and an inhibitory input preceding it by δ ms (G_inh =1). (G_ex =0.05.)

How does a favorably timed inhibitory input that precedes a subthreshold excitatory input lead to a spike? To address this question, we consider a resting membrane and subject it to an isolated pair of subthreshold excitatory and leading inhibitory input conductances [Fig. 2(b)]. As the lead time of inhibition (δ) is increased from 0 to a large value the membrane passes through a phase of hyperexcitability (time window, gray in figure) that resulted in a spike. The depression in the reverse correlations [Fig. 1(c)] is associated with the time range provided by this window that acquires the hyper-excitable nature due to a transient decrease in effective negative feedback of the system.

When the inputs are random, the arrival times of these i and e inputs are distributed with their time differences falling approximately in the window for hyperexcitability [Fig. 3(a)]. The phase of hyperexcitability occurs after the i-input, g_inh(t), has mostly decayed. Thus as τ_inh increases and g_inh(t) decays slower, the window for pairs shifts to larger δ values. Correspondingly, for the random input case, the distribution of favorable timings shifts to larger δ [Fig. 3(a)]. The mean of the distribution is shown in Fig. 3(b) (as filled circles) as a function of τ_inh. The points corresponding to 10% of the peak values are also marked for a few τ_inh values. As τ_inh increases, the recovery time of the membrane subsequent to, for example, a single isolated inhibitory input takes longer. In the present model, such a recovery is accompanied by an overshoot (due to a transient reduction of dynamic negative feedback in the system) of the membrane voltage above the rest level, V_rest. The time t^* at which V crosses V_rest upwardly depends continuously on τ_inh [solid line in Fig. 3(b)] and nearly coincides with the mean of the ie relative timing distributions. The finite spread of these distributions is reminiscent of the finite width of the excitable region shown in Fig. 2 (b), and this latter region is shown here again [gray in Fig. 3(b)] but now as a function of τ_inh. The width and extent of this gray PIF region (and thus the relative ie timing distribution widths) can be controlled by the level of G_ex. The relative hyperexcitability (i.e., effective threshold reduction), which is also reflected by the relative heights of the distributions, varies across the PIF window; it is dynamic and also depends on τ_inh. For example, at the point indicated by “+” (τ_inh =1 ms, δ=6.5 ms) a spike can be elicited with a G_ex value that is only 30% of the amount needed from rest.

FIG. 3.

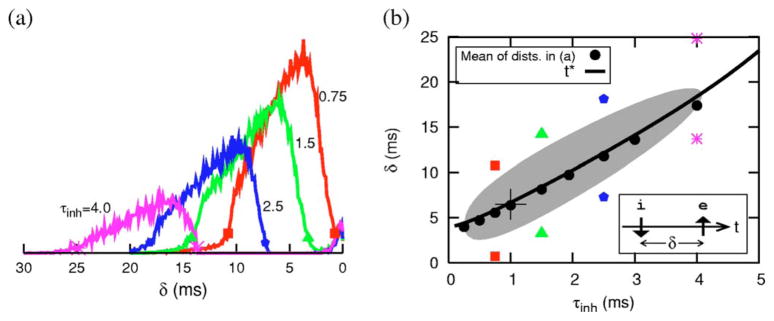
(Color online) δ-window distributions and comparison with response to isolated ie pairs. (a) Distribution of relative timing of i with respect to e immediately preceding a spike onset for different τ_inh. (b) The mean values of these distributions are plotted (as filled circles) as a function of τ_inh. The gray region shows the parametric dependence of the width of hypersensitive region shown in 2(b). The solid curve distinguishes two subregions where V > V_rest (gray portion with δ > t^*, see text) and where V < V_rest (δ < t^*) following an isolated inhibitory input. See text for other markings.

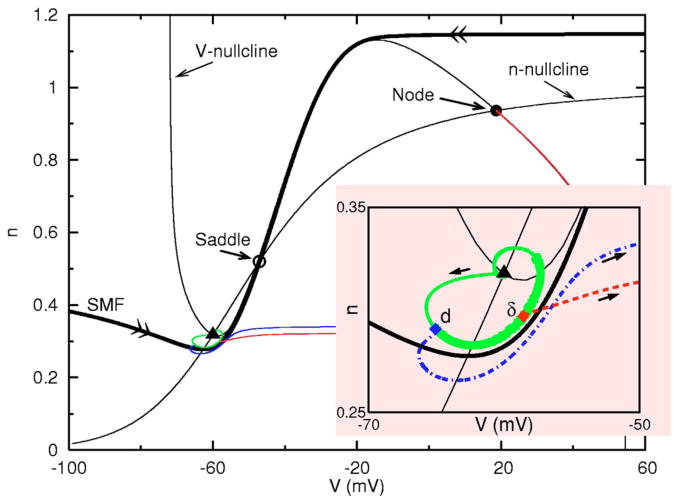
What actual biophysical mechanism is behind the enhancement phenomenon? To address this question we reduce the full model equations to a two-variable model [37] described by CV̇ =− I_fast(V) − G_Kⁿ⁴(V − E_K)− I_syn, ṅ = α_n(1 − n) − β_nn, where $I_{\mathit{fast}}(V)=G_{Na}{m}_{\infty }^3(V)h_0(V-E_{Na})+I_L$. And n is the negative feedback variable. The rest state at −60 mV is a focus, as in the full system, and as visualized in this phase plane (Fig. 4). In this reduced model, excitability corresponds to a spike-upstroke trajectory which is generated by a transient input that drives the V-n trajectory across the stable manifold (SMF) of the saddle. The SMF is the unique pair of phase plane trajectories (marked with double arrows in the figure) that enter the saddle point. Note that a SMF crossing could be evoked from a leftward-driving or rightward-driving stimulus. During a transient input, the V nullcline (i.e., the curve on which V̇ =0) and the SMF move dynamically; then, after the stimulus, the phase point moves along the flow lines of the resting system. An inhibitory input that is faster than the intrinsic relaxation time scale perturbs the phase point with nullclines and SMF virtually returned to their “resting” positions. For inputs that would be subthreshold from rest, there still are two mechanisms by which a spike upstroke can be achieved by temporally sequencing such inputs. For a subthreshold inhibitory input, the trajectory returns to the focus in a spiral (solid curve). If during this return toward rest the brief excitation (that would be subthreshold if applied at rest) is delivered (δ ms later, say at the point labeled δ in Fig. 4 inset) when the trajectory is close to the SMF the phase point is pushed rightward across the SMF and a spike results. For a given strength of inhibition, as before, a range of such favorable times (marked by the thick portion on the solid curve) can be found that define the δ-window where the spike threshold is effectively reduced and where PIF may occur. During some phases of this window the membrane is depolarized or hyperpolarized relative to rest [cf, t^* in Fig. 3(b)]. The transient reduction in threshold for a brief input depends on the instantaneous value of V and on the membrane resistance. The reduced value of n means increased resistance which enhances the effect of an input. Being closer horizontally to the SMF means less input is required for spike generation (for a given resistance). In some phases both factors contribute positively. The second mechanism (PIR) by which the trajectory can cross over the SMF is by using, instead of a delayed excitation, a second inhibitory input given d ms later. In this case, the trajectory crosses the manifold from right to left. Note that the counterclockwise flow during and after the inhibition leads to a trajectory along which during some phases the neuron is hyperexcitable (thickened portion, in Fig. 4 inset). Eventually the behavior of this trajectory locally is governed by the eigenstructure of the rest state. For this V-n model (in Fig. 4) and the full Hodgkin-Huxley model the rest state acts as a damped oscillator [29]. However, the counterclockwise flow does not require that the rest state be a focus and could persist even if it has a nodal structure [28]. For example, increasing G_L somewhat in the full and the reduced models changes the rest state structure from a resonator [30] to a nonresonator, but does not eliminate the counterclockwise flow or PIF.

FIG. 4.

(Color online) Demonstration of PIF and PIR in a 2D reduced model. Three trajectories emerging from the rest state in the direction of arrows are shown corresponding to a lone inhibition delivered at t =0 (solid curve, subthreshold oscillation), an inhibition (at t =0) followed by an identical inhibition delivered d(=3) ms later (dot-dashed curve, PIR), and an inhibition (at t =0) followed by an excitation delivered δ(=8)ms later (dashed curve, PIF). The thick portion of the solid curve indicates the reduced threshold region in which PIF may occur. (G_ex =0.05, G_inh =1.)

Using biophysical Hodgkin-Huxley model equations, we have shown that brief inhibitory synaptic inputs that are usually associated with spike-rate suppression can, in fact, enhance the spike rate. The enhancement of firing probability stems from favorable temporal pairings of inhibitory inputs with subthreshold excitatory inputs. Such pairings will occur in any neuronal system that is subjected to random inputs. Of course, some neurons or models will show less (or more) hyperexcitability. But surprisingly, previous studies have not considered these per chance timing effects between random excitatory and inhibitory inputs on the output response. This could partly be due to the fact that studies of response to stochastic input are often carried out with more analytically tractable leaky integrate-and-fire (LIF) type one-variable models. The LIF, for example, disallows the PIF mechanism since it has no negative feedback variable that could be transiently reduced from rest in response to an inhibitory input. The LIF formalism may be insufficient to capture the full implications of fast inhibition and may have to be modified appropriately. Our results carry implications for the role of fast inhibition both in recurrent networks and in feedforward contexts, say, in sensory pathways. Random brief inhibition could upregulate the spontaneous firing of sensory neurons, many of which have high spontaneous activity. We are reporting separately [28] experimental in vitro evidence for PIF behavior in auditory brain stem neurons, in circuitry where inhibition can be quite fast. The coincidence detecting sensitivity of such neurons, that carry out the neural computation for sound localization, is shaped by fast inhibition [13]. Recent in vitro studies have revealed that fast inhibition can promote synchronization and rhythmogenesis among neurons in hippocampal circuits [31] and in the subthalamic nucleus [26]. In the latter case, the timing of inhibition before excitation was shown to be especially effective. Suggestions that the transient hyperpolarizing current that preceded depolarizing input contributes to spike firing have been made based on reverse correlation analysis of random inputs and firings [32–34]. Our own theoretical extensions of the PIF phenomenon to the network level with noisy inputs showed that PIF mediated the onset of synchrony as well as an increase of the network’s frequency over control levels [35]. Our findings of the enhancement to firing probability (by per chance PIF events) should be considered in seeking to interpret the roles by brief inhibition in such networks.