Space can substitute for time in predicting climate-change effects on biodiversity

Abstract

“Space-for-time” substitution is widely used in biodiversity modeling to infer past or future trajectories of ecological systems from contemporary spatial patterns. However, the foundational assumption—that drivers of spatial gradients of species composition also drive temporal changes in diversity—rarely is tested. Here, we empirically test the space-for-time assumption by constructing orthogonal datasets of compositional turnover of plant taxa and climatic dissimilarity through time and across space from Late Quaternary pollen records in eastern North America, then modeling climate-driven compositional turnover. Predictions relying on space-for-time substitution were ∼72% as accurate as “time-for-time” predictions. However, space-for-time substitution performed poorly during the Holocene when temporal variation in climate was small relative to spatial variation and required subsampling to match the extent of spatial and temporal climatic gradients. Despite this caution, our results generally support the judicious use of space-for-time substitution in modeling community responses to climate change.

Viewed broadly, space-for-time substitution encompasses analyses in which contemporary spatial phenomena are used to understand and model temporal processes that are otherwise unobservable, most notably past and future events. Many fields have developed and debated methods relying on space-for-time substitution, such as ecological chronosequences to study long-term nutrient cycling and plant succession (1–3) and transfer functions for inferring past environmental changes from geological proxies (4, 5). The assumption of space-for-time substitutability has been queried and debated most closely in chronosequence studies, with conclusions ranging from strong support (6) to strong rejection (2) of space-for-time substitution. Increasingly, space-for-time substitution is being applied in biodiversity modeling to project climate-driven changes in species distributions, species richness, and compositional turnover (7–11). Examination of transferability of models for individual species has exposed concerns regarding the projection of these spatial models across time (12–15), and it has been suggested that models based on collective biodiversity properties might be more robust (9, 16, 17). However, the fundamental assumption that spatial relationships between climate and biodiversity can be used to project temporal trajectories of biodiversity under changing climates remains largely untested (but see refs. 16 and 18).

The turnover of species among communities is particularly well suited for testing space-for-time substitution because it can be quantified independently across space or through time and because compositional turnover strongly correlates to climate variations in both space and time (19–21). However, other factors, such as species history, site history, and species interactions, also influence compositional turnover, independently or interacting with climate (22–24). Even when climate is the main determinant of community composition, certain aspects of climate (e.g., temporal variability, covariance among critical variables) may be fundamentally more different across space than through time (25, 26). Understanding the extent to which compositional turnover is related to climate, and whether these relationships are the same across space and time, is essential to evaluating the accuracy of projections of compositional turnover with future climate change.

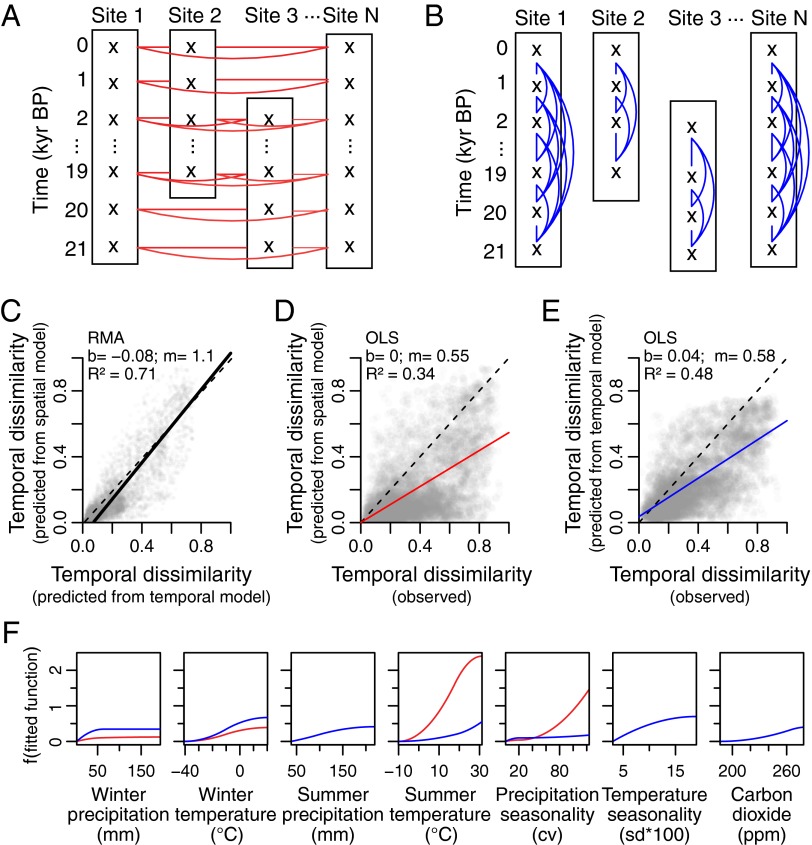
Here, we test whether the environmental influences on compositional turnover across space are the same as those through time, by constructing orthogonal spatial and temporal datasets of compositional turnover, then using these datasets to assess the predictive skill of models relying on “space-for-time” vs. “time-for-time” substitution (Fig. S1; see Materials and Methods and SI Materials and Methods for details). These datasets were constructed from fossil pollen assemblages from the Neotoma Paleoecology Database (www.neotomadb.org) and paleoclimate simulations from the National Center for Atmospheric Research Community Climate System Model version 3 (CCSM3) (27) for the past 21,000 y (i.e., the Late Quaternary) in eastern North America. In the spatial dataset, the compositional dissimilarities between all site pairs across space were calculated for a single time period then pooled with spatial comparisons from all other 1,000-y time slices over the past 21,000 y (Fig. 1A). In the temporal dataset, the compositional dissimilarities between all sample pairs at a single site through time were calculated then pooled with temporal comparisons for all other sites in eastern North America (Fig. 1B).

Fig. 1.

Spatial (A) and temporal (B) dataset construction, resulting predictions of temporal turnover (C–E), and fitted functions (F) for the Late Quaternary datasets (21–0 kyBP). In all cases, the red lines indicate spatial datasets, blue lines indicate temporal datasets, and dashed lines indicate the 1:1 line. (C) RMA regression between temporal turnover predicted by the temporal model and by the spatial model. (D) OLS regression between observed temporal turnover and temporal turnover predicted by the spatial model (space-for-time substitution). (E) OLS regression between observed temporal turnover and temporal turnover predicted by the temporal model (time-for-time substitution). (F) The fitted functions for each variable. b, Intercept of the regression line; cv, coefficient of variation; m, slope of the regression line; R², goodness of fit.

We calibrated generalized dissimilarity models (28) using these spatial and temporal dissimilarities then predicted compositional dissimilarity through time (temporal turnover) using either a spatial model (space-for-time) or a temporal model (time-for-time) (Fig. S1). Three expectations emerge if climate affects compositional turnover similarly across space and time: (i) predictions using space-for-time substitution should be as reliable as time-for-time predictions, (ii) the same environmental factors should emerge in explaining compositional turnover across space and time, and (iii) the rates and magnitudes of compositional turnover along environmental gradients should be similar across space and time.

Results and Discussion

Predictions of temporal turnover were comparable between the space-for-time and time-for-time analyses [reduced major axis (RMA) R² = 0.7116; Fig. 1C and Table S1]. The relationship between temporal turnover predicted by the spatial model (i.e., using space-for-time substitution) and observed temporal turnover was moderately strong [model-to-observation comparison, ordinary least-squares (OLS) R² = 0.3432; Fig. 1D and Table S2], particularly in comparison with the strength of the time-for-time predictions (model-to-observation comparison, OLS R² = 0.4773; Fig. 1E and Table S2). Overall, the predictive skill of models relying on space-for-time substitution was 72% as strong as models using time-for-time substitution, and space-for-time substitution resulted in only a small loss of predictive skill. This suggests that community and climate relationships across space may be applied to model compositional turnover over time.

However, some differences in the fitted spatial and temporal models underlying the predictions warrant further exploration. Although climatic factors alone explained a significant portion of the deviance in compositional turnover across both space and time (46.8% in the temporal model, 39.6% in the spatial model; SI Materials and Methods, Table S3), the remaining deviance in compositional turnover was not related only to climate (or at least to the specific climate variables used in this study). Moreover, the fitted relationships for individual climate gradients differed (Fig. 1F). In the temporal model, all seven environmental variables were significant predictors of variation in compositional turnover and no variable dominated (Fig. 1F). In contrast, two variables—summer temperature and precipitation seasonality—dominated the spatial model, with minor contributions from winter precipitation and temperature (Fig. 1F). Three variables are important through time but not across space: summer precipitation, temperature seasonality, and CO₂ concentration (which varies across time but not space). Even when the same variable is important across both space and time, the modeled rates and magnitudes of compositional turnover along environmental gradients differ markedly for some variables (Fig. 1F).

One likely reason for these differences is that this study encompasses two contrasting periods in earth history: the last glacial maximum (LGM) and deglaciation (i.e., the Late Pleistocene, 21,000–11,700 calibrated years B.P.), characterized by colder-than-present temperatures interspersed with periods of rapid warming and cooling, and the Holocene (11.7–0 kyBP), characterized by relatively stable temperatures but changing precipitation and temperature seasonality (29, 30). To explore the robustness of space-for-time predictions and diagnose the differences between fitted spatial and temporal models, we divided the datasets into their Late Pleistocene (21–11 kyBP) and Holocene (10–0 kyBP) subsets. We then repeated model training and prediction within each time period.

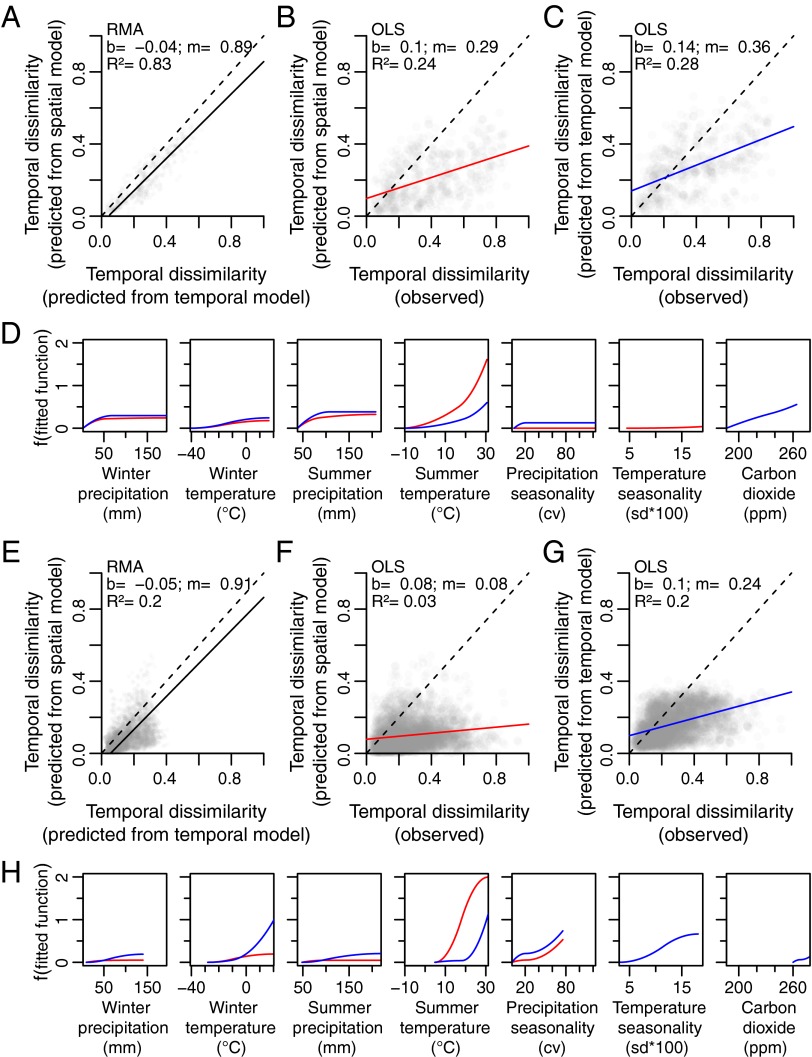
Space-for-time predictive skill and concordance between the influential variables of the temporal and spatial models improved for the Late Pleistocene but worsened for the Holocene (Table S2 and Fig. 2). For the Late Pleistocene, predictions of temporal turnover were similar between models (RMA R² = 0.8329; Fig. 2A and Table S1). The model-to-observation regressions weakened relative to the Late Quaternary datasets for both the space-for-time predictions (OLS R² = 0.2363; Fig. 2B and Table S2) and time-for-time predictions (OLS R² = 0.2839; Fig. 2C and Table S2), but the overall predictive skill of space-for-time substitution increased to 83% (Table S2). Climate explained a similar amount of deviance in compositional turnover in the spatial and temporal models (28.2% and 32.2%, respectively; Table S3) and produced similar rates and magnitudes of turnover along individual environmental gradients (Fig. 2D).

Fig. 2.

Predictions and fitted functions for the Late Pleistocene (21–11 kyBP) (A–D) and the Holocene (10–0 kyBP) (E–H). In all cases, the red lines indicate spatial datasets, blue lines indicate temporal datasets, and dashed lines indicate the 1:1 line. (A and E) Model-to-model RMA regression between temporal turnover predicted from the temporal model and from the spatial model. (B and F) Space-for-time OLS regression between observed temporal turnover and temporal turnover predicted from the spatial model. (C and G) Time-for-time OLS regression between observed temporal turnover and temporal turnover predicted from the temporal model. (D and H) Fitted functions for the spatial and temporal models. Abbreviations are as in Fig. 1.

However, space-for-time substitution performed poorly during the Holocene. The association between temporal turnover predictions from the spatial and temporal models was weak (RMA R² = 0.199; Fig. 2E and Table S1). Regressions between observed and predicted temporal turnover were even weaker (OLS R² = 0.0287 for predictions from the spatial model, Fig. 2F; OLS R² = 0.1984 for predictions from the temporal model, Fig. 2G), and the predictive skill of space-for-time substitution relative to time-for-time substitution dropped to 14% (Table S2). The amount of deviance explained by climate in each model differed substantially (44.1% for the spatial model and 21.7% for the temporal model; Table S3), and differences remained in the fitted functions comprising the spatial and temporal Holocene models (Fig. 2H).

The poor performance of space-for-time substitution in the Holocene is surprising because the spatial configuration of Holocene climates and communities is generally similar to that of the present. However, during the Holocene, the magnitude of climate change through time at millennial time steps is small relative to the spatial differences in climate between sites (Fig. 3 F and I). Although the spatial datasets (Fig. 3 A and F) always encompass a wider range of climate dissimilarities than the temporal datasets (Fig. 3 D and I) throughout the Late Quaternary, the discrepancy is particularly acute for the Holocene. This discrepancy mirrors that found by Adler and Levine (18) in their test of space-for-time substitution on much shorter time scales. Additionally, environmental gradients generally spanned a smaller range of values in the Holocene (see truncation along the x-axes in Fig. 2 H vs. D). Thus, although the fitted functions underlying the Holocene spatial model explain much of the deviance in the spatial relationship between climate and compositional turnover, the model is geared toward predicting large magnitudes of turnover and poorly predicts turnover given relatively small climatic changes during the Holocene. Conversely, the larger magnitudes of climate change through the Late Pleistocene better match the spatial gradients in climate.

Fig. 3.

Range of climate dissimilarity and model predictions for the Late Pleistocene (21–11 kyBP) (A–E) and Holocene (10–0 kyBP) (F–J). Light gray indicates the unsampled datasets, red indicates the climate-subsampled spatial datasets, and blue indicates the climate-subsampled temporal datasets. (A and F) Euclidean climate dissimilarity for the spatial datasets. (D and I) Euclidean climate dissimilarity for the temporal datasets. (B and G) Space-for-time OLS regression between observed temporal turnover and temporal turnover predicted by the spatial model. (E and J) Time-for-time OLS regression between observed temporal turnover and temporal turnover predicted by the temporal model. (C and H) Model-to-model RMA regression between temporal turnover predicted by the temporal model and by the spatial model for the climate-subsampled dataset (dark gray) and the unsampled dataset. Regression statistics for analyses based on the climate-subsampled datasets are indicated for each scatter plot. Abbreviations are as in Fig. 1.

By resampling the datasets so that the spatial and temporal models encompassed similar climate dissimilarities, we improved space-for-time substitution of compositional turnover during the Holocene (predictive skill increased from 14% to 47%) and did not affect space-for-time substitution detrimentally during the Late Pleistocene (Fig. 3, SI Materials and Methods, and Table S2). The Holocene improvement principally is the result of changes in the spatial model and greater concordance between the fitted spatial and temporal models (Fig. S2 E and F and Table S3) and predictions (Fig. 3 G, H, and J and Tables S1 and S2). However, although the Holocene model improved with subsampling based on climate, overall predictive skill was still lower than the Late Quaternary and Late Pleistocene analyses, suggesting that climatic factors not studied here [e.g., decadal- to centennial-scale hydrological variability (31)] or nonclimatic factors such as increasing human influence or altered biotic interactions (32, 33) may have played a role. Note that the well-known “no-analog” problem (26) does not quite apply in this analysis because the spatial and temporal datasets are drawn from the same population of climates and fossil assemblages. Insofar as there is a no-analog problem, it applies instead to time-for-space substitution during the Holocene (Fig. S3 and Tables S1 and S2), when the range of climatic and community dissimilarity over time is smaller than over space.

The success of space-for-time substitution in this study is partly a consequence of the strong interdependence among the processes by which climate governs species distributions and diversity across space and time. Compositional differences through time at a given point in space emerge from population-scale responses to climate change, manifested as abundance increases and decreases. Changes in abundance are the result of direct and indirect effects of climate on recruitment and mortality, with the rate of change influenced by the generation time (e.g., on the order of decades for the dominant pollen taxa in the assemblages) (25). Indirect effects emerge from climate-mediated shifts in species interactions and disturbance regime (33). Additionally, variations in atmospheric CO₂ may influence pollen productivity and relative abundance through time (e.g., refs. 34 and 35). Temporal turnover thus captures a cross-section of compositional differences through time for a single site and is influenced mainly by these population-scale processes, although spatial processes (see below) also may influence temporal turnover because they affect the timing of species arrival at individual sites.

Spatial shifts in species distributions due to climate change occur when climate favors abundance increases in one geographic region (including both increases within the historic range and the dispersal and successful establishment of populations outside the former range), with or without decreases (e.g., mortality and/or recruitment delays) in other parts of the range (36). Spatial processes such as dispersal limitation may slow range shifts at range margins and even within species range boundaries as climate change causes populations to shift between relatively favorable and marginal environments (37, 38). Hence, spatial gradients in species distributions and diversity ultimately emerge from the temporal responses of populations to climate change at individual sites, but also are affected by an additional overlay of spatial processes.

At shorter time scales (e.g., years to decades) or higher spatial resolutions (e.g., kilometers and less), factors such as dispersal limitation, stochastic processes, and semirandom processes, such as disturbance, may make space-for-time substitution less valid. However, this study compares temporal turnover over thousands of years with regional spatial processes, because fossil pollen integrates processes across whole landscapes (tens of kilometers) rather than at single sites. Thus, at the spatial and temporal scales of this study, compositional differences across space or through time are influenced by a similar set of biological processes.

In summary, these tests suggest that the climatic drivers of compositional turnover across space are similar to those that drive compositional turnover through time, at the spatiotemporal scales analyzed in this study. Although space-for-time substitution has been discussed and debated widely by ecologists studying chronosequences (2, 3, 6), it has been examined less closely in other contexts. Hence, this study provides an important and rare test of space-for-time substitution, and the methods developed here are applicable to other systems with rich spatiotemporal datasets of compositional turnover. However, this study also highlights the problem of scale mismatch; predictive skill in space-for-time substitution is reduced when the magnitude and nature of climate variability strongly differ between the spatial and temporal domains. This adds to recent results showing that predictive ability through time decreased for spatial models of turnover as the magnitude of climate change increased (39). There are other good reasons to exercise caution when applying empirically calibrated models to project biodiversity responses to 21st century climate change, including the prospect of shifting realized niches and emergent species interactions, the challenge of extrapolating models to no-analog climates, and the overarching question of whether ecological systems are computationally irreducible (15, 24, 26, 40). Nevertheless, this study complements studies that have focused on modeling changes in species richness (16, 18) and adds support to the prospect of projecting impacts to biodiversity as a result of climate change.

Materials and Methods

Fossil Pollen Data.

Fossil pollen data are based on those used in ref. 39. Briefly, fossil pollen sites from eastern North America from 21 kyBP to the present were drawn from the Neotoma Paleoecology Database (www.neotomadb.org) and represent genus-level pollen relative abundances for a suite of 106 genera across eastern North America. Age models were updated, recalibrated, and standardized across sites (41). The fossil pollen assemblage at each site thus consists of the relative abundances of pollen types in each sample, calculated relative to the sum of all upland pollen types. The fossil pollen taxonomy was standardized across sites, and only taxa identified to genus or better are included, except for closely related and palynologically indistinguishable genera such as Ostrya/Carpinus. If taxa were identified to a finer taxonomic resolution, they were binned into their constituent genus. The paleoclimate simulations are available at a 0.5 × 0.5° grid (∼50 × 50 km) (Paleoclimate Simulations); if more than one fossil pollen site occupied a climate grid cell, the relative abundance of each taxon across all sites within the cell was averaged. The final dataset encompasses 527 sites occupying 336 grid cells in eastern North America. Previous work with fossil pollen data has established that generalized dissimilarity modeling (GDM) is robust to variation in taxonomic level, sample size differences through time, climate models, and different methods of weighting the relative abundance of sites within climate grid cells (39).

Paleoclimate Simulations.

We paired the fossil pollen data with transient paleoclimate simulations from the National Center for Atmospheric Research CCSM3 (27). These data were debiased and downscaled to a 0.5 × 0.5° grid (∼50 × 50 km) and processed to infer seasonal temperatures and precipitation every 1,000 y since the LGM 21 kyBP (15). Downscaled paleoclimate simulations are available publicly through the University of Wisconsin Center for Climatic Research (http://purl.org/climate). We also included atmospheric CO₂ concentration as a predictor (42, 43), because this is an important influence on plant physiology and vegetation composition (44) that has varied through time and will continue to change in the future (45). CO₂ data were drawn from EPICA Dome C (42), an 800,000-y composite CO₂ record from East Antarctica on which the CO₂ data for 22–0 kyBP are based (46). The chronology was updated to EDC3_gas_a, the official chronology (47). Overall, final predictor variables used to construct models included six climatic predictors—mean precipitation and mean temperature for winter (December to February) and summer (June to August), plus indices of temperature seasonality and precipitation seasonality [equivalent to bioclimatic variables 4 and 15 in WorldClim (48)]—and CO₂. We tested the influence of CO₂ by removing this variable and refitting all models without CO₂.

The pollen and climate datasets were used previously to model the relationship between climate and compositional dissimilarity across space using GDM and to investigate the temporal stability of these spatial relationships (39). This prior work showed that the differences in fossil pollen assemblage composition across space were robust to choice of paleoclimate simulation (39), so here we use only the CCSM3 simulations.

GDM.

We used GDM to explore space-for-time substitution in fossil pollen assemblages from the past 21,000 y in eastern North America. GDM fits compositional dissimilarity as a function of environmental and/or geographic separation (28) and allows inference of the relative contribution of each environmental variable to overall compositional dissimilarity. Fitted functions for each variable indicate the rate of compositional turnover along the environmental gradient, and the maximum height attained on the y-axis indicates the relative importance of the variable to overall compositional dissimilarity.

We pooled data across all times for the spatial dataset and across all sites for the temporal dataset (Fig. 1 and Fig. S1). This approach pools community and climate data across multiple time periods and thus integrates across shifting niches, no-analog climates, and other factors to capture multiple realizations of community–climate relationships (49). Pooling also creates large datasets (383,287 pairwise dissimilarities in the spatial dataset and 18,584 in the temporal dataset), which increases analytical power. Finally, pooling controls for potential sources of bias and error; i.e., climate models may be inaccurate (50) and pollen data represent a biased sample of fossil plant taxa (51), but there is no reason to expect that these issues are differential in space vs. time.

To build and evaluate models, we split each dataset into training and evaluation partitions by randomly assigning 70% of the sample pairs from each dataset to a training partition to build the models and the remaining 30% of the sample pairs to an evaluation partition for testing model predictions. We used GDM to fit models of compositional dissimilarity in the training datasets (Fig. S1 and Table S3). All models in the main paper are fitted with environmental variables only (as opposed to environment plus geographic or temporal distance) to focus on the substitutability of environment-based models. Each model then was used to predict both spatial and temporal compositional dissimilarity in each of the evaluation datasets. When making predictions to the evaluation datasets, we reset the intercept to zero within the parameter file output for each model. Mantel tests cannot be used to assess significance owing to the nonindependence of each point (the same sample may be involved in many different pairwise comparisons, thus the individual points are not independent), the structure of the datasets (each dissimilarity matrix for an individual time or individual site was aggregated with the matrices for other sites or times; Fig. 1), and the sampling procedure for dividing the datasets into training and evaluation partitions, which was based on pairs of sites rather than single sites. Instead, we evaluated how well the predictions correlate to each other (model-to-model comparisons) using RMA regression, because there was no a priori expectation for independent vs. dependent variables and both predictions should have similar uncertainty. We used OLS regression to compare the predictions with observed compositional dissimilarity (model-to-observation comparisons), because here there is a clear dependence of predictions on observations. We report only the slope, intercept, and R² value for each model and not the significance level. We also quantify the “predictive skill” of space-for-time substitution as the performance of space-for-time substitution relative to time-for-time substitution, based on the R² values of the respective correlation tests (i.e., Table S2; predictive skill = R²_{space-for-time}/R²_{time-for-time}). To focus on the space-for-time transferability of climate-based models, we report only results of space-for-time substitution in the main paper. Time-for-space substitution results and sensitivity tests using different predictor variables are reported in SI Materials and Methods, Tables S1–S3, and Figs. S2–S6. We used a new version of the GDM software for R developed by Glenn Manion and Simon Ferrier to build models and make predictions to new data (GDM4Tables, version 1.0, available at http://purl.org/gdm). All other analyses also were done in R, version 2.15.1 (52).

Climate Subsampling.

We processed the Late Quaternary (21–0 kyBP), Late Pleistocene (21–11 kyBP), and Holocene (10–0 kyBP) training and evaluation datasets using coarsened exact matching with the R package MatchIt (53, 54). MatchIt considers the pairwise differences in each climate variable and extracts sets of sites in both the spatial and temporal datasets such that the underlying climate dissimilarities match as closely as possible. We did not include CO₂ in the set of variables to use for matching, because this variable varies across time only and not space. In effect, we preprocessed the datasets based only on their climate variables to give GDM the best chance possible at building models that are substitutable. This processing substantially reduced the size of the datasets [after processing, the spatial dataset included 3,086 dissimilarities for the Late Pleistocene (14.6% of the original dataset) and 15,441 (6.2% of the original dataset) for the Holocene, whereas the temporal dataset was reduced to 724 pairwise comparisons for the Late Pleistocene (72.4% of the original dataset) and 7,960 comparisons during the Holocene (99.3% of the original dataset)], and the resulting range of climate differences was comparable between the datasets (Fig. 3 and Fig. S6). We then refit models to each training dataset and predicted spatial and temporal dissimilarity of the subsampled evaluation datasets (Tables S1–S3 and Fig. S2).