Capillarity-induced ordering of spherical colloids on an interface with anisotropic curvature

Abstract

Objects floating at a liquid interface, such as breakfast cereals floating in a bowl of milk or bubbles at the surface of a soft drink, clump together as a result of capillary attraction. This attraction arises from deformation of the liquid interface due to gravitational forces; these deformations cause excess surface area that can be reduced if the particles move closer together. For micrometer-sized colloids, however, the gravitational force is too small to produce significant interfacial deformations, so capillary forces between spherical colloids at a flat interface are negligible. Here, we show that this is different when the confining liquid interface has a finite curvature that is also anisotropic. In that case, the condition of constant contact angle along the three-phase contact line can only be satisfied when the interface is deformed. We present experiments and numerical calculations that demonstrate how this leads to quadrupolar capillary interactions between the particles, giving rise to organization into regular square lattices. We demonstrate that the strength of the governing anisotropic interactions can be rescaled with the deviatoric curvature alone, irrespective of the exact shape of the liquid interface. Our results suggest that anisotropic interactions can easily be induced between isotropic colloids through tailoring of the interfacial curvature.

Colloidal self-assembly is a promising route toward the fabrication of new nano- and microstructured materials (1–3). Interesting superstructures can be obtained provided that the particle–particle interactions can be controlled, both in strength and in directionality. Recent examples include the formation of well-defined clusters (4, 5) or complex colloidal crystals (5, 6) using particles decorated with sticky patches. Many strategies to achieve directional interaction potentials rely on the use of anisometric particles, or particles that have patches of distinct chemical functionality at their surface (7, 8). Although effective, such particles are difficult to produce and typically only in low yields. Inducing anisotropic interactions between isotropic spherical particles requires the imposition of a directional external field or template; this has been achieved through application of electric or magnetic fields (9) or by immersing the particles in anisotropic fluids (10). Although liquid interfaces could be ideally suited as a template for self-assembly of nanoparticles or colloids (11–15), control of the directionality of the interactions is still lacking.

Colloidal particles adsorb strongly to the interface between two immiscible fluids, driven by a reduction of the interfacial area. For micrometer-sized colloids, the adsorption energy can be as large as 10⁷ times the thermal energy kT, making particle adsorption essentially irreversible. The lateral organization of the particles at the interface is determined by interparticle interactions. Isotropic repulsion, for example by electrostatic forces, leads to crystallization into a hexagonal lattice, once the particle density is high enough (16). Capillary interactions can also arise, if the particles locally deform the interface (17, 18). Such deformations increase the interfacial area and thus raise the interfacial free energy. When two particles approach each other, so that the deformations that they induce overlap, the area of the liquid interface changes, resulting in a capillary interaction between the particles. For colloidal particles of negligible weight, interface distortions can be caused by particle shape anisotropy (19–22) or by surface heterogeneities (23). In both cases, the undulating contact line induces orientation-dependent attractions and repulsions, causing particles to assemble with preferred orientations. Smooth, spherical colloids, however, can insert themselves in a flat interface without distorting the interface. The condition of a fixed contact angle along the particle perimeter, as required by Young’s law, can be satisfied simply by changing the vertical position of the particle. Such particles therefore do not experience any tangential forces at a flat interface.

The situation changes, however, if the liquid interface is not flat, but has an anisotropic curvature. In this case, it is no longer possible for an adsorbed particle to satisfy a uniform contact angle along the contact line without distorting the interface. Although it has been predicted that the distortion of an anisotropically curved interface leads to anisotropic capillary interactions between otherwise isotropic colloidal particles (24, 25), this has not been rigorously investigated experimentally. Here, we investigate how these interactions govern the self-assembly of particles adsorbed to interfaces of various different shapes. We study the organization of the particles and identify the characteristic measure for the interfacial shape that determines how the particles order. Numerical calculations are presented to explain our findings.

Results and Discussion

We create oil/water interfaces of different shapes by depositing oil droplets on glass slides patterned with hydrophobic patches (Methods) and covering these with a layer of water. Owing to strong pinning of the oil droplets on the hydrophobic patches, the droplets assume a shape that is completely determined by the shape of the hydrophobic patch and the volume of the oil droplet. We then add colloidal particles that consist of a fluorescently labeled polystyrene core and a poly(N-isopropylacrylamide-comethacrylic acid) shell, with a total radius a of 0.6 μm. Once adsorbed to the interface, the particles are no longer affected by gravity, as can be seen from the Bond number, which expresses the ratio between gravitational and interfacial energy: Bo = Δρga²/γ, where Δρ is the density difference between particle and liquid, g the gravitational acceleration, a the particle radius, and γ the interfacial tension between the two liquids. Here, Bo is ∼10⁻⁸; the interactions we observe are thus not caused by gravitational deformation of the interface, as observed for macroscopic objects (26).

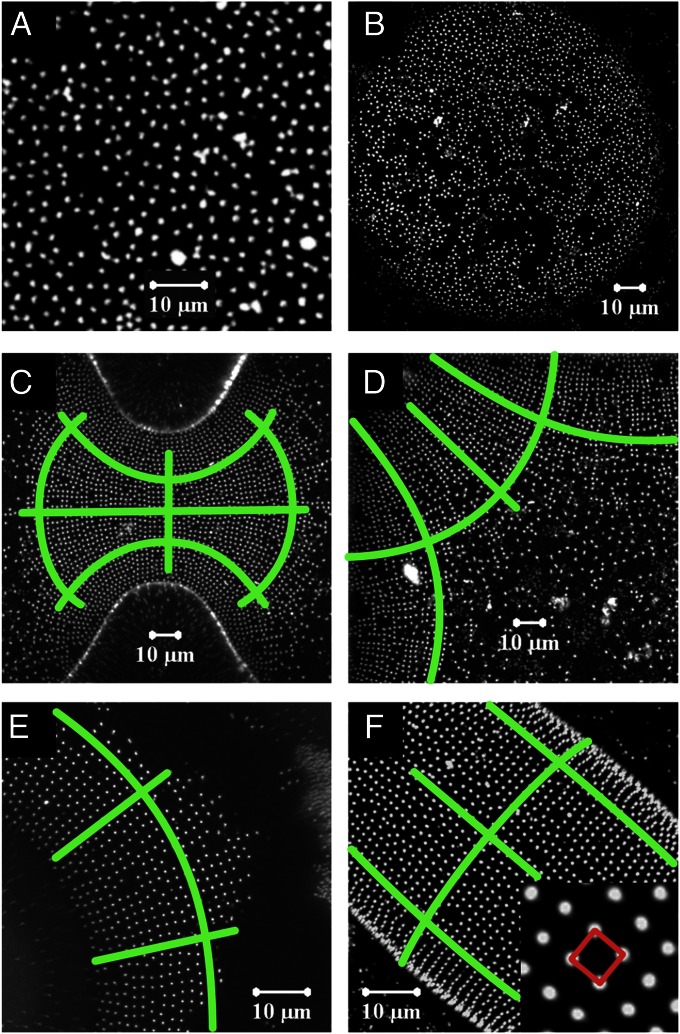
The organization of the particles on the oil/water interface is monitored using confocal microscopy. Fig. 1 shows maximum intensity projections of confocal z-stacks for droplets of various different shapes. On a flat interface or on a spherical cap, which has isotropic curvature, no signs of ordering are observed (Fig. 1 A and B). Particles move randomly at a flat interface without ordering or coming close to each other (Movie S1 and Fig. S4). This means that interactions due to pinning of the contact line on irregularities at the particle surface (23) or due to electro-capillary effects (27, 28) can be excluded for these particles. By contrast, on nonspherical droplets, the particles self-organize into ordered patterns, even when the coverage of the interface is still low, as shown for a variety of droplet shapes, ranging from dumbbells (Fig. 1C), rounded squares (Fig. 1D), and toroids (Fig. 1E) to prolate ellipsoids (Fig. 1F). On all these interfaces, the particles organize into an unusual square lattice (Fig. 1F, Inset). Movies S3, S4, S5, and S6 show the fluctuations of particles on an interface with anisotropic curvature for various particle densities. It is clear from these movies that the particles align in two perpendicular directions (Fig. S5). These findings are in agreement with theoretical predictions that show that capillary forces with quadrupolar symmetry arise between particles embedded in an anisotropic interface (24).

Fig. 1.

Particle organizations on oil/water interfaces of different shape. Maximum intensity projections of confocal z-stacks, showing fluorescently labeled particles on (A) a flat interface, (B) a spherical interface, (C) a dumbbell-shaped droplet, (D) a droplet pinned to a square patch (only one corner is shown), (E) a toroid-shaped droplet, and (F) a prolate ellipsoid. Inset in F shows square lattice organization. Green lines in C–F indicate the directions of principal curvature. Probability distributions of the angle ϕ between bonds and principal directions for each picture are shown in Fig. S6; values of order parameter 〈cos(4ϕ)〉: A, −0.031; B, −0.013; C, 0.44; D, 0.47; E, 0.40; and F, 0.37. (Scale bar, 10 μm in all images.)

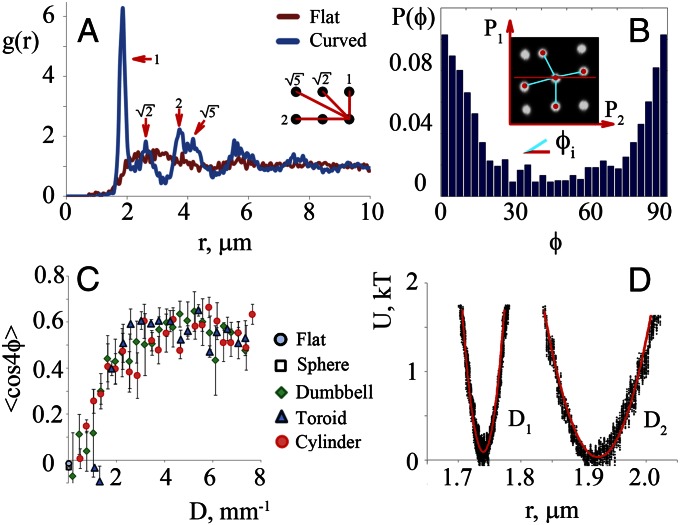
The radial distribution function of the particles (Fig. 2A) shows the characteristic peaks for a square lattice, at 1, √2, 2, and √5 times the lattice spacing. The first peak appears at a distance of ∼1.9 μm, which is larger than the particle diameter measured in water with dynamic light scattering (1.2 μm). This suggests that there is a distance of ∼700 nm between the particle surfaces. Apparently, the capillary attraction is balanced by a long-ranged repulsive interaction between the particles, so as to give a minimum at finite separation distance. This long-ranged repulsion is also seen for particles at a flat interface, for which the attractive interaction is absent: As shown in Movie S1 and Fig. S4, particles avoid each other on a flat interface, keeping a separation distance of at least 5 μm between them. This repulsive interaction may be an electrostatic repulsion, which can be very long-ranged for particles at an interface owing to asymmetric charging of the acid groups on the particle surface (16).

Fig. 2.

Analysis of particle organizations at interfaces with different deviatoric curvature. (A) Radial distribution function g(r) for particles on a dumbbell-shaped interface and for particles on a flat interface. On the anisotropic interface, g(r) shows the characteristic peaks for a square lattice organization, at 1, √2, 2, and √5 times the lattice spacing (1.9 μm in this case). (B) Probability distribution of angles ϕ between interparticle bonds and the local principal curvature axes on a dumbbell-shaped droplet. (C) Order parameter 〈cos(4ϕ)〉 as a function of the deviatoric curvature D for droplets of different shape. Average values and SDs are shown, obtained for ∼4,000 particles on three different droplets for shapes with D > 0 and for ∼2,000 particles on one droplet for D = 0. (D) Interparticle potential for two different deviatoric curvatures (D₁ = 0.016 μm⁻¹ and D₂ = 0.007 μm⁻¹) as obtained from measurement of the interparticle distance distribution (Fig. S8).

It can be seen in Fig. 1 C–F that the bonds between neighboring particles tend to align along the principal curvature axes of the interface. For example, in Fig. 1F, most interparticle bonds in the cylindrical region in the middle of the droplet are either along the long axis or along the short axis of the droplet. Spatial variations of the principal directions lead to distortions of the square lattice, as can be seen in Fig. 1 C–E. To quantify these observations, we obtain the local principal curvature directions in the vicinity of each particle from the images by interpolating the particle centroids and measure the probability distribution P(ϕ) of angles between each interparticle bond and the principal axis corresponding to the largest curvature (SI Text). An example of such a probability distribution for a dumbbell-shaped interface is shown in Fig. 2B; examples for other droplet shapes can be found in Figs. S4–S6. As shown in Fig. 2B, the distribution is strongly peaked at 0° and 90°, as expected for alignment along the principal axes. This indicates that the particles attract each other most strongly when they approach each other along one of the principal axes, in agreement with theoretical predictions (24). The distribution of Fig. 2B suggests that we can quantify the degree of ordering with an order parameter 〈cos(4ϕ)〉, which is unity when all interparticle bonds are aligned with either of the two principal axes and zero for a random organization. The values of 〈cos(4ϕ)〉 for the interfaces shown in Fig. 1 are given in the legend.

The images in Fig. 1 show that the ordering of the particles is related to the anisotropic shape of the interface. To study this relation more quantitatively, we need to find a quantity that characterizes the local shape anisotropy. This characteristic quantity is not the Gaussian curvature K = k₁k₂, where k₁ and k₂ are the local principal curvatures. Particle ordering occurs in regions of negative Gaussian curvature (Fig. 1 C and E), but also in some regions of positive Gaussian curvature (Fig. 1 D and F), whereas on a spherical interface (K > 0) no ordering is found (Fig. 1B). Instead, we argue that the relevant parameter that governs particle ordering is the deviatoric curvature, defined as 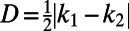(29). The deviatoric curvature is an invariant of the curvature tensor (SI Text) and is the simplest measure for the anisotropy of the interfacial curvature; it is larger than zero whenever the two principal curvatures are unequal. It should be noted that, in contrast to the mean curvature, the deviatoric curvature D is not a constant for a given droplet, but varies spatially. To test how the deviatoric curvature affects particle organization, we plot in Fig. 2C the order parameter 〈cos(4ϕ)〉, which measures the degree of ordering, as a function of D for droplets of different shapes. We find that the data for different droplet shapes indeed collapse on one master curve. For D < 0.001 μm⁻¹, 〈cos(4ϕ)〉 is small, indicating a random particle distribution. As D increases, the order parameter increases nearly linearly, and for D < 0.003 μm⁻¹, it reaches a plateau of ∼0.6. These findings indicate that the capillary interaction between the particles becomes stronger as the deviatoric curvature increases. The saturation of 〈cos(4ϕ)〉 at a value of 0.6 is caused by defects in the lattice; locally, in regions with few defects, 〈cos(4ϕ)〉 can reach higher values (Fig. S5 E and F). From the examples in Fig. 1 and Figs. S4–S6, we conclude that particle organizations can be considered to be ordered when 〈cos(4ϕ)〉 is larger than roughly 0.35.

We verify the effect of the deviatoric curvature on the ordering further by extracting the local confining potential from the probability distribution P(r) of the center-to-center distance r between neighboring particles in the lattice, by tracking all particles for several minutes (Movie S6 and Fig. S8). From this distribution, we estimate the potential well V(r) of a particle in the lattice by inverting the Boltzmann distribution (27), P(r) ∝ exp(−V(r)/kT). Fig. 2D shows the resulting potential for interfaces with two different values of D. Note that, because we analyze only the absolute distance between neighboring particles, the angular dependence of the potential is masked. Both potentials have a parabolic shape and can be fitted to the expected confining potential of a harmonic oscillator to extract an effective spring constant for the particle bonds. As D increases, the minimum of the potential shifts to smaller separations, whereas the effective spring constant increases from 1.4 μN/m for D = 0.007 μm⁻¹ to 8.2 μN/m for D = 0.016 μm⁻¹. This can be ascribed to an increase in the capillary attraction with increasing D.

The self-organization of the particles observed in our experiments can be explained by capillary interactions between the particles, induced by the anisotropy of the liquid interface. Theoretical work has shown that such interactions indeed arise and that they have a quadrupolar symmetry (24). However, the published interaction energies were derived only for the asymptotic regime of very large particle separations. To estimate the full strength of the interactions relevant for our experiments, near-field effects need to be considered (30). We therefore carry out numerical calculations to estimate the interactions. We do this by solving the Young–Laplace equation for the shape of the interface (Methods), which minimizes the interfacial area for given boundary conditions. Fig. 3A shows the calculated deformation of the interface induced by a spherical particle embedded in a saddle-shaped interface of zero mean curvature (a catenoid). The condition of fixed contact angle θ at the particle surface, as prescribed by Young’s law, leads to a quadrupolar deformation field around the particle. When two particles approach so that the quadrupolar deformations that they induce overlap, a capillary interaction between the particles arises, which depends on the relative orientation of the quadrupoles. The calculated interaction potentials are shown in Fig. 3B for particles approaching each other in two different directions. The particles attract each other if they approach along one of the principal curvature directions of the interface, but they repel each other when the angle between the direction of approach and the principal curvature directions is close to 45°. This orientation dependence of the interaction is the reason for the alignment of interparticle bonds with the principal axes, as observed in our experiments.

Fig. 3.

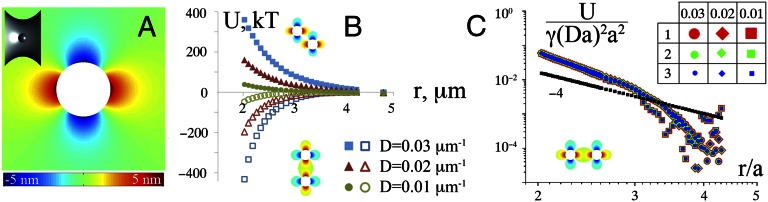
Calculated deformations and capillary interactions for colloidal particles on a saddle-shaped interface. (A) Calculated deformation field around a spherical particle with radius a = 1 μm on a catenoid interface with D = 0.02 μm⁻¹; blue regions indicate a depression of the interface and red regions a rise of the interface. (B) Calculated interaction energy between two particles (a = 1 μm) on catenoid interfaces of different curvature as a function of separation distance, for two relative orientations with respect to the principal curvature axis of the interface. Interfacial tension γ = 30 mN/m, and contact angle θ = 90° in these calculations. (C) Superimposed interaction curves for particles approaching along principal axis for different a and D, showing −U/[(γa²)(Da)²] as a function of (r/a). The black points indicate the analytical prediction for the far field (24).

Even though the deformation of the interface caused by the particles is at most a few nanometers (Fig. 3A), the interaction between the particles can still be many kT, because of the relatively large interfacial tension (34 mN/m, or ∼8 kT/nm²). As expected, the strength of the interaction increases with increasing deviatoric curvature of the interface. We find that the calculated interaction curves for different D and a can be superimposed by plotting −U/[(γa²)(Da)²] as a function of r/a (Fig. 3C). From this figure, we find that the strength of the attraction between two micrometer-sized particles in contact (r = 2a) is roughly equal to kT for D ≈ 0.003 μm⁻¹, which is very close to the value of D below which the ordering disappears in our experiments (Fig. 2C). Our numerical results differ from the far-field approximation derived in (24) and shown by the black points in Fig. 3C, where an r⁻⁴ dependence for the interaction energy was predicted for r ≫ a. Our results show that at short range the attractive interaction is a much steeper function of the interparticle separation.

The square lattices we observe in our experiment arise because this arrangement optimizes the attractive capillary interactions between the particles. However, when we increase the concentration of particles, the organization changes from square (Fig. 4A) into a hexagonal packing (Fig. 4B, Movies S2 and S7, and Fig. S9). We characterize this transition by calculating the local bond orientational order parameter

for each particle. Here, N_j indicates the number of neighbors of the particle and θ_j is the angle between the bond with a neighboring particle j and an arbitrary reference axis. The index n denotes the symmetry of the lattice: ψ₄ measures fourfold symmetry and ψ₆ measures sixfold symmetry. Fig. 4C shows both 〈|ψ₄|〉 and 〈|ψ₆|〉 as a function of the particle density at the interface for interfaces with D ∼0.006 μm⁻¹. At low densities, 〈|ψ₄|〉 > 〈|ψ₆|〉, indicating that the particles organize in a square lattice. However, at a density of ∼0.3 μm⁻², 〈|ψ₄|〉 drops rapidly, whereas 〈|ψ₆|〉 increases, indicating a transition from a square to a hexagonal packing. Sometimes, coexistence between square and hexagonal domains is seen on the same droplet (Fig. S9 C and D). The reason for the change in particle organization with increasing particle density is that the short-range repulsion is still isotropic and will eventually dominate because a higher packing density can be achieved for particles in a hexagonal lattice than for particles in a square lattice. The gain in adsorption energy outweighs the cost of the unfavorable capillary interactions. The smallest separation distance between particles in a square lattice is ∼1.73 μm, which corresponds to a maximum particle density of ∼0.33 μm⁻² for the square lattice (indicated by the red vertical dashed line in Fig. 4C). Above this density, regions of hexagonal organizations begin to appear. The maximum particle density for particles in a hexagonal lattice at the same particle separation corresponds to 0.39 μm⁻². This maximum density is indicated with a blue vertical dashed line in Fig. 4C.

Fig. 4.

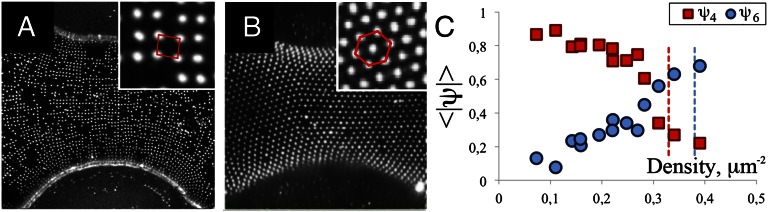
Transition from square to hexagonal packing at high particle densities. (A) Part of a dumbbell-shaped droplet covered with colloidal particles at relatively low density (0.16 μm⁻²). The particles organize in a square pattern: 〈|ψ₄|〉 = 0.81, 〈|ψ₆|〉 = 0.2. (B) At high density (0.5 μm⁻²) the particles are organized in a hexagonal lattice (Inset): 〈|ψ₄|〉 = 0.22, 〈|ψ₆|〉 = 0.74. (C) Bond order parameters for four- and sixfold symmetry as a function of particle density for interfaces with D = 0.006 μm⁻¹. The red and blue vertical dashed lines indicate maximum densities for a particle separation of 1.74 μm in a square and a hexagonal lattice, respectively.

In conclusion, we have demonstrated that anisotropically curved liquid interfaces induce quadrupolar capillary forces between adsorbed colloidal particles, which organize the particles in a square pattern aligned along the principal curvature axes. Our results show that a precise control over the curvature of the interface opens up new possibilities to direct the self-assembly of particles into complex arrangements. A similar curvature-induced interaction might also arise for particles embedded in a membrane. Anisotropically curved membranes occur for example in lipid mesophases, such as the cubic phase. Such phases have attracted attention, because they facilitate the crystallization of some membrane proteins (31). The mechanism underlying this crystallization method is poorly understood, but our data suggest that anisotropic interactions between proteins induced by the curvature field might play a role: From Fig. 4C we estimate the interaction between two 5-nm proteins to be on the order of kT for curvature radii of 20 nm.

Methods

Sample Preparation.

Core-shell particles consisting of a fluorescent polystyrene core and a shell of poly(N-isopropyl acrylamide-comethacrylic acid) were synthesized adopting a protocol described previously (32). After synthesis of a fluorescent polystyrene core particle through emulsion polymerization, with a diameter of ∼300 nm and polydispersity <5%, dyed with Pyromethene 546 (Exciton), a nonfluorescent microgel shell was grown through precipitation copolymerization of N-isopropylacrylamid (93 wt%), methacrylic acid (5 wt%), and the crosslinker bismethacrylamide (2 wt%). After extensive washing of the particles against deionized (DI) water, they are stored as a concentrated stock suspension at 4 °C. The final diameter of the core-shell particle was determined by dynamic light scattering and is 1.2 μm. The methacrylic acid groups make the shell of the particles negatively charged. A more detailed protocol of the colloid synthesis is given in SI Text.

Droplets with anisotropic curvature were prepared on substrates with patterned wettability. We prepared this through soft photolithography (Fig. S1A). First, a 25-μm-thick layer of SU-8 photoresist was spin-coated on a glass slide, which was then selectively cross-linked through a photomask. After washing the substrate with propylene glycol methyl ether acetate (Sigma-Aldrich), we obtained slides with wells in a 25-μm-thick layer of hydrophobic photoresist. Then, 5 μL of oil was deposited on the substrate and treated with weak air stream to remove excessive oil, leaving oil droplets only in the wells. Then, 200 μL of an oil-in-water emulsion (2% vol/vol) stabilized by the colloidal particles was carefully placed on top. The emulsion droplets fused with the droplets in the wells, after which the particles could spread over the oil/water interface. Because the contact line of the oil droplet is pinned strongly to the edge of the well, the shape of the interface is determined completely by the shape of the well and the volume of the droplet. Each slide contained ∼20–40 droplets of various shapes. To prevent evaporation, samples were sealed in a glass chamber (Fig. S1B).

Samples were imaged using a Zeiss Axiovert 200M-Exciter confocal laser scanning microscope, using a 100×/1.4 N.A. oil-immersion objective. The pinhole was 60 μm, corresponding to a slice thickness of 0.4 μm. Three-dimensional image stacks were obtained and centroids of the particles were determined in three dimensions using standard particle tracking algorithms (33) with a resolution of ∼20 nm in plane and 50 nm in the z-direction. The principle radii of curvature and their directions were then reconstructed by interpolating the particle. A detailed description of the different analysis steps is given in SI Text and Figs. S2 and S3.

Numerical Calculations of Interfacial Deformations and Capillary Interactions.

The expected shape of the liquid interface with embedded spherical particles is calculated by solving the Young–Laplace equation for the curvature of the interface, assuming that the contact angle at the three-phase (particle–liquid–liquid) contact line is fixed by Young’s law. We use a nonlinear finite element scheme to solve the equations. The force exerted on a particle is then calculated as

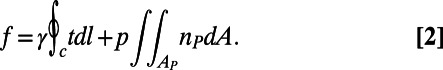Here the first contribution is the contribution of the capillary force, with t a unit vector normal to the contact line and tangential to the meniscus, and the second contribution is due to the Laplace pressure. For a minimal surface, such as the catenoid surface used in Fig. 3, this contribution vanishes. The vertical position of the particle is adjusted until the force in the direction normal to the interface vanishes. The interaction energy between two particles is calculated by integrating the force as the particles are brought into contact.