Heat transport in bubbling turbulent convection

Abstract

Boiling is an extremely effective way to promote heat transfer from a hot surface to a liquid due to numerous mechanisms, many of which are not understood in quantitative detail. An important component of the overall process is that the buoyancy of the bubble compounds with that of the liquid to give rise to a much-enhanced natural convection. In this article, we focus specifically on this enhancement and present a numerical study of the resulting two-phase Rayleigh–Bénard convection process in a cylindrical cell with a diameter equal to its height. We make no attempt to model other aspects of the boiling process such as bubble nucleation and detachment. The cell base and top are held at temperatures above and below the boiling point of the liquid, respectively. By keeping this difference constant, we study the effect of the liquid superheat in a Rayleigh number range that, in the absence of boiling, would be between 2 × 10⁶ and 5 × 10⁹. We find a considerable enhancement of the heat transfer and study its dependence on the number of bubbles, the degree of superheat of the hot cell bottom, and the Rayleigh number. The increased buoyancy provided by the bubbles leads to more energetic hot plumes detaching from the cell bottom, and the strength of the circulation in the cell is significantly increased. Our results are in general agreement with recent experiments on boiling Rayleigh–Bénard convection.

The greatly enhanced heat transfer brought about by the boiling process is believed to be due to several interacting components (1–3). With their growth the bubbles cause a microconvective motion on the heating surface, and as they detach by buoyancy, the volume they vacate tends to be replaced by cooler liquid. Especially in subcooled conditions, the liquid in the relatively stagnant microlayer under the bubbles can evaporate and condense on the cooler bubble top. This process provides for the direct transport of latent heat, which is thus able to bypass the low-velocity liquid region adjacent to the heated surface due to the no-slip condition. The bubble growth process itself requires latent heat and, therefore, also removes heat from the heated surface and the neighboring hot liquid. Finally, with their buoyancy, the bubbles enhance the convective motion in the liquid beyond the level caused by the well-known single-phase Rayleigh–Bénard (RB) convection mechanisms (4, 5). This last process is the aspect on which we focus in the present article.

In classical single-phase RB convection, the dimensionless heat transport, , the Nusselt number, is defined as the ratio of the total heat transported through the cell to the heat that would be transported by pure conduction with a quiescent fluid. This ratio increases well above 1 as the Rayleigh number is increased due to the onset of convective motion in the cell. Here g is the acceleration of gravity, β the isobaric thermal expansion coefficient, the difference between the temperature of the hot bottom plate and the temperature of the cold top plate, L the height of the cell, ν the kinematic viscosity, and κ the thermal diffusivity. Further, depends on the shape of the cell, its aspect ratio (defined for a cylindrical cell of diameter D as ), and the Prandtl number of the liquid. For in the range and in the range , the heat transport satisfies an approximate scaling relation (4, 5).

How is this scaling modified if the hot plate temperature is above the fluid saturation temperature , so that phase change can occur? The present article addresses this question by focusing on the enhanced convection caused by the bubble buoyancy, rather than attempting a comprehensive modeling of the actual boiling process in all its complexity. We carry out numerical simulations in the range for a cylindrical cell with aspect ratio for , which is appropriate for water at 100 °C under normal conditions.

This work differs in two major respects from our earlier studies of the problem. In the first place, we are now able to reach a much higher Rayleigh number, as opposed to as in ref 6, and to include three times as many bubbles. Secondly, we now study the effect of the liquid superheat, which was held fixed before.

The extensive literature on boiling leads to the expectation that the appearance of bubbles would cause a substantial increase in with respect to single-phase convection (1). For RB convection, the effect of phase change has recently been studied in ref. 7 for the case of ethane near the critical point, and indeed a major increase of the heat transport has been found.

Model

The present article is based on the same mathematical model and numerical method that we have used in ref. 6. and several other recent papers (8, 9). Briefly, under the Boussinesq approximation, conservation of mass, momentum, and thermal energy equations for the liquid are:

and

Here u, p, and T are the liquid velocity, pressure, and temperature, and ρ and are the liquid density and specific heat, while is the total number of bubbles. The bubbles are modeled as point sources of momentum and heat for the liquid. The i-th bubble offers a mechanical forcing and a thermal forcing . Here is the radius of the i-th bubble, the bubble heat transfer coefficient, and the liquid temperature and acceleration are evaluated at the location of the bubble; is the bubble surface temperature assumed to be at saturation with respect to the static pressure.

The motion of each bubble, envisaged as a sphere, is followed in a Lagrangian way by means of an equation that, in addition to buoyancy, includes drag, added mass, and lift:

where , are the added mass and lift coefficients, and is the bubble velocity. C_D is the drag coefficient (see ref. 6).

In its mechanical aspects, therefore, the model is similar to existing ones, which have been extensively used in the literature to simulate dilute disperse flows with bubbles and particles (10, 11). The novelty of our model lies in the addition of the thermal component. The heat exchange between the bubble and the liquid in its vicinity is modeled by means of a heat transfer coefficient dependent on the Péclet number of the bubble–liquid relative motion and on the Prandtl number of the liquid. The radial motion of the bubbles is slow enough that the vapor pressure remains essentially equal to the ambient pressure, which implies that the bubble surface temperature can be assumed to remain at the saturation value. The bubble volume, on which the enhanced buoyancy effect depends, is calculated by assuming that the entire heat absorbed by a bubble is used to generate vapor at the saturation density and pressure (for complete details, see ref. 6).

The calculation is carried out on a finite-difference grid based on cylindrical coordinates. The standard staggered-grid arrangement is used for the flow variables and the projection method for the calculation of the pressure and time stepping (12). No-slip conditions are applied on the bottom and top of the cell, and also on the lateral boundary. The Lagrangian treatment of the bubbles proceeds by means of a third-order Runge–Kutta method. The energy and force imparted by each bubble to the liquid are interpolated to the grid points of the cell containing the bubble in such a way as to preserve the total energy and the resultant and moment of the force.

Simulations are carried out on computational grids with the angular, radial, and axial directions discretized by means of , , , and nodes for , , , and . The simulations are therefore well resolved according to the requirements specified in refs. 13 and 14. We have also checked the global balances of appendix B in ref. 6, finding that they were satisfied to within .

When a bubble reaches the top cold plate, it is removed from the calculation to model condensation and a new bubble is introduced at a random position on the bottom hot plate so that the total number of bubbles in the calculation remains constant. We do not attempt to model the nucleation process, which, with the present state of knowledge, cannot be done on the basis of first principles and which would require addressing extremely complex multiscale issues. For our limited purpose of studying the bubble-induced increased buoyancy, it is sufficient to simply generate a new bubble at the hot plate. We do not model the process by which the bubble detaches from the plate but assume that it is free to rise immediately as it is introduced. The initial bubble radius is arbitrarily set at 38 μm. As shown in ref. 9, the initial bubble size is immaterial provided it is in the range of a few tens of microns. In view of their smallness, the latent heat necessary for their generation is very small and is neglected. We show results for three values of the total number of bubbles , namely , 50,000, and 150,000. Another parameter we vary is the degree of superheat, , which we express in the dimensionless form .

The Nusselt number shown in the following is defined as , where k is the liquid thermal conductivity and is the heat flux into the bottom plate. This quantity differs from , the heat flux at the upper plate, due to the heat stored in the bubbles. [The Nusselt number shown in our previous papers (6, 8, 9) are based on the average between and .] An important parameter introduced by the bubbles is the Jakob number , where ρ and are the densities of liquid and vapor and is the latent heat for vaporization. Physically, expresses the balance between the available thermal energy and the energy required for vaporization. With ^oC, varies between 0 and 1.68 as ξ varies between 0 and 1/2. For , the bubbles introduced at the hot plate can only encounter liquid at saturation temperature or colder, and therefore they cannot grow but will mostly collapse. On the other hand, for , they have significant potential for growth.

To give an impression of the physical situation corresponding to our parameter choices, we may mention that 100 °C water in a 15-cm-high cylinder with an imposed temperature difference °C would correspond to . The Kolmogorov length scale based on the volume- and time-averaged kinetic energy dissipation in single-phase RB convection is 3 mm for and 0.5 mm for (5) and is therefore always much larger than the initial size of the bubbles (e.g., 13 times larger for the highest Rayleigh number). In our simulations bubbles grow at most to a diameter of 130 d_inj (see Fig. 5). The bubble volume fractions are less than 0.01% and hence use of the point bubble model is justified.

Fig. 5.

Bubble size (given in bubble diameters ) distributions at various heights in the cylinder: (A–E) bubble density versus bubble diameter, and (F–J) PDF versus bubble diameter for and . From top to bottom, (A+F), 0.2 (B+G), 0.3 (C+H), 0.4 (D+I), and 0.5 (E+J). The bubble injection diameter at the hot plate is microns. Data symbols for different vertical heights (red squares), 0.25 (blue circles), 0.5 (green diamonds), 0.75 (brown triangles), and 0.95 (black stars). Note that all of the vertical axes are logarithmic except D and E.

Observations on Heat Transport and Flow Organization

In Fig. 1, the dependence of on the Rayleigh number and the dimensionless superheat ξ is shown for bubbles. Here is normalized by , the single-phase Nusselt number corresponding to the same value of . Each symbol shows the result of a separate simulation carried out for the corresponding values of and ξ. A colored surface is interpolated through the computed results with the color red corresponding to and the color blue to .

Fig. 1.

for boiling convection normalized by the corresponding single-phase value for bubbles. Here ξ is the normalized superheat, . The symbols correspond to (square), (triangles), (circles), and (stars).

The same data are shown on a 2D plot of versus ξ in Fig. 2A for four different Rayleigh numbers in descending order; here the dashed lines are drawn as guides to the eye. It is evident that the relative enhancement of the heat transport is a decreasing function . This statement, however, does not apply to the absolute heat transport shown in Fig. 2B, where is not normalized by the single-phase value. Here increases in ascending order, which shows that the bubbles always have a beneficial effect on the heat transport. For very small superheat, the heat transport approaches the single-phase value as shown in the inset of Fig. 2B.

Fig. 2.

(A) and (B) as functions of the normalized superheat ξ for 50,000 bubbles. The symbols correspond to (squares), (triangles), (circles), and (stars). The inset shows a detail for small superheat ξ for (squares) and (triangles) with quadratic fits to the data.

Figs. 1 and 2 show results calculated keeping the bubble number fixed. This procedure, therefore, does not faithfully reflect physical reality, as it is well known that the number of bubbles is an increasing function of superheat. The dependence is actually quite strong, with the number of bubbles proportional to raised to a power between 3 and 4 (1). However, varying independently and ξ permits us to investigate separately the effect of these quantities.

The effect of changing the bubble number from 50,000 to 150,000 at the same ξ is shown in Fig. 3 A and B for and , respectively. In the latter case, we also include results for . For small ξ, the heat transfer enhancement is small as the bubbles will mostly encounter colder liquid, condense, and add very little to the system buoyancy. As the superheat ξ increases, however, the effect of the bubbles becomes stronger and stronger, and larger the larger their number.

Fig. 3.

versus ξ for three different bubble numbers, (squares, B), 50,000 (triangles), and 150,000 (circles); A is for and B for . The curved dash line is a fit to the experimental data of Zhong et al. (7) shown by the filled symbols. The inset is a blow-up for the range . Error bars are shown inside the hollow symbols.

In Fig. 3B, the solid symbols are the data of ref. 7 taken at a higher Rayleigh number, . (This article reports data for both increasing and decreasing superheat. We show here only the latter data because, for increasing superheat, there is a threshold for fully developed boiling conditions that pushes the onset of bubble appearance beyond . For decreasing ξ, on the other hand, fully developed boiling conditions prevail all the way to small values of ξ.) The inset in the figure shows our computed results and the experimental data for . A major difference between our simulations and the experiment is that, in the latter, the number of bubbles increases with the superheat, while it remains constant with ξ in the simulations. We can nevertheless attempt a comparison as follows. Quadratic interpolation using our results for the three values of suggests that, to match the experimental values, we would need for and for . If, as suggested by experiment, the actual physical process results in a relation of the form , we find , which falls in the experimental range mentioned before. With this value of m, we can estimate the number of bubbles necessary to account for the measured at . Using , we find for and for . These values are in agreement and consistent with the fact that our computed result at is somewhat higher than the measured value for . The picture that emerges from these considerations is therefore in reasonable agreement with the experiment. A similar exercise cannot be carried out for larger values of ξ as in the experiment bubbles then become so large that they coalesce and form slugs with nonnegligible dimensions. Our model, in which the vapor volume fraction is assumed to be so small as to be negligible, clearly cannot be applied to this situation.

The heat transport in single-phase RB convection can be approximated by an effective scaling law . In the present range, the experimental data are well represented with the choices and . How does the effective scaling law change for boiling convection? Fig. 4A shows the Nusselt number versus Rayleigh number for different values of ξ for bubbles. The two solid lines have slopes and , while the dashed line shows the single-phase values. If we fit for the boiling case again with an effective scaling law , we obtain the effective exponents shown in the inset of the figure (as squares). Of course, and, as ξ increases, decreases to a value close to 0.20. In the range , the numerical results for are well represented by , which monotonically increases from 1 to 34.15 for . How strongly does the prefactor and the effective scaling exponent depend on ? In the inset of the same figure, we show for bubbles (see circles), to compare with the case. The functional dependence is very close for the two cases. Further, we find for 150,000 bubbles—that is, a stronger ξ dependence compared with the case, reflecting the enhanced number of bubbles.

Fig. 4.

(A) versus and (B) versus ξ for 50,000 bubbles. In A, the numerical results are shown as crosses , squares , triangles , circles , diamonds , and stars . Simulations without bubbles are also shown for comparison as a dashed line joining small dots and data from the LB simulations of ref. 15 as filled circles, light gray for no-boiling, and dark gray for boiling. In the inset, the effective scaling exponent obtained from power-law fits of the form is shown as a function of ξ for 50,000 (squares) and 150,000 (circles) bubbles. In B, the effective buoyancy has been computed from Eq. 5. The symbols are the same as in Fig. 2A. Error bars are shown inside the hollow symbols.

It is tempting to regard the increased heat transport as due to the additional buoyancy provided by the bubbles. In this view, the Rayleigh number should be based on an effective buoyancy in place of the pure liquid buoyancy β. An expression for can then be found by equating to with the result:

The quantity as given by this relation is shown in Fig. 4B as function of ξ and for . For the same ξ, decreases as increases as expected on the basis of Figs. 1 and 2. For fixed , increases with ξ, also as expected. It is quite striking that can exceed β by nearly three orders of magnitude for and small Rayleigh number. Note that one cannot directly compare the numerical values for shown in Fig. 4B with an experiment in which ξ is increased in a given cell, as in our plot is fixed, whereas in the experiment with as discussed above.

A recent Lattice–Boltzmann (LB) simulation of finite-size bubbles also found heat transport enhancement (15). The results of this study for are shown by filled circles in Fig. 4A. The heat transfer enhancements achieved are much smaller than ours, most likely due to the significantly smaller number of bubbles (only a few hundreds), as well as other differences (the values of 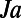, , etc.) of lesser importance.

Where are the bubbles in the flow, and how are they distributed in size, depending on their location? In Fig. 5, the statistics on the bubble diameter computed at different vertical heights in the cylinder are shown. To get an immediate impression on how large the bubbles have grown, we have normalized the bubble diameter with the initial injection diameter microns. We calculate the time-averaged bubble density in thin horizontal slices positioned at five different vertical heights in the cylinder for various diameter ranges (Fig. 5 A–E). For small superheat , the bubble nuclei do not grow much: most of them only up to a diameter 12 times the injection size and only very few toward 25 times the injection diameter (Fig. 5A). Moreover, they do not make it up to one-quarter of the cell height, as they encounter cold liquid and condense. As we increase ξ, the bubbles grow to larger sizes and can even reach the top plate (Fig. 5 B–E). Although the number density at a given cross-section decreases, a wide range of bubble size emerges, leading to poly-dispersity. The bubbles can grow up to a size of even 100 times the initial injection diameter. Note that for large and even more at , at any plane away from the boundary layers, the number density shows a similar trend for bubble size distribution, reflecting the homogeneously boiling situation. In the right column of Fig. 5 F–J, we show the corresponding probability density functions (PDFs) versus the bubble diameter, now all in log-linear form. Again we see that both the bubble maximum and the most probable diameter increase as we increase ξ.

We now come to the local flow organization. As well known, the boundary layers formed on the bottom (and top) plate are marginally stable and occasional intermittent eruptions of hot (or cold) liquid occur at their edges. Vapor bubbles subject these boundary layers to intense fluctuations, which enhance the convective effects. As an example, Fig. 6 shows sample time records of the dimensionless vertical velocity (Fig. 6A), and temperature (Fig. 6B) versus normalized time near the axis at —that is, just outside the hot thermal boundary layer. The velocity scale is defined by and . The dashed lines are results for the single-phase case. The immediate observation is that the small-scale fluctuations are much stronger in the two-phase case. As expected, the positive and negative velocity fluctuations are correlated with warm and cold temperature fluctuations, respectively.

Fig. 6.

The solid lines show the dimensionless vertical velocity (A) and temperature θ (B) as functions of dimensionless time in the hot liquid at a height near the axis. The dashed lines show similar results for simulations without bubbles; here , , and .

To give an impression of the difference brought about by the presence of bubbles on the convective motions in the cell, we show in Fig. 7 snapshots of the dimensionless temperature in a vertical plane through the axis of the cell for in the single-phase (Fig. 7A) and two-phase (Fig. 7B) cases, the latter for and . We notice that bubbles considerably thicken the layer of hot fluid near the base and make it more energetic compared with the single-phase situation. Chunks of hot liquid can be seen all of the way up near the cold plate, presumably caused by the latent heat deposited by condensing bubbles in the bulk liquid. The up–down symmetry of the single-phase case that can be seen in Fig. 7A is markedly absent in the two-phase case because of the tendentially upward motion of the bubbles, which condense on encountering liquid colder than . This mechanism is evidently quite different from the symmetry-breaking process observed in non-Boussinesq systems, which is due to the temperature dependence of viscosity (16).

Fig. 7.

Instantaneous dimensionless temperature field in a vertical plane through the cell axis for convection without bubbles (A) and with bubbles (B). The color varies from red for to blue for ; here , , and .

It is found that, for , the time- and area-averaged mean temperature in the cell is very close to 0.5—that is, , except in the two boundary layers near the plates. A detailed view of the temperature distribution in these layers is provided in Fig. 8. The figure makes evident that the temperature distribution in the upper and lower layers is not symmetric. Furthermore, the layers become thinner as increases, a clear manifestation of the enhanced convective circulation promoted by the bubbles.

Fig. 8.

(A) versus near cold plate, and (B) versus near hot plate. Symbols are circles (RB), triangles , and squares . Boundary layer thickness based on the wall gradient is also indicated in B for single-phase convection. Here and .

For the hot plate, one can define the thermal boundary layer thickness as , where is the mean temperature gradient at the hot plate. Replotting the data of the bottom panel in Fig. 8 as functions of , we find that the three sets of data collapse on a single line in the range (Fig. 9). The small differences farther away from the wall reflect differences in the shape factor of the boundary layers.

Fig. 9.

Normalized mean temperature 1 − versus in the hot thermal boundary layer. Here ξ = 0.5, Ra = 2 × 10⁸, and N_b = 0 (circles), 50,000 (triangles), and 150,000 (squares).

Summary and Conclusions

In summary, our investigation of a simple model of RB convection with boiling has demonstrated the effect of the degree of superheat and of the bubble number on heat transport. Comparison with existing data suggests a basic conformity of our results with some physical features of a real system. Vapor bubbles significantly enhance the heat transport primarily by increasing the strength of the circulatory motion in the cell. The velocity and thermal fluctuations of the boundary layers are increased and, by releasing their latent heat upon condensation in the bulk fluid, the bubbles also act as direct carriers of energy. We have shown that the heat transfer enhancement can be interpreted in terms of an enhanced buoyancy, which is shown in Eq. 1 and Fig. 4B. The relative effect of the bubbles diminishes as increases.