Movement trajectory smoothness is not associated with the endpoint accuracy of rapid multi-joint arm movements in young and older adults

Abstract

The minimum variance theory proposes that motor commands are corrupted by signal-dependent noise and smooth trajectories with low noise levels are selected to minimize endpoint error and endpoint variability. The purpose of the study was to determine the contribution of trajectory smoothness to the endpoint accuracy and endpoint variability of rapid multi-joint arm movements. Young and older adults performed arm movements (4 blocks of 25 trials) as fast and as accurately as possible to a target with the right (dominant) arm. Endpoint accuracy and endpoint variability along with trajectory smoothness and error were quantified for each block of trials. Endpoint error and endpoint variance were greater in older adults compared with young adults, but decreased at a similar rate with practice for the two age groups. The greater endpoint error and endpoint variance exhibited by older adults were primarily due to impairments in movement extent control and not movement direction control. The normalized jerk was similar for the two age groups, but was not strongly associated with endpoint error or endpoint variance for either group. However, endpoint variance was strongly associated with endpoint error for both the young and older adults. Finally, trajectory error was similar for both groups and was weakly associated with endpoint error for the older adults. The findings are not consistent with the predictions of the minimum variance theory, but support and extend previous observations that movement trajectories and endpoints are planned independently.

1. Introduction

The minimum variance theory is a prominent model of motor control developed to explain the planning, execution, and inherent variability of human movement (Hamilton, Jones, & Wolpert, 2004; Hamilton & Wolpert, 2002; Harris & Wolpert, 1998; Jones, Hamilton, & Wolpert, 2002; Wolpert & Ghahramani, 2000). In the original version of the theory (Harris & Wolpert, 1998), an optimization model was formulated that could successfully predict the trajectories and endpoint distributions of arm and eye movements. The model was based on the concepts that motor commands are corrupted by noise that increases with the size of the neural command signal and smooth trajectories with low noise levels are selected to minimize endpoint error and endpoint variability. Accordingly, the cost to be optimized is the endpoint error or endpoint variance across a group of trials, both of which should be dependent upon the smoothness of the trial trajectories. The theory has several compelling appealing aspects such as applicability to feedforward control (Todorov, 2004), relevance to motor learning processes (Wolpert & Ghahramani, 2000), and a relatively low central nervous system (CNS) computational requirement (Harris & Wolpert, 1998).

Several recent experimental studies have examined the major predictions of the minimum variance theory. However, the results have been mixed with some studies being consistent with the theory (Christou, Shinohara, & Enoka, 2003; Jones et al., 2002), whereas others have provided contradictory (Gribble, Mullin, Cothros, & Mattar, 2003; Osu et al., 2004; Tanaka, Krakauer, & Qian, 2006) or only partial supporting evidence (Christou, Poston, Enoka, & Enoka, 2007; Poston, Christou, Enoka, & Enoka, 2010; Poston, Enoka, & Enoka, 2008a). For example, Christou et al. (2003) found that the ability to accurately match a constant velocity template was strongly associated with the degree of trajectory smoothness during both eccentric and concentric contractions. In contrast, Osu et al. (2004) demonstrated that increases in cocontraction can improve endpoint accuracy, which refuted the prediction of the minimum variance theory that an increase in the size of the motor command always decreases endpoint accuracy. However, the previous studies either used isometric contractions (Christou et al., 2007; Jones et al., 2002; Poston et al., 2010; Poston et al., 2008a), constant velocity movements without an endpoint (Christou et al., 2003), or single-joint movements with a highly constrained trajectory (Osu et al., 2004). Therefore, none of these studies provided a test of the minimum variance theory for the primary task for which it was formulated, nor for the specific prediction that smooth trajectories are selected to minimize endpoint error and endpoint variability.

Based on these aforementioned limitations, the present study examined unconstrained, multi-joint arm movements that finished with the limb near zero velocity at a target to provide a more appropriate test of the minimum variance theory. Therefore, the purpose of the study was to determine the influence of trajectory smoothness on the endpoint accuracy and endpoint variability of multi-joint arm movements. Since previous findings have shown that less smooth trajectories can negatively impact movement accuracy to a greater degree in older adults compared with young adults (Christou et al., 2003), a group of older adults were also included in the study. Thus, a secondary purpose to determine if trajectory control and endpoint performance are impaired in older adults. It was hypothesized, based on the minimum variance theory, that movement trajectory smoothness would be associated with measures of endpoint performance (Harris & Wolpert, 1998). Finally, it was anticipated that less smooth trajectories would have a greater negative influence on movement accuracy for older compared with young adults (Christou et al., 2003).

2. Material and methods

2.1 Subjects

Sixteen young (9 women and 7 men, 24 ± 5 years) and 15 older adults (9 men and 6 women, 71 ± 5 years) volunteered to participate in the study. All subjects were strongly right-handed according to the Edinburgh Handedness Inventory (Oldfield, 1971), reported no known neurological impairments or medications known to influence neurological function, and had normal or corrected-to-normal vision. Subjects provided written, informed consent before participating in the study and the institutional review board at Arizona State University approved all experimental procedures.

2.2 Experimental arrangement

Subjects were seated in a dental chair and facing a computer monitor located 1 meter away at eye level. A table was situated between the subject and the computer monitor with the height of the chair adjusted so that the top of the table was at approximately waist level for each subject. A Wacom Intuos digitizer tablet was placed on the table and positioned in front and to the right of the midline of the subjects. The computer monitor displayed the workspace provided by the digitizer surface along with two circles that indicated a home and a target circle, respectively. The digitizer was oriented relative to the subjects so that the when the subjects placed the pen into the home circle they could assume a constant starting posture (joint angles) for each movement trial. Specifically, the right arm was abducted to ~45°, the elbow joint was flexed to ~90°, and the forearm was semi-supinated with the wrist in a neutral posture (Figure 1). Thus, the task required elbow extension and shoulder flexion to move the digitizer pen away from the body to acquire the target.

Figure 1.

Experimental arrangement. Subjects were seated and facing a monitor with a digitizer tablet positioned on a table in front and to the right of the subject’s midline. Subjects held a digitizer pen in the right hand and performed aiming movements by sliding the pen tip across the digitizer tablet from a home circle to a target circle that were displayed on the monitor.

Subjects held the digitizer pen in the right hand using a normal pen grip (dynamic tripod grasp) and executed aiming movements by sliding the digitizer pen tip across the digitizer tablet. The surface of the digitizer was defined by an x-y coordinate system with the x-axis oriented in the medio-lateral direction, whereas the y-axis was oriented in the anterio-posterior direction, perpendicular to the x-axis. The home circle was located near the bottom and middle of the digitizer and the center of the target circle was located 24.35 cm from the center of the home circle in a straight line away from the subject. The diameters of the home and target circles were 1.5 and 0.5 cm, respectively. This very small target size was used to ensure that the task would be sufficiently difficult so that performance would continue to improve over the course of the experiment. The diameters of the home and target circles along with the distance between them were held constant throughout the experiment (stylus-cursor gain of 1). Finally, the distance from the home to the target circle on the digitizer was the same as the distance between these positions displayed on the monitor.

2.3 Experimental procedures

Subjects reported to the laboratory for a single experimental session. Prior to beginning the experimental session, subjects received a written description of the project and signed informed consent forms. In addition, all subjects were given a visual demonstration of the experimental procedures by one of the investigators, affirmed that they could clearly see the visual display on the monitor, and were required to demonstrate that they understood how to interpret the visual feedback that was provided after each trial (described below). Subjects were then asked to perform a series of familiarization trials followed by experimental endpoint accuracy trials that involved aiming movements from a home circle to a target circle.

2.3.1 Familiarization trials

The familiarization trials were conducted to allow the subjects sufficient practice to correctly execute the following global aspects of the task correctly: (1) perform the task within the constraints and instructions provided on each trial by the data acquisition program; (2) hold the digitizer pen with the proper grip throughout the trial; (3) place the digitizer pen into the home position and hold it stationary until movement initiation; (4) perform a single, uncorrected movement and stop and hold the maximum movement extent position; and (5) execute the aiming movement very rapidly. An important aspect of the familiarization trials was that a target circle was not shown on the monitor in these trials to preclude a learning effect before the actual experimental trials began. Instead, a line was displayed on the monitor and subjects were merely instructed to move as fast as possible past the line and stop at some point afterward (see point 5 above). Subjects performed these trials until both the investigators and each subject were confident they could perform the task as instructed. Overall, the young adults normally required ~5–8 familiarization trials to become proficient in the aforementioned aspects of the task, whereas the older adults needed ~10–12 trials.

2.3.2 Experimental endpoint accuracy trials

Subjects were required to perform the endpoint accuracy trials as fast and as accurately as possible using a single, uncorrected movement. Furthermore, subjects were instructed to hold the final limb position after movement termination until post-trial visual feedback disappeared (see below). Prior to each trial, the computer monitor displayed the workspace of the digitizer along with the home circle and the target circle. Initially, the location of the digitizer pen on the tablet was displayed on the monitor as a computer cursor. To begin a trial, subjects slide the digitizer pen into the home circle. At this time, visual feedback of the cursor was extinguished and the computer program displayed a “GET READY” message above the home circle for 1 second. Once the pen remained stationary for 1 second, the computer presented a “GO” message and subjects performed the endpoint accuracy trial at their convenience (no reaction time component).

The cursor indicating the pen position remained hidden from the subject for the duration of the trial. Therefore, visual feedback of the movement trajectory taken from the home circle to the target circle was never provided. However, subjects were provided with visual feedback of their endpoint performance (a red circle relative to the blue target circle) 1 second after each trial and this feedback was displayed for 3 seconds. Therefore, subjects could determine the endpoint error produced in each trial as indicated by the distance between the endpoint of the trajectory (red circle) and the center of the target (blue circle). Subjects were instructed to attempt to minimize this distance on each successive trial. Following the 3 second display of the endpoint feedback, the endpoint target circle disappeared and subjects moved the pen back to the home circle to start the next trial. Each subject performed 4 blocks of 25 trials for a total of 100 trials and three minutes of rest were given between each block of trials to minimize the possible influence of muscle fatigue.

2.4 Data Analysis

All data collected during the experiments were using a custom-written data acquisition script in Matlab (Mathworks Inc., Natick, Massachusetts, USA) and stored on a personal computer. Similarly, data were analyzed off-line using additional custom-written Matlab programs. The position signals from the digitizer pen were sampled at 200 Hz with a spatial resolution of 0.001 cm and smoothed using a 4^th order Butterworth dual pass digital filter with an optimal cut-off frequency of 7 Hz. Trials were rejected online and repeated if the subject left the home circle before the “GO” command, however, this was rare as the task was self-paced and not a reaction time paradigm. Trials characterized by overt corrections, multiple velocity peaks, or lifting the pen off the digitizer tablet during movement were rejected offline. In total, 45 of the 3100 trials (~1.5%) were excluded using this approach.

2.4.1 Movement velocity

The movement onsets and movement offsets were estimated by a fixed criterion of 5% of the peak resultant velocity for each trial. After estimation, these segmentation points were modified by a search for the time point corresponding to the nearest zero crossing or local minimum of the acceleration profile for movement onset and offset, before or after the 5% criterion (Poston, Van Gemmert, Barduson, & Stelmach, 2009; Romero, Van Gemmert, Adler, Bekkering, & Stelmach, 2003a, 2003b). Movement time was quantified as the elapsed time between movement onset and offset. The average velocity was calculated as the average velocity value in the y direction for the entire movement, whereas the peak velocity was quantified as the maximum velocity value in the y direction between movement onset and offset. Since movement time, average velocity, and peak velocity are all mathematically related and gave the equivalent statistical results, only the average velocity is reported in the current study.

2.4.2 Endpoint accuracy

The endpoint accuracy was quantified as the endpoint error, x-absolute constant error and the y-absolute constant error for each trial. The endpoint error was calculated as the shortest distance between the x-y coordinates of the center of the target circle and the final endpoint of the trajectory for each trial using the Pythagorean Theorem. Therefore, endpoint error represented the absolute distance from the target and provided an overall measure of endpoint accuracy (Bagesteiro & Sainburg, 2002; Christou et al., 2007; Poston et al., 2008a; Poston, Enoka, & Enoka, 2008b; Sainburg & Kalakanis, 2000; Schaefer, Haaland, & Sainburg, 2009). In addition, the absolute distance from the target of the final trajectory endpoint in the x and y directions were quantified separately as the absolute x-absolute constant error and the y-absolute constant error. These absolute value based constant errors were reported instead of signed (positive or negative values) constant errors because neither group exhibited an overt bias to overshoot or undershoot the target or systematically terminate the movement medially or laterally relative to the target. Therefore, the signed constant errors cancelled out (exhibited values close to zero) and could not provide information regarding errors in distance from the target when averaged over all trials or blocks of trials.

2.4.3 Endpoint variability

The endpoint variability in performance was quantified with three measures: endpoint variance, x-endpoint variance, and y-endpoint variance. The endpoint variance provided an overall measure of endpoint variability and was determined as the sum of the variances of the final endpoints of the trajectories in x and y directions (van Beers, Haggard, & Wolpert, 2004). Therefore, the endpoint variance gave an overall measure of the variability of the distribution of endpoint locations relative to the average performance of each subject. Note that although endpoint variance can contribute to endpoint error, the two variables are disassociated when a consistent performance is produced that has an asymmetric distribution or bias relative to the target (Christou et al., 2007; Muller & Sternad, 2004; Schmidt & Lee, 1999; van Beers et al., 2004). In addition, the variance of the final trajectory endpoint distributions in the x and y directions were quantified separately as the x-endpoint variance and the y-endpoint variance.

2.4.4 Trajectory smoothness

Trajectory smoothness or smoothness of the overall movement within each trial (Romero et al., 2003a; van Gemmert, Teulings, & Stelmach, 1998) was quantified as the normalized jerk, which is a commonly used variable to determine smoothness. Normalized jerk has been shown to be greater in elderly adults (Contreras-Vidal, Teulings, & Stelmach, 1998; Yan, 2000) and patient populations (Alberts, Saling, Adler, & Stelmach, 2000; van Gemmert et al., 1998) than in healthy controls. Normalized jerk is a unitless measure, because it is normalized for both the amplitude and duration of movement (Teulings, Contreras-Vidal, Stelmach, & Adler, 1997). High normalized jerk values indicate less smooth movements, whereas low values indicate more smooth movements.

2.4.5 Trajectory error

In general, trajectory error has traditionally been referred to as the degree to which trajectories deviate from a theoretically optimal straight line from the initial position to the target. There are several different commonly used methods (i.e. linearity ratio, perpendicular displacement, absolute perpendicular distance, trajectory area, and curvature) to quantify trajectory error and all measures can give similar overall results (Sergio & Scott, 1998). Therefore, preliminary analyses were performed to quantify these measures of trajectory error, examine their relation to the primary dependent variables of the current study, and determine which measures to include in the final analysis. In the end, only the absolute perpendicular distance was selected as an index of trajectory error for the following reasons: (1) Linearity ratio, trajectory area, and curvature all yielded similar results to each other and all have the limitation of having movement extent components in their calculation and, therefore are not pure measures of trajectory error (Sergio & Scott, 1998); (2) Perpendicular displacement was not chosen because it is signed and the signed perpendicular displacement errors cancelled out (exhibited values close to zero) and could not provide information regarding errors in distance from the optimal straight line when averaged over all trials or blocks of trials; (3) Absolute perpendicular distance was selected because it has no movement extent component making it a pure measure of trajectory error (path deviation from a straight line). In addition, absolute perpendicular distance had weak, but significant correlations with endpoint error, at least for the older adults. Finally, the term trajectory error will be used hereafter as opposed to the term trajectory curvature.

2.5 Statistical analysis

The dependent variables were: (1) average velocity; (2) endpoint error; (3) y-absolute constant error; (4) x-absolute constant error; (5) endpoint variance; (6) x-endpoint variance; (7) y-endpoint variance; (8) normalized jerk; and (9) absolute perpendicular distance. Two-way ANOVAs (2 age × 4 block) with repeated measures on block were used to compare the dependent variables. Paired contrasts (t-tests with Bonferroni corrections) were used to locate differences among pairs of means when appropriate. Bivariate linear regressions were used to examine the associations between selected measures of endpoint accuracy, endpoint variability, and trajectory performance. A significance level was set at P < 0.05 for all statistical tests, except when modified by Bonferroni corrections. Data are indicated as means ± standard errors in the figures.

3. Results

3.1 Endpoint accuracy

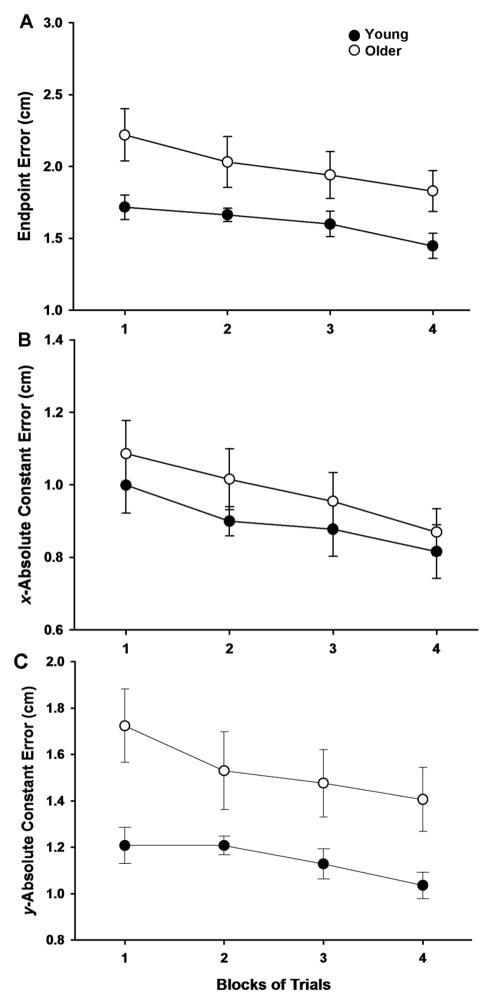
The endpoint error was greater for the older adults compared with the young adults when averaged over the four blocks of trials (age main effect: F[1, 29] = 6.640, P = 0.015; Figure 2A). There was also a significant (F[3, 87] = 5.434, P = 0.002) main effect for block and post hoc analysis indicated that the endpoint error was greater for first and second trial blocks compared with the fourth trial block (P = 0.007 and P = 0.018, respectively). All other pairwise comparisons between trial blocks did not reach significance. Finally, the age × block interaction was not significant (F[3, 87] = 0.363, P = 0.78), which indicated that the rate of decline in endpoint error across blocks of trials was similar for the two age groups. The x-absolute constant error was similar for the young and older adults when averaged over the four blocks of trials (F[1, 29] = 0.925, P = 0.344; Figure 2B). However, there was a significant (F[3, 87] = 5.416, P = 0.002) main effect for block and post hoc analysis indicated that the x-absolute constant error was greater for the first compared with the fourth trial block (P = 0.02). The difference between the fourth and the second trial blocks just failed to reach statistical significance (P = 0.061). All other pairwise comparisons between trial blocks were not significant. In addition, the age × block interaction was not significant (F[3, 87] = 0.130, P = 0.942), which indicated that the rate of decline in x-absolute constant error across blocks of trials was similar for the two age groups. The y-absolute constant error was greater for the older adults compared with the young adults when averaged over the four blocks of trials (age main effect: F[1, 29] = 8.914, P = 0.006; Figure 2C). There was also a significant (F[3, 87] = 3.051, P = 0.033) main effect for block, although post hoc analysis indicated that the difference between the fourth and the first trial blocks just failed statistical significance (P = 0.088). All other pairwise comparisons between trial blocks were not significant. Furthermore, the age × block interaction was not significant (F[3, 87] = 0.536, P = 0.659), which indicated that the rate of decline in y-absolute constant error across blocks of trials was similar for the two age groups.

Figure 2.

Endpoint error, x-absolute constant error, and y-absolute constant error for the young and older adults as a function of trial block. Each data point corresponds to the mean ± SE for 1 block of 25 trials for the young (filled circles) and older (open circles) adults. A. The endpoint error was greater for the older compared with the young adults (P = 0.015), declined as a function of trial block (P = 0.002), and the rate of decline was similar for the two age groups (no age × block interaction: P = 0.78). B. The x-absolute constant error was similar for the young and older adults (P = 0.344), declined as a function of trial block (P = 0.002), and the rate of decline was similar for the two age groups (no age × block interaction: P = 0.942). C. The y-absolute constant error was greater for the older compared with the young adults (P = 0.006), declined as a function of trial block (P = 0.033), and the rate of decline was similar for the two age groups (no age × block interaction: P = 0.659).

3.2 Endpoint variability

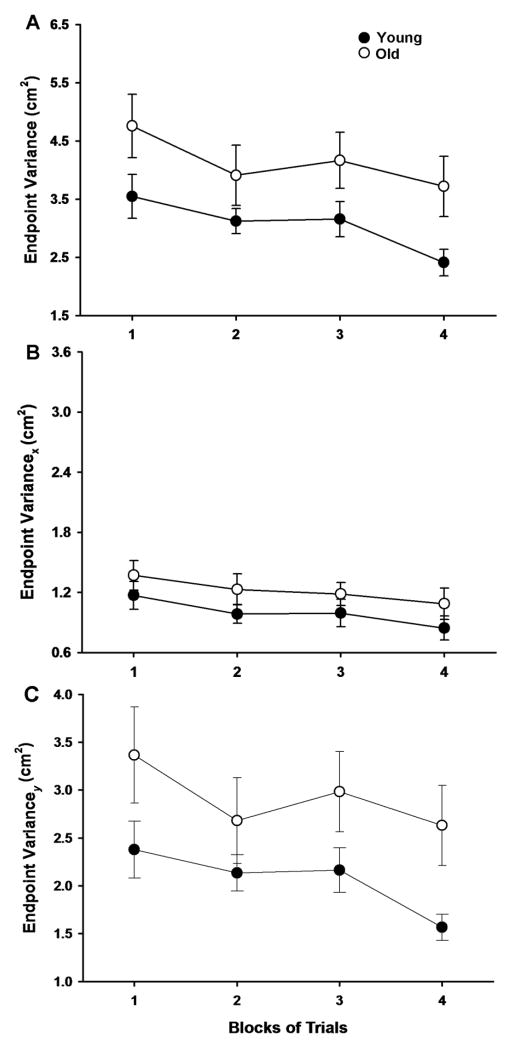
The endpoint variance was greater for the older adults compared with the young adults when averaged over the four blocks of trials (age main effect: F[1, 29] = 5.306, P = 0.029; Figure 3A). There was also a significant (F[3, 87] = 4.587, P = 0.005) main effect for block and post hoc analysis indicated that the endpoint variance was greater for the first compared with the fourth trial block (P = 0.023). The difference between the fourth and the second trial blocks just failed statistical significance (P = 0.079). All other pairwise comparisons between trial blocks did not reach significance. Finally, the age × block interaction was not significant (F[3, 87] = 0.207, P = 0.891), which indicated that the rate of decline in endpoint variance across blocks of trials was similar for the two age groups. The x-endpoint variance was similar for the young and older adults when averaged over the four blocks of trials (F[1, 29] = 2.006, P = 0.167; Figure 3B). However, there was a significant (F[3, 87] = 3.636, P = 0.016) main effect for block and post hoc analysis indicated that the x-endpoint variance was greater for the first compared with the fourth trial block (P = 0.023). All other pairwise comparisons between trial blocks did not reach significance. In addition, the age × block interaction was not significant (F[3, 87] = 0. 030, P = 0.993), which indicated that the rate of decline in x-endpoint variance across blocks of trials was similar for the two age groups. The y-endpoint variance was greater for the older adults compared with the young adults when averaged over the four blocks of trials (age main effect: F[1, 29] = 5.331, P = 0.028; Figure 3C). There was also a significant (F[3, 87] = 2.834; P = 0.043) main effect for block, however, post hoc analysis indicated that all pairwise comparisons between trial blocks did not reach significance. Furthermore, the age × block interaction was not significant (F[3, 87] = 0.263, P = 0.852), which indicated that the rate of decline in y-endpoint variance across blocks of trials was similar for the two age groups.

Figure 3.

Endpoint variance, x-endpoint variance, and y-endpoint variance for the young and older adults as a function of trial block. Each data point corresponds to the mean ± SE for 1 block of 25 trials for the young (filled circles) and older (open circles) adults. A. The endpoint variance was greater for the older compared with the young adults (P = 0.029), declined as a function of trial block (P = 0.005), and the rate of decline was similar for the two age groups (no age × block interaction: P = 0.931). B. The x-endpoint variance was similar for the young and older adults (P = 0.167), declined as a function of trial block (P < 0.016), and the rate of decline was similar for the two age groups (no age × block interaction: P < 0.993). C. The y-endpoint variance was greater for the older compared with the young adults (P = 0.028), declined as a function of trial block (P = 0.043), and the rate of decline was similar for the two age groups (no age × block interaction: P = 0.852).

3.3 Movement velocity, trajectory smoothness, and trajectory error

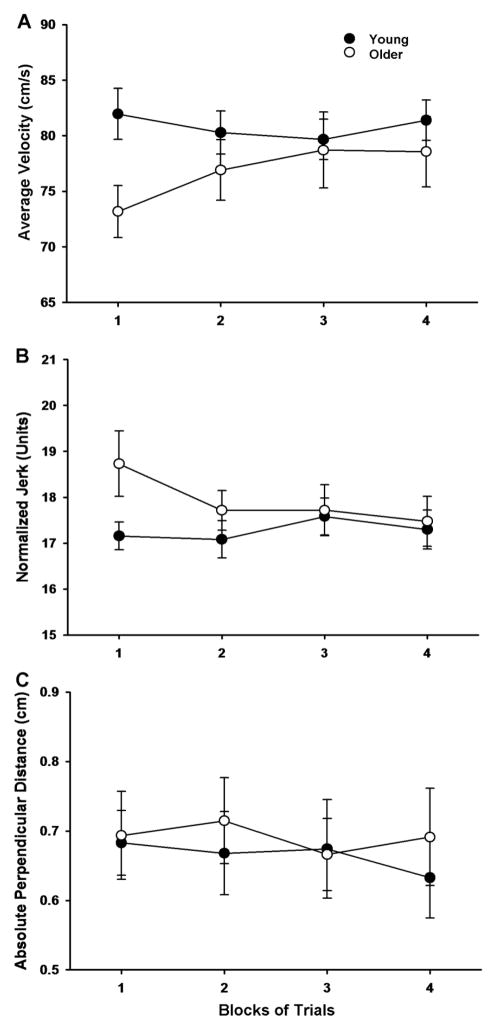
There was a significant age × block interaction for the average velocity (F[3, 87] = 3.966, P = 0.011; Figure 4A). Post hoc analysis indicated that average velocity was lower for older adults compared with the young adults, but only in the first block of trials (P = 0.013). However, the main effect for age was not significant (F[1, 29] = 1.495, P = 0.231). Furthermore, the main effect for block was not significant (F[3, 87] = 1.451, P = 0.233). For normalized jerk, both the main effect for age and block were not significant (F[1, 29] = 1.090, P = 0.305 and F[3, 87] = 1.792, P = 0.155, respectively). However, there was a significant (F[3, 87] = 2.902, P = 0.039; Figure 4B) age × block interaction. However, post hoc analysis of the interaction only revealed a trend for greater normalized jerk for the older compared with the young adults in the first block of trials (P = 0.053). The absolute perpendicular distance was similar for the older adults compared with the young adults when averaged over the four blocks of trials (F[1, 29] = 0.146, P = 0.705; Figure 4C). Furthermore, the main effect for block and the age × block interaction were not significant (F[3, 87] = 0.231, P = 0.875 and F[3, 87] = 0.278, P = 0.841, respectively).

Figure 4.

Average velocity, normalized jerk, and absolute perpendicular distance for the young and older adults as a function of trial block. Each data point corresponds to the mean ± SE for 1 block of 25 trials for the young (filled circles) and older (open circles) adults. A. The average velocity was lower for the older compared with the young adults, but only for the first block of trials (age × block interaction: P = 0.011). B. The normalized jerk was similar for the young and older adults, although there was a trend (P = 0.053) for greater normalized jerk for the older compared with the young adults in the first block of trials. C. The absolute perpendicular distance was similar for the young and older adults (P = 0.705) and across trial block (P = 0.875). In addition, the age × block interaction was not significant (P = 0.841).

3.4 Endpoint performance and trajectory smoothness associations

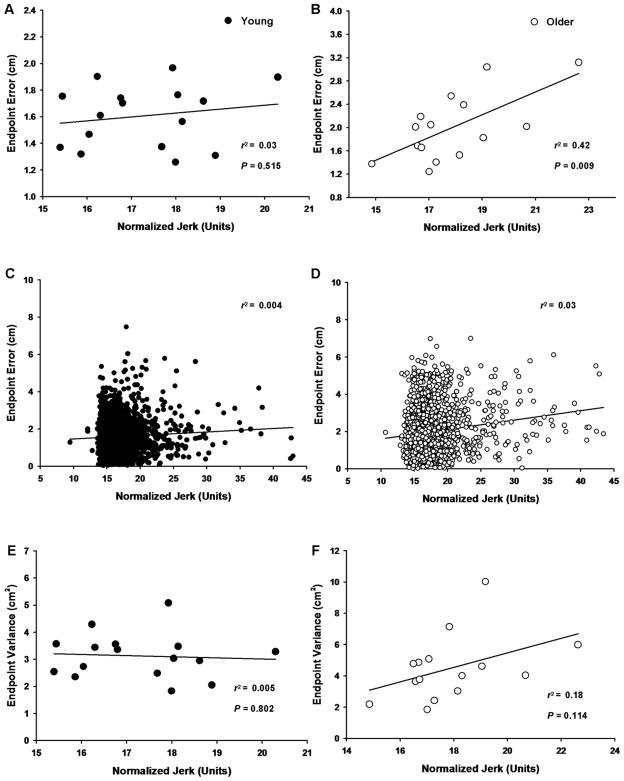
The association between normalized jerk and endpoint error for both the young and older adults was examined using the means of all 100 trials of each subject for the two variables. Normalized jerk did not significantly correlate with endpoint error (r² = 0.03, P = 0.515; Figure 5A) for the young adults, but the correlation was significant for the older adults (r² = 0.42, P = 0.009; Figure 5B). Similarly, the association between normalized jerk and endpoint variance was examined for the young and older adults using the data obtained from all 100 trials of each subject for the two variables. Normalized jerk was not significantly correlated with endpoint variance (r² = 0.005, P = 0.802; Figure 5E) for the young adults or for the older adults (r² = 0.18, P = 0.114; Figure 5F).

Figure 5.

The associations between normalized jerk and endpoint error for the young and older adults and between normalized jerk and endpoint variance for the young and older adults. In panels A, B, E, and F, each data point corresponds to the mean for all 100 trials for the young (filled circles) and older (open circles) adults, whereas in panels C and D each data point corresponds to a single trial for all the trials performed by the young (filled circles) and older adults (open circles). A. There was no correlation between normalized jerk and endpoint error for the young adults. B. There was a significant positive correlation between normalized jerk and endpoint error for the older adults. C. There was no correlation between normalized jerk and endpoint error for the young adults. D. There was no correlation between normalized jerk and endpoint error for the older adults. E. There was no correlation between normalized jerk and endpoint variance for the young adults. F. There was no correlation between normalized jerk and endpoint variance for the older adults.

Based on the somewhat different results obtained for the associations between normalized jerk and endpoint error for the young and older adults, the normalized jerk and endpoint error values for each trial in young and older adults were used to examine in more detail the influence of the within-trial variability of the trajectory on endpoint accuracy. The analyses revealed that normalized jerk was not correlated with endpoint error for the young (r² = 0.004, Figure 5C) or the older adults (r² = 0.03; Figure 5D). [Figure 5]

3.5 Associations between endpoint error, endpoint variance, and trajectory error

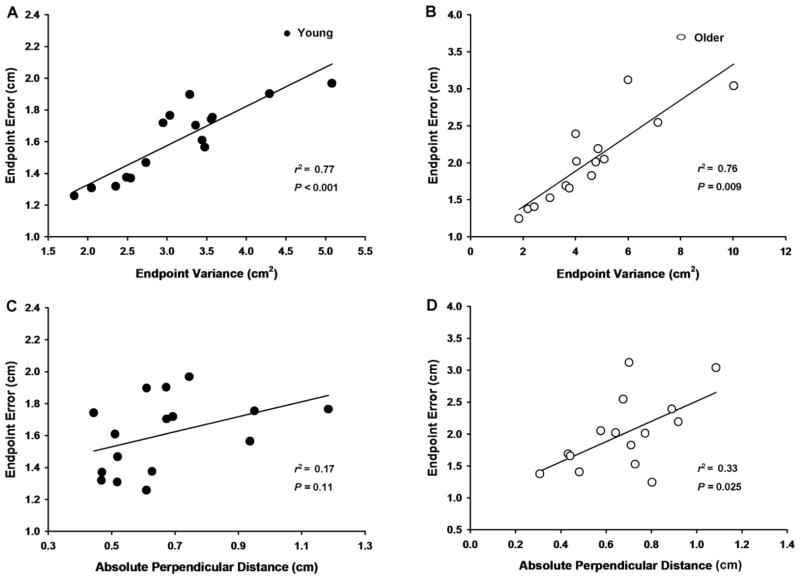
Endpoint variance was strongly associated with endpoint error for both the young (r² = 0.77, P < 0.001; Figure 6A) and older adults (r² = 0.76, P = 0.009; Figure 6B). However, the absolute perpendicular distance was not associated with endpoint error for the young (r² = 0.17, P = 0.11; Figure 6C) adults, but was weakly associated with endpoint error for the older adults (r² = 0.33, P = 0.025; Figure 6D).

Figure 6.

The associations between endpoint error and endpoint variance and between absolute perpendicular distance for the young and older adults. Each data point corresponds to the mean for all 100 trials for the young (filled circles) and older (open circles) adults. A. There was a significant positive correlation between endpoint variance and endpoint error for the young adults. B. There was a significant positive correlation between endpoint variance and endpoint error for the older adults. C. There was no correlation between absolute perpendicular distance and endpoint error for the young adults. D. There was a weak, but significant correlation between absolute perpendicular distance and endpoint error for older adults.

4. Discussion

The study produced four main findings on the relations between endpoint performance and trajectory control during rapid multi-joint arm movements in young and older adults. First, endpoint error and endpoint variance were greater in older compared to young adults despite similar average movement velocities. Second, every measure of endpoint performance changed (improved) with practice for the two age groups, whereas the smoothness of the trial trajectories remained invariant throughout the course of the experiment. Third, the greater endpoint error and endpoint variance exhibited by older adults was primarily due to impairments in movement extent control and not movement direction control. Fourth, the endpoint error and endpoint variance were not strongly associated with trajectory smoothness (normalized jerk) for either age group. Taken together, these findings are not consistent with most of the predictions of the minimum variance theory (Harris & Wolpert, 1998), but support and extend previous observations which indicated that movement trajectories and endpoints are planned independently (Ghez et al., 2007; Gordon et al., 1994; Scheidt & Ghez, 2007).

4.1 Endpoint performance and practice

Older adults typically exhibit declines in neuromuscular performance such as reduced movement velocity, decreased movement accuracy, and greater motor output variability (Barry & Carson, 2004; Barry, Riek, & Carson, 2005; Christou, 2011; Enoka et al., 2003). Accordingly, movement velocity was lower for the older adults, but this difference was only statistically significant in the first trial block. These findings seem counterintuitive as arm movement velocity has generally been reported to decline with age (Ketcham, Seidler, Van Gemmert, & Stelmach, 2002). Nevertheless, movement velocities can be comparable between young and older adults during rapid arm movements (Cooke, Brown, & Cunningham, 1989; Darling, Cooke, & Brown, 1989). In addition, hand muscles can exhibit similar rates of force development (Christou et al., 2007; Poston et al., 2008a, 2008b) and maximum force levels in young and older adults (Burnett, Laidlaw, & Enoka, 2000; Shinohara, Keenan, & Enoka, 2005). The similar movement velocities for the young and older adults imply that differences observed in other task performance measures between the groups must be due to factors that are independent of movement velocity. Furthermore, the lack of a change in movement velocity for the young adults across the trial blocks indicates that endpoint and trajectory control adjustments with practice were solely the result of changes in motor skill (Reis et al., 2009). In contrast, the older adults demonstrated considerable skill improvements by increased both their movement velocity (after the first trial block) and simultaneously increased their endpoint performance.

In the present study, both the overall endpoint error and endpoint variance were significantly greater for the older compared with the young adults. These differences were present in the initial block of trials and remained evident over the course of all subsequent trial blocks. Thus, the rate of improvement with practice was similar between the two groups, but the performance of the older adults never equaled that of the young adults (Figs. 2A, 3A). Collectively, these findings are consistent with previous studies that have investigated endpoint accuracy and variability during rapid arm movements (Barry & Carson, 2004; Barry et al., 2005) or isometric contractions (Christou & Carlton, 2001; Poston et al., 2008a, 2008b) in young and older adults. In addition, these results support previous suggestions that differences in motor performance between older and young adults are most evident when the task is complex, requires the coordination of many muscle groups, and involves high movement speeds (Barry & Carson, 2004; Barry et al., 2005; Christou & Carlton, 2001; Poston et al., 2008a, 2008b).

The overall endpoint error is the most commonly used measure to quantify the final positional accuracy of goal-directed arm movements. Accordingly, subjects received explicit instructions to attempt to minimize the overall endpoint error in every trial. However, endpoint error is composed of errors in both the x and y directions, which may each be the result of different physiological mechanisms (Ghez et al., 2007; Gordon et al., 1994; Scheidt & Ghez, 2007) or differentially impaired with aging. Therefore, the absolute constant errors in these directions were also quantified separately. Independent of age, the y-absolute constant error was greater than the x-absolute constant error (Young: 1.15 vs. 0.9 cm; Old: 1.54 vs. 0.98 cm). Thus, errors in movement extent had a greater contribution to the overall endpoint error than errors in movement direction. Similar findings were obtained for endpoint variance in that the y-endpoint variance was greater than the x-endpoint variance for both age groups (Young: 2.11 vs. 1.02 cm²; Old: 3.24 vs. 1.26 cm²). This general pattern of results has been shown before in arm movements performed by young adults as evidenced by elongated endpoint ellipses in the direction of movement extent (Gordon et al., 1994; van Beers et al., 2004). Both the y-absolute constant error and y-endpoint variance, however, were much larger in the older compared with the young adults, which as direct consequence provided the primary contribution to the group differences in overall endpoint error and endpoint variance (Figs. 2C, 3C). In contrast, both the x-absolute constant error and x-endpoint variance were similar between the older and young adults and, therefore did not provide the primary contribution to the group differences in the overall endpoint error or endpoint variance (Figs. 2B, 3B). To our knowledge, this is the first study to show that the greater endpoint error and endpoint variance typically observed in older adults during aiming movements is due primarily to impairments in movement extent control.

4.2 Endpoint performance and trajectory control

A major prediction of the minimum variance theory is that smooth trajectories with low noise levels are selected to minimize endpoint error and endpoint variability. Specifically, Harris and Wolpert (1998) stated, “Noise in the final neural control signal (that is, noise in the firing of motor neurons) will cause trajectories to deviate from the desired path. These deviations will be accumulated over the duration of a movement leading to variability in the final position”. Furthermore, Wolpert and Ghahramani (2000) stated, “Non-smooth movements require large motor commands, which generate increased noise; smoothness thereby leads to accuracy” (see their Fig. 2 for a depiction of these concepts). Thus, smoothness of the trajectory should determine the magnitude of endpoint error within a trial and reductions in endpoint error and endpoint variability with practice should be directly associated with concomitant changes in trajectory smoothness. In this context, the primary aim of the study was to determine the influence of trajectory smoothness on the endpoint accuracy and endpoint variability of rapid arm movements. Previous studies that have tested this prediction of the minimum variance theory with experimental data are difficult to interpret because they either used isometric contractions (Christou et al., 2007; Poston et al., 2010; Poston et al., 2008a), constant velocity movements without an endpoint (Christou et al., 2003), or single-joint movements with a highly constrained trajectory (Osu et al., 2004). Because the minimum variance theory was formulated using natural arm movements that finished with the limb near zero velocity (Harris & Wolpert, 1998), none of these studies directly tested the theory under the task conditions for which it was developed. Therefore, the current study employed an unconstrained multi-joint arm movement to a target to provide an appropriate test of this prediction of the minimum variance theory.

The trajectory smoothness (normalized jerk) remained invariant with practice, except for a slightly greater (non-significant) normalized jerk in the first trial block for the older adults, which is consistent with previous findings that elderly typically exhibit less smooth movements than young individuals in unpracticed movements. As a result, trajectory smoothness did not change in parallel with the endpoint error or endpoint variance for either age group. These disassociations imply that endpoint performance was not dependent upon the smoothness of the trajectory to the target. Accordingly, endpoint error and endpoint variance were not correlated with normalized jerk for the young adults when using the 100 trial averages for these variables (Fig. 5A, 5E). However, the endpoint error and the endpoint variance were moderately and weakly associated with the normalized jerk in the older adults (Fig. 5B, 5F). Thus, the normalized jerk and endpoint error values for every individual trial in both age groups were used to examine in more detail the influence of the within-trial smoothness of the trajectory on endpoint accuracy. These analyses showed that there was no correlation between normalized jerk and endpoint error for either of the two age groups (Fig. 5C, 5D). Thus, trajectory smoothness was not strongly or systematically correlated with measures of endpoint performance for either the between-trial or within-trial associations. Furthermore, trajectory error (absolute perpendicular distance) was a weak predictor of endpoint error, but only for the older adults. In contrast, the endpoint variance was a strong predictor of endpoint error in both age groups (Fig. 6A, 6B), which is consistent with a sub-prediction of the minimum variance theory. However, this association has been known for some time (Schmidt & Lee, 1999) as long as the average endpoint distribution is centered relatively close to the target (Christou et al., 2007; Muller & Sternad, 2004).

Taken together, the observations that trajectory smoothness was not correlated with endpoint error or endpoint variance and did not change in parallel with these measures of endpoint performance, contradict many of the predictions of the minimum variance theory. The findings also differ from Christou et al. (2003) who found that trajectory smoothness during eccentric and concentric contractions was significantly associated with movement accuracy. However, the task used in that study involved constant velocity muscle contractions, which do not occur in natural movements, and the task did not have an endpoint target to attain. Although the authors concluded that the findings supported the minimum variance theory, the disparate findings are almost certainly due to the artificial task conditions, which did not allow for an appropriate test of many of the key features of the minimum variance theory.

However, the disassociations between trajectory and endpoint control in the present study are consistent with a series of studies by Ghez and colleagues (Ghez et al., 2007; Gordon et al., 1994; Scheidt & Ghez, 2007). In a classic study, Gordon et al. (1994) required subjects to perform arm movements to targets of varying extents. They found that variable errors increased non-linearly with increases in movement extent, whereas variable errors in direction remained constant for the different movement extents. Thus, the findings provided evidence that movement extent and direction control are planned separately and independently during arm movements to a target. Recently, Scheidt and Ghez (2007) used a visuomotor adaptation paradigm involving two arm movement tasks that required spatial accuracy at either the midpoint or movement endpoint. Lack of transfer in visuomotor learning between the two tasks along with computer simulations, control experiments, and a follow up experiment (Ghez et al., 2007) allowed these authors to differentiate between the neural strategies used for trajectory and endpoint control. Collectively, these studies concluded that separate control strategies and physiological mechanisms underlie trajectory and endpoint control, the control strategies are planned in separate frames of reference and implemented sequentially, and the findings do not support the predictions of theories such as the minimum variance theory that propose a unified kinematic plan for trajectory and endpoint control.

Other evidence supports the idea that trajectory and endpoint control are the result of separate control processes. For example, there are differences in trajectory and endpoint control between the dominant and non-dominant arms (Sainburg, 2002). In addition, separate cortical neuron populations regulate endpoint posture and movement (Kurtzer, Herter, & Scott, 2005). In the present study, the findings that only weak to moderate associations between trajectory error and endpoint error further supports the concept of separate control of trajectory and final position. Several other studies have also found similar low levels of association between trajectory error and endpoint error (Messier & Kalaska, 1997, 1999; van Beers et al., 2004), which may be partially due to early trajectory errors ultimately being compensated for by early alterations of agonist activity (Gordon & Ghez, 1987) or most likely antagonist muscle timing (Darling & Cooke, 1987) especially near the endpoint (see Section 4.4 below), both of which would not necessarily influence movement smoothness. Regardless of the exact mechanisms, neither trajectory error nor trajectory smoothness predict endpoint error or endpoint variance, which contradicts the minimum variance theory proposal that noise in the trajectory is minimized to optimize cost functions related to endpoint error or variance. Accordingly, computational studies have indicated that the CNS likely uses cost functions in addition to endpoint variance (Todorov, 2004) to plan and execute movements with their weighting being dependent on the task and the movement context (Tanaka et al., 2006).

4.3 Trajectory error in young and older adults

Numerous studies have provided evidence that trajectory error is an important control variable used by the CNS in the planning and execution of arm movements (Lackner & Dizio, 1994; Morasso, 1981; Shadmehr & Mussa-Ivaldi, 1994). For instance, straight trajectories are maintained under a variety of task conditions (Morasso, 1981), curved trajectory paths return to straightness after force field perturbation (Shadmehr & Mussa-Ivaldi, 1994), trajectory error is similar in blind and sighted individuals (Miall & Haggard, 1995; Sergio & Scott, 1998), and trajectory error is more greater in elbow and shoulder joint paths than end-effector hand paths (Sergio & Scott, 1998). Therefore, deviations in the movement trajectory from the theoretically optimal straight-line path have been regarded as movement errors due to inexact motor planning (Ghez et al., 2007; Gordon et al., 1994; Scheidt & Ghez, 2007; Uno, Kawato, & Suzuki, 1989). In contrast to the impaired endpoint performance of the older adults, the magnitude of trajectory error (absolute perpendicular distance) was similar for the two age groups and did not significantly improve with practice. These findings indicate that the associated physiological mechanisms underlying this facet of trajectory control is not impaired with aging. Therefore, the most prominent differences between young and older adults in the present task seem to be confined to endpoint performance, especially in the movement extent control component.

4.4 Factors responsible for motor performance differences between young and older adults

The aging process is associated with significant declines in motor performance, however, the neuromuscular mechanisms responsible and their relative contribution to reduced performance remains unclear. The most commonly cited degenerative aging related adaptations include: motor neurons apoptosis (Doherty, 2003), cortical neuron loss (Eisen, Entezari-Taher, & Stewart, 1996; Henderson, Tomlinson, & Gibson, 1980), subcortical degeneration (Marchand et al., 2011; Sjobeck, Dahlen, & Englund, 1999), impaired spinal reflexes (Corden & Lippold, 1996; Kido, Tanaka, & Stein, 2004), and an altered balance of excitatory and inhibitory circuits in the motor cortex (McGinley, Hoffman, Russ, Thomas, & Clark, 2010; Sale & Semmler, 2005). Therefore, the greater endpoint error and variability exhibited by the older adults in the present study is likely the result of deteriorations in multiple CNS regions. Regardless of the exact origins, research shows that the net effects as reflected in the motor output of older adults includes altered coordination of multi-joint synergists (Barry & Carson, 2004; Barry et al., 2005), excessive and inappropriate timed cocontraction of antagonist muscles (Christou, 2011; Christou et al., 2007; Darling et al., 1989; Seidler-Dobrin, He, & Stelmach, 1998), and enhanced variability of motor unit discharge rates in the agonist muscle (Enoka et al., 2003; Kornatz, Christou, & Enoka, 2005; Laidlaw, Bilodeau, & Enoka, 2000). These mechanisms or their combination likely explain, at least partially, the altered control of movement extent by the older adults as altered coordination patterns of agonist and antagonist muscles at multiple joints and trial-to-trial variability in the triphasic pattern of muscle activation would lead to excessive endpoint variability in movement extent. However, future research utilizing a variety of physiological approaches will be needed to determine the CNS sites responsible for the differences in motor performance and motor output variability in young and older adults.

4.5 Conclusions

Endpoint error and endpoint variance were greater in older compared with young adults with the differences due mainly to the impairments in movement extent control exhibited by older adults. Most importantly, endpoint error and endpoint variance were not associated with trajectory smoothness in either age group. Accordingly, endpoint error and endpoint variance improved with practice for both age groups, whereas trajectory error remained invariant and was only weakly associated with endpoint error. The results do not support many of the predictions of the minimum variance theory, but are consistent with findings indicating that movement trajectories and endpoints are independently planned (Ghez et al., 2007; Gordon et al., 1994; Scheidt & Ghez, 2007). Finally, the results suggest that the CNS uses cost functions in addition to endpoint variance to plan and execute arm movements (Tanaka et al., 2006; Todorov, 2004).