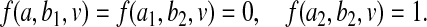Skip to main content
NCBI home page
Biostatistics (Oxford, England) logoLink to Biostatistics (Oxford, England)
. 2012 Dec 19;14(3):502–513. doi: 10.1093/biostatistics/kxs049

Deep determinism and the assessment of mechanistic interaction

Carlo Berzuini 1,*, A Philip Dawid 1
PMCID: PMC3677734  PMID: 23255363

Abstract

Given two variables that causally influence a binary response, we formalize the idea that their effects operate through a common mechanism, in which case we say that the two variables interact mechanistically. We introduce a mechanistic interaction relationship of “interference” that is asymmetric in the two causal factors. Conditions and assumptions under which such mechanistic interaction can be tested under a given regime of data collection, be it interventional or observational, are expressed in terms of conditional independence relationships between the problem variables, which can be manipulated with the aid of causal diagrams. The proposed method is able, under appropriate conditions, to test for interaction between direct effects, and to deal with the situation where one of the two factors is a dichotomized version of a continuous variable. The method is illustrated with the aid of a study on heart disease.

Keywords: Biological mechanism, Causal inference, Compositional epistasis, Direct effects, Directed acyclic graphs, Excess risk

1. Introduction

Suppose that we are interested in the causal effects of variables A and B on outcome Y , and, more specifically, in assessing whether these effects interfere with each other as a result of A and B being co-involved in a mechanism. Geneticists, for example, are interested in compositional epistasis (Bateson, 1909; Phillips, 2008; Cordell, 2009): the idea of a gene variant, A, that can nullify a phenotypic effect of gene variant B. More broadly, in this paper, A and B denote variables that can (conceivably if not technologically) be manipulated, such as treatments, or epidemiological or environmental exposures. In an attempt to embrace this spectrum, we shall refer to the above idea of interference as “mechanistic interaction”. For a discussion of interaction in the context of studies of molecular mechanisms of disease, see, e.g. Clayton (2009).

We would often wish to infer mechanistic interaction from data collected under an observational regime, e.g. from medical records. This problem has been tackled by several authors, including Rothman (1976); Greenland and Poole (1988); Rothman and Greenland (1998); VanderWeele and Robins (2008, 2009); VanderWeele (2009, 2010a, 2011); VanderWeele and Laird (2011); Skrondal (2003). Many of these consider the special case where A, B, and Y are binary, and show that the following conditions will, depending on assumptions, imply some form of mechanistic interaction:

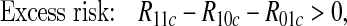1. (1.1)
1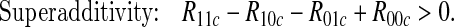. (1.2)

Here Rabc is the observational probability of the outcome event for an individual who has A=a and B=b, with a,b=0 or 1, conditional on an appropriately chosen set C of observed variables attaining value c (with C possibly empty and unaffected by (A,B)).

Current justifications of the above conditions are based on the potential outcomes (PO) formulation of causality (Rubin, 1974), or equivalent formulations. In the PO formulation, the value that Y would take in response to an intervention that sets (A,B) to values (a,b) (for a particular individual in particular circumstances) is regarded as a potential outcome, Y ab, existing even before the intervention on (A,B) is performed. As noted by Pearl (2011), this conception is formally equivalent to the assumption that there exists an “error variable” U, prior to and independent of (A,B), such that we can express Y as a deterministic function of A, B, and U, that is, Y =f(A,B,U). In this case, we shall have Y ab=f(a,b,U); conversely, if we start by assuming the prior existence of all the potential outcomes, we can define U to be the collection of all of these, with the function f simply picking out the component indexed by (a,b).

An important distinction (Dawid and Didelez, 2012), fundamental to our approach here, is between the case where U can be treated as a real and potentially measurable quantity in the physical world, and that where it is not (as will, for example, be the case when U is taken to be the collection of all potential outcomes, which by their very definition are not simultaneously observable). In the latter case, the functional relation Y ab=f(a;b;U) might be termed “formally deterministic”, and does not require or imply any form of determinism in the real world. In the contrary case where U can be regarded as a pretreatment variable that could (in principle at least) be measured in the real world, the above functional relationship grows teeth, and asserts genuine real-world deterministic behavior. In this special case, we say that the functional relation Y ab=f(a;b;U) is “deeply deterministic” and we can indeed regard each potential outcome Y ab, which is a function of U, as a real-world pretreatment variable. Whereas it is generally possible to produce formal determinism by purely mathematical manipulations, this is not so for deep determinism, which imposes strong restrictions on how the world behaves, and may or may not be appropriate according to circumstances.

In the PO approach, mechanistic interaction is interpreted as the existence of at least one individual who would develop the outcome Y =1 if both A and B are set to 1, but not if only one of them is: formally, Y 11=1,Y 01=Y 10=0. If we construe the probability Rabc as the expected value of Y ab over the individuals in stratum C=c, then, under suitable assumptions of no confounding and monotonicity of the potential outcomes, the excess risk and superadditivity conditions of (1.1)–(1.2) imply that the event

1. (1.3)

has positive probability in stratum C=c, which implies mechanistic interaction by definition (VanderWeele and Robins, 2008). We regard this as meaningful only when we can conceive of the Y ab as real-world, coexisting variables that characterize the individual prior to any intervention on (A,B). This requires the existence of a deeply deterministic functional relationship Y =f(A;B;C;U), where U is potentially—if not actually—observable and unaffected by (A,B).

A further assumption, which we call full determinism, is required in the typical PO formulation: that each variable on a causal path from (A,B) to Y depends on its direct causes via a functional relationship. Full determinism is a necessary assumption in many approaches to mechanistic interaction, e.g. in the sufficient causation approach (VanderWeele and Robins, 2008; VanderWeele, 2010b). Again, in these approaches, we can and should also distinguish between formal and deep determinism.

In our view, when no appropriate assumption of deep determinism for Y can be made, mechanistic interaction ceases to be meaningful. We do, however, extend our analysis beyond full determinism, by considering situations where some “mediator” variables along a causal path from (A,B) to Y depend stochastically on their causes. It is not obvious how we should tackle such situations within the PO framework.

We abandon the PO framework in favor of Dawid's (2000, 2002) decision-theoretic approach to causal inference. The present formulation and justification of mechanistic interaction are therefore novel, as is our analysis of the rôle of deep determinism in the problem. Under assumptions of full and deep determinism for Y, our approach to mechanistic interaction will lead to the same mathematical analysis as the previous, PO-based, methods. But in the presence of a stochastic mediator of the effect of (A,B) on Y , we show in §4.1 that an analysis of mechanistic interaction between total effects is no longer justified, whereas an analysis of interaction between direct effects (that operate when the value of the stochastic mediator is fixed by a real or hypothetical intervention) may—under an additional assumption—be justified.

A further contribution of the paper is to extend analysis of mechanistic interaction to situations where one of A and B has been obtained by dichotomizing a continuous measurement. We compare this with the recent independent proposal of VanderWeele and others (2011) for a similar situation. We present an illustrative study in cardiology.

2. Main example

According to the diagrams of Figure 1, the risk of an early infarction, Y =1, is directly influenced by a genetic variant, A, by physical activity, B, by a set W1 of proxies for social status, by a set U of unobserved variables, and by body mass, W2. The latter is, in turn, directly influenced by A,B,W1 and by a further set, U′, of unobserved variables. Further explanation is given in the figure caption. For the time being, ignore the σ nodes. Of interest is the question whether the effects of A and B on Y interact mechanistically.

Fig. 1.

Fig. 1.

Open in a new tab

These are two examples of an augmented causal diagram (ACD) (see §4.2) that represent different sets of assumptions about the same epidemiological study. The binary outcome variable Y indicates early occurrence (between ages 40 and 45) of an acute myocardial infarction. The binary factor A represents deleterious homozygosity (presence of two copies of the deleterious allele, A=1) at diallelic locus rs9939609. This locus is believed to exert a regulatory influence on more than one gene, thus possibly influencing unrelated molecular pathways, represented in the diagrams by non-overlapping paths from A to Y . The factor B represents “average number of days per week of at least 20 min of strenuous physical exercise”. In both diagrams, A and B influence Y directly, and indirectly through changes in body mass W2. Node W1 represents a collection of variables related to social status, including profession, geographical area of origin, and drinking habit. Both diagrams contain the assumption that, conditionally on W1, none of the unobserved influences on Y , denoted as U, further influences body mass. Full arrowheads denote functional dependence, whereas indented arrowheads represent fully stochastic dependence. While in (a) dependence of W2 on its direct influences is taken to be deterministic, in (b) it is taken to be fully stochastic, so that, in the latter figure, W2 acts as a stochastic mediator. The two diagrams contain decision nodes representing regime indicators, σAB and σW2, indicating whether the corresponding variables—to which they send arrows—are manipulated or simply observed (see §4).

Although Figures 1(a) and (b) represent the same epidemiological study, assumptional differences between them impact on the assessment of mechanistic interaction. One difference is that the full arrowheads into W2 of Figure 1(a) are replaced in Figure 1(b) by indented arrowheads. This is intended to indicate that dependence of W2 on its direct influences is taken to be deterministic in the former diagram, and fully stochastic in the latter diagram. Figure 1(a) embodies the following assumed functional relationships:

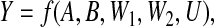2. (2.1)
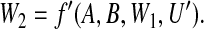2. (2.2)

On substituting for W2 in (2.1) from (2.2), we see that variable Y can be expressed as a deterministic function of (A,B) and variables unaffected by (A,B): Y =f′′(A,B,W1,U,U′). Figure 1(a) thus incorporates full determinism.

The functional relationships (2.1)–(2.2) require genuine deterministic dependence of myocardial infarction, Y , and body mass, W2, on prior variables: assumptions that deserve scrutiny. Our study experts feel comfortable with (2.1), on the grounds that a relatively small set of measurable conditions (e.g. disturbances in lipoprotein handling, vulnerability of endothelial integrity, altered arterial inflammation, and disruption of the normal process of clot and thrombus formation) could, depending also on obesity and physical activity, be assumed to make the infarction inevitable.

In contrast, the experts perceive the restriction imposed by (2.2) on the behavior of body mass as incompatible with their view of this variable as the resultant of a complex dynamic process of interaction between the individual's genetic and psychological characteristics and the cultural and social environment. This shifts interest from the model of Figure 1(a) to the reduced determinism model of Figure 1(b).

We will show that mechanistic inference about the total effects of A and B on Y is justified under the model of Figure 1(a), but not under that of Figure 1(b). We will also show that—under additional assumptions—the latter model justifies mechanistic inference about the direct (as opposed to total) effects of A and B on Y , controlling for W2. We shall also examine the conditions under which the required dichotomization of variable B, originally elicited as the number of days per week of physical exercise, does not affect the validity of the analysis.

3. Deep determinism and interference

Let the binary random variable Y indicate occurrence (Y =1) or non-occurrence (Y =0) of an outcome event of interest, depending causally (in a sense to be later clarified) on factors of interest A and B. The response Y will, in general, depend on a set of additional context variables V some of which may be unknown. Let the set of possible values of A (respectively, B, V) be denoted by 𝒜 (respectively, ℬ,𝒱); these may be arbitrary sets.

Our fundamental assumption—which would need justification in any application—is that, under any interventional regime that sets the values of A and B to some configuration (a,b), the response Y would be fully determined, without further variation, by (a,b,V); that is

3. (3.1)

for any value of V and some (typically unknown) deterministic function f. This is our deep determinism assumption. The set V may contain variables affected by A and/or B.

We wish to investigate context-specific causal effects—the effects of A and B upon Y in a given “context” V =v. More specifically, we shall investigate whether, in some context V =v, the effects (on Y) of manipulating A and B interfere with each other, in some sense. The following definition is one way of formalizing this notion of interference, under the deep determinism assumption (3.1).

Definition 3.1 (Interference) —

We say that B interferes with A in producing the event Y =1 if there are values b1,b2∈ℬ such that, in some context V =v, setting B=b1 causes Y to be 0, no matter how we manipulate A; whereas, in the same context, when we set B=b2, the value imposed on A makes a difference to Y . Formally, there is some v∈𝒱 such that, for some a1,a2∈𝒜 and b1,b2∈ℬ, all a∈𝒜:

graphic file with name M7.gif (3.2)

The above definition does not capture all the patterns we might intuitively associate with the idea of mechanistic interaction. In particular, it does not address qualitative interaction, where changing the value of one factor changes the sign of the effect of the other. This exclusion is mitigated by the existence of tests for qualitative interaction (see, for example, Azzalini and Cox, 1984); these do not require assumptions of determinism, essentially because qualitative interaction cannot be removed by model transformation.

Our definition of interference captures a possible asymmetry of the interference relationship. This is illustrated by the electrical example of Figure 2 (see figure caption for a description of the example), where switch A interferes with switch B, but not vice versa, as a consequence of the circuit structure. However, when A and B are both binary, the mathematical framework is unable to capture such asymmetries—even though, in certain applications, we might consider only one of the two possible directions of the interference relationship as meaningful (e.g. “the antiviral drug interferes with the effect of an exposure to virus”).

Fig. 2.

Fig. 2.

Open in a new tab

In this electrical circuit, imagine that an electrical voltage is applied between pins Inline graphic and Inline graphic. Let Y =1 indicate the absence of current between these two pins. Let Y =0 indicate the presence of current between these two pins. Switches A1,A2,B, and V may be OPEN or CLOSED; variable A indexes the four possible configurations of the A-switches, and variable B the two positions of the B-switch, while switch V acts as the unobserved context variable. A voltage is applied between pins Inline graphic and Inline graphic, and current will flow (Y =1) if there is a path between the two pins along which all switches are closed; otherwise, there is no current (Y =0). Then, in context V =CLOSED, the action of opening A2 causes Y to be 0, no matter how we set B. However, in the same context, when A2 is CLOSED and A1 is OPEN, the value of Y will depend on the position of B. Hence, A interferes with B in producing the event Y =1. The reader may verify that B does not interfere with A in producing Y =1.

A referee has remarked that, in the binary case, the above notion of interference is not invariant to recodings of the variables, (A,B,Y), that switch 0s with 1s. But we do not want invariance. Mechanistic interaction in producing the event Y =1 is a different thing from interaction in preventing it. One should always specify whether interest lies in “production” or “prevention”, with the specific application suggesting the choice. The default interpretation of “interference” will hereafter be “interference in producing”.

4. Assumptions and testing

Variable B will hereafter be ordered categorical or continuous, while A will be ordered categorical. Our method requires A and B to be dichotomized to produce binary (0,1) variables α and β, respectively. Variable A will have to be dichotomized at its highest level, that is, α=1 must correspond to A taking on its highest value amax, whereas B can be dichotomized at an arbitrary level. We shall continue to make use of inequalities (1.1) and (1.2), but with the reinterpretation Rijc=P(Y =1|α=i,β=j,C=c) (in the observational regime). In general, interference between A and B in producing Y =1 will not be testable by applying the excess risk or superadditivity condition to observational data, owing to confounding and/or selection, and, even when it is, the validity of the test will depend on appropriate choice of stratifying variables C. The following two sets of conditions are jointly sufficient for the testability of interference of B with A in producing Y =1, as defined by (3.2), by applying the excess risk condition to observational data.

Condition 4.1 (Structural conditions) —

  1. Variable A is ordered categorical, and Y is binary.

  2. The deep determinism assumption of (3.1) holds, with context variable V =(W,U), where the (possibly empty) set of variables W is observed and U unobserved. Thus, Y =f(A,B,W,U).

  3. (Monotonicity of the effect of A) For any fixed (w,u), either f(a,b,w,u) is a non-decreasing function of a for all b, or it is a non-increasing function of a for all b.

VanderWeele (2011) has provided, within a PO approach to the problem, empirical tests for interference that do not require the monotonicity assumption above. Our main motivation for keeping this assumption is our decision to focus on the consequences of dichotomizing a continuous causal factor for the mechanistic interaction tests. Further conditions are needed because our aim is to test for a property (interference) that refers to an interventional regime of manipulation of (A,B), by using data collected under an observational regime, in which A and B are not manipulated. Let the observational and interventional regimes of manipulation of (A,B) be denoted by o and e, respectively, and let σAB denote the regime indicator for (A,B), with values o and e. We use, for example, the symbol p(Y |A=a,B=b,σAB=e) to denote the distribution of Y under an intervention that sets A to value a, and B to value b, whereas we use p(Y |A=a,B=b,σAB=o) to denote the distribution of Y in a subject characterized by variables A and B being observed to take values a and b, respectively. These two distributions will, in general, be different. Inference about causative interaction is only possible if the two distributions have certain similarities that can be expressed using the conditional independence notation of Dawid (1979, 2002) as follows.

Condition 4.2 (Causal conditions) —

There is a set C of observed variables, with Inline graphic, such that:

  1. Y ⊥⊥ σAB|(A,B,W,U);

  2. U ⊥⊥ (A,B,σAB)|C;

  3. (unnecessary if β=1 corresponds to just one value of B): A ⊥⊥ B|(C,σAB).

Condition 4.2(1) requires that the functional relationship (3.2), which was assumed to hold when A and B are set by intervention, should also hold, unchanged, under observational circumstances. Informally stated, this means requiring that the effects of A and B on Y be unconfounded, given U and W. In §4.2, we show that this condition is straightforwardly checked with the aid of a causal diagram. Condition 4.2(2) requires that, in stratum C=c, the distribution of U be the same under both interventional and observational conditions and, further, be independent of A and B. Finally, Condition 4.2(3) requires that, in stratum C=c, variables A and B be independent in the observational regime (under an interventional regime this property will hold vacuously).

Theorem 4.1 —

Assume that the above structural and causal conditions are satisfied. Then if, in the observational regime, the excess risk condition (1.1) holds in some stratum C=c of the population, variable B interferes with A in producing the event Y = 1.

For a proof of the theorem, see §S.1 of supplementary material available at Biostatistics online.

In certain applications, one may be able to replace the above monotonicity assumption by the stronger assumption that the effects of A and B on Y are both positive monotonic. This asserts that an increase in either A or B does not induce a decrease in Y , whatever be the values of the other variables. Under this assumption, Theorem 4.1 remains valid if we replace the excess risk condition (1.1) by the weaker superadditivity condition (1.2).

The above theorem embraces those situations where β is obtained by dichotomizing a continuous variable. Results on the analysis of continuous variables have been independently obtained by VanderWeele and others (2011) under a PO framework. These results are in substantial agreement with our method, although they focus attention on the situation in which one of the factors is binary.

4.1. Total vs. direct effects

The model of Figure 1(a) admits either of the following two functional relationships for Y :

4.1. (4.1)
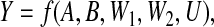4.1. (4.2)

where f and f′ are deterministic functions. Of the two relationships, the latter is mediator free, in the sense that none of its input variables is affected by (A,B). Such a relationship relies on the assumption that W2 depends on its influences in a deterministic way. Because the model of Figure 1(a) admits a mediator-free functional relationship for Y , it is called “fully deterministic”. Under a fully deterministic model, it may be possible—subject to the structural and causal conditions of Theorem 4.1—to assess mechanistic interaction between the total effects of A and B on Y , via excess risk or superadditivity. In particular, under the model of Figure 1(a), this is possible under our theory by choosing the conditioning variable to be C≡W1, which then leads to essentially the same analysis one would perform within the traditional PO approach to mechanistic interaction. Note that (4.2) defines a set of potential outcomes for Y, given (A,B), which are available a priori if (U,U′) are potentially observable, real-world quantities.

Things are different in those situations (illustrated by the model of Figure 1(b)) where the mediator (variable W2 in our example) is modeled stochastically, which precludes the existence of a mediator-free functional relationship for Y of the type illustrated by (4.2). Under such reduced determinism models, because our theory prescribes conditioning on the stochastic mediator, we can no longer analyze interaction between total effects of A and B on Y . What we, in certain situations, can explore is interaction between the direct effects of A and B on Y controlling for the mediator (Pearl, 2005). These are defined as the effects that operate under a hypothetical intervention that fixes the value of the mediator in all individuals. The additional assumptions for a valid analysis of mechanistic interaction between controlled direct effects are discussed in the following.

Let H⊆W be the mediator of the effect of (A,B) on Y that is involved as an input variable in the functional relationship for Y . In order that inference about direct effects of A and B on Y , controlling for H, be justified, we require the following stronger version of causal condition (1):

4.1.

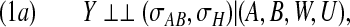where the regime indicator σH indicates whether H is manipulated or simply observed. This condition can be informally described as requiring that the effects of A, B, and H on Y be unconfounded, conditional on U and W. More formally, it requires that the functional dependence of Y on (A,B,W,U) continue to hold, and remain unchanged, when, in addition to A and B, also the values of the H variables are set by intervention. It then follows that with a reduced determinism model, under property (1a), when we condition on H, the relationship Y =f(A,B,W,U) describes the response we would observe were we able to intervene on A and B while, at the same time, interventionally fixing the H variables to a specific value. In such a case, if the remaining conditions of Theorem 4.1 are also satisfied, the method may provide evidence that B interferes with the direct effect of A on Y , controlled for H.

4.2. Augmented causal diagrams

It will often be possible to represent the assumed relationships between the various variables and regimes by means of an augmented causal diagram (ACD) (Dawid, 2002). Exemplified by Figures 1(a) and (b), this class of diagrams includes the relevant regime indicators in the form of additional (decision) nodes sending arrows into the variables they refer to. Figure 1(b), for example, contains the regime indicators σAB and σW2, this latter indicating whether W2 is manipulated or observed. Our causal conditions, as long as expressed in terms of conditional independence relationships between variables and indicators, can be checked on an ACD such as those of Figure 1 with the aid of such graphical criteria as d-separation (Geiger and others, 1990) or its moralization equivalent (Lauritzen and others, 1990). In particular, causal condition (1) and its stronger version, (1a), will hold so long as the set (A,B,W,U) contains all the parents of Y in the diagram.

5. Illustrative study

We shall now analyze data from the retrospective study (Ardissino and others, 2011) described by Figure 1. For each incoming case, a corresponding control was selected by matching on the basis of the W1 proxies for social status. 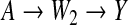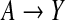Experimental evidence suggests that the genetic variant represented by A, deleterious homozygosity at rs9939609, influences susceptibility to infarction through changes in eating behavior (Dina and others, 2007) and in the regulation of entry into cell division (Jowett and others, 2010), these two independent mechanisms being represented in Figure 1 by the non-overlapping paths Inline graphic and Inline graphic, respectively. The mentioned studies support the assumption that both these pathways convey a monotonically increasing pro-infarction effect of A. In the following analysis, we let α=1 indicate A=1, with α=0 indicating otherwise. Under the positive monotonicity assumption that a decrease in B (average number of days per week of physical exercise) will not reduce the risk of infarction, we dichotomize this variable into β, which takes value 1 in the case of inactivity (B=0), and value 0 otherwise. We shall now carry out, and compare, analyses based on the full determinism model of Figure 1(a) and on the reduced determinism model of Figure 1(b).

5.1. Analysis under full determinism

We have seen in §2 that under the fully deterministic model of Figure 1(a), a functional dependence of Y on (A,B,W1) can be assumed, formally Y =f(A,B,W1,U,U′). If we then redefine U=(U,U′), then our causal and structural conditions are satisfied. This, in conjunction with the above-mentioned assumptions of monotonicity, justifies the use of the superadditivity condition (1.2) for testing mechanistic interaction between the total effects of A and B upon infarction. We perform this test by a logistic regression analysis, in which the conditioning on C≡W1 is effected through the matching. More formally, let the ij subscript index the jth member of matched pair i (with i=1,…,n). Then we assume that

5.1.

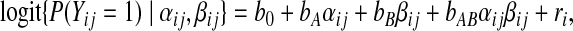where ri is the random effect for matched pair i. Maximum conditional likelihood estimates for (bA,bB,bAB) are reported in Table 1. It can be shown that the function of the unknown model parameters

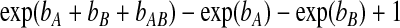5.1. (5.1)

yields the so-called relative excess risk due to interaction (RERI), defined by

5.1.

As noted by Rothman (1976) and Skrondal (2003), RERI is a function of relative risks and, hence, under mild assumptions about the sampling process, it can be estimated from case–control data. Positivity of RERI implies superadditivity, so that the problem reduces to testing for the positivity of (5.1). An approximate confidence interval for RERI can be constructed from the variance–covariance matrix of the parameter estimates via the delta method. Our data yielded an estimated value for RERI of 0.338, with a 95% confidence interval of (−0.4,1.3), representing insufficient evidence of interference of physical activity with the total effect of rs9939609 on infarction.

Table 1.

Results from the fitting of a conditional logistic model for the risk of premature myocardial infarction to the entire sample of matched cases and controls in the illustrative study on premature myocardial infarction

Effect estimate Relative risk Standard error z-value p-value
Minor homozygous at rs9939609 0.18 1.20 0.13 1.41 0.16
Physical inactivity 0.50 1.65 0.13 3.85 0.00
Minor homozygous × inactivity 0.10 1.11 0.16 0.65 0.51
Open in a new tab

The following variables were included as explanatory in the model: the presence of two copies of the minor rs9939609 allele (so-called minor homozygosity), and physical inactivity.

5.2. Analysis under reduced determinism

Consider now the reduced determinism model of Figure 1(b). We have seen in §4.1 that this model does not admit a mediator-free functional relationship for Y . It does, however, admit a functional relationship of the form Y =f(A,B,W1,W2,U), which leads to an analysis conditional on C=(W1,W2). With this proviso, the problem satisfies our causal and structural conditions, including (1a) because all the parents of Y belong to (A,B,U,W). Note that structural condition (3) is irrelevant here because β has been defined to take value 1 when B takes its lowest value. We conclude that superadditivity is here a valid condition for mechanistic interaction between the direct effects of A and B on Y , controlled for W2. These are, in fact, of primary scientific interest in the present study.

We adopt a regression approach to the analysis. We condition on W1 by matching cases with controls with respect to most of these variables, adjustment for the remaining ones being performed in the regression. We condition on W2 by restricting analysis to the stratum with a body mass index below 25 kg/m2, that is, by eliminating all matched pairs where at least one member exceeds the mentioned threshold, and by allowing the regression model to adjust for within-stratum variation of W2. See §2 of supplementary material available at Biostatistics online for a justification of the method. The fitting of a conditional logistic regression model for Y yielded the estimates of Table 2, which correspond to an estimated value for RERI of 1, with a 95% confidence interval of (0.4,1.85), representing strong evidence of superadditivity. This result suggests that physical activity may eliminate part of the rs9939609 pro-infarction effect that is not mediated by body mass. This conclusion we take with caution as it depends on the assumptions of Figure 1(b), notably on assuming the relationship between W2 and Y to be unconfounded conditional on W1.

Table 2.

Results from an analysis of the stratum of non-obese (1-to-1 matched) cases and controls in the illustrative study on premature myocardial infarction

Effect estimate Relative risk Standard error z-value p-value
Minor homozygous at rs9939609 −0.22 0.81 0.32 −0.68 0.50
Physical inactivity −0.12 0.89 0.32 −0.36 0.72
Body mass index −0.03 0.97 0.05 −0.62 0.54
Drinking habit 0.37 1.45 0.20 1.89 0.058
Triglycerides 0.01 1.01 0.00 5.05 4.39×10−7
Minor homozygous × inactivity 0.86 2.36 0.39 2.21 0.027
Open in a new tab

These have been obtained by fitting of a conditional logistic model for risk, with the variables included as explanatory: presence of two copies of the minor rs9939609 allele (so-called minor homozygosity), physical inactivity, body mass index, triglycerides, and drinking habit. Further variables like sex, profession, age of the case at first infarction, and geographical origin are taken into account by the matching.

6. Discussion

Mechanistic interaction has traditionally been tackled within a PO conceptualization of causality. Here, we have examined the problem from a decision-theoretic point of view (Dawid, 2012), with special attention to the necessary assumptions of determinism. These include the “full determinism” assumption that all the variables along the paths from the causal factors to the outcome depend on their influences in a deterministic way, and the assumption that the functional relationships be deterministic in a “deep” (rather than “formal”) sense. Both assumptions are illustrated by Figure 1(a), where Y and the mediator W2 depend on their causes in a deterministic way, so that Y depends on (A,B) in a functional way. We have argued that full determinism is essential to justifying an analysis of mechanistic interaction between the total effects of A and B on Y .

The literature on mechanistic interaction has mostly insisted on total effects. But one will often be interested in mechanistic interaction between the direct effects of A and B on Y , controlling for a mediator. In such a case, we do not need to assume determinism about the mediator, but we do need to make a (possibly strong) assumption of no confounding of the mediator–outcome relationship. Strong assumptions of the latter kind are common in mediation analysis. Our method assists the researcher—whether interested in total or direct effects—in verifying whether the necessary conditions can be assumed to hold in the application of interest. Because these conditions take the form of conditional independence relationships, they can be checked with the aid of a causal diagram of the problem, when this exists. As a further methodological contribution, we have derived conditions under which the tests of mechanistic interaction are valid when one of A and B has been obtained by dichotomizing a continuous measurement.

In requiring the functional dependence of the output Y on its inputs, our development here has been in line with the approach taken in most current treatments of mechanistic interaction. An exception to this is the “stochastic counterfactuals” reformulation of VanderWeele and Robins (2012). We plan to explore, in future work, the possibility of an analogous relaxation within our own framework. It appears to us that, at any rate in its current formulation, this approach still fails to address stochastic mediator problems such as that of Figure 1(b).

Supplementary material

Sections 1 and 2 of the supplementary material, available at http://www.biostatistics.oxfordjournals.org, contain a proof of Theorem 4.1, and a justification of our “reduced determinism” analysis.

Funding

The authors acknowledge support from the UK Medical Research Council Grant no. G0802320 (www.mrc.ac.uk).

Supplementary Material

Supplementary Data
supp_14_3_502__index.html (772B, html)

Acknowledgments

Conflict of Interest: None declared.

References

  1. Ardissino D., Berzuini C., Merlini P., Mannucci P., Surti A., Burtt N., Voight B., Tubaro M., Peyvandi F., Spreafico M. Influence of 9p21.3 genetic variants on clinical and angiographic outcomes in early-onset myocardial infarction. Journal of the American College of Cardiology. 2011;58:426–434. doi: 10.1016/j.jacc.2010.11.075. and others. [DOI] [PubMed] [Google Scholar]
  2. Azzalini A., Cox D. R. Two new tests associated with analysis of variance. Journal of the Royal Statistical Society. Series B (Methodological) 1984;46:335–343. [Google Scholar]
  3. Bateson W. Mendel's Principles of Heredity. Cambridge: Cambridge University Press; 1909. [Google Scholar]
  4. Clayton D. G. Prediction and interaction in complex disease genetics: experience in type 1 diabetes. PLoS Genetics. 2009;5:e1000540. doi: 10.1371/journal.pgen.1000540. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Cordell H. Detecting gene-gene interactions that underlie human diseases. Nature Reviews Genetics. 2009;10:392–404. doi: 10.1038/nrg2579. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Dawid A. P. Conditional independence in statistical theory. Journal of the Royal Statistical Society, Series B. 1979;41:1–31. [Google Scholar]
  7. Dawid A. P. Causal inference without counterfactuals. Journal of the American Statistical Association. 2000;95:407–424. [Google Scholar]
  8. Dawid A. P. Influence diagrams for causal modelling and inference. International Statistical Review. 2002;70:161–189. Corrigenda, ibid., 437. [Google Scholar]
  9. Dawid A. P. The decision-theoretic approach to causal inference. In: Berzuini C., Dawid A. P., Bernardinelli L., editors. Causality: Statistical Perspectives and Applications. Chichester: Wiley and Sons; 2012. pp. 25–42. Chapter 4. [Google Scholar]
  10. Dawid A. P., Didelez V. Imagine a can opener—the magic of principal stratum analysis. The International Journal of Biostatistics. 2012;8:19. doi: 10.1515/1557-4679.1391. [DOI] [PubMed] [Google Scholar]
  11. Dina C., Meyre D., Gallina S., Durand E., Körner A., Jacobson P., Carlsson L. M., Kiess W., Vatin V., Lecoeur C., others Variation in FTO contributes to childhood obesity and severe adult obesity. Nature Genetics. 2007;39:724–726. doi: 10.1038/ng2048. [DOI] [PubMed] [Google Scholar]
  12. Geiger D., Verma T., Pearl J. Identifying independence in Bayesian networks. Networks. 1990;20:507–534. [Google Scholar]
  13. Greenland S., Poole C. Invariants and noninvariants in the concept of interdependent effects. Scandinavian Journal of Work, Environment and Health. 1988;14:125–129. doi: 10.5271/sjweh.1945. [DOI] [PubMed] [Google Scholar]
  14. Jowett J. B., Curran J. E., Johnson M. P., Carless M. A., Goering H. H., Dyer T. D., Cole S. A., Comuzzie A. G., MacCluer J. W., Moses E. K., others Genetic variation at the FTO locus influences RBL2 gene expression. Diabetes. 2010;59:726–732. doi: 10.2337/db09-1277. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Lauritzen S. L., Dawid A. P., Larsen B. N., Leimer H. G. Independence properties of directed Markov fields. Networks. 1990;20:491–505. [Google Scholar]
  16. Pearl J. Proceedings of the American Statistical Association Joint Statistical Meetings. Minneapolis: MIRA Digital Publishing; 2005. Direct and indirect effects; pp. 1572–1581. [Google Scholar]
  17. Pearl J. Principal stratification—a goal or a tool? The International Journal of Biostatistics. 2011;7:20. doi: 10.2202/1557-4679.1322. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Phillips P. C. Epistasis—the essential role of gene interactions in the structure and evolution of genetic systems. Nature Reviews Genetics. 2008;9:855–867. doi: 10.1038/nrg2452. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Rothman K. J. Causes. American Journal of Epidemiology. 1976;104:587–592. doi: 10.1093/oxfordjournals.aje.a112335. [DOI] [PubMed] [Google Scholar]
  20. Rothman K. J., Greenland S. Modern Epidemiology. Philadelphia: Lippincott-Raven; 1998. [Google Scholar]
  21. Rubin D. B. Estimating causal effects of treatments in randomized and nonrandomized studies. Journal of Educational Psychology. 1974;66:688–701. [Google Scholar]
  22. Skrondal A. Interaction as departure from additivity in case-control studies: a cautionary note. American Journal of Epidemiology. 2003;158:251–258. doi: 10.1093/aje/kwg113. [DOI] [PubMed] [Google Scholar]
  23. VanderWeele T. J. Sufficient cause interactions and statistical interactions. Epidemiology. 2009;20:6–13. doi: 10.1097/EDE.0b013e31818f69e7. [DOI] [PubMed] [Google Scholar]
  24. VanderWeele T. J. Epistatic interactions. Statistical Applications in Genetics and Molecular Biology. 2010a;1:1–22. doi: 10.2202/1544-6115.1517. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. VanderWeele T. J. Sufficient cause interactions for categorical and ordinal exposures with three levels. Biometrika. 2010b;97:647–659. doi: 10.1093/biomet/asq030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. VanderWeele T. J. Empirical tests for compositional epistasis. Nature Reviews Genetics. 2011;11:166. doi: 10.1038/nrg2579-c1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. VanderWeele T. J., Chen Y., Ahsan H. Inference for causal interactions for continuous exposures under dichotomization. Biometrics. 2011;67:1414–1421. doi: 10.1111/j.1541-0420.2011.01629.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. VanderWeele T. J., Laird N. M. Tests for compositional epistasis under single interaction-parameter models. Annals of Human Genetics. 2011;75:146–156. doi: 10.1111/j.1469-1809.2010.00600.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. VanderWeele T. J., Robins J. M. Empirical and counterfactual conditions for sufficient cause interactions. Biometrika. 2008;95:49–61. [Google Scholar]
  30. VanderWeele T. J., Robins J. M. Minimal sufficient causation and directed acyclic graphs. Annals of Statistics. 2009;37:1437–1465. [Google Scholar]
  31. VanderWeele T. J., Robins J. M. Stochastic counterfactuals and sufficient causes. Statistica Sinica. 2012;22:379–392. doi: 10.5705/ss.2008.186. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_14_3_502__index.html (772B, html)
supp_kxs049_kxs049supp.pdf (175.9KB, pdf)

Articles from Biostatistics (Oxford, England) are provided here courtesy of Oxford University Press

RESOURCES