Simultaneously reconstructing viral cross-species transmission history and identifying the underlying constraints

Abstract

The factors that determine the origin and fate of cross-species transmission events remain unclear for the majority of human pathogens, despite being central for the development of predictive models and assessing the efficacy of prevention strategies. Here, we describe a flexible Bayesian statistical framework to reconstruct virus transmission between different host species based on viral gene sequences, while simultaneously testing and estimating the contribution of several potential predictors of cross-species transmission. Specifically, we use a generalized linear model extension of phylogenetic diffusion to perform Bayesian model averaging over candidate predictors. By further extending this model with branch partitioning, we allow for distinct host transition processes on external and internal branches, thus discriminating between recent cross-species transmissions, many of which are likely to result in dead-end infections, and host shifts that reflect successful onwards transmission in the new host species. Our approach corroborates genetic distance between hosts as a key determinant of both host shifts and cross-species transmissions of rabies virus in North American bats. Furthermore, our results indicate that geographical range overlap is a modest predictor for cross-species transmission, but not for host shifts. Although our evolutionary framework focused on the multi-host reservoir dynamics of bat rabies virus, it is applicable to other pathogens and to other discrete state transition processes.

1. Introduction

Many devastating infectious diseases have emerged from zoonotic viruses that have successfully jumped the ecological and evolutionary species barriers to generate sustained epidemics [1]. Jumps of viruses from their natural reservoirs can, however, have a range of distinct outcomes. Cross-species transmissions (CSTs) may trigger major epidemics such as those caused by HIV/AIDS, influenza type A virus and SARS coronavirus. Conversely, infections caused by CST can result in little or no onwards transmission in the recipient species, such as in Ebola virus and rabies virus infection in humans [2]. Although an understanding of the factors underlying the initial stages of viral emergence is central to public health strategies [3,4], these remain poorly understood for most important human pathogens.

As a multi-host pathogen that persists in independent cycles in numerous mammalian reservoir species [5,6], rabies provides an ideal candidate model to investigate CST dynamics at its earliest phases. Rabies is also one of the best-studied zoonotic pathogens [7–9], and its epidemic and evolutionary dynamics have frequently been explored using viral genetic data [10–12]. In North American bat species, rabies establishes different host-associated lineages through a process of frequent CST, mostly resulting in dead-end infections (CST spillover), but occasionally leading to successful and preferential transmission in the new host species (host shifts) [13]. A key question that naturally arises from this observation concerns the determinants underlying different stages of the CST dynamics: what factors govern the process of CST and host shifts of the virus? This has recently been addressed by a population genetic study of a comprehensive set of rabies virus gene sequences from distinct bat species, which demonstrated that lower degrees of host divergence between different species increase the chances of CST spillover and historical host shifts [5]. To a lesser extent, range overlap also played a role in the CST dynamics. So, despite the tremendous evolutionary potential that is generally ascribed to rapidly evolving viruses, which has sometimes led to the expectation that CST will be limited by ecological boundaries [4,14], CST is mainly restricted by host divergence in North American bat rabies populations.

The phylogenetic structuring into host-associated lineages, each maintained by a dominant bat species (figure 1), allowed Streicker et al. [5] to use an operational definition of host shifts and CST: while inferred changes in host in the ancestral history between these lineages reflects host shifting, viral jumps between the dominant host and other bat species within each lineage were considered to represent CST. To quantify rabies CST, Streicker et al. [5] applied a structured population genetics approach to viral sequence subsets for pairs of host species. For each pair of species that was infected by a common viral lineage, different hypotheses of CST directionality were tested, and estimates for the migration rate β_ij from bat species i to j were obtained using Migrate [15]. These migration rates were subsequently used to calculate per capita CST rates (R_ij), which can be interpreted as the expected number of infections in bat species i resulting from a single-infected individual from species j, based on 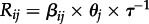, where θ_j represents an estimate of the genetic diversity for the viral population in bat species j and τ is the generation time. The latter is the sum of the incubation and infectious periods and taken to be 29 days based on controlled infection studies in insectivorous bats [16]. Finally, several factors were assessed as potential predictors for the R_ij estimates using standard generalized linear model (GLM) testing. Not only does this procedure require a series of population genetic analyses on subsets of viral sequence data, but also the considerable uncertainty that is generally associated with such estimation is necessarily ignored prior to statistical assessment. Although CST was the primary focus of the study by Streicker et al. [5], the authors also explored host shifts using a phylogenetic diffusion approach [17], and found some support for a correlation between host shifting and phylogenetic similarity between the hosts.

Figure 1.

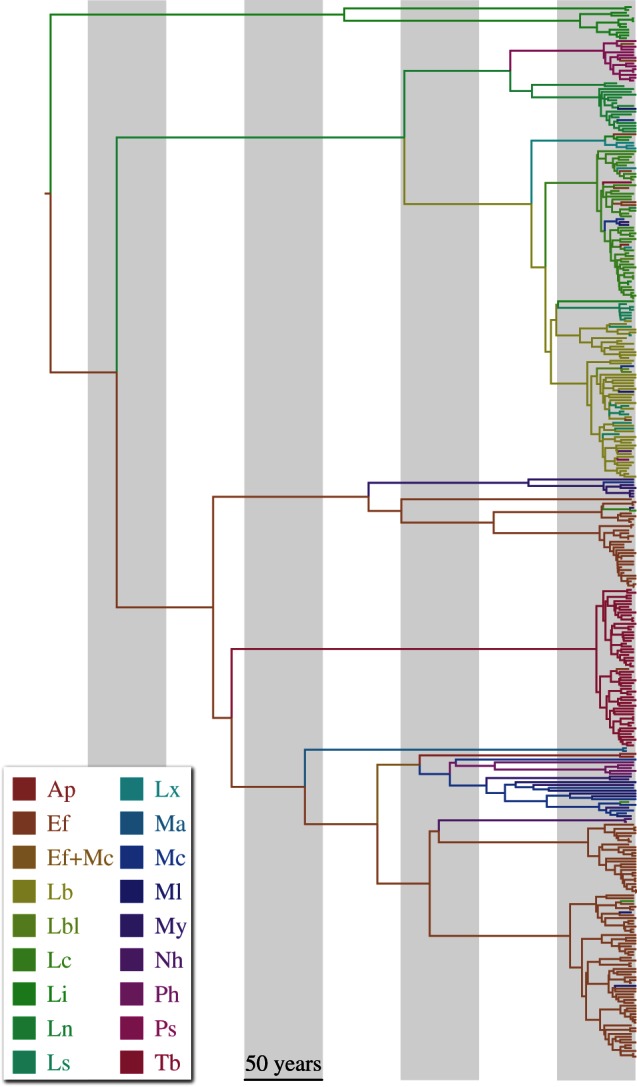
Time-calibrated maximum clade credibility (MCC) tree inferred for 372 nucleoprotein gene sequences sampled from 17 bat species. Branches were coloured according to most probable host species, indicated in the colour legend. Ap = Antrozous pallidus, Ef = Eptesicus fuscus, Lb = Lasiurus borealis, Lbl = Lasiurus blossevillii, Lc = Lasiurus cinereus, Li = Lasiurus intermedius, Ln = Lasionycteris noctivagans, Ls = Lasiurus seminolus, Lx = Lasiurus xanthinus, Ma = Myotis austroriparious, Mc = Myotis californicus complex, Ml = Myotis lucifugus complex, My = Myotis yumanensis, Nh = Nycticeius humeralis, Ph = Parastrellus hesperus, Ps = Perimyotis subflavus, Tb = Tadarida brasiliensis.

Here, we advance the application of phylogenetic diffusion models to processes of host transitioning, and describe a flexible Bayesian statistical framework to reconstruct virus transmission between different host species while simultaneously testing and quantifying the contribution of multiple ecological and evolutionary drivers of both CST spillover and host shifting. For this purpose, we parametrize the infinitesimal rates of a stochastic discrete diffusion process as a GLM, and perform Bayesian model averaging over several potential predictors of viral dispersal among host species. To discriminate between dead-end infection and sustained transmission in the new recipient species, we extend the diffusion approach to allow for a different host transition process on external and internal branches. Because understanding viral distributions within host ranges is important for anticipating emergence and developing appropriate strategies for prevention [7,10], we use a separate GLM diffusion model to identify potential predictors of viral spread in geographical space.

Finally, we demonstrate how a Bayesian stochastic search variable selection (BSSVS) procedure is able to estimate the connectivity in terms of viral transmission among host species, whereas Markov jump counts quantify the transmission intensity along these connections. We compare these estimates to per capita CST rates represented in a transmission network [5], which were obtained by the pairwise population genetic estimation procedure.

2. Material and methods

(a). Genetic and epidemiological data

Host species, spatial locations and sampling collection year were annotated for 372 nucleoprotein gene sequences (nucleotide positions: 594–1353). This data comprised a total of 17 bat species sampled between 1997 and 2006 across 14 states in the United States [5]. Two additional species that had been excluded from the original analysis owing to a limited amount of available sequences, Myotis austroriparius (Ma) and Parastrellus hesperus (Ph), were now included. We also included a virus sequence with an unknown sampling date (accession no. TX5275), sampled in Texas from Lasiurus borealis, and estimate its sampling date [18].

For the predictors of CST, we considered phylogenetic distances between bat species, geographical range overlap, ecological similarities in roost structures, wing aspect ratio, wing loading capacity and similarities in body sizes (described in detail in Streicker et al. [5]). Geographic range overlap was estimated as the percentage of overlap between the geographical range occupied by the recipient and donor species. Wing aspect ratio is defined as the ratio of the length of the wing to the width of the wing. Wing loading capacity is defined as the weight of a bat species divided by the area of the wings (in units of kg m⁻²). To relate the overlap of roost structures among all species, a binary matrix was used.

To test different determinants of viral dispersal between localities, we considered three distinct predictors: great-circle distances between each pair of locations (taken as the centroid of the county where each bat species was found), the number of rabies virus cases in bats in each of the relevant US states during 2010 [19] (a crude proxy for population size in the absence of such numbers for each bat species) and the geographical area in square kilometres of each federate state.

(b). Generalized linear model diffusion and branch partitioning

We model CST spillover and host shifting in the rabies virus evolutionary history as a stochastic diffusion process among a set of discrete states (in this case, bat species) in a Bayesian framework. This approach uses a continuous-time Markov chain (CTMC) to model discrete outcomes as a continuous function of time in temporally calibrated phylogenetic trees and has been introduced for phylogeographic estimation in which case locations make up the discrete states [17]. In our host transition application, we can represent the Markov process as a directed graph of host states among which viruses are transmitted. The rates or intensities at which viruses transition among pairs of hosts are typically denoted as the ijth elements (Λ_ij) of a transition rate matrix Λ. Standard Bayesian inference under this model, including a parametrization that aims to infer a sparse transition matrix through Bayesian stochastic search variable selection (BSSVS) procedure, has been described in Lemey et al. [17].

To test predictors for the CTMC transition rates among pairs of hosts (Λ_ij), we use a recent extension of the phylogenetic diffusion model that parametrizes these rates as a log-linear function of an arbitrary number of predictors [20]. Briefly, this GLM specifies coefficients (β_i) for each predictor p_i, allowing the estimation of their contribution to the diffusion process, as well as (0,1)-indicator variables (δ_i) to model the inclusion or exclusion of each predictor, such that the following relationship holds:

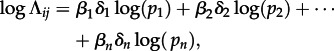2.1

for each Λ_ij and the n predictors.

By considering the potential contribution of all predictors simultaneously and jointly estimating both their importance (δ_i) and relative size (β_i), we efficiently perform Bayesian model averaging over all potential predictors for the discretized host transitioning process while simultaneously reconstructing this process. Lemey et al. [20] discuss a Metropolis–Hastings transition kernel for 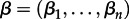that exploits the fixed correlation structure between predictors. We also refer to Drummond & Suchard [21] for a transition kernel on 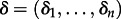. Based on the prior and posterior expectation for δ_i, which can be considered as the inclusion probability for a predictor p_i, the support for each predictor can be expressed as a Bayes factor (BF) [20].

Here, we extend the phylogenetic diffusion model, including the GLM parametrization, by allowing a different transition process on external (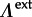) and internal (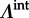) branches in order to discriminate between recent CSTs, many of which are likely to result in dead-end infections, and host shifts deeper in the evolutionary history that reflect successful onwards transmission in the new host species.

We follow standard phylogenetic practice in Bayesian inference by sharing evolutionary models among all branches throughout the evolutionary history, except for the GLM specific parameters (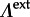 and 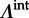), including the effect sizes ( 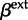and 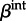) for the predictors and the indicator variables ( 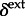and 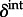) that determine the inclusion of these predictors.

All predictors were log transformed and standardized, except for the overlap of roost structures, which was coded as a vector of binary indicators for sharing or not sharing roost structures (see the electronic supplementary material). While the external/internal GLM branch partitioning (BP) was used to investigate predictors of CST and host shifts, we apply this partitioning simultaneously with a separate homogeneous GLM diffusion model [20] to investigate predictors of spatial diffusion.

(c). BEAST with BEAGLE inference

Discrete phylogenetic diffusion analyses were performed under an asymmetric diffusion model [22] using Markov chain Monte Carlo (MCMC) implemented in BEAST v. 1.7 [23]. Two chains of 2.5 × 10⁸ steps, sub-sampled every 50,000th generation were combined after discarding 10 per cent of the generations from each as burn-in. Analyses were performed under a general time reversible nucleotide substitution model, with 4Γ rate categories and a proportion I of invariant sites, and using a flexible Bayesian skyride demographic prior [24] and an uncorrelated lognormal-relaxed molecular clock [25]. A BSSVS procedure was used to identify significant pathways of host and spatial diffusion [17]. As a measure of statistical support for rates between discrete traits, e.g. host species or spatial locations, the BSSVS approach delivers a BF test by comparing the posterior with the prior odds that a particular rate is required to explain the diffusion process [17]. We follow standard terminology in BF interpretation [26], in which the strength of evidence for a particular rate is substantial when BF > 3, strong if BF > 10, very strong if BF > 30 and decisive if BF > 100. In addition to estimating support for diffusion pathways, we also used a robust counting procedure [12,27] to estimate the posterior expectations of the number of host transitions (Markov jumps) along the branches of the unknown tree [28]. Convergence of the MCMC output was inspected using Tracer and a maximum clade credibility (MCC) tree was summarized using TreeAnnotator and visualized using Figtree graphical user-interface (available at http://tree.bio.ed.ac.uk/). All analyses were performed using the BEAGLE library to enhance computation speed [29,30].

3. Results

(a). Determinants of cross-species transmission spillover and host shifts in the bat rabies virus evolutionary history

We analyse a heterochronous dataset comprising 372 nucleoprotein gene sequences sampled from 17 bat species using a full probabilistic model that encompasses components of timed sequence evolution, hosts transitioning and spatial dispersal. As an illustration of the former, our Bayesian inference procedure arrives at an estimate of the bat virus nucleoprotein gene evolutionary rate of 2.77 × 10⁻⁴ (95% Bayesian credible interval, BCI: 1.25 × 10⁻⁴ to 4.32 × 10⁻⁴) substitutions per site per year, and a most recent common ancestor of bat rabies in North America dated back to 1631 (95% BCI: 1353–1847; figure 1).

To identify the factors that determine CST spillover and its fate in the new host, we first adopted a recently developed GLM extension of a Bayesian phylogenetic diffusion model that has been introduced in a phylogeographic context [20]. Here, we refer to this as the ‘homogeneous GLM diffusion model’ and use this to simultaneously reconstruct host transition processes in the entire viral evolutionary history while identifying the variables that contribute significantly to this process. We follow Streicker et al. [5] and consider host genetic distance, geographical range overlap and similarities in roost structures, wing aspect ratio, wing loading and body size as potential predictors of the host diffusion process.

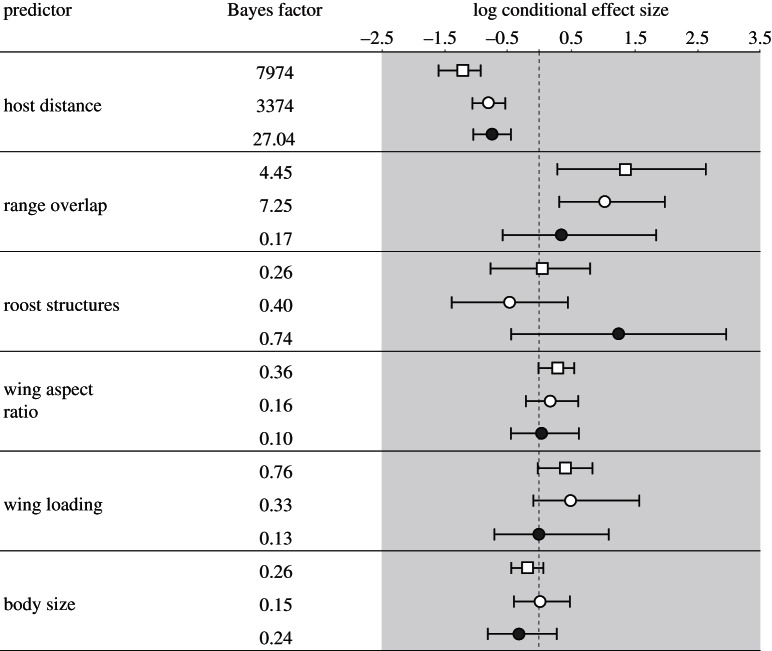
Figure 2 lists BF support for each predictor as well as the conditional effect sizes (cESs) on a log scale; the latter summarizes the coefficients conditional on the predictor being included in the GLM model (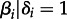). The negative conditional cES obtained using the homogeneous GLM diffusion model (open squares) for host distance (−1.21 (95% BCI: −1.64, −0.85)) imply that lower genetic distances between host species are predictive of higher rates of viral host jumping with a decisive statistical support (BF = 7974). Conversely, coefficients above zero indicate a positive correlation between the intensity of viral host jumping and the extent of geographical range overlap (ES = 1.03 (95% BCI: 0.28, 1.96)), albeit with only a modest support (BF = 4.45).

Figure 2.

Predictors of CST spillover and historical host shifts for bat rabies virus sampled in North America. For each potential predictor, the Bayes factor (BF) support and the conditional effect sizes (cESs) obtained using a homogeneous (squares) and a branch-partitioned GLM diffusion approach (circles) implemented in BEAST are shown (posterior mean and 95% Bayesian credible interval, BCI). The contribution of external (related to CST spillover) and internal (historical host shifts) branch substitution processes is shown separately using empty and filled circles, respectively. Note that the credible intervals for the cES of the predictors with BF above three exclude zero, which can be considered as an additional indication for its importance.

To further discriminate between recent CSTs and successfully established host shifts that reflect onwards transmission in the new host species, we extend the phylogenetic diffusion approach in BEAST to allow for a separate discrete diffusion process on both internal and external branches in the phylogeny. This BP allows the separation of recent CST, which likely represent evolutionary dead-ends in the new host species as expected from the typical short terminal branch length of such tips [5], from historical host shifts that occurred deeper in the evolutionary history.

The branch-partitioned GLM diffusion model reveals that genetic distance between hosts is a strong predictor for both CST spillover and historical host shifts (figure 2). This is corroborated by the decisive BF rates obtained for host genetic similarity using both the internal branch GLM (BF = 3374) and the external branch GLM (BF = 27.04). In the two cases, we also obtain cES estimates close to −1 (−0.82 (95% BCI: −1.14, −0.52) and −0.78 (95% BCI: −1.10, −0.40), respectively). For geographical range overlap, we obtain moderate support BF = 7.24) and a positive cES of 1.03 with credible intervals that exclude zero (0.28, 1.96) for the external branches. However, we did not find support for an impact of geographical range overlap in host shifting (BF = 0.16 and cES estimates of 0.29 (95% BCI: −0.63, 1.80)). Taken together, the results obtained using the branch-partitioned GLM diffusion model strongly support that the intensity of both recent CST and historical host shifts is predicted by host genetic similarity, and for recent CST this implies that merely establishing an infection of a single individual of a naïve host species may depend on its genetic relatedness to the donor bat species, even if this results in a dead-end infection. Moreover, our results also show that some degree of geographical range overlap is required for recent CST spillover, but it is not a significant predictor of established host shifts.

In agreement with previous findings [5], our analysis did not reveal a significant role for roost structures, wing aspect ratio, wing loading and body size, which represent ecological predictors in our GLM approach.

(b). Determinants of spatial dispersal

We further explore the application of a homogeneous GLM diffusion model [20] to identify possible predictors of viral dispersal among the 14 states in the US. This was done simultaneously with the host jump inference, and further illustrates the flexibility of our approach in incorporating different data types in a single probabilistic framework. Our results indicate a key role of spatial distance in viral spread between spatial localities (BF = 6516, with a cES of −1.14 (95% BCI: −1.43, −0.86); figure 3). This provides decisive support for the notion that viral dispersal occurs mostly between closely located regions rather than through long distance dispersal, despite the mobility of some bat species. Such knowledge may be useful to take into account in phylogeographic inferences that necessarily operate on sparse data. Furthermore, our analysis did not reveal evidence for the predictive role of the number of rabies cases or the geographical area of each of the US states considered.

Figure 3.

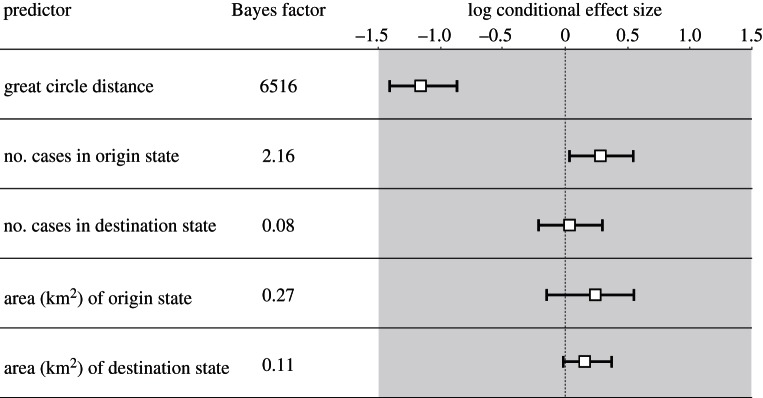
Determinants of geographical dispersal for bat rabies virus in North America. For each potential predictor, the BF support and the cES estimate obtained using a homogeneous GLM diffusion approach are shown (mean and 95% BCI).

(c). Transmission connectivity and magnitude of host transitioning

Based on a series of structured coalescent analyses of viral migration among pairs of host species, Streicker et al. [5] quantified per capita transmission rates and represented these in a ‘transmission web’ network. The species pairs considered for this network consisted of each combination of major bat host species associated with a viral lineage and the assumed recipient species in these lineages. Therefore, the connectivity only represents the CST dynamics implied within the host-associated lineages; the viral transmission along these connections is an estimated quantity obtained by genealogy-based population genetic inference.

Here, we first attempt to capture the connectivity among bat species using a BSSVS procedure under an asymmetric model of host diffusion [17]. In this case, the connectivity is estimated by identifying highly supported host transition rates without conditioning on the observation of host-associated lineages. This procedure considers the complete viral evolutionary history and not only the host pairs involved in CST.

Figure 4a shows the rates that were supported by a relatively strong BF support (BF > 10). The BSSVS procedure identifies support for a total of 19 host transition rates, whereas a total of 31 CST connections were implied by the transmission web in Streicker et al. [5]. Fifteen out of the 19 well-supported rates (80%) are represented by connections in the previously published transmission web. The four additional host-transitioning rates inferred with strong support by our approach (starred arrows in figure 4a) may reflect host jumps ancestral to the host-associated lineages or more subtle CST dynamics within those lineages. An example of the latter is the host transition rate from Lx to Ap species that is supported in our analysis by a BF of 28.5. A close inspection of our MCC tree shows that within the Lc-associated lineage, the discrete diffusion approach reconstructs a transmission from species Lc to Lx and then subsequently from Lx to Ap, instead of the transition from Lc to Ap inferred in the original analysis [5]. Similar scenarios can be identified for the other additional rates. Because Streicker et al. [5] considers the Lc species to be the major host associated with this lineage, and as a consequence, Lx and Ap to be recipient species within this lineage, transmission to potentially intermediate hosts as Lx are not represented by connections in the transmission web. The existence of such intermediate hosts is particularly plausible when the two spillover hosts are found in the same geographical region in the same time frame. This is the case for at least Lbl and Mc [5]. Another possible explanation is that local dynamics within the reservoir species lead to multiple CSTs, while by chance the reservoir host is not sampled and thus the two recent spillover hosts seem very closely related. Our connectivity inference does not question the assumptions of major host species being associated with different viral lineages, but simply demonstrates that CSTs additional to those from these major host species cannot always be excluded by the data.

Figure 4.

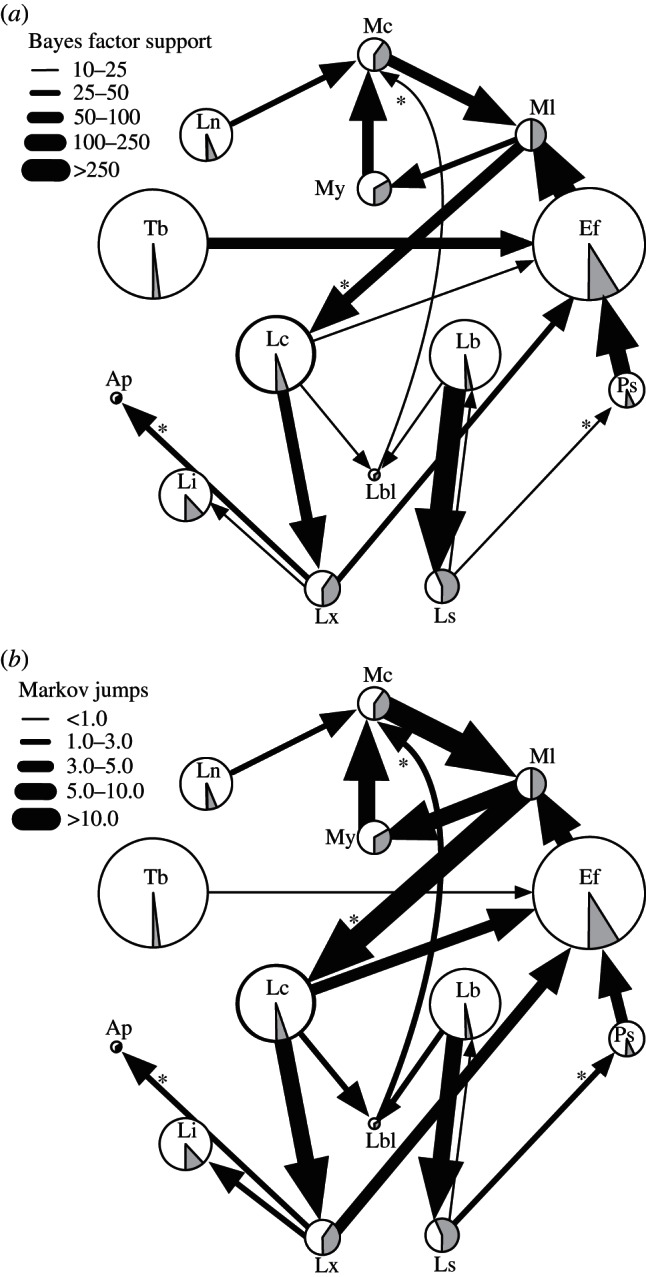
Connectivity and magnitude of host transitioning between bat species. In (a), the width of host transition rate reflects its statistical support in terms of BF. Only host transition rates supported by a strong BF > 10 and the species involved in these rates are shown. In (b), the width of the transitions between pairs of host species reflects the magnitude of the strongly supported transition rates. Rates inferred by our homogeneous BSSVS diffusion approach that are not represented by corresponding connections in Streicker et al. [5] are denoted with asterisks. Pie charts in grey show the observed proportion of each species infected by CST as implied within the host-associated lineages, and pie charts diameter is proportionate to the number-sampled bats as in the original transmission web [5]. The naming of the bat species is consistent with the legend of figure 1.

When the BF cut-off was lowered to a moderate support of 5, our connectivity approach identifies support for a total of 31 host transitioning rates, with 20 of these well-supported rates (65%) being represented in the CST transmission web [5]. The decrease in consistency with the previous CST transmission web [5] can be explained by the fact that a lower BF invokes many more uncertain rates that yield less convincing support for their involvement in CST, and also rates involved with ancestral host shifts may become more prominent under lower cut-offs.

While the BSSVS procedure delivers the statistical support for particular host transitions, it does not provide a quantification of the magnitude of these host transitions. For the latter, we use Markov jump estimations based on robust counting techniques [12,27,28] and summarize the expected number of jumps along the connectivity identified by BSSVS in figure 4b. It is interesting to note that not all the strongly supported BF rates actually correspond to a high magnitude in host transition rates. For example, while we obtain a very strong BF support of 97 for the host jump between Tb and Ef, we estimate only a mean of 1 Markov jump between these hosts. Conversely, we estimate 3 Markov jumps from Lc to Ef, but with a BF support of 12 for this connection.

4. Discussion

In this study, we present a flexible phylogenetic diffusion approach as an alternative to coalescent estimation for investigating CST and host switching based on viral genetic data. Phylogenetic diffusion models are now frequently being used for phylogeographic analyses [31], but also the inference of host jumping has become of interest [32,33]. The most important contribution of the current work is the extension of a GLM diffusion model that allows the inference of the discrete state transition history while simultaneously identifying the underlying predictors. The GLM diffusion model avoids post hoc statistical analyses of genetic estimates, which generally involves operating on mean estimates and ignores associated uncertainty that can be considerably large. The Bayesian inference approach enables model averaging over a number of potential diffusion predictors and estimates the support and contribution of each predictor while marginalizing over phylogenetic history. Our results based on a homogeneous GLM diffusion approach corroborate that host genetic distances and, at a lesser extent, geographical range overlap pose important constraints for rabies CST [5].

Importantly, we extend the phylogenetic diffusion approach to allow for different processes, in the form of different CTMC matrices, for different branch sets in the phylogeny. In the case of rabies transmission, we use this to separate out and test the determinants of host transitioning on both external and internal branches, which, respectively, reflect CST spillover and historical shifts among various bat hosts. We believe that the BP represents an important extension of the phylogenetic diffusion approach in order to distinguish two crucial stages in viral emergence. Whereas the determinants of CST had been scrutinized by estimating per capita rate estimates and subsequently testing these using a standard GLM approach, a similar test procedure was not available for ancestral host jumps [5].

However, external and internal BP only serves as an approximation to discriminate between CST and ancestral host jumps. Reassuringly, the rabies phylogeny is generally characterized by very short tips (figure 1), and Streicker et al. [5] showed that they were no more genetically divergent than donor lineage viruses. This suggested that external branches of the rabies phylogeny most likely represented dead-end infections than infections occurring within stuttering chains of transmission in the recipient species, that is, chains that will propagate for a few generations in the new host species before dying out. However, this does not formally rule out the possibility of stuttering chains along the external branches. Stuttering chains of human-to-human transmission of H5N1 avian influenza provide an example for this [34]. Importantly, host shifts at internal branches that are phylogenetically close to the external branches can also correspond to such stuttering chains of transmission. Thus, an absolute phylogenetic distinction in terms of the outcome of CST remains difficult. The external/internal BP essentially offers an operational prior distinction between jumps leading to generally ‘less’ and ‘more’ successful propagation in the new host. Further work may be aimed at methodology, perhaps in the form of mixture models, to provide better posterior classifications in terms of the outcome of host jumps in the phylogeny.

The observation that host genetic distances represent important constraints for both CST spillover and host shifts is not a stand-alone finding. The ability of sigma viruses to persist and replicate in Drosophila species has also been explained by the host phylogeny, with viral titres declining with increasing distance from the reservoir species [35]. For fungal pathogens infecting plants, a similar relation was found between phylogenetic distance between the plant host and the likelihood of infection [36]. More generally, the idea that phylogenetically similar species exchange viruses with higher probability of success has been well acknowledged in the field of pathogen emergence [3,37,38]. However, in very few cases has it been possible to isolate at which stage of a host shift such barriers may act. The strength of the current approach and Streicker et al. [5] is the ability to demonstrate phylogenetic barriers at two stages: emergence and establishment. Although the findings by Londgon et al. [35] in Drosophila sigma viruses are consistent with this scenario, the generality of this phenomenon remains to be investigated in other systems.

Our results also confirm that geographical range overlap is a modest, but non-negligible, predictor of CST spillover. For viral host jumps to result in onwards transmission to the recipient species, initial exposure of the new host species to the pathogen is required [2]. For example, ecological opportunity, determined by ecological changes driven by the process of economic development and land use, have previously been implicated as a determinant of successful CST from animal reservoir species to humans [3,39,40].

The fact that geographical range overlap is apparently not required to explain the host shift diffusion process could have many explanations. First, it may reflect the ability of some bat species to fly long distances during seasonal migrations [41]. However, our spatial analyses revealed that closer geographical distances are predictive of higher viral migration rates, suggesting that viral transmission occurs predominantly at a local scale. Although the BSSVS analysis identified support for viral migration between exceptionally distant spatial locations which could possibly be related with host migration (not shown), the finding that geographic distances and genetic distances are correlated has also been shown for fox and raccoon rabies virus [10,11]. Second, the currently observed range overlap for bat species may not have remained constant throughout bat rabies evolutionary history, which dates back several centuries for the current sample according to the divergence date estimates. Our estimates of the time of rabies evolutionary history in North America are in reasonable agreement with previous estimates [13,42], but even the estimates of a relatively longstanding rabies transmission dynamics may represent only a small part of the history of rabies in North America, because the common ancestor of modern viral strains does not necessarily extend back to the origin of the virus [43]. Third, there could be missing lineages in the tree (undiscovered viruses), and some inferred host shifts may actually have involved different donor species. Fourth, it is plausible that the relatively limited number of host shifts on internal branches yields less power to inform a GLM model applied to this branch set. Finally, and because the ranges of most bat species used for this analysis do overlap, it would be interesting to revisit the extent of range overlap as a predictor of CST and host shifts when larger datasets from other geographical locations become available.

In general, we cannot rule out the lack of power to explain lack of support for particular diffusion predictors, such as ecological predictors for CST (roost structures, wing aspect ratio, wing loading and body size). Phylogenetic diffusion models inevitably operate on sparse data, and whereas the GLM approach model generally has much fewer parameters than a standard diffusion model, it remains uncertain whether all factors contributing to the historical diffusion process can be inferred from the distribution of host or their locations at the tips of a phylogeny. In addition, sample sizes may affect the GLM parameter estimates and we cannot exclude that predictors other than the ones we specified might be involved with host transitioning or spatial dispersal. For example, spatial diffusion might be predicted by bat population sizes, but the number of rabies cases per state used in this study might be too crude a proxy for population size.

The summary of per capita transmission rates in the ‘transmission web’ differs in many aspects from our phylogenetic diffusion approach and a direct comparison is, therefore, difficult to make. Whereas the connectivity in the previously constructed transmission web is hypothesized based on the interpretation of CST within the host-associated lineages [5], our Bayesian phylogenetic diffusion approach attempts to estimate this connectivity, and because it considers the entire phylogenetic history, the connectivity estimate may also represent ancestral host jumps. In addition to measuring statistical support for host jumps between pairs of species, we also estimate the number of jumps along a set of strongly supported host transition pairs using robust counting techniques. A comparison of BF support for rates of diffusion (figure 4a) and posterior estimates of the number of jumps (figure 4b) indicates that high support for connectivity does not necessarily translate into a consistently high intensity of jumps. We note that this may also be important to bear in mind when interpreting phylogeographic applications of the discrete diffusion models and BSSVS, where a well-supported rate may for example be represented by only one migration event as long that is clearly evident from the data. The distinction between support and magnitude is one that we also make in our GLM model, through effect sizes and indicators, and can be important when predictors exist on different scales. As a quantification of the magnitude of host transitioning among only strongly supported rates, the robust counting procedure should produce estimates that are more comparable to the population genetic migration rates estimated by Streicker et al. [5]. In this respect, it is interesting to note that the three pairs of bat species exhibiting the highest number of host transitions (species Mc and Ml, Lc and Lx, and Lb and Ls), are consistent with the population genetic estimates [5]. We note, however, that population genetic estimates are more appropriate than phylogenetic transition estimates to approximate per capita CST rates, because the former adequately takes into account the ‘genetic size’ of the donor and recipient hosts of rabies transmission.

The work on rabies CST in North American bats species has recently been extended by an investigation of evolutionary rate shifts associated with ancestral host shifts [42]. Based on a phylogenetic analysis using the same Bayesian software in which we implemented our discrete diffusion models, Streicker et al. [42] demonstrate that rabies lineages associated with subtropical bat populations evolve nearly four times faster than those associated with temperate species. To find statistical evidence for this, the authors adopted hierarchical phylogenetic model (HPM) methodology [44] and incorporate fixed effects to allow to test differences in the evolutionary rate estimate for different groups of viral lineages (e.g., grouped according to host geography [42]). Although the fixed-effect HPM model and the discrete GLM-diffusion model are very different approaches, performing Bayesian estimation for these models relies on similar inference methodology, because the fixed effects in the HPM are also specified through coefficients that quantify the effect size and effect indicators that represent the inclusion probability or support.

5. Conclusion

In conclusion, the development and extension of a flexible approach to reconstruct discrete state transition processes while simultaneously identifying their determinants provides an useful framework to scrutinize CST and host shifts. The identification of risk factors that control or influence host transitioning may have important implications in the prediction, surveillance and control of new epidemic diseases [4]. We believe that the rabies example presented here makes a substantive contribution to this discussion.

Although we focused on multi-host reservoir dynamics of bat rabies virus, this approach is generally applicable to other pathogens and to other discrete state transition processes beyond spatial or host diffusion such as, for instances, viral diffusion between body organs and tissues. We hope that this framework will be useful to understand the key drivers of cross species dynamics for a broad range of zoonotic pathogens.