Uncovering epidemiological dynamics in heterogeneous host populations using phylogenetic methods

Abstract

Host population structure has a major influence on epidemiological dynamics. However, in particular for sexually transmitted diseases, quantitative data on population contact structure are hard to obtain. Here, we introduce a new method that quantifies host population structure based on phylogenetic trees, which are obtained from pathogen genetic sequence data. Our method is based on a maximum-likelihood framework and uses a multi-type branching process, under which each host is assigned to a type (subpopulation). In a simulation study, we show that our method produces accurate parameter estimates for phylogenetic trees in which each tip is assigned to a type, as well for phylogenetic trees in which the type of the tip is unknown. We apply the method to a Latvian HIV-1 dataset, quantifying the impact of the intravenous drug user epidemic on the heterosexual epidemic (known tip states), and identifying superspreader dynamics within the men-having-sex-with-men epidemic (unknown tip states).

1. Introduction

Epidemiological dynamics shape the genetic structure of measurably evolving populations such as RNA viruses. Increasing amounts of viral genetic sequence data together with novel statistical tools allow a better understanding of the epidemiological dynamics based on viral sequence data to be obtained. The general idea is to reconstruct the phylogeny of viral sequence data sampled from different infected hosts in an epidemic. The resulting phylogeny is a proxy for the transmission chain. This transmission chain is typically incomplete as often only a fraction of all infected individuals are sampled for any given epidemic. Characteristics of the phylogeny, identified using statistical methods, reveal epidemiological dynamics. For example, the basic reproductive number of hepatitis C virus [1], the geographical spread of influenza [2,3] and dengue [4], the interaction between transmission groups in HIV [5] or the dynamics of norovirus outbreaks [6] have been investigated.

Recently, new methods were introduced which in addition allow the quantification of transmission rates parametrized by standard epidemiological models [7–9]. The underlying models assume a homogeneous mixing population, implying that an average transmission rate for the whole population is estimated. However, in particular, for sexually transmitted diseases, we expect heterogeneous transmission dynamics owing to a heterogeneous contact structure. For example, it has been observed that in the Swiss HIV epidemic, the transmission group men-having-sex-with-men (MSM) maintain a subepidemic, whereas the heterosexuals (HETs) together with the intravenous drug users (IDUs) form transmission clusters [5]. In that study, the tips of a phylogenetic tree were labelled with the corresponding transmission group (MSM, HET, IDU), and the transmission group composition of large clusters was investigated. A further study of population structure in the Swiss HIV epidemic [10] showed a significant amount of structure also within these two subepidemics, MSMs and HETs/IDUs. This result was obtained by comparing phylogenetic trees that were simulated assuming a homogeneous mixing population to phylogenetic trees assuming a structured population. The comparison revealed that phylogenetic trees from a structured population are significantly less balanced than phylogenetic trees from a homogeneous mixing population. The empirical HIV trees were found to be more similar to simulated trees from a structured population than to trees from a homogeneous mixing population.

Here, we develop a method that allows quantification of the transmission dynamics in structured populations. Our method is based on a multi-type birth–death branching (MTBD) process. Under such a process, each individual is characterized by a type, and gives rise to secondary infections with type-dependent transmission rates. Furthermore, each type has its characteristic death or recovery rate. We derive a set of differential equations for the likelihood of the MTBD parameters given a phylogeny under the MTBD process. The likelihood is evaluated by solving the differential equations numerically.

Our maximum-likelihood method allows estimation of the type-dependent epidemiological parameters based on phylogenetic trees in which each tip is assigned to a type. In a second step, this method is extended to identify and quantify heterogeneous transmission patterns from trees in which the tips are not assigned a priori to types.

We first demonstrate the performance of our method in a simulation study. We then illustrate the method on a Latvian HIV dataset [11,12]. Focusing on the subtype A epidemic among HETs and IDUs, we assign the tips to the corresponding transmission group, and quantify the direction and amount of mixing between the two transmission groups. By focusing on the subtype B epidemic among MSMs, we use the method to detect evidence for superspreaders. Because we do not know a priori whether or not an individual is a superspreader, we analyse the observed phylogenetic tree without assigning types to the tips of the tree. The simulation procedures are available in the R package TreeSim [13], and the likelihood inference method is available in the R package TreePar [14].

2. Methods

(a). The multi-type birth–death branching model

The MTBD process generalizes a constant rate birth–death process as a model for transmission [8,15]. Under the MTBD-m process, each individual has a unique state out of m possible states . The process starts with a single individual in one of the m possible states, where the initial state might be chosen according to different rules (e.g. fixed state, or each state is equally likely, or the state is picked from an equilibrium distribution, see below). Through time, each individual in state i gives birth (transmission) to an individual in state j with rate λ_i,j. Each individual dies with a rate d_i. Upon death, the individual may be sampled with probability s_i. The process is stopped after time t₀. In summary, the parameters of the model are

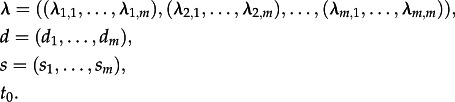The MTBD-m process gives rise to a tree with sampled and non-sampled individuals. The tree spanning only the sampled individuals is called the sampled tree (figure 1). In the sampled tree, the states of the tips are recorded, whereas all ancestral states are omitted.

Figure 1.

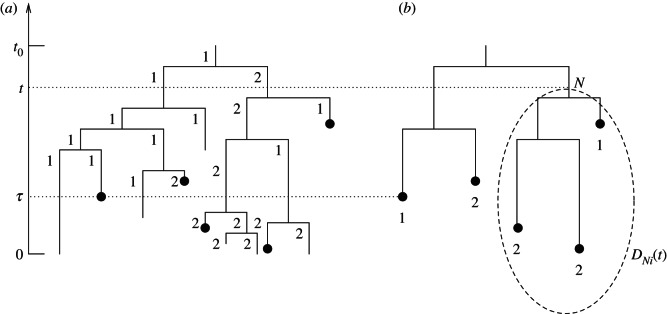
The MTBD model trees. (a) Complete transmission tree induced by the MTBD-2 model, the black dots correspond to sampled individuals. (b) Sampled tree obtained by pruning all non-sampled tips from the complete tree. Note that in the sampled tree, we record only the state of the tips, but not the state of the ancestral lineages (as in the data, we also know only the states of sampled individuals). When calculating the likelihood for a sampled tree, we calculate D_Ni(t) along the tree, where D_Ni(t) is the probability density that an individual N at time t in state i produces the observed sampled tree (here indicated with the dashed oval). The initial values for D_Ni(t) are calculated at the tip times, here the left tip was sampled at time τ.

In the epidemiological context, a state might be a transmission group, birth corresponds to a transmission event, and death is ‘becoming-non-infectious’ (which might be due to host death, recovery, behaviour change or successful treatment). Sampling corresponds to the infected individual being enrolled into the study such that the pathogen sequence data can be used to infer a sampled tree using phylogenetic methods. In the sampled tree, we typically have information about the states of the sampled tips, but no information about ancestral tips.

(b). Basic reproductive number of the MTBD-m model

The basic reproductive number R₀ is defined as the expected number of secondary infections caused by a single infected individual [16]. Clearly, if R₀ > 1, then the epidemic may spread, whereas R₀ < 1 causes the epidemic to die out.

The probability that an individual in state i infects k individuals during its lifespan is

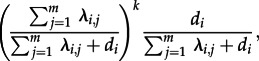which is a geometric distribution. The expected number of infections caused by an individual in state i is

Note that an individual may cause in expectation more than one secondary infection but the epidemic will nevertheless die out: for example, with m = 2, we may have 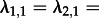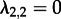and 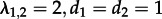, meaning an individual in state 1 infects on average two individuals (of state 2), but because individuals in state 2 cannot transmit, the epidemic will die out.

In fact, for calculating R₀, we need to consider f_i, the fraction of individuals in state i when the process is in equilibrium (i.e. the proportions of the different states do not change; an expression for f_i is provided in the electronic supplementary material, equation (S2) for the case m = 2). We obtain the basic reproductive number of the process (Keeling & Rohani [17]),

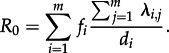2.1

We will compare the basic reproductive number of the MTBD-m process to the basic reproductive number assuming the states are isolated (i.e. λ_i,j = 0 iff i≠j),

(c). Calculating the likelihood given a tree

Our goal in this section is to calculate the probability density of a sampled tree given the parameters λ,d,s,t₀, i.e. we want to calculate the likelihood of the parameters given the data (sampled tree). For the calculation of the likelihood, we use ideas developed by Maddison [18].

We define time at present to be 0 and time to be increasing going into the past, i.e. we measure the time between today and an ancestral event. For an arbitrary edge N of the sampled tree, we define the probability density D_Ni(t) as follows. Let the individual being represented by edge N at time t to be in state i. D_Ni(t) is the probability density that this individual evolved between time t and the present as the sampled tree (figure 1). We note that D_Ni(t₀) is the probability density of the sampled tree with the initial individual being in state i. In order to calculate D_Ni(t₀), we additionally require E_i(t), the probability that an individual in state i (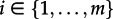) is not sampled and has no sampled descendants after time t.

(i). Calculating D_Ni(t)

We calculate D_Ni(t) backwards in time, starting at the leaves of the sampled tree. Consider a leaf of the sampled tree in state j, having been sampled at time τ in the past (figure 1). An individual at time τ in state i produces the tree as observed (i.e. a sampled leaf in state j) if j = i and the individual at time τ is sampled instantaneously. Recall that sampling occurs with probability s_i directly after becoming-non-infectious with rate d_i. Thus,

2.2

Now, we derive a system of differential equations for D_Ni(t) for t > τ. Based on D_Ni(t), we calculate 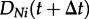, where Δt is a very small time step. Along edge N during time step Δt, either no event happens or birth events happen:

For , we obtain

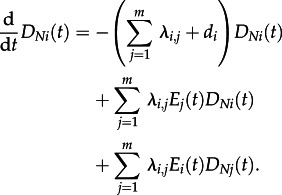This differential equation will be used to obtain the quantity D_Ni(t₀). However, in order to solve this differential equation, we need an expression for E_i(t), which is derived in the following section.

(ii). Calculating E_i(t)

In this section, we derive a differential equation for E_i(t). An individual, at time t = 0, is not sampled (otherwise, the individual would have become non-infectious and thus been removed), i.e. we have for ,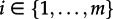

2.4

We derive differential equations for E_i(t) analogous to above. Suppose that for time t, we obtained the probability E_i(t). Then,

For , we obtain

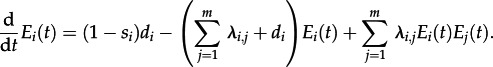2.5

Solving the differential equations for E_i(t) (equation (2.5)) and D_Ni(t) (equation (2.3)) with the initial values given in equations (2.4) and (2.2) allows us to calculate D_Ni(t) along an edge N. Section 2c(iii) explains how to proceed at the branching events in the sampled tree.

(iii). Pruning two subtrees

We now calculate the probability of obtaining the two subtrees descending from the bifurcation event A at time t in state i, D_Ai(t). Let the two edges descending from A be N,M. We have two scenarios, either the individual corresponding to N has given birth (i.e. transmitted) to the individual corresponding to M or the individual corresponding to M has given birth to the individual corresponding to N. Therefore,

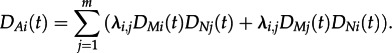2.6

(iv). At the root

Solving the differential equations and pruning the subtrees going backwards in time until time t₀ (the origin of the process and thus of the sampled tree) yields the probability density of the sampled tree given the root is in state i, D_Ni(t₀) for 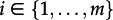. It was shown that rate estimates are more accurate if the initial individual at time t₀ is conditioned to give rise to at least one sampled individual [19]. This conditioning makes intuitive sense: in all analyses, we neglect non-sampled transmission chains, thus we should calculate the likelihood given we have a sampled chain. Thus, we divide the tree probability densities by the probability of obtaining at least one sample: .

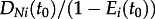Overall, the probability density of a tree with the first individual at time t₀ and conditioned on observing at least one sampled individual is, with f_i being the probability that an individual at time t₀ is in state i,

2.7

It remains to specify a distribution for f_i. We could assume that f_i = 1/m for 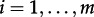. However, if we assume that the relative number of individuals in each state reached the equilibrium, we can use the equilibrium frequency for each state, which is calculated in the electronic supplementary material for the MTBD-2 model (see the electronic supplementary material, equation (S2)). Note that 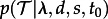is the likelihood of the parameters given the data (i.e. the sampled tree), meaning this function is used for parameter inference.

In the electronic supplementary material, we further show that equation (2.7) for the MTBD-1 process is equivalent to the equations derived for the constant rate birth–death process (which is the MTBD-1 process) [8,15].

(d). Unknown states

Until now, we have assumed that we know the state of each sampled individual. For a sampled tree where not all states of the sampled individuals are known, we can use the framework provided in this section for the unknown states.

Furthermore, with the framework in this section, we can investigate scenarios under which we do not know the state of any of the sampled individuals. Having no knowledge about states is for example the case when considering sexually transmitted diseases with the two states being ‘regular’ individuals and superspreaders (i.e. individuals who transmit the disease much more rapidly than regular individuals).

For obtaining the probabilities D_Ni(t) for a sampled tree with unknown tip states, we have to change the initial conditions of D_Ni(τ) for the tips with unknown states: the rate of an individual in state i to be sampled instantaneously at time τ is s_id_i, which leads to the initial condition for all i,

It is easy to check that the differential equations for D_Ni(t) (equation (2.3)) remain unchanged. For E_i(t), the initial conditions (equation (2.4)) and the differential equation (equation (2.5)) remain the same.

(e). Model extensions

The framework introduced earlier can easily be generalized in a number of different directions to accommodate particular properties of the various infectious diseases and datasets. We briefly discuss two extensions.

(i). State change of an individual

We can extend the MTBD-m model such that additional to the events transmission, death and sampling, each individual may change from state i to state j with rate γ_i,j. Thus, we have m²−m additional parameters,

with γ_i,i = 0 for 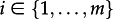. Changing states might for example be due to migration between geographical locations, or due to change of infection state (e.g. acute versus chronic infection; drug-sensitive versus drug-resistant infection).

The initial conditions for D and E remain as above (equations (2.2) and (2.4)). The differential equations are modified to:

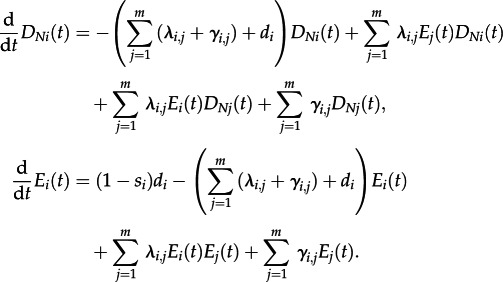The equilibrium frequencies are provided under the extended MTBD-2 model in the electronic supplementary material.

(ii). Contemporaneous sampling

In some circumstances, individuals may be preferentially sampled today, meaning that an individual in state i at present (time 0) is sampled with probability ρ_i. Compared with above, only the initial values change. For a tip in state j sampled at present, we have

Further,

Parameter combinations ψ = 0 and ρ > 0 (i.e. only sampling of contemporaneous individuals) correspond to models introduced for species phylogenies: Maddison [18], FitzJohn et al. [20] for λ_i,j = 0 iff i ≠ j, and γ ≥ 0; Magnuson-Ford & Otto [21], Goldberg & Igić [22] for general λ and γ. Note that for ψ = 0 and ρ = 1, E_i(t) is the probability of an individual giving rise to no extant individuals after time t, i.e. the probability of clade extinction.

(f). Parameter estimation

Calculating the likelihood of the MTBD-2 parameters given a sampled tree based on equation (2.7) is implemented in the R package TreePar [14], assuming an MTBD-2 model. Finding the maximum-likelihood parameters is done using the optimization function optim in R (with maxit = 10 000, others default).

For the MTBD-1 process, the three parameters λ, d and s are non-identifiable, and only two of the three parameters can be estimated: when conditioning the process on survival, the likelihood depends only on λ−d and λds while a third parameter is free to vary [23]. Thus, we fix s throughout (the probability of an individual being sampled when becoming non-infectious). We fix s (rather than any other parameter), because for this parameter, we can get a priori information based on the individual cohort studies from which the considered data is taken. We emphasize that we could not generalize the MTBD-1 result towards stating all parameter correlations in an MTBD-m process analytically.

(g). Simulation study

We implemented a forward-in-time simulation algorithm available in the R package TreeSim [13] in order to obtain sampled trees. We stop the simulation algorithm once a fixed number of sampled individuals is obtained (but one could easily implement other stopping criteria such as the age of the tree). We performed a number of different simulations in order to investigate the accuracy and power of the method. Always, the first individual was assumed to be in a random state taken from the equilibrium distribution; for each parameter combination we simulated 100 sampled trees.

We present the results for simulated trees with 200 tips and a sampling probability of 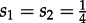in the main text. In order to further investigate the impact of sampling probability and tree size, we modified this setting by simulating trees using s₁ = s₂ = 0.05 and 200 tips as well as s₁ = s₂ = 0.05 and 50 tips (see the electronic supplementary material).

We asked the following three questions:

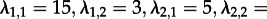
• — Can we accurately estimate λ and d? We simulated sampled trees using parameters 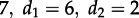and re-estimated the maximum-likelihood parameters assuming an MTBD-2 model and known tip states.

• — Can we distinguish a heterogeneous population from a homogeneous population? We re-estimated parameters based on the trees with tip states from the previous paragraph), assuming that an individual in any state i infects an individual in state j with the same rate λ_i,j (i.e. state-independent rate) and that all individuals die at the same rate. In the case of two states, we thus have 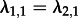, 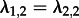and d₁ = d₂. Note that 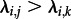accounts for a larger host population j than k, whereas all individuals transmit and become non-infectious under the same dynamics ( 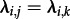would furthermore enforce the same size of population j and k, which may rarely be the case). We performed likelihood ratio tests to investigate how often the model with identical states is correctly rejected.

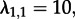
  Vice versa, we simulated 100 trees with 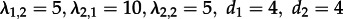, i.e. a scenario where both states are identical as each individual gives rise to a secondary infection with rate 15 and becomes non-infectious with rate 4 (note though that the state-1 population is twice as large as the state-2 population). Again, we re-estimated parameters under non-identical and identical states. We performed likelihood ratio tests to investigate how often the model with identical states is accurately not rejected.

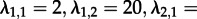
• — Can we identify superspreader dynamics? We simulated sampled trees using parameters 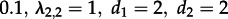. We re-estimated maximum-likelihood parameters assuming an MTBD-1 model as well as an MTBD-2 model. We did not use the tip states for the re-estimation but assumed that the states are unknown (§2d). Vice versa, we simulated trees under MTBD-1 (λ = 4, d = 2) and re-estimated the parameters assuming MTBD-1 as well as MTBD-2. Note that in contrast to the simulations in the previous paragraph, we can simulate under MTBD-1 directly and then analyse under MTBD-2, as we neglect the states in this analysis for both models. In all of these analyses, we fixed the death rate (arguing that in that respect all individuals are alike) as well as constraint .

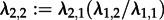  We point out that our parameter choice indeed reflects a superspreader scenario: individuals in state 1 have an x (here 20) times higher transmission rate than individuals in state 2 (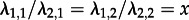). Furthermore, the population consists of y (here 10) times more ‘regular’ spreaders than superspreaders (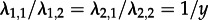). These superspreader parameters yield 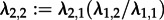which we fix in the inference. Furthermore, these constraints yield the fraction of superspreaders in the population at equilibrium which is #S/(#S + y × #S) = λ_1,1/(λ_1,1 + λ_1,2), where #S is defined as the number of superspreaders in the population. Equivalently, the fraction of superspreaders can also be established using the electronic supplementary material, equation (S2)), which simplifies to .

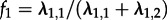Based on our parameter choices, a superspreader infects on average 11 and a ‘regular’ individual infects on average 0.55 individuals (i.e. the ‘regular’ individuals could not maintain an epidemic). Because 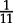of the population is superspreaders, the average R₀ is 1.5.

(h). Empirical study: Latvian HIV

We analysed a previously published dataset from the Latvian HIV-1 epidemic [11,12], using the MTBD-2 model. We obtained from Balode et al. [12] the alignment of HIV subtype A sequences both from the p17 and the V3 region (229 and 235 sequences). Furthermore, we obtained the alignment of HIV subtype B sequences from the V3 region (65 sequences). The obtained subtype B p17 sequences (n = 63) were unaligned. We aligned them using MAFFT [24], excluding sites 340–435 as this region contained many insertions and deletions. One sequence was excluded as it contained only gaps beyond site 435.

Previously, three independent transmission clusters were identified in the subtype B dataset [12]. We focused on the largest MSM transmission cluster (39 sequences for p17 and 40 sequences for V3).

We obtained posterior distributions of phylogenetic trees based on the four alignments using BEAST [25]. We chose a 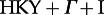substitution model with estimated base frequencies. The sites were partitioned into codon positions 1 + 2 and 3. Rate heterogeneity across branches was accounted for by a lognormal-relaxed clock (uncorrelated). We used the coalescent skyline plot (with 10 categories) as a prior on trees, as this prior does not enforce us to assume a particular population size change, such as exponential growth. An additional prior for the root age was applied to the B-p17 dataset, as otherwise the root was estimated far too old: we assumed a normal distribution with mean of 18 years and s.d. 2.5, truncated at the time of the oldest sample (7 years prior to the youngest sample that was collected in 2005, i.e. the ‘present’) and 29 years prior to the youngest sample. We ran the chain for 10⁸ steps (subtype B), and 10⁹ steps (subtype A) and excluded 10 per cent as burn-in. The four analyses converged with sufficiently high effective sampling sizes (several hundreds for all parameters, smallest was 160). In all four posterior tree sets, we analysed 90 trees from the posterior (i.e. every millionth tree for subtype B and every 10 millionth tree for subtype A).

The subtype A dataset was used to investigate the contribution of HETs and IDUs to the subtype A epidemic. As only eight sequences of A-p17 and seven sequences of A-V3 were not HET or IDU, we excluded them, yielding trees of size 221 and 228. Tips with unknown status were kept as these tips most likely are of unknown states as they either belong to HETs or IDUs. The subtype B dataset represents an MSM cluster, and we omitted tips with unknown states as they might be non-MSM, yielding trees with 36 tips for p17 as well as for V3.

Using our new implementation in TreePar [14], we fitted the MTBD-2 model to the subtype A trees with HET being state 1 (denoted by H in the following), and IDU being state 2 (denoted by I in the following). Because it is assumed that HETs are sampled more frequently than IDUs [12], we analysed the dataset for s_H = 0.1 and s_I = 0.01. To investigate sensitivity of the analysis towards that setting, we additionally analysed the dataset for s_H = s_I = 0.1 and s_H = s_I = 0.01.

For analysis of the subtype B datasets, we assigned state 1 to a superspreader (denoted by S in the following) and state 2 to a normal spreader (denoted by N in the following). We emphasize that we do not know the state of any of the tips, but we estimated the transmission dynamics associated with the two states, acknowledging that tip states are unknown. We assumed no difference in the sampling intensity of the normal spreaders and superspreaders, and thus we analysed the datasets for s_S = s_N = 0.1 and s_S = s_N = 0.01.

3. Results

(a). Simulation study

(i). Can we accurately estimate λ and d?

The analysis of the 100 trees simulated under scenario 1 yields accurate maximum-likelihood parameter estimates (table 1 and electronic supplementary material, tables S1 and S2).

Table 1.

Maximum-likelihood parameter estimates obtained from 100 simulated trees with 200 sampled tips (sampling probability s₁ = s₂ = 0.25). Upper part (a) shows parameter estimates under MTBD-2, lower part (b) assumes state-independent transmission. Sixty trees correctly reject the state-independent transmission model in favour of the MTBD-2 model (at the 0.8 level). Eighty-four trees correctly accept the state-independent transmission model over the MTBD-2 model (at the 0.8 level).

		true	median	2.5%	97.5%	true	median	2.5%	97.5%
(a)	λ1,1	15.00	15.29	8.56	16.50	10.00	10.36	0.00	14.13
	λ1,2	3.00	2.89	0.75	12.49	5.00	4.13	0.19	12.55
	λ2,1	5.00	4.22	0	20.97	10.00	8.09	0	25.33
	λ2,2	7.00	6.49	0	10.42	5.00	5.80	0	13.10
	d1	6.00	5.73	3.85	15.36	4.00	3.88	2.56	11.26
	d2	2.00	2.31	0.69	10.60	4.00	4.06	1.45	20.87
(b)	λ1,1 = λ2,1		14.07	12.71	15.53	10.00	9.97	8.88	11.28
	λ2,2 = λ1,2		2.19	1.28	3.30	5.00	5.05	4.06	6.04
	d1 = d2		4.99	3.73	6.07	4.00	3.97	3.15	4.89

(ii). Can we distinguish between 1 and 2 states?

In 60 per cent of the trees simulated under the MTBD-2 process, we correctly rejected state-independent transmission in favour of state-dependent transmission when performing a likelihood ratio test, using the χ²-distribution as approximation of the test statistic at the 0.8 level. In 84 per cent of the trees simulated under the MTBD-1 process, we correctly accepted state-independent transmission over state-dependent transmission (0.8 level). For the individual parameter estimates, see the table 1. For further parameter combinations, see the electronic supplementary material, tables S1 and S2.

(iii). Can we identify superspreader dynamics?

We analysed the trees simulated under our superspreader parameters, treating all states as unknown (as typically we have no information whether an individual is a superspreader or not). Again, the parameter estimates were very accurate (table 2 and electronic supplementary material, tables S3 and S4). Furthermore, statistical power for choosing the correct model was very high for the chosen parameters in the main analysis (table 2). In 100 per cent of the simulated trees, we correctly rejected homogeneous mixing in favour of superspreader dynamics (0.8 level). In 83 per cent of the simulated trees, we correctly accepted homogeneous mixing over superspreader dynamics (0.8 level).

Table 2.

Maximum-likelihood parameter estimates obtained from 100 simulated trees with 200 sampled tips (sampling probability s₁ = s₂ = 0.25). The states are assumed to be unknown (superspreader scenario). Upper part (a) shows parameter estimates under MTBD-2, lower part (b) assumes state-independent transmission. One hundred trees correctly reject the MTBD-1 model in favour of the MTBD-2 model (at the 0.8 level). Eighty-three trees correctly accept the MTBD-1 model over the MTBD-2 model (at the 0.8 level).

		true	median	2.5%	97.5%	true	median	2.5%	97.5%
(a)	λ1,1	2.00	2.11	1.60	2.62		1.59	0.01	3.10
	λ1,2	20.00	19.79	14.08	26.37		1.73	0.25	18.00
	λ2,1	0.10	0.10	0.05	0.19		0.88	0.00	2.82
	λ2,2	1.00	1.02	0.49	1.63		1.52	0.00	2.85
	d1 = d2	2.00	1.93	1.53	2.35		1.95	1.63	2.38
(b)	λ		3.93	3.31	4.76	3.00	3.02	2.75	3.31
	d		2.80	2.39	3.19	2.00	1.96	1.71	2.24

Obviously, the acceptance/rejection percentages and the accuracy of estimates depend on the choice of parameters for the simulated trees, and should therefore be regarded as examples showing that the method works in general. We chose these parameters in a range that should be realistic for epidemic dynamics. Below, we present further simulation results based on the parameter estimates obtained from the empirical data.

(b). Empirical study: Latvian HIV

(i). Subtype A: dynamics of the HET/IDU epidemic

The analyses of the subtype A trees yield the same parameter estimates if considering the V3 region or the p17 region (figure 2). All 90 trees rejected the simpler model in favour of the MTBD model at the 0.8 level. IDUs are estimated to have a significantly higher transmission rate than HETs, and in fact while IDUs transmit to HETs (median 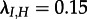), transmission from HET to IDU appears to be negligible (median ).

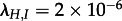Figure 2.

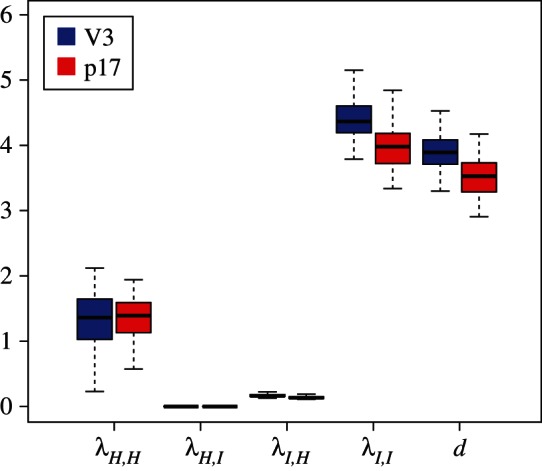
Transmission rate estimates for the Latvian subtype A dataset for s_H = 0.1, s_I = 0.01. (Online version in colour.)

Based on the estimates for λ and d, we calculated the median basic reproductive number R₀ = 1.13 using equation (2.1). For HETs, in isolation from IDUs, we estimate a median 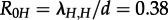which is significantly lower than 1, meaning the HET epidemic would die out without the IDUs. For IDUs in isolation, we estimated a median 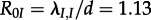which is also equal to the overall R₀ estimate (figure 3).

Figure 3.

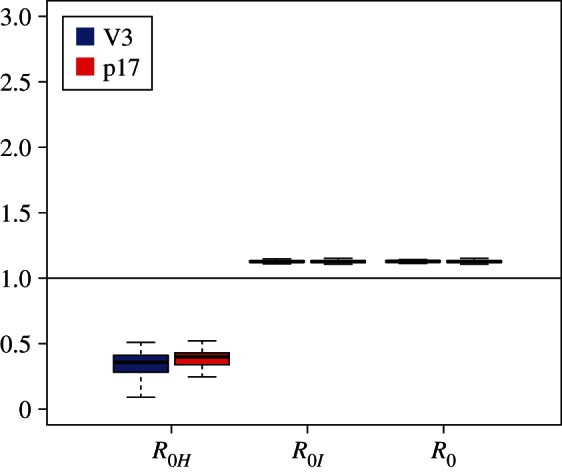
R₀ estimates for the Latvian subtype A dataset for s_H = 0.1, s_I = 0.01. (Online version in colour.)

By using equation (S2) in the electronic supplementary material, we predict about 5.1 per cent of this HIV epidemic to be HET (median based on V3 is 5.2 per cent, median based on p17 is 5.0 per cent). However, owing to the assumption of more sampling in HETs (10% versus 1% for IDUs), we expect a fraction of 0.51/(0.51 + 0.949) = 0.35 of our samples to be HETs. In fact our p17 dataset consisted of 65 HETs and 131 IDUs meaning 33 per cent are HETs (the remaining 25 individuals were of unknown state). The V3 dataset consisted of 68 HETs and 131 IDUs meaning 34 per cent are HETs (29 individuals were of unknown state).

The above results were all obtained assuming s_H = 0.1, s_I = 0.01, accounting for the intensified sampling of the HET population. Figures S1–S4 in the electronic supplementary material show the results for s_H = s_I = 0.1 and s_H = s_I = 0.01. The results are qualitatively equivalent to above.

In a further analysis, we considered again s_H = 0.1,s_I = 0.01, but allowed d_H to be different from d_I. The results are shown in the electronic supplementary material, figure S5. We note that we obtain a d_H that is close to zero while d_I is rather high, and such a general model is favoured over equal death rates when doing a likelihood ratio test. Only if 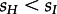, we estimate d_I and d_H to be of similar magnitude (see the electronic supplementary material, figure S6 for s_H = 0.01, s_I = 0.1). We found no evidence from other data sources that 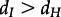. However, we found evidence for 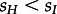being implausible [12]: the Latvian HIV-1 subtype A epidemic is dominated by IDUs, and thus HETs were sampled with more effort than IDUs as otherwise almost only IDUs would be sampled. As the general model yields implausible results or requires implausible assumptions, we focused our analysis assuming d_I = d_H . A reason for the statistical support of the general model may be the poor performance of model selection in some parts of parameter space, also see below.

Finally, we investigated how the method performs when analysing the subtype A trees using an MTBD-2 model, but not assigning the states (i.e. HET or IDU) to the tips. We assumed that type 1 is sampled with s₁ = 0.1 and type 2 is sampled with s₂ = 0.01. Three parameters are being estimated similar to the analysis when the tip states are known (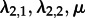) (see the electronic supplementary material, figure S7). The other two parameters 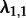and 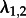are different. These two parameters turn out to be hard to estimate accurately, in general, as revealed by the following simulations.

In the simulation study, we investigated the accuracy and power of our method for general parameter combinations. In order to investigate the performance of our method for the parameter range suggested by the subtype A dataset, we simulated and re-analysed trees using the median parameter estimates under 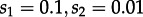(figure 1).

Table 3 shows the parameter estimates. 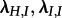and d are estimated very accurately, whereas 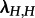and 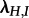have large confidence intervals. At the 0.8 level, 92 per cent of the trees correctly reject the simple model in favour of the MTBD-2 model, whereas only 22 per cent correctly accept the state-independent transmission model (if increasing the level to 0.9999, we obtain 27 and 79 instead of 22 and 92). We note that the power in model selection is significantly worse for this parameter choice than for the parameters used in the simulation study (tables 1 and 2).

Table 3.

Maximum-likelihood parameter estimates obtained from 100 simulated trees with 200 sampled tips (sampling probability s₁ = 0.1 and s₂ = 0.01). The parameters λ and d are the median estimates from the Latvian subtype A data analysis. Upper part (a) shows parameter estimates under MTBD-2, lower part (b) assumes state-independent transmission. Ninety-two trees correctly reject the state-independent transmission model in favour of the MTBD-2 model (at the 0.8 level). Twenty-two trees correctly accept the state-independent transmission model over the MTBD-2 model (at the 0.8 level).

		true	median	2.5%	97.5%	true	median	2.5%	97.5%
(a)	λ1,1	1.38	0.53	0.01	1.78	0.20	0.35	0.00	1.31
	λ1,2	0	4.07	0	5.93	3.96	4.13	0.68	7.81
	λ2,1	0.15	0.20	0.12	0.31	0.20	0.20	0.13	0.28
	λ2,2	4.17	4.04	3.29	4.68	3.96	3.94	3.36	4.53
	d1 = d2	3.71	3.75	3.19	4.33	3.70	3.68	3.26	4.30
(b)	λ1,1 = λ2,1		0.21	0.17	0.27	0.20	0.20	0.15	0.26
	λ2,2 = λ1,2		3.91	3.36	4.41	3.96	3.87	3.54	4.41
	d1 = d2		3.68	3.14	4.16	3.70	3.62	3.25	4.09

While having rejected the simple model on all 90 HIV-A trees based on V3 as well as p17 suggesting some support for the MTBD-2 model, the high type-1 error revealed by simulations does not allow us to draw a final, statistically well-supported conclusion.

(ii). Subtype B: superspreading in MSMs

Again, the analyses of the subtype B trees yield the same parameter estimates for the V3 region and the p17 region (figure 4). When considering the V3 (resp. p17) region, 63 per cent (resp. 78%) of the trees reject homogeneous mixing in favour of superspreader dynamics. The parameter estimates show significantly higher transmission rates for superspreaders, on average 9 (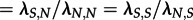) times as high as normal spreaders, whereas normal spreaders are about 17 () times as frequent as superspreaders (figure 5).

Figure 4.

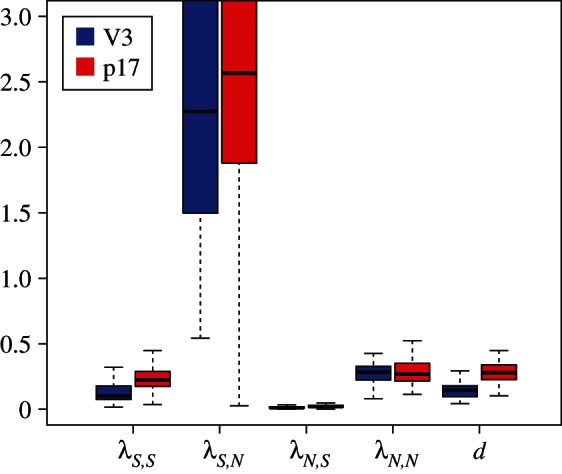
Transmission rate estimates for the Latvian subtype B dataset for s_S = 0.1, s_N = 0.1. (Online version in colour.)

Figure 5.

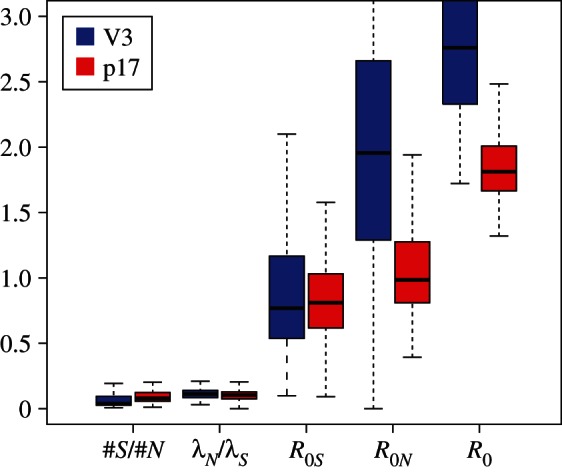
R₀ estimates for the Latvian subtype B dataset for s_S = 0.1, s_N = 0.1. (Online version in colour.)

The R₀ estimates for superspreaders and normal spreaders are largely overlapping (figure 5). Important to note is that owing to the interaction between groups, the overall R₀ is significantly higher than if the two populations were separated.

The results were obtained assuming s_S = s_N = 0.1. Results are comparable when assuming s_S = s_N = 0.1 (see the electronic supplementary material, figures S8 and S9).

In the simulation study, we investigated the accuracy and power of our method for general parameter combinations. In order to investigate the performance of our method for the parameter range suggested by the subtype B dataset, we simulated and re-analysed trees using the estimated median parameters under s_S = s_N = 0.1 (figure 4). Table 4 shows the parameter estimates. All parameters are estimated very accurately. At the 0.8 level, 78 per cent of the trees correctly reject the homogeneous mixing model in favour of the superspreader dynamics, whereas 84 per cent of trees correctly accept the homogeneous mixing model.

Table 4.

Maximum-likelihood parameter estimates obtained from 100 simulated trees with 200 sampled tips (sampling probability s₁ = s₂ = 0.1). The parameters λ and d are the median estimates from the Latvian subtype B data analysis. The states are assumed to be unknown (superspreader scenario). Upper part (a) shows parameter estimates under MTBD-2, lower part (b) assumes state-independent transmission. Seventy-eight trees correctly reject the MTBD-1 model in favour of the MTBD-2 model (at the 0.8 level). Eighty-four trees correctly accept the MTBD-1 model over the MTBD-2 model (at the 0.8 level).

		true	median	2.5%	97.5%	true	median	2.5%	97.5%
(a)	λ1,1	0.16	0.14	0.01	0.35		0.11	0.00	0.46
	λ1,2	2.42	2.56	0.85	4.67		0.94	0.31	4.10
	λ2,1	0.02	0.02	0	0.06		0.01	0	0.24
	λ2,2	0.28	0.31	0.11	0.50		0.41	0.00	0.56
	d1 = d2	0.21	0.20	0.08	0.31		0.21	0.08	0.37
(b)	λ		0.50	0.40	0.64	0.52	0.51	0.45	0.62
	d		0.27	0.17	0.39	0.26	0.24	0.14	0.38

Again, with 63 per cent (resp. 78%) of the empirical trees based on the V3 (resp. p17) region rejecting the homogeneous mixing model in favour of superspreader dynamics, we have some support for superspreading, but cannot draw a statistically significant conclusion.

4. Discussion

The amount of structure in a host population together with the amount of interaction between subpopulations is crucial for the ability of a pathogen to spread [26–28]. For example, an isolated population may have a basic reproductive number R₀ < 1, meaning the epidemic is dying out, whereas the same population having some interactions with other populations may lead to an R₀ > 1. Our Latvian HIV-1 subtype A analysis revealed for HETs an R₀ < 1, but since the HETs interact to some extent with the IDUs, HIV is maintained in the HET population.

Successful public health strategies rely on a detailed understanding of epidemiological dynamics. In the above example, targeting IDUs will clearly have a broader impact on decreasing the epidemic, as the HET epidemic will be decelerated as well. In particular if the IDU epidemic is stopped, then the HET epidemic will die out as this epidemic has an R₀ < 1. Vice versa, if HETs were the main target of public health interventions, only small transmission chains may be interrupted, whereas the main IDU epidemic (with an R₀ > 1) would remain unchanged.

Furthermore, it is unclear to what extent sexually transmitted diseases are driven by superspreader dynamics, i.e. by few individuals who overproportionally transmit the disease. To our knowledge, our epidemiological estimates for Latvian HIV-1 subtype B are the first estimates quantifying the amount of superspreading (in an MSM population), revealing about one in 18 superspreaders, with a roughly nine times higher transmission rate for superspreaders than regular spreaders.

Previous studies identified IDUs as main drivers of the HIV-1 epidemic in Switzerland [5] and Latvia [29]. Both studies did not aim at quantifying the epidemiological parameters. Our analysis of the Latvian dataset supports the hypothesis of IDUs being a main driver of the HIV-1 epidemic. In Graw et al. [29], it was estimated that about 66 per cent of the new HET infections are caused by IDU transmission. In fact, we estimated a transmission rate between HETs of about 1.38 and a transmission rate from IDUs to HETs of about 0.15; with our estimate of 5.1 per cent of the infected HET/IDU population being HETs, we overall expect 0.15 × 94.9/(5.1 × 1.38 + 0.15 × 94.9) = 67% of the newly infected HETs being infected by IDUs. With our new method, we further quantified the transmission rates in addition to the proportion of new introductions. Furthermore, our method does not rely on the assumption that new introductions of the pathogen into a transmission group from a different transmission group happen only in one direction (e.g. always from IDU to HET and never from HET to IDU). Compared with the previous studies [5,29], we could not test for changes of the epidemiological dynamics through time though (see also below).

We quantified the amount of structure and the dynamics of interactions between subpopulations by developing new phylogenetic tools. Based on a phylogenetic tree, we estimate the transmission rates within and between subpopulations using our new maximum-likelihood framework. The tips of the phylogenetic tree are assigned to the subpopulations to which they belong. If the state of the tips is unknown (e.g. in the case of superspreaders), the method can be applied to test whether there is evidence for population structure in the epidemic. Our simulations revealed that the parameters can be inferred accurately for trees of medium size (50–200 sequences), whereas model selection performs poor under some parameter combinations for that tree size, meaning that the appropriate model (e.g. d₁ = d₂ versus d₁ ≠ d₂) should ideally be chosen based on data independent of the genetic sequences.

Several methods have been introduced to take structured populations into account when performing phylogenetic analysis [30,31]. These methods allow estimation of the ancestral states together with migration rates between subpopulations, based on a phylogeny where the tips are assigned to the subpopulations. However, a quantification of the transmission rate, death rate and the basic reproductive number was not possible directly, as the underlying model, namely a Markov chain describing state changes on a given phylogeny, does not parametrize these quantities.

Recently, progress has been made towards explicitly parametrizing transmission and ‘becoming-non-infectious’ rates in structured populations [32]. This method is based on the coalescent, and thus relies on the assumption of small sample sizes compared with the total population. A future next step will be a comparison of our birth–death-based method and the coalescent-based method. In particular, this comparison will reveal the impact of the major assumptions of the two models towards parameter estimates. The main differences are (i) that birth–death-based models allow for stochastically varying population sizes, whereas coalescent-based approaches assume a deterministic population size (and thus are appropriate if the number of lineages in a tree is much smaller than the population size) and (ii) that the birth–death models take the sampling times as part of the data, while the coalescent conditions on these times.

Our model is a direct extension of methods developed for the analysis of species phylogenies [18,20–22], with species being of different types, and the speciation and extinction rates being type-dependent (rather than hosts being of different types, and the transmission and ‘becoming-non-infectious’ rates being type-dependent). As species trees are typically on extant species, the methods work for trees in which all tips are sampled at one point in time.

A limitation of our epidemiological method as well as the species methods [18,20–22] is that constant birth and death rates per type are assumed, which implies that for an R₀ > 1 we obtain an exponential growth of infected population. For species phylogenies as well as virus phylogenies, recent methods allow for a saturation effect, meaning the initial exponential growth of the tree is decelerated by having a limited number of ecological niches (macroevolution [33,34]) or a limited number of susceptible hosts (epidemiology [23]). It remains a future challenge to combine the type-dependent models with saturation effects.

Ideally, such models will be directly incorporated into a statistical framework inferring the phylogeny together with the transmission rates, rather than, as done in this paper, first inferring the tree (here using BEAST [25]) and then in a second step fitting a transmission model to the tree (here using TreePar 14]). In such a joint analysis, the likelihood has to be calculated for each proposed tree. Thus, a fast method for numerically evaluating the differential equations specifying the likelihood is required for a joint estimation of rates and trees and thus for bringing us closer towards unifying epidemiological and evolutionary methodology.