Abstract
This paper describes a computational model of use-dependent recovery of movement strength following a stroke. The model frames the problem of strength recovery as that of learning appropriate activations of residual corticospinal neurons to their target motoneuronal pools. For example, for an agonist/antagonist muscle pair, we assume the motor system must learn to activate preserved agonist-exciting corticospinal neurons and deactivate preserved antagonist-exciting corticospinal neurons. The model incorporates a biologically plausible reinforcement learning algorithm for adjusting cell activation patterns – stochastic search – using generated limb force as the teaching signal to adjust the synaptic weights that determine cell activations. The model makes predictions consistent with clinical and brain imaging data, such as that patients can achieve an increase in strength after appearing to reach a recovery plateau (i.e., “residual capacity”), that the differential effect of a dose of movement practice will be greater earlier in recovery, and that force-related brain activation will increase in secondary motor areas following a stroke. An interesting prediction that could be explored clinically is that temporarily inhibiting subpopulations of more powerfully connected corticospinal neurons during late movement training will allow the motor system to optimize corticospinal neurons with a weaker influence, whose optimization was blocked by the rapid optimization of more strongly connected neurons early in training.
Keywords: Stroke, Motor control, Reinforcement learning, Use-dependent plasticity
1. Introduction
Over 700,000 people experience a stroke in the US each year (Broderick et al., 1998). About 80% of acute stroke survivors experience hemiparesis, with this percentage decreasing to about 50% in chronic stroke (Gresham, Duncan, & Stason, 1995). Stroke patients typically undergo several months of rehabilitative movement training aimed at improving strength and coordination, but the neural mechanisms that promote motor recovery in response to movement practice are not well understood. There are currently intensive efforts to develop new stroke rehabilitation techniques (Langhorne, Coupar, & Pollock, 2009), including robotic and virtual reality approaches (Brochard, Robertson, Médée, & Rémy-Néris, 2010), but there is a lack of rigorous, theoretical frameworks to guide these efforts.
Developing mathematical models of stroke recovery could improve the understanding of stroke motor recovery and help guide the design of new therapies. Currently, however, only a few previous studies have used a computational approach to model motor function following stroke. The focus of these studies has primarily been on explaining changes in receptive fields or cortical maps following stroke (Goodall, Reggia, Chen, Ruppin, & Whitney, 1997; Lytton, Stark, Yamasaki, & Sober, 1999; Sober, Stark, Yamasaki, & Lytton, 1997) or on explaining kinematic features of movement impairment such as decreased smoothness and increased variability (Reinkensmeyer, Iobbi, Kahn, Kamper, & Takahashi, 2003; Rohrer et al., 2002) rather than on the dynamics of motor performance recovery. One recent exception is the model by Han, Arbib, and Schweighofer (2008), which modeled the phenomenon of “learned non-use”, in which a stroke patient will chose to not use their weakened limb because of difficulty in using it effectively; this non-use is hypothesized to result in further deterioration in the ability to control the limb. The Han et al. model used a population vector coding paradigm with simulated lesions to model directional errors in a center-out reaching task, and an action-choice module that learned by reinforcement learning the value of using each arm for reaching in different directions. They found that if motor training brought directional reaching errors below a threshold, then spontaneous use of the arm continued to train the arm, and they were able to model cortical reorganization as a redistribution of population vector directions due to the training. The model was supported by self-reports of functional activity from a large multi-site randomized controlled trial of constraint-induced therapy (Schweighofer, Han, Wolf, Arbib, & Winstein, 2009).
The Han et al. model focused on a cognitive issue—the choice whether or not to use the impaired arm, relating directional errors to functional use. The goal of the work described in this paper was to develop a computational model of motor recovery following stroke, and specifically, of the recovery of the ability to generate force using disrupted corticospinal pathways. We focused on the recovery of distal upper limb strength because strength strongly predicts upper extremity functional activity (Bohannon, Warren, & Cogman, 1991; Canning, Ada, Adams, & O’Dwyer, 2004; Harris & Eng, 2007; Lang, Wagner, Edwards, & Dromerick, 2007), and thus understanding its recovery might be expected to generalize to a wide range of functions. In addition, it was possible to base a model of force production on single cell neurophysiological studies of wrist force production in primates (Fetz & Cheney, 1980; Kasser & Cheney, 1985; Maier, Perlmutter, & Fetz, 1998; Mewes & Cheney, 1991; Perlmutter, Maier, & Fetz, 1998).
An initial goal in developing this model was to gain insight into the phenomenon of “residual capacity” or “functional potential”, which refers to the finding that additional movement training can improve motor function, including strength, even years following a stroke (Page, Gater, & Bach-Y-Rita, 2004; Rijntjes, 2006; Stinear, 2007). Upper extremity motor recovery following a stroke reaches an apparent plateau in the first year after the initial incident by clinical (Duncan et al., 1994; Heller et al., 1987; Sunderland, Tinson, Bradley, & Hewer, 1989) and biomechanical measures (Mirbagheri, Tsao, & Rymer, 2008) (Fig. 1). However, there is now extensive evidence that the time course of recovery is not fixed, but rather that additional movement practice can enhance movement and strength in both the sub-acute and chronic phases following a stroke (Ada, Dorsch, & Canning, 2006; Barreca, Wolf, Fasoli, & Bohannon, 2003; French et al., 2007; Kwakkel, Kollen, & Krebs, 2008; Kwakkel et al., 2004; van der Lee et al., 2001) (Fig. 1). The effect size of additional movement practice is typically small (French et al., 2007; Kwakkel et al., 2004) leaving patients short of a full recovery, but additional recovery is statistically significant. Understanding the possible neural bases of residual capacity should provide an insight into how to improve recovery. We sought to gain an insight into these neural bases by modeling the recovery of strength as a reinforcement learning problem in which the limb force experienced on attempts to move the limb guides the refinement of activation in preserved corticospinal pathways. Portions of this work have been published in abstract form (Reinkensmeyer et al., 2009).
Fig. 1.
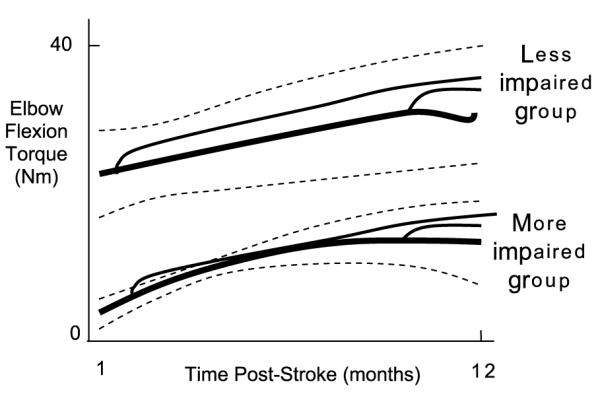
Strength recovery and residual capacity following a stroke. The strength recovery curves (thick solid lines), which were identified by measuring maximum isometric elbow flexion torque from 20 stroke patients 5 times over a 12 month period, and grouping more and less impaired patients into two groups using a growth-mixture model technique (thick solid line = mean, dashed lines ±1 standard deviation (SD)). For reference, unimpaired age-matched maximum elbow flexion strength is about 80 N m (Dewald & Beer, 2001). The superimposed thin, solid lines show the hand-drawn, predicted effects of strength training in the acute and chronic phase following a stroke based on a systematic review of 14 strength training studies (Ada et al., 2006). In the Ada review, the average effect size for strengthening acute weak patients was 0.33 SD, and for chronic patients 0.18 SD. Source: The strength recovery curves (thick solid lines) are copied from Mirbagheri et al. (2008).
2. Methods
2.1. Model description
The model presented here is intended to model strokes that cause weakness by damaging motor areas that give rise to descending white matter tracts. The model ignores muscle plasticity since it has been shown that electrical stimulation of muscle can produce near normal limb forces after chronic stroke, indicating that muscle atrophy is not the main cause of weakness (Landau & Sahrmann, 2002). We apply the model to the task of activating motor networks to generate a flexion force with the wrist, a task commonly used in primate neurophysiological studies. We propose that the motor system must learn appropriate activation of residual corticospinal (CS) cells from movement practice. Other potential mechanisms for recovery after a stroke include structural changes in dendrites and dendritic trees, activation of neural stem cells, and changes in the extracellular matrix (Cramer, 2008), but we focus here on the following question: “To what extent can the dynamics of stroke motor recovery be explained by the process of optimizing activity in residual, fixed pathways to motoneurons, based on experience of movement practice?” The model is characterized by two key features.
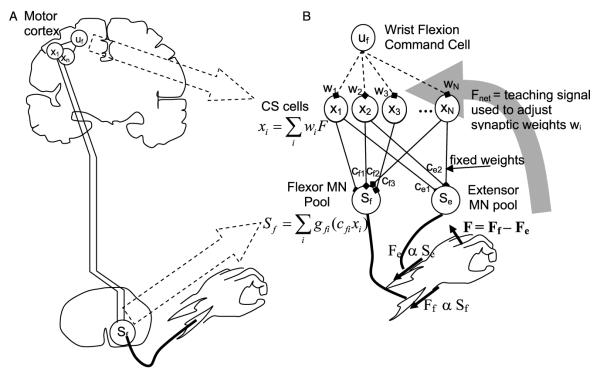
2.1.1. Model feature 1: summed activity from corticospinal cells determines muscle force
The first key feature is that the force the wrist muscles generate is determined by the weighted, summed activity of CS cells that activate the wrist motoneurons (MNs) (Fig. 2). The influence of both mono-synaptically connected systems (i.e. corticomotoneuronal CM cells) and multi-synaptically connected systems are captured by fixed, functional connectivity weights cfi and cei that represent the net excitatory or inhibitory effect of the cell on the MN pool. We modeled the distribution of these weights based on the primary motor cortex CM system because it is likely the most functionally important of the premotor systems for humans, and has been well characterized using spike-triggered averaging techniques in primates (Fetz & Cheney, 1980; Kasser & Cheney, 1985). Most CM cells (99%) originating from primary motor cortex facilitate either the flexor or extensor muscle groups for wrist flexion/extension movement; about a third or less of these cells at the same time inhibit the antagonist (see Fig. 17 in Perlmutter et al. (1998)). Changing the percentage of reciprocal or inhibitory connections did not alter the basic findings from the model, except that when no inhibitory cells were included, the levels of simulated co-contraction tended to be higher. Note that a basic feature of the model is simply that each descending neuron influences a motoneuron to increase or decrease muscle activity, regardless of whether the effect is through an interneuron or a direct connection. Therefore we will refer to the simulated descending neurons as CS cells rather than specifically CM cells.
Fig. 2.
A. The model proposes that the nervous system learns the best activations xi of N residual corticospinal (CS) cells in response to a flexion command uf to maximize wrist flexion force F following stroke. B. In more detail, the model proposes that the nervous system adjusts the synaptic weights wi that determine the activations xi of the N residual CS cells given a flexion command uf, in order to maximize the net force output F of the wrist, based on measurements of F generated during practice movements. CS cell activity is assumed to sum in the spinal cord, activating flexor and extensor motoneuronal pools. The resulting network architecture is a two-layer, feedforward neural network. The network is nonlinear in that the contribution of an individual CS cell to motoneuronal synaptic drive is assumed to saturate at higher firing rates xi, as represented mathematically by cell-specific saturation functions gi. Synaptic connectivity in the spinal cord is assumed to remain fixed (the cfi and cei weights are modeled as fixed weights, the distributions of which are taken from primate studies).
Muscle force production is typically proportional to the firing rate of neurons in motor cortex (Ashe, 1997) and also of CM and other premotor cells (Fetz, Cheney, Mewes, & Palmer, 1989; Mewes & Cheney, 1991; Maier et al., 1998). We therefore assumed that increases in the firing rate of a single CS cell caused proportional increases in muscle force, up to a saturation limit, with the proportionality constant determined by the connection weights cfi or cei (Fig. 2). A mechanistic way to view this model property is that CS cell activity sums at the level of the motoneuron pool to create a net excitatory drive proportional to muscle force, consistent with previously proposed models of muscle recruitment (Fuglevand, Winter, & Patla, 1993). We included a saturation constraint on the relationship between CS cell firing rate and net excitatory drive (and thus force output) because increases in cell firing rate cannot indefinitely increase excitatory drive to motoneurons, because of synaptic limitations. This saturation, well-documented experimentally (Powers & Binder, 2001) and included in many models of the motoneuron pool (Fuglevand et al., 1993; Zhou, Suresh, & Rymer, 2007), was a key factor that influenced the simulated recovery dynamics, as described below.
To map muscle force to wrist force, we grouped wrist extensor muscles into one equivalent agonist muscle, and wrist flexor muscles into an equivalent antagonist muscle, then subtracted their output to calculate net isometric force output of the wrist.
2.1.2. Feature 2: reinforcement learning of CS network activations
There is a globally optimal solution to the problem of maximizing force output given such a network of CS cells: maximize the summed firing output from CS cells that facilitate agonist muscles and inhibit antagonist muscles, and minimize summed output from antagonist-facilitating and agonist-inhibiting CS cells. We assume that the motor system must find this solution by evaluating the results of movement practice using a reinforcement learning algorithm (Sutton & Barto, 1998). Reinforcement learning uses only summary feedback of motor performance to update synaptic weights, and can be achieved with computations implemented locally at synapses, and is thus considered biologically plausible (Anderson, Omidvar, & Dayhoff, 1988; Mazzoni, Andersen, & Jordan, 1991; Werfel, Xie, & Seung, 2005; Williams, 1992). We assume that the teaching signal available to the reinforcement learning algorithm is the net force output of the wrist, which the motor system estimates using a blend of afferent and efferent information (Carson, Riek, & Shahbazpour, 2002).
Finding the optimal pattern of CS cell activity by trial-and-error using only net force produced by the wrist as a teaching signal is difficult because of a spatial credit-assignment problem: an observed increase in force output is difficult to attribute to an individual neuron from among the many that may have contributed to it. A biologically plausible reinforcement learning strategy that can solve the spatial credit assignment problem is stochastic local search (Anderson et al., 1988; Mazzoni et al.,1991; Werfel et al., 2005; Williams, 1992). Stochastic local search algorithms rely on a noise process to generate candidate activation patterns that are randomly perturbed from a nominal pattern, and then evaluate the candidate activation patterns by the effect they produce on the teaching signal. In the model, noise is assumed to be an inherent property of the CS firing patterns.
2.2. Model definition
With this background, the model can be defined mathematically as follows. Consider N CS cells, each with firing rate xi > 0. Define cfi and cei to be the fixed connection weights that determine the strength of synaptic drive to the flexor and extensor motoneuronal pools, respectively, from CS cell i. Since we assume that force is proportional to net excitatory drive to the motoneuronal pools, these constants also determine the force output from the muscle. The force F produced by the wrist is therefore:
where A is a scaling unit to convert to the correct units of force (set to be 1 in the simulations, so force is reported unitless), and gfi() and gei() are saturation nonlinearities. The cell-specific functions gfi() and gei() have a positive saturation limit for excitatory cells (cfi or cei > 0) and a negative saturation limit for inhibitory cells (cfi or cei < 0). For flexor CS cells, we set the weights cfi and cei to be +1 and 0 for 70% of cells, and +1 and −1 for 30% of cells, and vice versa for extensor CS cells (Perlmutter et al., 1998). We experimented with versions of the model in which the saturation limits for each cell were drawn from different random distributions; the results from such models did not differ from a model in which the saturation limits were all set at the same constant, so, for simplicity, we present only the constant limit model.
For conceptual convenience, we apply the update to the activation pattern X rather than the weights wi; the two are equivalent since we assume a single fixed flexion command working through the weights to create the activations (Fig. 2(B)). Given this formulation, the optimal activation pattern X* that makes flexion force F from the agonist/antagonist pair equal the maximum possible flexion force is the one that maximally activates CS cells that differentially excite the flexor or inhibit the extensor, and minimally activate cells that differentially excite the extensor or inhibit the flexor (assuming xi > 0).
For the below simulations, we randomized the starting activation X0 to a uniform random distribution. We reasoned that cell loss, and associated changes in synaptic connectivity due to sprouting, for example, would have the effect of inappropriately randomizing the inhibitory and excitatory inputs from the command motor system to the CS system. Other initial activation patterns, such as uniform low activity, produced similar results.
There are two simple ways to implement a local, stochastic search: a best first algorithm (Anderson et al., 1988), in which random patterns are tried, then accepted or rejected based on their outcome (i.e. based on the reward signal of whether they caused greater force production than that previously achieved), and a stochastic gradient descent (Werfel et al., 2005; Williams,1992), which changes the activations with a proportionality to the relative increase or decrease in force. We thought it was important to see if the results were dependent on a specific implementation of stochastic search. The best first algorithm can be summarized as follows:
2.2.1. Best-first algorithm: given an initial activation pattern X0 that produced a force F0
Activate CS cells with pattern Xi = X0 + νi, where νi is random noise, and measure the force Fi produced by this pattern.
Memorize the new pattern Xi if the force Fi it produces is greater than F0; i.e. if Fi > F0, then let X0 = Xi and F0 = Fi.
Repeat.
We assume that the noise ν is drawn from a zero-mean normal distribution with standard deviation σ, although other noise distributions, such as signal-dependent noise, are possible and considered below.
The stochastic gradient descent algorithm can be summarized as follows (Werfel et al., 2005; Williams, 1992):
2.2.2. Stochastic gradient descent algorithm: given an initial activation pattern X0 that produced a force F0
Activate CS cells with pattern Xi = X0 + νι, where νi is random noise, and measure the force Fi produced by this pattern.
- Update the activation pattern and the stored force:
where g is the learning gain. Repeat.
Again, the main difference between the algorithms is that the gradient descent algorithm changes the activation pattern with a proportional gain g, and also changes the activation in the opposite direction of the noise if the noise-perturbed activation pattern did not produce a greater force. This algorithm can be proven to optimize the reinforcement signal on average using a gradient descent on the reinforcement signal (Werfel et al., 2005;Williams, 1992). Note that in both cases the reinforcement signal is the difference between the achieved force Fi and the maximum achieved force Fo that was achieved previously. We compared the two learning algorithms to determine if the differences between these two basic ways to achieve stochastic local search altered the simulation results. The algorithms produced comparable results, so for brevity we present the results with the best-first algorithm.
3. Results
We simulated the process of relearning to generate a large wrist flexion force after stroke (i.e. strength recovery) as a reinforcement learning problem in which the motor system must learn appropriate activations of residual corticospinal (CS) cells preserved by the stroke, using wrist force experienced during practice movements as the teaching signal. We first demonstrate that the simulations predict existing clinical data such as residual capacity. We then describe two interesting predictions that could be explored clinically.
3.1. Predicting clinical data: residual capacity, timing, and severity effects
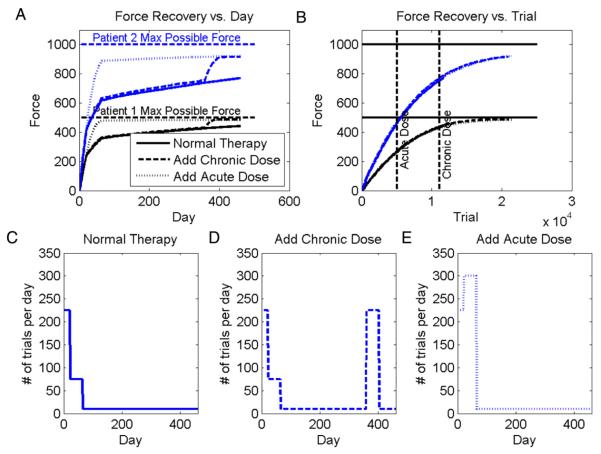
To relate the model output to residual capacity, we analyzed the simulation outcomes for two hypothetical subjects with different numbers of residual CS cells. We assumed a severely impaired subject had 1000 residual CS neurons that the motor system could potentially use to increase force output from the wrist, and a moderately impaired subject had 2000 residual CS neurons. The number of neurons was chosen arbitrarily; simulations with larger neurons produced similar results, except learning was slower. We compared three rehabilitation exercise protocols: “standard”, “standard additional subacute exercise” and “standard + additional chronic + exercise”. We estimated the number of wrist movements that a patient might make each day during these rehabilitation protocols, then used this estimate to plot the force recovery versus day rather than versus movement attempt. We plotted force recovery versus day because recovery data is commonly presented in this fashion in the rehabilitation literature.
Fig. 3 shows the response of the model to these three rehabilitation regimens, with the bottom row of panels defining the number of trials simulated per day of rehabilitation. Key results can be summarized as follows:
Both simulated patients exhibited residual capacity, as is apparent by their increased force output in response to the extra doses of subacute or chronic therapy. This is consistent with clinical evidence reviewed in Ada et al. (2006), Barreca et al. (2003), French et al. (2007), Kwakkel et al. (2008, 2004) and van der Lee et al. (2001).
The patient with the larger residual CS network learned to produce more force. This is consistent with both transcanial magnetic stimulation (TMS) and diffusion tensor imaging studies (DTI). Motor evoked potentials (MEP) elicited by TMS provide information related to the size of the CS cell population in the primary motor cortex. MEP amplitude is significantly correlated with grip strength following stroke (Brouwer,2006; Lindberg, Schmitz, Forssberg, Engardt, & Borg, 2004;Thickbroom, 2002), consistent with the model. DTI provides a quantitative estimate of the integrity of corticospinal tracts originating from multiple cortical areas (Lindberg, Schmitz, Engardt, Forssberg, & Borg, 2007). These authors found a strong correlation (r = 0.96) between white matter integrity, measured using fractional anisotropy (FA) with DTI, and maximum grip force in seven chronic stroke patients. These data support the basic structure of the model in which residual CS population size determines the maximum strength a stroke patient can recover.
The same dose of exercise given subacutely had a larger differential effect than when given chronically. This result is consistent with evidence reviewed in Teasell, Bitensky, Salter, and Bayona (2005).
The same dose of exercise had a smaller effect when given to the more severely impaired patient (Parry, Lincoln, & Vass, 1999).
The total number of movement repetitions determined the final force recovery (Fig. 6(B)). Data measuring how total upper extremity movement practice predicts recovery is lacking because it is difficult to precisely quantify upper extremity movement practice.
Fig. 3.
Residual capacity predicted by model. A: force recovery versus day for two simulated patients with 1000 and 2000 residual CS neurons, respectively, with σ = 0.04. The plot shows temporal recovery curves predicted for three different exercise protocols, which are defined in the bottom row of graphs. Adding an additional dose of therapy increased strength recovery, consistent with the clinical finding of residual capacity. B: force recovery versus movement repetition trial for the same two simulated patients. Bottom row: The simulations use an estimated number of movement repetitions per day. C: for the standard protocol, in the acute phase (first 21 days after the stroke), the patient exercises frequently, in the sub-acute phase (the next 42 days after the stroke) less, and in the chronic phase less. D: for the chronic-enhanced protocol, the patients receive an extra dose of movement training in the chronic phase following a stroke. E: for the acute-enhanced protocol, the patients received an extra dose of movement training in the sub-acute phase following a stroke. The number of estimated movement repetitions per day approximate research rehabilitation exercise protocols presented in the literature. The number of repetitions is small in the chronic phase, because we assumed the impaired wrist was difficult for the patient to use effectively, that formal therapy was discontinued, and that the patient preserved a “good” hand that he could instead use to achieve desired daily function, limiting the use of the impaired hand. The simulation results were robust to the specific numbers of repetitions used, unless very few or very many movements were used, in which case the interesting, residual-capacity effects became decreasingly small. The simulation results were also robust to changes in network parameters such as number of cells, amount of noise, or optimization algorithm (local or gradient search).
Fig. 6.
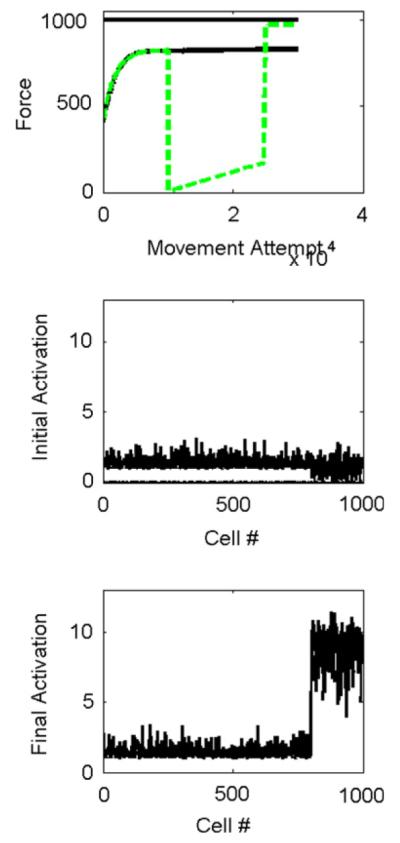
Effect of temporarily suppressing output from strongly connected cells. The network was the same as that considered in Fig. 4, with 800 strongly-connected cells in M1 (cells 1–800 in B and C), and 200 weakly connected cells in SMA (cells 801–1000 in B and C). A: force production versus movement attempt without suppression (solid) and with suppression of the M1 cells (dashed) for 10,000 movement attempts (dashed). The solid horizontal line at the top shows the maximum force the network is capable of achieving. Temporarily suppressing the output of the M1 cells allowed the network to learn to produce more force. B: cell activations after 10,000 movement attempts, before suppression. The simulated SMA cells (cells 801–1000) were not well optimized because of their weaker influence on the motoneuronal pools C: cell activations after 10,000 more movements with M1 suppressed. The simulated SMA cells (cells 801–1000) were better optimized after movement practice without the M1 cells present. For these plots σ = 0.02.
We also performed simulations in which we removed the saturation in the relationships between individual CS cell firing rates and muscle force. This caused the network to increase its force linearly to the maximum possible output of the network. Thus the presence of the saturation was key for the network to demonstrate residual capacity.
3.2. Predicting brain imaging results: spread of force-related activation to secondary motor areas
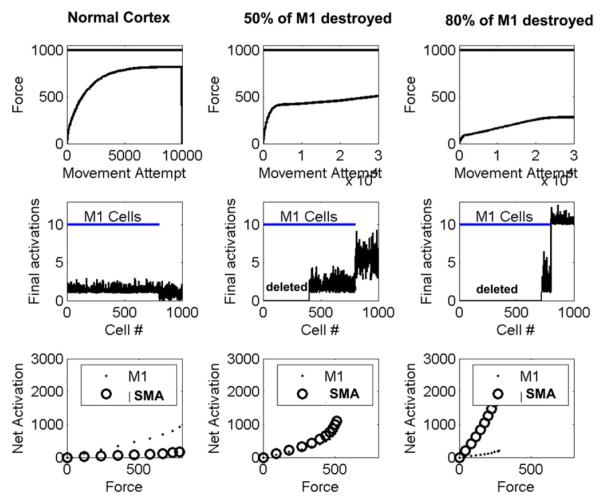
By incorporating simple anatomical assumptions, the model predicts the spread of force-dependent cell activity into secondary motor areas, as has been observed in brain imaging studies (Ward et al., 2007). We simulated a situation in which the primary motor cortex (M1), in its normal, pre-stroke state, had 80% of the total population of agonist-related CS cells, and a secondary motor area (assumed here to be supplementary motor area, SMA) had 20% of the population (for simplicity of presentation, we ignored antagonist-related cells; the results were similar when we included them). We assumed that connection weights to the motoneuronal pool for the SMA cells were 10% of the strength of those for the M1 cells (Lemon et al., 2002). We first allowed the optimization process to run for this “normal” cortex, and found that the stochastic local search more quickly optimized the M1 output than the SMA output (Fig. 4 first column). This can be accounted for because a random change in a M1 CS cell activation pattern was more likely to produce an increase in force earlier in recovery, due to its greater connection weight. Next, we assumed that a stroke destroyed 50% of M1 cells. We allowed the optimization to run again, and found that the learning algorithm now increased the activities of the SMA cells (Fig. 4, second column). Assuming the stroke killed 80% of M1 cells caused further increases in SMA cell activity (third column). The increase in cell activity also manifested as an increase in the slope of the relationship between total neuronal firing in the SMA and force. Thus, the model predicted an increase in force-related activation in a secondary motor area following a stroke that damages output from the primary motor area.
Fig. 4.
Spread of activation into secondary motor area following a stroke in the primary motor cortex. First column: the recovery dynamics for a “normal” cortex with 800 agonist-related cells in M1 (cells 1–800 in the middle row), and 200 in a secondary area, assumed to be supplementary motor area (SMA, cells 801–1000 in the middle row). The cells in SMA had 10% of the connection strength of the M1 cells. The top graph in the first column shows learned force as a function of movement attempt; the solid horizontal line shows the maximum force the network is capable of achieving. The middle graph in the first column shows the cell activities following 10 000 movement attempts; the SMA cells (cells 800–1000) remain poorly optimized due to their weaker connections. The bottom graph in the first column shows the net activation of the cells, which estimates the fMRI BOLD signal, as a function of force. In the normal cortex, the net activation was greater for M1, and showed greater force-dependence for M1 (first column, third row). The second column shows the recovery process after 50% of the M1 cells of the optimized healthy cortex were destroyed. There was an increase in force-related SMA activity following optimization (second column, bottom row). The third column shows the recovery process after 80% of the cells of the optimized healthy cortex were destroyed. There was a further increase in force-related SMA activity (third column, bottom row). For these plots, σ = 0.02.
Longitudinal studies of brain activation after stroke have noted a greater activation of secondary motor areas (Feydy et al., 2002). Even more specific and consistent with the model, Ward et al. found a spread of force-related activity following a stroke (Ward et al., 2007). In chronic human stroke subjects with a subcortical stroke, fMRI activation in multiple brain areas was graded to grip force production. Subjects in whom corticospinal tract disruption was more severe (gauged by MEP) had greater force-dependent activation in secondary motor areas, which is precisely what the model predicts (Fig. 4, bottom row).
3.3. Predicting strategies for improving recovery: clinically testable hypotheses
We devised two strategies for improving force recovery of the network. First, in sensitivity analyses, we observed the amount of force recovery increased when a decreased firing rate noise level was used to drive the search, but this slowed the learning rate. This observation suggested the strategy of decreasing noise as recovery proceeds to improve the completeness of late learning while not affecting the speed of early learning (a strategy analogous to “simulated annealing” in the neural network literature). Fig. 5 shows that this strategy resulted in better force recovery. Movement-related cortical neurons typically exhibit signal-dependent noise, in which the variability of their firing rate increases with increases in firing rate (Lee, Port, Kruse, & Georgopoulos, 1998; Stein, 2005). Including signal-dependent noise had a similar beneficial effect on the recovery pattern (Fig. 5).
Fig. 5.
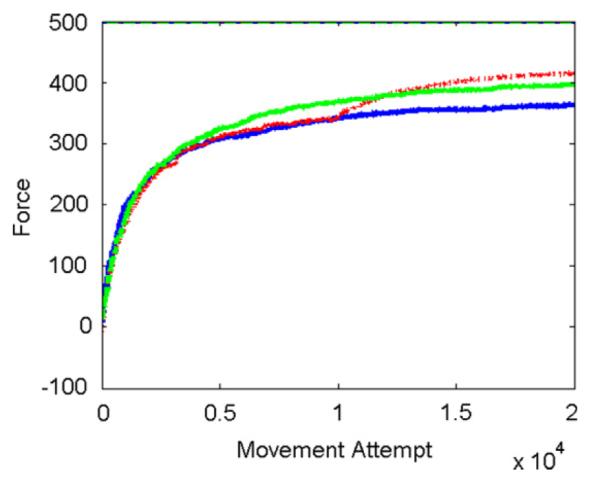
Effect of changing noise amplitude on force recovery. The three curves show learning with a fixed noise level (blue, normally-distributed noise with standard deviation σ = 0.04), learning in which noise amplitude was decreased at movement attempt 10 000 (red, σ = 0.04 until trial 10 000, and 0.01 after), and learning with signal-dependent noise (green, σ = 0.03 + 0.02x, where x is activation of CS cell). Network of 1000 cells optimized with best-first search. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
The second putative clinical strategy arose from two observations. First, as explained above, the network tended to optimize the activity of more strongly-connected cells first. Second, learning took longer as more cells were included in the network. These observations suggested the strategy of temporarily inhibiting already-optimized cells from the network, training the remaining, smaller, less-optimized network, then re-introducing the inhibited network. We applied this strategy to a network that simulated the connectivity of M1 and SMA, identical to the one described in the previous section. Inhibiting M1 cells during a training period allowed the more weakly connected SMA cell activities to become better optimized (Fig. 6). This strategy allowed the network to substantially increase its force output to levels unobtainable during training with the entire intact network.
4. Discussion
We developed a model of use-dependent strength recovery based on three ideas: (1) CS cell activity sums to create a net excitatory flexor or extensor drive to a joint (2) The relationship between a CS cell’s activity and its individual contribution to the excitatory drive on flexor and extensor motoneuronal pools is linear up to a peak firing rate, then saturates for higher activity levels; (3) The motor system optimizes CS cell activity based on repetitive movement experiences using a reinforcement learning algorithm – stochastic search – with limb force output as the teaching signal. Simplifying assumptions we permitted included: simplified CS cells with fixed effects on their target muscles, a linear recruitment model, a two-muscle, single-joint biomechanical model, and no horizontal interactions between CS cells. We ignored other possible mechanisms of plasticity, and assumed initial CS activity patterns were randomized by stroke. We neglected other aspects of motor behavior important to functional movement such as multiple-muscle coordination and muscle tone.
Within this framework of assumptions, we found that the model was adequate to predict many clinically-important behavioral results, such as exponential-like strength recovery curves, residual capacity, and the dependency of strength recovery amount on therapy timing and impairment severity. The model also predicted functional imaging results related to the spreading of force-dependent activation to secondary motor areas. Two key mechanisms driving the observed network dynamics are (1) the saturation in the relationship between CS cell firing rate and muscle force acts to slow late learning, because saturated neurons bias random candidate activation patterns so as to be less likely to increase force output; and (2) the activations of more strongly connected cells tend to be optimized first, as changes in their activations are more likely to increase force output.
We first briefly discuss the mechanisms of the observed dynamics, then assess the relevance of the model by the extent to which it suggests interesting directions for future experiments.
4.1. Mechanisms of the observed dynamics
Analysis of the model is difficult because of its nonlinearity, but it is useful to ask what caused the exponential shape to the observed force recovery curves, and the residual capacity of the network. As observed above, removing the saturation in the relationships between individual CS cell firing rates and muscle force caused the network to increase its force linearly to the maximum possible output of the network. Thus, this saturation constraint caused the exponential recovery curve and the residual capacity. To gain an insight into how, we analyzed the percentage of randomly-perturbed firing patterns that produced differentially greater force output when different percentages of cells were operating in the saturation regime of their firing-rate/force output relationship. When no cells operated in the saturation regime, the percentage of patterns that randomly improved strength was 50% and therefore optimization of force output proceeded rapidly since, on average, every other candidate pattern increased force output. However, as cells entered the saturation regime, the percentage of candidate patterns that randomly improved strength rapidly decreased toward zero. This was because the saturated cells biased the mean of the distribution of candidate patterns.
This biasing process due to saturation can be accounted for as follows. The differential increase in force output produced by a differential change in activations of the CS cells is the sum of random variables—i.e. the sum of the zero-mean Gaussian noise added to each unit to generate the candidate pattern, subject to the saturation constraints of the force production process. The mean of this sum is the sum of the means of the individual units’ contributions. Saturated units contribute a random variable to the sum with a negative mean, since positive noise does not increase their force contribution due to the saturation. As more units saturate, the more negative their summed contribution becomes, on average. This in turn increases the probability that a candidate activation pattern will decrease rather than increase force output. A percentage of candidate patterns will still increase force no matter how many cells operate in the saturation regime because the summed noise is a random variable, but this percentage becomes smaller as more cells operate in the saturation regime.
4.2. Quantifying the relationship between amount of practice, CS cell population size, and residual capacity
The model predicts that stroke patients can make further gains with additional practice, but that the amount of gain possible will depend on the history of exercise and the size of the residual population of CS cells. Therefore, the model suggests that it is essential to experimentally define the relationship between residual capacity, the history of movement practice, and CS population cell size. This relationship has not been defined previously at least in part because of experimental difficulties in measuring movement practice and CS population sizes. However, it is now experimentally feasible using low-cost, lightweight motion sensors to track limb use both during therapy and daily life (e.g. Lang et al., 2007). In addition, the development of DTI imaging techniques allows a degree of quantification of anatomical tract size from CS cell populations.
Along these lines, Stinear (2007) recently assessed the relationship between corticospinal tract (CST) integrity in stroke patients, quantified using TMS and DTI, and the patient’s response to a dose of movement training. Some patients had MEPs, indicating availability of CST originating from primary motor cortex. These patients improved motor ability with training, and the amount of improvement was predicted by time since stroke. In patients without MEPs, the integrity of the CST, quantified using DTI, predicted the behavioral response to therapy. Restating these results in the framework of the present model, residual capacity was apparently best for patients with larger CS networks that were less optimized, that is, for those networks for which time since stroke was shorter, and thus less movement practice had presumably occurred. The model predicts that with more cumulative movement practice, there is less room for recovery, as the networks are already optimized. Thus, the model suggests that the Stinear et al. study should be duplicated but using a quantitative history of limb use (rather than the inexact surrogate of time since stroke).
4.3. Strategies for improving recovery: clinically testable hypotheses
The model exhibits what might be called “latent residual capacity”, which is an amount of additional force that the CS network is capable of generating, but which reinforcement learning is not normally competent to access, or can access only very slowly (see Fig. 3(A), for example). The model predicted that this inaccessible residual capacity could be quite large – 50%–80% of the theoretical maximum force production – for large networks. This finding provides a mechanistic basis for the working hypothesis that seems to drive much rehabilitation research: that brain networks are inherently capable of generating substantially more output than rehabilitation currently achieves. The model suggests designing therapies to alter the activity of CS cells that are poorly optimized for force output.
We identified two possible strategies along these lines based on experience with the model. The first was to decrease cell firing rate noise later in recovery. The motor system may already have mechanisms that implement this strategy. For example, firing rate noise has been shown to decrease for primary motor cortex cells as rats learn a reach to grasp task (Kargo & Nitz, 2004). Signal-dependent noise (Lee et al., 1998; Stein, 2005) might also serve a role in improving force optimization. An interesting direction for future research is to identify ways to exogenously manipulate firing rate variability at key times during rehabilitative training.
A second strategy for improving recovery was to temporarily inhibit cells that are already optimized, train the remaining cells, and then release the inhibited cells. The cells that the stochastic local search process will tend to optimize first are those with stronger effects on muscles, since random changes in the firing rates of these cells are more likely to produce a net force benefit. Once these cells are optimized and operating in their saturation regime, they block further optimization of other cells because they negatively bias the distribution of forces improvements that can result from new, random, candidate activation patterns. Temporarily inhibiting these optimized cells allows the non-optimized cells to come into play and become optimized, resulting in increased force output when the inhibited cells are reintroduced.
The concept of inhibiting one group of cells to allow training of another group has not been well studied in the rehabilitation literature, but at least two therapeutic strategies may relate to this concept. Repetitive TMS has been used to temporarily upregulate the excitability of ipsilesional cortex, or downregulate the excitability of the inhibiting, contralesional cortex during training, sometimes resulting in greater efficacy of training (see review: Bolognini, Pascual-Leone, & Fregni, 2009). The mechanisms of this effect are unknown, but are speculated to be analogous to long-term potentiation, possibly involving TMS-induced changes in endogenous neurotransmitters or gene expression. The model presented provides an alternative, mathematical basis for how TMS could improve motor training: TMS may temporarily disrupt the function of optimized cells in the areas closer to the TMS delivery point, allowing cells in other areas to become optimized.
In another study, anesthesia delivered into selected parts of the brachial plexus was used to functionally deafferent shoulder and hand sensory motor cortex during hand movement training after a stroke, resulting in larger improvements in hand movement ability than were possible with training without the anesthesia (Muellbacher et al., 2002). The rationale behind this study was that a preference for training shoulder and elbow movement in normal rehabilitation may lead to a lack of cortical resources available for the hand; temporarily freeing shoulder cells through deafferentation might free those cells to learn to become hand-related cells. The model presented shows a quantitative mechanism by which disrupting cells whose activity is already optimized (e.g. shoulder cells) might allow non-optimized cells (e.g. hand cells) to become optimized. Besides TMS or anesthesia-produced deafferentation, drugs such as muscimol which can locally and temporarily inhibit cell activity might be useful to temporarily remove optimized cells during training.
4.4. Defining the teaching signal used for use-dependent strength recovery
Finally, the model highlights the importance of experimentally defining the teaching signal that directs the reinforcement learning of CS cell activity. We assumed that the teaching signal was limb force, and that a single, accurate estimate of limb force was broadcast to all CS cells following every movement attempt, as well as an accurate representation of the previously-achieved peak limb force for comparison. There are few experimental studies focused on defining the features of the reinforcement signals used for strength increases attributable to neural plasticity. One possible lead is that rats with induced focal M1 lesions require basal forebrain cholinergic systems to recover grasping ability. It has been suggested that these cholinergic systems enhance cortical responsiveness to relevant sensory inputs (Conner, Chiba, & Tuszynski, 2005), which suggest in turn that they may be related to or control teaching signals. Another possibility is dopaminergic projections to M1 that appear to enable motor learning (Luft & Schwarz, 2009). Clarifying exactly what the reinforcement signal is that drives neural strength gains, and how the motor system evaluates this signal with respect to the history of motor activity, may suggest ways to enhance this signal and improve the efficiency of motor recovery after a stroke.
References
- Ada L, Dorsch S, Canning CG. Strengthening interventions increase strength and improve activity after stroke: a systematic review. The Australian Journal of Physiotherapy. 2006;52(4):241–248. doi: 10.1016/s0004-9514(06)70003-4. [DOI] [PubMed] [Google Scholar]
- Anderson RW, Omidvar OM, Dayhoff J. Progress in neural networks. Academic Press; Boston: 1988. Random-walk learning: a neurobiological correlate to trial-and-error; pp. 221–244. [Google Scholar]
- Ashe J. Force and the motor cortex. Behavioural Brain Research. 1997;87(2):255–269. doi: 10.1016/s0166-4328(97)00752-3. [DOI] [PubMed] [Google Scholar]
- Barreca S, Wolf SL, Fasoli S, Bohannon R. Treatment interventions for the paretic upper limb of stroke survivors: a critical review. Neurorehabilitation and Neural Repair. 2003;17(4):220–226. doi: 10.1177/0888439003259415. [DOI] [PubMed] [Google Scholar]
- Bohannon RW, Warren ME, Cogman KA. Motor variables correlated with the hand-to-mouth maneuver in stroke patients. Archives of Physical Medicine and Rehabilitation. 1991;7:682–684. [PubMed] [Google Scholar]
- Bolognini N, Pascual-Leone A, Fregni F. Using non-invasive brain stimulation to augment motor training-induced plasticity. Journal of NeuroEngineering and Rehabilitation. 2009;6:8. doi: 10.1186/1743-0003-6-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brochard S, Robertson J, Médée B, Rémy-Néris O. What’s new in new technologies for upper extremity rehabilitation? Current Opinion in Neurology. 2010 doi: 10.1097/WCO.0b013e32833f61ce. [DOI] [PubMed] [Google Scholar]
- Broderick J, Brott T, Kothari R, Miller R, Khoury J, Pancioli A, et al. The greater Cincinnati/Northern Kentucky Stroke study: preliminary first-ever and total incidence rates of stroke among blacks. Stroke. 1998:415–421. doi: 10.1161/01.str.29.2.415. [DOI] [PubMed] [Google Scholar]
- Brouwer BJ. Hand function and motor cortical output poststroke: are they related? Archives of Physical Medicine and Rehabilitation. 2006;87(5):627–634. doi: 10.1016/j.apmr.2006.02.006. [DOI] [PubMed] [Google Scholar]
- Canning CG, Ada L, Adams R, O’Dwyer NJ. Loss of strength contributes more to physical disability after stroke than loss of dexterity. Clinical Rehabilitation. 2004;18(3):300–308. doi: 10.1191/0269215504cr715oa. [DOI] [PubMed] [Google Scholar]
- Carson RG, Riek S, Shahbazpour N. Central and peripheral mediation of human force sensation following eccentric or concentric contractions. Journal of Physiology. 2002;539(3):913–925. doi: 10.1113/jphysiol.2001.013385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conner JM, Chiba AA, Tuszynski MH. The basal forebrain cholinergic system is essential for cortical plasticity and functional recovery following brain injury. Neuron. 2005;46(2):173–179. doi: 10.1016/j.neuron.2005.03.003. [DOI] [PubMed] [Google Scholar]
- Cramer SC. Repairing the human brain after stroke: I. Mechanisms of spontaneous recovery. Annals of Neurology. 2008;63(3):272–287. doi: 10.1002/ana.21393. [DOI] [PubMed] [Google Scholar]
- Dewald JP, Beer RF. Abnormal joint torque patterns in the paretic upper limb of subjects with hemiparesis. Muscle and Nerve. 2001;24(2):273–283. doi: 10.1002/1097-4598(200102)24:2<273::aid-mus130>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- Duncan PW, Goldstein LB, Horner RD, Landsman PB, Samsa GP, Matchar DB. Similar motor recovery of upper and lower extremities after stroke. Stroke. 1994;25(6):1181–1188. doi: 10.1161/01.str.25.6.1181. [DOI] [PubMed] [Google Scholar]
- Fetz EE, Cheney PD. Postspike facilitation of forelimb muscle activity by primate corticomotoneuronal cells. Journal of Neurophysiology. 1980;44(4):751–772. doi: 10.1152/jn.1980.44.4.751. [DOI] [PubMed] [Google Scholar]
- Fetz EE, Cheney PD, Mewes K, Palmer S. Control of forelimb muscle activity by populations of corticomotoneuronal and rubromotoneuronal cells. Progress in Brain Research. 1989;80:437–449. doi: 10.1016/s0079-6123(08)62241-4. [DOI] [PubMed] [Google Scholar]
- Feydy A, Carlier R, Roby-Brami A, Bussel B, Cazalis F, Pierot L, et al. Longitudinal study of motor recovery after stroke: recruitment and focusing of brain activation. Stroke: A Journal of Cerebral Circulation. 2002;33(6):1610–1617. doi: 10.1161/01.str.0000017100.68294.52. [DOI] [PubMed] [Google Scholar]
- French B, Thomas LH, Leathley MJ, Sutton CJ, McAdam J, Forster A, et al. Repetitive task training for improving functional ability after stroke. Cochrane Database of Systematic Reviews (Online) 2007;(4):CD006073. doi: 10.1002/14651858.CD006073.pub2. [DOI] [PubMed] [Google Scholar]
- Fuglevand AJ, Winter DA, Patla AE. Models of recruitment and rate coding organization in motor-unit pools. Journal of Neurophysiology. 1993;70(6):2470–2488. doi: 10.1152/jn.1993.70.6.2470. [DOI] [PubMed] [Google Scholar]
- Goodall S, Reggia JA, Chen Y, Ruppin E, Whitney C. A computational model of acute focal cortical lesions. Stroke. 1997;28(1):101–109. doi: 10.1161/01.str.28.1.101. [DOI] [PubMed] [Google Scholar]
- Gresham GE, Duncan PW, Stason WB. Post-stroke rehabilitation. US Dept. Health and Human Services, Agency for Health Care Policy and Research; Rockville, MD: 1995. [Google Scholar]
- Han CE, Arbib MA, Schweighofer N. Stroke rehabilitation reaches a threshold. PLoS Computational Biology. 2008;4:e1000133. doi: 10.1371/journal.pcbi.1000133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris JE, Eng JJ. Paretic upper-limb strength best explains arm activity in people with stroke. Physical Therapy. 2007;87(1):88–97. doi: 10.2522/ptj.20060065. [DOI] [PubMed] [Google Scholar]
- Heller A, Wade DT, Wood VA, Sunderland A, Hewer RL, Ward E. Arm function after stroke: measurement and recovery over the first three months. Journal of Neurology, Neurosurgery and Psychiatry. 1987;50(6):714–719. doi: 10.1136/jnnp.50.6.714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kargo WJ, Nitz DA. Improvements in the signal-to-noise ratio of motor cortex cells distinguish early versus late phases of motor skill learning. The Journal of Neuroscience. 2004;24(24):5560–5569. doi: 10.1523/JNEUROSCI.0562-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kasser RJ, Cheney PD. Characteristics of corticomotoneuronal postspike facilitation and reciprocal suppression of EMG activity in the monkey. Journal of Neurophysiology. 1985;53(4):959–978. doi: 10.1152/jn.1985.53.4.959. [DOI] [PubMed] [Google Scholar]
- Kwakkel G, Kollen BJ, Krebs HI. Effects of robot-assisted therapy on upper limb recovery after stroke: a systematic review. Neurorehabilitation and Neural Repair. 2008;22(2):111–121. doi: 10.1177/1545968307305457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwakkel G, van Peppen R, Wagenaar RC, Wood Dauphinee S, Richards C, Ashburn A, et al. Effects of augmented exercise therapy time after stroke: a meta-analysis. Stroke: A Journal of Cerebral Circulation. 2004;35(11):2529–2539. doi: 10.1161/01.STR.0000143153.76460.7d. [DOI] [PubMed] [Google Scholar]
- Landau WM, Sahrmann SA. Preservation of directly stimulated muscle strength in hemiplegia due to stroke. Archives of Neurology. 2002;59(9):1453–1457. doi: 10.1001/archneur.59.9.1453. [DOI] [PubMed] [Google Scholar]
- Lang CE, Wagner JM, Edwards DF, Dromerick AW. Upper extremity use in people with hemiparesis in the first few weeks after stroke. Journal of Neurologic Physical Therapy: JNPT. 2007;31(2):56–63. doi: 10.1097/NPT.0b013e31806748bd. [DOI] [PubMed] [Google Scholar]
- Langhorne P, Coupar F, Pollock A. Motor recovery after stroke: a systematic review. Lancet Neurology. 2009;8(8):741–754. doi: 10.1016/S1474-4422(09)70150-4. [DOI] [PubMed] [Google Scholar]
- Lee D, Port NL, Kruse W, Georgopoulos AP. Variability and correlated noise in the discharge of neurons in motor and parietal areas of the primate cortex. The Journal of Neuroscience. 1998;18:1161–1170. doi: 10.1523/JNEUROSCI.18-03-01161.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemon RN, Davis JN, Yang HW, Kirkwood PA, Armand J, Maier MA. Differences in the corticospinal projection from primary motor cortex and supplementary motor area to macaque upper limb motoneurons: an anatomical and electrophysiological study. Cerebral Cortex. 2002;12(3):281–296. doi: 10.1093/cercor/12.3.281. [DOI] [PubMed] [Google Scholar]
- Lindberg PG, Schmitz C, Engardt M, Forssberg H, Borg J. Use-dependent up- and down-regulation of sensorimotor brain circuits in stroke patients. Neurorehabilitation and Neural Repair. 2007;21(4):315–326. doi: 10.1177/1545968306296965. [DOI] [PubMed] [Google Scholar]
- Lindberg P, Schmitz C, Forssberg H, Engardt M, Borg J. Effects of passive-active movement training on upper limb motor function and cortical activation in chronic patients with stroke: a pilot study. Journal of Rehabilitation Medicine: Official Journal of the UEMS European Board of Physical and Rehabilitation Medicine. 2004;36(3):117–123. [PubMed] [Google Scholar]
- Luft AR, Schwarz S. Dopaminergic signals in primary motor cortex. International Journal of Developmental Neuroscience. 2009;27(5):415–421. doi: 10.1016/j.ijdevneu.2009.05.004. [DOI] [PubMed] [Google Scholar]
- Lytton WW, Stark JM, Yamasaki DS, Sober SJ. Computer models of stroke recovery: implications for neurorehabilitation. Neuroscientist. 1999;5:100–111. [Google Scholar]
- Maier MA, Perlmutter SI, Fetz EE. Response patterns and force relations of monkey spinal interneurons during active wrist movement. Journal of Neurophysiology. 1998;80(5):2495–2513. doi: 10.1152/jn.1998.80.5.2495. [DOI] [PubMed] [Google Scholar]
- Mazzoni P, Andersen RA, Jordan MI. A more biologically plausible learning rule for neural networks. Proceedings of the National Academy of Sciences of the United States of America. 1991;88(10):4433–4437. doi: 10.1073/pnas.88.10.4433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mewes K, Cheney PD. Facilitation and suppression of wrist and digit muscles from single rubromotoneuronal cells in the awake monkey. Journal of Neurophysiology. 1991;66(6):1965–1977. doi: 10.1152/jn.1991.66.6.1965. [DOI] [PubMed] [Google Scholar]
- Mirbagheri MM, Tsao CC, Rymer WZ. Changes of elbow kinematics and kinetics during 1 year after stroke. Muscle and Nerve. 2008;37(3):387–395. doi: 10.1002/mus.20965. [DOI] [PubMed] [Google Scholar]
- Muellbacher W, Richards C, Ziemann U, Wittenberg G, Weltz D, Boroojerdi B, et al. Improving hand function in chronic stroke. Archives of Neurology. 2002;59(8):1278–1282. doi: 10.1001/archneur.59.8.1278. [DOI] [PubMed] [Google Scholar]
- Page SJ, Gater DR, Bach-Y-Rita P. Reconsidering the motor recovery plateau in stroke rehabilitation. Archives of Physical Medicine and Rehabilitation. 2004;85(8):1377–1381. doi: 10.1016/j.apmr.2003.12.031. [DOI] [PubMed] [Google Scholar]
- Parry RH, Lincoln NB, Vass CD. Effect of severity of arm impairment on response to additional physiotherapy early after stroke. Clinical Rehabilitation. 1999;13(3):187–198. doi: 10.1177/026921559901300302. [DOI] [PubMed] [Google Scholar]
- Perlmutter SI, Maier MA, Fetz EE. Activity of spinal interneurons and their effects on forearm muscles during voluntary wrist movements in the monkey. Journal of Neurophysiology. 1998;80(5):2475–2494. doi: 10.1152/jn.1998.80.5.2475. [DOI] [PubMed] [Google Scholar]
- Powers RK, Binder MD. Input–output functions of mammalian motoneurons. Reviews of Physiology, Biochemistry and Pharmacology. 2001;143:137–263. doi: 10.1007/BFb0115594. [DOI] [PubMed] [Google Scholar]
- Reinkensmeyer DJ, Iobbi MG, Kahn LE, Kamper DG, Takahashi CD. Modeling reaching impairment after stroke using a population vector model of movement control that incorporates neural firing rate variability. Neural Computation. 2003;15(11):2619–2642. doi: 10.1162/089976603322385090. [DOI] [PubMed] [Google Scholar]
- Reinkensmeyer DJ, Maier MA, Guigon E, Chan V, Akoner OM, Wolbrecht ET, et al. Do robotic and non-robotic arm movement training drive motor recovery after stroke by a common neural mechanism? experimental evidence and a computational model. Proceedings of the 2009 IEEE engineering in medicine and biology conference; 2009. pp. 2439–2441. 2009. [DOI] [PubMed] [Google Scholar]
- Rijntjes M. Mechanisms of recovery in stroke patients with hemiparesis or aphasia: new insights, old questions and the meaning of therapies. Current Opinion in Neurology. 2006;19(1):76–83. doi: 10.1097/01.wco.0000203886.28068.38. [DOI] [PubMed] [Google Scholar]
- Rohrer B, Fasoli S, Krebs HI, Hughes R, Volpe B, Frontera WR, et al. Movement smoothness changes during stroke recovery. The Journal of Neuroscience. 2002;22(18):8297–8304. doi: 10.1523/JNEUROSCI.22-18-08297.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schweighofer N, Han CE, Wolf SL, Arbib MA, Winstein CJ. A functional threshold for long-term use of hand and arm function can be determined: predictions from a computational model and supporting data from the extremity constraint-induced therapy evaluation (EXCITE) trial. Physical Therapy. 2009;89(12):1327–1336. doi: 10.2522/ptj.20080402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sober SJ, Stark JM, Yamasaki DS, Lytton WW. Receptive field changes after strokelike cortical ablation: a role for activation dynamics. Journal of Neurophysiology. 1997;78(6):3438–3443. doi: 10.1152/jn.1997.78.6.3438. [DOI] [PubMed] [Google Scholar]
- Stein RB. Neuronal variability: noise or part of the signal? Nature Reviews Neuroscience. 2005;6(5):389–397. doi: 10.1038/nrn1668. [DOI] [PubMed] [Google Scholar]
- Stinear CM. Functional potential in chronic stroke patients depends on corticospinal tract integrity. Brain. 2007;130(Pt. 1):170–180. doi: 10.1093/brain/awl333. [DOI] [PubMed] [Google Scholar]
- Sunderland A, Tinson D, Bradley L, Hewer RL. Arm function after stroke. An evaluation of grip strength as a measure of recovery and a prognostic indicator. Journal of Neurology, Neurosurgery and Psychiatry. 1989;52(11):1267–1272. doi: 10.1136/jnnp.52.11.1267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton RS, Barto AG. Reinforcement learning: an introduction. MIT Press; Cambridge, MA: 1998. [Google Scholar]
- Teasell R, Bitensky J, Salter K, Bayona NA. The role of timing and intensity of rehabilitation therapies. Topics in Stroke Rehabilitation. 2005;12(3):46–57. doi: 10.1310/ETDP-6DR4-D617-VMVF. [DOI] [PubMed] [Google Scholar]
- Thickbroom GW. Motor outcome after subcortical stroke: MEPs correlate with hand strength but not dexterity. Clinical Neurophysiology. 2002;113(12):2025–2029. doi: 10.1016/s1388-2457(02)00318-8. [DOI] [PubMed] [Google Scholar]
- van der Lee J, Snels I, Beckerman H, Lankhorst G, Wagenaar R, Bouter L. Exercise therapy for arm function in stroke patients: a systematic review of randomized controlled trial. Clinical Rehabilitation. 2001;15:20–31. doi: 10.1191/026921501677557755. [DOI] [PubMed] [Google Scholar]
- Ward NS, Newton JM, Swayne OB, Lee L, Frackowiak RS, Thompson AJ, et al. The relationship between brain activity and peak grip force is modulated by corticospinal system integrity after subcortical stroke. The European Journal of Neuroscience. 2007;25(6):1865–1873. doi: 10.1111/j.1460-9568.2007.05434.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Werfel J, Xie X, Seung HS. Learning curves for stochastic gradient descent in linear feedforward networks. Neural Computation. 2005;17(12):2699–2718. doi: 10.1162/089976605774320539. [DOI] [PubMed] [Google Scholar]
- Williams RJ. Simple statistical gradient following algorithms for connectionist reinforcement learning. Machine Learning. 1992;8:229–256. [Google Scholar]
- Zhou P, Suresh NL, Rymer WZ. Model based sensitivity analysis of EMG-force relation with respect to motor unit properties: applications to muscle paresis in stroke. Annals of Biomedical Engineering. 2007;35(9):1521–1531. doi: 10.1007/s10439-007-9329-3. [DOI] [PubMed] [Google Scholar]