Using Bayesian networks to explore the role of weather as a potential determinant of disease in pigs

Abstract

Many pathogens are sensitive to climatic variables and this is reflected in their seasonality of occurrence and transmission. The identification of environmental conditions that influence disease occurrence can be subtle, particularly considering their complex interdependencies in addition to those relationships between climate and disease. Statistical treatment of environmental variables is often dependent on their correlations and thus descriptions of climate are often restricted to means rather than accounting for the more precise aspects (including mean, maximum, minimum, variability). Here we utilize a novel multivariate statistical modelling approach, additive Bayesian network (ABN) analyses, to identify the inter-linkages of different weather variables to better capture short-term environmental conditions that are important drivers of disease.

We present a case study that explores weather as a driver of disease in livestock systems. We utilize quality assurance health scheme data on ten major diseases of pigs from 875 finishing pig herds distributed across the United Kingdom over 7 years (2005–2011). We examine the relationship between the occurrence of these pathologies and contemporary weather conditions measured by local meteorological stations.

All ten pathologies were associated with at least 2 other pathologies (maximum 6). Three pathologies were associated directly with temperature variables: papular dermatitis, enzootic pneumonia and milk spots. Latitude was strongly associated with multiple pathologies, though associations with longitude were eliminated when clustering for repeated observations of farms was assessed. The identification of relationships between climatic factors and different (potentially related) diseases offers a more comprehensive insight into the complex role of seasonal drivers and herd health status than traditional analytical methods.

1. Introduction

Pathogens play an important role in the productivity of farms: diseased animals have poorer performance. The transmission of many pathogens is sensitive to climatic factors that drive observed patterns of seasonality. For example, the survival of bacterial pathogens, helminthes and arthropod vectors are influenced by temperature and humidity that together influence their abundance and viability (Mas-Coma et al., 2008; Rogers and Randolph, 2006; Tang, 2009; Webster, 1981). Consequently, of particular current interest is how a changing climate will influence the dynamics of disease – in terms of economic productivity (Fofana et al., 2009; Gale et al., 2009; Kenyon et al., 2009; McInerney et al., 1992), food safety (Miraglia et al., 2009), food security (Gregory et al., 2005; McMichael, 2011) and zoonotic disease (Daszak et al., 2000).

In intensive livestock production systems – such as pig farms – considerable efforts are made to control or mitigate changes in the environment (Baxter, 1984; Feddes et al., 1983); examples include the management of airflows, reduction of dust, types of flooring and control of humidity to eliminate respiratory pathogens (Banhazi et al., 2008; Dawson, 1990; Heber et al., 1988; Stärk, 1999). Several reports indicate the presence of seasonal changes in disease occurrence in farmed pigs, suggesting that climatic factors play a substantial role driving pathogen (Sanchez-Vazquez et al., 2012b; Wagner and Polley, 1999) or disease patterns (Sanchez-Vazquez et al., 2012c; Stärk, 2000).

The environment is a complex multi-factorial combination of variables. In analyses whose main focus is identifying environmental risk factors or disease determinants, choices are often made about summarizing a few key variables, for example, through stepwise selection (Acevedo et al., 2010; McCluskey et al., 2003), data reduction with principle component analysis (Duchateau et al., 1997; Estrada-peña and Venzal, 2007) and partial Fourier series (Purse et al., 2007). These variables are then incorporated into modelling frameworks that might include regressions of bio-geographic variables on the presence of disease (Gilbert et al., 2005), pattern matching disease observations with climatic descriptors (Olwoch et al., 2003; Purse et al., 2007, 2004), utilizing expert opinion of major risk factors (Sumption et al., 2008) or comparison of time series (Sanchez-Vazquez et al., 2012c).

Here we present a case study which utilizes an additive Bayesian network (ABN) approach (Lewis and McCormick, 2012; Lewis et al., 2011) to examine the inter-linkages between a series of putative environmental risk factors and disease pathologies. Given that weather variables are highly interdependent, the ABN approach allows the separation of those weather factors that are directly connected from those that have co-dependence mediated through a series of intermediate factors (Lewis and McCormick, 2012) without excluding variables from an analysis on a statistical (rather than biological) basis. For example, although temperature (in the sense of average annual patterns) maybe predictive of broad ecological patterns such as the national burden of a particular pathology (Gilbert et al., 2005; Purse et al., 2007), what happens on an individual farm is a function of where that farm is located, local circumstances and the corresponding farm response.

In addition to the inclusion of weather factors, multiple disease conditions are included in the analyses presented to demonstrate that, by considering the holistic joint probabilities of inter-connected risks, the balance between climatic and non-climatic drivers can be incorporated into a single model and their relative influence assessed. The presence of any one disease may predispose animals to another; analytically, the first pathogen may not be related to weather, but through the association with a secondary pathogen that is climatically determined, there can be indirect association between environmental factors and the first pathogen. In contrast, more traditional generalized linear modelling (GLM) models that do not consider all joint probabilities of important components of a disease system are unable to distinguish between those risks that are directly or indirectly connected to health outcomes (Lewis and McCormick, 2012).

In this case study we use information on pig herd health, obtained from abattoir surveillance data, to contrast a number of pathologies that respond differently to climatic factors (Sanchez-Vazquez et al., 2012b,c, 2010). The collection of ten pathologies that are of importance to the economic productivity of farms describe a number of different aetiological routes; for example, papular dermatitis is related to sarcoptic mange (Cargill et al., 1997), enzootic-pneumonia is most closely associated with Mycoplasma hyopneumoniae (Maes et al., 1996) and milk spots are the result of Ascaris suum infection (Bindseil, 1973). These pathologies describe a complex web of interacting animal health challenges in which successive health insults can accumulate to weaken immune responses to otherwise unusual pathologies (Sanchez-Vazquez et al., 2012a). The presence of particular infections is known to influence the presence of other pathogens and some particular pathologies have been shown to follow seasonal patterns (Davies etal., 1991; Jacobs and Dunn, 1969; Sanchez-Vazquez etal., 2012c).

We describe here an application of ABN modelling which identifies potential relationships between climate and disease through analyses of readily available abattoir data. Through these results we show the utility of the ABN approach for elucidating complex environmental drivers of disease, in which the method presented is generic and applicable to many different diseases and food animal production systems.

2. Materials and methods

2.1. Pathology data

The BPEX Pig Health Scheme (BPHS) (Sanchez-Vazquez et al., 2011; Stärk and Nevel, 2009) provided abattoir surveillance data for 904 farms with batches of pigs sent for slaughter between July 2005 and June 2011, inclusive. The main objective of the BPHS is to improve awareness of the occurrence of economically important pig diseases, urging the implementation of strategies to improve productivity of the British pig industry. Approximately 33% of all British pig producers registered with assurance schemes are members of the BPHS, which is run as a voluntary scheme to provide farm-level information on diseases that manifest as gross lesions present at the abattoir (Stärk and Nevel, 2009). The BPHS farms are representative of approximately 75% of the English and Welsh commercial finishing pig population (Sanchez-Vazquez et al., 2011).

The number of farms included in the analysis was reduced to 875 when those missing covariate data were removed. This resulted in a total of 12,380 observed movements (a mean of 13.7 movements per farm). Pigs are moved to slaughter in batches (median 120 pigs per batch) that come from the same herd and a specialist swine veterinarian assesses a sample of each batch (median 50 animals from each batch) as they move down the slaughter line. Further details of the BPHS methodology can be found in Sanchez-Vazquez et al. (2011).

Ten batch-level conditions were included in the analysis as binary variables (the presence or absence of each pathology in at least one pig from a batch): enzootic-pneumonia, pleurisy, milk spots, hepatic scarring, pericarditis, peritonitis, lung abscess, pyaemia, tail damage, and papular dermatitis.

2.2. Weather data

Weather data, concurrent with the pig batches analyzed, were extracted from UK meteorological station records (UK Meteorological Office, 2012). Daily temperature, rainfall and wind speed data were averaged across stations within a 10 km radius of each farm. Although 10 km is geographically inclusive and likely to contain substantial variability across the area (Daniel, 1978), it was selected to ensure at least one meteorological station (based on the rarest of the weather variables – wind) per farm and still to capture the temporal variability in the weather associated with different batches of pigs. It is worth noting that the correlation between close meteorological stations is very high (e.g., see Hansen and Lebedeff, 1987) and using the more commonly utilized gridded climate data such as long term monthly averages (Hijmans et al., 2004; Mitchell et al., 2004; New et al., 2002) would homogenize the dates of pig batches to long-term monthly averages; and also that the grid cells are statistical interpolations of the raw meteorological station data (Hijmans et al., 2004; New et al., 2002).

Given that weather is changeable and that the relative impact of one or two days may not have substantial influence over a disease condition that requires several days to establish (by the time of slaughter, for example, for Ascaris eggs to develop, Seamster, 1950), the weather variables for the preceding 14 days were averaged (or summed in the case of rainfall). In this sense, the weather variables describe the average conditions when climatic conditions were (or not) consistently permissive for disease transmission or establishment rather than be biased by unusual anomalies at or near the time of slaughter (e.g., a single day that has a temperature suitable for bacterial growth is unlikely to result in a detectable lesion, whereas a period of consecutive days allows colonization).

For each batch of pigs the calculated weather variables were the mean minimum and maximum temperatures; the total degree-day warming (the sum of each degree ≥10 ° C per day); the total rainfall and the mean wind speed. Summaries of the variables available to the model are shown in Table S1 (supplementary information).

A sensitivity analysis was conducted to assess the impact of varying both the spatial and temporal windows. Meteorological data were summarized over a range of 1, 2.5, 5, 10, 20 and 50 km around each farm and from the preceding 5,7,10,14 and 21 days. The total number of arcs retained was compared and the frequency that any given arc between two variables was present in the Directed Acyclic Graph (DAG) was counted. The number of farms retained for each model in the sensitivity analysis was based on the most exclusive combination of time and distance (that is, meteorological stations ≤1 km away and only for the 5 days preceding slaughter) to ensure that the input observations were consistent for every iteration. The alternative would be to exclude only those farms that had missing data per combination of time and distance thresholds.

2.3. Bayesian networks

There is a considerable body of technical literature on Bayesian network modelling Key articles include: Friedman et al. (1999), Heckerman et al. (1995), Koivisto and Sood (2004). There exists, however, a paucity of articles dealing with models that are directly analogous to multivariate GLM and multivariate generalized linear mixed modelling (GLMM), which is what we utilize here. Note that we are referring to multivariate in the context of multiple dependent variables, as opposed to the usual multivariable GLM and GLMMs which comprise only one dependent and multiple independent covariates. Using the ABN methodology it is straightforward to construct fully multivariate GLM/GLMMs that are simply direct extensions of the usual regression models to include multiple dependent variables, that is a holistic statistical inference model comprising multiply inter-dependent variables, which we refer to as an additive Bayesian network model. This is a form of graphical modelling and ABN models comprise of two mutually dependent parts: a Directed Acyclic Graph (DAG); and a set of parameters. Each node in the DAG is the equivalent of the dependent variable in a (Bayesian) GLM or GLMM regression model potentially comprising the remaining nodes in the DAG. The ABN methodology is ideally suited to, and indeed arguably essential for, statistical analyses of data from highly complex epidemiological systems comprising many inter-dependent variables. We include in this definition both biological, ecological and environmental components. The specific statistical techniques used here are as previously described by Lewis and McCormick (2012).

A three-part procedure was used to determine an optimal ABN model for our case study data. First, we identify the single best model – specifically the DAG with optimal goodness of fit to the available data. The key part of this analysis is determining how to optimally combine all the individual component regression models (each individual node) into a single, probabilistically cohesive model describing all the joint relationships in the observed data (or technically the joint probability distribution of the data). Determining an optimal DAG is referred to in the technical literature as structure learning or structure discovery (Friedman et al., 1999; Heckerman et al., 1995). We utilize an established globally optimal search approach (Koivisto and Sood, 2004) which identifies a DAG whose goodness of fit is equal to the best possible goodness of fit of any DAG. Because this is a Bayesian analysis, prior distributions must be defined and a uniform structural prior was used – all DAG structures were equally supported in the absence of any data. We also used uninformative priors for all parameters at each node: specifically Gaussian distributions, with mean zero and variance 1000 for the additive (expectation) parameters and a diffuse Gamma distribution for the precision parameter in Gaussian nodes. Note that it is simply impractical to attempt to specify informative parameter priors because these would need to be given (and justifiable) for each and every combination of variables across the vast number of different models (DAG structures) being compared. At the end of this first step in the structure discovery process we will have identified a single best fitting multivariate GLM (ABN).

In the second step, the optimal DAG structure from the first step is pruned – arcs removed – to adjust for over-fitting. Over-fitting is an ever present and critical issue in statistical model comparison (Babyak, 2004). A standard and very robust, but extremely computationally intensive, parametric bootstrapping approach (Friedman et al., 1999) was used. This involves using Markov chain Monte Carlo (MCMC) simulation (in JAGS; Plummer, 2003) to generate realisations – simulated datasets of an identical size as the original – from the optimal model found in step one. An identical exact search for an optimal model structure was then performed exactly as used in the first step, but applied to the bootstrap rather than original data. This process was repeated many times and the frequency of each arc recorded. The general idea is to determine how much structure (arcs) can be reasonably recovered given a data set of the same size as the original. The bigger a data set, the more statistical power and therefore the more structure it can support. Arcs present in less than 50% of the globally optimal DAGs estimated from the bootstrap data were considered not to be robust and pruned from the DAG generated in the first step. A threshold of 50% structural support is the usual cut-off in BN analyses (Lewis and McCormick, 2012; Poon et al., 2007). At the end of this second step in the structure discovery process we will have identified a single most robust – that is a model fully adjusted for over-fitting – multivariate GLM (ABN).

The third and final step in the structure discovery process is to address potential within-group correlations. Batches of pigs from the same farm are potentially correlated as they are present within the same farm environment and likely subject to the same management processes. Not explicitly accounting for such within-group clustering can result in an underestimation of variance (reducing the reliability of confidence intervals and model goodness of fit estimates). The usual solution to this in regression analyses is to move from a GLM to a GLMM. We adopt a similar procedure where we introduce an independent Gaussian (mean 0, variance 1000) random effect (to adjust for within-farm correlation – each random effect comprises 875 terms, one for each farm) into each variable in our multivariate model. That is, each node in the DAG from step two becomes a GLMM rather than a GLM as previously – and so we now have a multivariate GLMM (ABN). This model was fitted to the observed data using MCMC (again via JAGS) following all the usual good practice measures (Congdon and Congdon, 2001) such as running multiple chains, visual inspection and use of the Gelman–Rubin convergence diagnostic, along with relatively large effective sample sizes (e.g., >1000 per parameter estimated). After including these random effect terms some arcs, which have so far been retained in the model, may no longer be supported due to the now potential increase in variance. Each arc denotes a marginal log odds ratio (binary node) or marginal mean (Gaussian node) and any arcs whose 95% credible intervals included zero were then dropped from the model. At the end of this final step in the structure discovery process we identify a single most robust joint statistical model of the observed data – fully adjusted for over-fitting and for within-groups correlation across all variables. This now gives us our optimal multivariate GLMM of the data – an additive Bayesian network model that describes all the statistically significant relationships with our complex epidemiological system of disease and environment.

2.4. GLM regression

The ABN approach was contrasted with more traditional GLM models. The purpose of such a comparison is to provide an example of the type of observation made in the well known Yule–Simpson paradox (Hand et al., 1997) – that taking a narrow univariate (single dependent variables/multivariable regression) – approach to risk factor analyses will, in general, not give the same results as a joint and truly multivariate approach (for more details also see Lewis and McCormick, 2012). This analysis is included for illustration only because in general it is not statistically valid to combine separately derived GLM models (each of which can be represented as a DAG with a single terminal node) into a single joint probability model. This would typically produce a graph with one or more cycles. Moreover, it is then highly subjective as to how these conflicting results can be resolved. This problem does not arise in ABN modelling because these are – by construction – joint probability models and therefore always acyclic. The GLM results presented are directly comparable with the ABN from the first step in the ABN model search process, as the best possible GLM is found for each node considering every possible combination of covariates. Also, identical parameter and structural priors are used as in the ABN analysis, and so the only difference here is that in the GLM search each response variable is considered separately, whereas in the ABN all variables are considered jointly. Note that while we use a GLMM approach to derive our final model (in step three above) that has no impact on this current comparison since the purpose here is to demonstrate the difference between a multivariable and multivariate regression. The inclusion or exclusion of random effects is irrelevant to this comparison.

All analyses were conducted using the authors' abn package for R (R Development Core Team, 2008) which is available from CRAN (cran.r-project.org) with additional documentation and case studies at www.r-bayesian-networks.org. The resultant networks (DAGs) were visualized with GraphViz (Ellson et al., 2003).

3. Results

3.1. Globally optimal DAG - multivariate GLM (ABN)

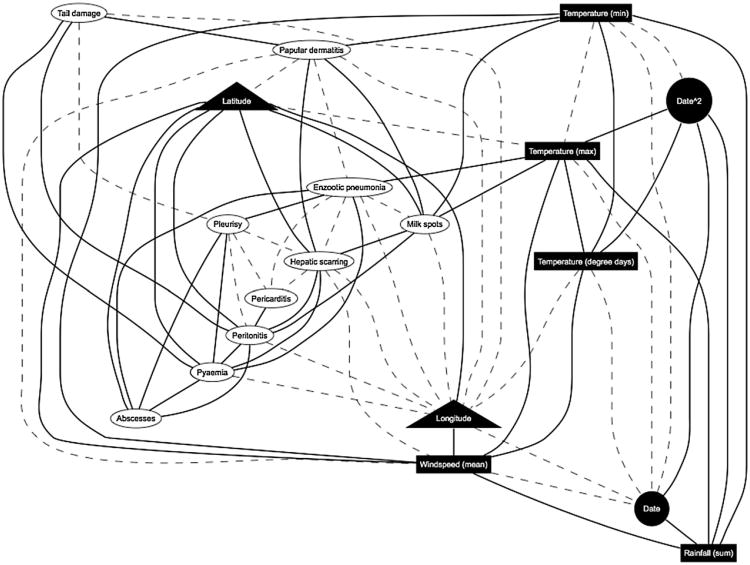
The best fitting global DAG is shown in Fig. 1 and comprises a total of 71 arcs. The presence of each and every arc resulted in an improved goodness of fit (as determined by the standard metric in Bayesian model comparison – the log marginal likelihood). This DAG was found by increasing the maximum number of parents allowed per node (number of covariates in each regression model at each node) until the goodness of fit no longer improved and therefore the same – and globally optimal – DAG was identified. The parent limit was increased from 1 to 10 and the goodness of fit no longer increased beyond nine parents per node. Increasing the parent limit gradually rather than simply setting it to be 18 (total number of nodes minus one) saves a vast amount of computing time as the structural search takes much longer each time the parent limit is increased. It took approximately 12 h (on a 3.2 Ghz, cpu) to identify the best possible DAG with eight parents and in excess of 20 h for the nine parents.

Fig. 1.

Most probable DAG (see Table 1 for variable names). Geographic variables, triangles; weather variables, rectangles; disease pathologies, ovals. Continuous nodes are shown in black, and binary variables in white. Dashed arcs are those lacking 50% support from bootstrapping, though present in the single best fitting DAG.

3.2. Sensitivity analysis of meteorological data selection

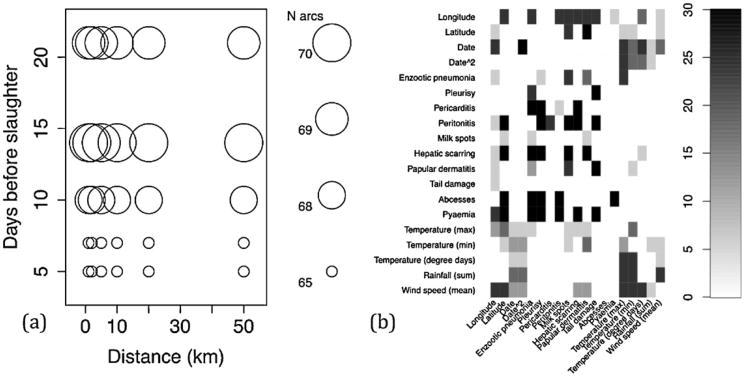
Changing the length of the temporal window preceding the movements of pigs to slaughter and the geographic radius within which to summarize the meteorological stations was used to assess the sensitivity of the optimal DAG to assumptions about the weather data. The total number of arcs found in the optimal DAG when the temporal and geographic thresholds for including weather data were changed ranged from 65 to 70. The number of arcs was insensitive to changing the geographic distance over which meteorological stations were averaged, but varied by number of days preceding the slaughter of pigs for which the weather was averaged (Fig. 2a). The specific identity of the arcs changed between iterations of the sensitivity analysis, although 28 were present in every combination of temporal and geographic windows and another 28 were present in 24 combinations (Fig. 2b). Those arcs that had less consistent support tended to include a weather node.

Fig. 2.

(a) The sensitivity of the total number of arcs identified in each combination of temporal and geographic window. (b) The number of times arcs were identified by each of the 30 combinations of time and geographic windows. Darker colours indicate more robust arcs.

3.3. Adjustment for over-fitting using parametric bootstrapping

A total of 256 bootstrapping analyses were performed, each comprising the generation of a data set and then performing an exact structural search using a parent limit of nine parents per node, as above. This took approximately 34 h across 128 × 2.8 Ghz processors on a grid computer. Tabulating the frequency that each arc (present in the globally optimal DAG identified using the original data) was recovered showed that 25 arcs did not meet the necessary 50% level of structural support to be considered sufficiently robust for inclusion in a reliable model of the data as the number of arcs was reduced from 71 to 46 (Fig. 1). Identical results were achieved by taking random subsets of size 128 from the 256 bootstrap analyses and computing how many arcs were recovered in at least 64 of these. This is convincing evidence that sufficient bootstrap analyses were run to achieve robust results.

3.4. Adjustment for correlated data - multivariate GLMM

Sixteen independent Monte Carlo Markov chains were run, each taking approximately 24 h to complete 50,000 iterations. Convergence diagnostics and visual inspection of the results confirmed that most – but crucially not all – parameters in the ABN were reliable. Fig. S2 (supplementary material) shows an example of a well-mixed chain for the parameter (posterior marginal log odds ratio) for the arc between hepatic scaring and peritonitis. Contrast this with the mixing in Fig. S3 (supplementary material) for the posterior marginal log odds ratio for the arc between latitude and peritonitis. By inspecting each of the parameters in the DAG there was a clear pattern that any arc involving either latitude or longitude had unreliable mixing, whereas all other parameters were well estimated. This behaviour was also apparent when the chains were run for 100,000 iterations and so this behaviour is unrelated to issues of convergence and burn-in; rather, this appears to be more an issue of model formulation and we return to this important issue in the context of environmental and climate variables in the discussion.

Based on the rather unusual – potentially unreliable – mixing in the above MCMC analyses, these were repeated but excluding latitude and longitude variables – temporarily – from the DAG. This resulted in well-behaved estimates for all parameters.

The purpose of the MCMC sampling was to assess whether some arcs are no longer robust after the inclusion of additional variance due to within-farm correlation. These new results suggest that almost all arcs were robust – they have posterior marginal log odds ratios (or mean effects) whose 95% confidence (credible) interval does not cross zero. There was one exception, the arc between the mean wind speed and Papular Dermatitis, whose 95% credibility interval overlapped zero and was therefore removed from the model (Fig. 1). All posterior densities are provided in the Supplementary material (Fig. 1). The median parameter estimates per node in the DAG, with the 95% credibility interval, are shown in Table 1. The final DAG (solid black arcs, Fig. 1) shows the most robust joint statistical model of our epidemiological system of interest: diseases and weather factors in pig production.

Table 1.

Parameter estimates for arcs remaining after pruning for within farm clustering and over fitting. The median and 95% credibility interval of the parameter estimate of each arc is shown.

Arc		Log odds (or mean effect)
Child	Parent	Median	Credibility Interval
		50%	2.50%	97.50%
Rainfall (sum)	Date ^ 2	−129	−149	−109
Rainfall (sum)	Temperature (max)	−16	−17	−16
Wind speed (mean)	Temperature (max)	−0.64	−0.67	−0.62
Milk spots	Temperature (max)	−0.044	−0.087	−0.0044
Enzootic pneumonia	Temperature (max)	−0.031	−0.044	−0.019
Wind speed (mean)	Temperature (degree days)	−0.0057	−0.0063	−0.005
Papular dermatitis	Temperature (min)	0.052	0.04	0.064
Milk spots	Temperature (min)	0.072	0.025	0.12
Abscesses	Peritonitis	0.23	0.11	0.36
Peritonitis	Milk spots	0.27	0.15	0.4
Milk spots	Papular dermatitis	0.32	0.2	0.45
Hepatic scarring	Papular dermatitis	0.33	0.23	0.44
Pyaemia	Peritonitis	0.4	0.22	0.56
Peritonitis	Tail damage	0.46	0.28	0.63
Pyaemia	Pleurisy	0.55	0.31	0.8
Pyaemia	Hepatic scarring	0.68	0.52	0.84
Abscesses	Enzootic pneumonia	0.71	0.52	0.92
Pyaemia	Enzootic pneumonia	0.75	0.45	1.1
Peritonitis	Pleurisy	0.77	0.58	0.96
Wind speed (mean)	Temperature (min)	0.78	0.75	0.82
Hepatic scarring	Milk spots	0.79	0.68	0.89
Papular dermatitis	Tail damage	0.79	0.62	0.96
Abscesses	Pyaemia	0.82	0.66	0.97
Pleurisy	Enzootic pneumonia	0.91	0.76	1.1
Peritonitis	Pericarditis	1	0.88	1.2
Peritonitis	Hepatic scarring	1	0.91	1.2
Abscesses	Pleurisy	1.2	1	1.4
Pyaemia	Tail damage	1.6	1.5	1.8
Temperature (max)	Date 2	2.6	2.3	2.9
Rainfall (sum)	Wind speed (mean)	6.1	5.7	6.5
Temperature (degree days)	Temperature (min)	6.8	5.8	7.9
Temperature (degree days)	Temperature (max)	17	16	17
Rainfall (sum)	Temperature (min)	19	18	20

3.5. Traditional multivariable (single dependent variable) GLMs

Comparison between the globally optimal DAG (all arcs shown in Fig. 1) and univariate GLMs (Fig. S6, supplementary information) highlighted four relationships in the GLMs that were in addition to those in the optimal DAG, and two that were not present (Table S3, supplementary information). Of the additional arcs in the GLM models, two were between temperature variables and latitude or longitude. These arcs that included latitude or longitude may be accounted for in the globally optimal model through other, better parameterized indirect relationships (e.g., minimum temperature might be more strongly correlated to both rainfall and maximum temperature than the latter are to each other). The GLM results failed to capture two relationships involving pleurisy – one in which pleurisy is statistically dependent with longitude and one where it is dependent with hepatic scaring.

4. Discussion

4.1. Biological interpretation

The optimal DAG contained two distinct clusters of the weather variables and almost entirely separately, the diseases. These two clusters had few (4) direct connections between one another, and those all included temperature variables.

Of the 41 arc there were just four direct arcs between weather and pathologies preserved after bootstrapping: minimum temperature and papular dermatitis; minimum temperature and milk spots; maximum temperature and milk spots; and maximum temperature and enzootic pneumonia. It is biologically plausible that papular dermatitis is related to temperatures since it is related to skin lesions from mites that are highly sensitive to temperatures, for example, surviving longer off-host at cooler temperatures (Arlian et al., 1989, 1984). Milk spots are associated with A. suum migration, the development of which have been shown to be sensitive to temperature with both upper and lower limits (Wagner and Polley, 1999). Enzootic pneumonia is a Mycoplasma caused respiratory disease associated with air circulation and pollutants (such as dust) and the structure of housing designed to mitigate external environmental conditions (Dawson, 1990; Stärk, 2000).

Total rainfall, wind speed and temperature were all interconnected. The identity of arcs between the weather variables tended to be intuitive, with for example, both the minimum and maximum temperatures associated with the degree-day warming. Similarly, the mean wind speed and total rainfall were negatively associated with maximum temperature.

Considering that the environment of pig production is strictly controlled (Baxter, 1984), it is not surprising that there are few direct relationships between weather variables and disease signs. What is interesting, however, is that there are many indirect connections that are mediated through geographic variables. Both latitude and longitude have extensive associations with pathologies and additional arcs to weather variables, though it is worth noting that the bootstrapping dramatically reduced the connectivity of longitude to other variables (with just 2 out of 11 arcs supported). This situation could be due to real regional differences in the health status (presence or absence of specific pathogens) that account for factors other than weather. One example might be the presence of a small number of large production enterprises and veterinary practices and their respective health programmes that are common to multiple farms within a geographic region (Sanchez-Vazquez et al., 2010). We have assumed that the farms subscribing to the BPHS and included in this analysis are a random sample, and therefore do not introduce systematic biases (e.g., due to different pig breeds). However, given that subscription to the BPHS is voluntary there is potential for particular enterprises to be over-represented. Additionally, the geography of the UK has a strong influence on the climate – particularly along a diagonal south-west to north-east axis. In this way many management factors based around fixed infrastructure (such as type of flooring and positioning of fans) are influenced by longer term climatic patterns and are likely to be captured more by the geographic coordinates than the specific weather conditions at the time of the movement of pigs to slaughter.

The sensitivity analysis suggests that the geographic area over which the weather was summarized did not play a substantial role in influencing the relationship between weather and the presence of pathologies. This was not true of the temporal window preceding the movement of pigs to slaughter. Given that different pathologies are likely to have different time courses for manifestation of clinical signs it is unsurprising that changing the temporal window influenced the total number of arcs identified – the longer the temporal window, overall the more relationships were identified.

4.2. Some statistical considerations

Accounting for correlation between farms proved rather more complex than originally envisaged, though retrospectively this was readily understood given the nature of the variables included in the modelling. A random effect was introduced into each variable (node) to allow for over-dispersion at individual farm level, that is, to allow farms with the same covariate pattern to be more different from each other than would normally be allowed under assumed Gaussian sampling. However, there is a potential difficulty with this approach when one or more of the covariates also takes a unique value for each farm – in this case, latitude and longitude – as this also allows something akin to a unique farm level adjustment. As the effect of latitude and longitude is included as the average effect over all farms in the data, it is then theoretically conceivable that they could be estimated in addition to the usual farm specific random effect term. However, as we observe with our data, this is likely data set specific. In our case, the effect of latitude and longitude is relatively poorly estimated. The results do strongly suggest that the data have updated the uninformative prior to some extent (e.g., in Fig. S3 the density does definitely not cross zero). The trace plots are so different that to be sure these results were reliable the chains would need to be run for a vastly longer duration – computationally challenging, given it took 24 h for each chain shown. This may be something to consider in a future study where perhaps it is necessary to develop a custom MCMC sampler rather than use either JAGS or WinBUGS (which are flexible but much slower than bespoke code). The other option (as was done here) is simply to remove these variables from the final adjustment under the assumption that they are not sufficiently well estimated to be reliable when included along with farm level (i.e., geographically unique) correlation adjustment.

4.3. Contrast with standard multivariable modelling approaches

A fair comparison between GLMs and using an ABN (without attempts to account for random effects – only comparing the globally optimal DAG, produced in step 1 and GLMs) resulted in differing results between the two approaches. This then raises the question of which is to be preferred. The Yule–Simpson paradox strongly suggests the ABN approach based on conceptual grounds. Moreover, because an ABN is simply a direct generalization of a GLM/GLMM to multiple dimensions, then it arguably makes little sense to choose a special case of this methodology over the more general approach. Finally, as already mentioned and as demonstrated in our results, there is an inherent statistical difficulty in treating multivariate data as individually dependent variables and then combing the analyses. While this approach is rather intuitive and very simple to implement in practice, it can provide both contradictory results and an acyclic model (which is not permitted in usual probability calculus). This then introduces into the analyses an unavoidably ad hoc judgement about which arcs are to be included or not, and in which direction to avoid cycles and therefore produce a valid statistical model. It is better to start with a fully joint regression model, that is, an ABN.

It is also important to note that the ABN does not attempt to attribute causality or direction of association. In contrast to the language of ‘predictors’ that is common to more traditional GLM type models, the ABN estimates the co-dependency of all available variables. To a priori selectively ban particular relationships yields a complicated mix of causal and statistical relationships that are conceptually difficult to disentangle (Heckerman et al., 1995). For example, the aim of the ABN is to identify the presence of statistical dependency (the presence of an arc) whereas the direction of an arc is essentially a secondary issue that requires more detailed experimental analysis to establish causality.

5. Conclusion

A novel multivariate modelling approach – additive Bayesian networks (ABN) – is presented. It is analogous to multivariate (multiple dependent variables) generalized linear/generalized linear mixed modelling. The ABN framework is a form of graphical modelling and allows ready interpretation of complex epidemiological systems. Given the highly inter-dependent relationships between climatic factors, their role in driving patterns of disease is complex. Whether climatic factors drive the seasonality of diseases directly, or act through a chain of intermediate variables, is helpful in understanding possible breakpoints that might lend themselves to interventions.

A wide range of diseases, identified through abattoir monitoring of pig carcasses, were shown to be highly inter-dependent. Two diseases, enzoonotic pneumonia and papular dermatitis, both with biologically plausible associations with climatic factors were shown to have direct links to climatic variables. The clustering of weather variables, with just four direct links to the pig diseases, suggests that in this case climate is an indirect contributing factor to the remaining diseases studied. However strong linkages between geographical coordinates, unique to each farm and both the clusters of disease and climatic variables, suggest that other farm-specific factors (including the physical structure and management of farms as influenced by more general climatic patterns) are likely to be stronger predictors of disease rather than the weather immediately preceding slaughter.

The case study presented focuses on pig production and porcine diseases. However, the multivariate analytical approach presented is generic and widely applicable to studies of complex systems consisting of epidemiological, ecological and environmental aspects for any species of food animal.