Registration of histological whole slide images guided by vessel structures

Abstract

Introduction:

The registration of histological whole slide images is an important prerequisite for modern histological image analysis. A partial reconstruction of the original volume allows e.g. colocalization analysis of tissue parameters or high-detail reconstructions of anatomical structures in 3D.

Methods:

In this paper, we present an automatic staining-invariant registration method, and as part of that, introduce a novel vessel-based rigid registration algorithm using a custom similarity measure. The method is based on an iterative best-fit matching of prominent vessel structures.

Results:

We evaluated our method on a sophisticated synthetic dataset as well as on real histological whole slide images. Based on labeled vessel structures we compared the relative differences for corresponding structures. The average positional error was close to 0, the median for the size change factor was 1, and the median overlap was 0.77.

Conclusion:

The results show that our approach is very robust and creates high quality reconstructions. The key element for the resulting quality is our novel rigid registration algorithm.

INTRODUCTION

The introduction of histological whole slide scanners was a significant step forward in histology and histopathology, since they enable a digitized workflow and a broader application of software tools for analysis. With this, new opportunities as well as new challenges arise for digital processing, one of which is the registration of histological slides, which always undergo deformations during the acquisition process. A partial reconstruction of the original volume is an essential step for example in the colocalization analysis of tissue parameters. Furthermore, a reconstructed histological 3-Dimensional (3D) volume allows insights into anatomical and tissue structures at scales that modern 3D acquisition methods such as microtomoraphy (MicroCT) are not able to deliver. Difficulties for registration algorithms, besides the deformations, are different stainings applied to the slides to exhibit various tissue parameters, leading to virtually unpredictable visual appearances.

In this paper, we present a robust staining-invariant method for the registration of consecutive histological slides, by combining rigid and elastic approaches. We especially focus on the rigid registration, since its robustness is essential for a successful subsequent elastic registration. We introduce a novel vessel-based rigid registration algorithm that employs a new similarity measure. The example cases employed in this paper are tissue sections of rat liver, but the algorithm is designed to be generally applicable to any tissue that exhibits vessel structures.

Several works have been published on the registration of histological slides. However, they usually give little consideration to the rigid deformations. Sharma, et al.,[1] and Wirtz et al.,[2] perform a principal component analysis for pre-alignment, which is prone to errors especially if the tissue sample is of rather circular shape. Feuerstein, et al.,[3] and Dauguet, et al.,[4] use block face images as external reference. However, such images are, in most cases, not available since they require additional effort and hardware during the slide acquisition. Ourselin, et al.,[5] and Cifor, et al.,[6] utilize a block matching algorithm, but their method relies on an intensity-based similarity matching, a constraint also shared by the methods of Tan, et al.,[7] as well as Bağci and Bai.[8] Schmitt, et al.,[9] published a detailed description on an intensity-based method for reconstructing a whole rat brain.

METHODS

During the acquisition of histological whole slide images two types of deformations occur: Non-linear deformations are introduced by the cutting process with the microtome and while mounting the tissue section on the microscope slide. At best, only small non-linear deformations occur, but in the worst case the tissue can have jags and disruptions. Mounting the tissue on the slide also introduces larger linear deformations composed by rotation and translation.

Our method addresses the two types of deformations in independent steps. First, a rigid pre-registration, which is the main focus of this paper, aims to align consecutive slides to roughly match their alignment in the original tissue sample block. Afterwards, non-linear registration is applied, which is based on established registration techniques and is, therefore, addressed only briefly in this paper.

When registering histological slides, intensity-based methods are vulnerable to consecutive slides being stained differently. Therefore, in both steps of our method we rely on vessel structures as features to guide the registration, since they are detectable despite different staining.

VESSEL EXTRACTION

Our method is designed to work on images that exhibit vessel structures, which are washed out during preparation of the tissue, and thus, appear significantly brighter on the image. Therefore, the required extraction method is rather simple, especially since the rigid registration is robustly designed to be able to deal with a coarse segmentation, which may even miss several vessel structures.

Thus, to roughly extract the vessel structures of a slide [see Figure 2a for an example slide], we first convert the red, green, blue (RGB) colors to gray values, using the lightness method: Grayvalue = 0.5 · (max (R,G,B) + min (R,G,B)). We then invert the gray values and apply Otsu's thresholding. From the resulting mask image we select the largest connected component and apply a closing operation to remove small noise. The closing kernel was set to 3 × 3 for our input images on which we selected a magnification level with a pixel spacing of around 30 μm. We reach our final vessel mask image by inverting the image values, keeping only those individual components of the mask image which are not connected to the image border.

Figure 2.

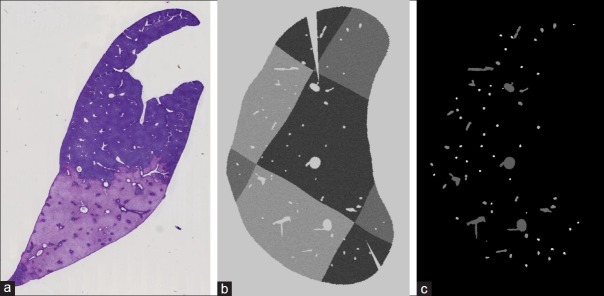
(a) A real histological slide of a rat liver. (b) A synthetic histological slide. (c) Corresponding label slide for automatic evaluation. Each vessel label in each slide has a unique ID throughout the whole dataset

It has to be noted that what we call “vessel mask” does most likely not contain exclusively vessel structures. This is due to the fact that tissue artifacts like discrete holes and disruptions also appear bright on the image and are thus included in the vessel mask. However, the rigid registration method, as described in the following section, is especially designed to deal not only with the fact that in the mask image some vessel structures might be missing but also that artifacts might be present.

RIGID PRE-REGISTRATION

Our rigid registration method considers the individual connected components of two consecutive vessel mask image slides as feature objects a_i ∈A and b_k ∈B. A classic approach to match those two sets of objects would be the iterative closest point (ICP) algorithm.[10] However, the difficulty in our case is that several of the objects a_i ∈ A might not have a corresponding object b_k ∈ B (and vice versa). Reasons for this can be that the object is an artifact or that the vessel-extraction step (see section Vessel Extraction) missed the vessel in the other slide. In any case, this makes the ICP approach inapplicable.

The basic idea of our method is to take subsets A₀ ⊂ A and B₀ ⊂ B containing some prominent structures that are most likely vessels, then from the subsets take a pair (a_i,a_j) and a pair (b_k,b_l) and compute a transformation that aligns the two pairs. Now we evaluate how well that transformation matches the whole set A₀ with B₀, and in the evaluation measure, we consider the fact that some objects from one set are allowed to have no corresponding objects in the other set. This process is repeated for all possible pair combinations of A₀ and B₀ to find the transformation that produces the best match. In detail the procedure works as follows:

To select the subsets of A and B, we require the following features for each object o ∈ A ∪ B:

with μ_pq (0) being the central moments of the image mask region that corresponds to o, λ₁≤λ₂ being the eigenvalues of the two principal components of that mask region, size(o) being the area and perimeter(o) the perimeter of the mask region. Further, let o.x and o.y be the x and y coordinates of the center of gravity of the corresponding mask region.

In the subsets A₀ ⊂ A and B₀ ⊂ B we include objects with size(o) ≥ 600 μm² and ellipticity – (1 – (ellipticity – eccentricity)) > 0. The size constraint rules out small objects, since on the one hand it is difficult to decide if they are actual vessels or artifacts, and on the other hand, even if they are vessels, the small objects are the ones most likely to be missed by the vessel extraction, thus not having corresponding objects in the other set. The purpose of the second term is to select only objects that have an elliptic shape while not allowing the ellipse to be stretched too much. The ellipticity measure alone is already a good indicator if an object is a vessel or not; including the eccentricity constraint rules out tears in the tissue as well as vessels that run rather in-plane with the tissue slide. This is important because we are looking for vessels that run rather perpendicular to the tissue slide and thus are supposed to have a good continuation and overlap on the next slide. Furthermore, the objects are sorted by their size and only the 15 biggest are taken into each subset, thus considering the more prominent structures.

Based on the two sets A₀ and B₀, we try different transformations to determine the one creating the best match between A₀ and B₀. For that we iterate over all possible combinations of double pairs {(a_i,a_j),(b_k,b_l)}, with a_i,a_j ∈ A₀; b_k,b_l ∈ B₀ and a_i≠a_j; b_k≠b_l.

In each iteration step, we compute the transformation matrix 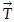that will translate b_k onto a_i and rotate the positions such that a_i,a_j,b_k and b_l are in line [see also Figure 1]:

Figure 1.

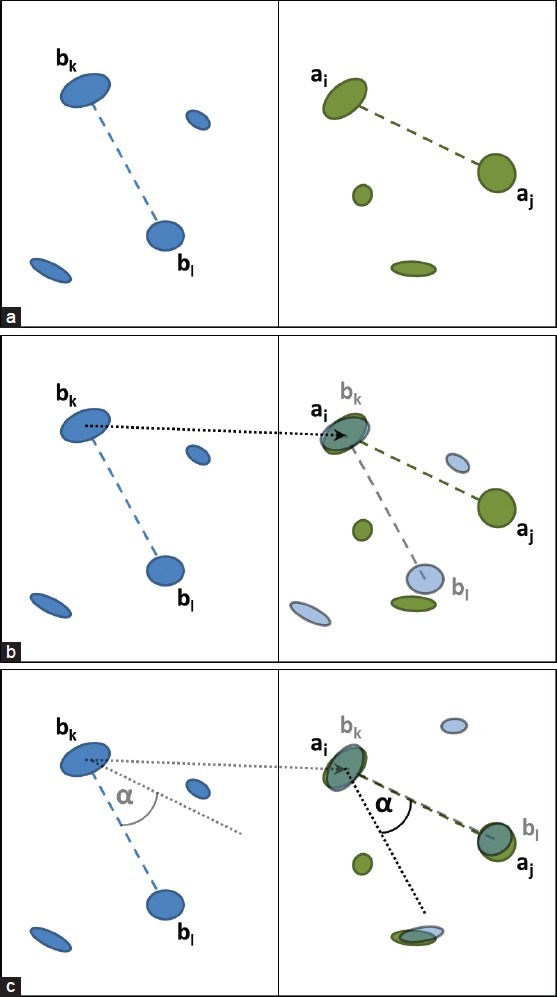
Compute a transformation based on a double pair: (a) Original configuration. (b) Translate b_k onto a_i. (c) Pivot around a_i to align a_j and b_l.

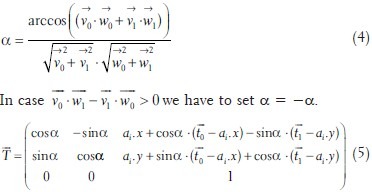
Then we change the positions of all b_m∈B₀ by applying the transformation 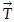. Those objects with the altered position we denote .

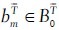To assess the matching quality between A₀ and 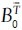we use a custom similarity measure denoted σ_T. The similarity measure has to reflect that a good registration transformation needs to result in an overall good continuation between objects from A₀ to objects from 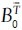. To be able to assess this in the computation of σ_T, we first define the matching cost δ_m,n between a 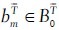and an a_n ∈ A₀:

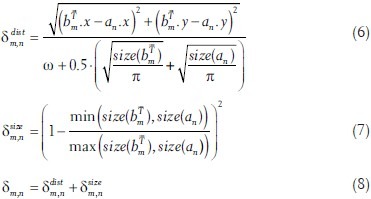
This matching cost considers two things: First, 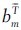and a_n are more likely to be a good match, the closer they are located to each other. The ω in the denominator of equation 6 is a variable that might be adjusted by the user to adjust the distance range. However, in all our tests, we set ω = 750 μm. The further term in the denominator allows more distance for bigger objects. The second consideration is that objects are more likely to be a match if their size difference is small, which is reflected in equation 7.

As mentioned before, our similarity measure also has to consider the possibility that some objects of one set might not have a corresponding object in the other set. To be able to include this in the similarity measure we also define a fixed cost, in case a 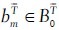is not assigned to an a_n ∈ A₀ or vice versa (symbolized by ɸ):

δ_m,ɸ = 1      (9)

δ_ɸ,n = 1      (10)

Since we, obviously, do not know the correct assignments between objects from 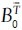and A₀, our similarity measure σ_T is calculated by finding the assignments that yield the lowest overall matching cost. This works as follows: Let 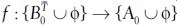be a function of assignments between the objects from 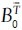and A₀, such that each 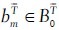and each a_n ∈ A₀ appear exactly once while ɸ may appear arbitrarily often with the restriction that ɸ → ɸ is forbidden. Further, let Ƒ be the set {ƒ₁,..,ƒ_p} that represents all possible permutations of assignment functions. Note that we explicitly allow assignment functions where objects from 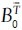are assigned to ɸ while at the same time ɸ is assigned to objects from A₀. This accounts for the fact that several objects in 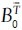actually might not have a matching object in A₀ and vice versa. This consideration contributes significantly to the robustness of the registration strategy.

We compute the similarity value σ_T for the current transformation 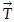by finding the assignment ƒ ∈ F that yields the minimal sum of matching costs:

Since we are iterating over all plausible transformations 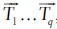the final transformation 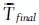for the rigid registration is selected such that σ_Tfinal = min(σ_T1,..,α_Tq).

ELASTIC REGISTRATION

Tissue deformations introduced during slide preparation are compensated using a non-linear image registration scheme. As these changes are typically unpredictable, a generic deformable registration approach is employed, performing a pair-wise consecutive alignment of two-dimensional slice images. The method is implemented as part of a modular software framework, integrating a multi-resolution strategy and efficient parallel computations.[11] It uses non-parametric transformations with Dirichlet boundary conditions.[12] Regularization of the calculated displacement field is enforced by explicit a-posteriori kernel-filtering with the discrete linear-elastic potential,[13] producing smooth and divergence-free deformations. Successive iterates of the displacement are concatenated by composition of the deformations.[14]

Contrary to other approaches, the proposed registration is performed entirely on the distance-weighted vessel mask images. As adjacent image slices are, therefore, invariant to local intensity distributions and particular variations in staining, the intensity-based sum-of-squared-differences measure can be used to guide the registration process.[12] Finally, computed displacements are applied to the original slice images.

EVALUATION

To evaluate our method against a human independent ground truth, we created a synthetic dataset resembling a rat liver.* For that we computed a vascular tree model by constrained constructive optimization. To simulate the effect of the staining, a checkerboard pattern of three different intensities was applied to the simulated liver tissue and Gaussian noise (σ =7.0) was added. To simulate the cutting and mounting process, an elastic deformation with a random field was applied to each simulated histological slide, followed by a rigid deformation with a random rotation and translation. Additional cuts were introduced at random positions. See Figure 2b for an example of a synthetic slide. The pixel spacing of our synthetic data is 30 μm, the resolution is 827 × 827 per slide. To be able to evaluate the registration automatically, for each simulated histological slide, we also generated a corresponding label image with individual labels for each single vessel structure on each slide. To those slides we applied the same deformations as to the corresponding synthetic histological slides. See Figure 2c for an example of such a label slide.

For evaluation, we selected 100 consecutive slides from the middle of the synthetic dataset. Starting with the first of those slides, each slide was automatically registered to its preceding slide. To be able to automatically compare the result to the ground truth we registered the first slide to its preceding non-deformed slice. The resulting deformation fields were then used to apply the same registration to the corresponding deformed label slides.

First we will look at the quality of the rigid registration, since this step is crucial for the success of the subsequent elastic registration. We compared the rotation and translation resulting from the rigid registration with the transformation matrix that was originally applied. The top row of Figure 3 shows the observed rotation and transformation errors. The error accumulates with increasing slice number, but remains still moderate considering the max. rotation error being around 15° and the max. translation error around 150 μm (5 pixels). The average and max. inter-slide error in rotation is 1.06° and 5.75°, respectively. Hence, the results indicate a very good and robust quality of the rigid registration method. Furthermore, these errors are mainly due to the elastic deformations and are thus impossible to be completely compensated by the rigid registration. This became apparent, when we evaluated the rigid registration on the same synthetic dataset, but only applied the rigid deformation without the additional elastic deformation during the construction. As the bottom row in Figure 3 shows, the rigid registration errors are significantly lower in this case.

Figure 3.

Rigid registration errors: (a) Rotation error on rigid + elastic (top) and only rigid (bottom) deformed synthetic data. (b) Translation error (Euclidean distance) on rigid + elastic (top) and only rigid (bottom) deformed synthetic data

The automatic evaluation of the overall registration (rigid + elastic) was done by comparing the original (non-deformed) with the registered (and previously deformed) label slides (with overall more than 6,000 labels). The labels allowed us to follow the continuations of the vessels through the slides and to measure the differences in those continuations between the original and the registered dataset.

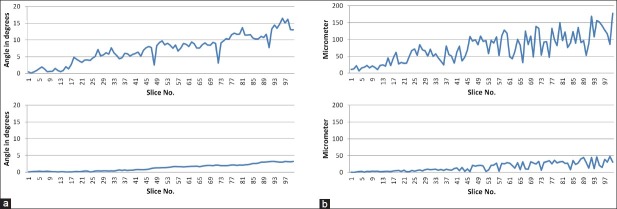
The first measure investigated to assess the registration quality was the direction and distance of the continuations of all labeled vessel structures from one slide to the next. We compared the relative differences for corresponding structures in the original and registered image slides. Figure 4a shows that the two inner quartiles stay very close to the optimum (0). Also the 1.5 interquartile ranges (IQRs) are still within a range of ±120 μm. Thus for most vessel structures the inter-slice continuation error is below 4 pixels.

Figure 4.

Boxplots of overall registration errors (red line = median, left/right end of box = lower/upper quartile, whiskers = 1.5 interquartile range (IQR)): (a) Relative inter-slice position error. (b) Size changes and inter-slice overlap changes

As second and third measures, we assessed the changes in size that were introduced by the registration as well as the effect to the overlap of continuing structures [Figure 4b]. The factor of size change stays within a reasonable range: The median is 1, the two inner quartiles are 1.08 and 0.9, and the 1.5 IQRs range from 0.65-1.3. The general tendency of the overlap in the registered slides is to decrease (median is 0.77) due to the positional and size changes, but rarely loses continuation completely.

The average computation time for the rigid registration was 9.18 seconds per synthetic slide and for the elastic registration 80.81 seconds per slide, measured on a HP EliteBook 8540w, Intel Core i7 CPU Q820 @ 1.73GHz and 16GB RAM.

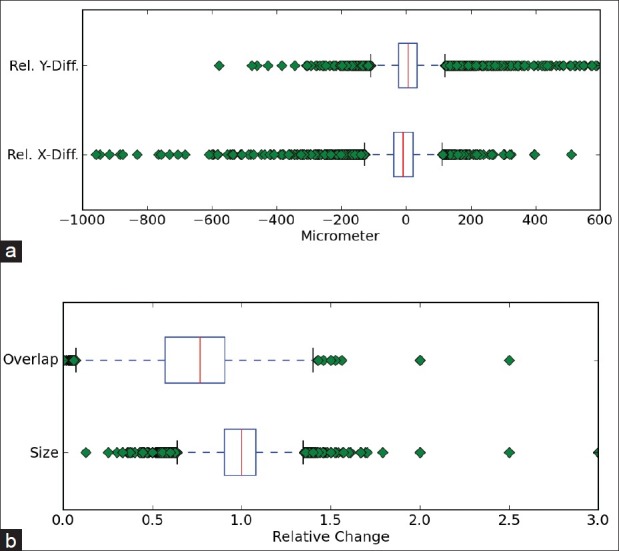
We also tested our method on three different histological whole slide stacks of rat livers with 144, 108, and 30 slides. For each stack, we selected the magnification which was closest to 30 μm pixel spacing (29.1 μm, 29.1 μm and 29.7 μm). Only the second example stack caused problems in 12 of the 108 slices. Those 12 slides were then sorted out, because they showed severe disruptions [see Figure 5 for some examples of those slides], hence, they could not be used for further analysis anyway. The visual inspection confirmed the quality and robustness of our registration method as indicated by the results on the synthetic dataset. See Figure 6 for examples of some successfully registered slides of one dataset. Figures 7a and 7b show cross sections of the according unregistered and registered stacks of slides. The rigid registration aligns the slides already very well, but we can also clearly see the improvement in detail the elastic registration is able to gain.

Figure 5.

Some example slides that failed to be correctly registered due to severe disruptions

Figure 6.

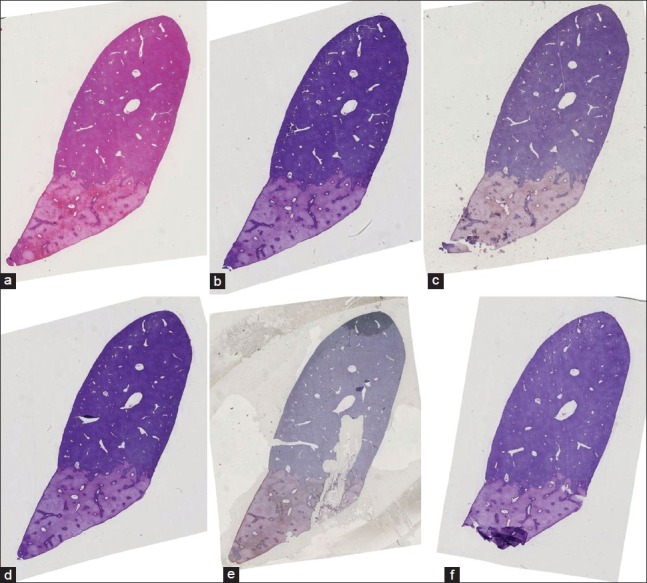
Example of six consecutive slides that have been registered successfully even though some rather difficult cases are apparent

Figure 7.

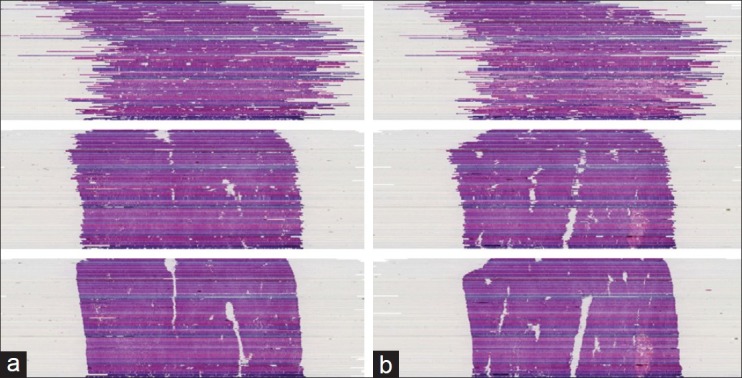
(a) (b) Example cross sections of a registered histological dataset. Top: No registration. Middle: Only rigid registration. Bottom: Full registration (rigid + elastic)

CONCLUSION

In this paper, we presented an automatic registration method to create 3D reconstructions of stacks of histological whole slide images for samples that exhibit vessel structures. We introduced a novel vessel-based rigid registration algorithm that uses a new similarity measure and is invariant to different stainings. Our approach focuses on the rigid registration while for the elastic registration, we employed established and reliable components. This is due to the fact that the non-linear deformations are expected to be moderate, since the tissue is very fragile and severe deformations would render the tissue useless for analysis and diagnosis anyway.

We performed a thorough evaluation of our method on a synthetic dataset as well as a visual evaluation on histological images, demonstrating the robustness and quality of our registration. For now, our method was only tested on rat liver examples. However, it was designed to work also for other organ types (e.g. kidney) and species - as long as the samples exhibit vessel structures - by merely adapting size parameters. The evaluation on that remains future work.

Further future work is to be done on the refinement of the elastic registration. Our current approach performs the registration only on a low magnification level (around 30 μm pixel spacing), which means that it does not make use of the higher details available on higher magnifications. While our registration already delivers good results, we expect to be able to even improve the registration quality in the future by introducing a multi-resolution registration strategy.

The rigid registration as main contribution of this paper, however, already proved to be robust and precise to serve as a fully automatic pre-registration step for any subsequent elastic registration. Our method can be used to enable colocalization analysis for differently stained consecutive tissue slides in clinical practice. Furthermore it is an important step towards full reconstructions of 3D histological volumes.