Intensity Invariant Dynamics and Odor-Specific Latencies in Olfactory Receptor Neuron Response

Abstract

Odors elicit spatiotemporal patterns of activity in the brain. Spatial patterns arise from the specificity of the interaction between odorants and odorant receptors expressed in different olfactory receptor neurons (ORNs), but the origin of temporal patterns of activity and their role in odor coding remain unclear. We investigate how physiological aspects of ORN response and physical aspects of odor stimuli give rise to diverse responses in Drosophila ORNs. We show that odor stimuli have intrinsic dynamics that depend on odor type and strongly affect ORN response. Using linear–nonlinear modeling to remove the contribution of the stimulus dynamics from the ORN dynamics, we study the physiological properties of the response to different odorants and concentrations. For several odorants and receptor types, the ORN response dynamics normalized by the peak response are independent of stimulus intensity for a large portion of the dynamic range of the neuron. Adaptation to a background odor changes the gain and dynamic range of the response but does not affect normalized response dynamics. Stimulating ORNs with various odorants reveals significant odor-dependent delays in the ORN response functions. However, these differences can be dominated by differences in stimulus dynamics. In one case the response of one ORN to two odorants is predicted solely from measurements of the odor signals. Within a large portion of their dynamic range, ORNs can capture information about stimulus dynamics independently from intensity while introducing odor-dependent delays. How insects might use odor-specific stimulus dynamics and ORN dynamics in discrimination and navigation tasks remains an open question.

Introduction

Insects and vertebrates olfactory receptor neurons (ORNs) project to segregated regions of the brain called glomeruli, in which they make synaptic connections with second-order neurons according to the odorant receptor they express (Su et al., 2009). Most odorants elicit distinct patterns of activity in the population of ORNs and in the glomeruli, suggesting that odors are encoded in spatial combinatorial maps (Malnic et al., 1999; Duchamp-Viret et al., 2000; Hallem and Carlson, 2006).

In locusts, flies, and moths, odor-evoked firing patterns are organized not only in space but also in time (Stopfer et al., 2003; Daly et al., 2004; Lei et al., 2004; Wilson et al., 2004). Fruit flies with only one functional class of ORNs can discriminate between odors (DasGupta and Waddell, 2008). These and other studies in vertebrates (Mozell, 1964b; Friedrich and Laurent, 2001; Spors et al., 2006; Schaefer and Margrie, 2007; Junek et al., 2010; Smear et al., 2011) suggested that information about odor stimuli might be encoded in temporal patterns in addition to spatial patterns of neural activity. In the locust, independent information about identity and intensity of odor stimuli can be extracted from the analysis of spatiotemporal patterns of activity of projection neurons (PNs; the neural targets of ORN) (Stopfer et al., 2003), even in the presence of temporally structured stimuli (Brown et al., 2005). Temporally diverse PN responses likely originate from temporally diverse ORN responses (Raman et al., 2010), raising the question of what determines the dynamics of the ORN responses.

In Drosophila, the diversity of ORN response dynamics has been attributed to the kinetics of interaction between odorants and receptors (Hallem and Carlson, 2006; Nagel and Wilson, 2011). However, characterization of the ORN response dynamics has been complicated by their dependency on odor concentration (Hallem and Carlson, 2006). Moreover, with few exceptions (Nagel and Wilson, 2011), previous studies have assumed that stimulus dynamics are independent of odor identity, but recent results show that response dynamics to a mixture of excitatory and inhibitory odorants might be affected by the odor-specific dynamics of the stimulus itself (Su et al., 2011) and depend on odor-dependent physico-chemical processes (Andersson et al., 2012). Hence, odor-receptor identity, odorant concentration, and odor-specific stimulus dynamics may all contribute to ORN response dynamics.

We combined single-sensillum recordings from the fly antennae and maxillary palps with direct measurements of the time-dependent concentration of the odor. To separate physiological aspects of ORN response from physical aspect of the odor-dependent stimulus dynamics, we used linear–nonlinear (LN) modeling. We found that, for a large portion of the ORN dynamic range, response dynamics tend to be phasic and independent of stimulus and background intensities. Near the bottom of the dynamic range, ORN response dynamics tend to be more tonic but transition to phasic as odor concentration is increased. Saturating stimuli tend to elicit prolonged responses. Removal of stimulus dynamics from ORN response revealed that different odorants induce different response delays (up to 18 ms in our dataset) and only marginally affect the shape of the response function.

Materials and Methods

Fly stocks.

Recordings from the ORNs ab3A, ab2A, ab7A, and pb1A were performed on adult female Canton-S flies 5 d after eclosion. To facilitate sorting of ab3B spikes, we killed the ab3A neuron by expressing UAS–reaper (w; UAS–rpr; Or22a–GAL4) (Su et al., 2011); recordings were performed on adult females flies 7 d after eclosion.

Electrophysiology.

Single sensillum recordings were performed as described previously (de Bruyne et al., 2001). Electrical signal was amplified using an Iso-DAM amplifier (World Precision Instruments), bandpass filtered (300 Hz to 2kHz), digitized at 10 kHz (NI-USB6221 digital acquisition board), and acquired in LabView. Spikes were sorted using a custom MATLAB routine.

Odor delivery.

All odor dilutions were prepared in paraffin oil (volumetric ratio). (1) For single puffs (see Figs. 1, 3, 5), as described previously (de Bruyne et al., 2001), 50 μl of odor dilution was placed in a paper filter contained in a Pasteur pipette; a three-way solenoid valve redirected an airstream (3 ml/s) through the pipette that was manually placed into a hole on the side of the main delivery tube in which a clean airstream (30 ml/s) was continuously running (see Fig. 1a). This setup allows the delivery of multiple concentrations of odor on the same neuron. When the photoionization detector (PID) was not used, the main airstream was humidified by passing it through a bottle containing distilled water. (2) For random stimulation (see Figs. 7–9), 20 ml of odor dilution were placed in a bottle (100 ml). A small three-way solenoid valve (The Lee Company) was placed in a hole on the side of the main delivery tube and was used to redirect the odor airstream from the exhaust to the delivery tube. Before starting recordings, the odor bottle was placed in the setup for 10–15 min to let the odor gas-phase reach equilibrium. We used a magnetic stirrer to facilitate equilibration of the liquid-phase preparation. A new solenoid valve was used for each odor. (3) For adaptation to a background (see Fig. 4), a constant background was delivered through the bottle into the main airstream, and puffs of increasing concentration were delivered through the Pasteur pipette as described above. Note that odor dilutions prepared in the Pasteur pipette do not result in the same gas-phase concentration as odor dilution prepared in the bottle. For methyl butyrate, the secondary airstream was 3 ml/s, and different background intensities were obtained with different dilutions of odor in paraffin oil (10⁻⁴, 3 × 10⁻⁴, 10⁻³). For ethyl acetate, we used two dilutions (10⁻², 10⁻³), but we observed a slow drift in the background intensity due to the slow depletion of odor concentration in the bottle. The drift is not significant within a trial but becomes significant when comparing different trials. Therefore, for the data analysis of Figure 4, we grouped the available trials based on PID measurements of the background stimulus. For ethyl butyrate, we used a fixed dilution (10⁻⁵) and changed the secondary flow rate to obtain different background intensities (0.5 and 1.2 ml/s). A lower flow rate allows maintaining a stable background for longer time. We checked that the specific method used to change the background intensity does not affect the results. (4) “Natural” stimuli used for Figure 2 were generated as depicted in Figure 2, a and b.

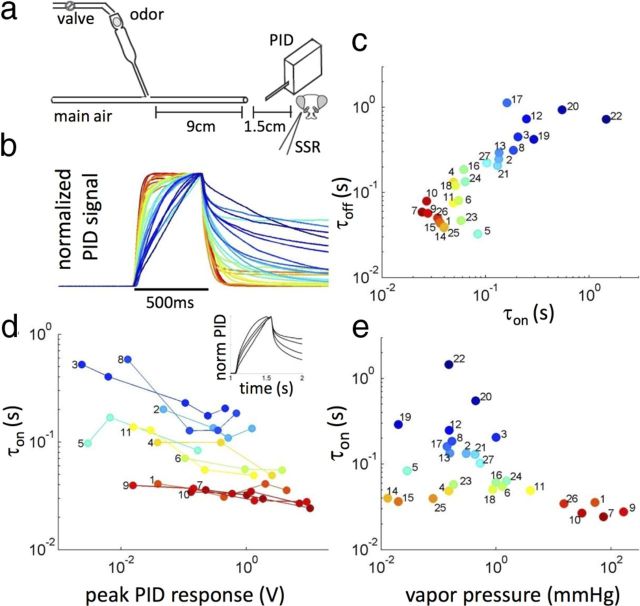
Figure 1.

Common odors exhibit a broad range of dynamics. a, Odor stimuli were generated driving an airstream through a Pasteur pipette containing odor dilution (see Materials and Methods). PID measurements were performed at the normal locus of the fly, ∼1.5 cm downstream from the exit of the delivery tube. b, Mean PID signal measured for 27 odors and normalized by peak response (n = 3–6). c, Rising and decay timescales τ_on(off) were estimated by fitting a double-exponential function to the PID signal (see Materials and Methods). Rising and decay timescales are correlated but not identical (r = 0.84, p = 10⁻⁷). d, Dependence of rising timescale on odor concentration. Connected dots represent different concentrations of the same odor and are plotted as a function of peak PID signal. Different odors are colored as in b and c. Inset, Normalized PID signal for linalool (dilutions, 3 × 10⁻³, 10⁻², 3 × 10⁻², 10⁻¹). e, Vapor pressure is anticorrelated with the rising timescale τ_on (r = −0.45, p = 0.018). The odors include the following: 1, 2,3-butanedione; 2, 2-methylphenol; 3, 4-methylphenol; 4, 6-methyl-5-hepten-2-on; 5, α-terpineol; 6, benzaldehyde; 7, ethyl acetate; 8, linalool; 9, methyl acetate; 10, methyl butyrate; 11, methyl hexanoate; 12, γ-hexalactone; 13, 3-methylthio-1-propanol; 14, geraniol; 15, β-citronellol; 16, 1-hexanol; 17, 1-octanol; 18, E2-hexenol; 19, ethyl octanoate; 20, diethyl succinate; 21, butyric acid; 22, pentanoic acid; 23, hexanoic acid; 24, isobutyric acid; 25, nerol; 26, isobutyl acetate; 27, 1-octen-3-ol.

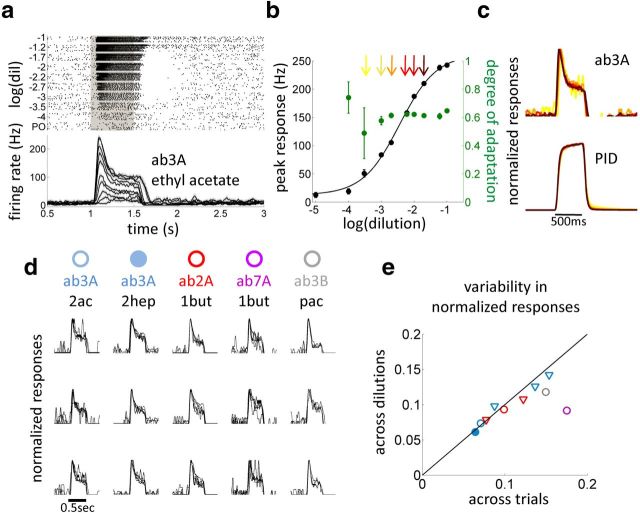
Figure 3.

Intensity invariant ORN response dynamics. a, Raster and PSTH of ab3A response to 500 ms puffs (gray) of increasing concentrations of ethyl acetate (dilutions prepared in paraffin oil as labeled). Dark gray, Standard error on 12 ORNs from 4 flies. b, Black, Peak response of ab3A as a function of ethyl acetate dilutions. Green, Degree of adaptation measured as the peak response minus the adapted response (measured 500 ms after stimulus onset) divided by the peak response. c, PSTHs and PID signals normalized by peak response collapse onto single curves for the odor concentrations arrowed in b. d, Normalized PSTH of single neuron responses are independent of stimulus intensity. Three neurons showed for each odor–receptor combination (2ac, ethyl acetate; 2hept, 2-heptanone; 1but, methyl butyrate; pac, propyl acetate). In each plot, different curves represent the response to different concentrations of the same odorant. e, Variability of normalized responses (see Materials and Methods) calculated across dilutions is smaller or equal than the variability across trials (repetition of the experiment were performed on 12 ORNs of the same type recorded from 3 to 4 animals). Circles correspond to the same odor–receptor combinations as in d, blue triangles correspond to ab3A response to methyl butyrate, methyl acetate, and 1-pentanol, and red triangles correspond to ab2A response to methyl acetate and ethyl acetate.

Figure 5.

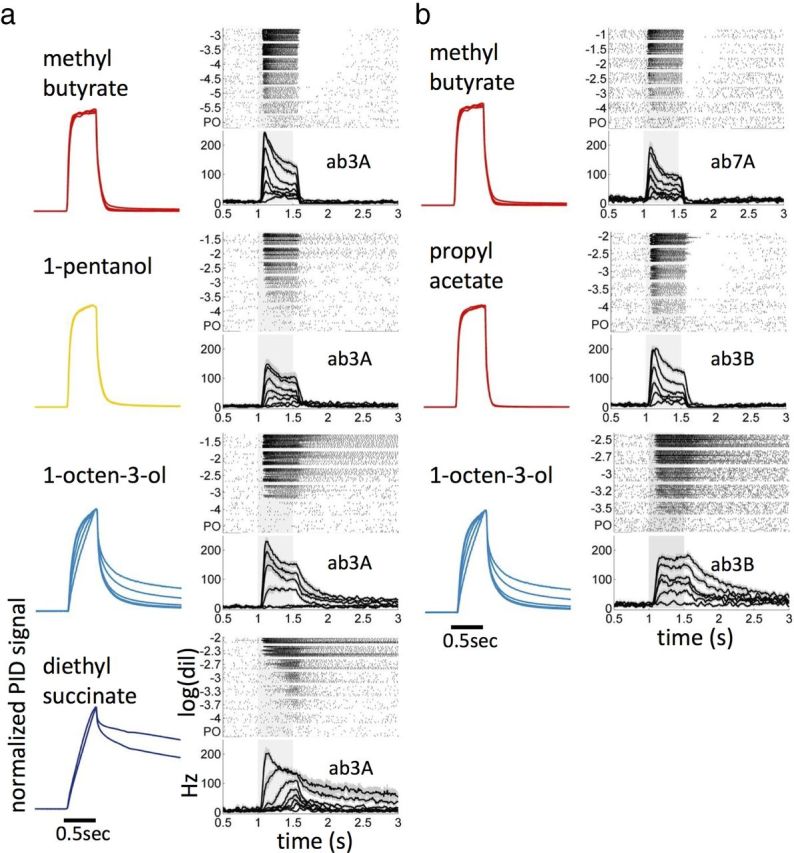
Stimulus dynamics depends on odorant type and affect ORN response dynamics. a, Left column, Normalized PID traces for multiple dilutions of the odor signal measured at the fly position when a short square puff is generated in the delivery tube. For fast odorants, the stimulus dynamics is invariant with respect to concentration, whereas for slow odorants it depends on the liquid dilution (Fig. 1d). Right column, Raster plot and PSTH of ab3A response to the corresponding odorants at increasing dilutions. b, Same as a for different odor–receptor combinations. Note that we were not able to obtain a PID measurement for all the dilutions used to stimulate the ORN due to the lower sensitivity of the PID compared with that of the ORN. Dilutions used for the PID measurements: methyl butyrate, 10⁻³, 5 × 10⁻³, 10⁻², 10⁻¹; 1-pentanol, 10⁻², 3 × 10⁻²,10⁻¹, 3 × 10⁻¹; 1-octen-3-ol, 10⁻³, 3 × 10⁻³, 10⁻², 3 × 10⁻², 10⁻¹; diethyl succinate, 3 × 10⁻², 10⁻¹; propyl acetate, 10⁻², 3 × 10⁻², 10⁻¹.

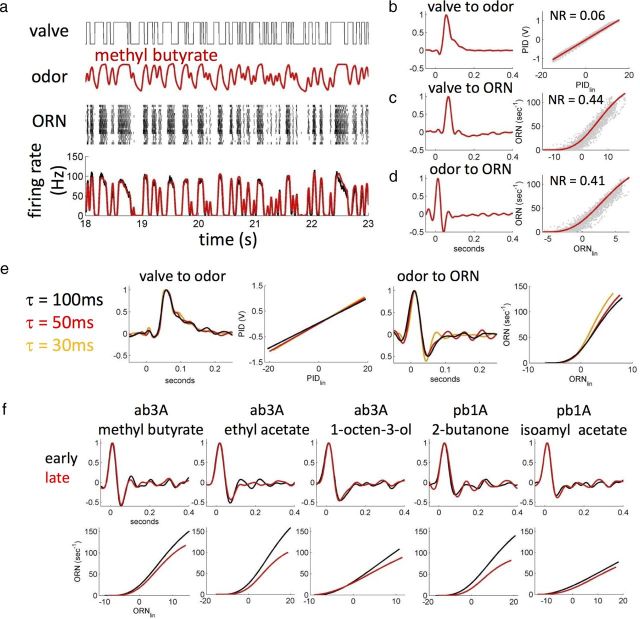
Figure 7.

Adaptive properties of ab3A response quantified using an LN model. a, Top to bottom, On–Off state of the valve driving the odor; PID response measured at the fly; and raster plot and PSTH of ab3A response (black, n = 18) and prediction from LN model obtained using the filter shown in d (red). Stimulus sequence was 30 s long with 30 ms correlation time. b–d, LN models for valve-to-odor, valve-to-ab3A, and odor-to-ab3A transformations. Left to right, Linear filter k(t) and nonlinear static transformation N. NR indicates the quality of the model prediction, and a value <1 means that the prediction is within the variance of the response (see Materials and Methods). e, Adaptive response to flickering stimuli with different correlation times. All three correlation times were tested on each neuron (n = 13), and the stimulus sequences was 30 s long. Left, Valve-to-odor transformation is independent from the stimulus correlation time. Right, Odor-to-ab3A transformation shows a faster negative lobe for shorter correlation times. f, After the onset of a stationary flickering stimulus, ab3A and pb1A adapt their gain but not their response kinetics. Filters and static functions were extracted for the first 10 s (early response) and the last 10 s (late response) of a 60-s-long flickering sequence with 100 ms correlation time. Top, Linear filters are identical for early and late responses for all odor–receptor combinations. Bottom, The static function shows a decrease in slope of different degree for the different odor–receptor combinations.

Figure 8.

ab3A response to a slow odor can be predicted using the LN model fitted to the response to methyl butyrate. a, Top to bottom, On–Off state of the valve driving the odor; PID response measured at the fly; and raster plot and PSTH of ab3A response (black, n = 18) and prediction from LN model obtained using the odor-to-ORN filter (blue). Both 1-octen-3-ol and methyl butyrate (Fig. 7) were presented in series on the same neurons. A stimulus sequence was 30 s long with 30 ms correlation time. A recovery time of 3–5 min was allowed between stimulations. b, Linear filters for valve-to-odor, valve-to-ab3A, and odor-to-ab3A transformations for both methyl butyrate (red) and 1-octen-3-ol (blue). c, Prediction (purple) of the measured response of ab3A (black) to 1-octen-3-ol (PID; blue) using the model of ab3A (red) built from the response to methyl butyrate. Odor signal was shifted by 4 ms to take into account the shift in the response function (see also Fig. 9). It was also appropriately normalized to take into account the different gains of the PID and ORN responses to the different odorants.

Figure 9.

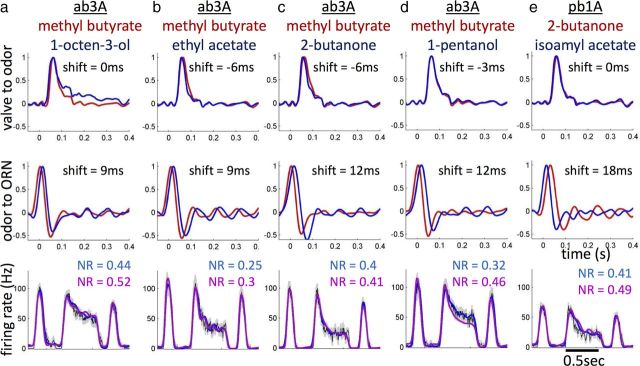
Odor-dependent delays in the ORN response function. Top and middle, Linear filters extracted for valve-to-odor and odor-to-ORN transformations for different odor–receptor combinations. Odor pairs were tested on the same neurons by presenting two 60-s-long time series of stimulus flickering at 100 ms correlation time one after the other. A recovery time of 3–5 min was allowed between stimulations. The shift between the two filters was estimated as the difference in the time-to-peak between the odor in red and the one in dark blue. A negative shift in the valve-to-odor filters is due to the fact that the odor in dark blue is delivered through a valve that is slightly closer to the exit of the delivery tube. A variation in the secondary flow rate of 1% was allowed to adjust stimulus concentration: this caused different values of the delay for different odor pairs. All delays measured in the valve-to-odor filters were consistent with the delay estimated from the speed of the airstream and the relative position of the two valves. The delays quantified for the odor-to-ORN linear filters already account for the differences in the position of the valve and represent delays in the physiological response of the neurons. Bottom, Cross-prediction of the response to the odor in blue given the filter extracted for the odor in red. Black, Mean firing rate in response to the “blue” odor; blue, firing rate predicted using the filter in blue; purple, firing rate predicted using the filter in red.

Figure 4.

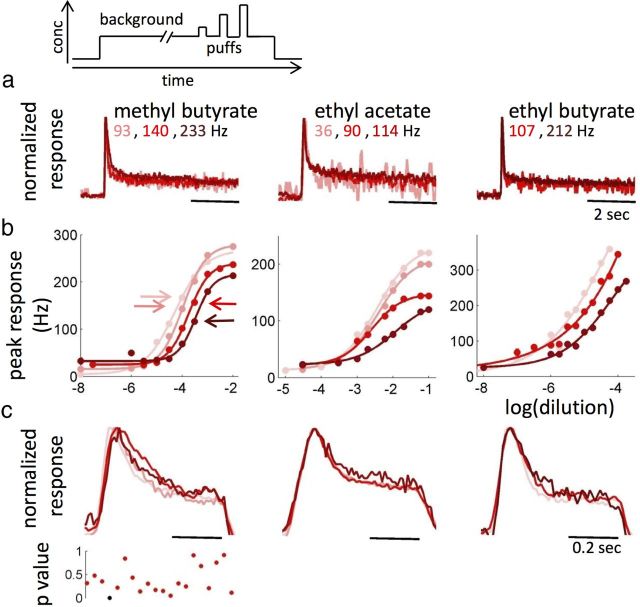
Normalized response dynamics is independent of background intensity. Experimental procedure (top and Materials and Methods): a constant stable background of odorant was used to adapt the neuron response. After ∼1 min, 500 ms puffs of increasing concentrations of the same odor were applied. a, PSTH of ab3A response to the background stimulus normalized by peak response. Labels correspond to the peak response used to normalize each curve (methyl butyrate, n = 12; ethyl acetate, n = 5–8; ethyl butyrate, n = 12). b, Peak response to the puffs applied on top of the background as a function of dilution for different background intensities. Dots indicate mean ± SEM peak response; error bars are too small to be visible. Lines are fit with $y=B+A\frac{x^n}{x^n+K^n}$. c, Top, PSTH of the response to 500 ms puffs normalized by peak response. One concentration for each background as arrowed in b. Bottom, p value obtained by ANOVA performed on the mean responses at each time point (bins of 30 ms); red indicates p > 0.05.

Figure 2.

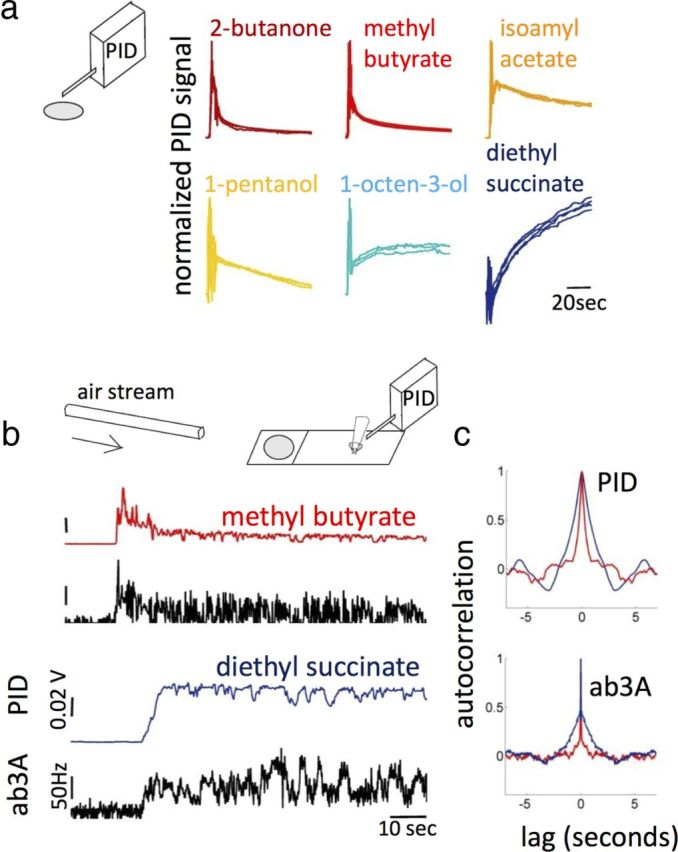
Dynamics of odor stimuli in more natural delivery conditions. a, Odor concentration measured 1.5 cm above a liquid source in the absence of wind (apart for the small suction of the PID): n = 4, all traces shown. The initial transient is due to the preparation of the odor source. b, Odor stimulus carried by a wind downstream from the source. PID traces (colored) and PSTH from ab3A responses (black). Distances are as follows: mouth of tube to odor source, 2.5 cm; odor source to fly and PID, 3 cm; fly to PID perpendicular to the flow, 0.7 cm. c, Autocorrelation of the fluctuations around the mean of odor stimulus (top) and ab3A response (bottom). Only the last 70 s of data were used to calculate the autocorrelation. Mean value of the PID trace was removed using the MATLAB function “detrend.”

PID measurements.

A fast-response mini-PID (200a; Aurora Scientific) was used to measure gas-phase concentration of the odor stimuli (Vetter et al., 2006; Schuckel et al., 2008). Linearity of the PID response was tested using a tracer gas (propylene). Timescales plotted in Figures 1 and 2 were obtained by fitting A_{on, off} e^{−t/τ_{on, off}} + A_{on, off}¹ e^{−t/τ_{on, off}1} to the rising and decaying phase of the PID traces. The first exponential captures the amplitude and the speed of the response to a change in stimulus, and the corresponding parameters have been plotted in Figures 1 and 2. The second exponential has a much smaller amplitude (A¹ ≪ A) and a slower timescale (τ¹ ≫ τ).

Data analyses.

Data analysis was performed in MATLAB. Unless otherwise specified, peristimulus time histograms (PSTH) were calculated as the average firing rate across n trials in 10 ms bins smoothed by a 50 ms squared window (n = 10–12 trials). PID measurements were averaged in the same way (n = 4–12 trials). For normalized responses, basal activity (mean activity in 1 s before stimulus) was subtracted before dividing by peak response. In Figure 3e, for each odor–receptor combination, we considered all the trials (n = 10–12) and three dilutions within the dynamic range. We defined r_id(t) as the normalized time-dependent response of neuron i to concentration d and calculated the variance between different trials averaged over all the dilutions as P_trial = 〈〈〈(r_id(t) − 〈r_id(t)〉_i)²〉_i〉_t〉_d and the variance between different dilutions averaged over all trials as P_dil = 〈〈〈(r_id(t) − 〈r_id(t)〉_d)²〉_d〉_t〉_i. In Figure 6, ab3A firing rate was normalized, and the first 3 s after the stimulus onset were considered for the analysis. Each time bin corresponds to a dimension, and the time-dependent firing rate for each odor represents a point in an n-dimensional space (n = 301 time bins). Principal component analysis (PCA) was used to visualize the distribution of firing traces in the temporal space and was performed using the MATLAB routine “princomp. ” Dendrograms were built from pairwise Euclidean distances between the normalized traces using the MATLAB routine “dendrogram.”

Figure 6.

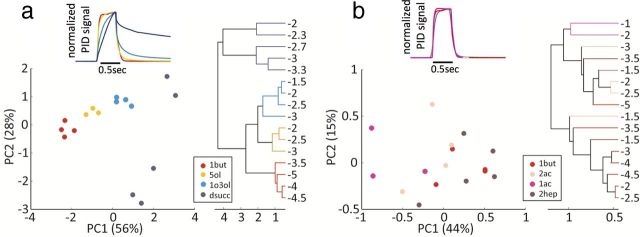
Temporal differences in ORN responses could enhance discrimination between odors of different speed. a, PCA and hierarchical clustering of ab3A response dynamics shown in Figure 5a normalized by peak response (only concentrations within the sensitive regime of the neuron were used). The 3 s after stimulus onset were considered for the analysis. Projection onto the first two principal components shows that responses to different concentrations of the same odor cluster together and odor types are clearly separated in this representation. 1but, methyl butyrate; 5ol, 1-pentanol; 1o3ol, 1-octen-3-ol; dsucc, diethyl succinate. Inset, PID measurements of the same four odorants illustrate the differences in stimulus dynamics. b, Same analysis as in a for the response of ab3A to four odors with similar dynamics (inset). Responses to the different odors are very similar, and simple classification algorithm cannot separate odor type from intensity. 1but, methyl butyrate; 2ac, ethyl acetate; 1ac, methyl acetate; 2hep, 2-heptanone.

LN model.

An LN model assumes that the neuron response can be decomposed into a linear filter k(t) and a static nonlinear function N such that the response r_LN(t) to a time-dependent stimulus s(t) is r_LN(t) = N(∫_−∞^ts(t′)k(t − t′)dt′) (Dayan and Abbott, 2001). We extracted linear filters from data by performing a linear regression to minimize the squared error between predicted r_lin(t) = ∫_−∞^ts(t′)k(t − t′)dt′ and measured response r(t). A random stimulus was generated by opening and closing the valve placed on the delivery tube according to a pseudorandom sequence of zeros (closed) and ones (open) (Geffen et al., 2009; Nagel and Wilson, 2011). The state of the valve was updated at time intervals of length τ. We considered values of τ between 30 and 100 ms. The full sequence was L = 30–60 s long depending on the dataset. The resulting stimulus had a flat power spectrum up to a cutoff frequency imposed by the minimum length of the on and off intervals, τ. Because the input stimulus has relatively low power at high frequencies, estimation of the filter is very sensitive to high-frequency noise. Filters were regularized using elasticnet method (Zou and Hastie, 2005) that allows both L1 and L2 constraints to the linear regression: K = argmin_K (||R − ΣK||² + λ₂ ||K||² + λ₁ ||K||₁), where K is the linear filter, R is the neuron response, Σ is the matrix of the time-shifted stimulus, and λ₁ and λ₂ are regularization parameters. We used the same set of parameters for all the datasets that we compare. Linear filters were normalized by their maximum value (normalization by the variance gave similar results but made more difficult visualization of the change in the nonlinear function in Fig. 7f). The nonlinear function N was estimated by plotting the measured firing rate against the predicted linear response and fitting the data with a Hill function, r = 1/(1 + (H/r_lin)ⁿ), where H is the half maximum. For filter estimation, the PSTH was calculated on 3 ms time bins and smoothed with a 30 ms squared window. The accuracy of the filter prediction was calculated as the ratio between the residual of the fit and the noise in the response (Geffen et al., 2009), $\sqrt{P_R/P_N}$ where P_N = 〈〈(r_i(t) − r(t))²〉_i)_t, P_R = 〈(r(t) − f_LN(t))²〉_t, and r(t) = 〈r_i(t)〉_i. A value of NR smaller than one indicates a model prediction that is more accurate than the variability in the data. We used two-thirds of the length of the recording to estimate the filter and the remaining one-third to test the prediction.

Results

Laboratory odor stimuli exhibit a large diversity of odor-specific temporal dynamics

In a previous study, we showed that stimulus dynamics can depend on odor identity (Su et al., 2011). We wondered how diverse are the dynamics of odor stimuli delivered in the laboratory for a larger set of monomolecular odors. We selected 27 compounds from the panel used previously (Hallem and Carlson, 2006) that contains odorants from different chemical classes that are relevant to the ecology of the fruit fly. Odor dilutions were prepared in a Pasteur pipette, and the time-dependent concentration of odorant reaching the fly position was measured with a PID (Fig. 1a and Materials and Methods). The timescales of the rise and decay phases of the PID traces are broadly distributed (Fig. 1b,c) between 30 ms and 1 s. Rise and decay phases are correlated but not identical. Stimulus dynamics is fairly independent of concentration for “fast” odors, but we measured differences up to hundreds of milliseconds for different concentrations of “slow” odors (Fig. 1d).

These observations suggest the presence of nonlinearity in the delivery system, likely associated with interactions between odor molecules and the surfaces of the delivery system. In the absence of any interaction, we would expect the system to be linear with the concentration of odor, and the on and off timescales to be similar (except for a 10% difference due to the different flow rates during the rising and decaying phases of the puff) and independent of concentration. In contrast, when interactions with surfaces become significant, this linear scaling breaks down; the rates of adsorption and desorption of odorant to surfaces depend on the relative coverage of the surface by odor molecules, which itself is a nonlinear function of the gas-phase concentration [e.g., a hyperbolic function in the simple case of a Langmuir adsorption isotherm (Langmuir, 1932), but more complex isotherms are also possible (Rabe et al., 2011)]. Hence, in this case, we expect the stimulus dynamics to depend on the odor concentration in the gas phase (Fig. 1d).

The concentration of odor in gas phase depends on the concentration in liquid phase and scales linearly with vapor pressure through the Raoult's law (Teixeira et al., 2009). Accordingly, stimulus dynamics also depends on the vapor pressure of the odorant (Fig. 1e). In particular, all odors with long rising time (>100 ms) had low vapor pressure (<1 mmHg). We noticed that the three outliers (in orange) are all acyclic monoterpenes, suggesting that other properties of the odorants (e.g., binding affinity to the tube surface) likely contribute to the time dependency of the odor signal as well.

Although the temporal dynamics of the stimulus reaching the fly is likely determined by the particular delivery method used (Vetter et al., 2006; Andersson et al., 2012), we found consistent differences between slow and fast odors when using different variations of our delivery system (Su et al., 2011). To make such comparisons easier throughout the text, we use “cold” blue colors to plot PID measurements of “slow” odorants and “warm” red colors for “fast” odorant.

What about more natural conditions? We considered two situations likely to occur in nature. First, we investigated stimulus dynamics in the absence of strong wind, mimicking what might happen in the head space of a flower, for example, when an insect is at close range. We placed 50 μl of odor dilution on a paper filter and recorded the gas-phase concentration of the head space 1.5 cm above it (Fig. 2a). In this situation, odor dynamics is governed by evaporation from the liquid source, transport by convection and advection by small flow due to the PID suction. We observed a continuum of dynamics ranging from fast depletion for ethyl acetate to slow increase for diethyl succinate (Fig. 2a). In this case, the dependency of the stimulus dynamics on vapor pressure likely reflects the linear relationship between evaporation rate (defined as minus the rate of change of the odor concentration in liquid phase) and vapor pressure, which has been experimentally observed (van Wesenbeeck et al., 2008), as well as deviations due to interactions between the paraffin oil and the odorant molecules in the liquid phase (Teixeira et al., 2009).

Next we asked whether differences between slow and fast odors would still be noticeable if the odor was transported downstream from the source by wind but still in the vicinity of surfaces. We blew a continuous airstream onto a paper filter containing 50 μl of odorant dilution and measured the odor concentrations 3 cm downstream from the odor source (Fig. 2b). To determine whether an ORN can detect these differences, we recorded the response of ab3A simultaneously with the stimulus concentration (Fig. 2b). Although the stimulus signal depends on the position of the detector and the particular configuration of the experiment, we found consistent differences in stimulus dynamics between a fast and a slow odorant. The overall trend of the stimulus concentration seems to reflect the evaporation dynamics shown in Figure 2a (fast depletion for methyl butyrate and slow increase for diethyl succinate). To quantify the statistics of the fluctuations around the evaporation trend, we calculated the autocorrelation function of the fluctuations around the mean for the last 70 s of the traces. The decay time in the autocorrelation function of the PID signal was longer for the slow odorant diethyl succinate than for the fast odorant methyl butyrate. Importantly, the autocorrelation functions for the ab3A responses show similar differences (Fig. 2c). This result suggests that the physico-chemical properties of odorant molecules can affect the temporal statistics of odor signals that reach the sensory system and that ORNs can detect such differences. Farther away from the source and away from surfaces, these differences should be eliminated by turbulent mixing. Note that, even away from surfaces, the edges of an odorant plume might still exhibit small delays between compounds coming from the same source because of different diffusivities of the odorants. What physiological properties enable the neuron to capture such differences in the temporal statistics of odor signals?

ORN response dynamics are independent of stimulus intensity for a large part of their dynamic range

Previous studies have shown that the response of ORNs to odor puffs exhibit diverse dynamics ranging from tonic to phasic depending on the particular odor–receptor combination (Hallem and Carlson, 2006; Nagel and Wilson, 2011). We reasoned that, to compare the response of ORNs to different odors, we should first characterize the dependence of the response on concentration, thus taking into account the fact that ORNs have odor-specific sensitivities (Ito et al., 2009). For this purpose, we considered only fast odorants for which stimulus dynamics is fairly independent from the particular dilution used (Figs. 1d, 3c).

ab3A response to 500 ms puffs (see Materials and Methods) of ethyl acetate is tonic at low concentrations, more phasic at concentrations close to the half-maximal response, and prolonged for saturating stimuli (Fig. 3a). A poststimulus silent period can be observed with intermediate concentrations. We measured the peak firing rate (Fig. 3b, black) and the degree of adaptation (Fig. 3b, green) defined as the decrease in firing rate relative to the peak, as a function of the odor dilution. The peak response follows the typical sigmoidal dependency on concentration and shows saturation for the two highest dilutions used. Surprisingly, the degree of adaptation is nearly constant for all the dilutions in the middle of the dynamic range in which the peak response is nearly linear with log changes in concentration (between 10 and 90% of the maximum firing rate, p > 0.6, ANOVA).

To analyze the response dynamics independently from the amplitude, we plotted the time-dependent firing rate normalized by its peak response. In the middle of the dynamic range (Fig. 3b, arrows), the curves are remarkably similar (Fig. 3c, p > 0.05, ANOVA performed on each time bin). Thus, not only the degree of adaptation but the entire response dynamics are independent of odor dilution. We used the PID to measure the intensity of the stimulus in the vicinity of the fly. A change in the dilution of ethyl acetate only affected the amplitude of the stimulus reaching the fly but not its dynamics (Fig. 3c).

We asked whether the invariance of normalized responses (Fig. 3d) was a property of the population average or a property of the individual ORNs. For all 12 neurons examined individually within their dynamic range, the normalized response dynamics are remarkably similar (Fig. 3d, first column, three individual cells shown). For four ORNs (ab2A, ab3A, ab3B, and ab7A) and the different odorants tested, normalized responses of single neurons are also concentration invariant (Fig. 3d). Moreover trial-to-trial variability of the normalized response dynamics is equal or larger than dilution-to-dilution variability (Fig. 3e and Materials and Methods), suggesting that, for concentrations in the middle of the dynamic range, invariance to stimulus intensity is a robust feature of ORN responses.

In summary, we identified three regimes of response dynamics. Stimuli at the lower end of the dynamic range usually elicit a tonic response that is probably concentration dependent (Nagel and Wilson, 2011). Response becomes more phasic and concentration invariant for stimuli in the middle of the dynamic range. Stimuli near the upper end of the neuron dynamic range elicit saturated responses characterized by prolonged dynamics.

Independence of ORN response dynamics with background intensity

In nature, odor stimuli are often encountered on top of a background. This poses a challenge to sensory systems, which must remain sensitive to changes in the signal over a wide range of background intensities. We asked whether the invariance of the normalized ORN response dynamics with respect to odor intensity still holds in the presence of a background of the same odorant.

We adapted ab3A to a stable concentration of methyl butyrate, and superimposed on this background, we administered short puffs of increasing concentration of the same odorant (Fig. 4a and Materials and Methods). Prolonged stimulation with methyl butyrate caused the neuron to adapt within few seconds to a stationary firing rate that is concentration dependent. When normalized by the peak response, the dynamics are independent of odor intensity (Fig. 4a), confirming the results obtained with short puffs (Fig. 3c).

Adaptation to the background induces a shift in the dose–response curve toward higher doses and decreases the dynamic range (Fig. 4b), similarly to what has been found in frog olfactory cells (Reisert and Matthews, 1999). Remarkably, in the middle of the dynamic range of the different adapted states (Fig. 4b, arrows), ab3A responds to odor puffs with firing dynamics that are very similar across background intensities when normalized by peak amplitude (Fig. 4c). Apart from one time point (Fig. 4c, black point bottom left), the differences between the curves are not significant (p > 0.05; Fig. 4c, bottom, tested on 30 ms time bins). For ethyl acetate and ethyl butyrate, there was no significant difference (p > 0.05) between the curves for all the time points (Fig. 4, second and third columns).

Thus, adaptation capabilities of ab3A are responsible for generating response dynamics that are independent of stimulus intensity, even in the presence of background stimuli. These results suggest that the dynamics of odor stimuli may be encoded in the ORN response independently of stimulus intensity.

Odor-dependent stimulus dynamics strongly affect ORN response dynamics

We showed in Figure 1 that the odor stimulus reaching the fly exhibited different temporal profiles depending on the odor used. We therefore asked to what extent ORN dynamics depend on stimulus dynamics in addition to the different physiological processes that can affect the response.

We measured the responses of ab3A, ab3B, and ab7A to five odorants ranging from fast to slow (Fig. 5). For fast odorants (methyl butyrate and propyl acetate in red), the stimulus measured at the fly closely follows the opening and closing of the valve, whereas ORNs (ab3A, ab7A, and ab3B) show a phasic response with a degree of adaptation ∼0.5 (as defined above). In contrast, for slow odorants, PID signals and neuron responses do not follow the opening and closing of the valve as well. ORN responses to slow odorants tend to be more tonic (lower degree of adaptation) and exhibit prolonged dynamics that reflects the long decay of the odor after the closing of the valve (ab3A and ab3B responses to 1-octen-3-ol and diethyl succinate).

Although for fast odors a change in dilution only affects the amplitude of the stimulus (Figs. 1d, 3c, 5, top), for slower odors a change in dilution can affect both the amplitude and the dynamics of the stimulus (Figs. 1d, 5, bottom). Thus, unlike for fast odors (Figs. 3, 5 top), the ORNs responses to puffs of slow odorants should not be expected to rescale with liquid dilution because the signal arriving on the fly does not rescale (see ab3A and ab3B responses to 1-octen-3-ol and diethyl succinate; Fig. 5, bottom). However, we expect the ORN response to rescale with the intensity of the odorant reaching the fly for both slow and fast odors as considered below (see Fig. 10). For very slow odorants, the dependency of stimulus dynamics on odor dilution can cause concentration-dependent delays in the neuron response to odor puffs (diethyl succinate; Fig. 5a), possibly related to the time needed for the odor concentration to reach the neuron detection threshold.

Figure 10.

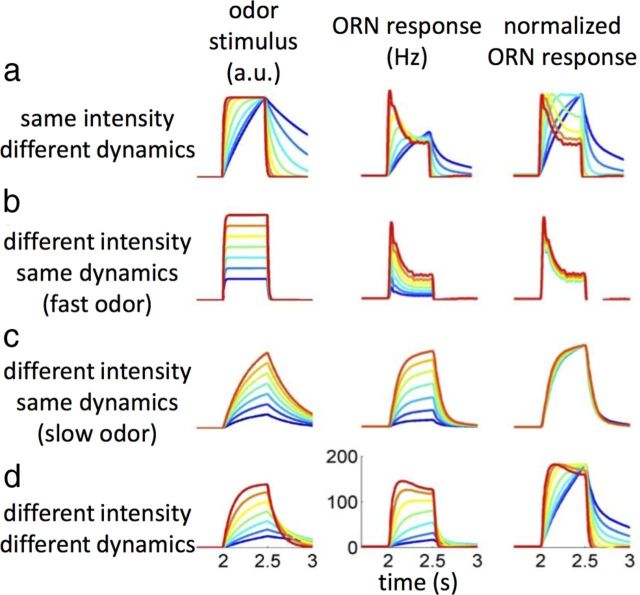
Modeling the effect of different stimulus dynamics and intensity on ORN response dynamics. The same LN model (Fig. 7d) is used for all simulations. Simulated stimuli (first column) were all 500 ms long with exponential rising and decay timescale τ and produced nonsaturated responses. a, Response to stimuli with identical intensities but different timescales (τ = 13–800 ms). b, Response to stimuli with different amplitudes but identical timescales (τ = 10 ms). c, Same as in b but for a slow odor (τ = 300 ms). d, Same as in c but now τ decreases with stimulus intensity as we observed for slow odors (Fig. 1d) (τ = 0.1–1 s).

Although these examples indicate that odor-dependent stimulus dynamics does affect ORN response dynamics, Figure 5 also shows that physiological processes alone can introduce differences in the ORN dynamics as reported previously (Nagel and Wilson, 2011): for example, the responses of ab3A and ab3B to 1-octen-3-ol are different, with ab3B response being more tonic.

To quantify to what extent stimulus dynamics might affect ORN response dynamics, we asked how easy it would be to discriminate between odorants on the basis of the time-dependent activity of ab3A only. Following the same approach that was used in previous studies (Stopfer et al., 2003; Raman et al., 2010), we performed PCA and hierarchical clustering on ab3A responses to the four odorants used in Figure 5a. Because of the similarity of ab3A response to different concentrations of the same odorant, responses to the same odor fall very close to each other in the PCA plot (Fig. 6a). Responses to different concentrations of diethyl succinate are relatively more distant from each other than for other odorants, probably because of the stronger concentration dependency of the stimulus dynamics. Responses to all the concentrations of the same odor cluster together, and different odor types rank according to their characteristic “speed” (Fig. 6a and Materials and Methods). In contrast, ab3A responses to four odors with more similar dynamics do not cluster accordingly to odor type (Fig. 6b).

Using an LN model to extract ab3A response function

The data shown so far indicate that the observed ORN response dynamics is the result of the convolution of the odor-dependent stimulus dynamics and the ORN response function. To separate this two contributions, we estimated LN models (Dayan and Abbott, 2001; Kim et al., 2011; Nagel and Wilson, 2011) for the delivery system and for ab3A responses.

An LN model consist of a linear filter k(t) and a static nonlinear transformation N (see Materials and Methods). We approximated a white-noise stimulus by randomly opening and closing a three-way solenoid valve to redirect an odor stream into the delivery tube (Fig. 7a, top trace). The valve state (On–Off) was updated every τ = 30 ms (see Materials and Methods). In the following, we refer to τ as the “stimulus correlation time ” (the time for the autocorrelation function to decay to zero). We performed simultaneous recordings of the odor concentration reaching the fly together with ab3A firing activity (Fig. 7).

First, we built an LN model for the odor stimulus using the binary state of the valve as the input and the PID signal as the output (Fig. 7b). The resulting linear filter k(t) peaks at 56 ms, consistent with the air travel time, and exhibits a long tail (∼200 ms, hereafter “integration time”) indicative of some integration of the signal within the delivery tube. The function N is a straight line revealing that the delivery system is linear.

Next, we built a LN model using the state of the valve as the input and ab3A response as the output (Fig. 7c). Comparing the time-to-peak of this filter with the time-to-peak of the filter obtained for the signal (Fig. 7b), we estimated a 12 ms delay between the stimulus arrival and the ORN response. The function N has the shape of a rectifier (Fig. 7c) and was fitted with a Hill function (see Materials and Methods).

Finally, we built an LN model using the PID signal as input and ab3A firing rates as output (Fig. 7d). In this case, the ORN response function is deconvolved from the dynamical properties of the stimulus, and the filter only reflects the effects of physiological processes. We call this filter the response function of the ORN. As reported previously (Kim et al., 2011; Nagel and Wilson, 2011), the filter shows a positive and a negative lobe, suggesting that the neuron is taking a derivative of the odor stimulus. The area under the filter is not zero, in agreement with the fact that this ORN does not return to baseline activity after a step stimulus (Fig. 4a). The integration time for this ORN (estimated as the width of the filter) is ∼100 ms, much shorter than the integration time of the delivery system. Cross-validation (see Materials and Methods) shows that the estimated LN model can accurately predict the response of ab3A (NR = 0.41) (Fig. 7a, bottom, red).

Adaptive properties of ab3A response to a flickering stimulus

To what extent does the LN model depend on the statistics of the stimulus signal? Figure 7e shows LN models for the odor signal and ab3A extracted using stimulus sequences with different correlation times (τ = 30, 50, and 100 ms). The LN model for the valve-to-odor transformation is independent of τ, suggesting that our method to estimate the model is not affected by the stimulus correlation time (for the range of τ values considered here). In contrast, ab3A response function does exhibit a small dependency on τ. The filter becomes slightly wider as the correlation time of the input signal is increased, suggesting that the neuron may adapt its response kinetics to the dynamics of the stimulus (Hosoya et al., 2005). We will investigate this issue further in future studies.

The short ∼100 ms integration time of ab3A response function (Fig. 7d) is consistent with the initial phasic response of this neuron to step increases in methyl butyrate (Figs. 4a, 5a). However, it is too short to explain the slower adaptation of the ab3A response to prolonged stimuli reported in Figure 4b. To quantify how the neuron might adapt to the flickering stimulus, we followed a procedure used for the analysis of adaptation in the retina (Baccus and Meister, 2002). We estimated LN models for the early (first 10 s) and the late (last 10 s) response of ab3A to the flickering signal (Fig. 7f). Although the linear filter k(r) remains invariant, the nonlinear function N becomes less steep as the neuron adapts to the flickering stimulus. This result is consistent with our finding that the presence of an odor background induces a change in the dose response of ab3A but does not affect ab3A response dynamics (Fig. 4). We obtained similar results for the response of ab3A to ethyl acetate, 1-octen-3ol (Fig. 7f), 2-butanone, and 1-pentanol (data not shown), as well as for the response of the maxillary palp neuron pb1A to 2-butanone and isoamyl acetate (Fig 7f).

The change observed in the nonlinear function during adaptation depends on the particular odor–receptor combination: for example, pb1A shows greater adaptation to 2-butanone than to isoamyl acetate. Note that the early response function was estimated from the first 10 s of the time series, and it is very likely that some adaptation already takes place during this time. The limited amount of data does not allow us to extract LN models for segments shorter than 10 s.

Different odorants induce small temporal delays in the response functions of two ORNs located in the antenna and the maxillary palp

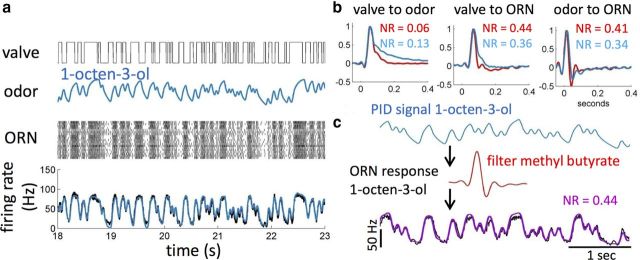
Finally, we investigated how the response function of ab3A and pb1A depend on odor identity. We generated a flickering stimulus of the slow odorant 1-octen-3-ol and compared the PID and ab3A responses (Fig. 8a) with those obtained with the fast odorant methyl butyrate (Fig. 7a). With 1-octen-3-ol, the PID trace is smoother and ab3A response appears more tonic. Neither odor concentration nor neuron firing goes to zero when the valve is closed (Fig. 8a). To identify the origin of such differences, we compared the filters obtained for the two odorants. The valve-to-odor filter peaks at the same time for both odorants but exhibits a longer tail for 1-octen-3-ol (Fig. 8b, left) with an integration time twice as long as for methyl butyrate, consistent with the slower stimulus dynamics of that odorant. The valve-to-ORN filter also shows a longer integration time with 1-octen-3-ol (Fig. 8b, middle). In addition, we observe a small 4 ms delay in the peak of the filter, which is consistent across single-neuron recordings (data not shown). Interestingly, apart from the same 4 ms delay, the filters obtained for the odor-to-ORN transformation (the response function of ab3A) exhibit less difference between the two odorants than those obtained for the valve-to-odor transformation (Fig. 8b, right). In particular the longer tail observed with 1-octen-3-ol in the valve-to-ORN filter is gone.

These results suggest that the large differences observed in ab3A dynamics between the two odorants (Figs. 7a, 8a) might be dominated by differences in stimulus dynamics. If this is true, it should be possible to use a single filter to predict the response to both odorants once a measure of the stimulus is provided. To test this hypothesis, we used PID measurements of 1-octen-3-ol concentration (appropriately scaled and shifted by 4 ms) as input into the LN model of ab3A obtained with methyl butyrate (Fig. 8c). The prediction of the response to the slow odor is remarkably good (NR = 0.44), comparable with the one obtained for methyl butyrate itself (NR = 0.41). Importantly, it was better than the prediction obtained doing the same cross-prediction with the valve-to-ORN filters (NR = 0.62). We attempted to extract similar LN models for other slow odors that activate ab3A, such as γ-hexalactone and diethyl succinate. However, ab3A is very sensitive to these odorants whereas the PID is not, and we were unable to obtain reliable measurements of the stimulus to use as input to the LN model.

We examined the response function of ab3A to a total of five odorants: (1) methyl butyrate; (2) 1-octen-3-ol; (3) ethyl acetate; (4) 2-butanone; and (5) 1-pentanol (Fig. 9a–d). To reduce the effect of cell-to-cell and fly-to-fly variability in our comparison, we tested two odors on each neuron and compared LN models obtained for each odor pair. A correlation time of 100 ms was used for the flickering stimulus. For 1-octen-3-ol, we obtained results similar to those measured with a 30 ms correlation time in the input (Fig. 8): apart from a small temporal shift, the filter extracted for methyl butyrate can be used to predict ab3A response to 1-octen-3-ol (Fig. 9a). For ethyl acetate, 2-butanone, and 1-pentanol, we do not observe any difference in the valve-to-odor filters (apart from a small shift due to the different position of the valves on the delivery tube) (Fig. 9b–d, top). The odor-to-ORN filters estimated for pairs of odors have different response delays with shifts of up to 12 ms and exhibit only minor differences in their shapes (Fig. 9b–d, middle). Given that the stimulus contribution was deconvolved from the ORN response, these differences in response delay can be entirely attributed to physiological processes. Once shifted in time by the appropriate amount, the filters obtained with methyl butyrate (in red) can be used to predict with good accuracy the response of ab3A to the other odorants (Fig. 9b–d, bottom) and this despite small differences in the filters shape. We note a larger difference for the ab3A 1-pentanol response. Consistent with the finding that the linear response of ab3A was invariant over the course of the flickering stimulus experiment (Fig. 7f), we found that the response delays measured for pairs of odorants at the very beginning of the flickering stimulus were the same as those measured at the end of the flickering stimulus. These odor-dependent latencies in the response of ab3A remained invariant, although the neuron sensitivity was adapting to the flickering stimulus.

We also measured the response function of pb1A, a neuron located in the maxillary palp, to 2-butanone and isoamyl acetate. Despite the different vapor pressure (Fig. 2b, 71 mmHg for 2-butanone and 5 mmHg for isoamyl acetate), we did not observe any difference in the dynamics of the two odor stimuli (Fig. 9e, top), likely because of the very low concentration of 2-butanone used to elicit a firing rate comparable with isoamyl acetate (∼100 Hz). The linear filter for the response of pb1A (Fig. 9e, bottom) has a smaller negative lobe than what was found for ab3A, suggesting that the response function depends on the neuron identity as reported previously (Nagel and Wilson, 2011). Like for ab3A, the main difference between the response functions of pb1A to the two odorants is a small delay (18 ms) between the corresponding filters. We demonstrated this by predicting the response of pb1A to a flickering stimulus of isoamyl acetate using the filter measured for 2-butanone (appropriately shifted in time by 18 ms) (NR = 0.49). A previous study reported larger differences in the responses of pb1A to these two odorants (Nagel and Wilson, 2011). Differences are to be expected if one of the two odorants is used at concentrations near the bottom of the dynamic range in which neural responses are close to the tonic-to-phasic transition. Indeed, the responses of pb1A to higher odorant concentrations (Nagel and Wilson, 2011, their Fig. 6) exhibit smaller differences between these two odorants. Another likely source of differences stems from the dependency of the ORN response on the correlation time in the stimulus (Fig. 7e). The cutoff frequency of the flickering stimulus is 100 ms in this study, much shorter that in the study by Nagel and Wilson (2011). Finally, the dependency of the stimulus dynamics on the delivery system configuration, odor type, and concentration may also contribute to the differences. For example, we noticed that the small difference in odor stimulus that we observed between methyl butyrate and 1-pentanol when delivered through the Pasteur pipette (Fig. 5a) is absent when the odor is delivered using a bottle (Fig. 9d, top). Similarly, ab3A response does not show a silent period after an odor puff, but it does show silent periods after the closing of the valve during the flickering odor stimulation. These observations support the importance of taking stimulus dynamics and neuron adaptation in account to study the contribution of physiological processes to ORN response dynamics.

Discussion

Here we identified three key aspects of ORN response dynamics. Our first result is that ORN response dynamics are independent of stimulus intensity in the middle of the neuron dynamic range (Fig. 3). Near the bottom of the dynamic range, responses become more tonic and often depend on concentration. For saturating stimuli, we observed prolonged responses that do not rescale. Adaptation at the level of both transduction and firing could be involved in the concentration invariance observed here (Liu and Wang, 2001). In photoreceptors and vertebrate ORNs, increases in stimulus intensity elicit faster response kinetics (Baylor and Nunn, 1986; Reisert and Matthews, 1999). Similarly, local field potential recordings from Drosophila ORNs show an increase in onset kinetics (Nagel and Wilson, 2011). Additional investigations are necessary to understand the mechanisms underlying the concentration invariance of the firing rate. In vision, adaptation to a background is usually accompanied by an acceleration of response kinetics (Baylor and Hodgkin, 1974; Burns and Baylor, 2001). In contrast, adaptation to a background in both vertebrate and insect ORNs has been shown to slow down the kinetics of the response to low stimulus concentrations (Reisert and Matthews, 1999; Nagel and Wilson, 2011). Here we show that adaptation to a background shifts and reduces the dynamic range, but in addition, we find that, for a large part of the adapted dynamic range, response dynamics to short puffs remain independent of the concentration of stimulus and background (Figs. 4, 7f).

These results suggest that, within a population of ORNs, neurons activated in this regime are able to encode the dynamics of the stimulus independently of its intensity. Hence, for each odorant, a relatively small number of ORNs might be sufficient to reliably capture the stimulus dynamics (Geffen et al., 2009). This property could be useful to maintain olfactory-driven navigation capabilities independent of signal intensity and background. A previous study (Asahina et al., 2009) suggested that, when climbing an odor gradient, Drosophila larvae rely on the response of various individual ORNs with distinct but overlapping dynamic ranges. A similar principle enhances the capability of bacteria to navigate chemical environments (Sourjik and Berg, 2002; Lazova et al., 2011). Additional investigations are needed to understand the role of low, saturated, and super-sustained responses (Montague et al., 2011). Concentration invariance of behavior may be achieved by processing in the antennal lobe (Asahina et al., 2009). Local inhibitory neurons in the antennal lobe have been shown to perform a normalization of the activity of a single glomerulus by the total activity of the ORN population (Olsen et al., 2010). These observations pose the question of whether processing in the Drosophila antennal lobe may provide the means to extract concentration-invariant information from temporal patterns of activity in the ORN population.

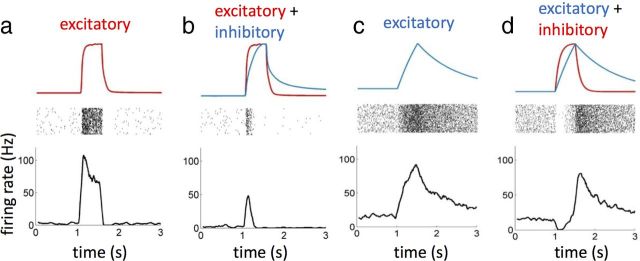
Our second result is that, under several conditions, ORN responses can be strongly affected by the odor-specific dynamics of the stimulus (Figs. 1, 2, 5, 6). In one case, we show that a single LN model can be used to predict the temporal response of an ORN to different odors, providing direct measurements of the odor stimuli reaching the fly (Figs. 8c, 9). In Figure 10, we use simulations to explore how the differences in stimulus dynamics might affect ORN dynamics. Assuming a single response function, ORN responses can be more or less phasic depending on the dynamics of the input stimulus (Fig. 10a). Consistent with what we observed in Figure 3, within the linear regime of the model, the ORN responds to different stimulus intensities with the same dynamics (Fig. 10b). Provided that the stimulus dynamics is concentration invariant, the model predicts concentration-invariant responses for fast and slow odorants (Fig. 10b,c). However, no rescaling of the ORN response should be expected when both the dynamics and intensity of the stimulus change (Fig. 10d). This seems similar to what we observed with most slow odorants we tested (Figs. 1d, 5). A better control of the stimulus is required to investigate experimentally the concentration dependency of the ORN response dynamics for slow odorants. We showed recently that ORNs respond to mixtures of excitatory and inhibitory odorants with distinct dynamics that reflect the physico-chemical properties of the odorants (Su et al., 2011). The LN model for ab3A can qualitatively account for the measured response dynamics solely from the different dynamics of the constituent odorants, assuming the contribution of the excitatory and inhibitory odorant to be additive (Fig. 11). Differences in stimulus dynamics alone could play an important role in the perception of odor mixtures.

Figure 11.

Simulation of the response to a mixture of an excitatory and an inhibitory odor qualitatively reproduce recent measurements (Su et al., 2011). a, Excitatory response to a puff of a fast odor. Top, Stimulus dynamics; middle, raster plot of the response generated using an LN Poisson model cascade; bottom, corresponding firing rate. The neuron response was simulated using the linear filter and the static nonlinear function estimated for ab3A (Fig. 7d). b, Response to a mixture of a fast excitatory and a slow inhibitory odorant. Response was calculated as above, using a linear combination of the two odors as stimulus. This simulation shows that a slow inhibitor can shorten and sharpen the response of a fast excitatory odor. c, Prolonged response to a puff of slow excitatory odor. d, Biphasic response to the sum of slow excitatory and fast inhibitory odorants.

Our third result is that, when differences in stimulus dynamics are carefully removed from the neuronal responses, ORN response dynamics still exhibit odor-dependent delays (Fig. 9). Other studies (Hallem and Carlson, 2006; Raman et al., 2010; Montague et al., 2011; Nagel and Wilson, 2011) have reported larger differences in the response of a single ORN to different odorants, suggesting that a bigger dataset might reveal greater variability than what we observed here. However, with few exceptions (Montague et al., 2011; Nagel and Wilson, 2011), most previous studies assumed stimuli to be independent of odor type and considered only one or few concentrations of the stimulus. Here we first quantified the dose response of each ORN–odor pair and then identified a regime of the dynamic range over which dynamics are concentration invariant. The response dynamics for different ORN–odor pairs were then compared within this regime. Moreover, we quantified the response function of the delivery system for each odorant and removed its contribution from the ORN response, obtaining response functions that only depend on physiological processes. Within this limited dataset, the shape of the response function only depends mildly on odorant identity but shows odor-dependent delays with differences up to 18 ms (Fig. 9). These delays remained constant between the beginning and end of the flickering stimulus, although the neuron sensitivity adapted to the stimulus (Fig. 7f). Odor-specific response delays have been observed previously in vertebrates ORNs and M/T cells (Spors et al., 2006; Junek et al., 2010). In the fly, odor-dependent delays could originate at different levels of the transduction process. For example, there could be rate-limiting events in the capture of odorant, their transport by odorant binding proteins, and their interaction with ORs.

Can odor-dependent differences in stimulus dynamics and odor-dependent delays in ORN response affect behavior?

Several experiments suggest that animals can use temporal information to distinguish between two olfactory stimuli. For example, mice can discriminate small delays of the order of 10 ms in the activation of the ORNs (Smear et al., 2011). Bees can discriminate two odor stimuli time shifted by only few milliseconds (Szyszka et al., 2012). Flies can discriminate between two odors using a single ORN type (DasGupta and Waddell, 2008). Moreover, odor speed affects the capacity of humans to discriminate mixtures of odorants and tastants (Mozell, 1964a; Kuznicki and Turner, 1988; Laing et al., 1994; Jinks and Laing, 1999).

It is widely accepted in perfumery that the composition of a fragrance changes over time as a result of differential evaporation of the individual components (Carles, 1962; Teixeira et al., 2009). Here we show that the concentration of the individual components can fluctuate differently depending on their physico-chemical properties. In ecology, much attention has been paid to the passive transport of odorants by turbulent flows (Murlis et al., 1992; Cardé and Willis, 2008; Riffell et al., 2008). While most of these works focused on situations in which the temporal dynamics of the stimulus are dominated by those of the air flow away from surfaces, here we examined what happens in the vicinity of surfaces. This situation is ecologically relevant to the fruit fly that spends a large amount of its lifetime walking (Carey et al., 2006). Interactions between odorant and surfaces introduce retardations in the stimulus dynamics that are odor specific (Figs. 1, 2a,c,d), and our results suggest that insects may be able to detect such relative temporal differences downwind of a nearby source (Fig. 2c). Behavioral experiments suggest that animals use fluctuations in odor concentration to identify different odor sources (Hopfield and Gelperin, 1989; Hopfield, 1991). It would be interesting in the future to investigate whether odor-dependent dynamics might be used to reveal the presence of different components within the same source.

Odor dependent differences in stimulus dynamics may affect tracking performance as well. For example the structure of an odor plume can greatly modify the way a moth tracks an odor signal down to its source (Baker et al., 1985; Mafraneto and Carde, 1994). Tracking capability in flies may also depend on odor identity (Krishnan et al., 2011), but whether this is attributable to differences in the input stimulus, ORN response, or downstream processing remains unclear.

The temporal aspect of ORN responses may add coding capacity to the spatial representation of odors at the periphery of the olfactory system. We have shown how ORN odor-specific dynamics originate in part from the stimulus itself in addition to the interactions between odorants and the periphery of the olfactory system. Whether and how the olfactory system uses the diversity in stimulus dynamics to enhance odor discrimination and tracking remains an open question.