The Role of Geometric and Biomechanical Factors in Abdominal Aortic Aneurysm Rupture Risk Assessment

Abstract

The current clinical management of abdominal aortic aneurysm (AAA) disease is based to a great extent on measuring the aneurysm maximum diameter to decide when timely intervention is required. Decades of clinical evidence show that aneurysm diameter is positively associated with the risk of rupture, but other parameters may also play a role in causing or predisposing the AAA to rupture. Geometric factors such as vessel tortuosity, intraluminal thrombus volume, and wall surface area are implicated in the differentiation of ruptured and unruptured AAAs. Biomechanical factors identified by means of computational modeling techniques, such as peak wall stress, have been positively correlated with rupture risk with a higher accuracy and sensitivity than maximum diameter alone. The objective of this review is to examine these factors, which are found to influence AAA disease progression, clinical management and rupture potential, as well as to highlight on-going research by our group in aneurysm modeling and rupture risk assessment.

1. INTRODUCTION

An abdominal aortic aneurysm (AAA) is a focal abnormal widening of the aorta to a size larger than approximately 1.5 times the normal healthy diameter (see Fig. 1). It is associated with degradation of connective tissue in the arterial wall and is most often found with a deposition within called intra-luminal-thrombus (ILT), consisting of fibrinous blood clots and cell debris. The hollow cavity through which blood flows is called the lumen.

Figure 1.

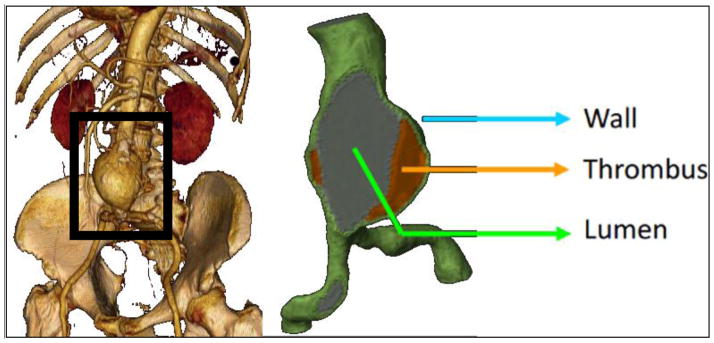
Aneurysmatic abdominal aorta (left frame is courtesy of University of California at Los Angeles).

AAAs are potentially life-threatening medical conditions often requiring surgical intervention. The underlying cause for the formation of an aneurysm can be either inherited (i.e., Marfan and Ehlers-Danlos syndromes) or acquired, with risk factors including hypertension, atherosclerosis, and smoking among others. The disorder is more common in men than in women, with prevalence rates estimated at between 1.3% and 8.9% in men and between 1.0% and 2.2% in women, accounting for more than 8,000 deaths in the United Kingdom and 15,000 deaths in the US every year.⁷³ Only 25% of AAAs rupture in an individual’s lifetime,¹⁰⁰ therefore clinicians compare the risk of rupture with the risk of repair, particularly because of the increased peri-operative mortality in elderly patients.⁸⁷ Typical guidelines currently used in the clinical management of AAAs are based on the maximum diameter derived metrics as a criterion for deciding the course of treatment. In clinical practice fusiform aneurysms larger than 5.5 cm are recommended for surgical intervention and those smaller than 4.0 cm are considered at low risk of rupture.⁹ Other morphological parameters are associated with risk of rupture, e.g. AAA volume,^12,65 rate of expansion,^7,43 ILT volume,⁸⁵ and asymmetry and tortuosity.⁵⁸

Recent research has pointed to the unsuitability of recommending intervention based solely on the maximum diameter criterion.^{19,23,27,29,100} It is known that small AAAs can rupture and large AAAs can remain stable. In an autopsy study of four hundred and seventy-three non-resected aneurysms¹³, 13% of aneurysms with a maximum diameter less than 5.0 cm ruptured and 60% with diameters greater than 5.0 cm remained intact. Therefore, other rupture risk parameters are needed as an alternative to the customary AAA size and expansion rate criteria. A biomechanics based approach correlated with geometric indices may be a viable option. Recent finite element (FE) simulation studies by Gasser et al³⁰ found that biomechanical parameters such as Peak Wall Stress (PWS) and Peak Wall Rupture Risk (PWRR) were 1.17 and 1.43 times higher in ruptured AAAs compared to those in diameter-matched unruptured aneurysms. McGloughlin and Doyle⁵¹ make a concise review on recent AAA biomechanics-based rupture risk biomarkers examining their potential for clinical decision-making tools. The scope of the present review is different from that of McGloughlin and Doyle⁵¹ and Vorp¹⁰⁰ in that it focuses exclusively on the computational aspects involved in the evaluation of biomechanics and geometry quantification as it relates to AAA rupture risk assessment.

There are many factors implicated in vascular wall biomechanical assessment (see Fig. 2) and the modeling strategies to address these differ greatly among researchers (see Tables 1–4). This manuscript reviews factors involved in AAA development and rupture risk, considering i) geometric features that discriminate AAA population subsets, and ii) biomechanical factors implicated in the assessment of rupture risk based on the AAA patient-specific geometry, wall structure, and mechanical response. In particular, we address the relative importance of wall mechanics vs. geometry quantification in the evaluation of AAA rupture risk, as the aneurysm geometry is believed to be the primary predictor of peak wall stress.

Figure 2.

Factors affecting evaluation of computational wall mechanics (exclusive of image segmentation errors).

Table 1.

Abbreviations used in Tables 2–4.

Abbreviation	Meaning
3DAO	3D Active Object
ALE	Arbitrary Lagrangian Eulerian coupling
Asym	Asymmetry
AxiSym	Axisymmetric
Avg Sys	Average of systolic pressure measured for each patient
Bifur	Bifurcation
BIM	Backward integral method
Ca	Calcification
E	Linear
GC-circle	Gauss curve for anterior and posterior with circular c/s fitted in between
HE	Hyperelastic isotropic
HEaniso	Hyperelastic anisotroic
I	Idealized
Implicit	Modeled implicitly by varying material properties of select elements in mesh
N	No
PC	Point cloud
PHE	Porohyperelastic
PS	Patient-specific
PWS	Peak wall stress
Quad-04	4 noded quadrilateral element
S	Shell
S3	3 noded shell element
S4	4 noded shell element
S8	8 noded shell element
SS	Surface smoothing
Tri-3	3 noded triangle
Y	Yes

Table 4.

Literature review summary – Fluid-structure interaction AAA modeling (Please refer to Table 1 for abbreviations used.)

Year	First Author	Coupling	Wall Material	ILT Material	Fluid	InletBC	OutletBC
2001	Di Martino	ALE	E-2.7 MPa	E=0.11 MPa	Newtonian	5xDia extension with Flat Velocity profile	time varying pressure
2005	Scotti	Iteratively Coupled	E-2.7 MPa	-	Newtonian	parabolic profile	time varying pressure
2005	Wolters	ALE, iterative coupling	E	-	Carreau–Yasuda model (Shear thinning)	plug profile	Zero-traction
2006	Leung	ALE, Fully Coupled	HE – 59	-	Newtonian	plug profile	time varying pressure
2007	Papaha- rilaou	decoupled	HE – 59	E=0.11 MPa	Newtonian	PS Womersley	Flow split (?)
2007	Scotti	ALE, Fully Coupled	HE – 59	HE	Newtonian	plug profile	time varying pressure
2006	Frauen- felder	Fully Coupled	E-10 MPa	-	Newtonian	plug profile	Zero-traction
2009	Rissland	Fully Coupled	HEaniso	E=0.11 MPa	Newtonian	plug profile	time varying pressure
2006	Li	Fully Coupled	E-4.66 MPa		non-Newtonian	parabolic profile	time varying pressure
2009	Bluestein	Decoupled	HE	E=0.11 MPa	Newtonian	steady plug flow	Zero-traction (?)

2. GEOMETRIC FACTORS

2.1 Baseline diameter and predisposition for AAA development

The role of size as a geometric factor involved in the aneurysmatic condition of the aorta and progression of the disease has been the basis for clinical management of AAA. In an interesting study by Solberg et al,⁸⁰ where 4,265 subjects with a normal sized aorta resulted in 116 AAAs diagnosed after 7 years, a statistical analysis revealed that the baseline diameter was a highly significant (p < 0.001), strong (95% CI: 7–76 times higher risk), and gender-independent risk factor for developing AAA. A smaller increase in diameter was noticed in patients with a smaller aorta when compared to the increase exhibited by patients with a larger aorta.⁸⁰ Moreover, when adjusted for age and aortic diameter, male sex was not significantly associated with AAA. This implies that geometry is more significant than gender in AAA development. The Solberg findings are in agreement with the previously reported fact that the growth rate of larger non-aneurysmatic aortas was higher than in smaller non-aneurysmatic aortas.⁵³

2.2 Importance of shape for wall mechanics estimation

The mechanics of the AAA wall and the resulting distribution of wall stress are influenced by the individual shape, in addition to the size, of the aneurysmal aorta. While precise soft tissue characterizations of the wall and ILT, as well as patient-specific blood flow velocity measurements, are imperative to achieve accurate computational predictions of the flow-induced wall stresses, the native, evolving AAA geometry is likely the most important feature to consider in evaluating the wall mechanics. A detailed discussion comparing various material property models in the ensuing wall stresses and strains can be found elsewhere.^66,68 Limiting the characterization of this geometry to the measurement of maximum diameter or expansion rate from medical images is not the best strategy to address the at-risk status of aneurysms on an individual basis. AAA shape is complex; most aneurysms are generally tortuous, asymmetric, and with amorphous multi-layered ILT.^2,22,100

Preliminary work in aneurysm biomechanics suggests that curvature quantification is more relevant than diameter for rupture risk assessment.^47,63 Ruptured AAAs seem to be less tortuous and have a larger cross-sectional diameter asymmetry,²⁸ which is consistent with FEA studies showing that the highest wall stress is obtained in AAAs with an asymmetric geometry.¹⁰² Moreover, the location of maximum stress is at the inflection point where the aneurysm curvature changes from concave to convex,²⁷ which was also observed in symmetric models.²⁵ Idealized fusiform and saccular models moreover yield an increase in wall stress with bulge diameter and asymmetry.^71,102 The potential for geometry based indices to assess AAA rupture risk is parallel to a recent study describing the derivation of a set of global indices quantifying size and shape of cerebral aneurysms to assess their rupture potential and for choosing the appropriate clinical treatment modality.⁵⁸

2.2.1 ILT as a geometric feature

ILT is a common presence in most AAAs and is known to alter the stress distribution of the aneurysmal wall^100,103 and directly affect AAA growth and rupture,^{8,40,52,84,85,101} making it relevant for the accuracy of AAA biomechanics. Nonlinear regression models for non-invasive wall strength estimations have used local ILT thickness as a modeling parameter.⁹⁶

2.2.2 Wall thickness as a geometric feature

A factor of significant importance in AAA rupture risk prediction is the individual, nonuniformity of the wall thickness. Figure 3 shows the estimation of AAA wall thickness distribution obtained from a contrast-enhanced CT scan.⁷⁸ Di Martino et al,¹⁶ using a laser micrometer, measured the thickness of AAA wall specimens obtained fresh in the operating room from patients undergoing surgical repair. A significant difference was found in wall thickness between ruptured (3.6 ± 0.3 mm) and electively repaired (2.5 ± 0.1 mm) aneurysms as well as an inverse correlation between wall thickness and local tissue strength. The tensile strength of ruptured AAA tissue was found to be lower than that of electively repaired tissue (54 N/cm² vs. 82 N/cm²), and AAA rupture was associated with aortic wall weakening, but not with wall stiffening. In an autopsy study, Raghavan et al⁶¹ analyzed the tissue properties of three un-ruptured and one ruptured AAA revealing that all aneurysms had considerable regional variation in wall thickness and there was a significant reduction in wall thickness near the rupture site. Similarly, Mower et al⁵⁵ demonstrated that wall thickness is a major parameter influencing wall stress distribution compared to aneurysm maximum diameter alone. It can be argued that the pathological state of the abdominal aorta results in an overall thicker, albeit weaker wall,¹⁶ even though AAA rupture, observed to occur at thin regions of the wall,⁶¹ is a local phenomenon triggered by the local wall mechanics. This observation underscores the need for appropriate wall thickness modeling techniques as well as the inadequacy of global size metrics such as diameter for patient specific risk assessment.

Figure 3.

Estimated wall thickness distribution (in mm) as a point cloud resulting from a segmented CT dataset.⁶⁸

2.2.3 Correlation of geometric features with peak wall stress

Geometric features have been shown to be significant predictors of peak wall stress (PWS) and subsequent risk of or predisposition to rupture.^27,29,97 Multiple regression analysis was performed on 39 patients and 17 features to assess the influence of the features on peak wall stress.³⁶ PWS was correlated with the mean centerline curvature, the maximum centerline curvature, and the maximum centerline torsion of the AAAs, with mean centerline curvature being the only significant predictor of PWS and subsequent rupture risk resulting from the multiple regression analysis. A multivariate analysis of 40 variables of 259 aneurysms revealed that ruptured aneurysms tend to be less tortuous and have a greater cross-sectional diameter asymmetry.²⁸ Similarly, Georgakarakos and colleagues³³ developed a linear model to associate PWS and geometric parameters. They report that the optimal predictive model can be formulated as follows: $\mathit{PWS}=8.791+2.3953\ast \mathit{MaxDiameter}+25.2923\ast \mathit{IntTortuosity}$, where MaxDiameter is the maximum in-plane diameter and IntTortuosity is the internal tortuosity. While it is difficult to reconcile these conflicting observations, the study by Fillinger et al²⁸ appears more reliable since the potential compounding effects of ILT do not play a role in the analysis, the population sample is larger, and the age, gender, and diameter matched approach makes the outcome more controlled.

2.2.4 Geometry quantification

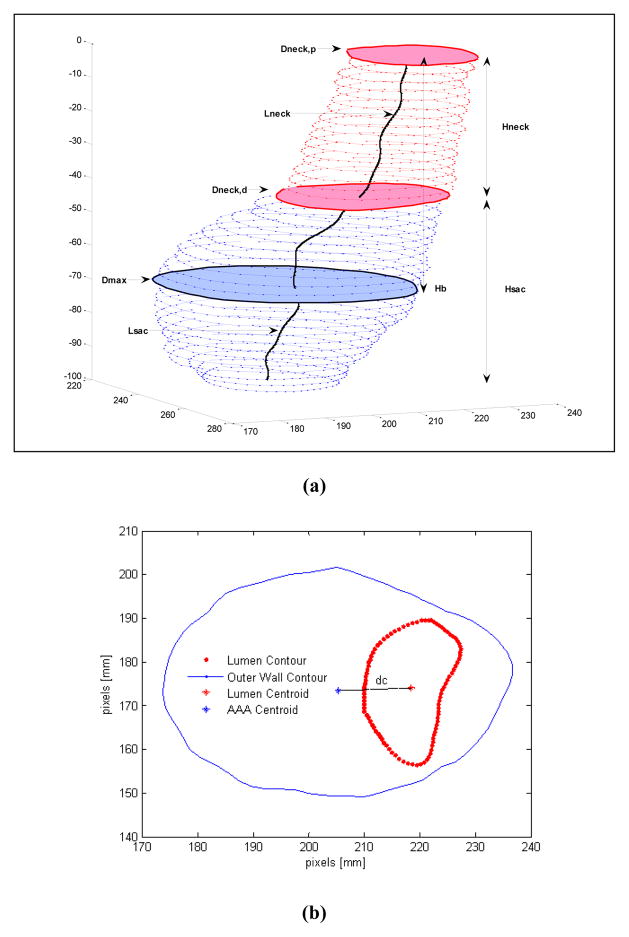
The ability to characterize the AAA geometry non-invasively from clinical images is an attractive strategy for rupture risk assessment as it can provide detailed information on the aneurysm morphology beyond what can be achieved by simple visual inspection of the images in the Radiology suite. To this end, Somkantha et al⁸¹ trained a Naïve Bayes classifier using three features (area, perimeter, and compactness) derived from image segmentation to discriminate between healthy and diseased arteries. Using 30 images for training and 20 images for testing, they obtained accuracy levels of 95%. However, as the aneurismal aorta is larger than a healthy aorta, it is expected that these size features can accurately discriminate between healthy and diseased aortas. Shum et al^78,79 developed a quantitative pipeline consisting of image segmentation and geometry quantification to compute 64 features that describe the size, shape,⁵⁰ wall thickness, and curvature for a subset of ruptured and unruptured aneurysms (see Fig. 4). Utilizing these features, a decision tree model (see Fig. 5) was trained on 76 AAAs and resulted in a prediction accuracy of 87% when including sac length, surface area, tortuosity, and the ratio of ILT to AAA sac volume as the classifying features.^77,79

Figure 4.

1-D size indices computed from segmented CT images: (a) maximum diameter (Dmax), proximal neck diameter (Dneck,p), distal neck diameter (Dneck,d), sac height (Hsac), neck height (Hneck), sac length (Lsac), neck length (Lneck), bulge height (Hb); (b) centroid distance at the maximum diameter (dc).⁶⁸

Figure 5.

Model learned by a J48 decision tree, based on highest information gain; L_sac, length of AAA sac; S, surface area; T, tortuosity; , ratio of intraluminal thrombus volume to aneurysm sac volume.⁶⁸

In addition to associating geometric features to rupture potential, five “geometric biomechanical factors” (deformation rate, asymmetry, saccular index, relative wall thickness, and growth rate) were recently combined to obtain a rupture risk qualitative indicator.⁹⁸ This indicator was defined to monitor the evolution of patients with aneurysms by integrating geometric information obtained from periodic checkups in an effort to improve the accuracy of rupture risk assessment. Validation studies were performed on one clinical case and three cases obtained from the literature, and a broader study enrolling more patients is currently in progress. Results show that the deformation and growth rates influence the aneurysm rupture potential more than maximum diameter alone, and that a rupture risk qualitative indicator greater than 0.64 (nondimensional, based on the weighted averages of the five geometric biomechanical factors) indicates elective repair should be considered.

3. BIOMECHANICAL FACTORS

From a purely biomechanical viewpoint, aneurysm rupture occurs when the mechanical stress within the dilating inner wall exceeds the failure strength of the vascular tissue. Therefore, a criterion for repair based on quantifying AAA wall stress and strength could facilitate a better method to predict at-risk AAAs. Unfortunately, obtaining in vivo patient-specific measurements of tissue stresses or strength non-invasively is currently not feasible. However, mathematical and computational models that accurately compute wall stress can be utilized to evaluate the AAA biomechanical environment at the organ scale. Therefore, rupture risk biomechanical parameters can be evaluated as an alternative to the standard AAA size and expansion rate.⁵¹ Such an approach has been extensively applied as a solution for rupture risk assessment, as evident by the extent of the literature now summarized in Tables 1–4, which include some of the relevant and highly cited works in the field of solid mechanics and fluid-structure-interaction AAA analysis. We note that the isotropic hyperelastic material model proposed by Raghavan and Vorp⁶⁴ has been used extensively in AAA numerical modeling.

3.1 Initial studies with idealized models

Early studies used the Law of Laplace to correlate AAA diameter and rupture.¹⁸ However, this approach ignores the complex aneurysm geometry and boundary conditions, as well as the presence of the ILT. In this regard, the calculation of peak wall stress by means of finite element analysis was first applied to a two dimensional AAA shape by Stringfellow et al.⁸⁶ Their work showed that AAA models with the same diameter but different geometry had different wall stress, pointing to the importance of AAA shape and the shortfall of Laplace’s law even for an idealized approximation of complex geometries. This observation was also corroborated by others.^25,39

3.2 Patient-specific AAA modeling

Fillinger et al^27,29 showed the feasibility of using finite element analysis (FEA) for patient-specific wall stress calculations and reported statistically significant differences in peak stress for ruptured/symptomatic AAAs (46.8 N/cm²) in comparison with those electively repaired (38.1 N/cm²). They also demonstrated that maximum wall stress correlated more closely with risk of rupture than maximum diameter.²⁷ In their study, wall stress was calculated by using FEA applied to a population of 103 patients, from which stress at a threshold of 44 N/cm² had 94% sensitivity and 85% accuracy in predicting rupture, compared to 81% sensitivity and 73% accuracy with maximum diameter at a threshold of 5.5 cm. A similar study was undertaken by Venkatasubramaniam et al⁹⁷ with 27 patients, from which 15 AAAs ruptured. They found that ruptured AAAs had significantly higher peak wall stress than non-ruptured AAAs (77 N/cm² vs. 55 N/cm²). Both studies^27,97 found a strong correlation between areas of high stress and the rupture site, based on quasi-static computational solid stress calculations applying a uniform intraluminal pressure directly on the wall. However, these findings were challenged by Georgakarakos et al.³⁴ They found the location of peak wall stress may not necessarily coincide with the site of rupture. It was reasoned that the wall strength is also an important factor to be considered for rupture risk assessment.

3.2.1 Metrics for material failure criteria

A logical follow up to the aforementioned studies is to compare wall stress against tissue strength. Vande Geest et al⁹² proposed a statistical model involving local ILT thickness, normalized transverse diameter, gender and family history to non-invasively estimate wall strength. In their work, the Rupture Potential Index (RPI) was proposed as a metric to quantify risk based on the ratio of wall stress and wall strength. Recent work by Maier et al⁴⁹ compared the efficacy of diameter, stress, and RPI to predict rupture. Maximum wall stress and maximum RPI were found to be high in symptomatic and ruptured cases compared to unruptured cases. An alternative approach in the field of hyperelasticity was proposed by Volokh⁹⁹ based on the use of strain energy density as a failure criterion. Strain energy density is the product of stress and strain at a given location within a structure. Thus, this quantity takes into account both load (~ stress) and deformation (~ strain). As per this theory, it is assumed that the structure fails when at any given location the strain energy exceeds the threshold level specific of the material.

3.2.2 AAA material behavior and constitutive models

An accurate and reliable analysis of AAA biomechanics requires not only a precise three-dimensional description of the aneurysm geometry but also an appropriate constitutive law for the material. The first studies on AAA wall mechanics relied on hyperelastic isotropic models^{16,17,25,27,29,60,86,88,97} assuming an incompressible behavior for the arterial wall. Such models have limited accuracy for AAA stress analysis since ex vivo biaxial experiments on human AAA tissue conducted by Vande Geest et al⁹³ demonstrated that the aneurysmal degeneration of the aorta leads to an increase in mechanical anisotropy, with the circumferential direction being the preferential stiffening direction. A number of anisotropic constitutive models have been proposed for AAA tissue,^31,71,107 the implementation of which yields significantly higher peak wall stress in both idealized and patient-specific geometries.^70,71,95 In this regard, anisotropic model results are more sensitive to geometric parameters such as symmetry and aneurysm length. A recent study conducted by Gasser et al³⁰ indicates that ILT has a major impact on AAA biomechanics and rupture risk, and hence, needs to be considered in meaningful FE simulations. In addition, they also claim that inter-patient variability might reduce the importance of considering anisotropic behavior, whereas the geometry is the most critical property to be considered in a structural analysis.

3.2.3 Influence of ILT on peak wall stress

The role of intraluminal thrombus (ILT) on AAA growth and remodeling is significant as it has been suggested that ILT growth and volume may be related to AAA risk of rupture.⁸⁵ ILT is found in most AAAs of clinically relevant size. A large ILT was found to be correlated with accelerated AAA growth rate but also reduced wall stress.¹⁰¹ Some studies have suggested that hypoxia of the AAA wall region covered by ILT causes degradation of the extracellular matrix and subsequent wall weakening, which is one of the precursors for aortic bulging.^56,103 Nevertheless, inclusion of ILT introduces many complexities in FEA modeling if obtaining an accurate wall stress distribution is the ultimate objective. For example, ILT internal fissures can lead to unrealistic stress concentrations; this can also occur at a sudden change in cross-sectional area at the ILT-wall-lumen interface; ILT can act as a buffer leading to lower stresses in those regions where a thick ILT is present. Clinically, a crescent shaped blood diffusion zone inside ILT has been correlated with rupture.⁷²

A reduced peak wall stress was found in patient-specific geometries when ILT is included in the FE model compared to the stress obtained using a wall-only model that ignores ILT.^30,35,94,103 In an interesting experimental study that supports these findings, Thubrikar et al⁸⁹ note that thrombus protects the aneurysm by diminishing and homogenizing strains on the aneurysm wall, although it does not restrict pressure transmission through it appreciably. A diameter matched approach was used by Gasser et al³⁰ to emphasize the inclusion of ILT and to improve the differentiation between ruptured and non-ruptured aneurysms. However, there is still lack of consensus regarding the protective role of ILT. Despite ILT’s impact on aneurysm disease, from a biomechanics perspective, thrombus development and its relation to aneurysm rupture is still not clearly understood. Whether it increases or decreases the risk of aneurysm rupture is still subject to debate. For example, hemoglobin-rich ILT causes oxidative and proteolytic injury to the wall⁵² and thicker ILT regions cause localized hypoxia of the underlying wall,¹⁰¹ thereby weakening it; ILT internal fissures cause stress concentrations at the wall,⁵⁹ while it also acts as a buffer against elevated wall stress.¹⁰⁰

From a mechanical point of view, ILT is usually considered as a homogeneous, incompressible, hyperelastic solid.^15,91,103 However, recent developments describe the ILT constitutive behavior using nonlinear viscoelasticity,⁹¹ an observation also supported by the recent work of Gasser and associates.³⁰ In this work they also found ILT to be vulnerable against cyclic loads and showing significant decrease in strength as a function of the number of load cycles; this increases the likelihood of ILT failure and the consequent overstress of the AAA wall.⁵⁹ Others have used local ILT wall thickness to model a reduction in wall strength.⁹² If indeed AAA geometry is the most important predictor of peak wall stress location, then the inclusion of ILT will lead to a more accurate spatial distribution of wall stress and a different spatially averaged wall stress (compared to wall-only models) without affecting significantly the statistical differences in peak wall stress. In a comparative analysis of large population groups, it is typically the statistical significance of the differences in peak wall stress of the groups that yields the assessment of rupture risk rather than the individual ILT-influenced peak wall stress estimations.

3.2.4 Influence of calcification

Most of AAAs exhibit localized calcifications in the tunica media, which have been taken into account recently for modeling of AAA biomechanics, leading to conflicting reports on whether the presence of calcification increases^45,82 or decreases⁴⁸ wall stress. There are challenges such as distinguishing calcification boundaries from lumen boundary during image segmentation and a 3D reconstruction becomes highly sensitive to this challenge given the relatively small size of the calcified regions compared to the extent of the lumen. Speelman et al⁸² modeled calcification implicitly by modifying the material property of the neighboring wall elements to account for the stiffer calcium content. Image mask operations were used by Maier et al⁴⁸ to model the multi-domain geometry with calcification beneath the wall embedded in the ILT region, whereas Li et al⁴⁵ modeled calcification embedded within the wall itself. Owing to the relatively thin AAA wall, such subtle differences in the modeling approaches are likely to yield significantly different wall stress estimations. In addition, constitutive material property models are scarce for calcification in the abdominal aorta.⁴⁵

3.2.5 Influence of the initial AAA configuration

Most computational models used for AAA finite element analysis are typically generated from multiple CT images acquired at one instant (gated) or multiple instants within the cardiac cycle, hence these models do not correspond to the geometry of the aorta in the unloaded state or at zero internal pressure. Thus, the application of a physiological pressure boundary condition to these pre-deformed geometries may have a significant effect on the wall stress distribution. Ideally, the boundary condition should be applied to either the unloaded geometry or a prestressed geometry to obtain physiologically realistic stresses.

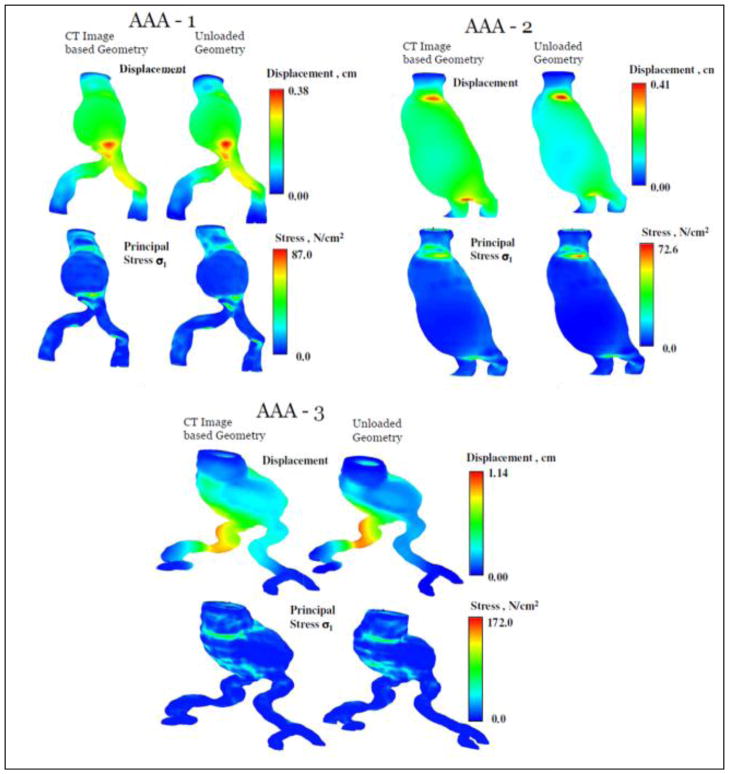
A number of numerical techniques have been developed to recover the approximate zero pressure configuration of an aneurysm.^14,46,62,83 These conclude that not accounting for the zero pressure configuration may lead to an overestimation of the maximum peak wall stress. The presence of the ILT has been neglected in these models and the AAA modeled as an isotropic material. Instead of focusing on the zero pressure geometry, the initial stress was estimated by Gee et al³² using a modified updated Lagrangian formulation while Hsu and Bazilevs³⁸ used an additive decomposition of the second Piola-Kirchoff stress tensor. A simulation based on the diastolic geometry without prestress consideration tends to overinflate the artery resulting in a significant difference in wall shear stress and wall tension.³⁸ In our laboratory, a new algorithm has been developed for zero pressure geometry estimation and applied to patient-specific AAA models that include ILT and regional variations of wall thickness.¹¹ Our two stage algorithm is designed to utilize the finite element mesh of an image based model (representing the geometry at diastolic pressure) and the outcome of FEA or FSI simulations for deriving the zero pressure geometry. In the first stage, the algorithm develops an initial approximation of the zero pressure geometry by extrapolating the nodal displacements of the outer wall mesh. In the second stage, a fixed point iterative algorithm is implemented to make incremental corrections to the nodal coordinates to minimize the error between the pressurized (at diastolic pressure) zero pressure geometry and the CT image based geometry. We tested this algorithm on three patient-specific models and were successful in deriving the zero pressure geometry in 5–9 iterations. Additional FEA simulations with peak systolic pressure were performed with the CT image based and zero pressure geometries of the three AAA models, and the displacements and stresses compared (as shown in Fig. 6). Assuming a nonlinear isotropic material for both the wall and the ILT, these results indicate that not accounting for the unloaded configuration may overestimate the maximum displacement of the AAA wall and underestimate the peak wall stress by as much as 20%.

Figure 6.

Displacement and stress distribution in three patient-specific geometries for both the CT image based analysis and the zero pressure configuration. Analysis based on the zero pressure configuration yielded a larger peak wall stress (reproduced from unpublished data).

Noteworthy is how an algorithm arrives at the geometry at zero pressure using the reference diastolic geometry. In particular, how the saddle shaped curvature regions are handled during this process may influence the ensuing maximum stress. Observing that local displacements are found to increase with the local characteristic radial distance and are less sensitive to local surface curvature⁶⁶ may be helpful when assessing the relative errors in implementation of zero pressure algorithms. In addition, it is desirable to use clinical images acquired at diastole using ECG gating rather than randomly acquired during the cardiac cycle and patient-specific diastolic blood pressure to increase the predictive accuracy of the algorithm.

3.2.6 Effect of blood flow

Most of the AAA wall stress calculations have been obtained from structural models by applying a uniform pressure on the inner surface of the aneurysm sac. The limitation of this approach is that the hemodynamics of blood flow through the aneurysm and the compliant nature of the AAA wall are not accounted for. One of the pioneering works that account for the effect of blood flow on the AAA peak wall stress was conducted by Di Martino et al.¹⁷ Their fluid-structure interaction (FSI) analysis of a realistic aneurysmatic aorta showed that the complex hemodynamics considerably affects the stress distribution, but also reported on the cushioning effect of ILT on the wall. However, in their work, the wall and ILT were considered linearly elastic materials. The nonlinear behavior of the wall and ILT as well as more complex pulsatile flow conditions were modeled in a series of studies conducted by Scotti et al,^74–76 which demonstrated the importance of considering the nonlinear elastic behavior of the structural domain. Moreover, the comparative study between FSI (coupled and decoupled) and structural analysis of patient-specific AAA performed by Scotti et al⁷⁵ show that the non-uniform pressure distribution on the inner AA surface due to the flow yielded a maximum peak wall stress up to 20% higher compared to that obtained with a static FEA when a uniform systolic pressure of 117 mmHg is applied. In these studies it is concluded that FSI analysis has the potential to capture the fluid dynamics inside a complex AAA structure accurately and hence is a better approach for calculating wall stress and studying rupture risk. Leung et al⁴⁴ also compared the stresses obtained from an FSI model and an FEA model, and reported that the combination of pulsatile fluid flow and a compliant wall can change the local stresses slightly but has a negligible effect on the peak wall stress. However, they created the wall domain by offsetting the lumen boundary, thereby ignoring ILT in the model, which therefore affected both the wall geometry as well as its mechanical contribution to the ensuing mechanics. One of the main conclusions that can be derived from these studies is that using a non-uniform pressure distribution on the AAA sac can substantially improve the accuracy of the structural analysis thereby avoiding a computationally extensive FSI analysis for assessing AAA rupture risk. Similar findings were reported by others using idealized and patient-specific geometries.^41,42,57

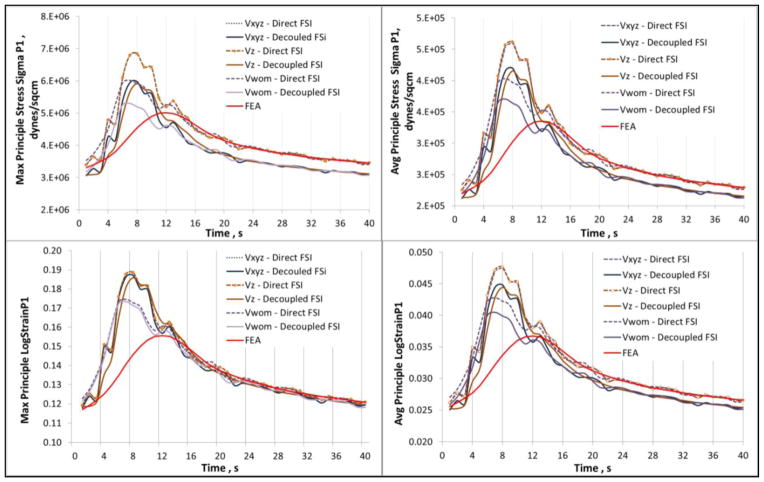
A recent study by Chandra et al¹⁰ demonstrates the effect of MRI derived inlet flow boundary conditions on AAA FSI modeling with ILT. The objective was to identify the effect of different inlet velocity distributions (Vwom: Womersley velocity profile, Vz: profile with longitudinal velocity component, Vxyz: profile with inclusion of all velocity components) on the computational assessment of stress and strain, and further draw comparisons with structural only (FEA) simulations. The study revealed that the contribution of the MRI derived longitudinal velocity component is significant in comparison to the in-plane components at the model inlet, and that a Womersley velocity profile leads to underestimation of wall stress. A comparison between fully coupled FSI, decoupled FSI, and transient FEA simulations revealed that the wall stress and strain distributions are largely influenced by the inclusion of the flow dynamics, as FEA underestimates both peak wall stress and strain. Further, the study demonstrates that peak stress and strain are not achieved at peak systolic pressure (see Fig. 7), therefore structural only simulations are inadequate for an accurate assessment of AAA biomechanics. The influence of material anisotropy in FSI simulations has been investigated by Rissland et al⁶⁹ and Xenos et al.¹⁰⁶ In their work, Rissland and colleagues introduced a new anisotropic material model of the AAA wall to perform FSI simulations of patient-specific AAA geometries to develop a more reliable predictor for the risk of rupture. With the ILT still modeled as a linearly elastic compressible material, these studies indicate that isotropic wall material properties yield a lower peak wall stress compared to anisotropic wall properties, resulting in an underestimation of the rupture risk.

Figure 7.

Maximum and average principal stress and strain waveforms for a patient-specific AAA obtained using direct FSI, uncoupled FSI, and transient FEA. The stress and strain follow the inlet velocity waveform rather than the pressure waveform boundary condition (reproduced from unpublished data).

4. MODELING CONSIDERATIONS AND RECOMMENDATIONS

If not performed accurately, numerical modeling can mislead AAA clinical management and pre-surgical planning recommendations. The following is an overview of the importance of computer aided analysis and its different stakeholders in AAA rupture risk assessment.

4.1 On the rationale for high stress and saddle shape correlation

AAA wall stress is typically maximum at a location that features the combined effects of large diameter and a local surface saddle point (i.e., a wall surface region that has local concavity when traversed along one direction and local convexity when traversed in a relatively perpendicular direction along the surface). The rationale for such behavior, under the assumption of a uniform wall thickness, can be explained by considering the schematic of Fig. 8. Consider two points A and B. A is located at a locally convex region in almost any plane passing through A. B is locally convex when a section cut by horizontal plane passing through B is considered; however, B is also locally concave when a section cut by vertical plane is considered, i.e. B represents a local saddle point. Consider a small region of wall near A and B isolated in space and forces acting on it as shown in Fig. 8. The in-plane forces (membrane forces) acting on this small region longitudinally have a component in the radial direction that augments the radially outward normal force acting from inside the AAA sac at point B. Hence, to maintain force equilibrium along the radial direction there is an increased demand on the membrane forces at B in the horizontal plane since those have a radially inward component acting on the small region under consideration. This scenario results in a higher wall stress. On the other hand, in-plane membrane forces in the vertical direction at A ease the load in the horizontal plane because of their radially inward component acting against the normal force. Thus higher stresses result from a combined and favorable action of local in-plane forces. Hence, stresses are also dependent on size since in-plane membrane stresses are simply dependent on the local diameter. Therefore, it is the combination of the local transverse dimension and local curvature that govern the wall stress distribution under the assumption that the wall thickness is uniform. This underscores the importance of quantifying accurately and non-invasively the individual AAA surface geometry and, evidently, regional variations of wall thickness from existing clinical imaging modalities, to obtain an accurate wall stress prediction.

Figure 8.

Rationale behind high stresses in saddle shaped surface region; (a) Typical stress distribution obtained by FE analysis under a uniform wall thickness assumption a cut section showing high stresses in the saddle shaped region; (b) Schematic with force directions explaining rationale behind saddle shape and high stress correlation.

4.2 On image based geometry reconstruction

It is evident that AAA geometry, especially its characterization by means of surface curvature and regionally varying wall thickness has a remarkable influence on computed biomechanical parameters such as stresses and strains. Consequently, the need for an accurate and realistic image based 3D reconstruction is emphasized in this work as a research opportunity. Some open questions remain in this regard, e.g. what is the extent of the error the image resolution introduces in the ensuing wall mechanics? Can it be ignored when performing numerical modeling? How is the accuracy of the 3D reconstruction affected by the unequal spacing of the image data originated from the in-plane resolution (pixel size) being small compared to the out-of-plane resolution (slice spacing)? Does the use of different image processing filters introduce additional uncertainty in the AAA geometry reconstruction? How much smoothing makes the reconstructed anatomy “smooth enough”? What is an appropriate metric to quantify smoothing-induced distortion of the geometry? Many of these questions arise in biomechanics modeling and are left either unanswered or as an end user’s judgment call, but can be addressed by quantifying inter-operator and intra-operator variations in the repeatability of 3D reconstructions. Our recent work⁶⁶ suggests that the sensitivity of linear tessellated surface representations toward smoothness-induced distortion caused by common Laplace and Taubin smoothing algorithms is higher for vessel regions with high curvature and larger element size. This implies that while the smoothing iterations are applied uniformly to the geometry, the ensuing changes in the surface are non-uniform and vary regionally.

4.3 On convergence assessment

The field of computational biomechanics has remarkable implications in the clinical management of vascular disease; however, it is important to understand the responsible use of the tools generated by researchers for this purpose. With accessibility to these tools, both in terms of software availability and hardware capabilities, a plethora of results without substantial thought on the proper setup of the simulations may attenuate the importance of the tools. Appropriate conventions and codes may be established in the near future for computational biomechanics similar to the ASTM international standards; such aspect is covered in more detail by Erdemir et al.²⁶ To this end, an analysis of numerical convergence poses a challenge for patient-specific modeling. There is no unique guideline that indicates the need to evaluate specifically stress or displacement or wall shear stress, etc., for convergence assessment. In biomedical applications, as the mesh element size is reduced, achieving convergence of the numerical solution to the governing equations, may not yield geometric accuracy (under the assumption of a consistent mesh quality during the mesh refinement process), making it difficult to arrive at some standard protocol. Ideally, a mesh refined for numerical convergence should be embedded within a coarser mesh,⁶ which is intricate to achieve in patient-specific modeling due to limitations related to high computational costs and parallelization of the solvers. For example, the number of elements in a hexahedral mesh would increase 8–27 times for a single step of isotropic refinement. Another problem of importance is the consideration given to the spatial location of the variables probed for convergence. In the case of patient-specific blood vessels with branches and bifurcations, it is not simple to define the probing location for different mesh resolutions due to the lack of mathematical equations that can define the tessellated geometry with precision. Preferably, mesh independence should be performed for each simulation; however, at least one reference mesh independence study should be completed for each combination of simulations parameters per patient-specific geometry.

4.4 On factors affecting wall mechanics

Computational assessment of wall mechanics is dependent on many factors, as shown previously in Fig. 2. Improved image segmentation algorithms are needed as current strategies do an inadequate job in identifying small features that have an impact on the wall mechanics, e.g. the inner wall boundary, extent of the calcified regions, etc. There are user dependent controls during 3D reconstruction such as image filters, morphological operation sequences, and mesh smoothing, for which there is no standard protocol to follow particularly in multi-domain vessel structures. Attempts to address inter-operator and intra-operator variability could improve reliability of these controls.^37,78 The use of shell vs. tetrahedral meshes and the inclusion of ILT were addressed by Doyle et al;²⁰ however, additional work is warranted by evaluating other features in AAA mechanics such as the geometry of the aorto-iliac bifurcation, patient-specific material properties, smoothness of the multi-domain interfaces, etc. Investigations such as the one reported by Doyle and colleagues,²¹ which verify computational techniques against experimental measurements or, alternatively, a peer-to-peer comparison of results for a common test problem that closely imitates the physiological environment should be encouraged as it would bring more credibility for computational biomechanics among the medical community. Moreover, the absence of a method for non-invasive, in vivo assessment of intraluminal pressure waveforms often leads to the use of simplified boundary conditions in the computational simulations. For patient-specific AAA rupture risk assessment, it would appear necessary to estimate the individual constitutive material properties of the vascular wall by means of nondestructive, in vivo methods as the aorta grows and remodels. This would lead to an unprecedented AAA multi-scale modeling approach, which would entail spatio-temporal variations of the wall mechanical properties as a function of the contributing cellular and subcellular components of the media and adventitia. Nevertheless, if the time rate of change of peak wall stress with respect to a baseline configuration (e.g., at the initial diagnosis of the AAA) is ultimately the sought-after biomechanical parameter that largely influences the rupture potential of an aneurysm, will complex growth and remodeling constitutive models lead to an increased accuracy in rupture risk assessment? In our laboratory, we have hypothesized that wall stress is largely influenced by the AAA shape and to a lesser extent by the constitutive material model used to represent the wall tissue properties. As wall stress computation is the result of force equilibrium equations, regionally-varying growth and remodeling constitutive models would presumably also play a limited role in the ensuing wall stresses compared to the driving time-course, evolving aneurysm shape. To this end, geometry reconstruction has a profound influence on the wall mechanics and hence preprocessing steps such as image segmentation, 3D reconstruction, and meshing require careful consideration.^1,3,66

Other important factors remain relatively unexplored as it relates to AAA wall stress estimation. First, the measurement and implementation of patient-specific non-uniform thickness of the arterial wall is a complex task, due primarily to limitations in the current technology to measure this parameter non-invasively. Patient-specific wall thickness variations based on ILT covered and uncovered regions of the wall³⁰ and truly image-derived variable wall thickness^66,67 have been implemented recently. Second is our limited knowledge regarding in vivo material property characterization, which will require in vivo intraluminal pressure measurement and 3D strain estimation. In this regard, 4D CT/MR images have been used to assess blood vessel deformation.^4,24,54 Recent work by Tierney et al⁹⁰ evaluates 2D strains in AAA cross sections and our own laboratory has contributed to 3D strain calculations using ECG gated MR images.⁶⁶ Consideration given to material properties subject to growth and remodeling (G&R theory)^5,104,105 remains an open research opportunity.

4.5 Clinical perspective

A computational tool that can calculate the regional and time-course variations of local surface curvatures automatically from segmented clinical images on the same day of AAA diagnosis or follow-up would be a resource with great translational potential in the vascular clinic. In our laboratory, local curvatures are believed to be the most important predictors of wall stress, which can be computed using membrane equilibrium equations on a patient-specific basis without the need to perform FEA (which would require specifying tissue material properties). Such a tool would need prior validation using a thorough biomechanics based approach to gain credibility in the medical community. Nevertheless, the comparative analysis of the various types of AAA (surveillance, electively repaired, symptomatic, and ruptured) by means of non-invasive, regional surface curvature quantification should yield the necessary metrics for rupture risk assessment without the need to derive population-based or individual constitutive material models.

Table 2.

Literature review summary - solid mechanics AAA modeling – Part 1 (Please refer to Table 1 for abbreviations used.)

First Author (year)	Focus	PS/I	Cases	Reconstruction Strategy	Bifur	ILT	Ca	FEA Solver	Pressure	Residual Stress	Element Type	Material Model
Fillinger (2003)	Rupture risk vs Max Dia	PS	103	PC, Decimation, SS	Y	N	N	ABAQUS	PS	N	S3 (?)	HE 59
Raghavan (2000)	Patient specific AAA analysis	PS	7	PC, Decimation, SS	N	N	N	ANSYS	PS	N	S4	HE 59
Fillinger (2002)	Wall stress and rupture risk	PS	48	PC, Decimation, SS	Y	N	N	ABAQUS	PS	N	S3 (?)	HE 59
Vorp (1998)	Geometry effect	I	10	GC-circle	N	N	N	ANSYS	120 mmHg	N	S4	E-5 MPa
Wang (2002)	ILT effect	PS	4	PC, decimation, SS, 3D Solid (Pro-E), Wall by extrusion const thk, PATRAN for meshing	N	Y	N	ABAQUS	PS	N	Tet-10	HE 59
Venkasubramaniam (2004)	rupture Vs non-rupture using PWS	PS	27	PC, Rhino Surface	N	N	N	ANSYS	120 mmHg	N	S6	HE 59
Inzoli (1993)	PWS and ILT	I	1	Axisym 2D	N	Y	N	BRAVO3	120 mmHg	N	Quad-04	E-2 MPa
Di Martino (1998)	ILT effect on AAA biomechanics (Expt+Sim)	I	1	2D, plane stress	N	Y	N	Patran	120 mmHg	N	Quad-04	E, HE
Elger (1996)	Shape and PWS	I	1	2D axisym	N	N	N	Analytical membrane theory	parameter	N	No FEM	E

Table 3.

Literature review summary - solid mechanics AAA modeling – Part 2 (Please refer to Table 1 for abbreviations used.)

First Author (year)	Focus	PS/I	Cases	Reconstruction Strategy	Bifur	ILT	Ca	FEA Solver	Pressure	Residual Stress	Element Type	Material Model
Stringfellow (1987)	PWS and geometry	I	2	Cyl and Sphere	N	N	N	Nastran	100 mmHg	N	Hex-08	E-3 MPa
Di Martino (2003)	Effect of ILT mat. prop. variation	I	1	Bell Curve Shaped	N	Y	N	ABAQUS	120 mmHg	N	Hex-08	HE
Speelman (2007)	Ca effect on AAA biomechanics	PS	6	?	N	Y	Y	ABAQUS	16 kPa	N	Quad-04	HE - 59
Truijers (2007)	PWS	PS	30	PC, decimation, SS Gaussian variation	N	N	N	ABAQUS	PS	N	S3 (?)	HE - 59
Rodriguez (2008)	Diameter, asym. and mat. Prop.	I	1	in Diameter and location of center	N	N	N	ABAQUS	16 KPa	N	Hex-08	HE , HEaniso
Doyle (2007)	Comparison of Modeling techniques	I	3	Marching Cube (Mimics)	N	Y	N	ABAQUS	120 mmHg	N	S3	E-4.66 MPa, HE 59
Li (2008)	ILT and Ca effect on AAA biomechanics	PS	20	Marching Cube (Simpleware)	Y	Y	Y	ABAQUS	AvgSys	N	Tet-4 (?)	HE - 59
Doyle (2009)	Vessel asym. as diagnostic tool	PS	15	Marching Cube (Mimics)	N	N	N	ABAQUS	120 mmHg	N	S3 (?)	HE - 59
Heng (2008)	PWS in rAAA and eAAA	PS	70	PC, Rhino Surface	N	N	N	ANSYS	PS	N	S8	HE - 59