Physical Factors Effecting Cerebral Aneurysm Pathophysiology

Abstract

Many factors that are either blood-, wall-, or hemodynamics-borne have been associated with the initiation, growth, and rupture of intracranial aneurysms. The distribution of cerebral aneurysms around the bifurcations of the circle of Willis has provided the impetus for numerous studies trying to link hemodynamic factors (flow impingement, pressure, and/or wall shear stress) to aneurysm pathophysiology. The focus of this review is to provide a broad overview of such hemodynamic associations as well as the subsumed aspects of vascular anatomy and wall structure. Hemodynamic factors seem to be correlated to the distribution of aneurysms on the intracranial arterial tree and complex, slow flow patterns seem to be associated with aneurysm growth and rupture. However, both the prevalence of aneurysms in the general population and the incidence of ruptures in the aneurysm population are extremely low. This suggests that hemodynamic factors and purely mechanical explanations by themselves may serve as necessary, but never as necessary and sufficient conditions of this disease’s causation. The ultimate cause is not yet known, but it is likely an additive or multiplicative effect of a handful of biochemical and biomechanical factors.

Introduction

Cerebral aneurysms are focal weakened pouches of arterial walls around bifurcations of the circle of Willis (Figure 1). Approximately 5% of the population (~15 million people in the United States) is estimated to have at least one cerebral aneurysm. About 0.2% of these aneurysms rupture every year (30,000 ruptures/year in the United States) leading to a subarachnoid hemorrhage.³³ This accounts for only about five percent of all strokes, but the consequences of aneurysmal hemorrhage are dire, carrying a mortality rate of about 50% and a morbidity rate among survivors of about 50%.¹⁴ The pathophysiology (term used to include aneurysm formation, growth, and rupture unless otherwise specified) of aneurysms leading to aneurysm growth and eventual rupture are not entirely clear, but research, especially because of the large number of groups studying aneurysms over the past decade or two, continues to converge on identification of the mechanisms responsible.

Figure 1.

Circle of Willis showing common locations of cerebral aneurysms. From Schievink 1997¹⁵⁶(N. Engl. J. Med., Schievink WI, Intracranial aneurysms, 336, pp.29, Copyright ©1997 Massachusetts Medical Society. Reprinted with permission from Massachusetts Medical Society)

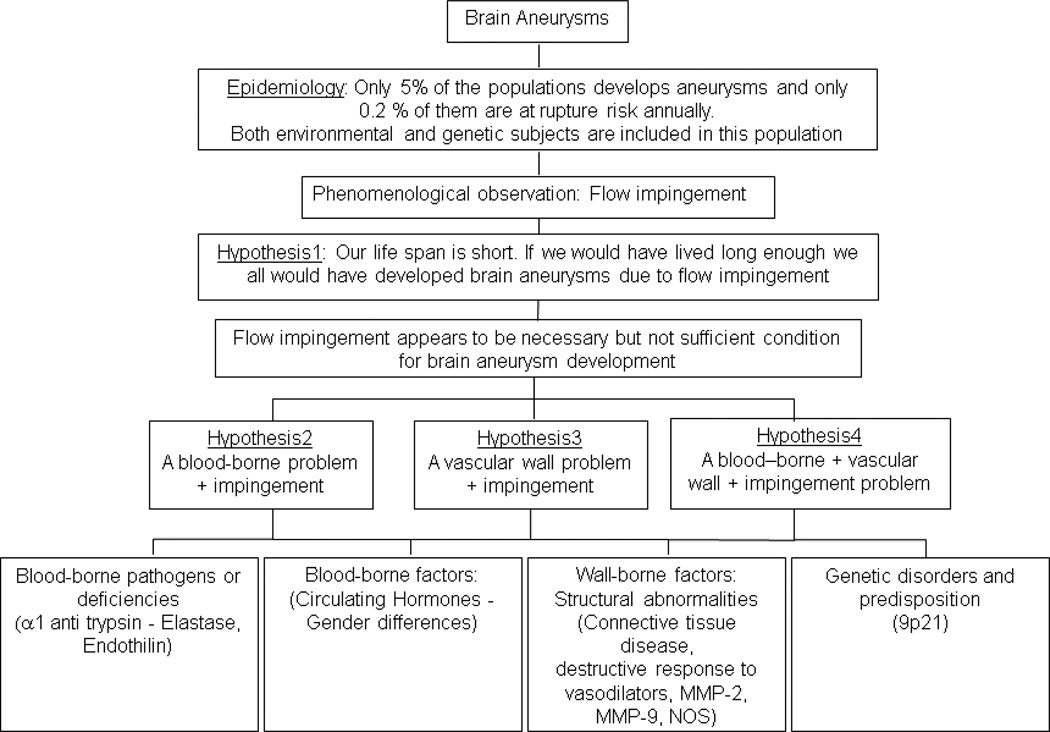
Reasonably, such dilations occur because of deleterious factors or deficiencies in the blood or because of structural deficiencies in the arterial walls, or both, with the focal nature of the disease being modulated by normal or abnormal (yet undefined) hemodynamics at the predisposed locations (Figure 2). The extent to which the pathophysiology is intrinsically predisposed or environmentally induced is also not clear. Epidemiologically, factors associated with aneurysms over the years include smoking, excessive alcohol consumption, female gender post-menopause (potentially protective role of estrogen), polycystic kidney disease, Ehlers-Danlos syndrome, α1-antitrypsin deficiency, increased levels of plasma elastase, altered expression or activity of matrix metalloproteinases and tissue inhibitors of metalloproteinases, alterations in molecules involved in tissue repair/vascular remodeling/extracellular matrix maintenance, growth factors, cellular adhesion molecules, familial history, genetic aberrations (genes or genetic regions encoding for collagens, elastin, endothelial nitric oxide synthase, α1-antitrypsin, matrix metalloproteinases (−1,−3,−9, and −12), tissue inhibitors of metalloproteinases, fibronectin, secreted protein acidic and rich in cysteine, polycystin, endoglin, transforming growth factor-β receptors, versican, perlecan, serpin, fibrillin), aneurysms with an irregular or multilobulated shape, aneurysms with higher aspect ratios (ratio of aneurysm height to neck), anomalies in the vascular tree around the circle of Willis, surgery or disease induced changes in flow in the affected parent artery, and larger aneurysm sizes^{28,36,80,82,88,94,96,98,109,126,137,146,150,151,156,164,204}

Figure 2.

A basic flowchart showing mechanistic possibilities of aneurysm pathophysiology

The list is not exhaustive but is illustrative of the fact that a plethora of factors have been associated with aneurysms and that all of them are blood-, wall-, or hemodynamics-borne. More important, the evidence shows that taken individually, all these factors are at best proximate causes of aneurysm pathophysiology. In so far as hemodynamic factors (flow impingement, pressure, wall shear stress (WSS)) are concerned, the phenomenological/epidemiological observation that the aneurysm occurrence rate is so low in the population demonstrates that these, by themselves, are insufficient conditions as causative factors of aneurysm initiation and formation. The ultimate cause is not yet known, but it is likely an additive or multiplicative effect of a handful of factors. Previous listed references may be consulted for cellular, molecular, and genetic factors associated with aneurysms. There are also several review articles written on the subject.^{14,49,96,98,126,151,156,164,189,213} The focus of this review is to address hemodynamic factors associated with aneurysm pathophysiology; also addressed are anatomical and structural factors as these inherently affect prevailing hemodynamics. We attempt to provide an overview of the breadth of the subject so different aspects are dealt with in varying degrees of depth and we briefly summarize salient (due to importance or popular use) variables or articles and note our conclusions from the evidence presented. Thus, broadly, the article represents our perspective on the status of physical variables that govern aneurysm pathophysiology. The reader may look to the references listed to gain additional information on different aspects or to educate themselves on different perspectives.

A search of the phrase ‘(cerebral OR intracranial) AND aneurysm AND (flow OR hemodynamics)’ in Pubmed, Medline, and Compendex gave 2891, 2350, and 331 results, respectively; search of ‘(cerebral OR intracranial) AND aneurysm AND biomechanic*’ gave 85, 75, and 108, results respectively. Results were limited to journal articles, duplicates were removed, and article titles were manually reviewed to condense the number of articles to 386. The reference list used here is a representative subset of the content of these ~400 articles.

Geometry

Flow patterns at arterial locations predisposed to aneurysm formation or within aneurysms (predisposed to rupture) are intrinsically governed by vascular anatomy. Several studies have evaluated such anatomical and morphological factors with the goal of elucidating differences in vascular anatomy between patient and control populations to determine geometrical factors causing aneurysm initiation and between ruptured and unruptured aneurysms to determine geometrical factors causing aneurysm rupture. Table 1 summarizes the arterial locations within and around the circle of Willis at which aneurysms are found. It should be noted that both ruptured and unruptured aneurysms are combined in the table and that the studies listed in the table may not precisely differentiate their results into the locations listed. For example, internal carotid aneurysms may include posterior communicating artery aneurysms while basilar artery aneurysms may include aneurysms of the vertebrobasilar system or list only basilar terminus aneurysms. The important point to note from the table, however, is that at least 70–75% of all intracranial aneurysms occur at one of three locations - the middle cerebral artery (at the bifurcation), the posterior communicating artery (at the internal carotid artery junction), and the anterior communicating artery (at the anterior cerebral artery junction). Internal carotid and basilar artery terminus aneurysms, which can be considered to be at ‘T’ junctions seem to constitute at most about 7% (at each terminus) of all aneurysms.^{4,14,34,46,50,76,91,114,145}

Table 1.

The location of aneurysms on the circle of Willis

Article	Number of aneurysms	ICA (%)	MCA (%)	ACA (%)	PComA (%)	AComA (%)	Basilar (%)
Crawford 195930	163	30 (18)	54 (34)	20 (12)	−	46 (28)	7 (4)
Kayembe 198491	67	12 (18)	15 (22)	2 (3)	−	27 (40)	4 (6)
Rinkel 1998a, 146	563	223 (42)	159 (30)	126 (24)	−	−	55 (10)b
Forget 200146	245	27 (11)	29 (12)	−	48 (20)	71 (29)	36 (15)
Joo 200978	889	131 (15)	258 (29)	−	152 (17)	284 (32)	−
Jeong 200976	239	20 (8)	61 (25)	14 (6)	52 (22)	66 (28)	13 (5)
De Rooij 200934	150	10 (7)	84 (56)	−	20 (13)	22 (15)	14 (9)
Carter 200617	1673	216 (13)	398 (24)	−	315 (19)	426 (26)	193 (12)
Ruiz- Sandoval 2009152	231	42 (18)	46 (20)	−	64 (28)	61 (26)	7 (3)
Hademenos 199859	74	18 (24)	3 (4)	−	11 (15)	4 (5)	24 (32)
Richardson 1941145	53	13 (25)	16 (30)	−	−	13 (25)	6 (11)
Nader- Sepahi 2004125	182	23 (13)	53 (29)	−	47 (26)	28 (15)	−
Juvela 200081	181	79 (44)	82 (45)	7 (4)	−	8 (4)	5 (3)
Weir 2002a, 204	3776	1437 (38)	797 (21)	−	−	1118 (30)	234 (6)b
McDonald 1939120	1023	165 (16)	294 (29)	121 (9)	66 (6)	158 (15)	143 (14)
Beck 20069	155	19 (12)	39 (25)	49 (32)c	20 (13)	−	28 (18)
Baharoglu 20124	271	52 (19)	40 (15)	5 (2)	49 (18)	58 (21)	12 (4)
Mackey 2012116	2930	1067 (36)	749 (26)	398 (14)c	374 (13)	−	342 (12)
Mean±Std Dev. %		21±11%	26±12%	12±10%	17±6%	23±10%	10±7%

^aLiterature review

^bPosterior circulation

^cIncludes AcomA

A large number of geometrical studies are driven by the goal of determining thresholds that will delineate unruptured from ruptured aneurysms. Various variables have been suggested, of which the maximal aneurysm size is the most widely used. There were early suggestions that a critical size threshold varying between 5–10 mm existed above which aneurysms are at increased rupture risk, or at least that unruptured aneurysms smaller than 10 mm have very low probabilities of rupture.^31,207 But given the data collected thus far, this position does not seem defensible in so far as predicting rupture risk of any given unruptured aneurysm smaller than 10 mm. In general, the data clearly show that the average size of ruptured aneurysm samples is greater than the average size of unruptured aneurysm samples (Table 2). The effect size (ruptured size – unruptured size), however, seems to be about 1.5 mm at best. Also, 70–85% of all ruptured aneurysm samples are smaller than 10 mm.^{9,46,76,78,125,204} Hypotheses suggesting that a certain class of aneurysms reach stability below the 10 mm size and thus rarely progress to rupture do not seem to be supported by the evidence.⁴⁶

Table 2.

Differences in size of ruptured and unruptured aneurysms

Article	Ruptured (mm)	Unruptured (mm)	Effect size (mm)	Effect Size (% of ruptured size)
Sadatomo 2008153	7.2	5.6	1.6	22%
Baharoglu 20124	7.8	6.4	1.4	18%
Weir 2002 (in Lall 2009102)	8	7	1	13%
Weir 2003 (in Lall 2009102)	10.8	7.8	3	28%
Hoh 2007 (in Lall 2009102)	6.2	4.3	1.9	31%
Juvela 2008 (in Lall 2009102)	5.6	4.9	0.7	13%
Baumann 2008 (in Lall 2009102)	7	4	3	43%
Beck 20069	6.7	5.7	1	15%
Yasuda 2011212	6.7	4.9	1.8	27%
Hademenos 199859	11.9	13.5	−1.6	−13%
Juvela 2000	5.6	4.9	0.7	13%
de la Monte 1985 (in Weir 2002204)	11.4	7.6	3.8	33%
Nader-Sepahi 2004125	7.7	5.1	2.6	34%
Carter 200617	8.2	8.4	−0.2	−2%
Rahman 2010142	7.9	6.2	1.7	22%
San Millán Ruíz 2006154	7.6	6.1	1.5	20%
Joo 200978	6.3	5.5	0.8	13%
Mean(std.error)			1.5(0.3)	19(3)%

Other geometrical variables have been constructed to include the aneurysm-parent vessel complex in an attempt to derive better descriptors of rupture. The aspect ratio (aneurysm height/aneurysm neck) of ruptured aneurysm samples has been found to be ~2.4, while that of unruptured aneurysms ~1.6.^{102,125,141,193} The size ratio (maximum aneurysm size/parent vessel diameter) of ruptured aneurysms is 4.1, while that of unruptured aneurysms, 2.6.¹⁴² The volume orifice area ratio (aneurysm volume/aneurysm neck area) of ruptured aneurysms is 14 and that of unruptured aneurysms 7.²¹² Ruptured aneurysms are often (40–60% of cases) multi-lobulated (presence of blebs) or have irregular surfaces.^31,59 Descriptors quantifying the shape of aneurysmal surfaces (surface undulations, ellipticity, non-sphericity, curvature) have also been found to have the potential to delineate ruptured from unruptured aneurysms.^34,141 Many other geometric variables have been constructed; the more popular ones have been reviewed previously.^4,102 The sensitivity of the predictive tests based on these factors is around 70–75%.^{125,141,142,212} Much larger data sets will be required to improve the predictive value of these tests if they are to be used to make clinical prognoses of individual aneurysms. Also, geometrical thresholds predicting rupture would be more accurate if they were obtained from prospective studies of unruptured aneurysms that are left untreated and then progress to rupture instead of the retrospective data being used for these tests,^114,206 but such prospective studies are difficult to conduct.

Anomalies in the geometry of the circle of Willis (such as hypoplasia, absence, asymmetry of paired vessels, fenestrations, triplication) have been suggested to occur more frequently in patients with aneurysms as compared to controls.^12,91,208 Statements that no such differences exist have been made.¹⁶³ Contradictory reports have also been published associating circle of Willis anomalies with ruptured aneurysms.^34,105 Such anomalous circles of Willis seem to exist in about 50% of the general population.⁸⁴ The overall evidence seems to be insufficient to conclude such association at this time. However, there does seem to be an association between asymmetry of the anterior cerebral arteries and the presence of anterior communicating artery aneurysms, with 25%–50% of circles with aneurysms having the asymmetry as compared to 5%–25% of non-aneurysmal circles.^91,115,163 There is marginal evidence indicating higher frequencies of asymmetry of the posterior communicating arteries in the patient population.⁹¹ Aneurysms seem to be more (as compared to controls) prevalent at bifurcations with greater bifurcation angles (angle between the daughter branches).^12,73,89 The longitudinal axis (aneurysm height) of aneurysms is more aligned with the direction of parent vessel flow in ruptured aneurysms as compared to unruptured aneurysms.^4,34,153,177 There is some evidence that the longitudinal axis of aneurysms clusters around specific angles with respect to the parent artery¹⁶⁶ and that more distal aneurysms have smaller sizes,¹⁷ but the effect of the perianeurysmal environment¹⁵⁴ must be considered along with such results. Advancements in software and hardware have enabled the quantification of much more sophisticated geometrical variables (or sophisticated combinations of geometrical variables) of the 3D aneurysm-parent vessel complex with relative ease^{104,111,138,139} and although it is difficult to imagine that a critical threshold predicting aneurysm rupture (or initiation) could be derived from purely geometrical factors, future evaluation may yield a geometrical predictive test with acceptable sensitivity and specificity to be clinically useful.

Flow

Flow patterns and pressure

Flow in cerebral aneurysms has generally been evaluated qualitatively by clinical and in vivo angiography and dye visualization in glass and elastomeric models and quantitatively by particle image and laser Doppler velocimetry in glass and elastomeric models and by numerical computational fluid dynamic (CFD) simulations. Figure 3 is a sampling of images from such varied studies showing the fundamental patterns of flow within aneurysms; the reader may look into these and other references to gain additional visual perspective on intraneurysmal flow. As represented in the figure, the gross qualitative features of flow in all aneurysms can be discerned from knowing the geometry of the aneurysm-parent vessel complex and estimates of volumetric flow in the arteries leading to and from the aneurysm. The traditional flow pattern is that of sidewall aneurysms, where the flow near the vessel wall closer to the aneurysm impinges on the distal neck of the aneurysm, enters the aneurysm, moves along the aneurysm wall in a circular/vortical manner and exits the aneurysm back into the parent vessel at the proximal neck of the aneurysm.^{51,67,71,110,135,168,169,180} Central regions of this vortex have very low flow activity.^53,128,136 This pattern, although simplistic, serves as a fundamental description of flow in all aneurysms. Complexity to the pattern is usually added by the prevailing geometry. Flow patterns in aneurysms at bifurcations, for example, are governed by the bifurcation angle, by the asymmetricity of the daughter branch diameters and by the flow distributions into these branches.¹⁶⁸ Flow from the parent artery tends to follow the trajectory along the longitudinal axis of the parent, tends to enter the aneurysm at the neck closer to the larger daughter branch, forms a vortex in the aneurysm, and exits at the opposite neck into the daughter branch closest to the exit.^136,175,192 The vortical structure may not be present if the aspect ratio of the aneurysm is very low (with flow maintaining its direction while deviating into the aneurysm) or a secondary vortex may form if the aspect ratio is high or if the aneurysm has a bleb.^110,135,192 Aneurysms with higher aspect ratios tend to have a lower ‘penetrance’ of flow or primary vortical structure into the aneurysm and tend to have flow stagnation zones near their domes.^147,192 Depending on the width and depth of this flow penetrance, a secondary vortex rotating in the opposite direction of the primary vortex may form in the aneurysm.^54,171 A greater part of the flow into anterior communicating artery aneurysms comes from the larger anterior cerebral artery but comprises of a mixing of streams from both anterior cerebrals and the intraneurysmal flow is additionally affected by the asymmetry of flow in the efferent A2 segments of the anterior cerebrals.^19,92 Basilar sidewall aneurysms may be affected by the asymmetry of flow distribution in the vertebrals, but the effect of this asymmetry is generally resolved in the length of the basilar artery by the time flow reaches basilar bifurcation aneurysms.¹⁹ Being under the influence of pulsatile flow, these aneurysmal patterns have a temporal quality so that, for example, portions of the fluid in the parent vessel can be driven into the aneurysm vortex during systole and then be distributed either into stagnation zones at the aneurysm dome or into the central vortical regions, while a greater portion (greater as compared to systole) of the intraneurysmal fluid exits the aneurysm during diastole.^53,107 The location near the distal neck where the flow impinges the aneurysm wall and the proportion of the neck area carrying flow into the aneurysm can vary during the cardiac cycle^54,180 and stable or oscillating vortical structures may persist throughout the cardiac cycle or they may be transient, existing only for parts of the cardiac cycle.^67,159 The flow in the parent vessel at the aneurysm neck is also generally disturbed (by the inflow and the outflow) and may contain portions of the intra-aneurysmal vortex, secondary flow structures including helical flow patterns, and recirculation zones.^110,135 Overall, the flow patterns in any given aneurysm in a patient are unique to that aneurysm because the geometry of the aneurysm-parent vessel complex and the parent vessel flow rates are unique to that aneurysm.

Figure 3.

Schematics of flow patterns in A) sidewall, B) bifurcation with symmetrical outflow, C) bifurcation with asymmetrical outflow, and D) asymmetric bifurcation. E) Laser induced fluorescence study in a sidewall channel at mid systolic acceleration; F) Dye visualization in an elastomer model of an anterior communicating artery aneurysm; asymmetrical internal carotid flow; G) Computational fluid dynamics in a giant internal carotid-posterior communicating artery aneurysm at early diastole; H) schematic of flow patterns in a high aspect ratio bifurcation aneurysm with a bleb; I) schematic at one instant in the cardiac cycle of different flow patterns obtained from computational fluid dynamics simulations in anatomically realistic aneurysms. Panels A–D from Steiger 1987¹⁶⁸ (With kind permission from Springer Science+Business Media: Heart Vessels, Basic flow structure in saccular aneurysms, 3, 1987, pp.57–61, Steiger HJ et al., Figures 3,7a,7b,8); panel E from Lieber 1997¹⁰⁷ (With kind permission from Springer Science+Business Media: Ann. Biomed. Eng., Alteration of hemodynamics in aneurysm models by stenting, 25, 1997, pp.463, Lieber BB et al., Figure 5A); panel F from Kerber 1999⁹² (CW Kerber et al., Flow dynamics in a lethal anterior communicating artery aneurysm, AJNR Am J Neuroradiol, 20, 10, pp.2000–3, 1999 © by American Society of Neuroradiology); panel G from Steinman 2003¹⁷¹ (DA Steinman et al., Image-based computational simulation of flow dynamics in a giant intracranial aneurysm, AJNR Am J Neuroradiol, 24, 4, pp.559–66, 2003 © by American Society of Neuroradiology); panel H from Ujiie 1999¹⁹² (Ujiie H et al., Effects of size and shape (aspect ratio) on the hemodynamics of saccular aneurysms, Neurosurgery, 45, 1, pp.119-29, 1999); panel I from Cebral 2005²³ (JR Cebral et al., Characterization of cerebral aneurysms for assessing risk of rupture by using patient-specific computational hemodynamics models, AJNR Am J Neuroradiol, 26, 10, pp.2550–9, 2005 © by American Society of Neuroradiology)

There is no difference in intraneurysmal and systemic pulsatile pressure as shown in 34 in vivo aneurysms,^130,157 in 8 patients intra-operatively³⁸ and endovascularly⁴¹, and in in vitro sidewall aneurysms.⁵³ There are in vivo experiments suggesting that pressures at the aneurysm dome are statistically lower (mean pressure lower by 10 mmHg in 5 cases,¹ systolic and diastolic lower by 6 mmHg in 80 cases⁶⁰) than systemic values, but the relative magnitude (5–15%) of these differences may have been effected by the recording methods. The augmentation index (ratio of reflected and primary amplitudes in the pressure waveform) at the carotid artery was 8% higher (statistically significant) in aneurysm patients as compared to controls; the index was recorded post-hemorrhage in 90% of the patients at least 2 months after the event,¹⁹⁰ but the effect of the hemorrhage on the difference needs to be investigated. Thus, the significance of pressure vis-à-vis aneurysm pathophysiology is manifested via the stress generated in the diseased arterial segment (i.e., the aneurysm) and the extent to which such stresses are sustainable by the progressively diseased wall.

Classification of Aneurysms and Wall Shear Stress

The quantification of aneurysmal velocities is largely driven by the goal of obtaining wall shear stress (WSS) values at the luminal surface of aneurysms (Figure 4). Intraneurysmal velocities are broadly about an order of magnitude lower than in the parent artery. In idealized aneurysms, velocites are suggested to be proportional to neck area and inversely proportional to the square of the maximum aneurysm diameter, with peak WSS values equaling those at arterial bifurcations (~50–150 dynes/cm²).^108,168 The flow patterns described above provide a picture of the relative velocities and WSS values in the aneurysm; regions near the neck that acts as a flow divider or regions in the aneurysm body where flow impinges have higher velocity and WSS values while regions where secondary flow structures prevail or regions of flow stagnation have lower velocity and WSS values. Peak velocities ranging from 10% to 150% of the velocity (axial or average) in the parent artery,^{10,60,63,108,110,182,183,192} maximal WSS values ranging from 10–1500 dynes/sq.cm,^{15,18–20,25,54,63,79,101,110,178} and cardiac cycle-averaged WSS values ranging from 10–220 dynes/sq.cm^{13,55,171,178,179} have been reported. Minimum values of velocities and WSS are, in general, in the sub-decimal range in almost all studies. WSS has been inversely related to the aspect ratio,^161,211 dome diameter,¹⁸¹ and the surface area⁷⁹ of aneurysms and low WSS and increased residence times are correlated to thrombosis.¹⁴⁴ Regardless of the value of the WSS or the method of its evaluation, it is important to emphasize that it is not only a difficult variable to evaluate with high fidelity but that the calculated values only represent a snapshot in the lifetime of an aneurysm.

Figure 4.

A) Velocity vectors obtained with laser Doppler velocimetry in acrylic casts of a middle cerebral artery aneurysm before and after it grew over a period of 1 year. Examples of wall shear stress magnitudes calculated with computational fluid dynamics in B) a posterior communicating artery and C) a middle cerebral artery aneurysm. Panel A from Tateshima 2007¹⁸³ (S Tateshima et al., Intra-aneurysmal hemodynamics during the growth of an unruptured aneurysm, AJNR Am J Neuroradiol, 28, 4, pp.622–7, 2007 © by American Society of Neuroradiology); Panel B from Kulcsár 2011¹⁰¹ (Z Kulcsár, et al., I Szikora, Hemodynamics of cerebral aneurysm initiation, AJNR Am J Neuroradiol, 32, 3, pp.587–94, 2011 © by American Society of Neuroradiology); Panel C from Shojima 2004¹⁶¹ (Shojima M et al., Magnitude and role of wall shear stress on cerebral aneurysm, Stroke, 35, 11, pp.2500–5, 2004)

Technological progress has enabled the development of sophisticated algorithms to extract surface geometries from patient medical imaging data that facilitate numerical simulations on geometries that are ‘patient-specific’.^{3,22,27,63,139} Such developments allow for numerical calculations of flow fields in the entire circle of Willis² or correlations of global morphological and hemodynamic variables to incidence and rupture patterns;¹³² the latter study finds tapers in the internal carotid artery to be associated with unruptured aneurysms while greater curvatures of the carotid siphon seem to be a deterrent to aneurysm formation. The ability to perform these numerical simulations with relative ease has also facilitated parametric studies where engineered arterial and aneurysmal geometries can be systematically varied to compare flow patterns and intraneurysmal velocities or where flow patterns can be calculated in several patient-derived geometries; attempts can then be made to extrapolate such results to classify patient morphologies according to hemodynamic patterns. Results include a negative correlation between dome size and intraneurysmal flow velocity,¹⁸¹ a correlation between aneurysm size at rupture and the diameter of associated side branches,⁶² greater flow activity in aneurysms on the outer curvature of arteries and invariance of velocities at the neck with changing aneurysm aspect ratio,^131,155 greater vorticity with decreasing alignment of the aneurysm height to inflow direction,¹⁷⁷ consideration of secondary flow structures in parent vessels with varying tortuosity affecting aneurysmal inflow,⁷⁰ secondary vortices/recirculation in terminus aneurysms only when the necks are eccentric to the parent vessel axis and when the eccentricity is less than the parent vessel diameter,¹²⁹ identification of a certain threshold of the angular displacement of the aneurysm center to the parent artery axis in one terminus aneurysm resulting in deeper jet penetrance and changed flow structure,⁴⁴ increasing complexity of flow patterns and increasing proportion of aneurysmal surface exposed to low (<5 dynes/cm²) WSS with increasing size ratio.¹⁸⁸

Cycle-averaged WSS values are found to be inversely proportional to aneurysmal growth displacement;¹³ 20–30% of the surface area at the dome of ruptured aneurysms is exposed to low WSS (<4 dynes/cm²) as compared to 5–10% of the area in unruptured aneurysms;^55,79 the minimum WSS in the group of ruptured aneurysms was found to be half (absolute value 0.2 dynes/cm²) of the unruptured group in 50 posterior communicating artery aneurysms, but no differences were found in 50 middle cerebral artery aneurysms;¹⁷⁸ areas of low WSS were not significantly different between ruptured and unruptured groups in one study.²⁵ The maximum WSS (absolute mean ~500 dynes/cm²) in ruptured aneurysms was found to be significantly higher than that in unruptured aneurysms; other studies support the notion of higher maximal WSS in the ruptured group with¹⁶¹ and without^79,178 statistical significance. An index of oscillation of the WSS was not significantly different between ruptured and unruptured groups in one study.¹⁷⁸ Ruptured aneurysms were found to more frequently have complex and unstable flow patterns with concentrated inflow regions and smaller impingement zones as compared to unruptured aneurysms.^23,24

In vitro and numerical studies have evaluated the WSS at arterial regions where aneurysms or bleb regions within aneurysms form by either artificially removing the blebs and aneurysms from geometries obtained post-formation^{26,54,118,160} or from geometries obtained pre-and post-formation.^{101,179,182,183} The results seem to consistently suggest that blood impinges at a location close to where the neck of the aneurysm or bleb forms with associated high and oscillating WSS (or WSS gradient) values while the region spanned by the neck of the future structure experiences flow recirculation or secondary flow with associated low and oscillating WSS values. After the blebs or aneurysms form, the WSS in these regions drops. Figure 4 shows one such aneurysm where the inflow impinges at the location where the bleb neck gains definition (high WSS), but a recirculation region that gains vortical structure (lower WSS) exists across the span of the bleb.¹⁸³ A range of about 20–200 dynes/cm² for peak WSS^26,54,183 and 400–600 dynes/cm²/mm for spatial WSS gradients¹⁰¹ have been reported at the pre-aneurysm/pre-bleb edges, minimum WSS values in growth regions are generally close to zero. An oscillatory index of the spatial gradient of the WSS has been associated with the location of aneurysm formation.¹⁶⁰ These results are from a total of 32 cases only and the study with largest sample size (20 cases)²⁶ states that 20% of blebs were not found at regions with the highest WSS, so additional data are needed to confirm this phenomenon. It is plausible that the search for the cause of aneurysm growth and rupture will require incorporation of the biology, and cannot depend solely on the physics of the flow and its derivative variables in the aneurysm.

Most studies use Newtonian fluid properties for ease of computation or experimentation, but blood is non-Newtonian with shear thinning properties. The non-Newtonian effect is mostly negligible in the parent vessel and near the aneurysm neck, but is much more apparent in low velocity regions.^{42,108,134,210} Experiments with non-Newtonian fluids report lower intraneurysmal velocities, weaker vortical structures, more stable and symmetric vortical structures, wider areas of low WSS, and displacement of low WSS regions as compared to Newtonian fluids.^{11,42,134,196} WSS values can be 20–50% lower than the lowest values predicted by Newtonian fluids in the low shear rate regions at aneurysm domes, while spatially averaged WSS over the dome regions are about 10–25% lower.^42,196,210 The error with the Newtonian assumption seems to be appreciable when the shear rate is below 10–15 s⁻¹ (WSS is less than ~1 dynes/cm²).^42,210

Numerical Simulations and Limitations

Numerical simulations are sensitive to the boundary conditions used for the calculations. For example, replacing the vasculature proximal to aneurysms with a straight pipe substantially reduced the impingement and high WSS values (differences of as much as 100–125 dynes/cm² at some locations) in the inflow zone.¹⁸ Recordings of flow waveforms in the internal carotid and vertebrobasilar arteries in 39 healthy subjects have suggested that an archetypal waveform for each artery could be constructed and then scaled to the average flow rate in the artery of a specific patient.^43,57 While such waveforms facilitate simulations when flow data from the individual patient are unavailable or they can be used to compare results across various geometries depending on study aims, the accuracy of the results generated with such idealized waveforms can be low if the goal is to quantify the hemodynamics in a specific aneurysm. The cycle-averaged WSS can differ as much as 40 dynes/cm² between results from idealized and patient-derived waveforms;⁸⁶ altering the flow ratios in the A1 segments by ~35% and 100% can change spatially-averaged WSS by 40% and time-averaged WSS by 100%, respectively.^87,201 Phase-contrast magnetic resonance imaging is becoming the standard mode of measuring flow waveforms in patients due to its non-invasiveness, but measurement of flow waveforms at all inlet and outlet sections of the vascular segment of interest are not yet practicable. Traditional outlet boundary conditions include constant zero pressure (the easiest to implement and the least accurate) and three-component (2 resistances and 1 capacitance) Windkessel, but several others exist;^56,202 differences of 50–70% in the time-averaged WSS have been reported with different boundary conditions.^119,143 Validation studies of numerical simulations with particle image and/or laser Doppler velocimetry and correlations with phase-contrast magnetic resonance imaging in patients have been conducted.^45,66,198 Gross flow structures are generally in agreement in such studies, with any quantitative differences between the numerical and in vitro studies mostly being due to geometry; substantial quantitative differences between the phase-contrast and numerical/in-vitro results can be found due to the lower spatio-temporal resolution of phase-contrast imaging.

Although the assumptions and limitations of numerical simulations are recognized, a couple of cautionary notes may need to be mentioned. All commercially available CFD codes and many of the homegrown codes are based on the Navier Stokes equations that merely describe the second law of Newton, and which are based on continuum mechanics. Blood, of course, is a complicated suspension of formed elements that are deformable and which react not only with each other but also with their surroundings. This interaction is not limited to only physical mechanics, but also biochemical interactions (cellular, molecular, genetic factors referred to in the introduction section). Unfortunately, the laws that govern such biological reactions have not been fully elucidated and thus cannot easily be incorporated into a computational scheme.

The term ‘patient specific’ has been often used in the titles and descriptions of reported simulation results. Although the term is applied loosely and is generally understood to mean ‘patient derived’, some caveats to the implication that the results are specific to the patient may be noted because these limitations also affect the use of these numerical results to explain causative mechanisms of aneurysm pathophysiology. As mentioned previously, since the late seventies, imaging and computer visualization of blood vessels has improved significantly so that three dimensional representations of the lumen of sections of the vascular tree are readily transferrable as structural meshes on which detailed flow calculations can be performed. Since in most cases the vascular wall geometry and mechanical properties are unknown, the common no slip boundary condition is applied. Unfortunately, even with the most up to date imaging equipment, small blood vessels that may branch off larger vessels cannot be visualized, the vasa vasorum^72,97 is invisible (possibly effecting accuracy of near-wall flow calculations) and the exact location of the boundary of the visible vessels themselves is uncertain, requiring a generally arbitrary threshold and smoothening algorithm to prevent the CFD program from encountering badly deformed elements. Additionally, to start the iterative calculations of the flow field within, entry and exit flow conditions into the region of interest are required. The inlet and outlet conditions are not obtained from the individual patient in most studies thus far. Finally, the obtained geometry is a snapshot in time and space and usually it undergoes geometrical changes; the inlet/outlet conditions also change depending on an individual’s posture and level of activity. Another cautionary note is with regards to the pressure fields generated by CFD simulations and the extrapolation of changes in pressure within the computational domain to the biological system. It is well accepted that CFD can produce physiologically relevant flow rates and flow velocities by simply imposing inlet flow conditions and zero pressure at the outlet(s). The CFD software then seeks iteratively to establish the pressure field that will drive fluid through the computational domain at the imposed inlet mass flow rate and distribute it throughout the region of interest. Imposing zero pressure at the outlet is justified by the fact that regardless of the absolute pressure at the outlet, the pressure gradient between the inlet and outlet remains the same. This is due to the fact that the pressure gradient only needs to overcome mainly viscous dissipation and some fluid inertia. However, in the circulatory system the boundaries that surround the blood do react to its presence in a viscoelastic fashion. Rapid pulsatile pressure changes are transmitted to the surrounding walls which work in harmony with the heart to absorb these rapid pressure changes and attenuate sharp pressure spikes. This is the well-known Windkessel effect and mathematically it is manifested as a substantial reduction in the wave propagation speed as compared to its value inside rigid boundaries. Thus, in a rigid domain all the energy produced by the heart is transmitted to the fluid whereas inside a viscoelastic domain, part of the energy is transmitted to the walls and retransmitted to the fluid in a delayed fashion. Therefore, the pressure flow relationship in the viscoelastic domain is vastly different than in the rigid domain both in terms of absolute changes in pressure values as well as in its phasic relations to the flow wave.

As the kinetic energy of flow impinges on the apices of bifurcations, it is converted to increased pressure and this increase has been speculated (especially from numerical simulations where only the requisite pressure gradient is used to impart flow) to be a factor in aneurysm pathophysiology,^39,47 but consideration of the total pressure at these regions suggests that this pressure increase in only about 2–4% and is unlikely to have any substantial effect.^106,162 There have been suggestions that turbulent flow regimes exist in aneurysms,^{39,40,60,148,194} which can drastically effect shear rates and accelerate wall degeneration, but it is much more likely that the recorded phenomena are due to highly disturbed or unstable flow patterns interacting with aneurysm wall fluctuations and not characteristic turbulence^{61,71,168,175,192} (characteristics of turbulence include disorder, irreproducibility in detail, efficient mixing and transport, and irregularly distributed three-dimensional vorticity over a wide range of length scales¹⁷²). In other words, such flow patterns may be a probabilistic phenomenon exhibiting complex laminar/transitional structures, and can neither be properly characterized as laminar flow (a deterministic phenomenon) nor as turbulent flow (a stochastic phenomenon). Large discrepancies in CFD results produced by various laboratories, especially in the transitional flow regime, were noted in a validation and verification study conducted by the Food and Drug Administration.¹⁷³ Transitional flow and other limiting assumptions (specificity of ‘patient-specific’ data, blood homogeneity, Newtonian properties, non-compliant walls) in numerical simulations noted above have been addressed before.¹⁷⁰ The overall clinical utility of CFD has also been discussed previously.^21,83,149

Wall Structure

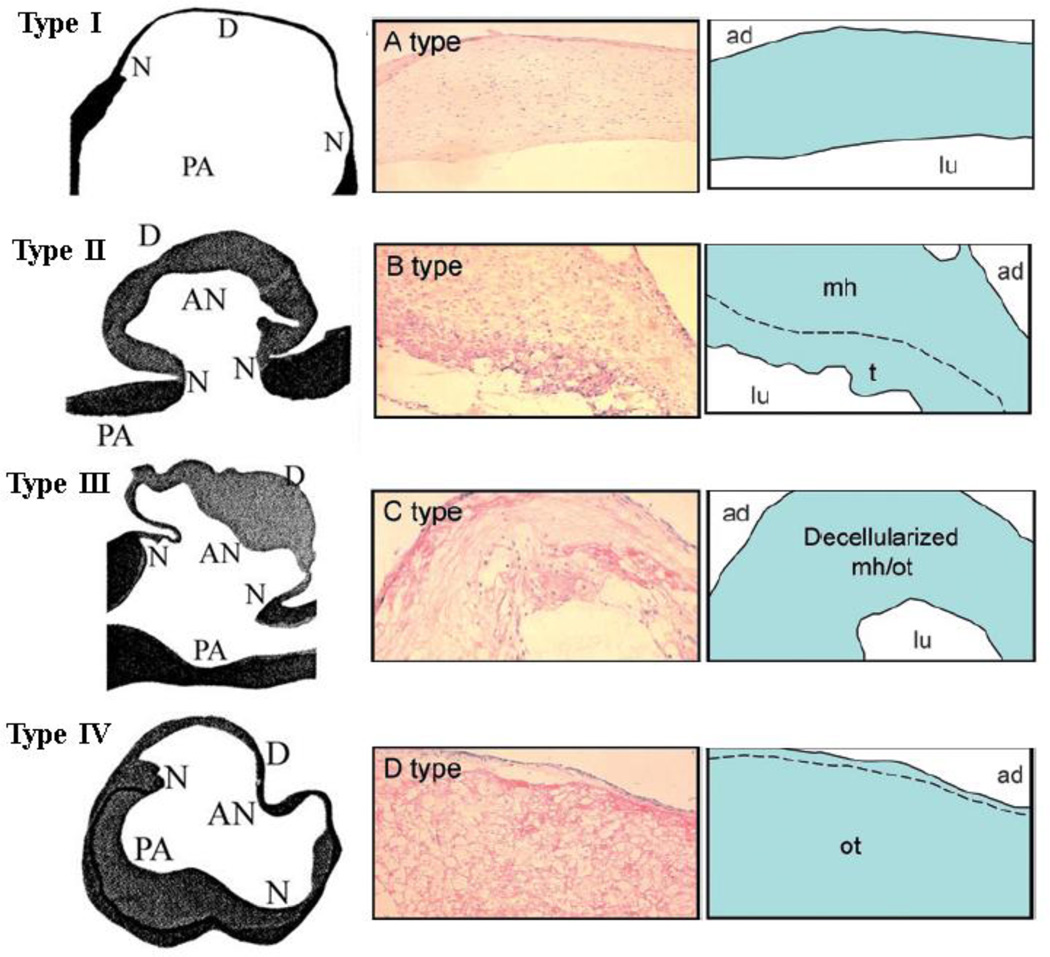
Histopathological and/or immunohistochemical evaluations of the walls of human cerebral aneurysms suggest that the walls of aneurysms can be differentiated into what are possibly different stages of progression to eventual rupture (Figure 5).^{48,49,176,189} Results from three studies^48,90,176 assessing a total of 74 unruptured and 108 ruptured aneurysms suggest that nascent or initial stage aneurysms seem to have their inner surfaces completely covered with endothelial cells with thin ‘smooth’ walls comprised of linearly organized smooth muscle cells, regular layers of collagen and very little evidence of inflammation. The wall subsequently degrades through two different observed types. The wall thickens, being comprised of fibroblasts and disorganized smooth muscle cells (intimal hyperplasia), but eventually starts to lose its gross ‘regularity’ and becomes hypocellular showing increased collagen content, and organizing luminal thrombosis. In what can be considered the final stage before rupture, the wall becomes irregular, extremely thin, and hypocellular with obscure layers of collagen and sparse smooth muscle cells. Ruptured aneurysm walls were mostly comprised of an acellular proteinacious structure (hyaline-like) with sparse smooth muscle cells and irregular collagenous layers with diffuse infiltration of macrophages and leukocytes. It may be noted that the temporal nature of degradation through these four wall types is only an inference based on literature evidence. Also the entire aneurysm wall does not necessarily delineate itself into these wall types; degeneration of the wall increases from the neck to the dome¹⁸⁹ and aneurysm ruptures mostly (80–85% of cases^30,31) occur at the dome.

Figure 5.

Four different types of aneurysm wall generally characterizing changes during progression to rupture. AN: aneurysm; PA: parent artery; N: neck; D: dome; ad: adventitial side; lu: luminal side; mh: myointimal hyperplasia; t: fresh thrombus; ot: organizing thrombus Left column with types I–IV from Suzuki 1978¹⁷⁶ (Suzuki J and Ohara H, Clinicopathological study of cerebral aneurysms, J. Neurosurg., 48, pp.505–14, 1978); right columns with types A–D from Tulamo 2010¹⁸⁹ (Adapted by permission from BMJ Publishing Group Limited. [J. Neurointerv. Surg., Tulamo R, Frösen J, Hernesniemi J, Niemelä M, 2, pp.120–30, 2010])

In comparison to peripheral arterial walls, cerebral arterial walls have negligible elastin in the medial and adventitial layers with no external elastic lamina, which makes cerebral arteries much stiffer (less distensible) than peripheral arteries.^39,65,124 Aneurysm wall thickness can range from 15 to 700 microns;^29,112 the anisotropy induced by collagen in the aneurysm wall has been measured;¹¹² the yield to breaking strength of aneurysm wall tissue seems to be around 0.5–2 MPa;^112,167 uniaxial tests of meridional strips of aneurysm tissue suggest a best-fit to a three-parameter Mooney-Rivlin model and show a statistical (n=16) difference in one of the model parameters between ruptured and unruptured aneurysms;²⁹ biaxial tests with best-fit Hookean and two-parameter Mooney Rivlin model parameters have been published.¹⁸⁷ The pulsatile motion of some aneurysm walls has been imaged^64,85 (average displacements of 40–300 microns are reported⁸⁵), but currently achievable spatio-temporal resolution can substantially effect accuracy. Further, attempts are being made to use such wall motion behavior to estimate the unknown material properties of the aneurysm wall through inverse analysis schemes.^6,99,214 Numerical schemes are also being developed to simulate wall remodeling (mostly by simulating collagen turnover) and growth of aneurysms.^{37,68,100,203}

Early suggestions that volume distension (ballooning) of aneurysm walls or mechanical fatigue made severe by resonant fluctuations can substantially contribute to aneurysm growth and rupture^58,123 do not seem to be valid.^{32,69,174,175,193} As smooth muscle cells in the medial layer are arranged circumferentially, there is a gap in the medial layer at the apices of bifurcations and this gap had been thought of as a weak point predisposed to aneurysm formation, but the fact that this region has abundant collagen fibers running along the gap,¹⁶ that these gaps occur in at least 60% to 100% of all bifurcations^16,52,205 (while aneurysms occur in 5% of patients), and that ex vivo pressures of 600 mmHg do not expose these spots as weak⁵² make these gaps unlikely to be a substantial factor. Due to the shear stress environment²¹⁵ at bifurcation apices, these regions tend to develop a cushion/pad-like region of intimal thickening over time (incidence ~20% by age 10 years, ~60% in adults²⁰⁵) that can project into the lumen. Although an ex-vivo steady flow study in rodent bifurcations suggests that flow stagnation exists distal to these intimal pads,¹²⁷ it is unclear if these can cause flow separation and substantially affect aneurysm initiation in patients; these structures are also widely prevalent at human bifurcations (at >60% of bifurcations²⁰⁵), which, again, does not match aneurysm prevalence.

Numerical simulations that incorporate deformable wall properties with pulsatile blood flow (called fluid-structure interaction, FSI) in artificial and patient-derived aneurysm geometries have also been carried out.^{5,110,184,185,195} In general, the use of deformable walls does not affect the gross flow patterns, but the secondary flow structures can be different with lower peak velocities and WSS values. In zones of low/stagnant flow, wall compliance can increase the minimal velocities (and minimal WSS).^110,186 Maximal aneurysm wall displacements ranging from 150 to 750 microns,^{7,185,186,195} percent reduction in maximal WSS due to deformable walls (as compared to rigid) ranging from 10–35%,^7,8,186 and maximal wall stress at the dome of around 0.2–0.3 MPa^5,7,8,195 are reported. Assuming a uniform wall thickness (300 microns) can reduce the maximal wall displacement by 40–45% and increase the spatially averaged systolic WSS by 60–90% as compared to an assumption of physiological variation in the wall thickness (300 microns at parent vessel to 50 microns at the dome).¹⁸⁵

Summary and Hypothesis

The hemodynamics of cerebral aneurysms has been reviewed before.^{75,103,133,158,159,209} The impetus of all the studies mentioned above can be categorized into one broad and one specific goal. The global goal is to identify physical mechanisms that are responsible for aneurysm pathophysiology and the more specific goal is the prognosis of a given (usually unruptured) aneurysm using these physical variables. The abundance of studies investigating variations in morphological and hemodynamic (and combinations of morphological and hemodynamic) parameters may facilitate achievement of the latter goal, but in general this seems far away. The prognostic relevance of these parameters has been questioned²⁰⁹ and, at the least, much larger sample sizes and multivariate analyses are required to distil predictive values. Aside from the assumptions made in numerical studies (which could be overcome with technological advancement), the biggest hurdle is that the predictive value of such studies may remain limited until biochemical degradation of the aneurysmal wall can be simulated and incorporated.^113,122 Ever more sophisticated computations incorporating the entire circle of Willis, pulsatile flow, wall deformability, and wall degeneration leading to aneurysm growth are being developed.³⁵ It is plausible, however, that advancements in medical imaging of flow in intracranial aneurysms^74,199 or of the aneurysmal wall^117,140 in individual patients will, in the near future, provide greater predictive values and obviate the need for simulations in this regard.

In terms of physical mechanisms facilitating aneurysm pathophysiology, it is clear that no geometrical factor(s) currently exists to classify aneurysms according to rupture status, no inherent anomalies in the circle of Willis clearly delineate the propensity of the vasculature to form aneurysms or to cause aneurysm rupture, and no hemodynamic discriminant (only WSS or its derivatives have really been evaluated) is currently able to predict aneurysm formation, growth or rupture. Some guidelines can, however, be gathered from the collected evidence. The results of these studies suggest that complex (or separated or recirculating or secondary or disturbed or unstable or oscillating) flow structures are involved in the growth and rupture of aneurysms and that the growth of aneurysms occurs at low flow (or slow or stagnant or low shear) regions. It is also sufficiently clear that aneurysm rupture occurs at the dome (at the dome of aneurysms or at the dome of blebs that may form on the aneurysm body). The current, generally accepted, hypothesis is that the initiation of aneurysms is related to (mechanical) degeneration of the bifurcation apex due to the high shear stress or high shear stress gradient in this region. Data also suggest that the initial location of aneurysms is distal to the bifurcation apices where shear gradient zones would be higher.^120,153,189 In vivo experiments have certainly demonstrated that artificially creating a high(er) hemodynamic stress environment at bifurcations leads to apparent degenerative changes in the elastic lamina near the apices with lesions resembling incipient aneurysms.^{93,95,121,165} To match the prevalence of aneurysms, this mechanism should reasonably imply that the shear stress at the middle cerebral artery bifurcation (~20% of aneurysms), the anterior cerebral-anterior communicating artery junction (~30%), and the internal carotid-posterior communicating artery junction (~25%) should be higher than that at the basilar or internal carotid bifurcations. Peak systolic velocities in the middle cerebral artery seem to be at least 30–50% higher than those in the basilar artery, but further evaluation is required to quantify the shear stress differences at these locations.

Another plausible physical mechanism that may contribute to aneurysm initiation is the fact that the stagnation point at the bifurcation apices (or within aneurysms) migrates at different parent artery flow rates.^101,191,211 The movement due to pulsatile flow is further exaggerated by heart-rate variability (60% variation in mean middle cerebral artery velocity has been noted²⁰⁰). This constant stochastic migration of the impingement point within a small area, or spot, subjects the endothelial cells to frequent changes in the shear direction and can facilitate the initiation of aneurysms. Heart rate variability and stagnation spots are yet to be evaluated in detail, but two previous experiments^77,197 clearly show the effect that vibration (an equivalent phenomenon) can have on transitional flows. It is thus plausible that one of the three indices of oscillatory shear stress that have been developed to correlate with aneurysm initiation,^118,160 or another such index, correlates better with locations of aneurysm initiation rather than just high WSS or WSS gradients. Further evaluation is needed to verify this mechanism. Hemodynamic factors may be correlated to the distribution of aneurysms within the circle of Willis, but all such mechanistic explanations will probably only serve as necessary but not sufficient causative conditions of aneurysm pathophysiology.