Estimating the ROC Curve in Studies that Match Controls to Cases on Covariates

Abstract

Rationale and Objectives

Studies evaluating a new diagnostic imaging test may select control subjects without disease who are similar to case subjects with disease in regards to factors potentially related to the imaging result. Selecting one or more controls that are matched to each case on factors such as age, co-morbidities or study site improves study validity by eliminating potential biases due to differential characteristics of readings for cases versus controls. However it is not widely appreciated that valid analysis requires that the receiver operating characteristic (ROC) curve be adjusted for covariates. We propose a new computationally simple method for estimating the covariate adjusted ROC curve that is appropriate in matched case-control studies.

Materials and Methods

We provide theoretical arguments for the validity of the estimator and demonstrate its application to data. We compare the statistical properties of the estimator with those of a previously proposed estimator of the covariate adjusted ROC curve. We demonstrate an application of the estimator to data derived from a study of emergency medical services (EMS) encounters where the goal is to diagnose critical illness in non-trauma, non-cardiac arrest patients. A novel bootstrap method is proposed for calculating confidence intervals.

Results

The new estimator is computationally very simple, yet we show it yields values that approximate the existing, more complicated estimator in simulated data sets. We found that the new estimator has excellent statistical properties, with bias and efficiency comparable with the existing method.

Conclusion

In matched case-control studies the ROC curve should be adjusted for matching covariates and can be estimated with the new computationally simple approach.

Many factors can influence the assessment provided by a radiologist reading a diagnostic image (1–2). Patient characteristics, for example breast density in reading mammograms, are one source of variability. Characteristics of the radiologist including expertise, training and malpractice concerns can influence assessments (3). Interpretations vary with institutions and they vary with health care norms that change over time (2).

In research concerning the accuracy of diagnostic tests such factors are called covariates and they must be taken into account in study design and analysis. Consider for example a study to evaluate the accuracy of computer-assisted mammography (CAD-mammography) in detecting breast cancer. Since breast cancer is more common in older women, a random set of breast cancer cases is likely to be older than a random set of controls without breast cancer. Therefore if controls are selected at random from the population of women who undergo mammography, differences in CAD-mammography assessments between cases and controls may be partly attributed to differences in their ages. In particular, a higher number of findings by CAD-mammography in cases may be partly due to the fact that it discovers anomalies more easily in fatty breast tissue that is more common in older women. Ignoring the covariate `age' that influences CAD-mammography assessments would lead to biased research results.

One common strategy to address covariate effects is to deliberately select controls for inclusion in the study that have similar covariate values as the cases. That is, for each case with disease one ascertains for the study a set of controls with the same covariate values as the case. This practice is called matching. Each case and its matched controls is called a matched set. Matching eliminates the potential for covariates to make the diagnostic test appear more accurate than it is. Choosing age-matched controls in the CAD-mammography study would eliminate any potential for age to confound results about accuracy.

Multi-center studies for new diagnostic tests often match for the “center” covariate by fixing the case-control ratio to be the same across centers. Multi-reader studies in which readers assess the same numbers of cases and controls implicitly match on the “reader” covariate. The motivation is again to avoid confounding. Without matching, if relatively more cases than controls are assessed by readers who have a tendency to use higher diagnostic categories, the accuracy of the diagnostic test will be over stated.

Although the practice of matching in retrospective studies is common, its impact is often ignored when evaluating the performance of a diagnostic test. Unfortunately, the receiver operating characteristic (ROC) curve and other measures of test performance are substantially biased when the data analysis does not acknowledge covariate matching. In particular, the ROC curve is attenuated in an analysis that simply pools data across centers, readers or other matching covariates (4–5).

One option for estimating the performance of a diagnostic test from a matched case-control study while acknowledging matching covariates is to calculate the covariate adjusted ROC curve (6) written AROC. The AROC describes the ROC for the test within strata of the population where matching factors are fixed and then averages the ROC curves across strata. For example, in a multi-center study the center adjusted ROC curve, AROC, is the average of the center specific ROC curves for the test. In a multi-reader study, the AROC is the average reader specific ROC curve. In a study that acknowledges that age may affect the interpretation of mammograms through its association with breast density, the age-adjusted ROC curve, AROC, is interpreted as the ROC curve of the diagnostic test in cases versus controls of the same age averaged across age

Statistical methods for estimating covariate adjusted ROC curves are available (5–9). One approach is to model the distributions of the diagnostic test as a function of covariates and disease status

These methods apply to studies that are matched but also to studies that are not matched. However, these methods are cumbersome in that they require modeling covariate effects on the distribution of the test result. In this paper we present a fundamental theoretical result that leads to a remarkably simple method for calculating the covariate adjusted ROC curve in matched case-control studies, a method that does not require modeling test result distributions.

MATERIALS AND METHODS

The Covariate Adjusted ROC Curve

We use D to denote disease status, D=1 for a case and D=0 for a control, Y for the diagnostic test result that is assumed to be higher in cases than in controls, and X for covariates. We suppose that the cases are a simple random sample from the relevant clinical population (10–11) and that for each case with covariate values X, K controls with the same value for X are selected randomly from the population. That is, the controls are frequency matched to cases on X. The x-covariate specific ROC curve, written ROC_x(f), is the ROC curve for Y in cases and controls with X=x. Formally, it is the proportion of cases with X=x whose values of Y exceed the threshold, y_x(f), above which lie test result values for the proportion f of controls with X=x. Mathematically we write:

$${\text{ROC}}_x\left(f\right)=\text{Prob}[Y>y_x(f)\mid D=1,X=x]$$

where f=Prob[Y>y_x(f) | D=0, X=x]. The covariate adjusted ROC curve, denoted by AROC, is the average covariate specific ROC curve where the averaging is made with respect to the distribution of the cases across covariate levels:

$$A\text{ROC}\left(\mathrm{f}\right)=\mathrm{E}\left\{{\text{ROC}}_{\mathrm{x}}\right(\mathrm{f}\left)\right\}.$$

If the diagnostic test performs similarly across covariate specific populations, in the sense that the covariate specific ROC curves are the same, the AROC is the common ROC curve. We focus on this setting. In other words, we assume that the diagnostic test result Y varies with the covariates in such a way as to keep the ROC curve constant.

Existing estimator of the AROC: the pv-AROC estimator

Suppose data are available for n cases and K×n controls:

$$\left\{\right(D_i=1,X_i,Y_i)i=1,\dots ,n;(D_j=0,X_j,Y_j)j=1,\dots ,K\times n\}$$

Currently there are two approaches to estimating the AROC curve. The first approach parametrically models the diagnostic test as a function of disease status and covariates, and then calculates the induced AROC using estimates of parameters in the model (7).

For example, if the diagnostic test is an ordinal rating, Y, of a diagnostic image, an ordinal probit regression model

$$\text{Prob}(Y<r\mid D,X)=\Phi \left(\frac{\{{\theta }_r-{\alpha }_{1}D-{\alpha }_{2}X\}}{\exp \left\{{\beta }_{1}D\right\}}\right)$$

can be fit to the data, where Φ is the standard normal cumulative distribution function (7). The AROC is then calculated from the estimated model parameters:

$$A\text{ROC}\left(f\right)=\Phi \left(\frac{{\alpha }_1+{\Phi }^1\left(f\right)}{\exp \left\{{\beta }_1\right\}}\right),$$

where f is the false positive rate. The second approach models the diagnostic test in controls only, using a semi-parametric method. This model provides covariate specific reference distributions for the test results with respect to which test results from cases are standardized (12). The AROC is then calculated non-parametrically from the standardized values of the test results among cases (6). Although the two approaches are related, the second approach is more general and requires fewer assumptions. We focus on it here, call it the percentile value method, and use pv-AROC to denote the resulting estimator of the AROC. For a thorough discussion of the relationships between the percentile value method and the parametric modeling method see (13) and (14).

There are three steps to calculating the pv-AROC (6, 15)

• (i)The first step is to calculate the x-specific cumulative distribution of Y in controls with covariate X=x, written as F^x(Y). If X has only a few categories, one can use the empirical cumulative distribution functions for controls in each category of X. However, if X is continuous or if X has many categories, use of regression modeling methods will be needed as described in (16).
• (ii)The second step is to convert values of Y for cases to corresponding covariate adjusted percentile values. Specifically, for each case with data (X=x,Y=y), we calculate the percentile of y within the control population with covariate values X=x. The percentile is written F^x(y). We also calculate 1− F^x(y) which is called the placement value (12).
• (iii)The percentile value estimate of the covariate adjusted ROC curve, denoted by pv-AROC, is the empirical cumulative distribution function of the case placement values. The corresponding area under the AROC is the average case percentile value, written pv-AAUC=average(F^X(Y) | D=1).

Interestingly, the pv-AROC estimator is simple and intuitive when X has only a few categories. It reduces to a weighted average of the X-category specific empirical ROC curves in that special case and the pv-AAUC is a weighted average of the X-category specific AUCs.

A New Method for Matched Data: the jm-AROC estimator

The new method we propose here is conceptually very different from the pv-AROC estimator.

• (i)
  The first step is to obtain an estimate of the risk function P(D=1 | X, Y) in the matched data. For example, one might fit a logistic regression model of the form:

  $$\mathrm{logit}P(D=1\mid X,Y)={\alpha }_0+{\alpha }_1\times X+{\alpha }_2\times Y+{\alpha }_3\times X\times Y$$

  to the matched data set, but alternative forms for the risk model could be used such as a model without interaction terms that we will consider later. Note here that the matching covariates are included as predictors in the risk model.
• (ii)The covariate adjusted ROC curve is then estimated with the empirical ROC curve for the fitted predictions, P(D=1 | X, Y), in the matched case-control dataset. We denote the resultant ROC estimator by jm-AROC where “jm” indicates joint modeling of Y and X in the risk model. The empirical area under the ROC curve for the fitted predictions estimates the covariate adjusted AUC and is written jm-AAUC.

Rationale for the jm-AROC estimator

We now provide arguments for why the jm-AROC estimator is valid in matched data. The arguments rely on the following general result that was proven in a recent article (17).

Result

Under the assumption that the AROC curve describes the common ROC performance of the diagnostic test across X-specific populations, the following statements are equivalent:

• (1)The ROC curve for the joint risk scores, P(D=1 | X, Y), is the same as the covariate adjusted ROC curve;

  if and only if

• (2)P(D=1 | X) = P(D=1);

(Note that the result as written in the Kerr and Pepe paper (17) uses somewhat different notation and has a small typo in the first item where ROC_X|Y should be ROC_Y|X).

The result states that in a population where equation (2) holds, equation (1) must hold as well. In other words, if disease prevalence does not vary with X, the ROC curve for the joint risk score, P(D=1| X,Y) is equal to the covariate adjusted ROC curve. Since matching in the design means that cases and controls are chosen to have the same distributions of X, equation (2) holds in a matched study. Therefore, any estimator of the ROC curve for the joint risk score, such as the jm-AROC estimator, can also be interpreted as an estimator of the covariate adjusted ROC curve since the result asserts that those two ROC curves are the same in matched data.

Data and Estimation Details for Simulation Studies

We simulated data in order to demonstrate and compare the two estimators of the covariate adjusted ROC curve. Data were simulated from a bivariate normal model in each of the case and control populations. Specifically we simulated data where the covariate and test result, (X,Y), are bivariate normal with variances 1 and covariance ρ, and the means are (0,0) in controls and (μ_X,μ_Y) in cases. In this setting the true covariate adjusted ROC curve (18) is

$$A\text{ROC}\left(f\right)=\Phi \left(\right({\mu }_Y-\rho \times {\mu }_X)∕\surd (1-{\rho }^2)+{\Phi }^{-1}(t\left)\right),$$

where Φ is the standard normal cumulative distribution function. Data were generated for a random sample of n=50 cases and n=50 random controls. To generate data for 50 matched controls, for each case with covariate value X_i we generated data from the distribution of Y conditional on D=0 and X=X_i, i.e. from a normal distribution with mean ρ×X_i and variance 1− ρ². In additional simulation studies, we chose unequal variances in cases versus controls and smaller sample sizes. Specifically, variances of X and Y were 1.5 in cases and 1.0 in controls, and samples of 20 cases and 20 controls were employed.

To calculate the pv-AROC estimator we had to estimate the distribution of Y as a function of X in controls. We did this by fitting a linear model to the distribution of Y conditional on X in controls: Y= β₀ + β₁×X+ε, with the distribution of ε estimated non-parametrically as the empirical distribution of the residuals. To calculate the jm-AROC estimator, we had to fit a model to the risk function, P(D=1 | X, Y). We did this by fitting a linear logistic model: logit P(D=1 | X, Y) = α₀ + α₁×X + α₂×Y. An interaction between X and Y was found to be non-significant in most simulations.

Observe that both estimators of the AROC, the pv-AROC and the jm-AROC estimators, require minimal assumptions about the data and therefore they are valid generally. The pv-estimator only requires correct specification of E(Y|X,D=0) and independence of ε from X in controls. The jm-estimator only requires correct specification of the risk function P(D=1|X,Y).

Data on a Diagnostic Test for Critical Illness

We applied the methods to an ongoing study that is evaluating diagnostic tests that could be measured by EMS personnel at the time a patient is being transported to hospital. The hypothesis of this study is that a rapid diagnostic test could be useful to improve the triage of patients prior to arrival for decisions about hospital destination or to provide advance notice to hospitals. Data derive from a previously described cohort (19) of 57,647 non-trauma, non-cardiac arrest patients. The primary outcome of this study is critical illness during hospitalization, defined as severe sepsis, delivery of mechanical ventilation, or death prior to hospital discharge. The dataset includes a previously developed clinical risk score based on age, sex, systolic blood pressure, respiratory rate, Glasgow Coma Scale score, pulse oximetry and residence in a nursing home. As studies are not yet complete, we simulated diagnostic test data in order to demonstrate the application of covariate-adjusted ROC methods in a matched, case-control study.

We generated Y for each patient in the cohort using the statistical model:

$$Y={\gamma }_0+{\gamma }_1\times X+{\gamma }_2\times D+\epsilon ,$$

where X is a 10-category version of the clinical risk score formed from the 10 deciles of the risk score in the cohort, D is the indicator of critical illness and ε is a standard normal random number. We chose γ₀ = 0, γ₁ = 5 and γ₂ = 0.742. For the matched case-control data set, we selected 200 case subjects at random from the cohort and for each case, we selected two random controls (without replacement) that had the same clinical risk category as the case. Thus controls were chosen to match cases on critical illness risk category.

The data were analyzed as described above for the simulation studies.

RESULTS

Results from Illustrative Datasets

In Figure 1 we show the true covariate adjusted ROC curve for Y and the ROC curve for Y that simply ignores the covariate using four simulated data sets. We see that the estimates that do not adjust for X are attenuated towards the 45° line relative to the true covariate adjusted ROC. In other words, the use of an unadjusted ROC curve with matched data leads to incorrect conclusions. That is, it appears that the diagnostic test does not perform as well as it actually performs within populations where X is constant.

Figure 1.

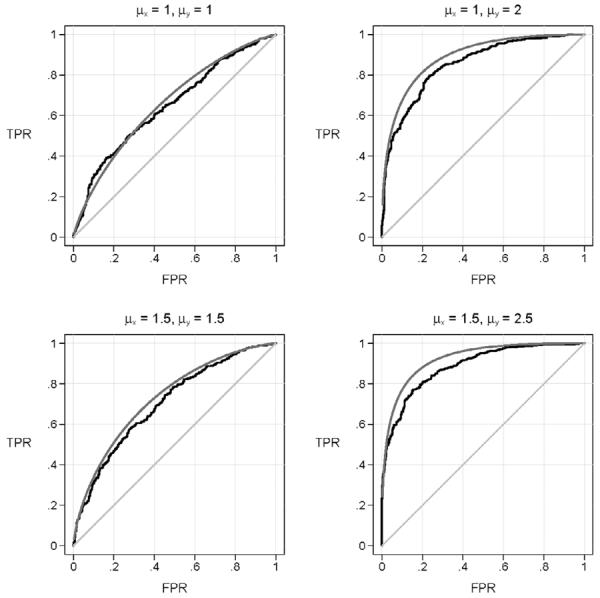
ROC curves for Y calculated on simulated data sets generated under four scenarios. Shown are the true covariate adjusted ROC curve (AROC), and the ROC curve that ignores the covariate (the unadjusted-ROC). The scenarios vary according to the associations between disease and both X and Y. The strength of association between D and X is quantified by the average of X in cases minus the average of X in controls, μ_X. Analogously, μ_Y, which is the average value of the test in cases minus the average in controls, quantifies the association between D and Y. The correlation between the test (Y) and the covariate (X) is ρ=0.5 in each scenario. The sample size is 500 cases and 500 matched controls.

The estimates of the covariate adjusted ROC curve are shown in Figure 2. We observe that the jm-AROC estimate and pv-AROC estimate are very similar but not exactly the same. In other words, the estimators are not simply reformulations of the same calculation but are distinct entities. Yet, since they are estimating the same quantity, namely the covariate adjusted ROC curve, it is not surprising that their values are very close in matched data.

Figure 2.

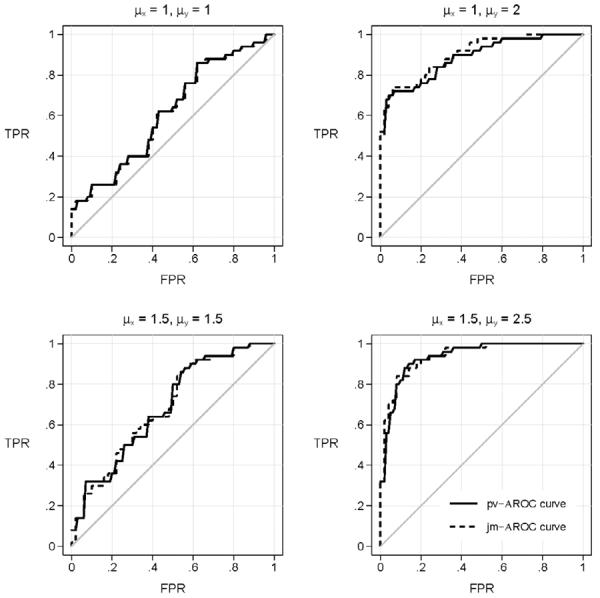
ROC curves calculated on simulated data sets generated under four scenarios. Shown are the estimated covariate adjusted ROC curve, calculated with the covariate adjusted percentile-value method, pv-AROC, and with the joint risk model method, jm-AROC. The scenarios are the same as those shown in Figure 1 but with smaller sample sizes, 50 cases and 50 matched controls.

Bias and Efficiency of Estimators in Simulated Data

We calculated estimates of the covariate adjusted ROC curve corresponding to a wide range of false positive rates=0.2, 0.5 and 0.7 as well as the area under the covariate adjusted ROC curve using 1000 simulated data sets. Low false positive rates are of interest in disease screening contexts while higher false positive rates corresponding to requirements for high true positive rates, are of interest in many diagnostic settings (11). Results displayed in Table 1 show that bias is negligible for both estimators across a wide range of scenarios. The relative efficiency of the estimators, defined as the ratio of their variances, was estimated as close to 100% in the many scenarios considered (Table 2). Qualitatively similar results were found in additional scenarios, the results of which are summarized in the Appendix.

Table 1.

Average over 1000 simulated data sets of estimates of points on the covariate adjusted ROC curve calculated with the pv-AROC and jm-AROC methods. ROC points corresponding to false positive rates of 0.2, 0.5 and 0.7 are displayed. Also shown are the estimated covariate adjusted AUCs. Data for 50 cases and 50 controls were generated in each simulation. In controls, the means of X and Y are zero. In cases, the means of X and Y are μ_X and μ_Y. Therefore larger values of μ_X and μ_Y imply larger associations with the outcome case-control status. The correlation between X and Y is denoted by ρ.

			AROC(0.2)			AROC(0.5)			AROC(0.7)			AAUC
μ X	μ Y	ρ	True	pv	jm	True	pv	jm	True	pv	jm	True	pv	jm
1	1	0.3	0.457	0.477	0.474	0.768	0.770	0.774	0.896	0.894	0.898	0.698	0.698	0.699
1	1	0.5	0.396	0.416	0.414	0.718	0.723	0.725	0.865	0.864	0.869	0.658	0.658	0.659
1	1	0.7	0.337	0.359	0.356	0.663	0.669	0.673	0.828	0.827	0.832	0.617	0.617	0.618
1	2	0.3	0.827	0.830	0.831	0.963	0.962	0.963	0.989	0.988	0.989	0.896	0.896	0.897
1	2	0.5	0.813	0.821	0.822	0.958	0.958	0.960	0.988	0.987	0.989	0.890	0.890	0.892
1	2	0.7	0.836	0.841	0.844	0.966	0.963	0.966	0.990	0.990	0.990	0.901	0.901	0.902
1.5	1.5	0.3	0.602	0.617	0.616	0.864	0.864	0.867	0.948	0.945	0.948	0.782	0.781	0.783
1.5	1.5	0.5	0.510	0.524	0.522	0.807	0.805	0.808	0.918	0.916	0.919	0.730	0.728	0.729
1.5	1.5	0.7	0.416	0.442	0.440	0.736	0.739	0.743	0.876	0.872	0.875	0.672	0.674	0.675
1.5	2.5	0.3	0.904	0.908	0.910	0.984	0.984	0.985	0.996	0.995	0.996	0.936	0.935	0.937
1.5	2.5	0.5	0.881	0.884	0.888	0.978	0.976	0.978	0.995	0.993	0.994	0.923	0.923	0.924
1.5	2.5	0.7	0.883	0.889	0.893	0.979	0.978	0.980	0.995	0.995	0.995	0.924	0.928	0.929

Table 2.

Standard deviations over 1000 simulated data sets of estimates of points on the covariate adjusted ROC curve and the AUCs calculated with the pv-AROC and jm-AROC methods. Settings chosen are the same as Table 1. The relative efficiency of the new jm method to the existing pv method is quantified by the ratio of the variances RE=variance(pv)/variance(jm). Data for 50 cases and 50 controls were generated in each simulation.

			AROC(0.2)			AROC(0.5)			AROC(0.7)			AAUC
μ X	μ Y	ρ	pv	jm	RE	pv	jm	RE	pv	jm	RE	pv	jm	RE
1	1	0.3	0.098	0.100	0.971	0.078	0.078	0.984	0.055	0.053	1.046	0.050	0.050	0.991
1	1	0.5	0.103	0.103	1.009	0.086	0.089	0.939	0.064	0.063	1.052	0.056	0.056	1.016
1	1	0.7	0.097	0.097	0.998	0.090	0.087	1.085	0.072	0.069	1.069	0.056	0.054	1.054
1	2	0.3	0.076	0.077	0.996	0.032	0.031	1.022	0.017	0.015	1.202	0.032	0.032	1.003
1	2	0.5	0.073	0.074	0.973	0.030	0.029	1.061	0.016	0.015	1.229	0.031	0.031	1.000
1	2	0.7	0.066	0.068	0.954	0.029	0.028	1.073	0.014	0.014	1.045	0.030	0.030	1.005
1.5	1.5	0.3	0.101	0.104	0.943	0.062	0.061	1.016	0.038	0.038	1.015	0.046	0.046	0.987
1.5	1.5	0.5	0.102	0.105	0.949	0.076	0.077	0.979	0.049	0.049	1.017	0.051	0.052	0.988
1.5	1.5	0.7	0.104	0.105	0.989	0.086	0.087	0.988	0.064	0.062	1.054	0.056	0.056	0.995
1.5	2.5	0.3	0.052	0.052	1.001	0.019	0.019	1.046	0.010	0.009	1.175	0.023	0.023	0.997
1.5	2.5	0.5	0.059	0.058	1.046	0.023	0.023	1.065	0.012	0.011	1.078	0.025	0.025	1.010
1.5	2.5	0.7	0.057	0.057	1.010	0.023	0.022	1.064	0.011	0.010	1.119	0.025	0.025	1.005

We conclude that the estimators are equally accurate and precise in the scenarios we simulated. In matched data, we see no statistical reason to prefer one estimator over the other. The choice depends on non-statistical factors such as available software and ease of computation.

Application to Diagnostic Tests for Critical Illness

Figure 3 shows ROC curves for the diagnostic test of critical illness adjusting for the clinical risk score category. The joint modeling and percentile value ROC estimators are visually indistinguishable again confirming the close relationship between them. The covariate adjusted AUCs were calculated as 0.722 with both the jm and pv methods.

Figure 3.

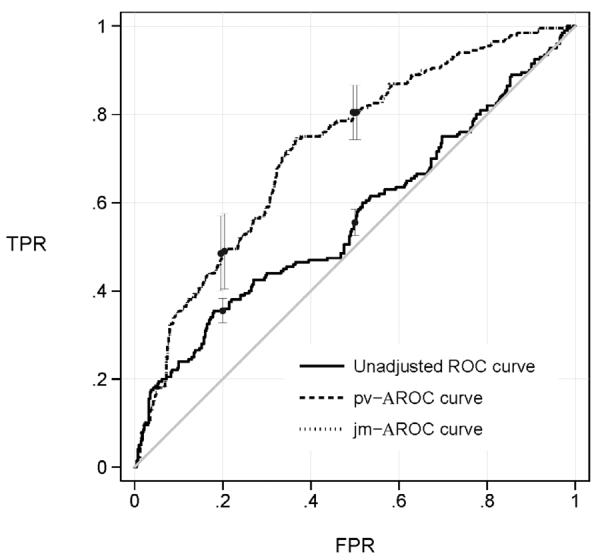
ROC curves for a point-of-care test of critical illness adjusted for clinical risk category using data for 200 cases and 400 matched controls. Also shown is the unadjusted ROC curve that

From the adjusted ROC curves we see that in a population where the clinical risk score category is the same for all subjects, the diagnostic test has an excellent capacity to discriminate cases from controls. For example, if we set the test threshold so that 20% of controls are allowed to test positive for critical illness, 49% of the cases are appropriately classified as such. On the other hand, if we ignore the risk score that was used in selecting the matched controls we get a very different impression. The unadjusted ROC curve indicates that only 36% of cases would be classified as positive for critical illness.

We used a novel bootstrap method to calculate confidence intervals for ROC points and the AAUC (Figure 3). Specifically, we first fit the linear model: Y= β₀ + β₁×X+ε, in controls with the distribution of ε estimated as the empirical distribution of the residuals. To generate a bootstrap sample, we randomly sampled with replacement 200 cases from the cases in our study. For each case, we then generated Y values for two controls by sampling two random residuals from the fitted linear model and adding them to β₁×X where X is the baseline risk value of the case. Observe that the cases are bootstrapped in the usual nonparametric way, with replacement from the study cases. However, to reflect the design of the study that selected matched controls, the bootstrap must select controls that are matched to the cases in the bootstrap sample. That is, for each case with covariate X=x in the bootstrap sample, K, controls must be selected to have the same covariate value. Our algorithm does exactly this by generating control Y values from the fitted distribution P(Y|D=0,X=x) that is derived from the semiparametric linear model. In other words, we used a semiparametric bootstrap procedure to generate matched control data. The ROC and AUC estimates were calculated for each of 1000 bootstrapped data sets. Using the standard deviation of the bootstrapped estimates, normal theory based confidence intervals were calculated. Interestingly, the confidence intervals for the adjusted and unadjusted ROC values did not even overlap, pointing to the extreme bias in the unadjusted estimate of the performance of the diagnostic test for critical illness.

DISCUSSION

Adjusting for covariates that may be associated with disease or other outcome is often proposed at the design stage of test accuracy studies by choosing controls that match cases on a priori covariates. Commonly used matching covariates include study center, reader, patient characteristics such as age or concomitant health conditions, radiologist characteristics such as experience or training, and imaging device. However, matching does not obviate the need to adjust for covariates in the analysis stage of the study. In fact, a matched study that does not adjust for covariates will underestimate the performance of the test within populations where all subjects have the same covariate value. This was shown previously (4–5) and we confirm this phenomenon in the current study (Figures 1 and 3). The importance of adjusting for matching covariates is also well described when modeling risk functions in epidemiologic research (6). In particular, it is well known that the odds ratio must be adjusted for matching covariates to avoid diluting exposure effects. The covariate adjusted ROC curve is the direct analogue of the covariate adjusted odds ratio in epidemiologic research. Both the covariate adjusted odds ratio and the covariate adjusted ROC curve pertain to entities calculated within populations that are homogeneous in regards to the covariate.

Our illustration was derived from the context of out-of-hospital critical care medicine. We chose controls that were matched to cases in regards to risk of the patient having a critical illness calculated on the basis of demographics and convenient clinical information. Diagnostic tests in this clinical setting are more likely to be biomarkers than imaging tests. However, the same statistical principals apply to both imaging and biomarker based diagnostic tests. Our data reflect the clinical question `Does this patient have critical illness?' which in practice is analogous to `Does this patient have pneumothorax?' We found that use of the AROC that accounted for matching was crucial for valid inference about test accuracy in our example.

Herein we propose a new estimator of the covariate adjusted ROC curve that is simple both computationally and conceptually. It requires fitting a risk model in which both the test result and the matching covariates are included as predictors, followed by the calculation of the simple empirical ROC curve with the fitted risk values. In many studies the relative risk associated with the test will be of interest in and of itself. Therefore estimation of the risk function will already be part of the analysis. The new jm-AROC estimator takes advantage of the fitted risk model and provides a coherent unified analysis approach. The estimator can be calculated in any standard statistical software package. In contrast, the existing estimator of the AROC curve that is based on covariate specific percentile values, requires additional computation and it requires modeling assumptions about the distribution of the biomarker as a function of covariates in controls.

The implementation of the new jm-AROC estimator may already occur in practice since investigators are apt to include covariates in the risk model as a means to “adjust for covariates,” a carry-over practice from epidemiology research. See for example a paper evaluating biomarker tests for acute kidney injury in a multi-center study where “center” was included as a covariate in the risk model and an empirical ROC curve was calculated with the predicted risks (20). Yet, a rigorous interpretation for the meaning of the ROC curve of the fitted risk values was not provided. We have shown here that in a matched study the ROC curve for the covariate adjusted estimates of risk is the covariate adjusted ROC curve defined previously by Janes and Pepe (6).

Several caveats associated with the new estimator of the AROC deserve mention. First, the new estimator only applies in a matched study or when adjustment is sought for a covariate that is marginally unrelated to disease. In unmatched data the new estimator does not estimate the AROC. Second, it is valid if the ROC performance of Y is approximately the same across populations with different values of X. Its interpretation is unclear if the ROC curve varies substantially with X.

In unmatched data, where cases and controls are simple random samples from the population, we noted above that the jm-AROC is not the covariate adjusted ROC curve but it is the ROC curve for the combination of X and Y together. In some settings the joint ROC curve for X and Y together may be of more interest than the covariate adjusted ROC curve. For example, one might want to compare the performance of X and Y together with that of X alone. Matching is strongly discouraged in such circumstances because the joint performance is impossible to estimate from a study that matches on X (5).