The Role of Naturally Occurring Stable Isotopes in Mass Spectrometry, Part II: The Instrumentation

Abstract

In the second instalment of this tutorial, the authors explain the instrumentation for measuring naturally occurring stable isotopes, specifically the magnetic sector mass spectrometer. This type of instrument remains unrivalled in its performance for isotope ratio mass spectrometry (IRMS) and the reader is reminded of its operation and its technical advantages for isotope measurements.

1. Introduction

The first instalment of this series focused on the theoretical aspects of stable isotopes and the calculation of their distribution patterns. In this second chapter, we will look at the technical measurement of stable isotopes using low-resolution magnetic sector mass spectrometers. We focus on magnetic sector instruments primarily because this mass spectrometer remains unrivalled in its performance for isotope ratio mass spectrometry (IRMS). Gas isotope ratio measurements require a much greater precision than that obtainable from other low-resolution instruments such as quadrupoles. The sector mass spectrometer also still prevails in other areas such as process control gas analysis (i.e., blast furnace top gas monitoring or coke oven gas analysis), which demand exceptional long-term stability and a high tolerance of changes in the nature of the sample gas from oxidising to reducing behaviour [1]. Furthermore in their most sophisticated form magnetic sector instruments remain the gold standard for petroleum analysis ultra-trace level determination of organic pollutants such as Polychlorinated dibenzo-para-dioxins (PCDD) and polychlorinated dibenzofurans ( PCDF) by GC/MS. The second reason for concentrating on magnet instruments in this tutorial series, is the increasing difficulty of finding detailed descriptions of the sector instrument’s theory and construction, particularly since the manufacturers’ manuals devote less and less space to these topics. Furthermore, different classes of mass analysers such as quadrupoles and its derivatives have increased in popularity to the extent that now there is a whole generation of mass spectrometry practitioners, many of whom have never considered the sector instruments. Therefore, the present authors found it worthwhile to remind mass spectrometrists of the technical principles of a mass spectrometry technique that still dominates particular areas of science. Readers interested in the technical descriptions of the other mass analysers (e.g., quadrupoles, ion traps, time-of-flight instruments, ion cyclotron resonance, orbitraps) are referred to ref [2,3].

With this in mind, this short tutorial article seeks to collate details of the low resolution magnetic sector instrument with the view of offering current and potential users of these instruments a description of their components in greater depth than is offered by elementary resources. For these, the components of the mass spectrometer instrument will be taken as the gas inlet system, the ion source, the magnetic sector and the detector. The construction of the vacuum chamber and its associated components such as pumps and vacuum gauges will not be discussed, nor will any detailed description of the electronics be given.

2. Gas Inlet Systems

Before we delve into the inner workings of the magnet sector instrument, it is useful to spend a few moments on the design of the interface between the gaseous sample and the vacuum of the mass spectrometer. To understand the transport and pressure reduction elements involved requires familiarity with vacuum techniques, and in particular the characteristics of gas flow over a wide range of working pressures. A full discussion of the vacuum science and technology required is outside the scope of this tutorial, however the salient points for our purposes are that the rate of material flow through a vaccum pump (throughput) is given by

$$\mathrm{F}=\mathrm{S}.\mathrm{P}$$ (1)

where S is the pump speed (usually quoted in L/s) and P the working pressure of the pump (usually quoted in mBar). Similarly the rate of material flow though a tube or other element of the vacuum system is given by

$$\mathrm{F}=\mathrm{C}.\Delta \mathrm{P}$$ (2)

where C is the conductance of the element, which is determined both by its physical dimensions and the operating pressure, and ΔP is the pressure drop across the element. For a more comprehensive discussion the reader is referred to www.vacuumlab.com, and the references which are cited there.

Although more details on the ionisation source will be explained in the following section, it is important, at this point, to estimate the gas flow requirements of the mass spectrometer, in order to discuss sample introduction systems compatible with these flow rates. The pressure in the main part of the vacuum chamber of the mass spectrometer is typically ~10⁻⁶ mBar. With a diffusion or turbo-molecular pump, a pumping speed of 100 Ls⁻¹ is readily available, and for a total conductance of the three apertures in the ionisation chamber of about 0.7 Ls⁻¹, the pressure in the ionising region is expected to be about 1.4×10⁻⁴ mBar, or approximately two orders of magnitude higher than that in the vacuum system proper. In passing, it is noted that from this calculation the throughput of sample gas is estimated to be 10⁻⁴ mBarLs⁻¹, or about 5 nmoles per second. Since sampling is usually performed from approximately atmospheric pressure, the required gas throughput necessitates a leak element with a conductance of 10⁻⁷ Ls⁻¹ for direct sampling. The obvious choice for this is a capillary. Representative dimensions are given in Table 1.

Table 1.

Viscous flow occurs through a capillary used to introduce gas at atmospheric pressure into a high vacuum system. Under these conditions, the conductance of the capillary is proportional D⁴/L, where D is the tube diameter and L its length.

I.D. (μm)	Length (m)
75	21.9
50	4.3
30	0.56
20	0.11

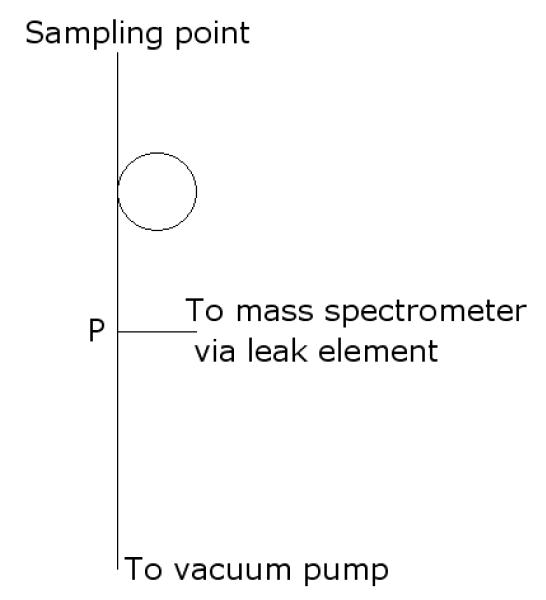
Capillaries of the smaller diameters are prone to blockage, and those with larger diameters have relatively slow transit times, and are therefore not sufficiently responsive if sample switching is required. To overcome this a two-part inlet system can be used with a bypass line fitted at the junction of the leak elements, which is taken to a vacuum pump (Figure 1). This system has fast response time, but care must be taken in its design if gas samples of widely differing viscosities are to be analysed. Optimal conditions are obtained if the flow from the sampling point to the tee-piece is viscous, and the flow from the tee-piece to the pump is molecular; however, some mixed flow conditions almost always exist. The pressure at the junction should be in the range 5-10 mBar, hence a leak element with conductance of about 10⁻⁵ mBarLs⁻¹ is required. A glass sinter is commonly used to provide a compact leak with a conductance in this range.

Figure 1.

The capillary inlet with a by-pass. The performance is set by the dimensions of the elements. Between the sampling point and point P, viscous flow through the capillary dictates the sampling rate. For example, for a tube of 0.25mm I.D. and 1.5 m long, the sampling rate from atmosphere will be fixed at about 10 ml/min. The element between the point P and the vacuum pump, through which flow is molecular, sets the pressure at point P. For the same capillary above, a tube from P to the vacuum pump of internal diameter 6mm and 1m long will give a pressure of about 7 mBar at the tee-piece.

A somewhat specialized system, which allows for rapid switching between two gas samples is often used in gas IRMS. The samples are held in reservoirs that are each connected to the ion source by a stainless steel capillary, which can be crimped in order to match the gas throughputs. Interposed between the capillaries and the source is a micro-valve, so arranged such that when one gas line is connected to the source the other is connected to a pump. In this way, gas is continuously bled from both reservoirs, and when stream switching is desired it is only a very small volume, which needs to be flushed before stable measurements can be made.

In recent years the continuous flow inlet has become fashionable, particularly for the analysis of ¹³CO₂ in breath, but the principle is applicable much more broadly. A typical system incorporates a multiport sampling valve configured with a sampling loop, although a considerable degree of complexity can arise (see for example [4]). However, all the sampling systems are designed to achieve the same purpose; to introduce a slug of sample gas into a stream of carrier gas. The mass spectrometer samples the carrier gas via on open split.

3. The Ion Source

A comprehensive discussion of the various types of ion source used with magnetic sector (and other) instruments has been given by Elliott [5]. For isotope ratio work the type of ion source usually employed is based on the design of Nier [6,7], which has been has been successfully used in these applications for many years (Figure 2). The sample gas is introduced into an ionisation chamber, which is essentially a closed box, with small holes for the entry and exit of the ionising electron beam, and also for the ions to exit. The purpose of keeping the ionisation chamber as gas-tight as possible is to create a region of relatively high pressure, so that the molecular density is sufficiently high for adequate ionisation to occur. The ions exit into the general vacuum chamber, which operates at a lower pressure where the mean free path of the residual gas molecules is sufficiently low that ion scattering is negligible.

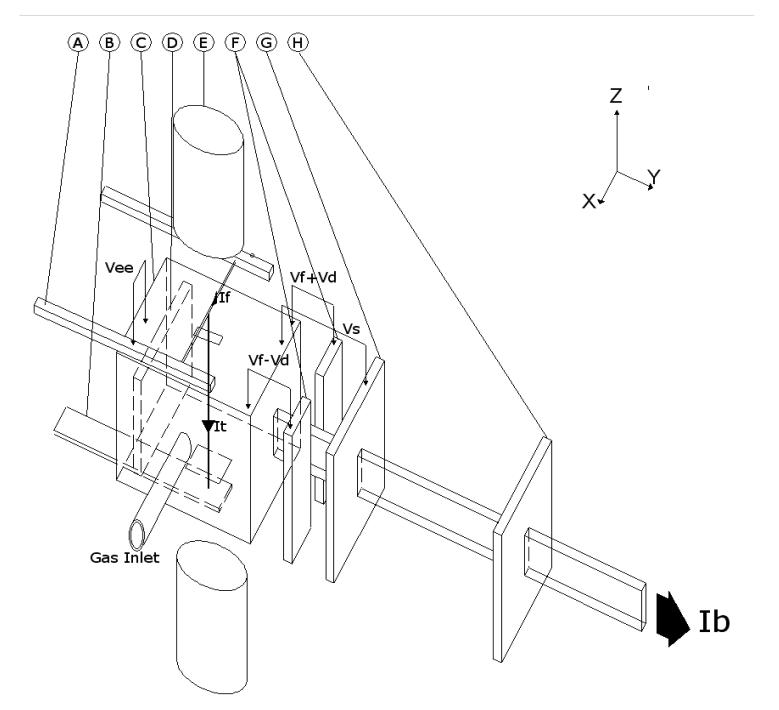
Figure 2.

Schematic of a typical ion source showing (A) Filament assembly, (B) electron trap, (C) ionisation chamber, (D) ion repeller, (E) source magnet, (F) half plates, (G) source slit, (H) alpha slit. Also shown are the filament and trap currents (I_f and I_t), the ion beam leaving the source (I_b) and the potentials defining the electron energy (V_ee), The ion energy (V_s), the focus (V_f) and the half-plate differential (V_d).

An electron beam is generated outside the ionisation chamber by thermionic emission from a heated filament. There have been various filament materials used over the years. Tungsten has been popular, but it is not ideal since it has a relatively high work function, and therefore needs a high temperature (approximately 2300°C) for photoemission to occur. As well, the performance requires a degree of carbonisation of the filament, giving high levels of background CO and CO₂. Rhenium has been proposed as an alternative, as have refractory oxides mounted on a conducting wire. ThO₂ coated iridium was used for many years, but recently has fallen out of favour since thorium emits alpha radiation, and therefore it has been replaced by Y₂O₃.

The filament is held at a slightly negative potential with respect to the ionisation chamber. This potential sets the electron energy, and therefore the ionising power of the electron beam. Under the influence of this potential, the electrons are accelerated towards the ionisation chamber, and pass through a narrow slit in one of its walls. The majority of them traverse the ionisation chamber, and exit through a second aperture in the wall directly opposite. Having passed through this exit hole, they strike the electron trap, which is another electrode set at a positive potential of ~50 V with respect to the ionisation chamber, in order to reduce the likelihood of secondary emission.

The electron beam is collimated by a coaxial magnetic field provided by a pair of magnets. The combination of this field and the electron energy results in the electrons adopting a spiral path through the ionisation chamber, and the ionising region is therefore a cylinder of relatively narrow radius. Besides keeping the ion beam well-defined the spiral nature of the ionising electron trajectory has the secondary advantage of increasing the pathlength of the electrons as they traverse the sample gas, with a corresponding increase in the ionisation efficiency (although it still remains poor at 10-100ppm). The ions are extracted through a narrow slit with its major axis parallel to that of the electron beam, and hence a ribbon-like beam of ions, with its long axis aligned with the electron path between filament and trap is ejected from the ionisation region towards the magnet.

The ions formed leave the chamber, which is maintained at a high positive potential (>2000 V) with respect to the rest of the vacuum system. In fact, extraction is achieved by a weak field due to a combination of field interpenetration from the half-plates, which lie just outside the ionising chamber, and a small electrode sited within it known as the ion repeller. The ion repeller is usually set in the range −20 to +20 V with respect to the ionisation chamber; the precise setting usually being determined by empirical optimisation of the source behaviour.

Having left the ionisation chamber, the ion beam is accelerated towards the source slit, which is at earth potential (Figure 1). The half plates in between the ionisation chamber and source slit are maintained at an intermediate potential to achieve focussing of the beam at the source slit itself. Additionally a differential voltage of up to about ±200 V can be applied to the half plate for beam steering purposes. Finally the beam passes through an alpha slit, again at earth potential, which limits the angular dispersion in the plane perpendicular to the magnetic field. Further refinements to the ion optic system are sometimes used, including extra beam steering plates, and plates designed to steer and focus the beam in the z-direction.

The operation and maintenance of the ion source requires the user to set and monitor a number of electronic parameters. These are described in more detail below.

Filament Current

As its name suggests, this is the current passing though the filament, causing it to heat to the point where thermionic emission occurs. The filament current depends on the nature of the filament material (its composition and dimensions), but is typically of the order of a few amperes. The amount of emission, and hence the number of electrons available for creating ions, is governed by the magnitude of this current. Therefore, it is regulated by means of a feedback system to stabilise the number of electrons passing through the ionisation chamber (see trap current below). As the filament ages it often thins, and its resistance rises, causing the filament current to drop. This is sometimes an early indication of a filament that is near the end of its life, and about to break.

Source Current

This is due to electrons leaving the filament, and colliding with the walls of the ionisation chamber, rather than traversing it and reaching the electron trap. In general, for an efficient source the source current should be approximately equal to the trap current. Exceptionally high source currents can indicate a filament that is poorly aligned. However, the practitioner should be aware that a second source of electron flow to the ionisation chamber is by ‘leakage’ from the body of the vacuum chamber through the ceramic spacers, which isolate it from the source. Therefore, an abnormally high source current can sometimes indicate contamination or dirt deposited on the source ceramics.

Trap Current

The trap current is due to electrons, which leave the filament and successfully traverse the ionisation region and arrive on the electron trap. Generally in the range of 50-500 μA, the trap current is maintained at a steady value using a feedback arrangement to control the voltage applied to the filament, and consequently the filament current and amount of emission. By these means it is possible to obtain trap current stability to better than 0.01%, which is necessary for the measurement of ion currents and ratios to the degree of precision required for isotope ratio work. In order to protect the filament from burning out due to an excessive demand for trap current, an upper limit on available filament current is usually imposed. If this limit is achieved, the trap regulation fails, and the ion beam exiting the source usually becomes unstable

Electron Energy

A potential difference is applied between the filament and the ionising chamber in order to attract the electrons leaving the filament so that they pass through the ionising region. This is the so-called electron energy, since it is responsible for imparting sufficient energy to the electrons for them to be able to promote ionisation. The magnitude of the electron energy dictates the number and types of positive ions formed. A typical chemical bond has an energy of 450kJ/mol, corresponding to about 5eV, and this corresponds to the ionisation potential. At electron energies slightly above the ionisation potential of the target molecule (soft ionisation), little molecular fragmentation occurs, but at higher electron energies (hard ionisation) all of the possible molecular fragments are produced. Inspection of the ionisation efficiency curves for a number of gases indicate that the maximal positive ion currents for the molecular ion and its fragments occur at very much the same electron energy, which is in the range 50-100 V.

It should be noted that if it is decided to reduce the electron energy in order to create ‘softer’ ionisation conditions, then the draw of the electrons from the filament through the ionisation chamber will be reduced, and the filament current needed to support a given trap current will increase, as will the source current to trap current ratio.

Repeller Voltage

This is the potential difference between the repeller plate and the ionisation chamber. As noted previously, the voltage applied is usually in the range −20 to +20 V, and is set to optimise performance. The term ‘ion repeller’ is therefore a misnomer, since when it is operated at a negative potential with respect to the ionisation chamber it clearly acts in the opposite manner. As previously mentioned ions are extracted from the ionisation chamber by a weak field due to a combination of field interpenetration from the half-plates, which lie just outsideof it and the repeller plate. Somewhat counter-intuitively it is often found that a negative potential applied to the repeller plate optimises the ion yield. However the term ion repeller is still in current usage.

When measuring isotope ratios of hydrogen, a relatively large positive voltage is usually chosen to minimise the residence time of the ionised hydrogen molecules in the source chamber, to lower the formation of H₃⁺ by molecular collisions.

Ion Energy

This is the potential of the ionisation chamber with respect to earth (the vacuum system). This voltage (in combination with the magnetic field) determines the radius of flight of the ions through the magnetic sector. The voltage can be scanned in order to detect ions of different m/z ratios, with higher m/z being selected by lower ion energy. It should be noted that many of the other ion source parameters have to be optimised for specific ion energies, and this somewhat limits the mass range, which can be covered. In order to achieve the best possible quantitative analysis with a low-resolution sector instrument, the ion energy should be stable to about 10 ppm.

Half Plate Potentials

The potentials applied to the half plates have two components, a common and a differential mode. The common mode voltage can be varied anywhere between the ion energy and earth. Frequently this voltage is expressed relative to the ion energy rather than earth, and often as a fraction of it. Therefore, if the ion energy is set to +3 kV with respect to earth a common half plate potential (sometimes called focus potential) of 10% means that +2.7 kV with respect to earth is supplied to the plates. It is best, however, to consult the manufacturer’s literature for a definitive description of how it is defined. The differential voltage is used for beam steering, is bipolar, and usually restricted to a small fraction of the common mode voltage.

4. Mass Separation by Magnetic Deflection

When particles of mass m (kg) and charge q (coulombs) are accelerated from rest through a potential difference V, the loss in potential energy (qV) results in a corresponding gain of velocity v and thus of translational energy (mv²/2), so that:

$${\mathrm{mv}}^2∕2=\mathrm{qV}$$ (3)

If such a beam of ions is introduced into a magnetic field produced by a sector magnet (basically the shape of a piece of cake sliced into two horizontally like a cream sponge, so that the ion beam can travel between the two halves), each ion experiences a force perpendicular to the (vertical) magnetic field direction and also perpendicular to the ion beam direction. (This is the same force that operates a DC electric motor since a beam of ions can be regarded as an electric current). The simplest case is that when the (horizontal) beam enters the sector field at right angles to the (vertical) sector boundary, when the magnitude of the magnetic force on an ion is given by Lorentz’s Law as (B.q.v) where B is the magnetic field strength. This causes the ion to travel in a circular trajectory in which this magnetic force is just balanced by the centripetal force (m.v²/r) associated with the circular motion where r is the radius of the orbit. Then:

$$\mathrm{B}.\mathrm{q}.\mathrm{v}={\mathrm{mv}}^2∕\mathrm{r},\text{whence}\mathrm{r}=\mathrm{Bq}∕\mathrm{mv}$$ (4)

Eliminating v from equations (1) and (2) gives:

$$\mathrm{r}={\left[\right(\mathrm{m}∕\mathrm{q}).(2\mathrm{V}∕{\mathrm{B}}^2\left)\right]}^{1∕2}={\left[\right(m∕z).({\mathrm{m}}_{\mathrm{u}}∕e).(2\mathrm{V}∕{\mathrm{B}}^2\left)\right]}^{1∕2}$$ (5)

where (m_u/e) is a constant = 1.0364×10⁻⁸ kg per coulomb. If V is in volts and B in tesla, r is in metres (an example of the coherence property of SI units). For a singly charged nitrogen molecule (m/z = 28)that has been accelerated through 2200V and traversing a magnetic field of 0.4T, the radius is found to be 0.09 m (9 cm)

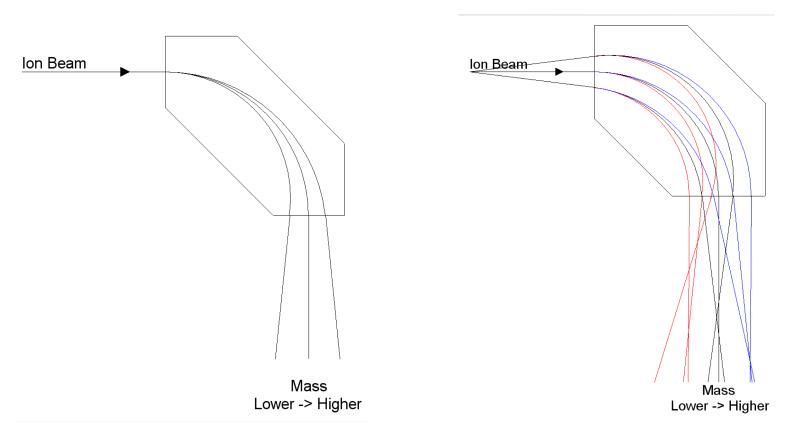
Clearly, as seen from eq. (5), the radius of flight increases with increasing mass (for a given charge), and on this basis the mass separation by a magnetic sector is often depicted as shown in Figure 3a. A magnetic sector, however, does more than simply separating ions in physical space, and it has properties beyond those of a mass filter such as a quadrupole. To illustrate this, we modified the diagram to show the incident ions not as a single ray, but as a divergent beam (Figure 3b). The figure illustrates that the magnetic sector also has the property of refocusing the ion beams. With the simple pole pieces shown, the focussing is not perfect, and is not as effective for the low masses as for the high ones. The ion beam divergence, however, is greatly exaggerated in the diagram (in a real instrument the divergence angle is less than 1°). The position of the image point depends not only on (i) the distance between the object (in this case the source slit) and the incident pole face of the magnet, and (ii) the radius of flight in the magnetic field, but also (iii) the angle of the incident and exit pole faces. It can be shown that the condition for a focussed image to be obtained is [8]

$$r^2\sin \theta \cos \alpha \cos \beta +r\left[a\cos \right(\theta -\alpha )\cos \beta +b\cos (\theta -\beta \left)\cos \alpha \right]-\mathit{ab}\sin (\theta -\alpha -\beta )=0$$ (6)

where a and b are the object and image distances, and α and β are the angles between the ‘central’ ray of the ion beam and the normals to the incident and exit pole faces, respectively, and θ the angle through which the ion beam is deflected. .

Figure 3.

An ion beam in a magnetic field: (a) the mass separation increases with increasing mass; that is, the radius of flight increases with increasing mass; (b) a divergent ion beam is refocused in a magnetic sector.

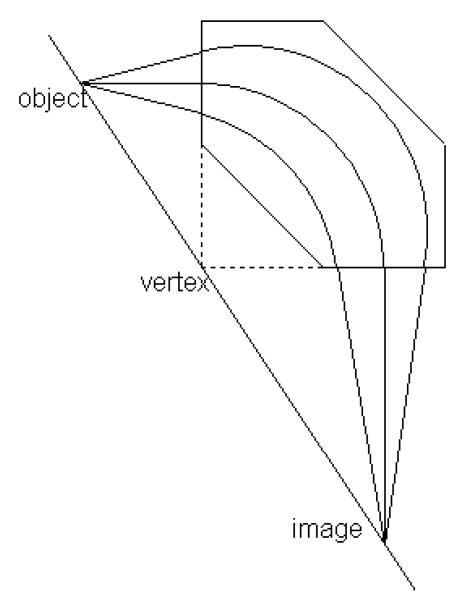
Furthermore, the angle of the pole faces has consequences for the trajectories of the ions in a direction parallel to the magnetic field (conventionally the magnetic field is said to define the z-axis of the system, with the ions being separated in the x-y plane). If the normal is on the outside of the beam with respect to the centre of curvature in the magnetic field the angle is taken to be positive, and the effect is to focus the beam in the z-direction. Conversely, if the normal is on the same side of the centre of curvature the angle is said to be negative, and the beam is defocused. From the diagram in Figure 4, it can be seen that for this case the low mass beam is z-focussed as it leaves the magnet, whilst the high mass beam will be caused to diverge slightly in the z-direction.

Figure 4.

If the pole faces are normal to the incoming and outgoing beams a special case of equation (4) is obtained:

$$(a+b)\cos \theta =(\mathit{ab}-1)\mathit{Sin}\theta$$ (4a)

This equation can be interpreted by the statement that “the object, image, and vertex of the sector lie on a straight line.” This is known as Barber’s rule.

These properties have been exploited in many analyser designs. In particular the geometry where the angle of deflection (θ) is 90° and the entrance and exit angles (α and β) are set to 26.57° the focal points in the x-y plane and in the z-plane are coincident. This geometry issometimes known as a double-focussing system.(although the same terminology is also used for instruments that focus for angular divergence using a magnet, and also ion velocity using an electric sector).

Flat-Topped Peaks

The resolving (detector) slit is placed at the point where the image of the source slit is located in the x-y plane. The ion beams can be scanned across the resolving slits by varying either the ion source accelerating potential or the magnetic field. If the resolving slit is wider than the focussed beam then the output of the amplifier from such a scan is in the form of a flat-topped peak (Figure 4a).

The advantage of operating in this mode is that unit resolution is achieved (i.e., ions of a particular integral value of m/z only are selected), but any small drifts in magnetic field or accelerating potential are insufficient to cause instability in the detected signal.

Since any slight misalignment in the ion optical system can have a profound effect on the precise point where the image is formed it is usual to make the magnet position adjustable. When the instrument is set up the optimal magnet position is located by observing the quality of the flat-topped peaks; i.e., by finding the position for which the top is flattest and the sides are steepest. The process of optimisation is often more difficult than might be anticipated, especially for operators inexperienced in the task.

Dispersion and Resolution

The dispersion of the ion optical system is defined as the separation between adjacent mass foci. Two masses are said to be resolved by the instrument if their beams are such that only one of them passes through the detector slit. Clearly, the maximum resolution would be achieved if the resolving slit was exactly the same as the beam width. However, as has been stated earlier, this is not the mode of operation with flat-topped peaks (Figure 5a). In these instruments, the resolving power R is the largest m/z ratio at which adjacent peaks of equal height have a 10% valley between them. This is equivalent to saying the m/z ratio at which the width of the peak measured at 5% of its height is equal to the separation between adjacent peaks. Clearly, the width of the resolving slit is a major factor in determining the resolution of such an instrument, as is the quality of the ion-optics alignment.

Figure 5.

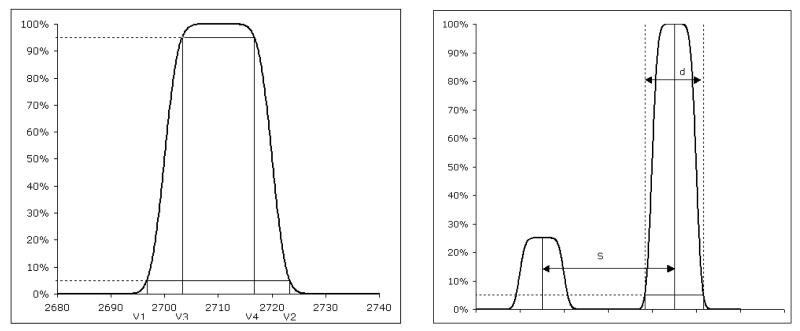
(a) Scanning the ion beam across the resolving slits by varying the ion source accelerating potential leads to a flat-topped peak if the resolving slit is wider than the focussed beam. Calculation of the resolving power is shown in eq. (5). (b) Alternatively, the resolution can be calculated directly from the spectrum (see eq. (6)).

From the peak shape, it is possible to obtain estimates of the beam width, slit width and working resolution of the instrument. The peak is scanned and the positions of the 5% and 95% peak-heights noted. As an example, a voltage scan performed across m/z 44 on a 6cm radius instrument is shown right in Figure 5a. The 5% points occur at 2696.7 (V₁) and 2723.3 volts (V₂), and the 95% points at 2703.3 (V₃) and 2716.7 volts (V₄). From these are calculated

$$\begin{array}{cc}\hfill & \text{Beam Width}=\frac{2(V_2-V_1-V_4+V_3)r}{(V_1+V_2+V_3+V_4)}=0.0146\mathit{cm}\hfill \\ \hfill & \text{Slit Width}=\frac{2(V_2-V_1+V_4-V_3)r}{(V_1+V_2+V_3+V_4)}=0.04443\mathit{cm}\hfill \\ \hfill & R=\frac{(V_1+V_2+V_3+V_4)r}{4(V_2-V_1)}=102\hfill \end{array}$$ (7)

Note the alternative expression for resolution, R = Radius/(Slit + Beam width)

A different method of measuring the resolution, useful if the absolute scale of the x-axis is unknown, is shown in Figure 5b. Here the width of the peak at 5% height and the separation between adjacent mass numbers are directly measured from the spectrum. In this example, showing peaks at m/z 45 and 44 where s = 99 and d = 43 units, the resolution is calculated as

$$R=\frac{\mathit{ms}}{d}=101$$ (8)

Abundance Sensitivity

In the preceding discussion it has been assumed that the ion beam distribution is well defined in space, and the overlap between adjacent beams for m/z well below the resolution has been assumed negligible. This is not the case – there are many reasons why the ions of a particular mass may contribute to the adjacent mass number. The measure of this is termed the abundance sensitivity, and is quite simply defined as the fractional intensity of a peak appearing at the neighbouring position. Typically the abundance sensitivity of the instrument should be a few parts per million (ppm).

5. The Collector

The ion collector is generally simple. It comprises a resolving slit (usually placed at the re-focussing point as described above) and behind it a detector. Although electron multipliers can be used as a detecting element, the requirements of high stability and precision of current applications usually demand that a Faraday bucket [9] (also called a Faraday cup) is used. Electrons ejected from the material of the bucket by the incoming ions are suppressed either by an electric field (a plate with a potential of about −70 V with respect to earth, or by small magnets.

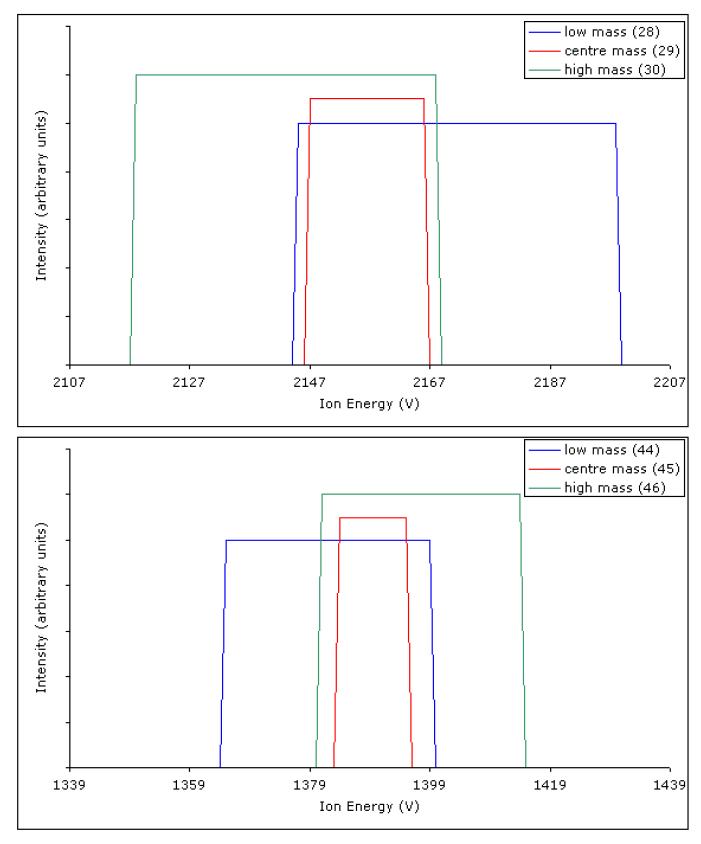
More than one collector can be fitted to the instrument in order to detect several masses simultaneously. For example, in gas IRMS research, a triple collector set to monitor three adjacent m/z values is often used, and the ion energy changed to select the particular mass group of interest. Substitution of values in the mass spectrometer equation will show, however, that the collector spacing is a function of the masses being measured. This can be partially overcome by making the two outer resolving slits much wider than the central one. Using this approach it is possible to construct a collector, which can used for measuring the stable isotopes of nitrogen (as nitrogen gas at m/z 28, 29 and 30), carbon or oxygen (as CO₂ at m/z 44, 45, and 46) and sulphur as SO₂ (m/z 64 and 66). The effect of effectively lowering the resolving power of two of the three detectors is shown in Figure 6. Note the difference in the overlap between the lowest and highest working m/z ratios for this particular design.

Figure 6.

Stylised scan output for a collector designed to monitor isotope ratios of N₂ and CO₂. In this system, the central resolving slit width is 0.4 mm and that of each of the outer slits is 1.1mm. Note the effect of the difference in spatial position between the N₂ and CO₂ mass clusters.

6. Concluding Remarks

In the preface to the second (1942) edition of his book ‘Mass Spectra and Isotopes’ [10], the pioneering mass spectrometrist F.W. Aston wrote “Since the publication of the first edition in 1933…..the subject may be said to have been closed. All the elements have now been analysed, and my main concern in writing this book is to tell how this has been done.”. At the time the explosion in the applications of mass spectroscopy in chemical and biochemical analysis could not have been foreseen. In some ways a similar comment might be applied today to the low resolution magnetic sector instrument, with many mass spectrometry practitioners dismissing them as old fashioned and obsolete. However, these instruments are irreplaceable in certain situations where a high degree of precision and long-term stability is required. Magnetic Sector instruments are also indispensable for the isotopic analysis of trace metals where an ICP source is commonly used, since they can be operated in high resolution mode which will allow measurements to be made in the presence of interfering species, not possible with mass analysers of lower resolution Although dismissed by some as ‘dinosaurs’, these instruments are currently far from extinct, and for those involved in the business of measuring isotopes, a thorough appreciation of their operation is necessary if an analytical performance of the highest quality is to be achieved.

The next instalment of this tutorial will explain state-of-the-art isotope application techniques such as mass isotopomer distribution analysis (MIDA) and position-specific isotope analysis (PSIA).

Biography

Professor Dietrich Volmer is Head of the Bioanalytical Sciences department at the Medical Research Council’s Human Nutrition Research institute in Cambridge, United Kingdom. He is interested in different areas of biological mass spectrometry, including biomarkers, metabolomics and structural elucidation techniques. Dr Les Bluck is a senior faculty member in Dr Volmer’s department, with strong interests in stable isotope tracer techniques and physiological modelling.