Abstract
The development of ultrasound-based elasticity imaging methods has been the focus of intense research activity since the mid-1990s. In characterizing the mechanical properties of soft tissues, these techniques image an entirely new subset of tissue properties that cannot be derived with conventional ultrasound techniques. Clinically, tissue elasticity is known to be associated with pathological condition and with the ability to image these features in vivo, elasticity imaging methods may prove to be invaluable tools for the diagnosis and/or monitoring of disease. This review focuses on ultrasound-based elasticity imaging methods that generate an acoustic radiation force to induce tissue displacements. These methods can be performed non-invasively during routine exams to provide either qualitative or quantitative metrics of tissue elasticity. A brief overview of soft tissue mechanics relevant to elasticity imaging is provided, including a derivation of acoustic radiation force, and an overview of the various acoustic radiation force elasticity imaging methods.
I. Introduction
The elasticity (i.e. stiffness) of soft tissues has been related to pathological condition since early medicine. In 400 B.C. Hippocrates noted that abdominal swellings that are “soft, free of pain, and yield when pressed with the finger, are more chronic” compared to those that “as are painful, hard, and large, indicate danger of speedy death” [1]. The use of manual palpation to assess tissue health and monitor disease progression is still commonly used in routine physical examinations. For instance, the presence of stiff masses found during routine breast exams is often an early indication of breast cancer [2–5]. While indispensable for medical diagnosis, manual palpation methods are relatively subjective and limited to superficial structures. With the ability to measure the elasticity of tissues deep within the body, ultrasound-based elasticity imaging techniques offer great clinical promise.
Unlike conventional B-mode imaging that differentiates features with dissimilar acoustic properties, elasticity imaging methods differentiate features and/or structures with different mechanical properties. To do this, the methods involve both the excitation of soft tissues and a monitoring of the deformation response. This response can be related to either a qualitative and/or quantitative measure of stiffness.
Several groups have been investigating the use of elasticity imaging methods in ultrasound. These methods can be classified according to the source of excitation used to deform the tissue. The first ultrasound-based elasticity imaging methods relied upon the use of an external force, such as a transducer to compress the skin as in elastography or strain imaging [6, 7]. Similarly, a mechanical vibrator can be used to vibrate the tissue at specific frequencies in sonoelasticity [8, 9]. Natural, physiological-based sources can also be used to deform the tissue. These methods take advantage of breathing, cardiac motion, or arterial pulsation to derive elasticity information [10–14]. In this paper, we will focus on the more recently developed acoustic radiation force (ARF) elasticity imaging methods that generate an acoustic radiation force excitation to cause localized displacements within the targeted region of interest. For more information on all these methods, the reader is refferred to excellent reviews provided by [15–18].
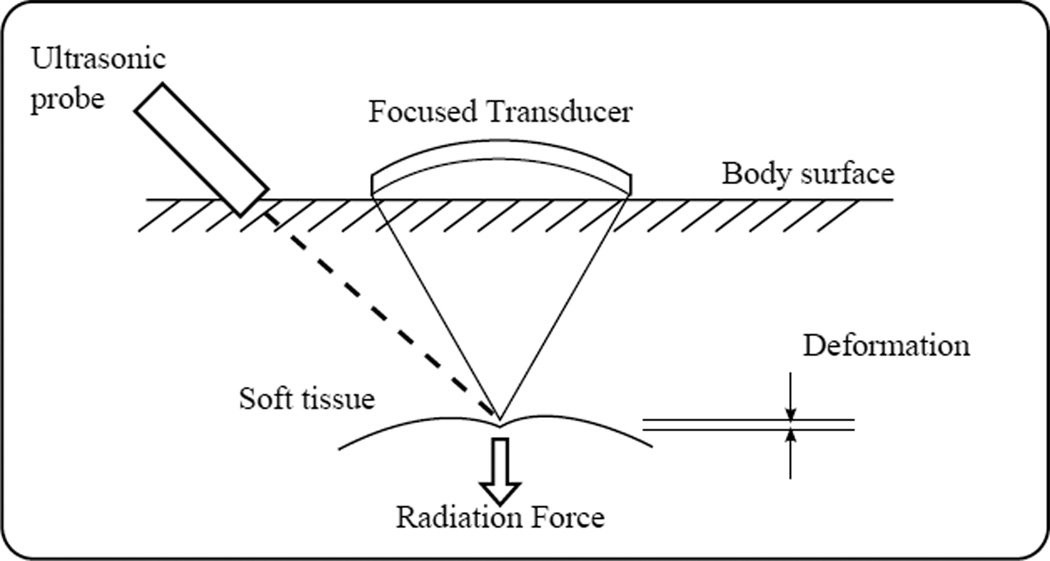
As shown in Figure 1, ARF methods use a focused remote device to generate a sufficient acoustic radiation force to cause localized displacements. Using either a separate or remote device, the deformation can be monitored spatially and temporally. Because the force is applied directly to the region of interest, ARF methods are associated with smaller strains, are less impacted by external boundaries, and unlike external excitation methods, they do not face problems associated with coupling the excitation within the targeted region.
Fig. 1.
General concept of ARF based elasticity imaging methods. 1) A focused ultrasound transducer is used to generate sufficient acoustic radiation force to cause localized tissue displacements. 2) The resulting deformation is monitored using the same or a separate remote device.
In this paper, a review of soft tissue biomechanics is provided to describe the common assumptions and elastic moduli often cited to quantify tissue elasticity. The phenomenon of acoustic radiation force is discussed with an accompanying derivation. Various ARF methods, classified according to the temporal duration of the applied acoustic radiation force and the location of the tracking beams, are discussed along with clinical applications and commercial implementations for selected methods. In looking at the future of ARF methods, current challenges and opportunities are discussed.
II. Background
A. Soft Tissue Biomechanics
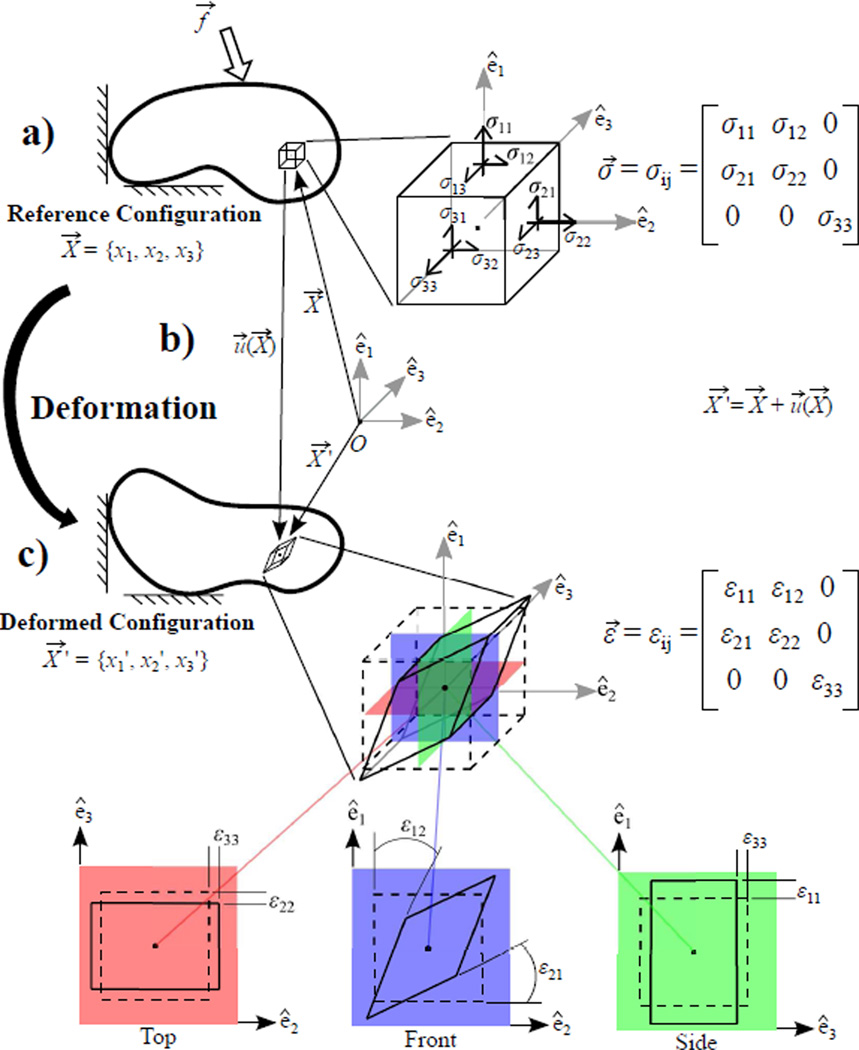
The deformation due to an applied force of a material body in a reference (i.e. initial) configuration to some deformed configuration is associated with 1) a restoring stress that satisfies equilibrium and 2) a strain describing the deformation. In continuum mechanics, a material body is idealized as being infinitely divisible such that the deformation, stress, and strain are functions of the position of each infinitely small volume within the continuum body. A brief review of these concepts is shown in Fig. 2, where a restoring stress and associated strain on a small infinitesimal volume are illustrated for an arbitrarily, yet physically realizable, prescribed loading. Note, stress and strain are tensor quantities (Table I) containing both normal (i.e. diagonal) and shear (i.e. off-diagonal) components. For a more in depth review of these concepts and mathematical operations, the reader is referred to any elementary mechanics reference including [19].
Fig. 2.
Brief overview depicting an arbitrary, yet physically realizable, restoring stress (σ⃗) and associated strain (ε⃗) that develops in an infinitesimal volume of a material body when an external force (f⃗) is applied. a) The restoring stress (σ⃗) satisfies equilibrium, according to (1), when an external force (f⃗) is applied to the body. b) The resulting deformation can be described by the displacement field (u⃗) related to the position of the infinitesimal volume in the reference (X⃗) and deformed (X⃗ ′) configurations. c) The associated strain (ε⃗) also describes the deformation and is related to the displacement (u⃗) according to (2). Here, the deformation is portrayed in 3 different orientations to illustrate both normal strains (ε11, ε22, and ε33) in the top and side views and shear strains (ε12 and ε21) in the front view.
TABLE I.
Nomenclature
| x1, x2, x3 | Euclidian space coordinates |
| i, j1 | Spatial vector and tensor subindices |
| δij | Kronecker delta |
| σ⃗ = σij | Cauchy stress tensor |
| ε⃗ = εij | Strain tesnor |
| u⃗ = ui | Particle displacement |
| υ⃗ = υi | Particle velocity |
| α⃗ = αi | Particle acceleration |
| f⃗ = fi | Applied force |
| ∇ | Spatial gradient operator |
| ∇ · | Divergence operator |
| ∇ × | Curl operator |
| ∇2 | Laplacian operator |
| 〈〉 | Time-average |
| λ | Lamé constant |
| μ | Lamé constant (shear modulus) |
| E | Young’s Modulus |
| ν | Poisson ratio |
| θ⃗ | Equivoluminal displacement |
| ψ | Dilatational displacement |
| ρ | Material Density |
| cL | Longitudinal wave speed |
| cT | Transverse wave speed |
| p | Scalar pressure |
| k | Bulk viscosity |
| μf | Shear Viscosity |
| F⃗ | Acoustic radiation force |
| I | Time-average Intensity |
| α | Absorption coefficient |
| F/# | F Number |
| z | Focal depth |
| D | Aperture width |
| σ | Jitter |
| fc | Center frequency |
| T | Correlation window length |
| B | Fractional Bandwidth |
| ρc | Correlation |
| SNR | Signal to Noise Ratio |
Following Einstein convention, summation is implied over repeated vector and tensor subindices. For an in depth review of vector and tensor notation and operations the reader is referred to [19].
Stress represents the force per unit area that serves to counteract the applied force. As an equation of equilibrium relating these quantities, Newton’s 2nd Law of motion can be expressed in terms of the Cauchy’s stress tensor (σ⃗) as (1), where f⃗ represents an externally applied force per unit volume and α⃗ is the particle acceleration [19].
| (1) |
The strain relates the deformed configuration of a material to its initial reference configuration; specifically representing the change in length per unit length. Normal strains correspond to pure compression and/or expansion, while shear strains involve a twist (Fig. 2). As a kinematic expression of particle motion, the strain can be written in terms of the displacement (u⃗) according to (2).
| (2) |
The elasticity of a material describes its tendency to deform in response to an applied force, such that the goal of elasticity imaging methods is to relate stress and strain. Note however, the equations of stress equilibrium and kinematics are indeterminate, such that a constitutive equation is needed to relate these quantities. For complex materials it is nearly impossible to derive a constitutive equation that can accurately model the material under any loading. As such, many assumptions are typically made in order to describe the material behavior under the particular loading conditions being investigated.
In general, soft tissues are viscoelastic, inhomogeneous, and anisotropic [20]. As viscoelastic materials, soft tissues exhibit properties of both elastic solids and viscous fluids, whose particular response is dependent upon the frequency of excitation [21]. Ignoring viscous forces and neglecting the non-linear terms in (2) (i.e. assuming small strains) soft tissues are often described to a first-order approximation as linear, elastic solids. If homogeneous and isotropic conditions are also assumed, a constitutive equation describing the relationship between stress and strain can be represented as (3), which depend on two material coefficients known as the Lamé constants (λ and μ).
| (3) |
Various elastic moduli exist to define the elasticity of a material. In the literature, the stiffness of a material is most commonly reported in terms of the Young’s Modulus (E), which describes a material’s resistance to deformation in uniaxial compression/tension. The shear modulus (μ) describes the resistance to shear. The Poisson’s ratio (ν) describes the deformation that occurs orthogonal to that of the applied force. For a homogeneous, isotropic, linear elastic material (3), these moduli completely define the elasticity of the material and are related according to (4–6). For incompressible materials ν = 0.5 and (6) reduces to μ = E/3.
| (4) |
| (5) |
| (6) |
Taking the spatial derivative of (3) according to (1) and expressing the particle acceleration in terms of the particle displacement , the governing equation for wave propagation in a linear, elastic, isotropic material can be expressed as (7). Here ∇ is the spatial gradient operator, ∇ · is the divergence operator, and ∇ × is the curl operator.
| (7) |
There are are two primary modes of wave propagation in soft tissues. In longitudinal (i.e. compressional or pressure) waves, the particles oscillate in the direction of wave propagation. With shear waves, the particles oscillate in a direction that is transverse with that of the wave propagation [21]. Helmholtz theorem can be used to decompose the displacement vector field into the curl-free, longitudinal, scalar potential (ψ) and the divergence-free, transverse, vector potential (θ⃗) according to (8) [22].
| (8) |
Separating components leads to two wave equations that separately describe the longitudinal and transverse propagation, defined according to (9) and (10) respectively. Note, the speed of the propagating longitudinal waves (cL) and transverse waves (cT) are expressed in terms of elastic moduli.
| (9) |
| (10) |
A common deviation from the linear elastic model assumed herein, accounts for the soft tissue being nonlinear such that the stiffness is dependent upon the strain magnitude. To account for dispersion, in which the stiffness is dependent upon the excitation frequency, soft tissues can also be modeled as viscoelastic solids [20].
B. Acoustic Radiation Force
The phenomenon of acoustic radiation force generation results from the transfer of momentum from an ultrasonic wave in an attenuating medium, where the pressure and particle velocity become out of phase. Note, at ultrasonic frequencies soft tissues do not support shear stresses and are more accurately modeled as viscous fluids [21, 23]. Therefore, the approach by Nyborg [24] and Eckart [25] is followed herein, using a linear viscous fluid model that, unlike the elastic model, can account for the appreciable loss of energy from the propagating wave to derive an equation for acoustic radiation force. For an incompressible material the constitutive equation for a linear viscous fluid can be described by (11); where represents the rate of deformation, (υ⃗) is the particle velocity, and p is a scalar pressure. The material constants k and μf represent the bulk viscosity and shear viscosity, respectively [19].
| (11) |
For a fluid particle, the acceleration can be expressed as the sum of the local particle acceleration and the convective acceleration according to (12) [26].
| (12) |
Combining (1) and (12) leads to the Navier-Stokes equation, which relates the equation of motion (1) in terms of the velocity components. For a linear viscous fluid model described by (11), this reduces to (13).
| (13) |
To approximate a solution to (13), a perturbation analysis [27] is used to expand the density, pressure, and velocity in terms of time-dependent approximations to the steady-state solutions with higher-order, time-independent correction terms. Applied to the right hand side of (13) and keeping up to the second-order terms, this approximation leads to (14). Here ρ0 represents the material density, and ρ1 are first-order approximations (i.e the sinusoidal time-varying response) for the particle velocity and density respectively, and is a higher-order correction term that represents the acoustic streaming velocity.
| (14) |
Taking the time-average (〈〉) of (14) leads to the following expression for radiation force (F⃗),
| (15) |
For an exponentially attenuating plane wave this force can be expressed in terms of the time-average intensity (I⃗) at any given spatial location as (16), where α represents the absorption coefficient and cL is the longitudinal wave speed [23, 24, 28].
| (16) |
Herein, an expression for the acoustic radiation force was derived from the right hand side of the Navier-Stokes equation (13). In performing a similar perturbation analysis and time-averaging to the left hand side of (13) and assuming that (∇ · υ⃗2) is negligible, as done in Nyborg [24], leads to (17); where p2 represents a second-order pressure term.
| (17) |
From this expression, the radiation force is described in terms of the shear viscosity operating on the Laplacian operator of the velocity field (i.e. a diffusion of momentum) such that the acoustic radiation force represents a transfer of momentum from the acoustic wave to the material [24]. In this derivation, any contribution from scattering has been ignored such that the momentum transfer is assumed to be only due to absorption of the acoustic energy alone. In soft tissues, where absorption dominates scattering, this assumption seems valid [29]. For this reason, the absorption coefficient is typically replaced with an attenuation coefficient.
Note that because this force is related to the time-average intensity, the excitation frequency of the resulting radiation force is much lower than that of the incident ultrasonic wave. Therefore, while a linear viscous fluid model was used to account for the generation of an acoustic radiation force, often a linear elastic solid model (3) is used to describe the response of soft tissues that occurs at these lower frequencies.
In conventional ultrasound imaging, the magnitude of acoustic radiation force is relatively small such that tissue displacements are negligible (< 1 µm). To generate sufficient acoustic radiation force, ARF methods use a focused transducer and longer and/or higher power acoustic pulses. Peak acoustic radiation force magnitudes are typically on the order of dynes for in vivo applications, creating tissue displacements in the range of 1 to 10 µm.
The acoustic radiation force field is spatially distributed under the active transducer aperture and is dependent upon the material properties and characteristics of the transmitted beam. As shown in (16), the acoustic radiation force is a function of the absorption (i.e. attenuation) and intensity. While higher attenuation increases the amount of momentum transfer to the medium, it decreases the intensity of the acoustic wave. Because attenuation is frequency and depth dependent, the optimal frequency used to generate an acoustic radiation force is application specific and involves a tradeoff between attenuation losses in the near field and focal point gain. In general, an increased attenuation or frequency is associated with more near field losses and a more uniformly distributed force [30]. The focal configuration of the transmitted excitation beam can be tailored to account for these effects. The transmit F/#, shown in (18), dictates the depth of field and beam width, where z is the focal depth and D is the aperture width.
| (18) |
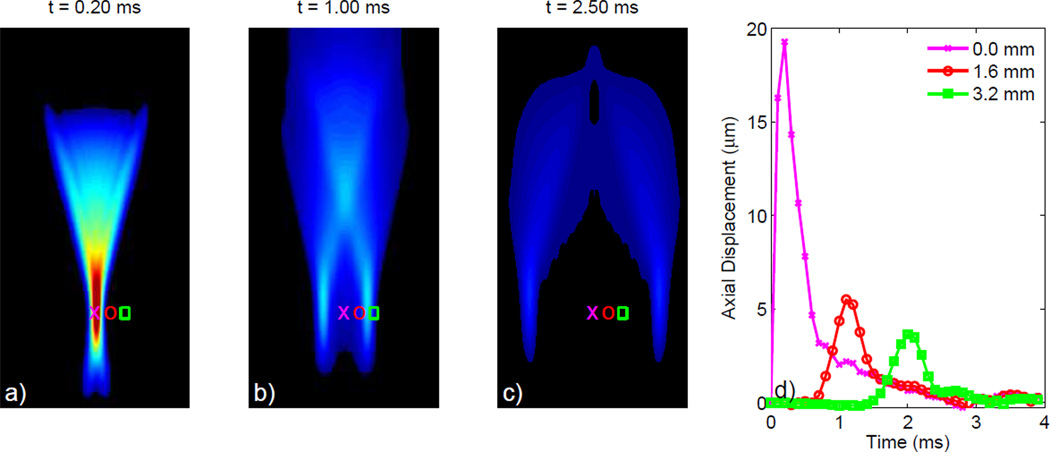
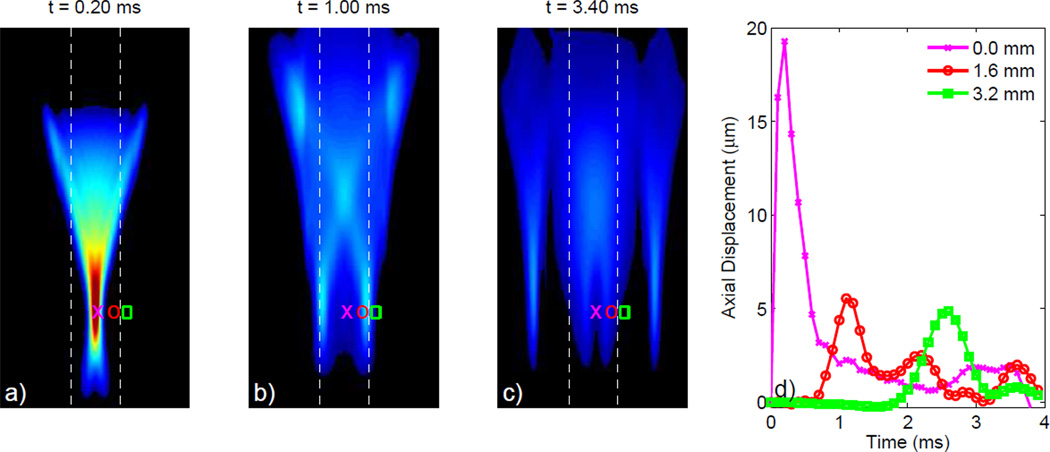
Shown in Figure 3 is a Finite-Element Method (FEM) simulation depicting the axial displacements induced in a 3-D, homogeneous, isotropic, linear, elastic solid model with E = 10 kPa by an impulse-like (i.e. short duration) 45 µs, F/1.3, 6.7 MHz acoustic radiation force excitation [23]. The response at 3 time steps following the application of the acoustic radiation force is portrayed in Figures 3a–c. Initially, the acoustic radiation force is localized within the focal zone, often referred to as the region-of-excitation (ROE), resulting in the peak displacement in Figure 3a. Shear waves created at the edges of the ROE propagate orthogonally to the direction of the applied force, causing off-axis displacements of decreased magnitude due to a spreading of the acoustic energy depicted in Figures 3b–c. The response recorded at three locations distributed across the lateral dimension within (pink x) and outside (red circle and green square) the ROE through time is depicted in Figure 3d. In heterogeneous soft tissues this dynamic response becomes much more complicated due to wave reflections at material boundaries and acoustic impedance mismatches [31]. With the white-dashed lines depicting the material boundaries between a E = 10 kPa centeral layer and two softer E = 2 kPa outer layers, Figure 4 portrays this more complicated response for the same transducer configuration represented in Figure 3. Note in Figure 4d, the presence of multiple distinct peaks indicative of the initial shear wave propagating away from the ROE, but also the reflected shear wave traveling back towards the ROE.
Fig. 3.
FEM simulated response in a 3-D, homogeneous, isotropic, linear, elastic solid (E = 10 kPa) depicting the axial displacements from an impulsive 45 µs, F/1.3, 6.7 MHz acoustic radiation force excitation. The axial displacements depicted at 3 different time steps following excitation in (a) through (c) show the propagation of shear waves away from the ROE. The displacement through time profiles depicted in (d) show the axial displacements occurring at the focal depth for each of 3 separate lateral locations, located both on-axis (pink X) and off-axis (red circle and green square). These profiles reflect the decreased displacement amplitude with increased distance from the ROE due to geometric spreading.
Fig. 4.
FEM simulated response depicting the axial displacements from an impulsive 45 µs, F/1.3, 6.7 MHz acoustic radiation force excitation in a 3-D linear, isotropic, elastic solid consisting of a stiffer material (E = 10 kPa) centered between two softer materials (E = 2 kPa). The material boundaries are indicated by the white dashed lines in (a) through (c), which depict the axial displacements at 3 distinct times following excitation. In (b) the shear waves have not reached the layer boundaries and only the initial shear waves propagating from the ROE are observed. In (c), just after the shear waves reached the center material boundary, the reflected and transmitted waves are depicted. Displacement through time profiles in (d) show multiple distinct peaks indicative of both the incident shear waves along with the reflected shear waves introduced by the material boundaries.
C. Monitoring the Deformation Response
To derive meaningful information, ARF methods rely upon the ability to accurately monitor the tissue motion induced by the applied acoustic radiation force. Using conventional pulse-echo ultrasound, the tissue motion can be monitored spatially and temporally. Typically performed using phase shift or cross-correlation based algorithms, an estimate of tissue displacement can be made between signals collected before the excitation (reference) and after the excitation (tracking).
1) Cross-Correlation Methods
Developed for estimating blood flow velocities from radiofrequency (RF) data the cross-correlation technique [46] measures the similarity between a windowed length of data from the reference and tracking signals. Often referred to as a time-delay estimation technique, the time shift that results in the maximum cross-correlation value indicates when the two signals are most similar and represents the time used to form a displacement estimate. With greater performance, the normalized cross-correlation method reduces the impact of bright scatterers and is often considered the gold standard for ultrasonic displacement estimation [47].
2) Phase Shift Methods
In 1985, real-time 2-D color flow imaging was made possible with a 1-D autocorrelation phase shift estimation method developed by Kasai et al. [48]. Unlike cross-correlation methods that operate in the time-domain on RF data, the phase-shift methods operate in the frequency domain utilizing the less memory intensive demodulated inphase and quadrature (IQ) data. Improved performance can be obtained using the 2-D autocorrelation method developed by Loupas et al. [49] that accounts for local variations in the center frequency of the received echo for each displacement estimate. For the small displacements typically encountered with ARF methods, the 2-D autocorrelation method performs reasonably well compared with normalized-cross correlation and is less computationally intensive [50].
3) Sources of Bias and Jitter
The ability to accurately estimate tissue motion is quantified by an estimator’s bias and jitter. Derived by Walker et al. [51] from the Cramer-Rao lower bound, a theoretical lower limit for the jitter (σ) of correlation-based tracking algorithms for partially correlated speckle signals assuming a flat power spectral density can be expressed as (19), where SNR is the signal-to-noise ratio, fc is the transducer center frequency, T is the correlation window length, B is the fractional bandwidth, and ρc is the correlation value between the signals.
| (19) |
Jitter, which can empirically range from 1 to 5 µm for typical diagnostic ultrasound results in noisy images and inaccurate moduli estimates [31, 50, 51]. For ARF methods, scatterer shearing beneath the point spread function can decrease the correlation between the reference and tracking pulses and result in increased jitter and an underestimation of the true displacement magnitude [52, 53]. Recently, harmonic methods for tracking the displacements induced by an acoustic radiation force excitation have been developed by Doherty et al. [54] to suppress clutter for improved jitter reduction and feature detection.
III. Imaging Methods
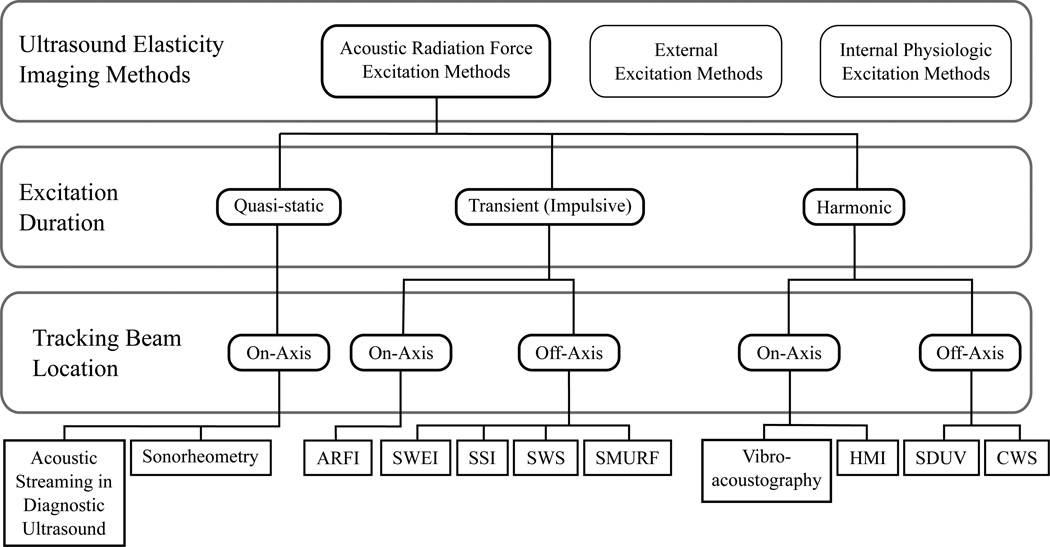
In 1990 Sugimoto et al. [55] proposed that “radiation force of ultrasound is used instead of fingers” as a means of extending palpation methods to internal organs. Since then, a variety of ARF methods have been investigated. As shown in Figure 5 these methods can be classified according to the temporal duration of the applied acoustic radiation force excitation and the location of the tracking beams used to measure the deformation response. In general, the excitation (pushing) pulses can be applied 1) quasi-statically to achieve a steady state response, 2) transiently in an impulse-like fashion or 3) harmonically to excite the tissue at specific frequencies.
Fig. 5.
Ultrasound-based elasticity imaging methods can be categorized by the excitation source used to deform soft tissue. As presented herein, Acoustic Radiation Force methods can be further classified according to the duration of the applied acoustic radiation force excitation and the location of tracking beams used to monitor the deformation response. These methods include: Acoustic Streaming in Diagnostic Ultrasound [32, 33], Sonorheometry [34], Acoustic Radiation Force Impulse (ARFI) Imaging [35, 36], Shear Wave Elasticity Imaging (SWEI) [37], Supersonic Shear Imaging (SSI) [38], Shear Wave Spectroscopy (SWS) [39], Spatially Modulated Ultrasound Radiation Force (SMURF) [40], Vibro-acoustography [41, 42], Harmonic Motion Imaging (HMI) [43], Shear Wave Ultrasound Dispersion Ultrasound Vibrometry (SDUV) [44], and Crawling Wave Spectroscopy (CWS) [45].
Tracking beams can be positioned either within the ROE (on-axis) or outside the ROE (off-axis). Note that with on-axis methods, wherein the deformation is monitored at the location of the applied excitation, the measured response is dependent upon the magnitude of the applied force. Because this force depends upon material properties, which are unknown in vivo, on-axis methods can generally only provide relative measures of elasticity and are often considered qualitative methods. This can be somewhat confusing however. For instance, in Sonorheometry [34], a force-free parameter can be estimated from on-axis measurements using a model-based approach. Because it does not depend upon the magnitude of the applied force, this can serve as a quantitative parameter that describes the tissue elasticity. In general, quantitative estimates are most commonly performed using off-axis methods by estimating the speed of shear waves propagating outside the ROE to estimate the shear modulus from relationships such as (10).
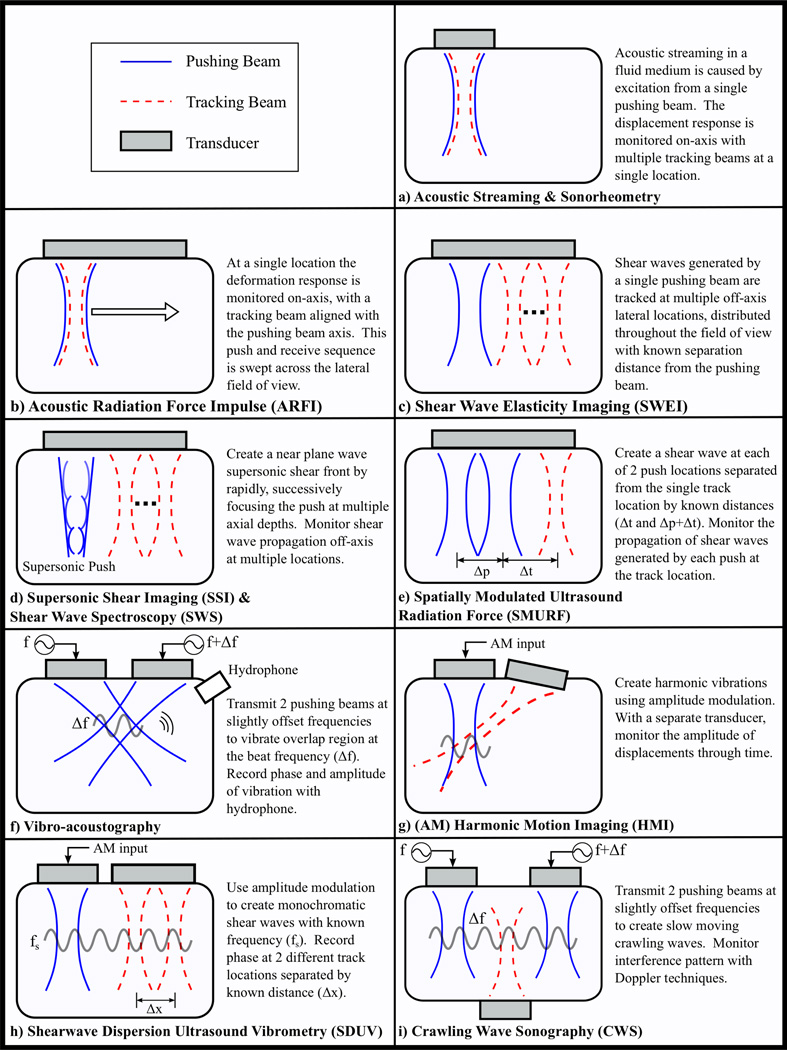
In the following sections, a short description of the various ARF methods that have been developed is presented. Clinical applications and implementations on commercially available scanners will be discussed for selected methods. An overview of these methods, depicting the different manners in which acoustic radiation force can be used to induce soft tissue deformation and the relationship between pushing beam and tracking beam locations, is provided in Figure 6.
Fig. 6.
Overview of Acoustic Radiation Force elasticity imaging methods in diagnostic ultrasound.
A. Quasi-static Methods
In quasi-static methods, a steady state tissue response can be attained by applying the acoustic radiation force excitation at a high pulse repetition frequency (PRF) for a relatively long duration. Because tissue heating can be a concern at a high PRF, quasi-static methods have generally been applied in fluids, where the forces required to achieve a measurable deformation are less than in soft tissue. The on-axis response can be monitored using either a separate monitoring device or the same transducer.
1) Acoustic Streaming in Diagnostic Ultrasound
Acoustic streaming is the fluid flow induced by acoustic radiation force in a viscous fluid. Using conventional Doppler techniques, the velocity of the induced fluid flow can be measured [32]. Clinically, this method was applied by Nightingale et al. [33] to differentiate fluid filled lesions (cysts) from solid lesions in breast tissue.
2) Sonorheometry
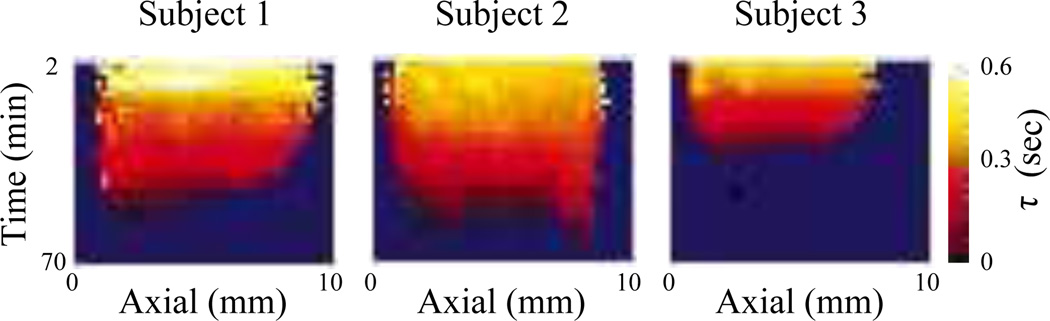
Developed by Viola et al. [34], the fluid/solid response of blood to a quasi-static acoustic radiation force excitation can be monitored to assess properties of coagulation in a method termed Sonorheometry. Using a model-based approach, the measured response can be fit to a viscoelastic Voigt fluid model to determine the time-constant (τ), a force-free parameter that provides a quantitative estimate of the rate of stiffening. Images of the time constant as function of time after a blood sample is withdrawn from a subject, Figure 7, indicate blood stiffening (i.e. decreased τ) over time and can be used to differentiate subjects with a clotting disorder (Subject 3) from normal subjects [34]. More recently, an adaptive force method that adjusts the PRF of the applied excitations based on the maximum displacement has been developed for an improved dynamic range of stiffness measurements [56].
Fig. 7.
Sonorheometry: Images portray a decrease in the force-free parameter (τ) indicative of blood stiffening with increasing time after the blood is withdrawn in three test subjects. The horizontal axis represents the axial depth within the cuvet containing the blood samples. In Subject 3, who had a history of a blood clotting disorder, the rate of stiffening is much greater than in Subject 1 and Subject 2. Image is modified from [34].
HemoSonics, LLC has recently introduced a portable analyzer based upon Sonorheometry for characterizing blood hemostasis in a number of settings.
B. Transient Methods
By applying an impulse-like (short duration) acoustic radiation force excitation, the transient deformation response of soft tissue can be monitored to derive elasticity information. Using conventional pulse-echo ultrasound the displacement response can be monitored both spatially and temporally. For more information on these methods, the reader is reffered to current reviews [30, 57].
1) Acoustic Radiation Force Impulse (ARFI) imaging
In Acoustic Radiation Force Impulse (ARFI) imaging, a single ultrasound transducer is used to both induce and monitor a deformation response [35]. At a single lateral location, a typical ARFI sequence consists of three pulse types: reference pulses(s) are used to establish a baseline position of the tissue prior to the acoustic radiation force, excitation (pushing) pulse(s) are used to generate the acoustic radiation force to induce localized deformation, and tracking pulses applied immediately following the pushing pulse(s) are used to monitor the deformation response and recovery of the soft tissue. This ensemble of reference, pushing, and tracking pulses can be translated across the aperture, similar to B-mode imaging, to acquire 2-D (lateral vs. axial) information. Using either cross-correlation or phase-shift algorithms, the axial displacements from a single reference pulse and all other tracking pulses, can be calculated to obtain displacement through time datasets that can be used to depict the relative stiffness of soft tissues. Images can be created to reflect the tissue displacement at a specific time following excitation, the maximum tissue displacement, or the time it takes to reach the maximum displacement [36]. In general, softer regions will displace farther, take longer to reach a maximum displacement, and recover more slowly than stiffer tissues [23, 31].
In a technique, related to both Sonorheometry [34] and ARFI [35, 36] is a method termed Monitored Steady-State Excitation and Recovery (MSSER) [59]. Here both the steady-state response and the transient recovery following the cessation of force application is monitored to form an estimate of the tissue elasticity and stiffness using a model based approach.
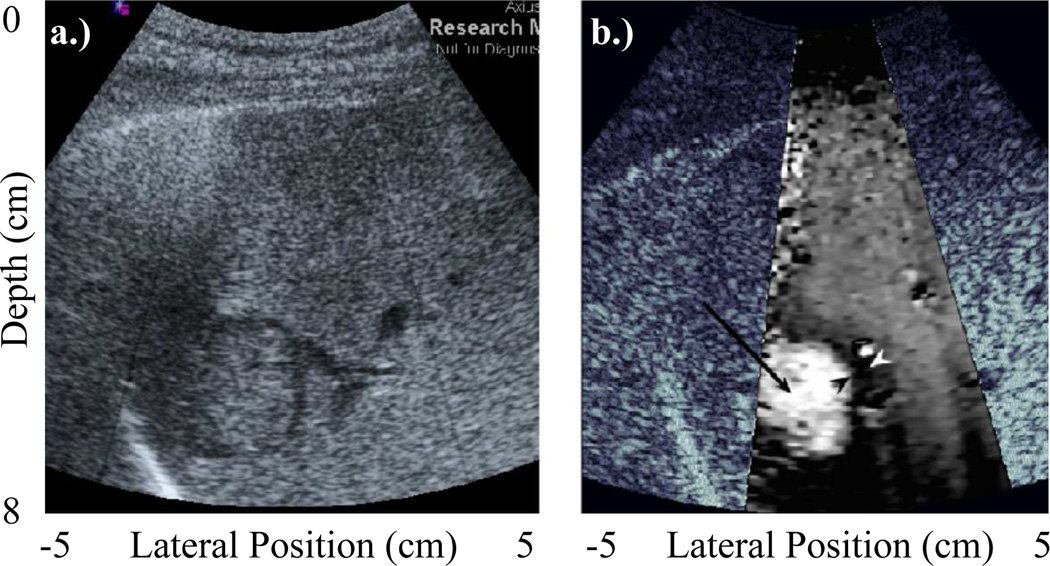
Clinically, ARFI imaging has been investigated for multiple applications. It has been used to assess changes in stiffness over the cardiac cycle in both vascular [60–62] and cardiac tissues [63, 64]. Capable of distinguishing ablated regions of myocardium, ARFI imaging has been used to guide thermal ablation procedures in the heart [65].With the goal of identifying patients more at risk of stroke and other sudden ischemic events, ARFI imaging has shown promise for its ability to distinguish soft, vulnerable plaques from otherwise stiffer, more stable regions [66, 67]. In cancer imaging, ARFI imaging has been also been used for tumor characterization in the breast [68], gastrointestinal [69], prostate [70, 71], and abdomen [58]. As shown in Figure 8, ARFI images often portray improved contrast over matched B-mode images [58, 71, 72].
Fig. 8.
ARFI: Comparing (a) B-mode and (b) ARFI in vivo images of a hepatocellular carcinoma (HCC) in a human liver. The overlaid ARFI grayscale represents normalized displacements, and indicates that the HCC displaced farther than the surrounding cirrhotic liver tissue. While HCC’s are known to be stiffer than normal liver (and would thus be expected to appear darker in an ARFI image), this patient was diagnosed with cirrhosis, which is associated with increased tissue stiffness. Image modified from [58].
Siemens Medical Solutions has implemented a version of ARFI imaging, termed Virtual Touch™ Tissue Imaging, on their ACUSON S2000™ ultrasound scanner [73]. Towards evaluating the utility of these methods, clinical studies have been ongoing in Europe and Asia [74–80].
2) Shear Wave Elasticity imaging (SWEI)
In 1998 Sarvazyan et al. used a high intensity focused ultrasound (HIFU) piston to induce shear waves that were monitored using MRI, to quantify tissue stiffness in a method they termed Shear Wave Elasticity Imaging (SWEI) to [37]. As applied by Nightingale et al. [81], SWEI can be performed using a single ultrasound transducer by applying an impulsive acoustic radiation force excitation to generates shear waves, whose propagation can be monitored using conventional pulse-echo ultrasound at locations outside the ROE. SWEI methods obtain similar information that is acquired in ARFI imaging, except that tracking beams are positioned outside the ROE. With displacement through time information at multiple lateral locations separated by a known distance from the excitation source, the speed of the propagating shear waves can be estimated. Although inversion of the wave equation (10) was originally employed for quantifying shear wave speeds [82], these methods are confounded by large jitter; where differentiation of noisy ultrasonic displacement estimates can lead to an amplification of the jitter and variable shear wave speed estimates. Therefore, shear wave speed estimates are typically determined using time-of-flight (TOF) methods that perform linear regression between the wave arrival time and lateral position data [83–86].
Clinically, acoustic radiation force based SWEI methods have been applied to non-invasively monitor liver fibrosis [87, 88]. Along with ARFI methods, TOF based shear wave speed quantification methods have been introduced as part of the Virtual Touch™ Tissue Quantification tool by Siemens Medical Solutions [73]. These tools have been utilized for quantifying the stiffness of various abdominal and thyroid tissues [80, 89–94].
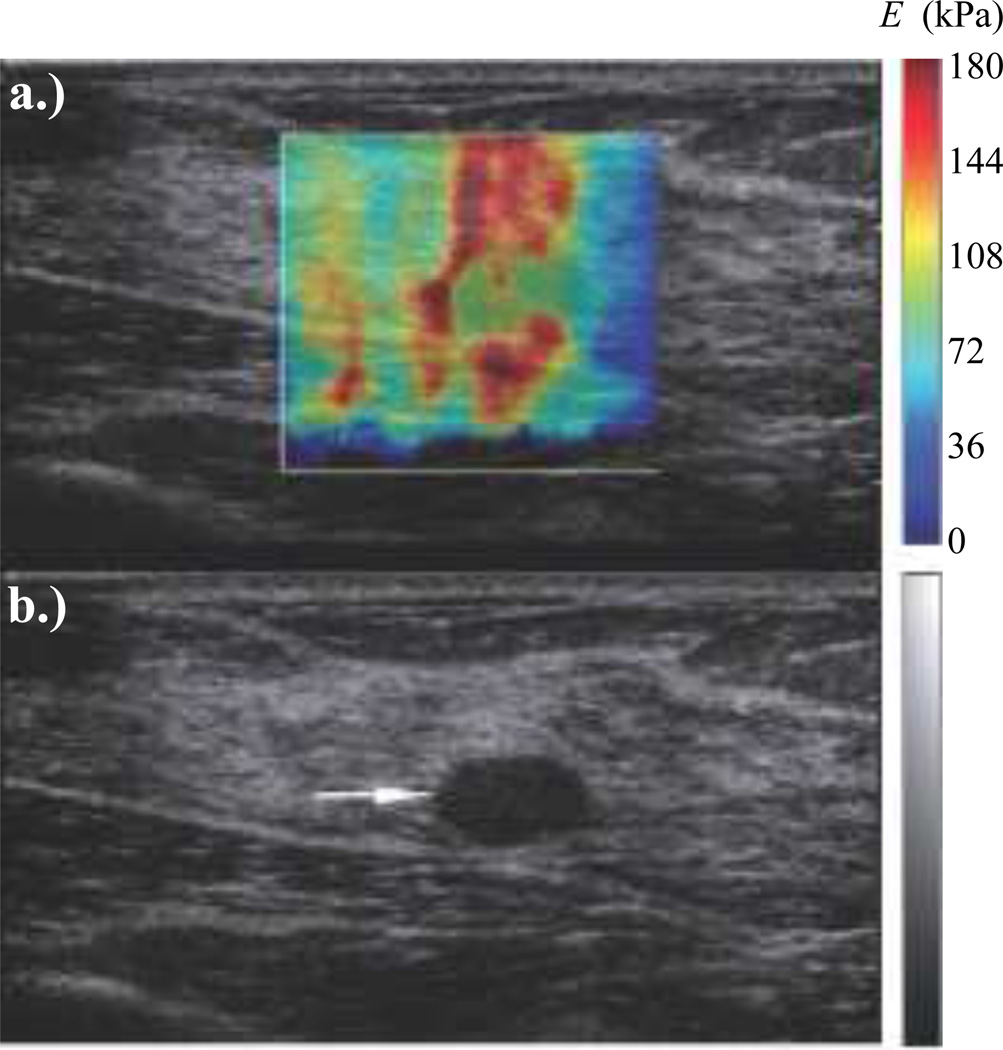
3) Supersonic Shear Imaging (SSI)
In Supersonic Shear Imaging (SSI), multiple acoustic radiation force excitations are applied at increasing focal depths to create a quasi-plane shear wave source. Developed by Bercoff et al. [38], the method relies upon applying the excitations at a supersonic speed (i.e. the excitation is moved faster than the shear wave speed) such that shear waves propagating away from the ROE sum constructively along a Mach cone to create an axially extended cylindrical shear wave. Utilizing extensively parallel beam-forming and plane wave transmits, SSI methods are capable of monitoring the deformation response simultaneously across a large field of view (FOV) at ultrafast (i.e. kHz) frame rates. Using TOF methods, shear wave speeds can be determined and used to form a quantitative estimate of tissue stiffness.
SSI has been utilized to detect breast cancer lesions [95], map hepatic viscoelasticity [96], assess stiffness in the muscoskeletal system [97], and for monitoring thermal ablation procedures [38]. Implemented on their Aixplorer™ ultrasound scanner, SuperSonic Imagine has commercialized SSI methods to create quantitative elasticity images [98]. Using this technology in a large multinational study, it was found that SSI methods improved the specificity of breast ultrasound mass assessment [99]. The heterogeneity in breast mass and surrounding tissue in the elastography image shown in Figure 9 is a suspicious sign for what was later identified as a grade III invasive ductal carcinoma biopsy [99].
Fig. 9.
SSI: Matched (a) elastographic and (b) B-mode in vivo images of an oval breast mass. The heterogeneously stiff breast mass and surrounding tissue are suspicious findings in the elastography image for the biopsy proven grade III invasive ductal carcinoma. Image is modified from [99].
4) Shear Wave Spectroscopy (SWS)
Towards evaluating dispersion in soft tissues, the method of Shear Wave Spectroscopy (SWS) monitors the propagation of shear waves with frequencies ranging from 75–600 Hz [39]. As an extension of SSI, the SWS method generates a quasi-plane shear wave source to induce displacements that can be monitored across the lateral field of view at ultrafast frame rates. Unlike conventional SWEI and SSI methods that attempt to estimate the shear wave group velocity, the goal of SWS is to form estimates of the shear wave velocity for individual frequency components. Because the energy within an individual component is much smaller than that of the entire signal, SWS methods are challenged by poor SNR. By assuming homogeneity within a large region of interest (ROI), the SNR can be improved at the expense of resolution. To assess dispersion, the method applies Fourier transforms to the propagating shear waves and evaluates the phase difference as a function of frequency.
5) Spatially Modulated Ultrasound Radiation Force (SMURF)
Rather than monitoring the propagation of shear waves at multiple lateral locations for a fixed excitation location, in Spatially Modulated Ultrasound Radiation Force (SMURF) [40], the propagation of shear waves generated at separated excitation locations is monitored at a single tracking location. By adjusting the spatial separation between successive excitations, shear waves of a specific wavelength can be designed. From time of arrival estimates, the time difference between the shear waves from each source can be estimated. With the known path length between these sources, a shear wave speed estimate can be obtained and related to the shear modulus using a model based approach. Because SMURF uses the time between arriving shear waves, any bias inherent to the time of arrival of an individual shear wave is removed, assuming that each shear wave would be subject to the same distortion. For this reason, SMURF is less susceptible to the varying biases that exist at multiple tracking locations used in other methods [100].
C. Harmonic Methods
Rather than using a mechanical vibrator as in sonoelasticity [8], harmonic ARF methods use multiple acoustic radiation force excitations to drive soft tissue at frequencies that typically range from 20 to 100 kHz. The frequency of the generated force can be modulated to elicit a vibratory response that is related to the mechanical properties of the soft tissue. A number of recent reviews of these methods have been provided to which the reader is referred for more detailed information [101–103].
1) Vibro-acoustography
In Vibro-acoustography, a method developed by Fatemi and Greenleaf [41, 42], a low frequency (kHz) radiation force excitation is generated to locally vibrate tissue, producing a sinusoidal acoustic compressional wave that depends upon the viscoelastic properties of the medium. This oscillatory radiation force can be generated using two continuous wave excitation pulses that are transmitted simultaneously, focused at the same location, but with slightly offset frequencies to vibrate the tissue at the difference (beat) frequency of the two pulses. As described by Urban et al. [104], a similar response can be achieved using a single amplitude modulated (AM) continuous excitation pulse. The amplitude and phase of the acoustic emission created by the vibrating tissue can be detected with a hydrophone. By mechanically translating the excitation beam(s) across the elevation-lateral plane, C-scan type images can be created that depict relative changes in the stiffness of the interrogated regions.
Towards reducing the acquisition time, recent efforts have focused on implementing the method using a single ultrasound scanner on a commercially available scanner [105]. With a spatial resolution <1mm, Vibroacoustography has been applied in vivo to detect microcalcifications in arteries [106] and for imaging ex vivo breast [107] and prostate tissues [108].
2) Harmonic Motion Imaging (HMI)
In Harmonic Motion Imaging [43], a separate ultrasonic imaging transducer can be used to monitor the harmonic motion generated by either a single AM excitation or the overlapping transmit beams utilized in Vibro-acoustography. From RF data collected with conventional pulse echo ultrasound, cross-correlation based algorithms can be used to estimate the induced tissue displacements within the interrogated region of interest to qualitatively reflect changes in material stiffness.
With a separate therapy and diagnostic transducer combined into a confocal configuration, these methods have been used to visualize thermal ablations created during focused ultrasound (FUS) therapy [109].
3) Shear Wave Dispersion Ultrasound Vibrometry (SDUV)
Shear Wave Dispersion Ultrasound Vibrometry (SDUV) [44] can be used to create monochromatic shear waves of a designed frequency to assess dispersion in a viscoelastic medium. The method combines Vibro-acoustography, to create harmonic shear waves with SWEI, to monitor off-axis propagation using diagnostic pulse-echo ultrasound. The phase-shift of the propagating shear wave between tracking locations separated by a known distance can be determined and used to estimate the shear wave speed. Applying this over a range of excitation frequencies, a quantitative estimates of tissue stiffness and viscosity can be derived using a model-based approached. For evaluating dispersion over a significant frequency bandwidth, where having to transmit multiple narrowband shear waves of different frequencies can require a long duration, SDUV methods have also been applied using AM techniques to transmit repeated tonebursts of ultrasound to generate broadband shear waves [110]. More recently, a model-free based approach for quantifying viscoelastic properties has been introduced that combines the creep response measured in the MSSER imaging method with SDUV shear wave speed estimation [111].
SDUV has been used in vitro to estimate shear wave velocities in blood vessels [112, 113], kidney tissue [114], and the prostate [115]. In vivo the method was used to investigate dispersion in the liver [110].
4) Crawling Wave Spectroscopy (CWS)
Rather than focusing multiple excitation sources in the same location as in Vibro-acoustography, the pushing beams can be spatially offset to create two shear vibration sources. This approach has been employed to provide the mechanical excitation for a sonoelastography [8] derived technique, termed Crawling Wave Spectroscopy (CWS) [45]. Here, the slow moving crawling wave that is generated between the two sources of slightly offset frequencies can be monitored in real-time using conventional Color Doppler techniques. The speed of the crawling waves are related to the mechanical properties of the tissue and can be used to form a quantitative estimate of stiffness. More recently, CWS efforts have been integrated on a commercial ultrasound imaging system [116, 117].
In excised prostate glands, CWS has been used to differentiate cancerous and normal tissue [118].
IV. DISCUSSION
The phenomenon of acoustic radiation force provides a novel means for determining the elasticity of tissues deep within the body. Unlike methods using cutaneous mechanical excitations such as Transient Elastography (TE) introduced by Fibroscan®, where the presence of ascites or fluid boundaries proximal to the targeted organ make it difficult/impossible to induce shear waves, ARF methods benefit from being able to generate an excitation that can be localized within the specific ROI [119]. However, the depth at which ARF methods can be applied is limited, due to attenuation effects discussed earlier. Early implementations of shear wave imaging systems in the liver have motivated the use of low frequency ARF excitations and the development of the Fibroscan® XL mechanical punch for TE methods in obese patients [58, 87, 89, 120, 121].
Each of the ultrasound-based ARF elasticity imaging methods discussed herein provides a unique mechanism of image contrast that may be useful for delineating and characterizing disease. Clinically relevant differences in parameters such as contrast, spatial resolution, temporal resolution (i.e. frame rate) make some methods more useful for a particular task. Generally, qualitative imaging methods such as ARFI and Vibro-acoustography have improved spatial resolution compared to shear wave based, quantitative imaging methods including SWEI, SSI, SWS, SMURF, SDUV, and CWS that typically require large regression kernels in order to achieve a more precise estimate of the tissue modulus [57]. For this reason, qualitative imaging methods may be more suited for identifying lesion boundaries and for visualizing structural information. On the other hand, quantitative methods may be more useful in cases where the abnormality is not confined to a particular region, where the lack of a background tissue cannot provide sufficient contrast [110]. Also important are differences in making point measurements compared to creating multi-dimensional images of tissue elasticity, for which the acquisition time may be important; especially when large motions can corrupt displacement estimates and lead to poor image quality or inaccurate modulus estimates. For example, methods such as HMI and Vibro-acoustography are confined to smaller regions due to long acquisition times and may be best suited for identifying suspected sites where biopsy may be performed for closer examination. As demonstrated recently, factors including imaging location and probe position can impact point measurements and also need to be considered [122]. On commercially available systems, both SuperSonic Imagine and Siemens provide quantitative based imaging modes that allow the user to choose different sized regions for which either an image or a specific point measurement of estimated shear wave speeds (or shear moduli) is provided [73, 98].
While ARF methods have been investigated in research settings since the mid-1990s, they are just recently emerging into the clinic on commercial systems. For instance, a surge in publications has occurred in the clinical literature surrounding the use of shear wave-based imaging modalities to noninvasively characterize liver fibrosis, a disease that currently relies on invasive needle biopsy to provide a limited sampling of liver tissue for histologic evaluation. This clinical literature has established the feasibility of using ARF elasticity imaging in this setting, and in Europe, recommendations are being made to concurrently acquire shear wave-based imaging data of the liver along with biopsy, if not even replacing the biopsy completely with the elasticity imaging stiffness estimates [88, 91, 120, 123–143].
The generation of elasticity metrics, such as shear wave speed, by an imaging system for clinical diagnoses introduces the need for some standardization of those metrics between different commercial systems and different user implementations in the clinical setting. To that end, the Radiological Society of North America (RSNA) Quantitative Imaging Biomarkers Alliance (QIBA) established in 2012 an Ultrasound Shear Wave Speed Technical Committee to explore the standardization of quantitative elasticity metrics for clinical applications [144]. The goal of this committee is to identify and address the system-dependent variability in shear wave based quantification systems, and to eliminate those variabilities to ease the clinical interpretation of these novel diagnostic data. Sources of variability may include, but are not limited to, assumptions in the shear wave reconstruction algorithms, viscous and nonlinear tissue behaviors, and other dependencies (i.e. heterogeneity) that may exist over the imaging region of interest. Additionally, when new clinical applications for elasticity imaging are explored, elasticity metrics need to be established for these specific healthy and diseased tissues [30]. This will likely require large scale studies and efforts to standardize imaging protocols.
In relative elasticity imaging (e.g., ARFI imaging), clinicians must be made aware that the relative stiffness of a structure may change depending on the health of the background tissue, as can be the case in studying focal liver lesions in the context of healthy versus fibrotic liver tissue [58, 74, 75, 143]. Elasticity imaging artifacts can also exist in quantitative methods, where assumption of tissue isotropy in areas of reconstruction may be violated. Sources of such artifact in shear wave imaging include reflections from structural boundaries and out-of-imaging-plane diffraction effects [86, 145].
In addition to establishing consistency between different imaging systems and training clinicians to interpret relative elasticity images, there are other factors that ARF imaging systems must consider when used in the clinical setting. For instance, in order to generate adequate acoustic radiation force to achieve a measurable displacement in soft tissues, ARF elasticity imaging methods may benefit from the use of higher intensity and/or longer duration excitation pulses that are currently constrained by FDA acoustic and thermal exposure guidelines [146, 147]. This is especially true at depth and when large lateral regions of interest are desired to observe shear wave propagation. Despite potential benefits of an increased mechanical index (MI), most ARF elasticity imaging methods maintain an MI <1.9 to satisfy regulatory limits and reduce the likelihood of cavitation. However, these regulatory guidelines are based on the output and efficacy of ultrasound systems produced before 1976 and are not based on specific scientific knowledge regarding bioeffects due to ultrasound [148]. The American Institute of Ultrasound in Medicine (AIUM) recently established a subcommittee to review the bioeffects literature and make recommendations regarding the use of transiently increased output (TIO) in non-fetal and non-contrast agent ultrasonic imaging.
Besides generating an acoustic radiation force, absorption of acoustic energy also leads to the generation of heat within soft tissue. For a single impulsive acoustic radiation force excitation, the maximum temperature increase is a maximum at the focal point and can range from 0.02°C to 0.2°C. When repeated acquisitions are used, the maximum temperature induced can shift to the location of maximum beam overlap [149]. For increased scan durations and a high PRF, transducer surface heating can be significant. In satisfying regulatory limits, ARF methods must balance image quality, frame rates, and scan durations to ensure that the maximum temperature stays <43°C [150].
Improvements in transducer technology and the development of probes specifically designed for ARF methods will likely allow for greater depth penetration with less transducer face heating. With enhanced parallel beamforming capabilities, both on-axis and off-axis information can be monitored simultaneously across a wider FOV. Additionally, transducers can be specifically designed that operate at different frequencies to deliver the ideal ARF excitation beams (typically lower frequency), with higher frequency tracking beams to reduce displacement estimate jitter and displacement underestimation bias due to scatterer shearing [31, 52, 151].
V. Conclusions
Elasticity imaging methods have been the subject of intense research activity in the field of ultrasound imaging. With the ability to characterize the mechanical properties of tissues, these methods provide entirely new information that can be used for the diagnosis of disease or monitoring disease progression. Compared with other ultrasound-based elasticity imaging methods, ARF techniques that generate an acoustic radiation force deep within the tissue allow for excitations to be targeted within the region of interest to generate localized displacements. Adapted for clinical use, many ARF methods have recently been implemented on commercially available systems. With increased evaluation of their utility, we can expect ARF elasticity imaging methods will likely become a standard part of diagnostic ultrasound imaging.
Acknowledgments
The authors would like to thank NIH grants R37HL096023, R01HL075485, R01EB2132, R01CA142824, and R21HD063031 for funding this work.
REFERENCES
- 1.Adams F. The Genuine Works of Hippocrates. William Wood and Company; 1891. [Google Scholar]
- 2.Tohno E, Cosgrove DO, Sloane JP. Ultrasound diagnosis of breast diseases. New York: Churchill Livingstone Inc.; 1994. [Google Scholar]
- 3.Wolfe JN. Xeroradiography of the breast. Springfield, IL: Thomas; 1972. [Google Scholar]
- 4.Bassett L, Gold R, Kimme-Smith C. Hand-held and automated breast ultrasound. Thorafore, NJ: Slack Inc.; 1986. [Google Scholar]
- 5.Donegan WL, Spratt JS. Cancer of the breast. Philadelphia: Suanders; 2002. [Google Scholar]
- 6.Ophir J, Cespedes I, Ponnekanti H, Yazdi Y, Li X. Elastography: a quantitative method for imaging the elasticity of biological tissues. Ultrasonic Imaging. 1991;vol. 13(no. 2):111–134. doi: 10.1177/016173469101300201. [DOI] [PubMed] [Google Scholar]
- 7.Ophir J, Srinivasan S, Righetti R, Thittai A. Elastography: A Decade of Progress (2000–2010) Current Medical Imaging Reviews. 2011;vol. 7(no. 4):292–312. [Google Scholar]
- 8.Lerner RM, Huang SR, Parker KJ. “Sonoelasticity” images derived from ultrasound signals in mechanically vibrated tissues. Ultrasound Med Biol. 1990;vol. 16(no. 3):231–239. doi: 10.1016/0301-5629(90)90002-t. [DOI] [PubMed] [Google Scholar]
- 9.Parker KJ. The Evolution of Vibration Sonoelastography. Current Medical Imaging Reviews. 2011;vol. 7(no. 4):283–291. [Google Scholar]
- 10.Wilson LS, Robinson DE. Ultrasonic measurement of small displacements and deformations of tissue. Ultrasonic Imaging. 1982;vol. 4(no. 1):71–82. doi: 10.1177/016173468200400105. [DOI] [PubMed] [Google Scholar]
- 11.Dickinson RJ, Hill CR. Measurement of soft tissue motion using correlation between A-scans. UBM. 1982;vol. 8(no. 3):263–271. doi: 10.1016/0301-5629(82)90032-1. [DOI] [PubMed] [Google Scholar]
- 12.Mai JJ, Insana MF. Strain imaging of internal deformation. Ultrasound Med Biol. 2002;vol. 28(no. 11–12):1475–1484. doi: 10.1016/s0301-5629(02)00645-2. [DOI] [PubMed] [Google Scholar]
- 13.de Korte CL, van der Steen AF. Intravascular ultrasound elastography: an overview. Ultrasonics. 2002;vol. 40(no. 1–8):859–865. doi: 10.1016/s0041-624x(02)00227-5. [DOI] [PubMed] [Google Scholar]
- 14.D’hooge J, Bijnens B, Thoen J, de Werf FV, Sutherland GR, Suetens P. Echocardiographic strain and strain-rate imaging:a new tool to study reqional myocardial function. IEEE Trans Med Imaging. 2002;vol. 21(no. 9):1022–1030. doi: 10.1109/TMI.2002.804440. [DOI] [PubMed] [Google Scholar]
- 15.Wells PN, Liang H. Medical ultrasound: imaging of soft tissue strain and elasticity. J. R. Soc. Interface. 2011;vol. 8(no. 64):1521–1549. doi: 10.1098/rsif.2011.0054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Greenleaf JF, Fatemi M, Insana MF. Selected methods for imaging elastic properties of biological tissues. Annual review of biomedical engineering. 2003 Jan;vol. 5(no. 1):57–78. doi: 10.1146/annurev.bioeng.5.040202.121623. [DOI] [PubMed] [Google Scholar]
- 17.Parker KJ, Taylor LS, Gracewski S. A unified view of imaging the elastic properties of tissue. J Acoust Soc Am. 2005;vol. 117(no. 5):2705–2712. doi: 10.1121/1.1880772. [DOI] [PubMed] [Google Scholar]
- 18.Sarvazyan AP, Hall TJ, Urban MW. Imaging, An Overview of Elastography-An Emerging Branch of Medical. 2Current Medical Imaging Reviews. 2011;vol. 4(no. 7):255–282. doi: 10.2174/157340511798038684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lai WM, Rubin D, Krempel E. Introduction to Continuum Mechanics. Burlington, MA: Butterworth-Heinmann; 1999. [Google Scholar]
- 20.Fung YC. Biomechanics: Mechanical Properties of Living Tissue 2nd Edition. New York: Springer-Verlag; 1993. [Google Scholar]
- 21.Kino GS. Acoustic waves: devices, imaging, and analog signal processing. Englewood Cliffs, NJ: Prentice-Hall Inc.; 1987. [Google Scholar]
- 22.Achenbach JD. Wave propagation in elastic solids. New York, NY: Elsevier Science; 1999. no. [Google Scholar]
- 23.Palmeri ML, Sharma AC, Bouchard RR, Nightingale RW, Nightingale KR. A finite-element method model of soft tissue response to impulsive acoustic radiation force. IEEE Trans Ultrason Ferroelect Freq Contr. 2005 Oct;vol. 52(no. 10):1699–1712. doi: 10.1109/tuffc.2005.1561624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Nyborg W. In: Acoustic streaming. W M, editor. New York: Academic; 1965. [Google Scholar]
- 25.Eckart C. Vortices and streams caused by sound waves. The American Physical Society. 1948;vol. 73(no. 1):68–76. [Google Scholar]
- 26.Fox R, McDonald A. Introduction to Fluid Mechanics. New York: Wiley; 1992. [Google Scholar]
- 27.Ginsberg JH. Perturbation Methods. In: Hamilton MF, Blackstock DT, editors. Nonlinear acoustics. Academic Press; 1998. [Google Scholar]
- 28.Torr GR. The acoustic radiation force. Am. J. Phys. 1984;vol. 52(no. 5):402–408. [Google Scholar]
- 29.Christensen DA. Ultrasonic Bioinstrumentation. New York: Wiley; 1988. [Google Scholar]
- 30.Palmeri ML, Nightingale KR. Acoustic radiation force-based elasticity imaging methods. Interface Focus. 2011 Aug;vol. 1(no. 4):553–564. doi: 10.1098/rsfs.2011.0023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Palmeri ML, Mcaleavey SA, Trahey GE, Nightingale KR. Dynamic Mechanical Response of Elastic Spherical Inclusions to Impulsive Acoustic Radiation Force Excitation. IEEE Trans Ultrason Ferroelect Freq Contr. 2006 Jul;vol. 53(no. 11):2065–2079. doi: 10.1109/tuffc.2006.146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Dymling SO, Persson HW, Hertz TG, Lindstrom K. A new ultrasonic method for fluid property measurements. Ultrasound Med Biol. 1991;vol. 17(no. 5):497–500. doi: 10.1016/0301-5629(91)90186-z. [DOI] [PubMed] [Google Scholar]
- 33.Nightingale KR, Kornguth PJ, Walker WF, McDermott BA. A novel ultrasonic technique for differentiating cysts from solid lesions: preliminary results in the breast. Ultrasound Med Biol. 1995;vol. 21(no. 6):745–751. doi: 10.1016/0301-5629(95)00020-r. [DOI] [PubMed] [Google Scholar]
- 34.Viola F, Kramer MD, Lawrence MB, Oberhauser JP, Walker WF. Sonorheometry: a noncontact method for the dynamic assessment of thrombosis. Ann Biomed Eng. 2004 May;vol. 32(no. 5):696–705. doi: 10.1023/b:abme.0000030235.72255.df. [DOI] [PubMed] [Google Scholar]
- 35.Nightingale KR, Palmeri ML, Nightingale RW, Trahey GE. On the Feasibility of Remote Palpation Using Acoustic Radiation Force. J Acoust Soc Am. 2001;vol. 110(no. 1):625–634. doi: 10.1121/1.1378344. [DOI] [PubMed] [Google Scholar]
- 36.Nightingale K, Soo MS, Nightingale RW, Trahey GE. Acoustic radiation force impulse imaging: in vivo demonstration of clinical feasibility. Ultrasound Med Biol. 2002;vol. 28(no. 2):227–235. doi: 10.1016/s0301-5629(01)00499-9. [DOI] [PubMed] [Google Scholar]
- 37.Sarvazyan AP, Rudenko OV, Swanson SD, Fowlkes JB, Emelianov SY. Shear wave elasticity imaging: a new ultrasonic technology of medical diagnostics. Ultrasound Med Biol. 1998;vol. 24(no. 9):1419–1435. doi: 10.1016/s0301-5629(98)00110-0. [DOI] [PubMed] [Google Scholar]
- 38.Bercoff J, Tanter M, Fink M. Supersonic shear imaging: a new technique for soft tissue elasticity mapping. IEEE Trans Ultrason Ferroelect Freq Contr. 2004;vol. 51(no. 4):396–409. doi: 10.1109/tuffc.2004.1295425. [DOI] [PubMed] [Google Scholar]
- 39.Deffieux T, Montaldo G, Tanter M, Fink M. Shear wave spectroscopy for in vivo quantification of human soft tissues viscoelasticity. IEEE Trans Med Imaging. 2009 Mar;vol. 28(no. 3):313–322. doi: 10.1109/TMI.2008.925077. [DOI] [PubMed] [Google Scholar]
- 40.McAleavey SA, Menon M, Orszulak J. Shear-modulus estimation by application of spatially-modulated impulsive acoustic radiation force. Ultrasonic Imaging. 2007;vol. 29(no. 2):87–104. doi: 10.1177/016173460702900202. [DOI] [PubMed] [Google Scholar]
- 41.Fatemi M, Greenleaf JF. Ultrasound-Stimulated Vibro-Acoustic Spectrography. Science. 1998 Apr;vol. 280(no. 5360):82–85. doi: 10.1126/science.280.5360.82. [DOI] [PubMed] [Google Scholar]
- 42.Fatemi M, Greenleaf JF. Vibro-acoustogaphy: An imaging modality based on ultrasoundstimulated acoustic emission. Proc. Natl. Acad. Sci. 1999 Jun;vol. 96(no. 6603–6608):6603–6608. doi: 10.1073/pnas.96.12.6603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Konofagou EE, Hynynen K. Localized harmonic motion imaging: theory,simulations and experiments. Ultrasound Med Biol. 2003 Oct;vol. 29(no. 10):1405–1413. doi: 10.1016/s0301-5629(03)00953-0. [DOI] [PubMed] [Google Scholar]
- 44.Chen SG, Fatemi M, Greenleaf JF. Quantifying elasticity and viscosity from measurement of shear wave speed dispersion. J Acoust Soc Am. 2004;vol. 115(no. 6):2781–2785. doi: 10.1121/1.1739480. [DOI] [PubMed] [Google Scholar]
- 45.Hah Z, Hazard C, Cho YT, Rubens D, Parker K. Crawling waves from radiation force excitation. Ultrasonic Imaging. 2010 Jul;vol. 32(no. 3):177–189. doi: 10.1177/016173461003200305. [DOI] [PubMed] [Google Scholar]
- 46.Bonnefous O, Pesque P. Time Domain Formulation of Pulse-Doppler Ultrasound and Blood Velocity Estimation by Cross Correlation. Ultrasonic Imaging. 1986;vol. 8:73–85. doi: 10.1177/016173468600800201. [DOI] [PubMed] [Google Scholar]
- 47.Embree P. Ph.D. dissertation. Urbana, Ill.: University of Illinois; 1985. The accurate ultrasonic measurement of the volume flow of blood by time-domain correlation. [Google Scholar]
- 48.Kasai C, Namekawa K, Koyano A, Omoto R. Real-time two-dimensional blood flow imaging using an autocorrelation technique. IEEE Trans Ultrason Ferroelect Freq Contr. 1985;vol. SU-32(no. 3):458–464. [Google Scholar]
- 49.Loupas T, Powers J, Gill R. An axial velocity estimator for ultrasound blood flow imaging, based on a full evaluation of the doppler equation by means of a two-dimensional autocorrelation approach. IEEE Trans Ultrason Ferroelect Freq Contr. 1995;vol. 42(no. 4):672–688. [Google Scholar]
- 50.Pinton GF, Dahl JJ, Trahey GE. Rapid tracking of small displacements with ultrasound. IEEE Trans Ultrason Ferroelect Freq Contr. 2006;vol. 53(no. 6) doi: 10.1109/tuffc.2006.1642509. [DOI] [PubMed] [Google Scholar]
- 51.Walker WF, Trahey GE. A fundamental limit on delay estimation using partially correlated speckle signals. IEEE Trans Ultrason Ferroelect Freq Contr. 1995;vol. 42(no. 2):301–308. [Google Scholar]
- 52.Palmeri ML, McAleavey SA, Trahey GE, Nightingale KR. Ultrasonic tracking of acoustic radiation force-induced displacements in homogeneous media. IEEE Trans Ultrason Ferroelectr Freq Control. 2006 Jul;vol. 53(no. 7):1300–1313. doi: 10.1109/tuffc.2006.1665078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.McAleavey SA, Nightingale KR, Trahey GE. Estimates of echo correlation and measurement bias in acoustic radiation force impulse imaging. IEEE Trans Ultrason Ferroelect Freq Contr. 2003;vol. 50(no. 6):631–641. doi: 10.1109/tuffc.2003.1209550. [DOI] [PubMed] [Google Scholar]
- 54.Doherty JR, Dahl JJ, Trahey GE. A Harmonic Tracking Method for Acoustic Radiation Force Impulse (ARFI) Imaging. Proceedings of the IEEE Ultrasonics Symposium. 2012 [Google Scholar]
- 55.Sugimoto T, Ueha S, Itoh K. Tissue Hardness Measurement Using the Radiation Force of Focused Ultrasound. IEEE Trans Ultrason Symposium. 1990:1377–1380. [Google Scholar]
- 56.Mauldin FWJ, Viola F, Hamer TC, Ahmed EM, Crawford SB, Haverstick DM, Lawrence MB, Walker WF. Adaptive force sonorheometry for assessment of whole blood coagulation. Clin Chim Acta. 2010 May;vol. 411(no. 9–10):638–644. doi: 10.1016/j.cca.2010.01.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Nightingale KR. Acoustic radiation force impulse (ARFI) imaging: A review. Current Medical Imaging Review. 2011;vol. 7(no. 4):328–339. doi: 10.2174/157340511798038657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Fahey BJ, Nelson RC, Bradway DP, Hsu SJ, Dumont DM, Trahey GE. In vivo visualization of abdominal malignancies with acoustic radiation force elastography. Phys Med Biol. 2008;vol. 53:279–293. doi: 10.1088/0031-9155/53/1/020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Mauldin FW, Haider Ma, Loboa EG, Behler RH, Euliss LE, Pfeiler TW, Gallippi CM. Monitored steady-state excitation and recovery (MSSER) radiation force imaging using viscoelastic models. IEEE transactions on ultrasonics, ferroelectrics, and frequency control. 2008 Jul;vol. 55(no. 7):1597–1610. doi: 10.1109/TUFFC.2008.836. [DOI] [PubMed] [Google Scholar]
- 60.Dumont DM, Dahl JJ, Miller EM, Allen JD, Fahey B, Trahey GE. Lower-limb vascular imaging with acoustic radiation force elastography: demonstration of in vivo feasibility. IEEE Trans Ultrason Ferroelectr Freq Control. 2009 May;vol. 56(no. 5):931–944. doi: 10.1109/TUFFC.2009.1126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Behler RH, Nichols TC, Zhu H, Merricks EP, Gallippi CM. ARFI imaging for noninvasive material characterization of atherosclerosis. Part II: toward in vivo characterization. Ultrasound Med Biol. 2009;vol. 35(no. 2):278–295. doi: 10.1016/j.ultrasmedbio.2008.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Trahey GE, Palmeri ML, Bentley RC, Nightingale KR. Acoustic radiation force impulse imaging of the mechanical properties of arteries: in vivo and ex vivo results. Ultrasound Med Biol. 2004 Sep;vol. 30(no. 9):1163–1171. doi: 10.1016/j.ultrasmedbio.2004.07.022. [DOI] [PubMed] [Google Scholar]
- 63.Hsu SJ, Bouchard RR, Dumont DM, Wolf PD, Trahey GE. In vivo assessment of myocardial stiffness with acoustic radiation force impulse imaging. Ultrasound Med Biol. 2007 Nov;vol. 33(no. 11):1706–1719. doi: 10.1016/j.ultrasmedbio.2007.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Hsu SJ, Hubert JL, Smith SW, Trahey GE. Intracardiac echocardiography and acoustic radiation force impulse imaging of a dynamic ex vivo ovine heart model. Ultrasonic Imaging. 2008;vol. 30(no. 2):63–77. doi: 10.1177/016173460803000201. [DOI] [PubMed] [Google Scholar]
- 65.Eyerly SA, Hsu SJ, Agashe SH, Trahey GE, Li y, Wolf PD. An in vitro assessment of acoustic radiation force impulse imaging for visualizing cardiac radiofrequency ablation lesions. J Cardiovasc Electrophysiol. 2010;vol. 21(no. 5):557–563. doi: 10.1111/j.1540-8167.2009.01664.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Dahl JJ, Dumont DM, Allen JD, Miller EM, Trahey GE. Acoustic radiation force impulse imaging for noninvasive characterization of carotid artery atherosclerotic plaques: a feasibility study. Ultrasound Med Biol. 2009;vol. 35(no. 5):707–716. doi: 10.1016/j.ultrasmedbio.2008.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Doherty JR, Dumont DM, Trahey GE, Palmeri ML. Acoustic radiation force impulse imaging of vulnerable plaques: a finite element method parametric analysis. 2012 Nov; doi: 10.1016/j.jbiomech.2012.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Sharma AC, Soo MS, Trahey GE, Nightingale KR. Acoustic radiation force impulse imaging of in vivo breast masses. 2004 IEEE Ultrasonics Symposium. 2004;vol. 1:728–731. [Google Scholar]
- 69.Palmeri ML, Frinkley KD, Bentley RC, Ludwig K, Gottfried M, Nightingale KR. Acoustic radiation force impulse (ARFI) imaging of the gastrointestinal tract. Ultrasonic Imaging. 2005;vol. 27:75–88. doi: 10.1177/016173460502700202. [DOI] [PubMed] [Google Scholar]
- 70.Zhai L, Polascik TJ, Foo WC, Rosenzweig SJ, Palmeri ML, Madden J, Nightingale KR, Mouraviev V. Acoustic radiation force impulse imaging of human prostates ex vivo. Ultrasound Med Biol. 2010;vol. 36(no. 4):576–588. doi: 10.1016/j.ultrasmedbio.2009.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Zhai L, Polascik TJ, Foo WC, Rosenzweig SJ, Palmeri ML, Madden J, Nightingale KR, Mouraviev V. Acoustic radiation force impulse imaging of human prostates: initial in vivo demonstration. Ultrasound Med Biol. 2012;vol. 38(no. 4):50–61. doi: 10.1016/j.ultrasmedbio.2011.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Palmeri ML, Dahl JJ, MacLeod DB, Grant SA, Nightingale KR. On the feasibility of imaging peripheral nerves using acoustic radiation force impulse imaging. Ultrason Imaging. 2009 Jul;vol. 31(no. 3):172–182. doi: 10.1177/016173460903100303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Lazebnik RS. Tissue Strain Analytics Virtual Touch Tissue Imaging and Quantification Tissue Strain Analytics Virtual Touch Tissue Imaging and Quantification. Siemens Healthcare White Paper. 2008 [Google Scholar]
- 74.Cho SH, Lee JY, Han JK, Choi BI. Acoustic Radiation Force Impulse Elastography for the Evaluation of Focal Solid Hepatic Lesions: Preliminary Findings. Ultrasound in medicine biology. 2010;vol. 36(no. 2):202–208. doi: 10.1016/j.ultrasmedbio.2009.10.009. [DOI] [PubMed] [Google Scholar]
- 75.Shuang-Ming T, Ping Z, Ying Q, Li-Rong C, Ping Z, Rui-Zhen L. Usefulness of acoustic radiation force impulse imaging in the differential diagnosis of benign and malignant liver lesions. Academic radiology. 2011 Jul;vol. 18(no. 7):810–815. doi: 10.1016/j.acra.2011.01.026. [DOI] [PubMed] [Google Scholar]
- 76.D’Onofrio M, Gallotti A, Salvia R, Capelli P, Mucelli RP. Acoustic radiation force impulse (ARFI) ultrasound imaging of pancreatic cystic lesions. European journal of radiology. 2011;vol. 80(no. 2):241–244. doi: 10.1016/j.ejrad.2010.06.015. [DOI] [PubMed] [Google Scholar]
- 77.Gallotti A, D’Onofrio M, Pozzi Mucelli R. Acoustic Radiation Force Impulse (ARFI) technique in ultrasound with Virtual Touch tissue quantification of the upper abdomen. Radiol Med. 2010 Sep;vol. 115(no. 6):889–897. doi: 10.1007/s11547-010-0504-5. [DOI] [PubMed] [Google Scholar]
- 78.Bai M, Du L, Gu J, Li F, Jia X. Virtual touch tissue quantification using acoustic radiation force impulse technology: initial clinical experience with solid breast masses. J Ultrasound Med. 2012 Feb;vol. 31(no. 2):289–294. doi: 10.7863/jum.2012.31.2.289. [DOI] [PubMed] [Google Scholar]
- 79.Clevert D-A, Stock K, Klein B, Slotta-Huspenina J, Prantl L, Heemann U, Reiser M. Evaluation of Acoustic Radiation Force Impulse (ARFI) imaging and contrast-enhanced ultrasound in renal tumors of unknown etiology in comparison to histological findings. Clin Hemorheol Microcirc. 2009;vol. 43(no. 1–2):95–107. doi: 10.3233/CH-2009-1224. [DOI] [PubMed] [Google Scholar]
- 80.Piscaglia F, Salvatore V, Di Donato R, D’Onofrio M, Gualandi S, Gallotti A, Peri E, Borghi A, Conti F, Fattovich G, Sagrini E, Cucchetti A, Andreone P, Bolondi L. Accuracy of VirtualTouch Acoustic Radiation Force Impulse (ARFI) imaging for the diagnosis of cirrhosis during liver ultrasonography. Ultraschall in der Medizin (Stuttgart, Germany: 1980) 2011 Apr;vol. 32(no. 2):167–175. doi: 10.1055/s-0029-1245948. [DOI] [PubMed] [Google Scholar]
- 81.Nightingale KR, McAleavey SA, Trahey GE. Shear-wave generation using acoustic radiation force: in vivo and ex vivo results. Ultrasound Med Biol. 2003 Dec;vol. 29(no. 12):1714–1723. doi: 10.1016/j.ultrasmedbio.2003.08.008. [DOI] [PubMed] [Google Scholar]
- 82.Oliphant TE, Manduca A, Ehman RL, Greenleaf JF. Complex-valued stiffness reconstruction for magnetic resonance elastography by algebraic inversion of the differential equation. Magnetic Resonance in Medicine. 2001;vol. 45:299–310. doi: 10.1002/1522-2594(200102)45:2<299::aid-mrm1039>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- 83.McLaughlin J, Renzi D. Shear wave speed recovery in transient elastography and supersonic imaging using propagating fronts. Inverse Problems. 2006;vol. 22:681–706. [Google Scholar]
- 84.Wang MH, Palmeri ML, Rotemberg VM, Rouze NC, Nightingale KR. Improving the robustness of time-of-flight based shear wave speed reconstruction methods using RANSAC in human liver in vivo. Ultrasound Med Biol. 2010;vol. 36(no. 5):802–813. doi: 10.1016/j.ultrasmedbio.2010.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Rouze NC, Wang MH, Palmeri ML, Nightingale KR. Robust estimation of time-of-flight shear wave speed using a radon sum transformation. IEEE Trans Ultrason Ferroelect Freq Contr. 2010;vol. 57(no. 12):2662–2670. doi: 10.1109/TUFFC.2010.1740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Rouze NC, Wang MH, Palmeri ML, Nightingale KR. Parameters affecting the resolution and accuracy of 2d quantitative shear wave images. IEEE Trans Ultrason Ferroelect Freq Contr. 2012;vol. 59(no. 8):1729–1740. doi: 10.1109/TUFFC.2012.2377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Palmeri ML, Wang MH, Dahl JJ, Frinkley KD, Nightingale KR. Quantifying hepatic shear modulus in vivo using acoustic radiation force. Ultrasound Med Biol. 2008;vol. 34(no. 4):546–558. doi: 10.1016/j.ultrasmedbio.2007.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Palmeri ML, Wang MH, Rouze NC, Abdelmalek MF, Guy CD, Moser B, Diehl AM, Nightingale KR. Noninvasive evaluation of hepatic fibrosis using acoustic radiation force-based shear stiffness in patients with nonalcoholic fatty liver diesease. J Hepatol. 2011;vol. 55(no. 3):666–672. doi: 10.1016/j.jhep.2010.12.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Friedrich-Rust M, Wunder K, Kriener S, Sotoudeh F, Richter S, Bojunga J, Herrmann E, Poynard T, Dietrich CF, Vermehren J, Zeuzem S, Sarrazin C. Liver Fibrosis in Viral Hepatitis: Non-invasive Assessment with Acoustic Radiation Force Impulse Imaging versus Transient Elastography1. Radiology. 2009;vol. 252(no. 2):595–604. doi: 10.1148/radiol.2523081928. [DOI] [PubMed] [Google Scholar]
- 90.Goertz RS, Amann K, Heide R, Bernatik T, Neurath MF, Strobel D. An abdominal and thyroid status with Acoustic Radiation Force Impulse Elastometry–A feasibility study: Acoustic Radiation Force Impulse Elastometry of human organs. European journal of radiology. 2011;vol. 80(no. 3):e226–e230. doi: 10.1016/j.ejrad.2010.09.025. [DOI] [PubMed] [Google Scholar]
- 91.Haque M, Robinson C, Owen D, Yoshida EM, Harris A. Comparison of acoustic radiation force impulse imaging (ARFI) to liver biopsy histologic scores in the evaluation of chronic liver disease: A pilot study. Annals of Hepatology. 2010;vol. 9(no. 3):289–293. [PubMed] [Google Scholar]
- 92.Horster S, Mandel P, Zachoval R, Clevert DA. Comparing acoustic radiation force impulse imaging to transient elastography to assess liver stiffness in healthy volunteers with and without valsalva manoeuvre. Clinical Hemorheology and Microcirculation. 2010;vol. 46(no. 2–3):159–168. doi: 10.3233/CH-2010-1342. [DOI] [PubMed] [Google Scholar]
- 93.Lupsor M, Badea R, Stefanescu H, Sparchez Z, Branda H, Serban A, Maniu A. Performance of a new elastographic method (ARFI technology) compared to unidimensional transient elastography in the noninvasive assessment of chronic hepatitis C. Preliminary results. Journal of gastrointestinal and liver diseases JGLD. 2009;vol. 18(no. 3):303–310. [PubMed] [Google Scholar]
- 94.Fierbinteanu-Braticevici C, Andronescu D, Usvat R, Cretoiu D, Baicus C, Marinoschi G. Acoustic radiation force imaging sonoelastography for noninvasive staging of liver fibrosis. World J. Gastroenterol. 2009;vol. 15(no. 4):5525–5532. doi: 10.3748/wjg.15.5525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Tanter M, Bercoff J, Athanasiou A, Deffieux T, Gennisson J-L, Montaldo G, Muller M, Tardivon A, Fink M. Quantitative assessment of breast lesion viscoelasticity: initial clinical results using supersonic shear imaging. Ultrasound Med Biol. 2008 Sep;vol. 34(no. 9):1373–1386. doi: 10.1016/j.ultrasmedbio.2008.02.002. [DOI] [PubMed] [Google Scholar]
- 96.Muller M, Gennisson J-L, Deffieux T, Tanter M, Fink M. Quantitative viscoelasticity mapping of human liver using supersonic shear imaging: preliminary in vivo feasibility study. Ultrasound in medicine biology. 2009;vol. 35(no. 2):219–229. doi: 10.1016/j.ultrasmedbio.2008.08.018. [DOI] [PubMed] [Google Scholar]
- 97.Deffieux T, Gennisson JL, Tanter M, Fink M. Assessment of the mechanical properties of the muscoskeletal system using 2-D and 3-D very high frame rate ultrasound. IEEE Trans Ultrason Ferroelect Freq Contr. 2008;vol. 55(no. 10):2177–2190. doi: 10.1109/TUFFC.917. [DOI] [PubMed] [Google Scholar]
- 98.Bercoff J. Shearwave elastography. Supersonic Imagine White Paper. 2008 [Google Scholar]
- 99.Berg WA, Cosgrove DO, Dore CJ, Schafer FKW, Svensson WE, Hooley RJ, Ohlinger R, Mendelson EB, Balu-Maestro C, Locatelli M, Tourasse C, Cavanaugh BC, Juhan V, Stavros AT, Tardivon A, Gay J, Henry J-P, Cohen-Bacrie C. Shearwave elastography improves the specificity of breast US: the BE1 multinational study of 939 masses. Radiology. 2012 Feb;vol. 262(no. 2):435–449. doi: 10.1148/radiol.11110640. [DOI] [PubMed] [Google Scholar]
- 100.McAleavey SA, Collins E, Johanna K, Elegbe E, Menon M. Validation of SMURF estimation of shear modulus in hydrogels. Ultrasonic Imaging. 2009;vol. 31(no. 2):131–150. doi: 10.1177/016173460903100204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Urban MW. A Review of Vibro-acoustography and its Applications in Medicine. Current Medical Imaging Reviews. 2011;vol. 7(no. 4):350–359. doi: 10.2174/157340511798038648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Konofagou EE, Maleke C, Vappou J. Harmonic Motion Imaging (HMI) for Tumor Imaging and Treatment Monitoring. Current Medical Imaging Review. 2012;vol. 8(no. 1):16–26. doi: 10.2174/157340512799220616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Urban MW, Chen SG, Fatemi M. A Review of Shearwave Dispersion Ultrasound Vibrometry (SDUV) and its Applications. Current Medical Imaging Reviews. 2012;vol. 8(no. 1):27–36. doi: 10.2174/157340512799220625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Urban MW, Fatemi M, Greenleaf JF. Modulation of ultrasound to produce multifrequency radiation force. J. Acoust. Soc. Am. 2010;vol. 127(no. 3):1228–1238. doi: 10.1121/1.3294487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Urban MW, Chalek C, Kinnick RR, Kinter TM, Haider B, Greenleaf JF, Thomenius KE, Fatemi M. Implementation of Vibro-Acoustography on a clinical ultrasound system. IEEE Trans Ultrason Ferroelect Freq Contr. 2011;vol. 58(no. 6):1169–1181. doi: 10.1109/TUFFC.2011.1927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Pislaru C, Kantor BK, Kinnick RR, Anderson JL, Aubry MC, Urban MW, Fatemi M, Greenleaf JF. In vivo Vibroacoustography of large peripheral arteries. Invest Radiol. 2008;vol. 43(no. 4):243–252. doi: 10.1097/RLI.0b013e31816085fc. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Fatemi M, Wold LE, Greenleaf JF. Vibro-Acoustic tissue mammography. IEEE Trans Med Imaging. 2002;vol. 21(no. 1):1–8. doi: 10.1109/42.981229. [DOI] [PubMed] [Google Scholar]
- 108.Mitri FG, Davis BJ, Alizad A, Greenleaf JF, Wilson TM, Mynderse LA, Fatemi M. Prostate cryotherapy monitoring using vibroacoustography: preliminary results of an ex vivo study and technical feasibility. IEEE Trans Biomed Egr. 2008 Nov;vol. 55(no. 11):2584–2592. doi: 10.1109/TBME.2008.2001284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Maleke C, Konofagou EE. Harmonic motion imaging for focused ultrasound (HMIFU): a fully integrated technique for sonification and monitoring of thermal ablation in tissues. Phys Med Biol. 2008 Mar;vol. 53(no. 6):1773–1793. doi: 10.1088/0031-9155/53/6/018. [DOI] [PubMed] [Google Scholar]
- 110.Chen S, Urban MW, Pislaru C, Kinnick R, Zheng Y, Yao A, Greenleaf JF. Shearwave dispersion ultrasound vibrometry (SDUV) for measuring tissue elasticity and viscosity. IEEE Trans Ultrason Ferroelectr Freq Control. 2009 Jan;vol. 56(no. 1):55–62. doi: 10.1109/TUFFC.2009.1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Amador C, Urban MW, Chen S, Greenleaf JF. Loss tangent and complex modulus estimated by acoustic radiation force creep and shear wave dispersion. Physics in medicine and biology. 2012 Mar;vol. 57(no. 5):1263–82. doi: 10.1088/0031-9155/57/5/1263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Zhang X, Kinnick RR, Fatemi M, Greenleaf JF. Noninvasive method for estimation of complex elastic modulus of arterial vessels. IEEE Trans Ultrason Ferroelect Freq Contr. 2005;vol. 52(no. 4):642–652. doi: 10.1109/tuffc.2005.1428047. [DOI] [PubMed] [Google Scholar]
- 113.Bernal M, Nenadic I, Urban MW, Greenleaf JF. Material property estimation for tubes and arteries using ultrasound radiation force and analysis of propagating modes. The Journal of the Acoustical Society of America. 2011 Mar;vol. 129(no. 3):1344–1354. doi: 10.1121/1.3533735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Amador C, Urban W, Greenleaf JF. Shearwave Dispersion Ultrasound Vibrometry (SDUV) on Swine Kidney. IEEE Trans Ultrason Ferroelect Freq Contr. 2011;vol. 58(no. 12):2608–2619. doi: 10.1109/TUFFC.2011.2124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Mitri FG, Urban MW, Fatemi M, Greenleaf JF. Shear wave dispersion ultrasonic vibrometry for measuring prostate shear stiffness and viscosity: an in vitro pilot study. IEEE transactions on bio-medical engineering. 2011 Feb;vol. 58(no. 2):235–242. doi: 10.1109/TBME.2010.2053928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Hazard C, Hah Z, Rubens D, Parker K. Integration of crawling waves in an ultrasound imaging system. Part 1: system and design considerations. Ultrasound in medicine & biology. 2012 Feb;vol. 38(no. 2):296–311. doi: 10.1016/j.ultrasmedbio.2011.10.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Hah Z, Hazard C, Mills B, Barry C, Rubens D, Parker K. Integration of crawling waves in an ultrasound imaging system. Part 2: signal processing and applications. Ultrasound in medicine & biology. 2012 Feb;vol. 38(no. 2):312–323. doi: 10.1016/j.ultrasmedbio.2011.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.An L, Mills B, Hah Z, Mao S, Yao J, Joseph J, Rubens DJ, Strang J, Parker KJ. Crawling wave detection of prostate cancer: preliminary in vitro results. Med Phys. 2011;vol. 38(no. 5):2563–2571. doi: 10.1118/1.3569578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Sandrin L, Fourquet B, Hasquenoph J-M, Yon S, Fournier C, Mal F, Christidis C, Ziol M, Poulet B, Kazemi F, Beaugrand M, Palau R. Transient elastography: a new noninvasive method for assessment of hepatic fibrosis. Ultrasound in Medicine & Biology. 2003 Dec;vol. 29(no. 12):1705–1713. doi: 10.1016/j.ultrasmedbio.2003.07.001. [DOI] [PubMed] [Google Scholar]
- 120.Myers RP, Pomier-Layrargues G, Kirsch R, Pollett A, Beaton M, Levstik M, Duarte-Rojo A, Wong D, Crotty P, Elkashab M. Feasibility and diagnostic performance of the FibroScan XL probe for liver stiffness measurement in overweight and obese patients. Journal of Hepatology. 2012;vol. 56(no. 3):564–570. doi: 10.1002/hep.24624. [DOI] [PubMed] [Google Scholar]
- 121.Sporea I. In: Hepatic Elastography Using Ultrasound Waves. Sporea I, Sirli R, editors. Bentham Books; 2012. [Google Scholar]
- 122.Ling W, Lu Q, Quan J, Ma L, Luo Y. Assessment of impact factors on shear wave based liver stiffness measurement. European journal of radiology. 2012 Oct;:1–7. doi: 10.1016/j.ejrad.2012.10.004. [DOI] [PubMed] [Google Scholar]
- 123.Myers RP, Crotty P, Pomier-Layrargues G, Ma M, Urbanski SJ, Elkashab M. Prevalence, risk factors and causes of discordance in fibrosis staging by transient elastography and liver biopsy. Liver Int. 2010 doi: 10.1111/j.1478-3231.2010.02331.x. [DOI] [PubMed] [Google Scholar]
- 124.Rigamonti C, Fraquelli M, Bastiampillai AJ, Caccamo L, Reggiani P, Rossi G, Colombo M, Donato MF. Transient elastography identifies liver recipients with “non-viral” graft disease after transplantation: A guidance for liver biopsy. Liver transplantation : official publication of the American Association for the Study of Liver Diseases and the International Liver Transplantation Society. 2012 doi: 10.1002/lt.23391. [DOI] [PubMed] [Google Scholar]
- 125.Sporea I, Sirli RL, Deleanu A, Popescu A, Focsa M, Danila M, Tudora A. Acoustic Radiation Force Impulse Elastography as Compared to Transient Elastography and Liver Biopsy in Patients with Chronic Hepatopathies. Ultraschall in der Medizin. 2010;vol. 32(Suppl 1):S46–S52. doi: 10.1055/s-0029-1245360. [DOI] [PubMed] [Google Scholar]
- 126.Sebastiani G, Alberti A. How far is noninvasive assessment of liver fibrosis from replacing liver biopsy in hepatitis C? Journal of viral hepatitis. 2012 Jan;vol. 19(Suppl 1):18–32. doi: 10.1111/j.1365-2893.2011.01518.x. [DOI] [PubMed] [Google Scholar]
- 127.Wong GL, Wong VW, Choi PC, Chan AW, Chum RH, Chan HK, Lau KK, Chim AM, Yiu KK, Chan FK, Sung JJ, Chan HL. Assessment of fibrosis by transient elastography compared with liver biopsy and morphometry in chronic liver diseases. Clin Gastroenterol Hepatol. 2008;vol. 6(no. 9):1027–1035. doi: 10.1016/j.cgh.2008.02.038. [DOI] [PubMed] [Google Scholar]
- 128.Gomez-Dominguez E, Mendoza J, Rubio S, Moreno-Monteagudo JA, Garcia-Buey L, Moreno-Otero R. Transient elastography: a valid alternative to biopsy in patients with chronic liver disease. Alimentary Pharmacology and Therapeutics. 2006;vol. 24(no. 3):513–518. doi: 10.1111/j.1365-2036.2006.02999.x. [DOI] [PubMed] [Google Scholar]
- 129.Chang PE, Lui HF, Chau YP, Lim KH, Yap WM, Tan CK, Chow WC. Prospective evaluation of transient elastography for the diagnosis of hepatic fibrosis in Asians: comparison with liver biopsy and aspartate transaminase platelet ratio index. Alimentary Pharmacology and Therapeutics. 2008;vol. 28(no. 1):51–61. doi: 10.1111/j.1365-2036.2008.03711.x. [DOI] [PubMed] [Google Scholar]
- 130.Stanciu C, Trifan A, Cojocariu C. Transient elastography–an alternative to liver biopsy in patients with chronic hepatitis C? Rev Med Chir Soc Med Nat Iasi. 2006;vol. 110(no. 4):765–770. [PubMed] [Google Scholar]
- 131.Masuzaki R, Tateishi R, Yoshida H, Goto E, Sato T, Ohki T, Goto T, Kanai F, Sugioka Y, Ikeda H, Shiina S, Kawabe T, Omata M. Comparison of liver biopsy and transient elastography based on clinical relevance. Canadian Journal of Gastroenterology. 2008;vol. 22(no. 9):753–757. doi: 10.1155/2008/306726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Castera L, Vergniol J, Foucher J, Le Bail B, Chanteloup E, Haaser M, Darriet M, Couzigou P, De Ledinghen V. Prospective comparison of transient elastography, Fibrotest, APRI, and liver biopsy for the assessment of fibrosis in chronic hepatitis C. Gastroenterology. 2005;vol. 128(no. 2):343–350. doi: 10.1053/j.gastro.2004.11.018. [DOI] [PubMed] [Google Scholar]
- 133.Sanchez-Conde M, Montes-Ramirez ML, Miralles P, Alvarez JM, Bellon JM, Ramirez M, Arribas JR, Gutierrez I, Lopez JC, Cosin J, Alvarez E, Gonzalez J, Berenguer J. Comparison of transient elastography and liver biopsy for the assessment of liver fibrosis in HIV/hepatitis C virus-coinfected patients and correlation with noninvasive serum markers. Journal of Viral Hepatitis. 2010;vol. 17(no. 4):280–286. doi: 10.1111/j.1365-2893.2009.01180.x. [DOI] [PubMed] [Google Scholar]
- 134.Sporea I, Sirli R, Deleanu A, Tudora A, Curescu M, Cornianu M, Lazar D. Comparison of the liver stiffness measurement by transient elastography with the liver biopsy. World J Gastroenterol. 2008;vol. 14(no. 42):6513–6517. doi: 10.3748/wjg.14.6513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Miailhes P, Pradat P, Chevallier M, Lacombe K, Bailly F, Cotte L, Trabaud MA, Boibieux A, Bottero J, Trepo C, Zoulim F. Proficiency of transient elastography compared to liver biopsy for the assessment of fibrosis in HIV/HBV-coinfected patients. Journal of Viral Hepatitis. 2010 doi: 10.1111/j.1365-2893.2010.01275.x. [DOI] [PubMed] [Google Scholar]
- 136.Calvaruso V, Camma C, Di Marco V, Maimone S, Bronte F, Enea M, Dardanoni V, Manousou P, Pleguezuelo M, Xirouchakis E, Attanasio M, Dusheiko G, Burroughs AK, Craxi A. Fibrosis staging in chronic hepatitis C: analysis of discordance between transient elastography and liver biopsy. Journal of Viral Hepatitis. 2010;vol. 17(no. 7):469–474. doi: 10.1111/j.1365-2893.2009.01199.x. [DOI] [PubMed] [Google Scholar]
- 137.Coco B, Oliveri F, Maina AM, Ciccorossi P, Sacco R, Colombatto P, Bonino F, Brunetto MR. Transient elastography: a new surrogate marker of liver fibrosis influenced by major changes of transaminases. Journal of Viral Hepatitis. 2007;vol. 14(no. 5):360–369. doi: 10.1111/j.1365-2893.2006.00811.x. [DOI] [PubMed] [Google Scholar]
- 138.Sporea I, Sirli R, Deleanu A, Popescu A, Cornianu M. Liver stiffness measurement by transient elastography in clinical practice. J Gastrointestin Liver Dis. 2008;vol. 17(no. 4):395–399. [PubMed] [Google Scholar]
- 139.Takahashi H, Ono N, Eguchi Y, Eguchi T, Kitajima Y, Kawaguchi Y, Nakashita S, Ozaki I, Mizuta T, Toda S, Kudo S, Miyoshi A, Miyazaki K, Fujimoto K. Evaluation of acoustic radiation force impulse elastography for fibrosis staging of chronic liver disease: a pilot study. Liver international : official journal of the International Association for the Study of the Liver. 2010;vol. 30(no. 4):538–545. doi: 10.1111/j.1478-3231.2009.02130.x. [DOI] [PubMed] [Google Scholar]
- 140.Corradi F, Piscaglia F, Flori S, D’Errico-Grigioni A, Vasuri F, Tame MR, Andreone P, Boni P, Gianstefani A, Bolondi L. Assessment of liver fibrosis in transplant recipients with recurrent HCV infection: usefulness of transient elastography. Dig Liver Dis. 2009;vol. 41(no. 3):217–225. doi: 10.1016/j.dld.2008.06.009. [DOI] [PubMed] [Google Scholar]
- 141.Stasi C, Arena U, Vizzutti F, Zignego AL, Monti M, Laffi G, Corti G, Pinzani M. Transient elastography for the assessment of liver fibrosis in patients with chronic viral hepatitis: the missing tool? Dig Liver Dis. 2009;vol. 41(no. 12):863–866. doi: 10.1016/j.dld.2009.04.002. [DOI] [PubMed] [Google Scholar]
- 142.Adebajo CO, Talwalkar JA, Poterucha JJ, Kim WR, Charlton MR. Ultrasound-based transient elastography for the detection of hepatic fibrosis in patients with recurrent hepatitis C virus after liver transplantation: A systematic review and meta-analysis. Liver transplantation : official publication of the American Association for the Study of Liver Diseases and the International Liver Transplantation Society. 2012;vol. 18(no. 3):323–331. doi: 10.1002/lt.22460. [DOI] [PubMed] [Google Scholar]
- 143.Rifai K, Cornberg J, Mederacke I, Bahr MJ, Wedemeyer H, Malinski P, Bantel H, Boozari B, Potthoff A, Manns MP, Gebel M. Clinical feasibility of liver elastography by acoustic radiation force impulse imaging (ARFI) Digestive and liver disease : official journal of the Italian Society of Gastroenterology and the Italian Association for the Study of the Liver. 2011 Jun;vol. 43(no. 6):491–497. doi: 10.1016/j.dld.2011.02.011. [DOI] [PubMed] [Google Scholar]
- 144.Quantitative Imaging Biomarkers Alliance (QIBA) Ultrasound Shear Wave Speed Technical Committee [Google Scholar]
- 145.Deffieux T, Gennisson J-L, Bercoff J, Tanter M. On the effects of reflected waves in transient shear wave elastography. IEEE transactions on ultrasonics, ferroelectrics, and frequency control. 2011 Oct;vol. 58(no. 10):2032–2035. doi: 10.1109/TUFFC.2011.2052. [DOI] [PubMed] [Google Scholar]
- 146.O’Brien WD. Ultrasound-biophysics mechanisms. Progress in biophysics and molecular biology. 2007;vol. 93(no. 1–3):212–255. doi: 10.1016/j.pbiomolbio.2006.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 147.Duck FA. Medical and non-medical protection standards for ultrasound and infrasound. Progress in biophysics and molecular biology. 2007;vol. 93:176–191. doi: 10.1016/j.pbiomolbio.2006.07.008. [DOI] [PubMed] [Google Scholar]
- 148.Fowlkes JB, Committee AB. American Institue of Ultrasound in Medicine Consensus Report on Potential Bioeffects of Diagnostic Ultrasound. J Ultrasound Med. 2008;vol. 27:503–515. doi: 10.7863/jum.2008.27.4.503. [DOI] [PubMed] [Google Scholar]
- 149.Palmeri ML, Nightingale KR. On the thermal effects associated with radiation force imaging of soft tissue. IEEE Trans Ultrason Ferroelect Freq Contr. 2004;vol. 51(no. 5):551–565. [PubMed] [Google Scholar]
- 150.Standard IECS. Particular requirements for the safety of ultrasonic medical diagnostic and monitoring equipment. Geneva, Switzerland: International Electrotechnical Committee; 2011. vol. Tech. Rep. [Google Scholar]
- 151.Dhanaliwala A, Hossack J, Mauldin F. Assessing and improving acoustic radiation force image quality using a 1.5-D transducer design. IEEE transactions on ultrasonics, ferroelectrics, and frequency control. 2012 Jul;vol. 59(no. 7):1602–1608. doi: 10.1109/TUFFC.2012.2360. [DOI] [PMC free article] [PubMed] [Google Scholar]