Abstract
Fluorescence tomography (FT) reconstructs the three-dimensional (3D) fluorescent reporter probe distribution inside biological tissue. These probes target molecules of biological function, e.g. cell surface receptors or enzymes, and emit fluorescence light upon illumination with an external light source. The fluorescence light is detected on the tissue surface and a source reconstruction algorithm based on the simplified spherical harmonics (SPN) equations calculates the unknown 3D probe distribution inside tissue. While current FT approaches require multiple external sources at a defined wavelength range, the proposed FT method uses only a white light source with tunable wavelength selection for fluorescence stimulation and further exploits the spectral dependence of tissue absorption for the purpose of 3D tomographic reconstruction. We will show the feasibility of the proposed hyperspectral excitation-resolved fluorescence tomography method with experimental data. In addition, we will demonstrate the performance and limitations of such a method under ideal and controlled conditions by means of a digital mouse model and synthetic measurement data. Moreover, we will address issues regarding the required amount of wavelength intervals for fluorescent source reconstruction. We will explore the impact of assumed spatially uniform and nonuniform optical parameter maps on the accuracy of the fluorescence source reconstruction. Last, we propose a spectral re-scaling method for overcoming the observed limitations in reconstructing accurate source distributions in optically non-uniform tissue when assuming only uniform optical property maps for the source reconstruction process.
1. Introduction
In vivo fluorescence molecular imaging reports on biological processes and functions on a cellular level by using light emitting probes (Frangioni 2003, Graves et al 2004, Rao et al 2007, Ntziachristos 2006). These reporter probes utilize a fluorophore that is targeted to a specific molecular indicator of interest studied in biological tissue. Many of the fluorescent reporter probes, including nanoparticles and quantum dots (Qdots), are currently used in pre-clinical imaging of small animal models of human disease (Gao et al 2004, Cai and Chen 2008, Michalet et al 2008, Smith et al 2008, Biju et al 2008, Debagge and Jaschke 2008). Here, the probes are administered to a small animal and fluorescence images are taken with an optical camera at the tissue surface upon illumination with an external light source. Due to strong light scattering in biological tissue, the two-dimensional (2D) surface images do not clearly reveal the three-dimensional (3D) location and emission strength of the imaged reporter probe. Thus, quantitative assessment of 3D reporter probe distributions in tissue is limited.
Therefore, fluorescence tomography (FT) has been developed in order to overcome the limitations of 2D imaging (Li et al 1996, O’Leary et al 1996, Chang et al 1997, Paithankar et al 1997, Hattery et al 2001, Ntziachristos and Weissleder 2001, Eppstein et al 2002, Lee and Sevick-Muraca 2002, Godavarty et al 2003, Graves et al 2003, Klose and Hielscher 2003, Milstein et al 2003, Thompson et al 2003, Hall et al 2004, Schulz et al 2004, 2006, Bloch et al 2005, Godavarty et al 2005, Klose et al 2005, Kumar et al 2005, 2006, 2008, Patwardhan et al 2005, Soubret et al 2005, 2006, Zacharakis et al 2005, Joshi et al 2006, Roy et al 2006, Corlu et al 2007, Deliolanis et al 2007, Herve et al 2007, Montet et al 2007, Roy et al 2007, Soloviev et al 2007, Panasyuk et al 2008, Zacharopoulos et al 2009, Dutta et al 2010, Venugopal et al 2010). FT utilizes computational methods, similar to emission tomography in nuclear medicine, that calculate the 3D probe concentration distributions inside tissue from a set of fluorescence surface images. Probing the tissue surface with light at different locations rs yields a spatially varying excitation field or photon flux Φx(r, rs) for fluorescence stimulation at location r inside the tissue. Hence, the measured fluorescence images provide linearly independent boundary datasets, which are utilized for tomographic reconstruction. Figure 1(a) shows a schematic of FT.
Figure 1.
(a) FT with source multiplexing: a fluorescence image is taken for each source position (rs). (b) HEFT with hyperspectral excitation: a fluorescence image is taken for each spectral band (λl). (A) Light source; (B) switch for source multiplexing (e.g. optical mirror); (C) source location rs on tissue surface (e.g. narrow laser beam or optical fiber tip); (D) wavelength-selective filter; (E) macro-illumination at specified wavelength λl; (F) tissue with fluorescent source at location r; (G) fluorescence emission filter, and (H) optical detector (e.g. CCD camera).
While current FT requires relatively complex imaging instrumentation with source–detector multiplexing for the purpose of tomographic reconstruction, e.g. (Graves et al 2003, Schulz et al 2006, Herve et al 2007, Roy et al 2007, Kumar et al 2008, Panasyuk et al 2008), the proposed method offers a different and less cumbersome approach to how tomography could be performed. Hyperspectral excitation-resolved fluorescence tomography (HEFT) uses only a single light source and, instead, exploits the spectral properties of tissue (oxy-)hemoglobin for fluorescence source reconstruction (Klose 2009a). HEFT uses a wavelength-dependent excitation field Φx(r, λ) for fluorescence stimulation, which generates linearly independent boundary data, i.e. 2D surface images, at the fluorescence wavelength for tomographic reconstruction. Because partially overlapping wavelength intervals or spectral bands for fluorescence stimulation are allowed (i.e. hyperspectral excitation), large sets of fluorescence boundary data (2D fluorescence images) can be taken despite the relatively narrow emission band of a fluorescence source. Furthermore, a white light source with macro-illumination instead of a point-like source, e.g. a focused laser beam, could be used for fluorescence stimulation. In fact, HEFT facilitates the imaging process in so far that no moving parts or optical switches for source–detector multiplexing are required. Figure 1(b) shows a schematic of HEFT.
The concept of using spectrally-resolved boundary measurements, instead of spectrally-resolved excitation, for reconstruction of spatial source distributions has already been applied in ocean optics and in bioluminescence tomography (BLT). Both applications do not use an excitation source for light emission stimulation, and thus no excitation field Φx for fluorescence stimulation is present. Instead, luminescence images are taken for different wavelength intervals pertaining to the emission spectrum of the unknown source distribution. In ocean and natural water optics, the estimation of bioluminescent sources from light-emitting marine organisms is performed with multispectral remote sensing of light escaping through the water surface (Chalhoub and de Campos Velho 2003). In BLT, multispectral images of a spectrally broad emitting luciferase reporter source are taken on the tissue surface for the purpose of 3D image reconstruction (Chaudhari et al 2005, Alexandrakis et al 2005, Dehghani et al 2006, Kuo et al 2007, Lv et al 2007, Lu et al 2009, Klose et al 2010).
Ideas about excitation-resolved FT have already been communicated (Klose 2009a, Chaudhari et al 2009) but have not experimentally been confirmed. Chaudhari et al (2009) compared different multispectral imaging approaches, including excitation and emission resolved, and discussed the performance of each modality and the combination thereof for image reconstruction. Based on a singular-value decomposition (SVD) study, they also pointed out that excitation-resolved FT leads to more accurate image reconstructions than FT with multispectral emission detection.
Klose (2009a) has shown in a simulation study the feasibility of excitation-resolved FT of Qdots. The extinction spectrum of Qdots extends over several hundreds of nanometers and overlaps with that part of the hemoglobin absorption spectrum between 560 and 660 nm that shows large changes in its extinction coefficient. Moreover, Qdots are characterized not only by favorable broad extinction spectra but also by relatively narrow emission spectra extending far into the near-infrared (NIR). This might have a few advantages for pre-clinical imaging of small animals. First, NIR-emitting Qdots could facilitate deep tissue imaging because only little light absorption and tissue auto-fluorescence are present in that spectral region. Second, the spectral distance between the excitation and emission wavelengths of Qdots is not limited to the relatively small Stokes shift of organic dyes. Therefore, imaging of Qdots provides a relatively easy means for spectral separation of fluorescence from ambient light.
Based on previous simulation studies (Klose 2009a), this paper demonstrates on numerical and experimental examples that the 3D spatial distribution of fluorescence sources inside tissue can be reconstructed from spectrally varying illumination alone. First, we will develop a HEFT reconstruction algorithm based on the simplified spherical harmonics (SPN) equations for curved tissue geometries. Second, we will show with experimental data that the spatial location of fluorescent Qdot sources in tissue can be reconstructed by means of spectrally resolved fluorescence stimulation. Next, we will perform HEFT simulations on a digital mouse model and will demonstrate the feasibility of HEFT for pre-clinical imaging of small animal models of human disease. We will evaluate the source reconstruction performance in optically nonuniform media by assuming either uniform or nonuniform optical tissue parameter distributions. Furthermore, we will study the impact of boundary measurement re-scaling on the outcome of image reconstruction results. Last, we will compare single and multi-view macro-illumination geometries with respect to improvement in source reconstructions.
2. Theory and method
FT consists of two main components: (i) imaging instrumentation, including a light source for fluorescence stimulation and an optical detector, and (ii) an image reconstruction algorithm. Hereby, a light source illuminates the tissue surface at location rs while stimulating optical probes at location r for light emission. These fluorescence sources are optically defined by their quantum yield, η, and extinction coefficient, ε. Furthermore, the target-specific probe uptake directly relates to the fluorophore concentration c. Following excitation, the partial current of fluorescence light is measured at the detector positions rd on the tissue surface. The excitation and the fluorescence light is strongly scattered and partially absorbed in tissue; and the optical tissue properties are defined by their absorption, μa, scattering, μs, and anisotropy, g, coefficient. Once the fluorescence boundary data have been measured, the 3D fluorophore concentration distribution is calculated with an image reconstruction algorithm, which employs a light propagation model F (Klose 2009b). F establishes a functional relationship between the fluorescence boundary current, J+(rd), and the emission strength or power density, Φx(r, rs)ηεc(r), of the fluorophore:
| (1) |
The excitation field Φx(r, rs) inside tissue at location r is a direct function of the excitation source at the surface location rs. Thus, the current J+ becomes a function of the excitation source location rs as well. The unknown boundary current can directly be calculated by means of F for a given excitation source and fluorophore distribution. Vice versa, the unknown fluorophore distribution could be calculated by means of F−1 for a given excitation source and boundary measurements Y, which represent the noise-corrupted J+(rd) or fluorescence surface images.
Instead of using multiple source positions for the purpose of tomographic source reconstruction, HEFT exploits the spectral properties of blood hemoglobin and transforms the collected fluorescence boundary measurements into 3D spatial information about the fluorophore concentration distribution inside tissue. It uses a white light source with a wavelength-tunable bandpass filter that emits light in partially overlapping or non-overlapping spectral bands centered at λl. Its photon flux φx inside tissue excites fluorophores for fluorescence stimulation. The emitted fluorescence light is collected by a camera on the tissue surface. Since partially overlapping spectral bands for fluorescence stimulation are allowed (i.e. hyperspectral excitation), large sets of fluorescence images can be taken each pertaining to a single spectral excitation band. Preferably, excitation wavelengths are chosen to be within the bounds of maximum variability of the (oxy-)hemoglobin extinction coefficient (i.e. 580–660 nm) (figure 2).
Figure 2.
Extinction spectrum of (oxy-)hemoglobin (Prahl 1999).
Using the light propagation model F, we obtain the partial boundary current of fluorescence light
| (2) |
as a function of the wavelength-dependent excitation field Φx(r, λ) inside tissue. Therefore, a set of fluorescence images taken at different spectral bands of the excitation light encodes for the spatial location r of the fluorescence source, and the nonlinearity between the boundary data and the excitation field can be used for tomographic reconstruction of c.
In comparison to current FT methods with J+(rd, rs) of different source–detector pairs (s, d), the partial current of HEFT, J+(rd, λ), is given by different pairs (d, λ) of detector positions and wavelengths. That strictly simplifies the measurement process because no multiple point-like sources are required at the tissue surface, but instead a single light source with uniform macro-illumination can be employed.
2.1. SP3 light propagation model
In general, F can be given by a high-order approximation, such as the discrete-ordinates (SN) (Case and Zweifel 1967), spherical harmonics (PN) (Case and Zweifel 1967), or simplified spherical harmonics (SPN) (Klose 2009b, Klose and Larsen 2006) approximation to the radiative transfer equation (RTE). At wavelengths of visible light, where light attenuation by (oxy-)hemoglobin in tissue becomes significant, imaging is performed far from the diffusion limit (i.e. ) (Case and Zweifel 1967). In addition, fluorophore distributions in the boundary proximity might lead to small source–detector separations. Thus, low-order approximations to the RTE, such as the diffusion equation, will have limitations for accurate prediction of the boundary current J+ (Klose and Larsen 2006, Hielscher et al 1998, Aydin et al 2002). Moreover, HEFT requires the solutions of F for multiple excitation wavelengths and for large sets of boundary data. Therefore, computationally expensive methods, including the SN and PN methods, lead to long processing times. Therefore, we need to pick a light propagation model that is more accurate than the diffusion model and computationally less expensive than full transport methods.
Solutions to the SPN equations have shown to be more accurate than the diffusion approximation for tissue with absorption coefficients larger than 1 cm−1 and, moreover, are significantly faster to obtain than SN and PN solutions (Klose and Larsen 2006). Therefore, SPN methods offer both relative accuracy and processing speed, and are most suitable for spectral imaging in strongly absorbing tissues. We solve the SPN equations of third order (SP3) for obtaining (i) the excitation field Φx(r, λl) at different wavelengths λl and (ii) the partial boundary current J+ of the fluorescence light.
The SP3 equations for fluorescence stimulation are given for the moments and with
| (3) |
The partial-reflective boundary conditions are given with
| (4) |
| (5) |
Here, S(λl, Ω) depicts an external light source that emits photons with energies within the wavelength interval Δλ centered at λl. The wavelength intervals of different λl can be partially overlapping and, hence, attribute to the term hyperspectral in HEFT. The source uniformly illuminates along Ω the tissue boundary with surface normal n. The optical parameters are wavelength dependent as well and need to be chosen accordingly. Last, the excitation field Φx(r, λl) is given by
| (6) |
Once the excitation field has been calculated, we will solve the SP3 equations for the fluorescence light originating from light emitting fluorophores:
| (7) |
The partial-reflective boundary conditions for fluorescence light are given with
| (8) |
| (9) |
Finally, the partial current of fluorescence light J+ at the boundary with surface normal n is obtained from and :
| (10) |
| (11) |
| (12) |
The coefficients A1, … , D1, … , A2, … , D2, the reflection moments R1, R2, R3, R4 and the absorption moments μa1, μa2 and μa3 can be found in Klose and Larsen (2006).
2.2. Blocking-off finite difference method for curved geometries
The blocking-off or blocked-off region method is a finite-difference (FD) technique for solving radiative transfer problems in media with curved geometries while using regular or structured Cartesian grids (Patankar 1980, Chai et al 1993, 1994, Byun et al 2003, Talukdar 2005, 2006, Klose et al 2010). We have implemented such blocking-off FD method for solving the SP3 and boundary equations for tissue models with curved surfaces such as small animals. FD methods on structured or regular grids have a few advantages as compared to methods on unstructured or irregular grids. For example, structured grid calculations are more computationally efficient and take less time than unstructured grid calculations. Neighboring grid points of structured grids are simply found by adding or subtracting 1 from grid point indices in a 3D data array. Thus, data storage and accessibility of neighboring grid points is relatively fast. Unstructured grids, however, require storage of cell-to-cell pointers in a one-dimensional data array, which provides a list of the connectivity between neighboring cells, leading to more storage and slower code execution.
Using the blocking-off method, the physical domain of the tissue is represented by a so-called nominal domain that is divided into two regions. First, the active region is part of the physical domain where the solution of the SP3 equations is sought. Second, the inactive region lies outside the physical boundary. The active region is generated by identifying all grid points that are enclosed by the physical boundary. Hence, the tissue boundary is approximated by grid points of the active region closest to the physical tissue boundary. The SP3 equations are solved for the moments ϕ1 and ϕ2 on the interior grid points of the active region, whereas the boundary equations are solved on the boundary grid points of the active region approximating the curved tissue geometry. For example, figure 3 shows the boundary grid points of a small animal model, which will be used in our numerical study.
Figure 3.
Boundary points of the active region that represent the curved surface of a mouse model. The SP3 equations are solved on the interior grid points (not shown) of the active region, whereas the boundary equations are solved on the surface points (shown).
2.3. Spectral re-scaling of measurement data
According to equation (2), the optical tissue parameters have a direct impact on the numerical calculation of the partial boundary current. Given only a uniform tissue without anatomical structure, the spectrally dependent absorption coefficients, μa(λ) = c · ε(λ), could easily be derived from the extinction spectrum and concentration of (oxy-)hemoglobin. A nonuniform tissue model with anatomical structure, however, also requires the spatial distribution of its optical parameters for accurately solving the light propagation model. Such anatomical information could, for instance, be obtained from computed tomography (CT) or magnetic resonance imaging (MRI) co-registration, or from an anatomical atlas. In the simplest case, however, such additional information is not available, and thus only a uniform tissue model can be assumed for calculating the boundary current. As a consequence, such simplification may directly impact the tomographic source reconstruction.
Therefore, we devised a spectral re-scaling method that partially corrects for the mismatch in the boundary current when a uniform tissue model is used for light propagation simulation in the presence of an optically nonuniform tissue. The proposed re-scaling method for the measured fluorescence data is a means for partially circumventing the need for accurate anatomical co-registration leading to nonuniform optical property maps. Hereby, the influences on the source reconstruction performance due to a mismatch of the assumed uniform optical parameter distribution for the reconstruction process to the actual nonuniform optical parameter distribution of the small animal can be reduced by referencing the boundary measurements at the emission wavelength λm to boundary measurements at a reference wavelength λr. Thus, the actual emission measurements Y+(rd, λl) obtained at the detector point rd and excitation wavelength λl are re-scaled by the calibration factor J+(rd, λr)/Y+(rd, λr), which is obtained for the reference wavelength λr. The reference wavelength was chosen to be the fluorescence emission wavelength. J+(rd, λr) are the numerical solutions of the boundary current for a uniform tissue model. Y+(rd, λr) are the actual in vivo measurements of the partial boundary current for the small animal. Thus, the re-scaled boundary measurements , which will be used for tomographic reconstruction, are given by the relation
| (13) |
Data re-scaling with respect to a single excitation wavelength, instead of the fluorescence emission wavelength, has already been proven to be successful in FT (Klose et al 2005). Such a method is similar to the normalized Born ratio approach (Ntziachristos and Weissleder 2001, Soubret et al 2005), and in vivo FT experiments have been demonstrated to deliver superior reconstruction performance in media with a high degree of tissue heterogeneity. Furthermore, they have been found to minimize the sensitivity of the image reconstruction to distortions arising from modeling errors, variations in optical tissue properties, and measurement signal noise (Lee and Sevick-Muraca 2002, Ntziachristos and Weissleder 2001, Soubret et al 2005).
2.4. Illumination and detection geometries
In general, HEFT employs only a single source for uniform macro-illumination of the tissue surface, while multiple fluorescence images are taken for different excitation wavelengths for the purpose of source reconstruction. The illumination is performed with a white light source (A in figure 4(a)), which has a continuous output spectrum of constant radiant power in the considered wavelength range. The excitation light of desired wavelength range for fluorescence stimulation can be thought of being generated using various discrete bandpass filters or with a single continuously tunable bandpass filter (B in figure 4(a)). An emission filter (C in figure 4(a)) separates the fluorescence light from the excitation light, and a CCD camera (D in figure 4(a)) is used for detecting the fluorescence light on either the same side as the source (epi-illumination) or on the side opposite to the source (trans-illumination). Figure 4 shows both (a) trans- and (b) epi-illumination geometries.
Figure 4.
(a) Trans-illumination geometry. (b) Epi-illumination geometry. Both geometries use a white light source for fluorescence stimulation (A), a wavelength discriminating bandpass filter (B), an emission filter (C), and a CCD camera (D).
HEFT with a single-view illumination (V = 1) constitutes the basic experimental imaging geometry. It consists of a static illumination-detection set-up with the light source and the detector in either trans- or epi-illumination geometry (figure 4). Measurement data in trans-illumination are acquired by consecutively illuminating the, for instance, dorsal side of a mouse model with different excitation wavelengths, while the corresponding fluorescence is detected at the ventral side. The same applies to epi-illumination for the source and detector being on the same side. Single-view HEFT does not consider tomographic data acquisition from multiple spatial projections (V > 1), and thus tomographic resolution is solely based on the spectral encoding of the excitation light in tissue.
Despite the fact that HEFT can be used with a single source–detector geometry either in epi- or trans-illumination, multiple views of such macro-illumination geometry, as illustrated in figure 5, could be further utilized to increase the amount of independent measurement data. Such approach promises to improve the source reconstruction process and image quality. In contrast to single-view HEFT, multi-view HEFT measurements are not restricted to a fixed illumination-detection arrangement relative to the imaged object. In multi-view HEFT, several spatial views of the object are employed in the data acquisition process by either stepwise rotating the fixed source–detector gantry around the object or rotating the object around its own symmetry axis relative to the source–detector gantry in fixed position, while measurement data are recorded at every stop position defined in the acquisition protocol. Multi-view imaging experiments increase the amount of linearly independent measurement data, which consequently decrease the ill-posedness of the inverse fluorescence source problem. Hence, it is expected that multi-view HEFT will yield qualitatively and quantitatively better results than single-view HEFT. In this study, multi-view HEFT is applied using two (dual-view) and four stop positions (quad-view) as shown in figures 5(b) and (c). In the dual-view (V = 2) configuration the object is first illuminated from the top (position 1) and then from the opposite side (position 2). In the quad-view (V = 4) configuration two additional views are added, one illuminating from lateral right (position 3) and one from lateral left (position 4).
Figure 5.
(a) Single-view HEFT set-up: V = 1. (b) Dual-view HEFT arrangement with two illumination positions: V = 2. (c) Quad-view HEFT arrangement with four illumination positions: V = 4.
2.5. Linear image reconstruction
Following the fluorescence data acquisition, the image reconstruction is performed by solving an algebraic system of linear equations
| (14) |
with being the vector of the unknown fluorophore concentration and being the vector of the measured boundary current. can be either the actual, Y+, or the re-scaled, , boundary measurements. The vector with components cm has the dimension of M voxels of the reconstruction domain that is defined on the structured grid. The vector has N·L·V elements with N being the number of detector points on the tissue surface, L being the number of excitation wavelengths, and V being the number of views. The elements of are ordered as follows: . A single element A[n,l,v],m of the matrix A[N·L·V]×M is defined as the partial boundary current J+(rn):
| (15) |
at a detector point rn, which is calculated by the light propagation model F based on the SP3 equations for a unit concentration c0(rm) at a voxel rm and excitation source Sv with wavelength λl. Last, the algebraic system of equations (14) is iteratively solved for with an expectation-maximization (EM) method and solutions are displayed as tomographic images (Wernick and Aarsvold 2004).
2.6. Tissue phantom
As experimental demonstration, the HEFT method for 3D source reconstruction will be tested on a tissue slab containing a capsule of fluorescent Qdots. A slice of chicken breast was embedded into an imaging bed with dimensions of 4 cm × 3 cm × 1.2 cm. The chicken tissue was contained in a fixed pose between two glass plates. An optically transparent plastic capsule with outer diameter of 0.2 cm and a length of 0.5 cm contained 2 nM of fluorescent Qdots (Qtracker705, Invitrogen, USA). The capsule was placed inside the tissue at a depth of 0.5 cm measured from the top plane. The bed was placed on top of the imaging stage of the Photon Imager (Biospace Lab, France). The Photon Imager is a light-tight box containing a white light source, an automatic filter system, and a cooled CCD camera. The imager operates in back-reflectance mode (epi-illumination), where the detection and illumination units are placed on the same side of the object. A halogen lamp with a tunable bandpass filter (10 nm spectral width) provided the light for fluorescence stimulation. The top surface of the tissue slab was consecutively illuminated with light of nine different λl from 580 to 660 nm using a wavelength interval of Δλ = 10 nm. A single fluorescence image at λ = 700 nm was taken by the CCD camera for each illumination wavelength in back-reflectance on the top side of the imaging bed. An edge-filter blocked the excitation light from entering the detection unit. A single image acquisition time was 4 s. The imaging bed was flipped by 180° and fluorescence images were taken from the bottom side in back-reflectance. Hence, we obtained a total of nine images for single view and 18 images for dual view using the epi-illumination geometry.
Prior to fluorescence source reconstruction, the spectrally dependent and strongly varying absorption coefficient, μa(λ), of the chicken breast tissue needed to be determined. Thus, we performed an additional epi-illumination experiment with a known fluorescence source position. The fluorescent capsule containing the Qdots was placed at the geometrical center beneath the imaging bed and was, hence, fully covered with the chicken breast. After uniform illumination of the tissue surface on the opposite side to the capsule, the fluorescence light was measured for all nine excitation wavelengths. Next, an evolution strategy (ES) for parameter optimization calculated the unknown absorption coefficients for all nine wavelengths. We obtained the following absorption coefficients (μa, λ): (0.02 cm−1, 660 nm), (0.08 cm−1, 650 nm), (0.12 cm−1, 640 nm), (0.16 cm−1, 630 nm), (0.23 cm−1, 620 nm), (0.31 cm−1, 610 nm), (0.39 cm−1, 600 nm), (0.53 cm−1, 590 nm), and (0.72 cm−1, 580 nm). More details about the ES can be found in Klose et al (2010).
2.7. Numerical mouse model
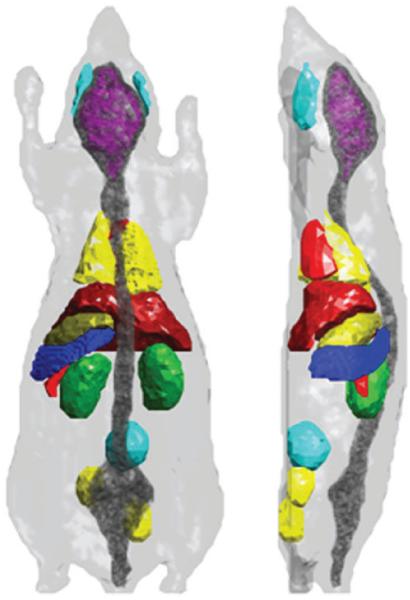
The application of the HEFT method for small animal imaging was tested on a numerical mouse model with synthetic measurement data, where we have complete control over all model parameters, including optical properties and anatomical structure. The used mouse model is a simplified version of the publicly available tessellated 3D Digimouse atlas (http://neuroimage.usc.edu/Digimouse.html) (Dogdas et al 2007, Stout et al 2002). The surface rendered 3D Digimouse model outlining several anatomically correct mapped organs is shown in figure 6.
Figure 6.
Surface rendering of the Digimouse atlas outlining the organs: mouse skin, whole brain, masseter muscles, spine and skull, heart, liver, lungs, stomach, spleen, pancreas, kidneys, bladder, and testes (left: posterior view; right: lateral left view).
As a modification, the unstructured tetrahedral tessellation (Delaunay tessellation) of the original mouse model was re-sampled on a structured Cartesian grid with the grid spacings Δx = Δy = Δz = 0.1 cm, making the mouse model accessible to the FD blocking-off region method. The resulting simplified model offers a total volume of 34 × 88 × 16 = 47 872 voxels (x–y–z-axis) giving a stack of 16 frontal slices, in which the re-sampled mouse body is embedded. As a further modification, the interstitial space between the organs and the outer tissue boundaries as well as the space between the extremities and the mouse body was padded out forming the bulk tissue of the mouse model. Figure 7 shows the re-sampled mouse model as a compilation of four different slices, z = 3, z = 6, z = 9, and z = 12, corresponding to the tissue depths of 0.3 cm, 0.6 cm, 0.9 cm, and 1.2 cm, respectively, where z = 0 refers to the ventral side and z = 16 to the dorsal side of the mouse body. For simplicity, the masseter muscles, pancreas, spleen, and lungs have been left out in the simplified model. All remaining organs in the model were assigned with optical properties as a function of wavelength following the method proposed by Alexandrakis et al (2005). This method provides estimations of realistic tissue optical properties of small animals based on published data. Although these values can only be seen as estimations of the real tissue parameters present in living small animals, they provide a good means to study FT in optically nonuniform tissue-like media on a comparable basis.
Figure 7.
(a)–(d) 3D mouse model in four different planes from anterior (slice 3) to posterior (slice 12) containing the following organs: brain, heart, bone, liver, stomach, bladder, testes, kidneys, and the bulk tissue (interstitial matter). (e) Corresponding frontal planes in the original Digimouse model.
Here, the reduced scattering coefficient, , given in cm−1 is approximated by an empirical function:
| (16) |
where a and b are the constants controlling the spectral variation of each tissue. Organ-specific values for the parameters a and b can be found in Alexandrakis et al (2005). The tissue absorption is assumed to depend only on the local oxy-hemoglobin (HbO2) and deoxy-hemoglobin (Hb) concentrations present in the respective organs. Therefore, the spectral absorption coefficient, μa(λ), given in cm−1 can be approximated as the weighted sum of the absorption coefficients μaHbO2(λ) and μaHb(λ):
| (17) |
where x = HbO2/(HbO2+Hb) is the ratio between oxy-hemoglobin and the total hemoglobin concentration. SB is a scaling factor to adjust the absorption coefficient to the respective organ. The spectral absorption data of HbO2 and Hb were derived from Prahl. Figure 8 shows the spectral variation of the assigned optical properties to the organs within the simplified mouse model. Here, the bulk tissue was considered as a compound of 90% adipose and 10% muscle tissue. Due to missing optical properties, the brain was set to the properties of adipose, and the bladder and testes were set to the properties of bulk tissue.
Figure 8.
Optical properties assigned to the simplified mouse model at nine different excitation wavelengths in the range of 580–660 nm, and a single emission wavelength at 700 nm (marked by dots). The absorption coefficient (a) and the reduced scattering coefficient (b) are given for the following organs: brain (pink), liver (brown), heart (red), stomach (blue), kidneys (green), bones (black), and bulk tissue (gray).
2.8. Measure of performance
All image reconstruction results, obtained either from the tissue phantom or from the numerical mouse model, were evaluated with different performance measures. These measures include the χ2-error norm, the correlation coefficient (corr), as well as the standard deviation (STD) of the reconstructed () with respect to the original () vectors of fluorophore concentration distribution. The χ2-error norm is defined as
| (18) |
with m specifying the index over all voxels. The correlation coefficient is given with
| (19) |
where 〈·〉 constitutes the mean value. Therefore, a small χ2, a large corr, and a small STD constitute a reconstructed fluorophore concentration distribution that is closest to its original distribution.
3. Results
First, we demonstrated the feasibility of HEFT by using ex vivo experimental data. We performed an imaging experiment with a fluorescent Qdot source of defined spatial location inside a tissue slab with uniform optical properties. Second, the image reconstructions were compared to reconstruction results obtained from a numerical model representing the tissue slab under ideal imaging conditions. We further demonstrated the tomographic imaging performance as a function of number of wavelengths and views. Last, whole-body small animal imaging or imaging of complex tissue anatomies inevitably involves nonuniform optical tissue property distributions that might impact the accuracy of the fluorescence source reconstructions. Therefore, we studied the impact of optical parameter maps on the outcome of source reconstructions by using a numerical mouse model and synthetic measurement data. By utilizing simulation studies, we had full control over the optical parameters and, hence, could test different image reconstruction scenarios including measurement re-scaling and multi-view geometries.
3.1. Tissue phantom experiment with uniform optical parameter distribution
The measured fluorescence data became input to the HEFT image reconstruction algorithm. The imaging bed with tissue was discretized on a structured grid with 48 × 60 × 13 = 37 440 grid points. The grid point separation was chosen to be 0.1 cm. The top plane of the tissue phantom is indicated by slice z = 12, whereas slice z = 0 depicts the bottom plane. The partial current of fluorescence light, J+, was calculated for 264 (single view: detection and illumination at z = 12) and 529 (dual view: detection and illumination at z = 0 and z = 12) grid boundary points on the glass plates of the bed. Thus, we obtained a matrix A with 37 440 columns and 264 × 9 (529 × 9) rows for single view (dual-view) and a maximum of nine wavelengths. The reconstructions were completed after 3000 iterations of the EM method using an Intel processor with 3 GHz clock rate.
3.1.1. Single view versus dual view
Figure 9 shows the measured fluorescence images on the top side (z = 12) of the imaging bed, which were taken at excitation wavelengths of 580–660 nm in epi-illumination geometry. Figure 10(a) shows a lateral x–y plane at z = 7 and a horizontal x–z plane at y = 20 of the reconstructed fluorophore distribution inside the tissue when using only a single-view epi-illumination configuration. We could find relatively good agreement between the reconstructed and original spatial position (green rectangle in figure 10) of the fluorescent capsule. Figure 10(b) shows the reconstructed source distribution for dual-view epi-illumination. An improvement in image reconstruction accuracy with better depth resolution along the z-axis can be observed. Lines 12 and 16 in table 1 show the χ2-error, the correlation coefficient, and the standard deviation for both reconstruction results.
Figure 9.
(a) Fluorescence images of Qdots inside tissue taken for different excitation wavelengths (580–660 nm) on the top side (z = 12) of the tissue phantom. A capsule of Qdots is located 0.5 cm (z = 7) beneath the top tissue surface.
Figure 10.
Image reconstructions of fluorescent Qdots embedded into chicken breast tissue for epi-illumination geometry and L = 9 wavelengths. Top row: lateral slices at depth z = 7. Bottom row: axial slices at y = 20. Original location of the capsule is depicted by a green-colored rectangle. (a) Single-view (V = 1) HEFT reconstructions. Detection and illumination plane is located at z = 12. (b) Dual-view (V = 2) HEFT reconstructions. Detection and illumination planes are located at z = 0 and z = 12.
Table 1.
Quantitative analysis of the impact of the number of wavelengths (L) and views (V) on the accuracy of the fluorescence source reconstruction. As a measure, the χ2-error, the correlation coefficient corr, and the standard deviation STD are given for simulated and experimentally obtained reconstructions.
| Case | V | L | χ 2 | Corr | STD | |
|---|---|---|---|---|---|---|
| 1. | Simulation | 1 | 1 | 6.6937 | 0.0749 | 0.1111 |
| 2. | Simulation | 1 | 3 | 3.5522 | 0.1572 | 0.0652 |
| 3. | Simulation | 1 | 5 | 3.0095 | 0.1915 | 0.0557 |
| 4. | Simulation | 1 | 9 | 1.8406 | 0.2937 | 0.0343 |
| 5. | Simulation | 2 | 1 | 7.2782 | 0.0735 | 0.1233 |
| 6. | Simulation | 2 | 3 | 2.9641 | 0.3122 | 0.0571 |
| 7. | Simulation | 2 | 5 | 2.2313 | 0.3737 | 0.0442 |
| 8. | Simulation | 2 | 9 | 1.2246 | 0.4889 | 0.0253 |
| 9. | Experiment | 1 | 1 | 8.7152 | 0.0372 | 0.1380 |
| 10. | Experiment | 1 | 3 | 5.1002 | 0.0491 | 0.0879 |
| 11. | Experiment | 1 | 5 | 4.9228 | 0.0988 | 0.0859 |
| 12. | Experiment | 1 | 9 | 3.9826 | 0.2017 | 0.0723 |
| 13. | Experiment | 2 | 1 | 6.3231 | 0.0362 | 0.1058 |
| 14. | Experiment | 2 | 3 | 4.3275 | 0.0824 | 0.0749 |
| 15. | Experiment | 2 | 5 | 4.2462 | 0.2121 | 0.0773 |
| 16. | Experiment | 2 | 9 | 2.2029 | 0.3649 | 0.0430 |
3.1.2. Reconstruction performance as function of wavelength
We further investigated the dependence of the excitation-resolved source reconstructions on the total number of used excitation wavelengths between 580 and 660 nm. Figure 11 shows two reconstructed lateral and horizontal cross-sections of the embedded Qdot source for different sets of excitation wavelengths (L = 1, 3, 5, 9). The reconstructions indicate that an increase of the number of wavelengths used for reconstruction improve the localization ability of the reconstruction. A precise and concisely confined source localization in the x–y-plane could only be obtained for L = 9. The lower the number of wavelengths involved in the reconstruction, the less is the capability of accurately resolving the source depth. In case of L = 1, almost all of the reconstructed source intensity is concentrated beneath the tissue boundary close to the detector plane, and only a low amount of intensity can be observed at the true depth of the fluorophore. Increasing the number of wavelengths, however, increases the depth information provided to the reconstruction, and hence the source localization starts to grow into the volume, which in parallel results in an increased amount of intensity at the position of the real fluorophore inclusion.
Figure 11.
Dual-view ex vivo reconstructions of fluorescent Qdots embedded into chicken breast tissue for (a) L = 1, (b) L = 3, (c) L = 5, and (d) L = 9 excitation wavelengths. Top row: lateral slices of Qdot distribution inside tissue at the depth z = 7. Bottom row: axial slices of Qdot distribution inside tissue at y = 20.
For comparison, source reconstructions were performed with synthetic measurement data eliminating measurement noise, uncertainty in optical properties, and mismatch of detector points’ alignment (figure 12). These source reconstructions provide a measure under ideal conditions.
Figure 12.
Dual-view reconstructions of synthetic measurement data for (a) L = 1, (b) L = 3, (c) L = 5, and (d) L = 9 excitation wavelengths. Top row: lateral slices of the fluorescence source inside the numerical model at the depth z = 7. Bottom row: axial slices of the fluorescence source inside the numerical model at y = 20.
3.2. Numerical mouse model with nonuniform optical parameter distribution
The preceding experimental and simulation studies dealt with a uniform tissue model with defined optical properties. Next, we will perform simulation studies using the numerical mouse model with nonuniform optical parameter distributions and trans-illumination geometry. We will (i) demonstrate the impact of single- and multi-view geometries on the image reconstruction performance, (ii) study the impact of a tissue model with an incorrectly assumed uniform optical parameter distribution (real case), and (iii) show the impact of re-scaled measurement data while using a tissue model with only uniform optical parameter maps for the reconstruction process (re-scaling case). Last, the reconstructions of the real case and re-scaling case with unknown optical parameter maps will be compared to reconstructions where the nonuniform optical parameter maps are known a priori (ideal case).
3.2.1. Single-view HEFT reconstruction
As a basis for the simulation, a single fluorescence source, mimicking Qdot nanoparticles QTracker® 705 (Invitrogen Inc., USA), was placed approximately at the center of the bowel region below the liver (coordinates: x = 18–19, y = 38–39, and z = 9–10 as depicted by the green-colored circle in figure 13). The source size was 2 × 2 × 2 voxels yielding a total volume of 8 mm3 (0.008 mL). Throughout all simulations, the Qdot concentration was assumed to be 100 nmol L−1 with an extinction of 0.4–1.2 × 106 cm−1 M−1 for wavelengths between 580 and 660 nm in descending order.
Figure 13.
Single-view HEFT reconstruction of a fluorescence source obtained for (a) the ideal case, i.e. with the original nonuniform optical parameter maps, (b) the real case with an assumed uniform optical parameter distribution, and (c) the re-scaling case with re-scaled measurement data based on a uniform optical parameter distribution. The top row of images shows frontal slices at z = 10. The bottom row of images shows transversal slices at (a) y = 37, (b) y = 35, and (c) y = 34. The original location of the fluorescence source is illustrated by a green circle.
The mouse model was uniformly illuminated on the ventral side by placing excitation sources on 1608 surface grid points. Fluorescence stimulation was chosen to be at L = 9 wavelength intervals between 580 and 660 nm in steps of 10 nm. The fluorescence emission was collected at a single wavelength of 700 nm. The optical parameters as a function of wavelength (figure 8) were assigned to the mouse model accordingly. The synthetic measurement data were calculated for 260 grid points on the dorsal side. Thus, the matrix A was composed of 260 × 9 = 2340 rows and 47 872 columns. All reconstructions were terminated after 350 iterations of the EM method. The single-view reconstruction results are shown for the ideal case, the real case, and the re-scaling case in figure 13.
Regarding the ideal case, the original nonuniform optical parameter distribution of the mouse model was assumed to be known during the image reconstruction process. This case constitutes an experimental situation under ideal conditions where the exact optical parameter distribution of the tissue is completely known. Therefore, the matrix A was built by solving equation (15) using the original nonuniform tissue parameter maps. Figure 13(a) shows the reconstructed source distribution, which is in good agreement with the original source location depicted by the green-colored circle. In the real case scenario, however, no information about the actual optical tissue nonuniformities was included into the reconstruction process. Therefore, the matrix elements in equation (15) were calculated by using only a uniform optical parameter distribution. Figure 13(b) shows a diverted source distribution with little depth resolution. We assume that the exclusion of the kidney and the liver with their large absorption coefficients have a major impact on the light propagation. Nevertheless, the source reconstructions gained on accuracy for the re-scaling case while still using uniform optical parameter distributions for building the matrix A. Here, the synthetic measurement data, Y+(λl), of the actual nonuniform mouse model at wavelength λl were re-scaled according to equation (13). The re-scaling factor was obtained from an additional set of synthetic measurement data, Y+(λr), for the nonuniform mouse model at a reference wavelength λr = 700 nm and a set of predicted partial boundary currents, J+(λr), for the uniform mouse model at the same wavelength. As can be seen from the reconstructed slices in figure 13(c), a significant improvement in recovering the original source localization within the x–y-plane could be achieved when compared to the real case. Lines 1, 2, and 3 in table 2 show the χ2-error, the correlation coefficient, and the standard deviation of the reconstructed with respect to the original source distribution for all three cases and V = 1. In fact, the χ2-error and the STD have been improved for the re-scaling case (χ2 = 1.5211, STD = 0.0148) and are smaller than for the real case (χ2 = 1.7843, STD = 0.0191).
Table 2.
Quantitative analysis of the nonuniform mouse model simulations distinguishing the ideal, real, and re-scaling cases as a function of number of views (V).
| Case | V | χ 2 | Corr | STD | |
|---|---|---|---|---|---|
| 1. | Ideal | 1 | 0.9874 | 0.6109 | 0.0155 |
| 2. | Real | 1 | 1.7843 | 0 | 0.0191 |
| 3. | Re-scaling | 1 | 1.5211 | 0 | 0.0148 |
| 4. | Ideal | 2 | 0.6248 | 0.7911 | 0.0119 |
| 5. | Real | 2 | 1.4297 | 0 | 0.0132 |
| 6. | Re-scaling | 2 | 0.5656 | 0.8340 | 0.0124 |
| 7. | Ideal | 4 | 0.6203 | 0.7892 | 0.0113 |
| 8. | Real | 4 | 1.4449 | 0 | 0.0135 |
| 9. | Re-scaling | 4 | 0.7377 | 0.7591 | 0.0143 |
The single-view reconstructions of the real case and the re-scaling case show, however, limitations in depth resolution along the z-axis within the x–z-plane (figures 13(b) and (c)) when compared to reconstructions of the ideal case. The false source reconstruction of the real case and re-scaling case in close proximity to the surface may be caused by (i) the relatively small amount of source and detector points and (ii) the partially illuminated surface area of the single view. The single-view geometry causes the sensitivity, , of the partial current with respect to the fluorescence source to be depth dependent. As a result, changes of q will cause larger changes in J+ when q is closer to the surface. Moreover, Φx is a function of the optical tissue parameters at wavelengths λl and, thus, has a direct impact on the depth-dependent sensitivity . Changes in q, which is a function of Φx(λl), due to partially wrong optical parameters of an assumed uniform tissue model will cause changes in J+. J+ will, however, be more sensitive to these wrongly assumed optical parameters when q is closer to the surface. Vice versa, the source reconstruction for a given partial current Y+ will also be more sensitive to changes in the excitation field due to wrong optical parameters. The source artifacts will disappear when more than a single view (V > 1), with an overall larger illumination area, is used for source reconstruction.
3.2.2. Multi-view HEFT reconstruction
So far, only a single view (V = 1) in trans-illumination geometry was employed for the acquisition of tomographic data from the numerical mouse model. Now the impact of multiple views on the source reconstruction will be demonstrated. We will consider a dual-view (V = 2) and a quad-view (V = 4) trans-illumination configuration. Similar to the prior studies using a single view, reconstructions were performed for the ideal-, real-, and re-scaling cases.
Dual-view HEFT utilizes imaging data obtained from two illumination views (figure 5(b)). The first data set is acquired using the single-view illumination-detector arrangement. Then, light source and detector switch places and a second data set is acquired. Quad-view HEFT expands the dual-view data acquisition by two additional illumination views, orthogonal to the dual-view, as illustrated in figure 5(c). Figure 14 shows the results presented as frontal and axial slices at the position of the recovered single fluorescence source. In all three cases, real, ideal and re-scaling, a confined source position could be recovered. We do not observe artifacts in the reconstructed domain. As can be seen from the axial slices (bottom row images in figure 14), in either of the simulation cases the correct depth of the fluorescence source could be found. Ideally, the ideal case reconstruction, as shown in figure 14(a), gives the correct spatial location of the fluorescence source in both cross-sectional planes. A small deviation (caudal shift of 0.3 cm) of the reconstructed source within the x–y plane, however, was observed for the real case in figure 14(b). Using re-scaled measurement data, this deviation could be fully compensated as shown in figure 14(c). Figure 15 gives a 3D rendering of the reconstructed source intensity, which was found in the real case reconstruction. A clear and uniquely localized source spot can be identified. The spot is of almost spherical shape, which indicates an imaging performance of similar resolution power in all three dimensions. Lines 4, 5, and 6 in table 2 show the χ2-error, the correlation coefficient, and the standard deviation of the reconstructed with respect to the original source distribution for all three cases and V = 2. As can be seen, all measures of performance have been improved for V = 2 in comparison to V = 1.
Figure 14.
Dual-view HEFT reconstruction of a single fluorescence source obtained for (a) the ideal case, (b) the real case, and (c) the re-scaling case. The top row of images shows frontal slices at z = 10. The bottom row of images shows transversal slices at (a) y = 38, (b) y = 34, and (c) y = 38. The original location of the fluorescence source is illustrated by a green circle.
Figure 15.

3D isosurface rendering of the source obtained for the real-case simulation using dual-view HEFT reconstruction.
The quad-view HEFT reconstructions are shown in figure 16. Compared to the dual-view reconstructions, almost no difference in the localization performance of the fluorescence source was observed. The χ2-error, the correlation coefficient, and the standard deviation of V = 4, given by lines 7, 8, and 9 in table 2, are similar to those of V = 2.
Figure 16.
Quad-view HEFT reconstruction of a single fluorescence source obtained for (a) the ideal case, (b) the real case, and (c) re-scaling case. The top row of images shows frontal slices at z = 10. The bottom row of images shows transversal slices at (a) y = 38, (b) y = 34, and (c) y = 38. The original location of the fluorescence source is illustrated by a green circle.
4. Conclusion
We have presented an excitation-resolved FT method, which reconstructs the 3D fluorescence source distribution inside scattering tissue. It exploits the large change of (oxy-)hemoglobin absorption in tissue for the purpose of 3D volume image reconstruction from 2D fluorescence surface images. Fluorophores with relatively broad extinction spectrum, such as quantum dots, will be excited for fluorescence stimulation with light at different wavelengths that overlap with the strongly varying absorption spectrum of (oxy-)hemoglobin between 580 and 660 nm. Therefore, HEFT simplifies the measurement process because its single excitation light source does not rely on complex fiber optics, source arrays, diode lasers, or optical switches for source–detector multiplexing, which are required for current FT image reconstruction methods. Instead, macro-illumination can be employed for fluorescence stimulation.
HEFT is not only an inexpensive alternative to current FT, but also existing 2D imaging technology could easily be retrofitted for 3D fluorescence tomography by only adding a wavelength-discriminating macro-illumination component. Therefore, we have demonstrated our excitation-resolved FT method on a commercially available fluorescence small animal imager (Photon Imager, Biospace Lab, France). The Photon Imager was originally designed for 2D small animal imaging but could readily be used for HEFT imaging by using its wavelength-selective fluorescence excitation capability. We demonstrated the functionality of HEFT in an ex vivo tissue phantom experiment under tightly controlled conditions, such as uniform optical tissue properties and defined tissue geometry. We were able to reconstruct the exact spatial location of an embedded fluorescent quantum dot capsule. We could show that at least L = 3 different wavelength bands are required for recovering the capsule location. Experimental and simulation results were best for L = 9 wavelengths. Further image reconstruction improvements could be achieved by illuminating the tissue from V = 2 different views.
Since our HEFT method uses the spectral dependence of hemoglobin absorption for 3D image reconstruction, we needed to develop a light propagation model that accurately models radiative transfer in tissue with strong light absorption up to 10 cm−1. RTE-based or Monte-Carlo models are suitable candidates for describing radiative transfer in scattering domains beyond the diffusion limit. Both methods, however, are computationally demanding and require relatively long processing times. Therefore, we developed a fluorescence light propagation model based on the SP3 equations, which consists of only two coupled diffusion equations. Moreover, we have implemented a blocking-off region finite-difference method for solving the SP3 equations in media with curved geometries such as small animals. Our simulation study based on synthetic measurement data yielded similar image reconstruction results as our experimental tissue phantom study. Good agreement between both studies demonstrates that the SP3 equations correctly describe the light transport in scattering tissue at a wide range of absorption coefficients.
Next, we have investigated the capability of HEFT for reconstructing a fluorescence source inside a nonuniform tissue model with curved geometries. This study goes beyond our previous ex vivo demonstration experiment with a uniform model and simple Cartesian geometry. Our current imaging instrumentation did, however, neither allow for registering curved tissue surfaces nor could it determine the accurate in vivo optical parameter distribution of a small animal. Therefore, we refrained to a numerical simulation study where we had full control over all experimental conditions, including the tissue surface geometry and the exact optical parameter distribution of an optically nonuniform mouse model. Our numerical reconstruction results show an accurate recovery of the unknown source location inside the mouse model when using the exact nonuniform optical tissue parameter distribution (ideal case) for the source reconstruction process. Our findings are in good agreement with our ex vivo experimental results. For example, very good image reconstruction results with accurate source recovery were obtained for V = 2 views, whereas a single-view (V = 1) reconstruction yielded only moderately satisfactory results with source artifacts close to the tissue boundary. V = 4 views did not significantly further improve the reconstruction.
HEFT uses a spectrally dependent excitation field for fluorescence stimulation, and thus the accurate absorption parameter distribution for a given excitation wavelength needs to be known (ideal case). Such stringent requirement is, however, difficult to be satisfied in a typical experimental setting under realistic conditions due to the lack of any anatomical information about the animal. The determination of accurate absorption maps would require a tomographic method such as diffuse optical tomography (DOT) (Arridge and Schweiger 1997, Arridge 1999, Gibson et al 2005, Gibson and Dehghani 2009, Dehghani et al 2009), which is a difficult and challenging task itself. Therefore we have investigated the real case scenario, where the optical parameters of different organs and tissue types are unknown for the purpose of image reconstruction. We found larger discrepancies in localizing the original source position, especially for V = 1. Using more than a single view, however, increased the 3D image quality significantly. Nevertheless, the reconstructed spatial location of the fluorescence source deviated from its original location by almost 0.3 cm.
The source reconstructions of the real case scenarios could significantly be improved by using a data re-scaling method while still using the uniform optical parameter distributions (re-scaling case). The re-scaling method partially corrects for the deteriorating impact of an assumed uniform tissue model on the source reconstruction. We re-scaled the measured fluorescence light intensities by a re-scaling factor prior to the image reconstruction process. The re-scaling factor is obtained from calculated fluorescence intensity data of a uniform tissue model and from additionally measured light intensities at the fluorescence wavelength and absence of a fluorescence source (i.e. the source is not stimulated for fluorescence emission). Typically, these measurements could be taken prior to the fluorescence experiment. We found that the obtained source reconstructions are in good agreement with the original source location for views larger than V = 1. Thus, the re-scaling method demonstrates the feasibility of reconstructing the fluorescence source inside animal tissue without the knowledge of the exact optical absorption map.
Acknowledgments
This work was supported in part by grants UL1RR024156 from the National Center For Research Resources (NCRR) and 1R21EB011772-01A1 from the National Institute of Biomedical Imaging and Bioengineering (NIBIB). We would like to thank Dr Serge Maitrejean and Dr Sebastien Bonzom from BiospaceLab for kindly providing the Photon Imager, Bradley Beattie from Memorial Sloan-Kettering Cancer Center for pre-processing the optical data, and Dr Lynne Johnson and Dr Yared Tekabe from the Department of Medicine of Columbia University for their helpful support. Additionally, the authors gratefully acknowledge funding of the Erlangen Graduate School in Advanced Optical Technologies (SAOT) by the German Research Foundation (DFG) in the framework of the German excellence initiative.
References
- Alexandrakis G, Rannou FR, Chatziioannou AF. Tomographic bioluminescence imaging by use of a combined optical-PET (OPET) system: a computer simulation feasibility study. Phys. Med. Biol. 2005;50:4225–41. doi: 10.1088/0031-9155/50/17/021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arridge SR. Optical tomography in medical imaging. Inverse Problems. 1999;15:R41–93. [Google Scholar]
- Arridge SR, Schweiger M. Image reconstruction in optical tomography. Phil. Trans. R. Soc. B. 1997;352:717–26. doi: 10.1098/rstb.1997.0054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aydin ED, de Oliveira CRE, Goddard AJH. A comparison between transport and diffusion calculations using a finite-element spherical harmonics radiation transport method. Med. Phys. 2002;29:2013–23. doi: 10.1118/1.1500404. [DOI] [PubMed] [Google Scholar]
- Biju V, Itoh T, Anas A, Sujith A, Ishikawa M. Semiconductor quantum dots and metal nanoparticles: syntheses, optical properties, and biological applications. Anal. Bioanal. Chem. 2008;391:2469–95. doi: 10.1007/s00216-008-2185-7. [DOI] [PubMed] [Google Scholar]
- Bloch S, Lesage F, Mackintosh L, Gandjbakche A, Liang K, Achilefu S. Whole-body fluorescence lifetime imaging of a tumortargeted near-infrared molecular probe in mice. J. Biomed. Opt. 2005;10:0540031. doi: 10.1117/1.2070148. [DOI] [PubMed] [Google Scholar]
- Byun DY, Baek SW, Kim MY. Investigation of radiative heat transfer in complex geometries using blocked-off, multiblock, and embedded boundary treatments. Numer. Heat Transfer A. 2003;43:807–25. [Google Scholar]
- Cai W, Chen X. Preparation of peptide conjugated quantum dots for tumor vasculature-targeted imaging. Nat. Protocols. 2008;3:89–96. doi: 10.1038/nprot.2007.478. [DOI] [PubMed] [Google Scholar]
- Case KM, Zweifel PF. Linear Transport Theory. Addison-Wesley; Reading, MA: 1967. [Google Scholar]
- Chai JC, Lee HS, Patankar SV. Proc. National Heat Transfer Conf. American Society of Mechanical Engineers; Atlanta: Aug 8–11, 1993. 1993. Treatment of irregular geometries using a Cartesian coordinates control-angle control-volume-based discrete-ordinate method; pp. 35–43. [Google Scholar]
- Chai JC, Lee HS, Patankar SV. Treatment of irregular geometries using a Cartesian coordinates finite volume radiation heat transfer procedure. Numer. Heat Transfer B. 1994;26:225–35. [Google Scholar]
- Chalhoub ES, de Campos Velho HF. Multispectral reconstruction of bioluminescence term in natural waters. Appl. Numer. Math. 2003;47:365–76. [Google Scholar]
- Chang J, Graber HL, Barbour RL. Imaging of fluorescence in highly scattering media. IEEE Trans. Biomed. Eng. 1997;44:810–22. doi: 10.1109/10.623050. [DOI] [PubMed] [Google Scholar]
- Chaudhari AJ, Ahn S, Levenson R, Badawi RD, Cherry SR, Leahy RM. Excitation spectroscopy in multispectral optical fluorescence tomography: methodology, feasibility and computer simulation studies. Phys. Med. Biol. 2009;54:4687–704. doi: 10.1088/0031-9155/54/15/004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaudhari AJ, Darvas F, Bading JR, Moats RA, Conti PS, Smith DJ, Cherry SR, Leahy RM. Hyperspectral and multispectral bioluminescence optical tomography for small animal imaging. Phys. Med. Biol. 2005;50:5421–41. doi: 10.1088/0031-9155/50/23/001. [DOI] [PubMed] [Google Scholar]
- Corlu A, Choe R, Durduran T, Rosen MA, Schweiger M, Arridge SR, Schnall MD, Yodh AG. Three-dimensional in vivo fluorescence diffuse optical tomography of breast cancer in humans. Opt. Express. 2007;15:6696–716. doi: 10.1364/oe.15.006696. [DOI] [PubMed] [Google Scholar]
- Debagge P, Jaschke W. Molecular imaging with nanoparticles: giant roles for dwarf actors. Histochem. Cell Biol. 2008;130:845–75. doi: 10.1007/s00418-008-0511-y. [DOI] [PubMed] [Google Scholar]
- Dehghani H, Davis SC, Jiang S, Pogue BW, Paulsen KD, Patterson MS. Spectrally resolved bioluminescence optical tomography. Opt. Lett. 2006;31:365–7. doi: 10.1364/ol.31.000365. [DOI] [PubMed] [Google Scholar]
- Dehghani H, Srinivasan S, Pogue BW, Gibson A. Numerical modelling and image reconstruction in diffuse optical tomography. Phil. Trans. R. Soc. A. 2009;367:3073–93. doi: 10.1098/rsta.2009.0090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deliolanis N, Lasser T, Hyde DD, Soubret A, Ripoll J, Ntziachristos V. Free-space fluorescence molecular tomography utilizing 360 degrees geometry projections. Opt. Lett. 2007;32:382–4. doi: 10.1364/ol.32.000382. [DOI] [PubMed] [Google Scholar]
- Dogdas B, Stout D, Chatziioannou AF, Leahy RM. Digimouse: a 3D whole body mouse atlas from CT and cryosection data. Phys. Med. Biol. 2007;52:577–87. doi: 10.1088/0031-9155/52/3/003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dutta J, Ahn S, Joshi AA, Leahy RM. Illumination pattern optimization for fluorescence tomography: theory and simulation studies. Phys. Med. Biol. 2010;55:2961–82. doi: 10.1088/0031-9155/55/10/011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eppstein MJ, Hawrysz DJ, Godavarty A, Sevick-Muraca EM. Three-dimensional bayesian image reconstruction from sparse and noisy data sets: near-infrared fluorescence tomography. Proc. Natl Acad. Sci. 2002;99:9619–24. doi: 10.1073/pnas.112217899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frangioni JV. In vivo near-infrared fluorescence imaging. Curr. Opin. Chem. Biol. 2003;7:626–34. doi: 10.1016/j.cbpa.2003.08.007. [DOI] [PubMed] [Google Scholar]
- Gao X, Cui Y, Levenson RM, Chung LWK, Nie S. In vivo cancer targeting and imaging with semiconductor quantum dots. Nat. Biotechnol. 2004;22:969–76. doi: 10.1038/nbt994. [DOI] [PubMed] [Google Scholar]
- Gibson A, Dehghani H. Diffuse optical imaging. Phil. Trans. R. Soc. A. 2009;367:3055–72. doi: 10.1098/rsta.2009.0080. [DOI] [PubMed] [Google Scholar]
- Gibson A, Hebden JC, Arridge SR. Recent advances in diffuse optical imaging. Phys. Med. Biol. 2005;50:R1–43. doi: 10.1088/0031-9155/50/4/r01. [DOI] [PubMed] [Google Scholar]
- Godavarty A, Eppstein MJ, Zhang CY, Theru S, Thompson AB, Gurfinkel M, Sevick-Muraca EM. Fluorescence-enhanced optical imaging in large tissue volumes using a gain modulated ICCD camera. Phys. Med. Biol. 2003;48:1701–20. doi: 10.1088/0031-9155/48/12/303. [DOI] [PubMed] [Google Scholar]
- Godavarty A, Sevick-Muraca EM, Eppstein MJ. Three-dimensional fluorescence lifetime tomography. Med. Phys. 2005;32:992–1000. doi: 10.1118/1.1861160. [DOI] [PubMed] [Google Scholar]
- Graves EE, Ripoll J, Weissleder R, Ntziachristos V. A submillimeter resolution fluorescence molecular imaging system for small animal imaging. Med. Phys. 2003;30:901–11. doi: 10.1118/1.1568977. [DOI] [PubMed] [Google Scholar]
- Graves EE, Weissleder R, Ntziachristos V. Fluorescence molecular imaging of small animal tumor models. Curr. Mol. Med. 2004;4:419–30. doi: 10.2174/1566524043360555. [DOI] [PubMed] [Google Scholar]
- Hall D, Ma G, Lesage F, Wang Y. Simple time-domain optical method for estimating the depth and concentration of a fluorescent inclusion in a turbid medium. Opt. Lett. 2004;29:2258–60. doi: 10.1364/ol.29.002258. [DOI] [PubMed] [Google Scholar]
- Hattery D, Chernomordik V, Loew M, Gannot I, Gandjbakhche A. Analytical solutions for time-resolved fluorescence lifetime imaging in a turbid medium such as tissue. J. Opt. Soc. Am. 2001;18:1523–30. doi: 10.1364/josaa.18.001523. [DOI] [PubMed] [Google Scholar]
- Herve L, et al. Noncontact fluorescence diffuse optical tomography of heterogeneous media. Appl. Opt. 2007;46:4896–906. doi: 10.1364/ao.46.004896. [DOI] [PubMed] [Google Scholar]
- Hielscher AH, Alcouffe RE, Barbour RL. Comparison of finite-difference transport and diffusion calculations for photon migration in homogeneous and heterogeneous tissues. Phys. Med. Biol. 1998;43:1285–302. doi: 10.1088/0031-9155/43/5/017. [DOI] [PubMed] [Google Scholar]
- Joshi A, Bangerth W, Sevick-Muraca EM. Non-contact fluorescence optical tomography with scanning patterned illumination. Opt. Express. 2006;14:6516–34. doi: 10.1364/oe.14.006516. [DOI] [PubMed] [Google Scholar]
- Klose AD. Hyperspectral excitation-resolved fluorescence tomography of quantum dots. Opt. Lett. 2009a;34:2477–9. doi: 10.1364/ol.34.002477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klose AD. Radiative transfer of luminescence light in biological tissue. In: Kokhanowsky AA, editor. Light Scattering Reviews. Vol. 4. Springer; Berlin: 2009b. pp. 293–345. [Google Scholar]
- Klose AD, Beattie BJ, Dehghani H, Vider L, Le C, Ponomarev V, Blasberg R. In vivo bioluminescence tomography with a blocking-off finite-difference SP3 method and MRI/CT coregistration. Med. Phys. 2010;37:329–38. doi: 10.1118/1.3273034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klose AD, Hielscher AH. Fluorescence tomography with simulated data based on the equation of radiative transfer. Opt. Lett. 2003;28:1019–21. doi: 10.1364/ol.28.001019. [DOI] [PubMed] [Google Scholar]
- Klose AD, Larsen EW. Light transport in biological tissue based on the simplified spherical harmonics equations. J. Comput. Phys. 2006;220:441–70. [Google Scholar]
- Klose AD, Ntziachristos V, Hielscher AH. The inverse source problem based on the radiative transfer equation in optical molecular imaging. J. Comput. Phys. 2005;202:323–45. [Google Scholar]
- Kumar ATN, Raymond SB, Boverman G, Boas DA, Bacskai BJ. Time resolved fluorescence tomography based on lifetime contrast. Opt. Express. 2006;14:12255–70. doi: 10.1364/oe.14.012255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar ATN, Raymond SB, Dunn AK, Bacskai BJ, Boas DA. A time domain fluorescence tomography system for small animal imaging. IEEE Trans. Med. Imaging. 2008;27:1152–63. doi: 10.1109/TMI.2008.918341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar ATN, Skoch J, Bacskai BJ, Boas DA, Dunn AK. Fluorescence-lifetime-based tomography for turbid media. Opt. Lett. 2005;30:3347–9. doi: 10.1364/ol.30.003347. [DOI] [PubMed] [Google Scholar]
- Kuo C, Coquoz O, Troy TL, Xu H, Rice BW. Three-dimensional reconstruction of in vivo bioluminescent sources based on multispectral imaging. J. Biomed. Opt. 2007;12:24007-1–24007-12. doi: 10.1117/1.2717898. [DOI] [PubMed] [Google Scholar]
- Lee J, Sevick-Muraca EM. Three-dimensional fluorescence enhanced optical tomography using referenced frequency-domain photon migration measurements at emission and excitation wavelengths. J. Opt. Soc. Am. A. 2002;19:759–71. doi: 10.1364/josaa.19.000759. [DOI] [PubMed] [Google Scholar]
- Li XD, O’Leary MA, Boas DA, Chance B, Yodh AG. Fluorescent diffuse photon density waves in homogeneous and heterogeneous turbid media: analytic solutions and applications. Appl. Opt. 1996;35:3746–58. doi: 10.1364/AO.35.003746. [DOI] [PubMed] [Google Scholar]
- Lu Y, Douraghy A, Machado H, Stout D, Herschman H, Chatziioannou A. Spectrally resolved bioluminescence tomography with the third-order simplified spherical harmonics approximation. Phys. Med. Biol. 2009;54:6477–93. doi: 10.1088/0031-9155/54/21/003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lv Y, Tian J, Cong W, Wang G, Yang W, Qin C, Xu M. Spectrally resolved bioluminescence tomography with adaptive finite element analysis: methodology and simulation. Phys. Med. Biol. 2007;52:4497–512. doi: 10.1088/0031-9155/52/15/009. [DOI] [PubMed] [Google Scholar]
- Michalet X, Bentolila LA, Weiss S. Advances in Medical Physics. Medical Physics Publishing; Madison, WI: 2008. chapter 8. [Google Scholar]
- Milstein AB, et al. Fluorescence optical diffusion tomography. Appl. Opt. 2003;42:3081–94. doi: 10.1364/ao.42.003081. [DOI] [PubMed] [Google Scholar]
- Montet X, Figueiredo JL, Alencar H, Ntziachristos V, Mahmood U, Weissleder R. Tomographic fluorescence imaging of tumor vascular volume in mice. Radiology. 2007;242:751–8. doi: 10.1148/radiol.2423052065. [DOI] [PubMed] [Google Scholar]
- Ntziachristos V. Fluorescence molecular imaging. Annu. Rev. Biomed. Eng. 2006;8:1–33. doi: 10.1146/annurev.bioeng.8.061505.095831. [DOI] [PubMed] [Google Scholar]
- Ntziachristos V, Weissleder R. Experimental three-dimensional fluorescence reconstruction of diffuse media by use of a normalized Born approximation. Opt. Lett. 2001;26:893–5. doi: 10.1364/ol.26.000893. [DOI] [PubMed] [Google Scholar]
- O’Leary MA, Boas DA, Li XD, Chance B, Yodh A. Fluorescence lifetime imaging in turbid media. Opt. Lett. 1996;21:158–60. doi: 10.1364/ol.21.000158. [DOI] [PubMed] [Google Scholar]
- Paithankar DY, Chen AU, Pogue BW, Patterson MS, Sevick-Muraca EM. Imaging of fluorescent yield and lifetime from multiply scattered light reemitted from random media. Appl. Opt. 1997;36:2260–72. doi: 10.1364/ao.36.002260. [DOI] [PubMed] [Google Scholar]
- Panasyuk GY, Wang ZM, Schotland JC, Markel VA. Fluorescent optical tomography with large data sets. Opt. Lett. 2008;33:1744–6. doi: 10.1364/ol.33.001744. [DOI] [PubMed] [Google Scholar]
- Patankar SV. Numerical Heat Transfer and Fluid Flow. Hemisphere; Washington, DC: 1980. [Google Scholar]
- Patwardhan SV, Bloch SR, Achilefu S, Culver JP. Time-dependent whole-body fluorescence tomography of probe bio-distributions in mice. Opt. Express. 2005;13:2564–77. doi: 10.1364/opex.13.002564. [DOI] [PubMed] [Google Scholar]
- Prahl SA. Oregon Medical Laser Clinic; 1999. http://omlc.ogi.edu/spectra/hemoglobin/index.html. [Google Scholar]
- Rao J, Dragulescu-Andrasi A, Yao H. Fluorescence imaging in vivo: recent advances. Curr. Opin. Biotech. 2007;18:17–25. doi: 10.1016/j.copbio.2007.01.003. [DOI] [PubMed] [Google Scholar]
- Roy R, Godavarty A, Sevick-Muraca EM. Fluorescence-enhanced optical tomography of a large tissue phantom using point illumination geometries. J. Biomed. Opt. 2006;11:044007. doi: 10.1117/1.2338807. [DOI] [PubMed] [Google Scholar]
- Roy R, Godavarty A, Sevick-Muraca EM. Fluorescence-enhanced three-dimensional lifetime imaging: a phantom study. Phys. Med. Biol. 2007;52:4155–70. doi: 10.1088/0031-9155/52/14/009. [DOI] [PubMed] [Google Scholar]
- Schulz RB, Peter J, Semmler W, D’Andrea C, Valentini G, Cubeddu R. Comparison of noncontact and fiber-based fluorescence mediated tomography. Opt. Lett. 2006;31:769–71. doi: 10.1364/ol.31.000769. [DOI] [PubMed] [Google Scholar]
- Schulz RB, Ripoll J, Ntziachristos V. Experimental fluorescence tomography of tissues with noncontact measurements. IEEE Trans. Med. Imaging. 2004;23:492–500. doi: 10.1109/TMI.2004.825633. [DOI] [PubMed] [Google Scholar]
- Smith AM, Duan H, Mohs AM, Nie S. Bioconjugated quantum dots for in vivo molecular and cellular imaging. Adv. Drug Deliv. Rev. 2008;60:1226–40. doi: 10.1016/j.addr.2008.03.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soloviev VY, McGinty J, Tahir KB, Neil MAA, Sardini A, Hajnal JV, Arridge SR, French PMW. Fluorescence lifetime tomography of live cells expressing enhanced green fluorescent protein embedded in a scattering medium exhibiting background autofluorescence. Opt. Lett. 2007;32:2034–6. doi: 10.1364/ol.32.002034. [DOI] [PubMed] [Google Scholar]
- Soubret A, Ntziachristos V. Fluorescence molecular tomography in the presence of background fluorescence. Phys. Med. Biol. 2006;51:3983–4001. doi: 10.1088/0031-9155/51/16/007. [DOI] [PubMed] [Google Scholar]
- Soubret A, Ripoll J, Ntziachristos V. Accuracy of fluorescent tomography in the presence of heterogeneities: study of the normalized born ratio. IEEE Trans. Med. Imaging. 2005;24:1377–86. doi: 10.1109/tmi.2005.857213. [DOI] [PubMed] [Google Scholar]
- Stout DB, Chow PL, Silverman R, Leahy RM, Lewis X, Gambhir S, Chatziioannou A. Creating a whole body digital mouse atlas with PET, CT and cryosection images. Mol. Imaging Biol. 2002;4:S27. [Google Scholar]
- Talukdar P. Radiative heat transfer for irregular geometries with the collapsed dimension method. Int. J. Therm. Sci. 2005;45:103–9. [Google Scholar]
- Talukdar P. Discrete transfer method with the concept of blocked-off region for irregular geometries. J. Quant. Spectrosc. Radiat. Tranfer. 2006;98:238–48. [Google Scholar]
- Thompson AB, Hawrysz DJ, Sevick-Muraca EM. Near-infrared fluorescence contrast-enhanced imaging with area illumination and area detection: the forward imaging problem. Appl. Opt. 2003;42:4125–36. doi: 10.1364/ao.42.004125. [DOI] [PubMed] [Google Scholar]
- Venugopal V, Chen J, Lesage F, Intes X. Full-field time-resolved fluorescence tomography of small animals. Opt. Lett. 2010;35:3189–91. doi: 10.1364/OL.35.003189. [DOI] [PubMed] [Google Scholar]
- Wernick MN, Aarsvold JN. Emission Tomography. Elsevier; Amsterdam: 2004. [Google Scholar]
- Zacharakis G, Ripoll J, Weissleder R, Ntziachristos V. Fluorescent protein tomography scanner for small animal imaging. IEEE Trans. Med. Imaging. 2005;24:878–85. doi: 10.1109/tmi.2004.843254. [DOI] [PubMed] [Google Scholar]
- Zacharopoulos AD, Svenmarker P, Axelsson J, Schweiger M, Arridge SR, Andersson-Engels S. A matrix-free algorithm for multiple wavelength fluorescence tomography. Opt. Express. 2009;17:3025–35. doi: 10.1364/oe.17.003042. [DOI] [PubMed] [Google Scholar]