Hippocampal CA1 pyramidal neurons exhibit type 1 phase-response curves and type 1 excitability

Abstract

Phase-resetting properties of neurons determine their functionality as integrators (type 1) vs. resonators (type 2), as well as their synchronization tendencies. We introduce a novel, bias-correction method to estimate the infinitesimal phase-resetting curve (iPRC) and confirm type 1 excitability in hippocampal pyramidal CA1 neurons in vitro by two independent methods. First, PRCs evoked using depolarizing pulses consisted only of advances, consistent with type 1. Second, the frequency/current (f/I) plots showed no minimum frequency, again consistent with type 1. Type 1 excitability was also confirmed by the absence of a resonant peak in the interspike interval histograms derived from the f/I data. The PRC bias correction assumed that the distribution of noisy phase resetting is truncated, because an input cannot advance a spike to a point in time before the input (the causal limit) and successfully removed the statistical bias for delays in the null PRC in response to zero-magnitude input by computing the phase resetting as the mean of the untruncated distribution. The PRC for depolarization peaked at late phases and decreased to zero by the end of the cycle, whereas delays observed in response to hyperpolarization increased monotonically. The bias correction did not affect this difference in shape, which was due instead to the causal limit obscuring the iPRC for depolarization but not hyperpolarization. Our results suggest that weak periodic hyperpolarizing drive can theoretically entrain CA1 pyramidal neurons at any phase but that strong excitation will preferentially phase-lock them with zero time lag.

hippocampal ca1 neurons participate in various brain rhythms in vivo, most notably in the gamma and theta bands (Buzsaki 2006; Buzsaki et al. 1983). Experiments have confirmed that inhibitory drive can phase-lock rhythmically firing CA1 neurons in the theta (Cobb et al. 1995), beta (Bibbig et al. 2007), and gamma (Whittington et al. 1997) bands, resulting in synchrony among groups of CA1 neurons. Phase-response curves, also called phase-resetting curves (PRCs) can be an important tool to study oscillations and synchronization (Glass and Mackey 1988; Kuramoto 1984; Winfree 2001). PRCs measure how much an input delays or advances the timing of the next spike in a rhythmically firing neuron. Intuitively, a neuron can fire with a constant time lag relative to a periodically applied input in the presence of jitter, only if the phase resetting tends to minimize the effect of jitter, defined as the inevitable variability in the spike times of actual neurons. Jitter is minimized when inputs arriving just before or just after the constant time lag advance the next spike less or delay it more than those arriving slightly earlier. Then, a spike that occurs “too early” relative to a periodic input on one cycle will occur later in the next, closer to the desired constant lag. Similarly, a spike that occurs “too late” relative to a periodic input on one cycle will occur earlier in the next, again closer to the desired constant lag. Thus advances must decrease with increasing phase, and delays must increase with increasing phase in the vicinity of an input that produces a spike with the desired constant time lag. This intuitive observation shows that the slope of the PRC at the point corresponding to the timing of this input is critical to the ability of neurons to phase-lock to a common periodic input. However, until recently, phase-resetting properties of CA1 neurons had not been measured directly. The effect of jitter on the measurement of the PRC presents a difficult problem of great current interest (Ermentrout et al. 2011; Phoka et al. 2010, Polhamus et al. 2012) that is partially addressed in this study.

The PRC in response to a specific finite input, such as a postsynaptic potential, has been called the spike time response curve (STRC) (Netoff et al. 2005b), whereas the PRC in response to a vanishingly small input is called the infinitesimal PRC (iPRC) (Ermentrout 2002; Rinzel and Ermentrout 1998). The iPRC can theoretically be used to predict the response to any arbitrary input or combination of inputs. PRCs in response to a depolarization can be type 1 (i.e., consisting solely of advances) or type 2 (i.e., consisting of both delays and advances) (Hansel et. al 1995). In addition, the PRC type is correlated with neuronal excitability type (Ermentrout 1996; Izhikevich 2007; Rinzel and Ermentrout 1998) (see discussion for exceptions), as defined by Hodgkin (1948): type 1 excitability is characterized by a gradual onset of spiking at low frequencies near the rheobase, whereas type 2 excitability is characterized by a sharp frequency threshold, below which they could not be induced to spike. Neurons with type 1 iPRCs have type 1 excitability, which allows them to function like integrators and spike at arbitrarily low frequencies. On the other hand, neurons with type 2 iPRCs have type 2 excitability, which allows them to operate more like resonators with a preferred frequency range. Typical type 1 PRCs tend to favor synchronization with zero phase lag to a periodic inhibition, whereas typical type 2 PRCs tend to favor synchronization with zero phase lag to a periodic excitation (Ermentrout 1996). These tendencies suggest that networks of type 1 neurons would synchronize due to reciprocal inhibitory coupling, whereas networks of type 2 neurons would synchronize with excitatory coupling. The PRC type also has been hypothesized to determine the tendency to synchronize a population receiving correlated noisy inputs (Galan et al. 2007). There are many techniques for measuring an iPRC [for a review, see Torben-Nielsen et al. (2010)], but here, we use a direct approach (Achuthan et al. 2011a; Galan et al. 2005) by applying small current pulses at various phases.

Most previous studies in pyramidal neurons measured the PRC or excitability type but not both. Layer 5 neocortical pyramidal neurons in rat motor (Tsubo et al. 2007), rat barrel (Stoop et al. 2000), and cat sensorimotor cortex (Reyes and Fetz 1993a, b) have mostly type 1 PRCs. On the other hand, layer 2/3 pyramidal cells in rat motor cortex tend to exhibit type 2 PRCs (Tsubo et al. 2007); however, in a different study, layer 2/3 pyramidal cells in rat somatosensory cortex displayed type 1 excitability (Tateno et al. 2004). A possible explanation of this variability is suggested by a study (Stiefel et al. 2008) in which rat layer 2/3 pyramidal neurons in visual cortex were equally likely to have type 1 or type 2 PRCs; the application of the cholinergic agonist carbachol favored a switch to type 1 PRCs, presumably by reducing the muscarine-sensitive potassium current. Here, we focus on hippocampal CA1 pyramidal neurons, which are thought to function as integrators (Prescott et al. 2008) with type 1 excitability (Gustafsson and Wigstrom 1981) but have recently been reported to have type 2 PRCs (Ota et al. 2011).

METHODS

Electrophysiology.

Transverse hippocampal slices (400 μm thick) were prepared from 7- to 10-wk-old male Sprague Dawley rats, according to methods approved by the Louisiana State University Health Sciences Center Institutional Animal Care and Use Committees, as described previously (Gasparini et al. 2007). Briefly, rats were anesthetized with an intraperitoneal injection of ketamine and xylazine, perfused through the ascending aorta with an oxygenated solution just before death, and decapitated. The external solution used for recordings contained (in mM) NaCl 125, KCl 2.5, NaHCO₃ 25, NaH₂PO₄ 1.25, CaCl₂ 2, MgCl₂ 1, and dextrose 25 and was saturated with 95% O₂ and 5% CO₂ at 34–36°C (pH 7.4). CA1 pyramidal neurons were visualized using a Zeiss Axioskop (Carl Zeiss, Oberkochen, Germany), equipped with infrared video microscopy and differential interference contrast optics. Somatic whole-cell patch-clamp recordings were performed using a BVC-700 amplifier (Dagan, Minneapolis, MN) in the active “bridge” mode. Patch pipettes had a resistance of 2–3 MΩ when filled with a solution containing (in mM) K-methylsulfonate 130, HEPES 10, NaCl 4, Mg₂ATP 4, Tris₂GTP 0.3, and phosphocreatine (di-Tris salt) 14 (pH 7.3). The series resistance was generally below 30 MΩ. The temperature of the recording chamber was kept at 34–36°C for the recordings. 6-Cyano-7-nitroquinoxaline-2,3-dione (20 μM), dl-2-amino-5-phosphonopentanoic acid (50 μM), and gabazine (12.5 μM) were added to the recording solutions to block AMPA and N-methyl-d-aspartate glutamatergic receptors and GABA_A receptors, respectively.

PRC data analysis.

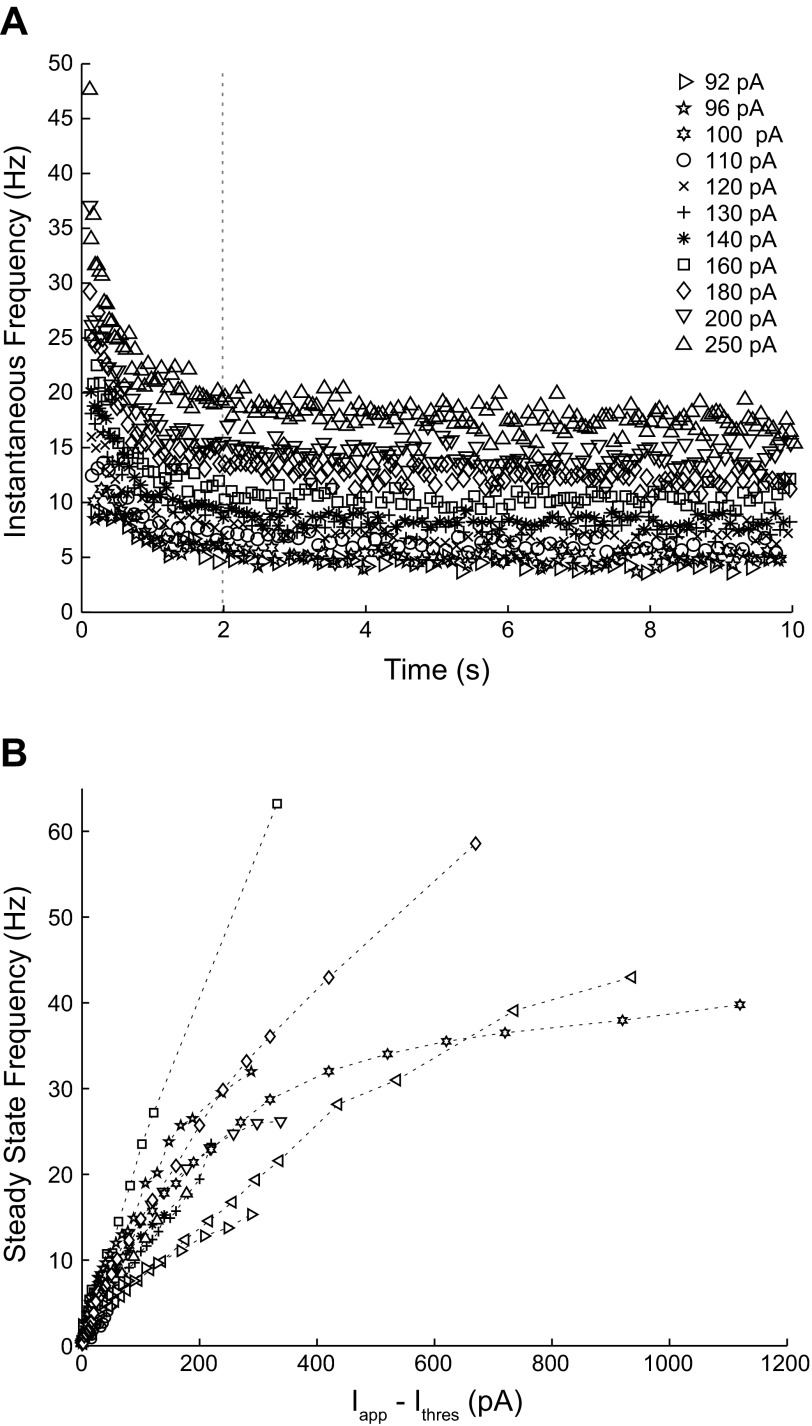
We injected sufficient levels (100–340 pA) of somatic current in the soma to evoke spike firing at 7–12 Hz. We allowed the firing rate to stabilize for 10 s, and we applied small, brief depolarizing or hyperpolarizing (Fig. 1, A1 and B1, respectively) current pulses every seventh cycle. The pulses were usually 3 ms long with an amplitude of 40–110 pA. A phase of zero was assigned to an upward threshold crossing of −14 mV and a phase of one to the next threshold crossing. Intermediate phases θ were calculated by normalizing the stimulus interval (ts) by the intrinsic period (P_i); P_i was calculated as the mean of three interspike intervals (ISIs) before the cycle that contains the perturbation. The phase resetting (Fig. 1, A2 and B2) was calculated by the following formula: f(θ) = (P₁ − P_i)/P_i, where P₁ is the period of the cycle that contains the perturbation. If the next spike time is delayed (advanced), the cycle period is lengthened (shortened), and the phase resetting by our convention is positive (negative). The mean phase resetting was calculated for 50 rolling bins (Fig. 1, A2 and B2). The bins were 0.05 phase units in width, with the first bin beginning at phase zero; then, each successive bin was shifted by 0.02 phase units to smooth the noisy data.

Fig. 1.

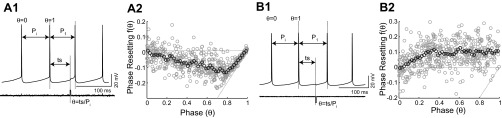
Direct measurement of infinitesimal phase-resetting curve (PRC) in CA1 pyramidal neurons. A1: a depolarizing current pulse, applied at a stimulus interval (ts) after a spike at a phase of θ, results in a cycle length (P₁) that may be different from the intrinsic period (P_i) which, in practice, is the average of the preceeding 3 cycle periods. A2: the phase resetting [f(θ); gray circles] due to depolarizing pulses is the normalized difference in cycle period. The data were smoothed using a rolling average (black circles). The causal limit (θ − 1) is indicated by the diagonal, dashed line. B1: same as A1 but for a hyperpolarizing pulse. B2: same as A2 but for a hyperpolarizing pulse.

Normalization of the PRCs was complicated by their noisy nature and by the difference in shape exhibited in response to depolarization and hyperpolarization. The former was rank ordered by the slope of the best linear fit at phases <0.8 and normalized by the peak value of the strongest resetting curve. The latter was rank ordered by the mean value between 0.8 and 1.0, where a plateau seemed to have been reached, and normalized by the peak value of the strongest resetting curve.

Frequency/current curves.

The steady-adapted rate was obtained by averaging the data after 2 s elapsed, provided that visual inspection confirmed the attainment of a steady rate.

Modeling.

The Morris-Lecar (1981) model with a fixed time step of 0.1 µs and zero mean white current noise was used to characterize the distribution of ISI histograms for type 1 and type 2 model neurons, as the constant baseline stimulus current (I) was increased. The parameters used for type 1 and type 2 regimes are given in Rinzel and Ermentrout (1998).

RESULTS

An analytical expression for the null PRC provides the correct null hypothesis for phase resetting.

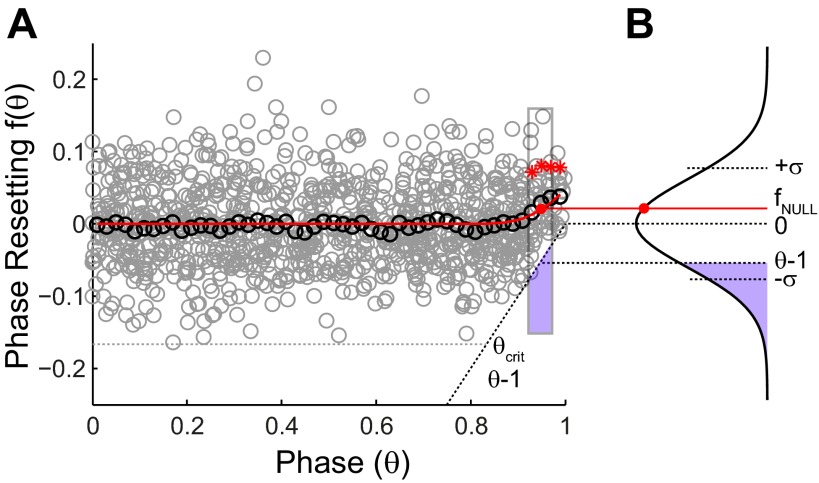
The phase resetting in the absence of any input perturbation was measured as a control in each of the 26 neurons examined. Phoka et al. (2010) and Polhamus et al. (2012) have demonstrated clearly that the PRC observed in response to no input, that is, the null PRC, is nonzero at late phases. Fig. 2 shows an example of a null PRC, in which a hypothetical, random input of zero magnitude was applied in cycles immediately preceding the cycle that was actually perturbed. Since no perturbation was actually delivered, no phase resetting should be observed. Nonetheless, for each neuron, a significant difference from zero was observed at P < 0.05 for the three to six contiguous points (Fig. 2A) to the left of a phase of one representing phases >0.88–0.94, respectively. Since an input cannot advance a spike to before the input was applied, there is a hard causal limit on the observed resetting, f_obs(θ). This limit on advances is equal in length and opposite in sign to the normalized time until the next spike is expected in the absence of an input, or θ − 1 (Fig. 2A). To account analytically for the shape of the null PRC, we need only assume that the measured PRC has a Gaussian distribution around the true value and that the postulated, normal distribution is left truncated (Fig. 2B) at a value of (θ − 1)/σ, where σ is the SD of the untruncated Gaussian. In the absence of input, the mean of the untruncated Gaussian distribution is clearly zero, because applying zero input should have zero effect on the resetting, but the mean of the truncated distribution will be >0 by an observable amount at late phases.

Fig. 2.

Null PRC. A: a hypothetical, 0-magnitude perturbation was analyzed analogously to the real perturbations in Fig. 1. The resetting (gray circles) and the smoothed average (black circles) were calculated in the same way. The red asterisks indicate resetting that differs significantly from 0 mean. The dashed line indicates the causal limit, and the phase at which its effect becomes evident is θ_crit. The correction is illustrated for a particular bin outlined in gray, with the portion truncated by the causal limit shown in purple. The red dot indicates the observed phase resetting. B: the SD (σ) was estimated from the values to the left of θ_crit. f_NULL, null resetting.

The mean of the truncated distribution (Greene 2003) for each phase θ is

$$f_{null}\left(\theta \right)=\frac{\sigma \phi \left(\frac{\theta -1}{\sigma }\right)}{1-\Phi \left(\frac{\theta -1}{\sigma }\right)}$$ (1)

Substituting in the formulas for the probability density function ϕ for the normal distribution, as well as for the cumulative probability distribution function Φ in terms of the error function (erf), we obtain

$$f_{null}\left(\theta \right)=\sigma \frac{\frac{1}{\sqrt{2\pi }}{e}^{\frac{-{\left(\theta -1\right)}^2}{2{\sigma }^2}}}{\frac{1}{2}-\frac{1}{2}erf\left(\frac{\theta -1}{\sigma \sqrt{2}}\right)}$$ (2)

The expression above has a single unknown—the SD σ of the null resetting—which was determined as follows. We estimated θ_crit by identifying the phase at which the Bermuda triangle (Phoka et al. 2010) of forbidden phase-resetting values becomes evident, and then we calculated the SD σ of the null phase resetting only for phases to the left of this limit, θ_crit. We neglected any dependence of the variance on phase (Ermentrout et al. 2011). The “observed” phase resetting was then binned and averaged (Fig. 2A; see methods) to compare it with the theoretical expression (Fig. 2A) derived from Eq. 2 above. The theoretical expression provides a reasonable fit to the data (Fig. 2A). Moreover, when significance was recalculated after subtracting the null PRC value from the data, the significance essentially disappears, as it should in the absence of an input. Specifically, of the 26 neurons considered, only two single-isolated bins in two different neurons achieved significance using the Student's t-test at a significance level of P < 0.05. Thus the correct null hypothesis for no input is given by Eq. 2, and the assumption of a truncated Gaussian distribution seems well supported.

Sampling bias for measured PRCs.

For resetting in response to an actual perturbation, we can no longer assume zero mean but must instead infer the true mean f_true(θ) of the phase-resetting value from the observed mean f_obs(θ). An approach analogous to that in Eq. 1 was taken to obtain the observed nonzero mean of the Gaussian in terms of the true mean

$$f_{obs}-f_{true}=\frac{\sigma \phi \left(\frac{\theta -1-f_{true}}{\sigma }\right)}{1-\Phi \left(\frac{\theta -1-f_{true}}{\sigma }\right)}$$ (3)

Substituting in the formula for the cumulative distribution in terms of the error function (erf) and rearranging, we obtain

$$f_{obs}\left(\theta \right)=f_{true}+\sigma \frac{\frac{1}{\sqrt{2\pi }}{e}^{\frac{-{\left(\theta -1-f_{true}\right)}^2}{2{\sigma }^2}}}{\frac{1}{2}-\frac{1}{2}erf\left(\frac{\theta -1-f_{true}}{\sigma \sqrt{2}}\right)}$$ (4)

We were not able to find a closed-form solution, but given σ, θ, and f_obs(θ), Eq. 4 can be solved numerically for f_true(θ) for phases greater than θ_crit.

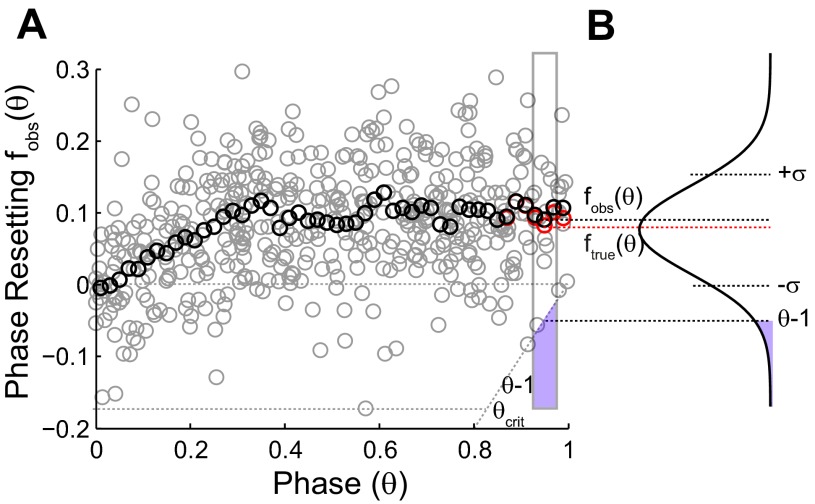
Fig. 3 illustrates how the bias was removed from a PRC in response to hyperpolarizing input pulses. The individual data points in Fig. 3A cannot fall below the causal limit (θ − 1), resulting in a truncation (Fig. 3B) of the distribution of the data points. Again, the dependence of the variance on the phase (Ermentrout et al. 2011) was ignored, and the variance in the causal-limit region was estimated using the variance of the points to the left of θ_crit. The estimate of the true mean for the bins to the right of θ_crit was calculated using Eq. 4. In sum, the PRC bias correction assumes a Gaussian distribution for noisy phase resetting that is truncated, because an input cannot advance a spike to a point in time before the input (the causal limit) and attempts to remove the resultant statistical bias for delays by computing the phase resetting as the mean of the untruncated distribution.

Fig. 3.

Correcting PRCs in response to inhibition for statistical bias. A: the raw phase-resetting data (gray circles) are smoothed (black circles) and corrected for bias (red circles). An example calculation is shown for the rectangular bin outlined in gray. The mean (black circle) at the center of the bin does not represent the true mean or peak of the distribution shown in B because of the purple region truncated by the causal-limit line, whereas the true mean (red circle) does. The SD σ was estimated from the values to the left of θ_crit. f_obs(θ), observed mean of phase resetting; f_true(θ), true mean of phase resetting.

Normalization shows the likely shape of the iPRC.

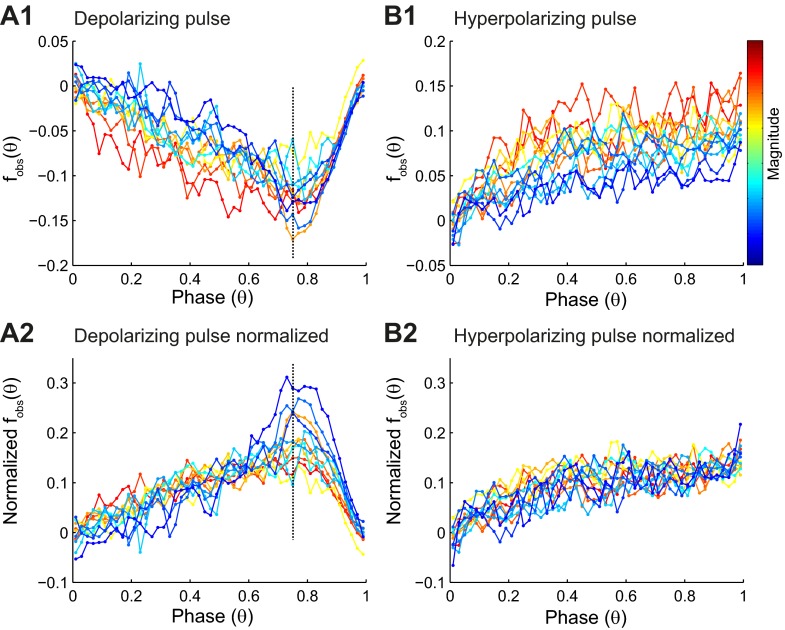
PRCs, measured in response to a depolarizing pulse (n = 12; Fig. 4A1), were clearly type 1, because only advances were observed in the mean values. A typical PRC decreased monotonically until a maximum absolute value was achieved between a phase of ∼0.75 and 0.8 and then returned to zero, mostly along the causal-limit line.

Fig. 4.

Summary of PRC data. A1: the binned averaged data (filled circles) for PRCs, measured in 12 different neurons in response to depolarizing pulse, are color coded for PRC magnitude, with red representing the strongest resetting. A2: PRCs normalized by the maximum resetting for each curve to illustrate that the shape is consistent prior to reaching the causal limit. Points to the right of the vertical, dashed line are influenced largely by the proximity of the causal limit. Note that normalization reverses the sign and facilitates comparison with PRCs measured in response to hyperpolarization in B2. B1: the binned averaged data as in A1 for PRCs measured in response to hyperpolarization (n = 14). B2: PRCs normalized by the maximum resetting for each curve. The shape is noisy but consistent across magnitudes.

The PRCs in response to a hyperpolarizing pulse (n = 14; Fig. 4B1) were also clearly type 1, because only delays were observed in the mean values. Theoretically, the response to a weak hyperpolarization should be opposite in sign but otherwise identical to that for a weak depolarization. However, typical PRCs in response to hyperpolarization did not show a peak but increased monotonically and appeared to plateau or at least increase more slowly after a phase of ∼0.3. The averaged data for each experiment are shown, color coded by PRC magnitude, determined as explained in methods. Discounting the causal-limit region in the PRCs in response to depolarization, the maximal sensitivity of spike timing to an input occurs late in the cycle.

The iPRC is the response to a weak input, and for very weak inputs, even a strong, nonlinear system behaves linearly, meaning that scaling the magnitude of the input should scale the observed phase resetting by the same factor. The theoretical scaling behavior is not observed if the pulse is too weak or too brief, because the PRC is lost in the noise. On the other hand, if the pulse is too strong, the measured PRC may no longer linearly scale with pulse strength so that the shape of the iPRC is not preserved. Therefore, the proof that the iPRC has been obtained is the identification of a scaling region (Achuthan et al. 2011a), in which the shape of the PRC is invariant to the magnitude of the resetting. Fig. 4A2 shows the normalized phase resetting measured in response to depolarizing pulses. To the left of the causal-limit region (Fig. 4, A1 and A2), normalization decreases the separation between the traces and shows that the shapes are quite similar. Near the causal limit, increasing the magnitude of the input does not affect the magnitude of the resetting very much, so normalization actually increases the separation between the traces at late phase, where causal-limit truncation is prominent. Fig. 4B2 shows the normalized phase resetting measured in response to hyperpolarizing pulses. The curves in Fig. 4B2 are self consistent in that the variability between traces is significantly less (P < 0.000006, using a Wald test) than the variability within traces. We can also compare them with the normalized PRCs in Fig. 4A2, because both curves are normalized to about the same peak value (0.15 delay or advance). The iPRCs for hyperpolarization are similar to those for depolarization if we only compare the curves prior to the artifact introduced by the severe causal-limit truncation. Because of this artifact, the shape in Fig. 4B2 may be a better approximation to the shape of the iPRC than that in Fig. 4A2.

Correction for bias fails in causal-limit region and has little effect on iPRC for hyperpolarization.

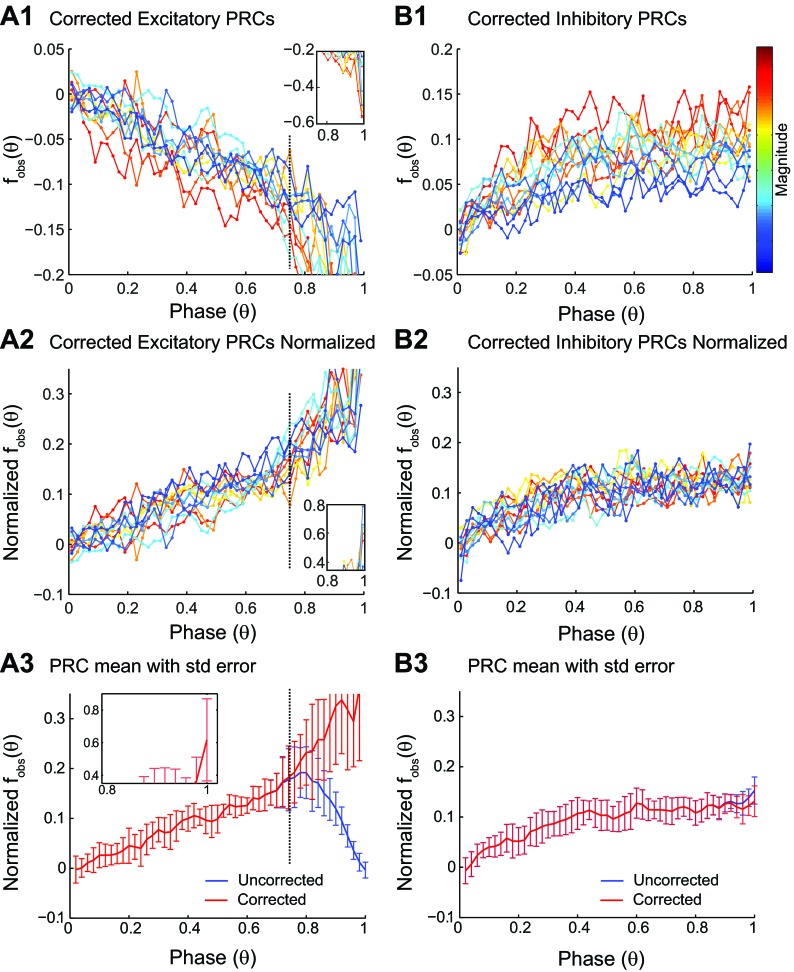
Figure 5 shows the effect of the correction for bias described in Fig. 3 to the data in Fig. 4. For PRCs in response to depolarizing pulses (Fig. 5A1), the phase resetting was so tightly clustered around the causal limit at late phases (see Fig. 1A2) that no useful information about the iPRC could be extracted at those late phases. With such small tails, it was difficult to estimate accurately the peak of the distribution, and the putative, corrected values fluctuated erratically (Fig. 5A1). Normalization (Fig. 5A2) only exacerbated this problem in the causal-limit region. The causal limit removes all information about phase resetting in response to depolarization, because in this region, an input is triggered immediately. Since the information is destroyed, no method can recover it, and applying a correction in this region simply increases the SE in the normalized PRC for depolarization (Fig. 5A3) but not for hyperpolarization (Fig. 5B3). The only real benefit that we derived from the bias correction of PRCs in response to depolarization is an explanation for the delays that are sometimes observed at very late phases (Wang et al. 2012) with excitation or depolarization; the explanation is that these delays are probably spurious and due to bias.

Fig. 5.

Effects of bias in PRC data. A1: the bias-corrected binned averaged data (filled circles) for PRCs, measured in 12 different neurons in response to depolarizing pulse, are color coded for PRC magnitude, with red representing the strongest resetting. The inset shows the presumably unreliable mean estimation from the residual remaining, severely truncated tail. A2: PRCs normalized by the maximum resetting for each curve to illustrate that the shape is consistent prior to reaching the causal limit, where the inset again shows the large fluctuations near the causal-limit region. Note that normalization reverses the sign and facilitates comparison with PRCs measured in response to hyperpolarization in B2. A3: SE (std error) for the corrected (but not the uncorrected curve) increases dramatically to the right of the dashed line, indicating the predominance of the causal-limit region. B1: the bias-corrected binned averaged data as in A1 for PRCs measured in response to hyperpolarization. B2: PRCs normalized by the maximum resetting for each curve. The shape is noisy but consistent across magnitudes. B3: no increase in SE is observed for the corrected vs. uncorrected version.

Theoretically (Ermentrout 2002), an iPRC is a periodic function that has the same value at zero and one. We hypothesized that the bias toward delays might be obscuring a downward trend at the end of the PRCs measured in response to hyperpolarizing pulses. However, the effect of the correction was not substantial, since Fig. 5, B1–B3, for the bias-corrected data closely resembles Fig. 4, B1 and B2, for the uncorrected data. We conclude that the effect of bias is not masking a trend in our data toward zero at the end, although the shape in Fig. 5B2 may be a slightly better approximation to the iPRC than Fig. 4B2, because of the slight bias correction that flattens the PRC at the end. The effect of an input at the end of a cycle (a phase of one) on the previous cycle is zero, because by definition, the previous cycle is over at a phase of one. Since the effect of an infinitesimally weak input should be continuous throughout the cycle (Ermentrout 2002), the true iPRC likely trends toward zero at a phase of one, despite the lack of a visible trend toward zero at a phase of one in the data. Due to the noisy scatter in the data that requires binning and averaging and the finite width of the pulse used to probe the iPRC, the resolution of the measurements is limited, and a sharp downward trend might not be detected. We further conclude that the actual peak of the PRC cannot be resolved experimentally, due to the limitations imposed by the noise; weaker inputs than the ones shown in this study did not produce significant resetting.

Excitability type of CA1 neurons.

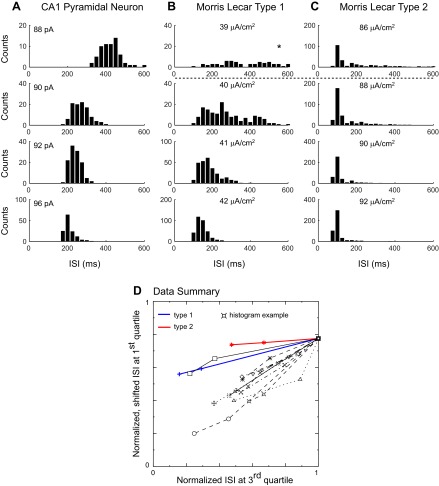
As stated in introduction, the iPRC type is thought to correlate with the excitability type, as defined by Hodgkin (1948). Therefore, we also measured spike frequency as a function of the level of injected current. As shown in Fig. 6A, CA1 pyramidal neurons exhibit spike frequency adaptation. Figure 6B shows the dependence of the steady, adapted frequency on the injected current (n = 13). The frequency/current (f/I) curve is approximately linear near the rheobase and flattens out at higher levels of the injected current. No abrupt frequency threshold is evident in Fig. 6B. However, the abrupt frequency threshold attributed to type 2 excitability may be difficult to detect in the presence of noise [see Fig. 7.12 in Izhikevich (2007)]. One approach (Tateno et al. 2004) is to use the pattern exhibited by the coefficient of variation (CV) of the ISIs, as the injected current is increased to distinguish between type 1 and type 2 excitability. We were not able to discriminate between excitability types using the CVs. Instead, we examined the distribution of the ISIs in the experimental data; a representative example is shown in Fig. 7A. We then compared the experimental data with templates created by using simulated, noisy Morris-Lecar (1981) model neurons. We found that as the levels of injected current were increased, the progressive alterations in the shape of the distribution of the ISIs were strikingly different for noisy type 1 (Fig. 7B) vs. type 2 (Fig. 7C) model neurons in the fluctuation-driven regime, in which the mean excitation level is below the rheobase. The distribution for type 1 was broad for currents that, in the absence of noise, were near the rheobase. As the levels of injected current were increased, the distribution became narrower, and its peak quite noticeably shifted to the left. On the other hand, the distribution for type 2 was highly asymmetric for currents that in the absence of noise were below the rheobase, with a prominent tail on the right and a sharp peak near the resonant frequency. As the levels of injected current were increased, the area under the right tail decreased, and the peak became sharper, but the location of the peak was shifted only slightly. Qualitatively representative histograms obtained from somatic recordings of CA1 pyramidal neurons (Fig. 7A) exhibited a pattern more consistent with type 1 (Fig. 7B). No resonant frequency peak accompanied by shrinking right tails was evident; instead, a gradual narrowing of the distributions and leftward shift were always observed. We quantified the change in the shapes of the distributions with an increasing applied current by plotting the value of ISIs at the end of the first quartile vs. that at the end of the third quartile of each distribution for three current levels near threshold (Fig. 7D). For the type 1 and type 2 model templates, these points are strikingly colinear, suggesting that at least near threshold, the slope of this plot may be constant. The preferential shrinkage of the right tail compared with the left one that is observed for type 2 is more prominent than for type 1, which translates to a flatter slope for type 2 compared with type 1. Most experimental neurons (n = 10) showed an even steeper slope than the type 1 template, consistent with the type 1 classification. This method was not able to classify the remaining three neurons.

Fig. 6.

CA1 pyramidal neuron frequency/current (f/I) curves exhibit type 1 excitability. A: time course of interspike intervals (ISIs) during applied depolarizing current steps (I_app) in a single neuron. Adaptation is evident at higher frequencies. B: the f/I curves for 13 CA1 pyramidal neurons have spiking onset at low frequency at the rheobase. Each symbol represents a different neuron and was calculated as the average of the data points measured after 2 s (vertical, dashed line in A). I_thres, current threshold.

Fig. 7.

CA1 neurons near the rheobase exhibit ISI histograms characteristic of type 1 excitability. A: ISI histograms for a representative CA1 neuron as the applied current is increased. After 2 s, the firing rate is generally flat. Only the ISIs after the 2-s adaptation period were included in the analysis at each level of current injected. B: ISI histograms for a type 1 Morris-Lecar (1981) model neuron as the applied current is increased. The rheobase in the absence of noise is 40 μA/cm², and the stimulus current I ranged from 39 (top) to 42 μA/cm², with SD (σ) = 0.005 for the current noise. The asterisk above the top histogram indicates that the mean was 963 ms, so most of the distribution was truncated to plot it on the same time scale as the others. C: ISI histograms for a type 2 Morris-Lecar (1981) model neuron as the applied current is increased. The rheobase in the absence of noise is 88 μA/cm² (actually, the model is bistable between 88 and 92 μA/cm²), and the stimulus current I ranged from 86 (top) to 92 μA/cm², with σ = 0.01 for the current noise. The horizontal, dashed line represents the rheobase in the absence of noise for the simulations. D: plot of the value of the 1st-quartile (the value of ISI >25% of the ISIs) point on the y-axis as a function of the value of the 3rd-quartile (the value of ISI >75% of the ISIs) point on the x-axis for 3 current levels near threshold. For each neuron, the ISIs were normalized by the 3rd-quartile value at the lowest applied current, and the y-axis points were shifted for easier comparison of the slopes. Neither of these manipulations affects the slope. The ISI distributions for type 1 and type 2 shift to the left (faster frequency and smaller ISIs) as the injected current is increased. However, for type 2, the right tail shrinks very rapidly with respect to the left tail, which causes a small shift in the 1st-quartile point compared with the 3rd. The flatter the slope, the smaller the relative shift of the 1st-quartile point with respect to the 3rd. In general, the experimental neurons do not exhibit the extreme flatness characteristic of type 2 near threshold. Ten experimental neurons exhibited slopes consistently steeper than the type 1 template; 1 had an inconsistent slope that might be either type, and 2 neurons were not plotted, because the data were sampled so sparsely that the slope reversed signs.

DISCUSSION

We have demonstrated, by two methods, that hippocampal CA1 pyramidal neurons in vitro are type 1; most studies measure the PRC or the f/I curve but not both. The type 1 iPRCs measured here are consistent with the type 1 excitability, as evidenced by the lack of an abrupt frequency threshold in the f/I curves and confirmed by the histogram method. We introduced two novel methods: one for correcting the sampling bias in the PRC and the other for confirmation of excitability type in the presence of noise. The correction for sampling bias assumes that the causal limit truncates a noisy Gaussian distribution of the phase resetting about the mean value and attempts to recover the true mean of the untruncated distribution. The use of ISI histograms to clearly distinguish between type 1 and type 2 excitability is consistent with the ideas in Izhikevich (2007) but, to our knowledge, has not been used previously. Although the classification of PRC and excitability type shown here is consistent for CA1 pyramidal neurons, this may not always be the case. For example, the PRC type did not strictly correspond to excitability type in interneurons of rat somatosensory neurons (Tateno and Robinson 2007). Also, correspondence of type 1 excitability and type 1 PRC is not exact but depends on the underlying bifurcation occurring at a point in the cycle at which a depolarizing stimulus will lead to an advance (Ermentrout et al. 2012).

Comparison with other approaches to correct for sampling bias.

Phoka et al. (2010) suggested another solution to eliminate the sampling bias. After calculating the phase and phase resetting the traditional way, the phase is recalculated by using the estimated intrinsic period to normalize the interval between the penultimate spike preceding the input and the input itself, instead of the interval between the spike immediately preceding the input and the input itself. In general, these recalculated points will have a phase greater than one. However, on some occasions when the interval between the two spikes immediately preceding the input is shorter than the estimate of the intrinsic period, the phase of the input will be less than one. Then, the phase resetting is calculated using the normalized difference between the ISI preceding the input and the estimated period and is always an advance, since the reference period must be less than the estimated period to give a phase less than one by the method described above. This “resetting” is not determined by the timing of the input that follows it and is therefore unconstrained by any causal limit. This approach appropriately flattens the null PRC so that it becomes zero everywhere. Since the extra points are not dependent on pulse timing or magnitude, it is not clear that this approach is adequate for cases in which there is actual resetting that is dependent on the timing of the applied pulse.

Alternatively, Polhamus et al. (2012) assumed that 1) the unperturbed ISIs are drawn randomly from a Gaussian distribution, and 2) the intrinsic period for a perturbed cycle must be greater than the stimulus interval between the most recent spike and the input time, which left-truncates the distribution of the cycle periods. The unperturbed periods were averaged across the entire experiment; however, only periods larger than the stimulus interval were averaged to obtain the intrinsic period used to calculate the phase for that stimulus interval. Calculated phases greater than one are eliminated, thereby increasing the sampling of late phases within the cycle, which is an advantage of this method. Farries and Wilson (2012) used this method to remove sampling bias and also addressed the causal-limit problem by normalizing the resetting by the fraction of the stimulus that was delivered prior to action-potential generation. This approach did not resolve the observed differences in PRCs for depolarizing vs. hyperpolarizing pulses in their study or in ours (data not shown). Although the Polhamus et al. (2012) method flattens the null PRC when the x-axis for the flattened PRC is given in units of time for the stimulus interval, the causal-limit sampling bias should persist to some degree if the x-axis were given instead in units of phase, which is critical for an iPRC. The same group suggested other methods to obtain a better estimate of the true mean of the untruncated distribution: fit the histogram of the ISIs to a truncated Gaussian distribution using maximum likelihood estimates, or use a nonparametric estimator of the discrete probability and cumulative probability distributions of the ISI histograms.

The method presented in this paper assumes that there is a deterministic, intrinsic period on any given cycle and considers the phase, rather than the period, to be the random variable. Under our model, the reason some unperturbed periods are longer, and some are shorter, is that each cycle experiences noisy phase resetting. The phase can be visualized as a point moving around the unit circle at a fixed angular velocity determined by the intrinsic period, but the exact location of this point is jittered backward and forward by a one-dimensional random walk (analogous to one-dimensional Brownian motion), due to the inevitable noise encountered in a biological system. This jitter is manifested as noise in the observed phase resetting. The intrinsic period is not actually constrained to be larger than the stimulus interval, because delays may have accumulated during the stimulus interval, causing it to be longer than the intrinsic period, even if the intrinsic period is shorter than the stimulus interval. We prefer to consider the phase resetting as the random variable for this reason. Another reason we prefer to consider the phase as the random variable is that period can drift (Achuthan et al. 2011b) during an experiment, so we use a rolling window to estimate the mean period rather than pooling values across the whole experiment.

Relationship to prior studies of CA1 pyramidal neurons.

Consistent with our observations, previous studies have shown that CA1 pyramidal neurons have the ability to maintain steady, low (<1 Hz)-frequency firing rates and exhibit a linear f/I curve for the steady, adapted firing rates near the rheobase (Gustafsson and Wigstrom 1981; Lanthorn et al. 1984). These results are consistent with a functional integrator with a type 1 iPRC, such as the ones we measured in this study (Ermentrout 1996; Izhikevich 2007). However, subthreshold membrane potential oscillations have been observed in these neurons using current injections near the spike threshold (Leung and Yim 1991), which is consistent with a resonator with a type 2 iPRC.

Prescott et al. (2008) used modeling studies to show that increasing the net steady-state potassium current contribution in these neurons in the subthreshold regime, whether via shunting in a high-conductance state or via adaptation, favors a transition from type 1 to type 2 excitability. This is consistent with the neocortical study (Stiefel et al. 2008) that reported a switch in the opposite direction, from type 2 to type 1 PRCs, when the muscarine-sensitive potassium current is decreased. Prescott et al. (2008) then used the dynamic clamp (Pinto et al. 2001) to add shunting and adaptation currents to real CA1 pyramidal neurons. They noted that “it is impossible to demonstrate experimentally that the neuron can spike at rates arbitrarily close to zero spikes per second” to prove that a neuron has type 1 excitability. However, in every case, the minimum observed frequency did increase as a result of the manipulations, so the transitions that they hypothesized are plausible. The histogram method presented here might have more definitively established the putative transitions in excitability type. In any case, it is likely that under different arousal and modulatory levels, the excitation dynamics of these neurons may vary.

Recently, Ota et al. (2011) measured the iPRCs in hippocampal CA1 pyramidal neurons via an indirect method using a 10-ms pulse for neurons induced to fire with an intrinsic period of 50–80 ms. Indirect methods involve optimizing the deconvolution of various signals (Netoff et al. 2005a; Ota et al. 2009; Preyer and Butera 2005) to retrieve the iPRC. Ota et al. (2011) observed mostly type 2 iPRCs with delays early or in some cases, during most of the cycle. It is likely that some systematic difference in protocol and/or analysis is responsible for our divergent results. Example STRCs reported for hippocampal CA1 pyramidal neurons [see Figs. 5.13 and 5.14 in Netoff et al. (2012)] appeared to be weakly type 2 (meaning only a small, initial region of phase resetting opposite to the predominant delays or advances). The results of Netoff et al. (2012) agreed with ours, in that they reported a different shape for excitatory vs. inhibitory PRCs and also attributed the differences in the observed shapes to the limitations imposed by causality.

Functional significance.

All CA1 neurons examined exhibited type 1 excitability and type 1 PRCs. The shape of the PRCs in response to depolarization and hyperpolarization is different, mainly because the causal limit prevents the accurate measurement of the normalized response to depolarization; hence, the PRC in response to small hyperpolarizations, provides a better estimate of the iPRC. We conclude that the slope of the iPRC in CA1 pyramidal neurons is positive at all observable phases for the response to hyperpolarization and infer that the converse is likely true for the response to depolarization. If a neuron is unidirectionally driven by a periodic input with a forcing period equal to the perturbed cycle length due to an input at phase θ, then a stable phase-locking can only result if the slope of the PRC at phase θ is positive (Dror et al. 1999; Perkel et al. 1964). Under a weak coupling theory, the sign of the slopes would be preserved for purely inhibitory or purely excitatory synaptic potentials. Therefore, the implication is that an inhibitory drive could stably entrain, or phase-lock, these neurons at any phase, but an excitatory drive could not stably entrain, or phase-lock, these neurons at any phase. The concept of the iPRC breaks down for inputs that immediately trigger an action potential, because the whole idea of the iPRC is that the phase resetting produced by weak inputs is additive, whereas phase resetting clearly saturates at the causal limit. Therefore, the relevance of the iPRC for depolarizing inputs arriving at late phases is questionable, since the causal limit prevents the realization of this shape with depolarizing inputs that are not lost in the noise. In practice, excitatory inputs that arrive late enough to trigger a spike almost immediately can stably entrain these neurons, because they would fall in a positive-slope region of the PRC.

Phase-resetting theory and one-to-one phase-locking are appropriately used to explain the pyramidal interneuron gamma rhythm using a coupled oscillator theory (Börgers and Kopell 2003) if at least a subpopulation of pyramidal neurons receives sufficient background excitation levels to function as oscillators. Although CA1 pyramidal neurons clearly participate in neuronal rhythms, they do not necessarily fire on every cycle of the population rhythm (Bragin et al. 1995), and alternate theories have been proposed for rhythm generation (Brunel and Wang 2003) that take into account the sparse firing of pyramidal cells during gamma rhythms in vivo. These mean field theories postulate instead that all neurons are in the noisy, fluctuation-driven regime below the rheobase (Fig. 7, B and C) and that a population rhythm is generated by the delayed inhibition of the pyramidal cells via disynaptic feedback inhibition. Two recent network models of gamma oscillations (De Sancristóbal et al. 2013; Moca et al. 2012) show that even in the noisy fluctuation-driven regime, type 1 and type 2 neurons have different effects on the ability to maintain a constant network frequency and to endow the network with different response properties. Therefore, it is important to demonstrate that CA1 neurons, as components of a hippocampal network, are type 1 neurons, as we did here.

We found that in CA1 pyramidal neurons, the response to hyperpolarization is more informative regarding the iPRC than that to depolarization. We successfully characterized the bias responsible for the counterintuitive significance of the null PRC observed when no perturbation is applied. Although accounting for this bias did not substantially change our best estimate of the iPRC, this method may well improve the estimate in data from other neurons. Similarly, the histogram method for distinguishing type 1 and type 2 excitability may be useful in other preparations.

GRANTS

Funding for this work was provided by Grants R01-MH085387 and R01-NS054281 (to C. C. Canavier), R01-NS069714 (to S. Gasparini), and P30-GM103340.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: C.C.C. and S.G. conception and design of research; M.M.M. performed experiments; S.W. and M.M.M. analyzed data; C.C.C. and S.G. interpreted results of experiments; S.W. prepared figures; C.C.C. drafted manuscript; S.G. edited and revised manuscript; S.W., M.M.M., C.C.C., and S.G. approved final version of manuscript.