State-based decoding of hand and finger kinematics using neuronal ensemble and LFP activity during dexterous reach-to-grasp movements

Abstract

The performance of brain-machine interfaces (BMIs) that continuously control upper limb neuroprostheses may benefit from distinguishing periods of posture and movement so as to prevent inappropriate movement of the prosthesis. Few studies, however, have investigated how decoding behavioral states and detecting the transitions between posture and movement could be used autonomously to trigger a kinematic decoder. We recorded simultaneous neuronal ensemble and local field potential (LFP) activity from microelectrode arrays in primary motor cortex (M1) and dorsal (PMd) and ventral (PMv) premotor areas of two male rhesus monkeys performing a center-out reach-and-grasp task, while upper limb kinematics were tracked with a motion capture system with markers on the dorsal aspect of the forearm, hand, and fingers. A state decoder was trained to distinguish four behavioral states (baseline, reaction, movement, hold), while a kinematic decoder was trained to continuously decode hand end point position and 18 joint angles of the wrist and fingers. LFP amplitude most accurately predicted transition into the reaction (62%) and movement (73%) states, while spikes most accurately decoded arm, hand, and finger kinematics during movement. Using an LFP-based state decoder to trigger a spike-based kinematic decoder [r = 0.72, root mean squared error (RMSE) = 0.15] significantly improved decoding of reach-to-grasp movements from baseline to final hold, compared with either a spike-based state decoder combined with a spike-based kinematic decoder (r = 0.70, RMSE = 0.17) or a spike-based kinematic decoder alone (r = 0.67, RMSE = 0.17). Combining LFP-based state decoding with spike-based kinematic decoding may be a valuable step toward the realization of BMI control of a multifingered neuroprosthesis performing dexterous manipulation.

both neuronal ensemble (Carmena et al. 2003; Fetz 1999; Hochberg et al. 2006, 2012; Humphrey et al. 1970; Serruya et al. 2002; Taylor et al. 2002, 2003; Velliste et al. 2008; Wessberg et al. 2000) and local field potential (LFP) (Heldman et al. 2006; Mehring et al. 2003; O'Leary and Hatsopoulos 2006; Rickert et al. 2005) activity from various cortical areas can be used to predict movement kinematics of a single effector, such as arm end point or position of a computer cursor. Recent studies have demonstrated continuous decoding of multiple degrees of freedom (DoFs), including individual fingers (Aggarwal et al. 2009) or complete kinematics of the upper limb (Bansal et al. 2011; Vargas-Irwin et al. 2010; Zhuang et al. 2010). These studies all have demonstrated the ability to decode movement kinematics during ongoing movement. However, neural activity is not necessarily quiescent during periods of steady posture (Crammond and Kalaska 1996; Humphrey and Reed 1983), and attempting to decode movement kinematics during postural epochs can lead to inappropriate decoding of motion (Bokil et al. 2006). Brain-machine interfaces (BMIs) that will control an upper limb neuroprosthesis at all times will need to distinguish between periods of posture and movement autonomously to prevent unintended jitter of the prosthetic limb. Therefore, decoding behavioral states—such as baseline, reaction, movement, and hold—could be helpful in gating a kinematic decoder.

Previous work has shown that for goal-directed, voluntary movements, neural activity modulates differently during preparatory periods prior to the initiation of the movement, during the perimovement periods accompanying the movement itself, and during stable hold periods after the movement is complete (Crammond and Kalaska 2000). Cortical ensemble activity therefore has been used to predict temporal intervals between movements and to distinguish delay periods from movement (Lebedev et al. 2008). Relatively few studies have investigated how a state decoder could autonomously trigger a movement decoder, however. Using a state-machine, neuronal ensemble activity recorded from the premotor cortex (PM) has been used to decode planning activity during an instructed delay task (Achtman et al. 2007; Kemere et al. 2008), and spectral LFP features from the posterior parietal cortex (PPC) have been used to decode movement onset in a self-paced reach task (Hwang and Andersen 2009), with the output from the movement onset decoders then being used to trigger spike-based decoding of target location. Likewise, the spiking activity of neurons in the primary motor cortex (M1) has been used to detect the onset of movement, triggering a movement classifier to asynchronously decode movements of individual fingers (Acharya et al. 2008; Aggarwal et al. 2008a), wrist rotation, or different grasp patterns (Aggarwal et al. 2008b). This two-stage decoding approach, while effective for decoding discrete classes of movement, has not been applied previously in paradigms that require continuously decoding the kinematics of multiple DoFs.

In monkeys making reach-to-grasp movements to four different objects in space, we therefore examined decoding of both the behavioral state (baseline, reaction, movement, hold)—i.e., state decoding—and the kinematics of the arm, hand, and fingers—i.e., kinematic decoding—from the same data set. Although spikes can be used to distinguish periods of movement versus posture (Ethier et al. 2011), LFP activity may provide better discrimination of planning and movement than spikes recorded from the same region (Pesaran et al. 2002; Scherberger et al. 2005). We therefore investigated the optimal features for both the state and kinematic decoders by designing separate decoding models using either spikes or LFPs recorded from either the primary motor or premotor cortex. We then examined the extent to which using an LFP-based state decoder to trigger a spike-based kinematic decoder—i.e., state-based kinematic decoding—improved decoding of upper limb kinematics during entire reach-to-grasp movements from baseline through movement execution to final hold.

METHODS

Behavioral task.

This work analyzed data collected from two male rhesus monkeys (Macaca mulatta, monkeys X and Y) that have been the subject of previous studies (Mollazadeh et al. 2011). Each monkey was trained to sit in a primate chair and was visually cued to reach toward, grasp, and manipulate one of four objects—sphere, perpendicularly mounted cylinder (mallet), pushbutton, or peripheral coaxial cylinder (pull handle)—arranged on a planar circle at 45° intervals (Fig. 1A). Each object was mounted on the end of a 2- to 3-ft., 0.5-in.-diameter aluminum rod, and manipulation of the object operated a microswitch mounted at the opposite end of the rod. The monkey was seated in a custom polycarbonate primate chair that restrained the torso, left upper extremity, and legs but permitted the monkey to reach out with the right hand. All studies were approved by the University of Rochester Institutional Animal Care and Use Committee.

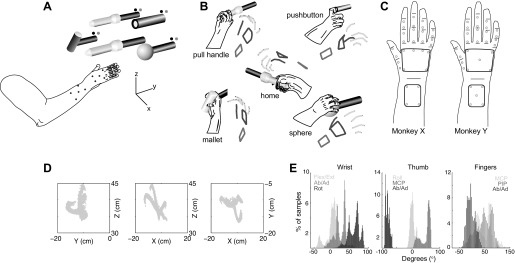
Fig. 1.

Experimental setup and task apparatus. A: subject was instructed to release a centrally located home object and reach toward, grasp, and manipulate 1 of 4 peripheral objects (sphere, mallet, pushbutton, pull handle) arranged in a planar circle. A set of blue LEDs cued which object to reach for, and green LEDs indicated when the object was manipulated. Upper limb kinematics were tracked with 30 optically reflective markers affixed to the monkey's right forearm, hand, and digits. B: drawings from digital video frames are shown adjacent to the reconstructed kinematics from the motion tracking system (stick figures). Grasping each object invoked a unique grasp conformation of the fingers and wrist. C: for monkey X, marker placement included 4 markers on the dorsal aspect of the forearm, 6 markers on the dorsal surface of the hand, 2 markers over the first metacarpal, 2 markers between the metacarpophalangeal (MCP) and proximal interphalangeal (PIP) joints for each digit, and 2 markers between the PIP and distal interphalangeal (DIP) joints for digits 2 through 5. For monkey Y, 5 markers were placed on the dorsal surface of the hand and the forearm. Distribution of kinematic data for monkey X is shown in Cartesian space (D; shown separately for x-, y-, and z-dimensions) and joint angle space (E; shown separately for joint angles of the wrist, thumb, and fingers).

Each behavioral trial began when the monkey first grasped a home cylindrical object and pulled it ∼1 cm against a small spring load. This home object was centrally located 13 cm from each of the peripheral objects and 32 cm directly in front of the monkey's right shoulder. After a variable initial hold period of 230–1,130 ms, during which the monkey was required to maintain its pull on the home cylinder, a blue LED [cue presentation (Cue)] next to one of the four peripheral objects instructed the monkey to release the home object [onset of movement (OM)] and reach toward and grasp the instructed peripheral object. Trials were aborted immediately if the monkey prematurely released the home object during the initial hold period or failed to release the home object within an allowed 1,000-ms reaction time.

Upon grasping the instructed peripheral object, the monkey was required to rotate the sphere object 45°, pull the perpendicularly mounted cylinder (mallet) object, depress the pushbutton object (12 mm diameter), or pull the peripheral coaxial cylinder object, each against its own small spring load. Illumination of a green LED next to the grasped object indicated successful completion of each manipulation [start of static hold (SH)]. The objects were selected to evoke a range of different grasp conformations that required fine manipulation of the fingers and wrist. Visual observation of the monkey performing the task indicated that manipulation of the mallet resulted in a large hand wrap, the pushbutton resulted in an index point, the coaxial cylinder (pull handle) resulted in a small hand wrap, and the sphere resulted in a finger-splayed wrap (Fig. 1B).

After grasp completion, the monkey was required to maintain the object in its final position for a 1,000-ms final hold period, at which time the blue LED was turned off [final hold complete (FH)] and the monkey received a food pellet reward (Bioserv, Frenchtown, NJ). After successful completion of a trial, the monkey was free to release the peripheral object and initiate another trial by once again pulling on the central home cylinder object. Trials were aborted immediately if the monkey manipulated a noninstructed object or released the instructed peripheral object before completion of the final hold period. Instructed objects were presented pseudorandomly, and error trials were repeated immediately for the same object until successfully completed. Table 1 summarizes the number of successful trials completed for each object type in each recording session, as well as their mean reaction times and movement times.

Table 1.

Summary of successful trials

	No. of Successful Trials
Recording Session	Sph	Mall	Pull	Push	Reaction Time, ms	Movement Time, ms
X0918	117	115	113	117	263 ± 100	274 ± 70
X1002	67	69	60	72	230 ± 51	295 ± 81
Y0211	168	167	164	171	445 ± 205	610 ± 300
Y0304	109	107	111	113	345 ± 49	490 ± 157

Reaction and movement times are reported as means ± SD. Sph, sphere; Mall, mallet; Pull, pull handle; Push, pushbutton.

Neural recording.

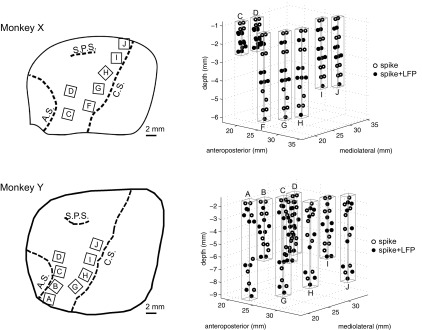
Spiking and LFP activity was recorded from multiple floating microelectrode arrays (FMAs; MicroProbes, Gaithersburg, MD) that were implanted in cortical motor areas contralateral to the trained hand. Each FMA included 16 Pt/Ir microwire recording electrodes with tip impedance of ∼0.5 MΩ, arranged in a triangular grid with an interelectrode spacing of 500 μm. Two additional low-impedance microelectrodes on each array served as reference and ground electrodes. Figure 2 illustrates the array configurations and implantation sites in the motor and premotor cortex from which the recordings analyzed here were obtained for each monkey, and additional details are given in Table 2. Five FMAs were implanted anterior to the central sulcus in monkey X (arrays F, G, H, I, J) and four in monkey Y (arrays G, H, I, J), such that they recorded from the anterior bank of buried cortex in the M1 upper extremity representation. Two additional FMAs in monkey X (arrays C, D) and four in monkey Y (arrays A, B, C, D) were implanted posterior to the arcuate sulcus in the dorsal (PMd) and ventral (PMv) premotor areas. Each FMA included recording electrodes of various lengths (from 1 to 9 mm) to permit sampling of neural activity both on the crown of the precentral gyrus and in the depths of the anterior bank of the central sulcus or posterior bank of the arcuate sulcus. Details of the surgical procedure have been reported previously (Mollazadeh et al. 2011).

Fig. 2.

Neural recording locations. Simultaneous spiking and local field potential (LFP) activity was recorded from multiple floating microarrays (FMAs) in primary motor cortex (M1) and dorsal (PMd) and ventral (PMv) premotor areas of 2 subjects (monkeys X and Y). Left: drawings traced from intraoperative photos show the location of implanted arrays in each monkey, relative to cortical sulci (C.S., central sulcus; A.S., arcuate sulcus; S.P.S. superior precentral sulcus). Only the arrays used in the present study are shown. Right: neural recording sites from electrodes of staggered (i.e., nonuniform) length are indicated by circles. Open circles identify spike recording sites, and filled circles identify simultaneous spike and LFP recording sites. Spikes were acquired from every electrode, while LFPs were acquired from every other electrode. Rectangular prisms outlined in gray outline indicate the approximate recording volume sampled by each FMA.

Table 2.

Summary of spike recordings and LFP channels by array

Monkey	Array	Implant Site	Electrode Length*	Spikes (SU + MU)†		LFP Channels‡
X				X0918	X1002	X0918	X1002
	C	PMv	Short	33 (39)	32 (35)	7 (8)	7 (8)
	D	PMd	Short	34 (41)	22 (29)	8 (8)	8 (8)
	F	M1	Long	9 (9)	16 (16)	8 (8)	8 (8)
	G	M1	Long	11 (11)	5 (7)	8 (8)	8 (8)
	H	M1	Long	13 (18)	9 (10)	8 (8)	8 (8)
	I	M1	Intermediate	17 (20)	17 (17)	8 (8)	8 (8)
	J	M1	Intermediate	17 (21)	15 (22)	8 (8)	8 (8)
Y				Y0211	Y0304	Y0211	Y0304
	A	PMv	Extra long	5 (7)	0 (2)	8 (8)	8 (8)
	B	PMv	Long	13 (16)	9 (12)	8 (8)	8 (8)
	C	PMv	Extra long	2 (5)	4 (5)	8 (8)	8 (8)
	D	PMv	Long	12 (21)	10 (14)	8 (8)	8 (8)
	G	M1	Long	14 (19)	8 (15)	8 (8)	8 (8)
	H	M1	Extra long	15 (18)	19 (25)	8 (8)	8 (8)
	I	M1	Long	12 (17)	11 (14)	8 (8)	8 (8)
	J	M1	Extra long	12 (16)	13 (13)	8 (8)	8 (8)

^*Floating microelectrode arrays (FMAs) with 3 different electrode length configurations were implanted in monkey X. In each configuration the 16 recording electrodes had staggered (i.e., nonuniform) lengths: short (1–4.5 mm), intermediate (1.5–6 mm), and long (2–9 mm). Four different FMA configurations were used in monkey Y, also with staggered (i.e., nonuniform) electrode lengths: intermediate (1–4.5 mm), long (1.5–6 mm), extra long (1.5–9 mm or 1.5–8 mm).

^†Spike recordings with firing rate >1 Hz (total spikes in parentheses) between cue presentation (Cue) and static hold (SH).

^‡Local field potential (LFP) channels with visible modulation (total LFP channels) between Cue and SH. SU, single unit; MU, multiunit.

Both spiking and LFP activity were recorded with a Plexon Multichannel Acquisition Processor (MAP) (Plexon, Dallas, TX). Signals were first amplified 20× through a head-stage amplifier and then hardware-filtered separately for LFPs [0.7 Hz (2 pole) to 175 Hz (4 pole)] and spikes [100 Hz (2 pole) to 8 kHz (4 pole)]. LFP activity was recorded from every other electrode and further hardware-amplified 50×. A National Instruments PXI-6071 (National Instruments, Austin, TX) analog-to-digital converter was used to sample the LFP data at 1 kHz. Spiking activity (single and multiunit) was recorded from each electrode and amplified to a final gain of 1,000 to 32,000×. Spike waveforms were sampled at 40 kHz, and Plexon's Offline Sorter was used for spike sorting. After off-line sorting, spike clusters with a waveform signal-to-noise ratio (SNR) > 3.0 and with no interspike intervals (ISIs) of ≤1 ms were considered well-isolated single-unit (SU) recordings, whereas spike clusters with SNR ≤ 3 or ISIs ≤ 1 ms were considered multiunit (MU) recordings.

The data presented were recorded in two experimental sessions for both monkey X (X0918, X1002) and monkey Y (Y0211, Y0304). These sessions were selected based on their having a relatively large number of successful trials, a good number of SUs and MUs, and artifact-free LFP recordings. In this study, SUs and MUs were combined for decoding purposes. However, only spike recordings (either SU or MU) with mean firing rate > 1 Hz, and LFP channels with modulation visible in the raw recording, were included in the present analysis. Table 2 summarizes the number of spike recordings and the number of LFP channels analyzed from the arrays in each session.

Tracking of hand and finger kinematics.

Simultaneously with neural recordings, upper limb kinematics were tracked with an 18-camera Vicon optical motion capture system (Vicon Motion Systems, Oxford, UK) at a frame rate of 200 Hz. Cameras were mounted on an aluminum frame measuring 60 in. in width and depth and 88 in. in height. Up to 30 optically reflective hemispheric markers (3-mm diameter) (Optitrack, Eugene, OR) were affixed to the dorsal aspect of the monkey's right forearm, hand, and digits with a self-adhesive (spirit gum), to allow tracking of the forearm, the hand, and the phalangeal segments of each finger (Fig. 1C). For monkey X, marker placement included four markers on the dorsal aspect of the forearm (2 over the ulna, 2 over the radius), six markers on the dorsal surface of the hand (1 proximally and 1 distally over the second and fifth metacarpals and 1 distally of the third and fourth metacarpals), two markers over the first metacarpal (proximally and distally), two markers between the metacarpophalangeal (MCP) and proximal interphalangeal (PIP) joint of each digit, and two markers between the PIP and distal interphalangeal (DIP) joints for digits 2 through 5. For monkey Y, marker placement was similar to that for monkey X except that an additional marker was used between the four on the forearm and only five markers were placed on the dorsal surface of the hand (2 proximally and distally over the second and fifth metacarpals and 1 midway along the third metacarpal).

In daily recording sessions, the monkey's forearm, hand, and digits were first shaved and cleaned before reflective markers were placed in the arrangements described above. For monkey Y, tattoo marks (∼2-mm diameter) were placed at each marker location to allow more consistent marker placement between daily recording sessions. Each subject's marker placement was then calibrated to a subject model in Vicon's Nexus software. After each recording session, motion capture data were processed in Nexus to ensure that markers were labeled correctly and any gaps were filled. Motion capture data were then exported from Nexus with the c3d file format and imported into MATLAB (MathWorks, Natick, MA) for further analysis.

The x, y, z position of each marker in Cartesian coordinates was converted into 18 relative joint angles of the wrist, thumb, and fingers with the methods described previously (Aggarwal et al. 2011). The PIP joint angles (θ_PIP2, θ_PIP3, θ_PIP4, θ_PIP5) were defined as the angles between a vector along the proximal phalanx and a vector along the middle phalanx of each digit. The MCP joint angles (θ_MCP2, θ_MCP3, θ_MCP4, θ_MCP5) were defined as the angles between a vector normal to the palmar surface and a vector along the proximal phalanx of each digit. The abduction-adduction angles (θ_AbAd2, θ_AbAd3, θ_AbAd4, θ_AbAd5) were defined as the angles between a vector horizontal with the palm and a vector along the proximal phalanx of each digit. Thumb flexion-extension (θ_MCP1) was taken as the angle between a vector along the thumb metacarpal and a vector along the thumb proximal phalanx. Thumb abduction-adduction (θ_AbAd1) was taken as the angle between a vector along the thumb metacarpal and a vector drawn between the base of the thumb and the base of the ring finger. Thumb opposition (θ_Opp) was taken as the angle between a vector normal to the palmar surface and a vector along the thumb metacarpal. Wrist flexion-extension (θ_FE) was taken as the angle between a vector normal to the forearm and a vector along the palm vertical. Wrist ulnar-radial deviation (θ_Dev) was defined as the angle between a vector horizontal with the forearm and a vector along the palm vertical. Figure 1, D and E, illustrate the distribution of kinematic data for monkey X in the original Cartesian space and joint angle space, respectively.

Behavioral event marker codes (8 bit) generated by the TEMPO (Reflective Computing, Olympia, WA) behavioral control system were acquired in parallel by the Plexon and Vicon data acquisition systems and used to enable synchronization of the two data streams.

Decoding behavioral states.

Each movement trial consisted of four different behavioral epochs: a baseline period consisting of the 300 ms immediately prior to Cue; a reaction period from Cue to OM, a movement period from OM to the start of SH; and a hold period from SH to completion of FH.

Linear discriminant analysis (LDA) was used to predict the instantaneous behavioral state using neural activity immediately preceding the decision time. Although earlier studies used both hidden Markov models (Kemere et al. 2008) and maximum likelihood-based approaches (Achtman et al. 2007) for state decoders, we chose LDA for computational efficiency and ease of implementation. Separate models were developed with the mean spike firing rate, LFP amplitude (time domain amplitude of LFP signals), or LFP power (frequency domain spectral amplitude) over a sliding temporal window of duration T_W that was shifting every T_S (for spikes and LFP amplitude, T_W = 100 ms and T_S = 20 ms; for LFP power, T_W = 250 ms and T_S = 20 ms). LFP power was computed with a windowed Fourier transform at discrete times t_k,

$$X\left(f,t_k\right)=\frac{1}{T_{\text{w}}}{\displaystyle \sum _{t_k}^{t_k+T_{\text{w}}}\left|F_k{\left(f,t_k\right)}^2\right|}$$ (1)

where F_k(f, t_k) is the spectral estimate of the continuous LFP signal. The LFP power was then log-transformed and averaged across five different frequency bands (6–14 Hz, 15–22 Hz, 25–40 Hz, 75–100 Hz and 100–175 Hz),

$$X_{\text{LFP}}\left(t_k\right)=\frac{1}{f_{\text{H}}-f_{\text{L}}}{\displaystyle \sum _{f_{\text{L}}}^{f_{\text{H}}}10\log X\left(f,t_k\right)}$$ (2)

where f_L and f_H represent the lower and upper bounds of each frequency band, respectively. Both the mean firing rate for each spike recording and LFP amplitude/power for each channel and frequency band were normalized to zero mean and unit SD across all training trials.

The conditional probability f_i(x) of belonging to class i was defined at discrete times t_k as

$$f_i\left(x\right)=X{\left(t_k\right)}^T{\Sigma }^{-1}{\mu }_i-\frac{1}{2}{\mu }_i^T{\Sigma }^{-1}{\mu }_i+\text{In}\left(p_i\right)$$ (3)

where i = 1, . ., 4 corresponded to the four behavioral states, X = [x₁ … x_N]^T, and x_n was the mean firing rate for each spike recording n or mean LFP amplitude/power for each LFP channel n, ∑ was the pooled within-group covariance matrix, μ_i was the mean for the ith group, and p_i was the prior estimate for the ith group. The decoded output, Y(t_k), was selected as the class with highest conditional probability,

$$Y\left(t_k\right)=\underset{i}{\arg \max }{f}_i\left(x\right)$$ (4)

Mutually exclusive sets of trials were used for training and testing, and results were averaged with fivefold cross-validation. Because the four behavioral states were of different durations, we normalized decoding accuracy by the total number of decision points for each state, making the chance behavioral state decoding accuracy 25%.

Decoding arm, hand, and finger kinematics.

For continuous prediction of arm, hand, and finger kinematics, a discrete Kalman filter was used to adaptively estimate the system state using observations of neural activity. Our earlier work showed that a Kalman filter outperforms a simple linear regresser when decoding the kinematics of multiple DoFs (Aggarwal et al. 2009). Separate models were developed using the same neural features as the state decoder—mean spike firing rate, LFP amplitude, and LFP power in five different frequency bands. To align the neural data with the motion capture data, all Vicon data were downsampled at 50 Hz (20 ms). As with the neural data, the kinematic data for each joint angle were also normalized to zero mean and unit SD across all training trials.

With the Kalman framework described in detail by Wu et al. (2006), separate state estimate models were built for each decoded parameter at discrete times t_k,

$$Y_i\left(t_k\right)=A{Y}_i\left(t_{k-1}\right)+w\left(t_{k-1}\right)$$ (5)

where Y_i was the kinematic output of one of the 18 relative joint angles or hand x, y, z end point position and A was a matrix that related the current system state to the previous system state in the presence of zero-mean Gaussian noise, w(t_k)∼N(0,W). The observation model assumed that the observed neural activity was Gaussian and linearly related to the current system state such that

$$X\left(t_k\right)=H{Y}_i\left(t_k\right)+q\left(t_k\right)$$ (6)

where X = [x₁, …, x_N]^T, x_n was the mean firing rate for each spike recording n or mean LFP amplitude/power for each LFP channel n, and H was an N × 1 matrix that related the current system state to the current observation in the presence of zero-mean Gaussian noise, q(t_k)∼N(0,Q). Both the state matrix A and the observation matrix H were assumed to be constant and calculated from the training data set with a least-squares approach.

$$\begin{array}{c}A={\left(Y{\left(t_{k-1}\right)}^{T}Y\left(t_{k-1}\right)\right)}^{-1}Y{\left(t_{k-1}\right)}^{T}Y\left(t_k\right)\\ H={\left(Y{\left(t_k\right)}^{T}Y\left(t_k\right)\right)}^{-1}Y{\left(t_k\right)}^{T}X\left(t_k\right)\end{array}$$ (7)

The noise covariance matrices W and Q were then estimated from A and H, respectively.

$$\begin{array}{c}W=\frac{\left(Y\left(t_k\right)-AY\left(t_{k-1}\right)\right){\left(Y\left(t_k\right)-AY\left(t_{k-1}\right)\right)}^T}{N-1}\\ Q=\frac{\left(X\left(t_k\right)-HY\left(t_k\right)\right){\left(X\left(t_k\right)-HY\left(t_k\right)\right)}^T}{N}\end{array}$$ (8)

The final a posteriori estimate for each kinematic variable was calculated recursively with the prediction and update equations for the Kalman filter described by Wu et al. (2006). The initial system state, Y_o, was reset every trial.

Mutually exclusive sets of trials again were used for training and testing, and results were averaged with fivefold cross-validation. Performance metrics include the Pearson's correlation coefficients (CC) and root mean square error (RMSE) between the actual and predicted kinematics. To allow comparison of different types of decoding, all features used in our analysis were normalized to zero mean and unit SD. RMSE therefore has units of normalized standard deviations throughout. To calculate chance decoding performance, surrogate validation data sets of the same length were created by randomly shuffling the predicted kinematic output across time while keeping the spatial order fixed. This was repeated 1,000 times, and the chance level was defined as the upper bound of the 95% confidence interval of chance correlations between the original predicted output and the new shuffled validation sets.

RESULTS

Neural activity and kinematics during reach and grasp.

Figure 3 illustrates representative data from monkey X for one movement type (pushbutton) in one session (X0918). Figure 3A shows the spiking activity of a single unit, along with LFP activity recorded from the same electrode. LFP activity is shown in both the time (LFP amplitude) and frequency (LFP power spectrogram) domains. Figure 3B shows simultaneous kinematic traces of representative joint angles and Cartesian hand position. Data from 10 individual trials are shown as dot rasters for the single unit and as overlaid gray traces for the LFP and kinematic data. The solid black traces for spiking and LFP amplitude activity are averages across all correctly performed trials for the given movement type, as are the LFP spectrograms. All trials were aligned at SH.

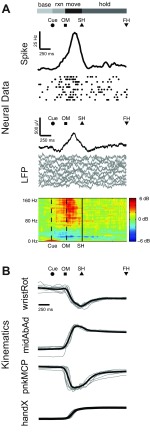
Fig. 3.

Neural and kinematic activity during reach and grasp. A: time-averaged traces of spiking activity, LFP amplitude, and LFP power for a representative single unit and LFP channel recorded from the same electrode, averaged across all correctly performed trials for 1 movement type in 1 session (monkey X: pushbutton in session X0918). Ten individual trials of spiking activity are shown as dot rasters directly below the histogram of spiking activity (black trace). Ten trials of LFP activity (gray traces) are shown directly below the average LFP amplitude (black trace). B: time-averaged traces of selected joint angles from the wrist (wristRot, wrist rotation) and fingers (midAbAd, middle abduction/adduction; pnkMCP, pinky metacarpal) as well as hand centroid position (handX, average of palm markers in x-dimension). Ten individual trials of kinematic data (gray traces) are shown overlaid with the average activity (black trace) for each degree of freedom (DoF). The average time of cue presentation (Cue), onset of movement (OM), start of static hold (SH), and final hold completion (FH) are indicated by symbols above each set of traces. Horizontal bars depict the behavioral states delimited by these event markers: baseline (base), period 300 ms prior to Cue; reaction (rxn), period from Cue to OM; movement (move), period from OM to SH; hold, period from SH to FH. For each DoF, the kinematic data were normalized to zero mean and unit standard deviation across all trials. All trials were aligned at SH.

Horizontal bars at the top of Fig. 3 illustrate the duration of the four behavioral states for each monkey, averaged across all successful trials for the given session and movement type. The average times of Cue, OM, SH, and FH are indicated by symbols above each set of traces. Both spiking and LFP activity show clear modulation with movement of the upper limb, increasing from baseline activity prior to Cue to peak activity after OM. These findings were consistent across all spike recordings and LFP channels, and across all recording sessions for both monkeys (data from monkey Y not shown).

Predicting behavioral states and upper limb kinematics.

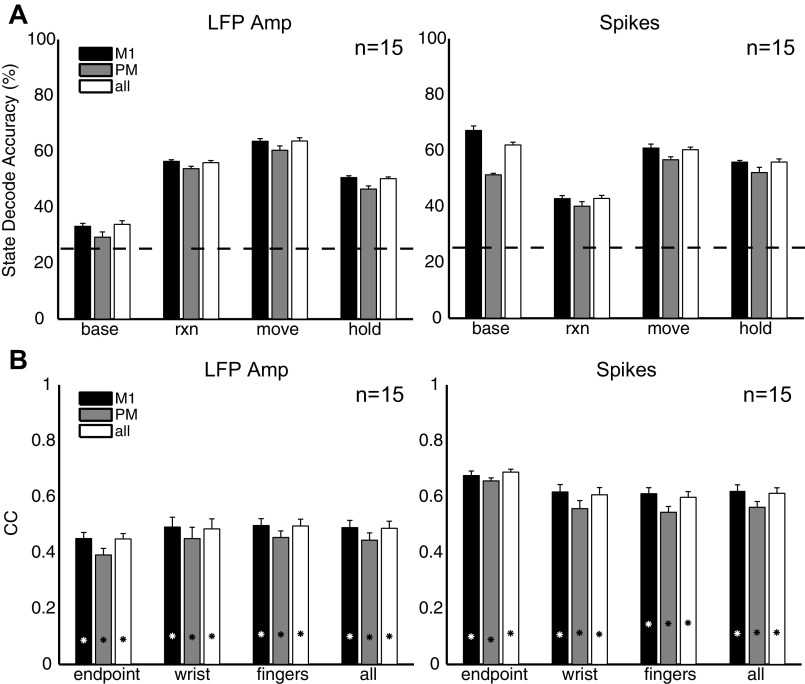
Figure 4A, top, shows the average state decoding accuracy using spikes, LFP amplitude, and LFP power in five different frequency bands as a function of the number of spike recordings or channels, n. State decoding accuracy was calculated as the number of correctly predicted samples divided by the total number of samples across all testing trials for each class and then averaged across all four classes. Spike recordings and LFP channels were selected randomly across all arrays, and results were averaged across 10 random subsets of a given number of input features. It is important to note that the smoothness of these curves reflects averaging across randomly selected ensembles of signals that may or may not contain the most informative signals. For both monkeys, decoding accuracy was greatest with spike recordings (at n = 55, accuracy = 73%; averaged across both monkeys and all 4 sessions), followed by LFP amplitude (62%) and high-frequency LFP power in the 100–175 Hz band (59%). LFP power in the 15–22 Hz band exhibited the poorest overall accuracy for state decoding.

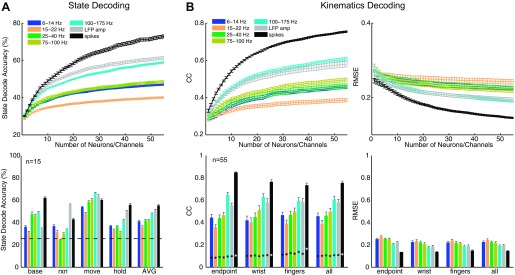
Fig. 4.

Predicting behavioral states and kinematics. A: average decoding accuracy for prediction of 4 behavioral states with LFP power in different frequency bands, LFP amplitude, and spike firing rate. Top: decoding results averaged across all 4 states as a function of the number of spike recordings or LFP channels. Bottom: decoding results for each state separately for a fixed common number of spike recordings or LFP channels (n = 15). Horizontal dashed line indicates chance state decoding accuracy (25%). B: average correlation coefficients (CC) and root mean square error (RMSE) for prediction of arm, hand, and finger kinematics from Cue to SH with LFP power in different frequency bands, LFP amplitude, and spike firing rate. Top: decoding results averaged across all 18 joint angle and 3 end point DoFs as a function of the number of spike recordings or LFP channels. Bottom: decoding results grouped separately for hand end point, average joint angles of the wrist, and average joint angles of each digit (thumb, index, middle, ring, little), for a common fixed number of spike recordings or LFP channels (n = 55). Asterisks indicate chance levels of kinematic correlations. All results shown are averaged across both monkeys and all 4 sessions. Error bars indicate SE.

Figure 4A, bottom, shows decoding accuracy for each behavioral state separately using n = 15 neural features. Although the baseline and final hold states were decoded most accurately with spikes, the reaction and movement states were predicted more accurately with LFPs. LFP amplitude predicted the reaction state more accurately (56%) than spikes (43%) (P < 0.05, 1-way ANOVA, Tukey-Kramer post hoc test), and both LFP amplitude (64%) and LFP power in the 100–175 Hz band (67%) predicted the movement state with higher accuracy than spikes (60%) (P < 0.05, 1-way ANOVA, Tukey-Kramer). While we would leverage all available input channels for ultimate decoding purposes, in order to best illustrate the differences between spikes and LFP we chose n = 15 as a special case so as to not mask the effects of having too many spikes saturating the decoding accuracy. Furthermore, this special case demonstrates that in the event that only a limited number of spikes are available (as can happen over time), LFPs, which typically can still be recorded on many channels, would be a viable alternative for state decoding.

Figure 4B, top, shows the average RMSE and correlation values (Pearson's correlation, r) for prediction of arm, hand, and finger kinematics during the reaction and movement periods between Cue and SH. Kinematic decoding accuracy was averaged across all 18 joint angles and hand end point. As for the state decoder, decoding results using spikes, LFP amplitude, and LFP power in the five different frequency bands are shown separately as a function of the number of randomly selected spike recordings or channels, n. For both monkeys, decoding performance was greatest with spike recordings (at n = 55, r = 0.76, RMSE = 0.14; averaged across both monkeys and all 4 sessions), followed by high-frequency LFP power in the 100–175 Hz band (r = 0.61, RMSE = 0.19) and LFP amplitude (r = 0.58, RMSE = 0.20). Although decoding accuracies were comparable for both monkeys when using spikes (X: r = 0.76, Y: r = 0.75), decoding accuracy was lower for monkey Y than for monkey X when using either LFP amplitude (X: r = 0.64, Y: r = 0.53) or 100–175 Hz LFP power (X: r = 0.64, Y: r = 0.58). As for state decoding, LFP power in the 15–22 Hz band had the lowest kinematic decoding accuracy. For both monkeys, the decoding accuracies for each DoF exceeded chance levels, and overall performance was comparable to results reported previously by others (Vargas-Irwin et al. 2010; Zhuang et al. 2010).

Examining decoding accuracy (n = 55) separately for the wrist (rotation: θ_Rot, flexion-extension: θ_FE, ulnar-radial deviation: θ_Dev), fingers (thumb opposition: θ_Opp, PIP: θ_PIPx, MCP: θ_MCPx, abduction-adduction: θ_AbAdx), and hand end point (hand_X, hand_Y, hand_Z) (Fig. 4B, bottom) revealed that spikes were better able to decode hand end point (r = 0.85) as well as kinematics of the wrist (r = 0.77) and fingers (r = 0.73) than other any other type of neurophysiological signal (P < 0.01, 1-way ANOVA, Tukey-Kramer post hoc tests). Although spikes decoded hand end point with higher accuracy than the wrist/finger joints (P < 0.01, 1-way ANOVA, Tukey-Kramer post hoc test), neither LFP amplitude (end point: r = 0.55, wrist: r = 0.58, fingers: r = 0.58) nor 100–175 Hz LFP power (end point: r = 0.65, wrist: r = 0.63, fingers: r = 0.60) (P > 0.05, 1-way ANOVA) exhibited such differences. Furthermore, decoding accuracies were quite similar across each of the individual joints for a given digit (results not shown). Whereas Fig. 4 shows results averaged across all four sessions, Table 3 and Table 4 summarize state and kinematic decoding performance, respectively, from both sessions in both monkeys.

Table 3.

Summary of state decoding results

Input Feature	X0918	X1002	Y0211	Y0304
Spikes	72.9 ± 0.9	74.7 ± 0.9	67.6 ± 0.9	76.6 ± 0.6
LFP amplitude	66.3 ± 1.0	58.7 ± 1.2	58.4 ± 1.2	62.4 ± 0.9
6–14 Hz	45.4 ± 1.1	46.4 ± 1.5	47.3 ± 0.9	48.8 ± 1.1
15–22 Hz	41.1 ± 1.0	39.9 ± 1.9	41.6 ± 0.7	37.5 ± 0.8
25–40 Hz	48.9 ± 0.9	44.5 ± 1.1	49.9 ± 0.8	51.1 ± 1.2
75–100 Hz	51.6 ± 1.2	50.5 ± 1.4	46.1 ± 0.8	46.1 ± 1.3
100–175 Hz	61.3 ± 1.2	58.4 ± 0.8	56.7 ± 0.7	59.5 ± 1.2

Values (in %) are mean ± SE accuracy for n = 55, where n refers to the number of spike recordings or LFP channels.

Table 4.

Summary of kinematic decoding results

	Correlation Coefficient				Root Mean Square Error
Input Feature	X0918	X1002	Y0211	Y0304	X0918	X1002	Y0211	Y0304
Spikes	0.78 ± 0.01	0.74 ± 0.01	0.77 ± 0.01	0.74 ± 0.01	0.14 ± 0.01	0.16 ± 0.01	0.15 ± 0.01	0.14 ± 0.01
LFP amplitude	0.66 ± 0.02	0.61 ± 0.02	0.49 ± 0.02	0.57 ± 0.01	0.18 ± 0.01	0.20 ± 0.01	0.23 ± 0.01	0.18 ± 0.01
6–14 Hz	0.45 ± 0.03	0.44 ± 0.05	0.45 ± 0.03	0.48 ± 0.02	0.23 ± 0.01	0.24 ± 0.01	0.23 ± 0.01	0.20 ± 0.01
15–22 Hz	0.38 ± 0.04	0.34 ± 0.04	0.42 ± 0.03	0.41 ± 0.01	0.25 ± 0.01	0.27 ± 0.01	0.24 ± 0.01	0.20 ± 0.01
25–40 Hz	0.44 ± 0.04	0.40 ± 0.03	0.49 ± 0.01	0.52 ± 0.02	0.24 ± 0.01	0.25 ± 0.01	0.23 ± 0.01	0.18 ± 0.01
75–100 Hz	0.54 ± 0.02	0.50 ± 0.05	0.46 ± 0.02	0.48 ± 0.04	0.21 ± 0.01	0.23 ± 0.01	0.24 ± 0.01	0.20 ± 0.01
100–175 Hz	0.65 ± 0.03	0.62 ± 0.02	0.56 ± 0.02	0.60 ± 0.03	0.18 ± 0.01	0.20 ± 0.01	0.21 ± 0.01	0.17 ± 0.01

Values are means ± SE for n = 55, where n refers to the number of spike recordings or LFP channels.

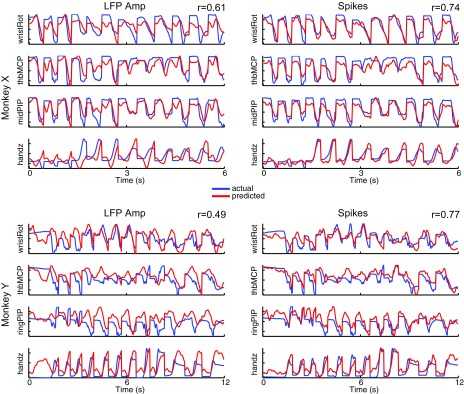
Figure 5 illustrates the simultaneous reconstruction of selected joint angles from the wrist, hand, and fingers using decoded output from either LFP amplitude (Fig. 5, left) or spike recordings (Fig. 5, right) from one session in each monkey (X1002, Y0211). For illustrative purposes, here we concatenated three trials of movements to each of the four object types (mallet, sphere, pushbutton, pull handle). The predicted output (red) closely tracked the actual output (blue) in all cases, although the predictive performance was better with spikes than LFP amplitude for both monkeys. In general, these results suggest that LFP amplitude can provide useful information for distinguishing between movement and nonmovement states, while spikes provide more accurate decoding of kinematics during reach-to-grasp movements per se.

Fig. 5.

Reconstruction of arm, hand, and finger kinematics. Reconstruction of selected joint angles from the wrist, hand, and fingers using decoded output from either LFP amplitude (left) or spike recordings (right) from 1 session in each monkey (X1002, Y0211). Results are shown for 3 sample trials of reach-to-grasp movements to each of the 4 object types (mallet, sphere, pushbutton, pull handle). Correlation coefficients (r) are reported as mean across all 18 joint angles and 3 end point DoFs.

Differences in decoding accuracy between M1 and PM.

We compared state and kinematic decoding accuracy obtained by using signals from both M1 and PM with that obtained by using either M1 or PM recordings alone. Spike recordings or LFP channels were selected randomly from the arrays within each of these two cortical regions, and results were averaged across 10 random subsets. Because the number of available spike recordings or LFP channels, n, differed between M1 and PM in each monkey, to compare decoding performance between these two regions we used a fixed common number of input features, n = 15.

Figure 6A shows decoding accuracy separately for each behavioral state. For both spikes and LFP amplitude, M1 was better able to decode the baseline state than PM (P < 0.05, 1-way ANOVA, Tukey-Kramer post hoc test). However, there was no difference between M1 and PM when decoding the reaction, movement, or hold states (P > 0.05, 1-way ANOVA). Similar trends were observed by using LFP power (results not shown), with the exception that M1 was better able to decode the movement state with 6–14 Hz or 100–175 LFP power or the reaction state with 6–14 Hz LFP power.

Fig. 6.

Decoding accuracy as a function of motor region. Mean state decoding accuracy (A) and kinematic correlation coefficients (B) using neural activity randomly sampled from only M1 arrays (monkey X: arrays F, G, H, I, J; monkey Y: arrays G, H, I, J), PMv/PMd arrays (monkey X: arrays C, D; monkey Y: arrays A, B, C, D), or all arrays. Results shown used a fixed common number of spike recordings or LFP channels (n = 15) and then were averaged across the 4 sessions, 2 from each monkey. Horizontal dashed line in A indicates chance state decoding accuracy (25%). Asterisks in B indicate chance kinematic correlations. Error bars indicate SE.

Figure 6B shows the kinematic decoding accuracy separately for arm (translational) end point and wrist and finger (rotational) DoFs. For both spikes and LFP amplitude, there was no difference between M1 and PM (P > 0.05, 1-way ANOVA) when decoding reach end point versus proximal and distal joints of the arm. Once again, similar trends were observed with LFP power (results not shown), with the exception that M1 was better able to decode finger joints with 6–14 Hz or 100–175 Hz LFP power (P < 0.05, 1-way ANOVA, Tukey-Kramer post hoc test).

Furthermore, there was no improvement in either state or kinematic decoding accuracy when neural activity from both M1 and PM was combined (P > 0.05, 1-way ANOVA). This suggests that the information present in the premotor areas during movement was redundant to that in the primary motor areas for decoding purposes.

Analysis of state transition times.

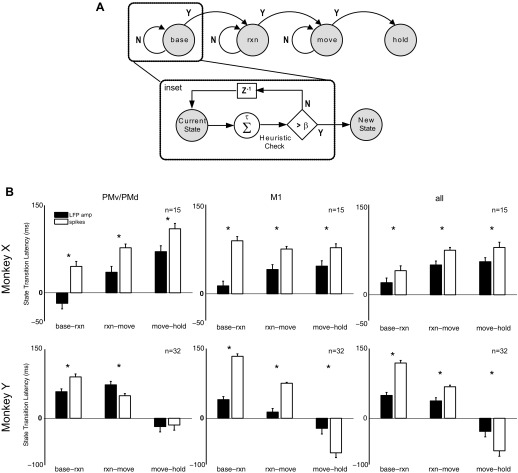
We also investigated the latency at which different types of neurophysiological signal detected the transition from one state to the next. Figure 7A illustrates schematically how we defined these transitions. We made the simplifying assumption that, given the current state in a correctly performed trial, a transition could occur only to the next state. Backward transitions to the previous state and forward transitions to a subsequent state could not occur. For example, from the reaction state the next transition could have been only to the movement state and not to the baseline or hold state. (Note that our assumption of an ordered baseline-reaction-movement-hold sequence would be directly applicable to only a subset of real-world situations.) Furthermore, to minimize spurious state transitions, the predicted transition times were defined as the time at which the state decoder correctly predicted the same immediate next state at least β times out of the previous τ decision points (where β < τ),

$$Y_{\text{state}}\left(t_k\right)=\{\begin{array}{cc}{Y}_{\text{state}}\left(t_k\right)+1& \text{if}{\displaystyle \sum _{t=t_k-\tau }^{t_k}\left(Y_{\text{state}}\left(t\right)=Y_{\text{state}}\left(t_k\right)+1\right)>\beta }\\ Y_{\text{state}}\left(t_k\right)& \text{else}\end{array}$$ (9)

where Y(t_k) = {1,2,3,4} is the output of the state decoder and was assigned an integer label for each of the four behavioral states; β and τ were constants optimized to minimize the difference between the predicted and actual state transition times and empirically selected to be β = 3, τ = 5. This heuristic classifier only transitioned to the immediate next state if the predicted new state was consistently different from the predicted current state, and did not rely on any knowledge of the actual current state. Note that this definition of transition times increased accuracy at the cost of increasing the latency at which state transitions were declared (Achtman et al. 2007). Each of the four state transition latencies was predicted separately for reach-to-grasp trials to each of the four objects in each of the four recording sessions from the two monkeys, using each of four neurophysiological signal types: spike recordings, LFP amplitude, 6–14 Hz LFP power, and 100–175 Hz LFP power.

Fig. 7.

State transition latencies. A: state diagram illustrates transition from one behavioral state to next. To eliminate spurious state transitions, predicted transition times were determined as the time at which the state decoder correctly predicted the new state at least β times out of the previous τ decision points (see inset). B: mean state transition latencies using LFP amplitude and spike recordings randomly sampled from only M1 arrays, PMv/PMd arrays, or all arrays. State transition latencies are reported as the difference between the predicted transition times and actual transition times as indicated by behavioral markers for Cue (baseline-reaction), OM (reaction-movement), and SH (movement-hold). Results were averaged across only those trials where decoding accuracy for each state was at least 25%. Asterisks indicate significant differences between state transition latencies. Error bars indicate SE.

Figure 7B shows the difference between the predicted and actual state transition times (i.e., latency of state transition prediction), averaged across all four object types, using spike recordings or LFP amplitude. (State transition latencies using LFP power in the 6–14 Hz and 100–175 Hz bands showed large variability reflecting the overall poorer state decoding accuracy obtained with these neurophysiological signal types, and therefore have not been illustrated here). Separate analyses were performed with fixed numbers of spike recordings and LFP channels drawn randomly from PM, M1, or both PM and M1. The actual state transition times were calculated on a trial-by-trial basis from the recorded times of the behavioral markers that demarcated state transitions: Cue (baseline-reaction transition), OM (reaction-move), and SH (move-hold). For this analysis, trials were used only if the decoding accuracy for each state (i.e., the number of correctly predicted samples divided by the total number of samples across all testing trials for that class) was at least chance or better (>25%). In monkey X, state transitions were consistently detected earlier with LFP amplitude than with spikes for each of the transition events (P < 0.01, 1-way ANOVA, Tukey-Kramer post hoc test), with the greatest difference observed for the baseline-reaction transition. Except with spike recordings from M1, the state transition latency was lowest for the baseline-reaction transition, followed by the reaction-move transition and then the move-hold transition. With PMv/PMd LFP amplitude, the mean base-reaction state transition latency was even negative (−18 ± 9.5 ms), indicating that the transition could be predicted before it occurred. In monkey Y, LFP amplitude also provided earlier state transition prediction latency than spikes for the baseline-reaction and reaction-move transitions (P < 0.01, 1-way ANOVA, Tukey-Kramer post hoc test), with the exception of using PMv/PMd LFP activity to predict the reaction-move transition time. In contrast, prediction of the move-hold transition in monkey Y did not differ significantly for LFP versus spike recordings using PMv/PMd channels and was earlier using spike recordings from M1. Furthermore, with LFP channels or spikes from all arrays, in monkey Y the state transition latency was latest for the base-reaction transition and earliest for the move-hold transition, a pattern opposite to that seen in monkey X. In addition, in monkey Y both LFP and spikes predicted the move-hold transition in advance of its actual occurrence.

Combined state-based kinematic decoding.

LFP amplitude had the highest state decoding accuracy for the reaction and movement states, while spiking activity had the highest kinematic decoding accuracy during the movement period from Cue to SH (Fig. 4). We therefore compared the performance of kinematic decoding (i.e., kinematics alone) to that of state-based kinematic decoding (i.e., combined state plus kinematics). We used spike recordings for kinematic decoding throughout, whereas state decoding was assessed with either spike recordings (Ethier et al. 2011) or LFP amplitude. In either case the state decoder was trained to distinguish between one of four behavioral states (baseline, reaction, movement, hold) while the kinematic decoder was trained to continuously decode hand end point position and 18 joint angles of the wrist and fingers.

The state-based kinematic decoder then operated in a hierarchical fashion, such that the output of the combined decoder, Y_comb(t_k), was held at a constant position until the output of the state decoder, Y_state(t_k), predicted a transition from the baseline period to the reaction period at time t_rxn. The output of the state-based kinematic decoder then tracked the output of the kinematic decoder, Y_kin(t_k), until the state decoder predicted a transition from the movement period to the hold period at time t_hold. At that time, the output of the state-based kinematic decoder was latched at a constant position for the remainder of the trial.

$$Y_{\text{state}+\text{kin}}\left(t_k\right)=\{\begin{array}{ccc}{Y}_{\text{kin}}\left(0\right)& \text{if}& Y_{\text{state}}\left(t_k\right)=\text{base}\\ Y_{\text{kin}}\left(t_k\right)& \text{if}& Y_{\text{state}}\left(t_k\right)=\text{reaction}\text{or}\text{move}\\ Y_{\text{kin}}\left(t_{\text{hold}}\right)& \text{if}& Y_{\text{state}}\left(t_k\right)=\text{hold}\end{array}$$ (10)

Supplemental videos illustrate the output of a spike-based kinematic decoder (Supplemental Video S1) versus an LFP-based state decoder combined with a spike-based kinematic decoder (Supplemental Video S2) used to drive a virtual macaque arm in Musculoskeletal Modeling Software (MSMS) (Davoodi and Loeb 2002; Davoodi et al. 2004).¹ In both videos, the decoded arm/hand kinematics (solid arm) are compared to the actual arm/hand kinematics (shadow arm) for movements to each of the four different objects. The state-based kinematic decoder eliminated the wavering motion of the kinematic decoder during the baseline and final hold periods at the expense of some inaccuracy in the maintained position.

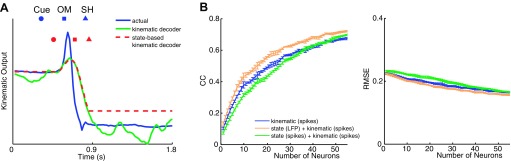
Figure 8A illustrates this difference for a single DoF, wristFE, in a sample trial from session X0918. The actual kinematics of wristFE are shown in blue, and the blue markers above indicate the time of cue presentation, onset of movement, and start of static hold for this particular trial. As can be seen, wristFE was relatively stable during the period prior to Cue while the subject was at the home position and during the period after SH when the subject was engaged in a stable hold after grasping the peripheral object. The predicted output of the kinematic decoder, trained using spiking activity for from 300 ms prior to Cue to the end of the final hold, is shown in green. The kinematic decoder provided a smooth output during movement of the joint from Cue to SH, but during both the baseline period before the cue and the hold period after the movement, the kinematic decoder produced a wavering motion around the actual stable joint position.

Fig. 8.

Combined state-based kinematic decoding. A: comparison of actual kinematics (blue) for a single DoF, wristFE, with predicted kinematics from a kinematic decoder using spike recordings (green) or a state-based kinematic decoder using LFP amplitude for state decoding and spikes for kinematic decoding (red). Results are shown for a sample trial from session X0918. B: average CC and RMSE for prediction of arm, hand, and finger kinematics from 300 ms prior to Cue to FH, from 1) only a spike-based kinematic decoder (blue); 2) a spike-based state decoder combined with a spike-based kinematic decoder (green); and 3) an LFP-based state decoder combined with a spike-based kinematic decoder (orange). Decoding results averaged across all 18 joint angle and 3 end point DoFs as a function of different numbers of randomly selected spike recordings for the kinematic decoder (x-axis). Error bars indicate SE.

The predicted output of the state-based kinematic decoder, which used LFP amplitude to decode state and spikes to decode kinematics, is shown in red in Fig. 8A. The markers in red above the decoded output trace indicate the time of predicted state transitions from baseline to reaction, reaction to move, and move to hold for this particular trial. As can be seen, the decoded output remained latched at a constant position until the state decoder predicted the baseline-reaction transition, at which point the kinematic decoder was activated. The output of the state-based kinematic decoder then tracked that of the kinematic decoder until the state decoder predicted the move-hold transition, at which point the kinematic decoder was deactivated and joint position was latched at a constant value for the remainder of the trial. Compared with the wavering output of the kinematic decoder, during the initial baseline and final stable hold periods, the stationary output of the state-based kinematic decoder produced a closer temporal correlation with the actual joint kinematics at the expense of a fixed inaccuracy in final position.

Figure 8B shows the average correlation values (Pearson's correlation, r) and RMSE for prediction of arm, hand, and finger kinematics over entire trials from 300 ms prior to Cue to FH, using a spike-based kinematic decoder (blue), a spike-based state decoder combined with spike-based kinematics decoder (green), or an LFP-based state decoder combined with a spike-based kinematic decoder (orange). Decoding results were averaged across all 18 joint angles and hand end point as a function of randomly selected spike recordings, n, for the kinematic decoder with the same varying number of spike recordings n (green) or a fixed number of LFP channels, n = 55 (orange), for state decoding. Across all values of n, the LFP state-based kinematic decoder performed significantly (at n = 55, r = 0.72, RMSE = 0.15) better than either the spike state-based kinematic decoder (at n = 55, r = 0.70, RMSE = 0.17) or the spike-based kinematic decoder (n = 55, r = 0.67, RMSE = 0.17) alone (P < 0.01, 2-way ANOVAs).

DISCUSSION

In monkeys performing a reach-to-grasp task, we investigated both state decoding and kinematic decoding of up to 21 DoFs of the arm, hand, and fingers using both LFPs and spikes recorded in both primary motor and premotor cortical areas. LFP features more accurately predicted different behavioral states, whereas spike features more accurately predicted the continuous kinematics of multiple DoFs. No noticeable differences in decoding performance were observed with velocity features, and thus only results from position decoding are presented. Using a state-based kinematic decoder improved overall decoding of reach-to-grasp movements from baseline through movement execution to final hold by eliminating the wavering output of the kinematic decoder during the initial and final periods of stationary posture. State-based kinematic decoding with LFP amplitude provided better overall performance than state-based kinematic decoding with spike recordings.

Our experimental paradigm involved voluntary goal-directed reaches to multiple objects arranged in a center-out fashion. The task-defined times of cue presentation, onset of movement, and start of the final, stable hold allowed us to segment trials into baseline, reaction, movement, and hold states. Neurophysiological signals from M1 and PM enabled us to predict all three state transitions: baseline to reaction, reaction to movement, and movement to hold. Furthermore, the mallet, sphere, pull handle, and pushbutton objects elicited distinct grasp conformations and allowed us to sample a significant range of motion for 18 joint angles of the wrist and fingers, as well as hand end point position.

Differences between LFPs and spikes in state and kinematic decoding performance.

Unlike spiking activity, which reflects the output activity of neurons, LFPs mainly reflect the synaptic activity of a large population of neurons from within 0.5–3 mm from the tip of the recording electrode (Fromm and Bond 1964; Gray et al. 1989; Mitzdorf 1985). As such, spiking and LFP activity are believed to be generated by different processes in the cortex. Although LFP activity can be predicted from multiunit spiking activity (Rasch et al. 2009), and conversely can predict summed spiking activity (Bansal et al. 2011), LFPs cannot predict the millisecond precision of spike timing (Rasch et al. 2008) that is essential for temporal coding (Mainen and Sejnowski 1995).

Although containing some redundant information, spikes and LFPs also may carry complementary information. For example, low-frequency LFP oscillations and spiking activity from the visual cortex have been shown to convey independent information about visual stimuli (Belitski et al. 2008). Furthermore, the spatiotemporal distribution of discriminable information about reach-to-grasp movements in M1 was found to differ for low-frequency LFP oscillations (1–4 Hz) and LFP amplitude compared with spikes (Mollazadeh et al. 2011).

We considered the possibility that the low-frequency components of the present LFPs might represent mechanical artifacts from the monkeys' movements. Low-frequency activity in LFPs appears 100 ms or more before the onset of movement (Hwang and Andersen 2009; Mollazadeh et al. 2011; Rickert et al. 2005), however, and hence cannot consist entirely of mechanical artifact. Indeed, in primate M1 and PMd low-frequency LFP responses to visual instructional cues peak <125 ms after the cue appears (O'Leary and Hatsopoulos 2006), and in humans making self-paced movements with no visual cues slow potentials from the surface of the brain or from the scalp over the supplementary motor area and premotor cortex begin several hundred milliseconds before movement onset, peaking over M1 shortly before movement onset (Hallett 1994; Tarkka and Hallett 1991). Both before and after movement onset, the topographic localization of these slow potentials over particular cortical areas, as well as over specific somatotopic representations, indicates their origin from neural activity rather than from generalized mechanical artifact (Tarkka and Hallett 1991). We therefore accept the low-frequency components of the present LFPs as neurophysiological signals.

In general, our results suggest that LFP features more accurately identified the reaction and movement states as well as the transition between them, while the kinematics of the reach-and-grasp movement itself could be decoded more accurately from spike recordings. Similarly, behavioral states have been found to be better encoded in LFPs and movement direction better encoded in spiking activity recorded from the parietal reach region (PRR) (Pesaran et al. 2002; Scherberger et al. 2005). Furthermore, as in these studies of the PRR, we observed that high-frequency LFP spectral features captured more movement-related information than low-frequency LFP spectral features, as evidenced by higher kinematic decoding accuracies as well as greater predictive power for detecting the movement state. This may reflect the fact that high-frequency LFP features may contain some residual spiking activity (Ray and Maunsell 2011). Because spikes and LFPs reflect different aspects of neural processing, a multimodal decoding scheme using different types of neurophysiological signals could improve the amount and quality of information that can be decoded.

Similarity of movement-related information in primary motor and premotor regions.

M1 is generally considered to encode kinematic and kinetic parameters of limb movement (Ashe 1997; Ashe and Georgopoulos 1994; Fu et al. 1995; Georgopoulos et al. 1988; Hendrix et al. 2009; Moran and Schwartz 1999b; Sergio et al. 2005). Consequently, movement kinematics can be decoded from neural activity in M1 (Aggarwal et al. 2009; Carmena et al. 2003; Moran and Schwartz 1999a; Taylor et al. 2002; Vargas-Irwin et al. 2010). In contrast, the premotor cortex is commonly viewed as representing more abstract aspects of movement. Neurons in PMd respond to arbitrary, abstract cues and show sustained activity during instructed delay periods as subjects plan which movement to perform (Cisek and Kalaska 2004; Weinrich et al. 1984). Neurons in PMv have visual receptive fields in peripersonal space as well as large somatosensory fields and discharge in relation to canonical uses of the hand (Rizzolatti et al. 1981a, 1981b, 1987, 1988). Yet we found, as have others (Bansal et al. 2011), that the kinematics of the multiple DoFs involved in hand and arm movements—including the end point of the arm and the joints of the wrist and each of the digits—can be decoded from neural activity in the premotor cortex almost as well as from that in M1. The lack of improvement in decoding accuracy when neural activity from M1 and PM were combined further supports the presence of redundant information about both state and kinematics in these two cortical regions.

These observations indicate that, along with representation of more abstract aspects of motor control, the kinematics of limb movements are well-represented in the premotor cortex. Although recent studies have emphasized activity related to movement planning in PMd and canonical grasps in PMv, neurons in both of these cortical motor areas are well known to discharge along with M1 neurons as subjects execute movements (Kurata 1993; Weinrich et al. 1984). Moreover, the firing rate of PMv neurons varies in relation to the direction and amplitude of wrist movements (Kurata 1993) and in relation to grasp force (Hepp-Reymond et al. 1994), and the discharge of PMd neurons depends on movement direction (Weinrich et al. 1984) and grasp dimension (Hendrix et al. 2009). Future investigations may reveal more detailed representations of movement kinematics and kinetics in the premotor cortex than previously appreciated.

State transition latencies.

Although the current behavioral state—baseline, reaction, movement, or hold—could be decoded accurately from spike recordings or from LFPs, we found that the transition from one state to another was detected somewhat earlier with LFP amplitude than with spikes, particularly in our monkey (X) with faster (shorter) reaction and movement times. LFPs generally are thought to reflect synaptic activity (Fromm and Bond 1964; Gray et al. 1989; Mitzdorf 1985), and the time required for synaptic integration to alter the spike firing rates of local neurons therefore may have contributed to a delay between the appearance of decodable information in LFPs and in spikes. The change in behavioral state from baseline to the reaction period of the present task, for example, was defined by the sudden appearance of a visual cue that instructed the monkey which movement to perform. In PMd and M1, LFPs aligned at the time of such a cue show “instruction-evoked potentials” that peak at average latencies of 114–123 ms in PMd and 105–122 ms in M1 (O'Leary and Hatsopoulos 2006). By comparison, spiking responses to visual cues in PMd are just beginning at an average latency of 138 ms (Weinrich et al. 1984). Such delays from LFP to spiking activity may contribute to decoding state changes somewhat earlier with LFPs than with spikes.

Impact of a combined state-based kinematic decoder for neuroprosthetics.

BMIs typically have relied on a priori information about movement periods in order to activate kinematic decoding algorithms at the appropriate time. Continuous control of an upper limb neuroprosthesis with many DoFs might be improved, however, by activating kinematic decoding only during periods of intended movement, without requiring external input to detect such periods. A few studies have investigated how a state decoder could autonomously trigger a decoder for discrete target positions (Hwang and Andersen 2009; Kemere et al. 2008), but previous studies have not used a state decoder to gate periods of continuous kinematic decoding. We found that a state-based kinematic decoder can improve the continuous decoding of multiple DoFs, although latching the output when the movement-to-hold transition is detected can result in a final joint angle error (Fig. 8A). Ultimately, the usability of a state-based kinematic decoder in a real prosthetic device will depend on high state classification accuracy and will need to be addressed in future work. Nevertheless, for neuroprosthetic applications a stationary limb with small final position errors may be more desirable than unintended movement of the limb during postural periods. Furthermore, triggering the neuroprosthesis to transition between posture and movement would ameliorate not only noise in the output from the neural decoder but also mechanical noise in a neuroprosthetic limb system.

Although this work presents off-line results, our state-based kinematic decoding scheme could be readily applied to online control of a prosthetic arm with little increase in computational complexity beyond that of a kinematic decoder alone. Both linear (Carmena et al. 2003; Hochberg et al. 2006; Serruya et al. 2002) and Kalman (Wu et al. 2004) filters have been employed previously in BMI systems and can be parallelized to run in real time in a hierarchical fashion (Aggarwal et al. 2008b). More recent work involving unscented Kalman filters augments the movement state variables with a state history into a single model (Li et al. 2009). Combined state-based kinematic decoding may represent an important step toward the realization of more accurate and smoother BMI control of a multifingered hand neuroprosthesis performing dexterous manipulation.

GRANTS

This work was sponsored in part by the Johns Hopkins University Applied Physics Laboratory under the Defense Advanced Research Projects Agency (DARPA) Revolutionizing Prosthetics program, contract N66001-06-C-8005; the DARPA REPAIR program, contract 19GM-1088724; National Institute of Neurological Disorders and Stroke R01 NS-040596-09S1; and the National Science and Engineering Research Council of Canada (NSERC).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).^…

AUTHOR CONTRIBUTIONS

Author contributions: V.A., M.M., and M.H.S. conception and design of research; V.A. and M.M. analyzed data; V.A., M.M., and M.H.S. interpreted results of experiments; V.A. prepared figures; V.A. drafted manuscript; V.A., M.M., A.G.D., M.H.S., and N.V.T. edited and revised manuscript; V.A., M.M., A.G.D., M.H.S., and N.V.T. approved final version of manuscript; A.G.D. and M.H.S. performed experiments.