Mammographic density as a mediator for breast cancer risk: analytic approaches

Abstract

Mammographic breast density has been found to be associated with breast cancer risk. Many of the traditional risk factors for breast cancer are themselves associated with mammographic breast density. A natural question that arises in this setting is the extent to which the effects of breast cancer risk factors are mediated by breast density and the extent to which such effects are through other pathways. We discuss analytic approaches to address these questions of mediation and also discuss how such approaches can accommodate potential interaction between risk factors and mammographic density and can accommodate case-control study designs.

Mammographic breast density is clearly a strong risk factor for breast cancer [1]. Certain traditional demographic, behavioral, and genetic risk factors for breast cancer have now also been shown to be related to breast density [2-7]. A question that therefore naturally arises in this context is the extent to which traditional risk factors for breast cancer influence breast cancer risk through their effects on breast density and the extent to which traditional risk factors might operate through other pathways. Stated another way, we may be interested in the extent to which the effect of traditional risk factors on breast cancer is mediated by breast density.

In their review, Boyd and colleagues discuss mediation in a number of contexts [7]. They comment that because breast density is strongly associated with risk of breast cancer, factors that influence density may also contribute to the causes of breast cancer. The authors note that breast density may be on the causal pathway for breast cancer for some or all of the known risk factors. They point out that if breast density is to serve as a surrogate for breast cancer prevention in intervention trials, then most of the effect of such interventions on breast cancer risk should be mediated by breast density.

Boyd and colleagues do not, however, discuss how one would analytically assess mediation. A very general approach has recently been developed to address questions of mediation that allows for considerable flexibility and can also be applied to case-control studies [8]. Let F denote a traditional risk factor, M the percentage mammographic density, B breast cancer, and C a set of baseline covariates. The conceptual relationships between these variables are given in Figure 1. If we are interested in the extent to which the effect of the risk factor is mediated through density (the F-M-B pathway) versus the extent to which the effect of the risk factor is independent of density (the F-B pathway(s)), we could proceed as follows. We could first fit a logistic regression model for breast cancer on the risk factor, the percentage density, and the baseline covariates:

Figure 1.

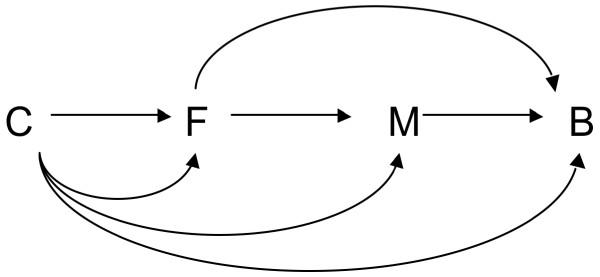
Conceptual relationships between variables illustrating mediation. Conceptual relationships illustrating mediation between a traditional breast cancer risk factor (F), mammographic density (M) and breast cancer (B), along with baseline confounding covariates (C).

$$\text{logit}\left[\text{P}\left(\text{B}=1|\text{F},\text{M},\text{C}\right)\right]={\mathrm{\theta }}_0+{\mathrm{\theta }}_1\text{F}+{\mathrm{\theta }}_2\text{M}+{\mathrm{\theta }}_3\text{FM}+{\mathrm{\theta }}_4\text{C}$$

This model allows us to assess the association of breast cancer risk with the risk factor of interest and with density. Note that this model also allows for potential interaction between the risk factor and density, a point to which we return below. Second, we could fit a linear regression model for density on the risk factor and covariates:

$$\text{M}={\mathrm{\beta }}_0+{\mathrm{\beta }}_1\text{F}+{\mathrm{\beta }}_2\text{C}+\epsilon$$

If the risk factor is binary, then - under some assumptions about confounding control described below - the mediated effect odds ratio is as follows [8]:

$$\text{Mediated effect}=\text{exp}\left({\mathrm{\beta }}_1{\mathrm{\theta }}_{\text{2}}+{\mathrm{\beta }}_1{\mathrm{\theta }}_3\right)$$

The direct effect odds ratio would be:

$$\text{Direct effect}=\text{exp}\left({\mathrm{\theta }}_1+{\mathrm{\theta }}_3{\mathrm{\beta }}_0+{\mathrm{\theta }}_3{\mathrm{\beta }}_2\text{C}+{\mathrm{\theta }}_3{\mathrm{\theta }}_2{\mathrm{\sigma }}^2+1/2{{\mathrm{\theta }}_3}^2{\mathrm{\sigma }}^2\right)$$

where σ² is the variance of the error term in the linear regression model for density. The total effect odds ratio is equal to the product of these direct effect and indirect effect odds ratios. The proportion mediated on a log odds scale can be calculated by taking the log of the mediated effect odds ratio divided by the log of the total effect odds ratio. Using a different transformation, the proportion mediated on a risk difference scale can also be calculated [8].

Expressions for nonbinary exposures and standard errors for these effects are given elsewhere [8]. SAS and SPSS macros are available to do this automatically; the programs and accompanying paper are available from the authors upon request and will also be accessible online [9].

The expressions above assume that adequate control has been made for confounding so that the associations from the statistical models reflect causal effects. Specifically, the expressions assume that the baseline covariates C suffice to control for confounding of the risk factor-breast cancer relationship, for confounding of the density-breast cancer relationship, and for confounding of the risk factor-density relationship. Stated another way, our covariates C need to control for the exposure-outcome, mediator-outcome, and exposure-mediator confounders.

The approach above applies to a cohort study if the outcome is rare. A modification is necessary for a case-control study. The same approach would work for a case-control study with a rare outcome provided that the linear regression model for mammographic density is fit only amongst the controls. This method takes into account the fact that the sample was selected based on breast cancer status, and allows the model for the mediator to approximate the mediator in the population - provided the breast cancer outcome is rare in the population.

The expressions above generalize approaches to mediation sometimes employed in the social science literature [10] to allow for exposure-mediator interaction (that is, interaction between the risk factor and density) and to allow for case-control sampling designs. Another approach to mediation, more common in epidemiology, is to fit the model for the breast cancer outcome both with and without the mediator, density (in both cases excluding the interaction), and examining whether the coefficient for the risk factor changes when the mediator is in the model. This is sometimes called the difference method. The social science techniques, the difference method, and the method described above all make the same assumptions about confounding if the direct and indirect effects are to be interpreted causally, although this is not always explicitly noted when these methods are used. The expressions given above, however, generalize the difference method approach to allow for exposure-mediator interaction.

Including such interactions can be important. For example, Boyd and colleagues discuss [7] a prevention trial using tamoxifen as an intervention in which, in the tamoxifen group, only those who experienced a reduction in density had a reduction in breast cancer risk compared with the control group; those with tamoxifen but no decline in density experienced no risk reduction; and in the control group the breast cancer risk was similar in subjects with and without breast density reduction [11]. In other words, tamoxifen and breast density appear to interact in this trial. Boyd and colleagues comment that no evidence was given that the change in density mediated the effect of tamoxifen on breast cancer risk. The methods described above would allow one to assess mediation even in the presence of interaction, as seems to have indeed been present in this trial.

The methods described above can be used to assess mediation in the context of such prevention trials. The methods could also be used to assess whether the effect of various traditional risk factors (genetic factors, age, weight, age at menarche, parity, hormone replacement therapy, and so forth) on breast cancer are mediated by breast density. Care needs to be taken in appropriate confounding control. For any particular risk factor under study, one needs to control not only for common causes of the risk factor and breast cancer but also for common causes of density and breast cancer. Because of the latter requirement, control should be made for other risk factors that may be related to both density and breast cancer, especially if they occur prior to the risk factor under study. Control for risk factors subsequent to the risk factor under study would be omitted if these also serve as mediators for the risk factor of interest. Appropriate confounding control is important in the analysis of direct and mediated effects. Sensitivity analysis techniques can be helpful in assessing the extent to which uncontrolled confounding may or may not substantially influence estimates [12]. We believe these contemporary methods for mediation will be useful in shedding further light on the role of mammographic density in the etiology of breast cancer.

Abbreviations

B: breast cancer; C: baseline covariates; F: risk factor; M: mammographic density.

Competing interests

The authors declare that they have no competing interests.

Acknowledgements

The research was supported by funding from the National Institutes of Health.