Combining Classifiers Using Their Receiver Operating Characteristics and Maximum Likelihood Estimation

Abstract

In any medical domain, it is common to have more than one test (classifier) to diagnose a disease. In image analysis, for example, there is often more than one reader or more than one algorithm applied to a certain data set. Combining of classifiers is often helpful, but determining the way in which classifiers should be combined is not trivial. Standard strategies are based on learning classifier combination functions from data. We describe a simple strategy to combine results from classifiers that have not been applied to a common data set, and therefore can not undergo this type of joint training. The strategy, which assumes conditional independence of classifiers, is based on the calculation of a combined Receiver Operating Characteristic (ROC) curve, using maximum likelihood analysis to determine a combination rule for each ROC operating point. We offer some insights into the use of ROC analysis in the field of medical imaging.

1 Introduction

It is often desirable in clinical practice to combine the results of two or more diagnostic tests or classifiers in order to obtain a more accurate and certain diagnosis. In the field of medical imaging, combinations of independent assessments based on multiple imaging modalities can be combined to create a joint classifier. See [2] for example. Results from segmentation or recognition algorithms can also be combined [8, 3] to produce an improved estimate of ground truth. Ideally, combination of classifiers would be done by joint training and analysis on a common dataset to which all classifiers can be applied. Standard methods in machine learning (logistic regression, PCA, SVMs, etc.) could then be used to find an optimized combined classification scheme [5, 6]. In practice, however, it is often the case that joint training data is not available, or is of insufficient quantity. Indeed, there is a “power rule” involved: if it takes roughly N data points to estimate a distribution in order to train a single classifier, it is reasonable to expect the need for on the order of N^c data points to estimate the joint distribution needed to train c classifiers. In light of initiatives established to encourage the sharing of algorithms, such as the ITK project (www.itk.org), the lack of sufficient quantities of data for joint training has become more apparent. Accordingly, we have developed the following simple algorithm, used to combine multiple classifiers without the need for joint training. It is based on the maximum likelihood analysis of ROC curves of classifiers.

Although ROC analysis is widespread and standard in the medical field wher-ever diagnostic tests are analyzed, it is far less common within the field of medical image analysis [9]. We feel this is unfortunate, and that a wider use of these techniques would help lead to general acceptance of image analysis algorithms, e.g. algorithms for detection, segmentation and registration, within the clinical community.

2 Background on ROC Analysis

We begin with some basic notions from the standard ROC theory. See [4] for a review of its use in biomedicine. Let I be an image, depending on a binary random variable T ∈ {0, 1} representing unknown “truth” and suppose we have a classification process, or test, A estimating T and depending on a vector of parameters k_A, so that A(I, k_A) ∈ {0, 1}. A simple example would be where I is a pixel in a CT image, k_A = (I_low, I_high) consists of a range for Hounsfield units used to segment some structure, and A is then either 1 or 0, indicating the absence or presence of said structure, i.e. whether or not the intensity lies in the range given by k_A. A more sophisticated example might be where A is a segmentation algorithm depending upon several parameters.

For each setting of the parameter k_A we define two probabilities, the true positive rate tp_A = Pr(A = 1ǀT = 1) and the false positive rate fp_A = Pr(A = 1ǀT = 0). The true positive rate is also known as the sensitivity of the classifier, while 1 – fp_A is known as A’s specificity. We would generally like a classifier to be specific and sensitive. Thus, these notions give us a partial ordering of the unit square [0, 1]² : an operating point $(f{p}_A^1,t{p}_A^1)$ is superior to $(f{p}_A^0,t{p}_A^0)$ if $f{p}_A^1\le f{p}_A^0$ and $t{p}_A^1\ge t{p}_A^0$.

The Receiver Operator Characteristic or ROC for A is the set of points {(fp_A(k_A), tp_A(k_A))} ⊂ [0, 1]², as k_A ranges over all of its possible values. When k_A is a single scalar value, the ROC is a curve in the unit square parameterized by k_A. We will assume that our ROC curves are concave, and that tp ≥ fp for each point one the curve. Concavity is a standard and mild assumption, for any ROC can be made concave by adding a stochastic component to the classifier [7]. Given concavity, tp ≥ fp on the ROC curve as long as it contains some points which are superior to (0, 0) and (1, 1). Our work is related to that of [7], who used stochastic methods to create a combined classifier having an ROC equal to the convex hull of the ROCs of the individual classifiers. Our method can produce superior classifiers, in the sense of having an ROC superior to this convex hull, but requires a conditional independence assumption.

3 Combining Classification Processes

3.1 Model Assumptions

Our model assumes that the classifiers A and B are conditionally independent. This means that given some unknown truth, positive (T = 1) for example, we assume that the output of A and B can be modeled as independent Bernoulli processes with respective probability of success tp_A and tp_B, i.e. the true-positive rates for the two processes. Note the we do not assume the independence of A and B; only the much weaker assumption of independence conditioned on the true underlying value is required. Conditional independence assumptions are common in machine learning and statistical and information theoretic image processing, especially in relation to maximum likelihood estimation. In the area of ROC analysis, and application to combinations of classifiers, the role of conditional independence is investigated in [1]. This work is related to our own, but differs in the combination technique, estimation of priors, and derivation of a joint statistic.

3.2 Maximum Likelihood Estimation

Let us assume we have two classifiers A and B, and that they are operating according to respective parameters k_A and k_B. We assume we know the ROC curves of the two processes, and the true positive and false positive rates for every value of the parameters k_A and k_B. Given some input, processes A and B will output either 0 (false) or 1 (true), giving us a total of 4 possible cases. For each case we have an expression for the maximum likelihood estimate (MLE) of the unknown truth T :

Each inequality (logical expression) in the rightmost column evaluates either to 0 or 1, and the resulting value is the maximum likelihood estimate of the truth T. If conditional independence is assumed, then Pr( A = 1 , B = 1 ǀ T = 1 ) = Pr( A = 1 ǀ T =1 ) Pr(B = 1 ǀ T = 1) = tp_A tp_B. See [1] for more details. Proceeding similarly for the other terms in the rightmost column above, we get the following table:

From our assumptions detailed above, tp_A tp_B ≥ fp_A fp_B and (1 – tp_A)(1 – fp_B) ≥ (1 – fp_A)(1 – fp_B), so the first and last rows of Table 2 are determined, and whenever A and B are in agreement their common output is the maximum likelihood estimate of T. Thus, only the middle two rows of the table above need to be determined, resulting in one of 4 possible MLE combination schemes, which we mnemonically name scheme “A and B,” scheme “A,” scheme “B,” and scheme “A or B.” These are summarized in the following table:

Table 2.

Binary Output for Classifiers A, B and the Maximum Likelihood Combination

A	B	Combined MLE of Truth T
1	1	tpA tpB ≥ fpA fpB
1	0	tpA(1 – tpB) ≥ fpA(1 – fpB)
0	1	(1 – tpA)tpB ≥ (1 – fpA)fpB
0	0	(1 – tpA)(1 – tpB) ≥ (1 – fpA)(1 – fpB)

It’s easy to calculate the false positive fp and true positive tp rates for these schemes, again using the assumption of conditional independence:

Thus, under the assumption of conditional independence, these rates can be calculated from information contained in the ROCs for A and B alone. In practice, this means that decision processes can be combined without retraining, since there is no need to estimate joint distributions for the output of A and B, nor the need to know the distribution of the underlying truth T.

3.3 Effect of the Combination Rules on Composite Accuracy

When operating under scheme “A and B,” we have fp = fp_A fp_B ≤ fp_A and similarly fp ≤ fp_B, tp ≤ tp_A, tp ≤ tp_B. We see that when compared to A or B alone, this rule generally decreases sensitivity tp but increases specificity 1 – fp, as one might expect for a scheme that requires a consensus to return a positive result. For the scheme “A or B,” we have fp = fp_A + fp_B − fp_A fp_B = fp_A + fp_b (1 – fp_A) ≥ fp_A, and similarly fp ≥ fp_B, tp ≥ tp_A, tp ≥ tp_B. So the “A or B” rule generally increases sensitivity but decreases specificity, again as one might expect. Thus in each of these cases the operating rate (fp, tp) is not demonstratably superior to either (fp_A, tp_A) or (fp_B, tp_B). However, an advantage is gained by an analysis of the entire range of operating rates, as we describe below.

3.4 Calculating Attainable True and False Positive Rates

To combine processes A and B, we begin by calculating for each value of the parameter pair (k_A, k_B), and corresponding 4–tuple of false-positive and true-positive rates (fp_A, tp_A, fp_B, tp_B), the correct ML scheme to use according to Table 2 above, and the resulting combined rates (fp, tp) for that scheme using the formulas in Table 4. In practice, we take discrete values for k_A and k_B, say by sampling them evenly. The resulting set of points (fp, tp) for two example ROCs are shown in Figure 1.

Table 4.

False (fp) and True (tp) Positive Rates by Combination Scheme

Scheme	fp	tp
“A and B”	fpA fpB	tpA tpB
“ A ”	fpA	tpA
“ B ”	fpB	tpB
“A or B”	fpA + fpB − fpA fpB	tpA + tpB − tpA tpB

Fig. 1.

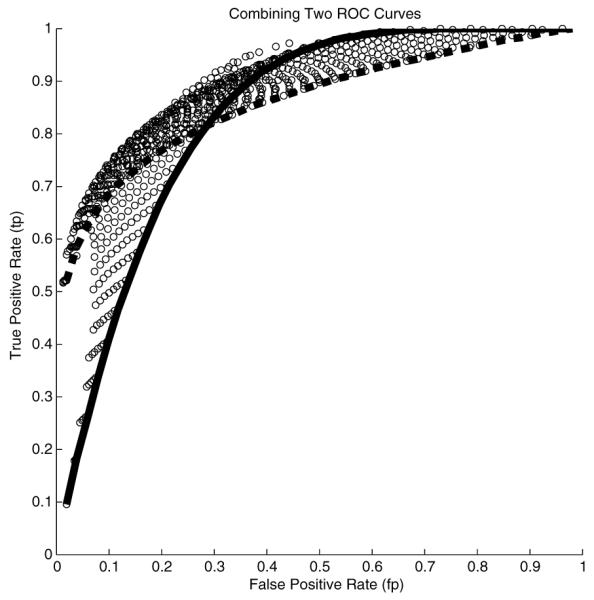
Two ROCs (solid line, broken line), together with set of points (circles), the outer boundary of which represents the ROC of the combined ML process

3.5 ROC Boundary Curve

The set of points (fp, tp) represent possible operating points for our joint process. However, we do not need to consider points in the interior of the region containing these points. For each point in the interior, there is a point on the outer boundary of the region which is superior, and thus a better operating point. For example, there is a point on the boundary which has the same false positive rate and a greater true positive rate. Thus, we discard these interior points, and consider only those points along the outer boundary. These points form a curve which is the ROC of our combined process. This combined ROC is the graph of the combined true positive rate thought of as a function of the combined false positive rate fp. We take fp ∈ [0, 1] to be the parameter of our combined process. In practice, the outer boundary ROC can be estimated by splitting the interval [0, 1] into a number of sub-intervals i.e. bins, and within each bin finding the pair (fp, tp) having the largest value of tp. The choice of the number of bins to use requires some care, but this is a common concern which appears whenever data histogramming is required, and standard solutions can be applied. We are currently researching a method by which an exact calculation of the joint ROC curve can be obtained. Along with each point (fp, tp) on the combined ROC curve, we keep track of a pair of parameters (k_A, k_B), and a ML combination scheme which allows us to operate at (fp, tp).

3.6 Calculating a Combined Statistic

In theory, the classifiers A and B can be any binary decision process governed by parameters k_A and k_B, where these parameters may be vector valued. In practice however, it is often the case that k_A and k_B are simple thresholds applied to scalar outputs s_A and s_B calculated as part of the A and B decision processes respectively. Thus A returns the estimate T = 1 if and only if k_A ≤ s_A, and similarly for B. In this case, it may be desirable to have a new derived statistic s for the combined process. Let C denote our combined classifier, created as described above. For a chosen operating point (fp, tp) on the ROC curve for C, we have associated thresholds k_A and k_B and an MLE combination rule to be applied in order to derive an estimate C ∈ {0, 1} of T based on the pair of statistics s_A and s_B. We define our joint statistic s as a function of s_A and s_B and the chosen operating level as follows:

To use s, we treat it as a statistic and return C = 1 if and only if s ≥ 0. It is easy to see that the true positive and false positive rates for this process are the same as the rates associated with the point on the joint ROC at which we wish to operate. We are currently refining a method by which a single joint statistic can be produced without the need for an apriori specification of an ROC operating point.

4 Illustration of the Method

We illustrate the method described above on a synthetic example. In Figure 2 we show two normal distributions for each of two classifiers A and B. One is the probability distribution for the statistic s_A or s_B given that T = 0, and the other is for these statistics given T = 1. The thresholds to use, shown as vertical lines, are determined by our algorithm after we choose an operating point (fp, tp) on the combined ROC curve, shown circled on the in Figure 3. Also displayed in Figure 3 are the ROC curves for A and B and the corresponding operating levels which result from the thresholds our algorithm chooses.

Fig. 2.

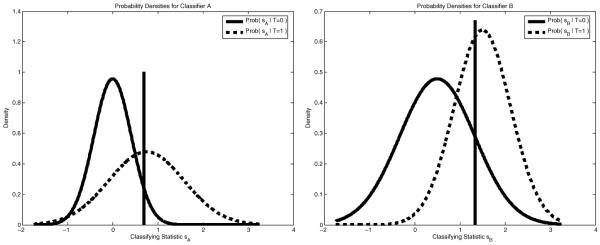
Distributions associated with the statistics s_A and of a thresholding classification scheme. The thresholds to use are determined by our algorithm.

Fig. 3.

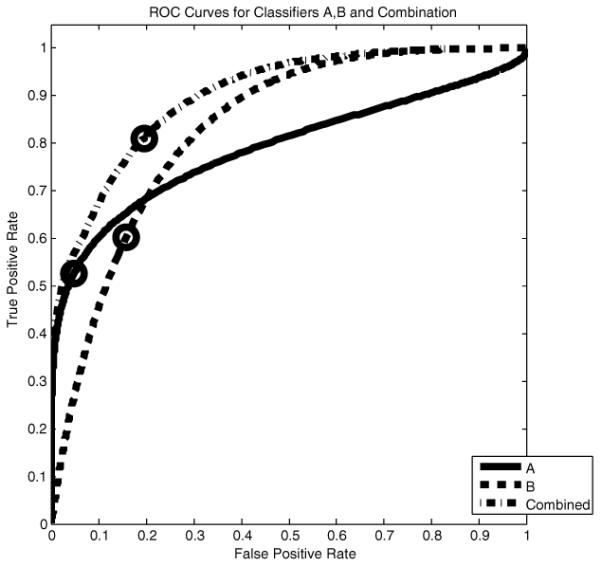
ROC curves for classifiers A and B. The circled point on the combined ROC curve represents a level at which we wish to operate. Our algorithm determines the thresholds to use to attain this level, shown in Figure 2, and the corresponding operating levels for A and B, shown circled on their respective ROC curves.

5 Conclusion and Discussion

We have developed a simple algorithm for combining multiple classifiers without the need for joint training, based on the maximum likelihood analysis of ROC curves of classifiers. Our work has been motivated by the general paucity of joint training data to use with a rapidly expanding array of new segmentation algorithms and diagnostic tests. Future work will include the testing of the method on a range of image and other clinical data, including an investigation of the validity of the conditional independence assumption across this range.

As mentioned before, ROC analysis, though standard in the medical community, has not been as widely adopted in the medical image processing field. Often, a segmentation or registration algorithm requires the specification of numerous parameters, such as kernel sizes, time steps, thresholds, weights applied in a weighted sum of functional terms, etc. The engineer typically varies these parameters to find the single point which gives a good result for a training data set, then applies them to a test data set. Yet finding this single point in parameter space is neither necessary nor desirable. What is more in tune with medical research outside of image processing is to report the ROC for the entire range of parameters, or the outer boundary of these possible operating points. Note that in the latter case, the outer boundary effectively reduces the degrees of freedom in the specification of parameters to one.

Medical image processing is maturing, with standardized algorithms for detection, segmentation and registration readily available to the general community in shared form through mechanisms like the ITK project. We believe more widespread use of ROC analysis will lead to greater clinical acceptance.

Table 1.

Binary Output for Classifiers A, B and the Maximum Likelihood Combination

A	B	Combined MLE of Truth T
1	1	Pr(A = 1, B = 1ǀ T = 1) ≥ Pr(A = 1, B = 1ǀ T = 0)
1	0	Pr(A = 1, B = 0ǀ T = 1) ≥ Pr(A = 1, B = 0ǀ T = 0)
0	1	Pr(A = 0, B = 1ǀ T = 1) ≥ Pr(A = 0, B = 1ǀ T = 0)
0	0	Pr(A = 0, B = 0ǀ T = 1) ≥ Pr(A = 0, B = 0ǀ T = 0)

Table 3.

Schemes for Combining Processes A and B

A	B	Scheme “A and B”	Scheme “A”	Scheme “B”	Scheme “A or B”
1	1	1	1	1	1
1	0	0	1	0	1
0	1	0	0	1	1
0	0	0	0	0	0

Table 5.

Formulas for Joint Statistic s

Scheme	Formula for s
“A and B”	min(sA – kA, sB – kB)
“ A ”	sA – kA
“ B ”	sB – kB
“A or B”	max(sA – kA, sB – kB)