Calcium dynamics and signaling in vascular regulation: computational models

Abstract

Calcium is a universal signaling molecule with a central role in a number of vascular functions including in the regulation of tone and blood flow. Experimentation has provided insights into signaling pathways that lead to or affected by Ca²⁺ mobilization in the vasculature. Mathematical modeling offers a systematic approach to the analysis of these mechanisms and can serve as a tool for data interpretation and for guiding new experimental studies. Comprehensive models of calcium dynamics are well advanced for some systems such as the heart. This review summarizes the progress that has been made in modeling Ca²⁺ dynamics and signaling in vascular cells. Model simulations show how Ca²⁺ signaling emerges as a result of complex, nonlinear interactions that cannot be properly analyzed using only a reductionist's approach. A strategy of integrative modeling in the vasculature is outlined that will allow linking macroscale pathophysiological responses to the underlying cellular mechanisms.

INTRODUCTION

An elaborate network of signaling pathways exists that regulates the intracellular concentration of free calcium [Ca²⁺]_i in endothelial cells (ECs) and smooth muscle cells (SMCs) of the vascular wall. This network includes intracellular signaling as well as cell-to-cell (intercellular) communication with paracrine factors or diffusion of species through homo-and hetero-cellular gap junctions. This assembly of signaling pathways creates multiple feedback loops that tightly regulate Ca²⁺ homeostasis and dynamics. Experimentation has begun to untangle this elaborate network and continuously provides new insights about the physiology of blood vessels and the mechanisms that regulate tone and blood flow. Mathematical modeling offers a systematic approach to system and data analysis and to guiding new experimental studies.

Mathematical models can assist in the elucidation of regulatory mechanisms behind phenomena of importance in vascular physiology. In the regulation of vasomotor responses for example, the importance of intercellular exchange of Ca²⁺ and other second messengers in myoendothelial communication is still under investigation.^1–3 Recent experiments suggest preferential expression of membrane components in specialized cellular extensions from the EC to the SMC across the internal elastic lamina (i.e., myoendothelial projections) and a key role of these structures in the regulation of vasoreactivity.^4–9 The phenomenon of spontaneous oscillations in vessel diameter, called vasomotion, is thought to play an important role in the regulation of tissue perfusion and oxygenation. The responsible cellular oscillator(s) and the mechanism that allows synchronization of individual cells are still under investigation.^10–13 Focal stimulation in some vessels leads to spreading vasomotor responses. This phenomenon is important for both the rapid and long-term coordination of microvascular function.¹⁴ In some tissues, these responses can spread over significant distances and secondary Ca²⁺ waves can be observed in some preparations, implying currently unidentified regenerative mechanisms for signal conduction.^15–18

Significant progress has been made in the development of comprehensive models of calcium dynamics for some systems such as in cardiac myocytes.^19–23 Often these models are integrated with descriptions for membrane electrophysiology, cell mechanics, metabolic and signal-transduction pathways.^24–29 Multicellular/multiscale models have emerged for the heart. Anatomically detailed models incorporate the cellular models to describe the electromechanical properties of the whole organ. These models are capable of describing function at the tissue level while integrating mechanisms at the subcellular/molecular level and have been utilized to investigate physiological function as well as disease states.^30–33 Unfortunately, the significant progress seen in the modeling of the heart has not been paralleled in the vasculature. Despite the existing differences in intracellular signaling, electrophysiology, mechanics, and geometry between the two systems, a similar approach for the development of multiscale models can be applied for the vasculature.

Although Ca²⁺ signaling in various cell types shows many common features and motifs,³⁴ there are significant differences in Ca²⁺ mobilization between cardiac and vascular cells.^35–40 In addition, the SMC differs from the electrically non-excitable EC in channel and receptor composition, and in the contribution of the various Ca²⁺ mobilization pathways. L-type Ca²⁺ channels and calcium-induced calcium release (CICR) from ryonodine receptor (RyR)-sensitive stores play a predominant role in myocytes, while the phosphatidylinositol pathway and capacitative calcium entry (CCE) have a significant role in ECs. Furthermore, the type and density of membrane ion channels exhibit significant differences among species and tissues, and probably change even within the same vascular bed with the size of vessel. This heterogeneity suggests a need for vessel-specific models of Ca²⁺ signaling and dynamics in the vasculature.

This review focuses on recent efforts in the development of mathematical models to describe Ca²⁺ dynamics in vascular SMCs and ECs. The level of detail in these models ranges from minimal models with phenomenological descriptions to models with detailed kinetic descriptions of transmembrane currents. Models exist that incorporate biophysical descriptions for the signaling pathways leading to or affected by the Ca²⁺ mobilization. Published models differ also in the level of detail in spatial organization, from models with a single cytosolic compartment with single or multiple internal stores to models with cytosolic subcompartments and spatial gradients.

EC MODELS

EC models have recently emerged that are based on earlier generic models of calcium dynamics in electrically non-excitable cells.^41–44 One of the first EC models was developed by Winston and coworkers⁴⁵ to study the effects of mechanical strain on cultured bovine pulmonary artery endothelial (BPAE) cells. Three Ca²⁺ sequestering mechanisms were incorporated as binding processes with reversible or irreversible kinetics (i.e., Ca²⁺ binding with intracellular proteins, Ca²⁺ binding with fluorescent dyes and Ca²⁺ pumping). In this simplistic model, free steady-state Ca²⁺ concentration was determined by the ratio of stretch-dependent permeability to pumping.

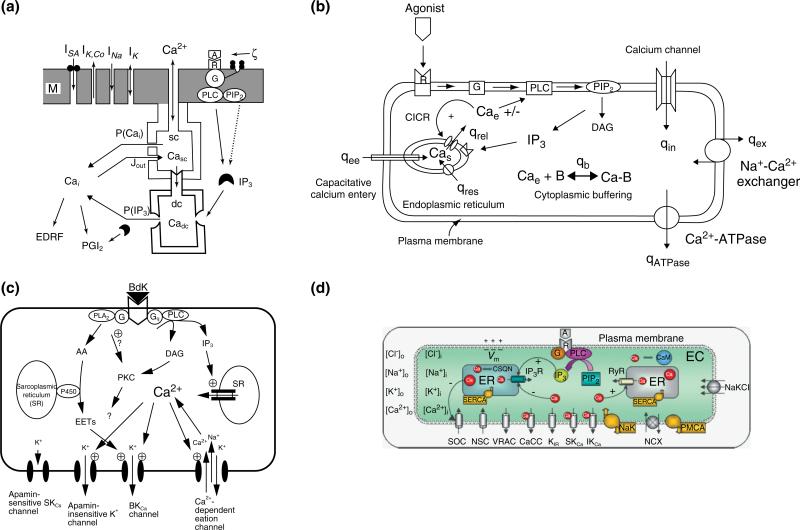
Ca²⁺ dynamics and electrical activity of vascular ECs were first examined in a model introduced by Wong and Klassen (Figure 1a).⁴⁶ Their model contained four transmembrane currents: a sodium current (INa), a potassium current (IK), a Ca²⁺-activated potassium current (IKCa), and a stretch-activated calcium current (ISa). The model also contained an internal calcium store that was divided into two compartments [superficial (sc) and deep (dc) compartments] to separate the effect of the Ca²⁺-induced Ca²⁺ release (CICR) mechanism from store release induced by IP₃. A Ca²⁺ flux refills the sc compartment of the store directly from the extracellular space which in turn replenishes the dc compartment. IP₃ was generated by stress and was inactivated by cytosolic Ca²⁺. Simulation results demonstrated the ability of the store to increase cytosolic Ca²⁺ in response to agonist stimulation. In a latter study,⁴⁷ they utilized this model to examine cell responses to shear stress. Pulsatile stimulation elicited two to three times higher Ca²⁺ transient than steady shear stress. The model responses were similar to those observed in cultured vascular ECs.

FIGURE 1.

Models of calcium dynamics in ECs. (a) A model introduced by Wong and Klassen.⁴⁷ The model contained an internal calcium store that was divided into a superficial (sc) and deep (dc) compartments and four transmembrane currents: a sodium current (I_Na), a potassium current (I_K), a Ca²⁺-activated potassium current (I_K,Ca), and a stretch-activated calcium current (I_SA). (b) A calcium dynamics model in human umbilical vein endothelial cells (HUVECS) introduced by Wiesner and coworkers.⁴⁸ The model includes descriptions for CICR, CCE, kinetics for IP₃ formations following thrombin receptor activation, and Ca²⁺ buffering. Formulations for the NCX and the PMCA pump were also included. (c) A model of endothelial cell electrophysiology presented by Schuster and coworkers (reprinted with permission from Ref 50. Copyright 2003 Springer). Model focuses on K⁺ currents from bradykinin-sensitive channels (i.e., the large-conductance BKCa channel, the apamin-insensitive small-conductance SKCa channel, and an NSC channel) and the apamin-sensitive SKCa channel that is not gated by bradykinin. (d) An endothelial cell electrophysiology/ionic dynamics model introduced by Silva et al.⁵¹ Model contains several transmembrane currents from: store-operated Ca²⁺ channels (SOC); nonselective cation (NSC) channels; voltage-regulated anion channel (VRAC); Ca²⁺-activated Cl^– channels (CACC); inward rectifier K⁺ channels; Ca²⁺-activated K⁺ channels (small-conductance SKCa, intermediate-conductance IKCa); Na⁺-K⁺-ATPase (NaK) pumps; plasma membrane Ca²⁺-ATPase (PMCA) pumps; Na⁺/Ca²⁺ exchanger (NCX). The model accounts for changes in membrane potential (V_m) and in the intracellular concentrations of the four main ionic species following agonist induced IP₃ release.

An in-depth model of calcium dynamics in human umbilical vein endothelial cells (HUVECS) was presented by Wiesner and coworkers⁴⁸ (Figure 1b). Their model incorporated detailed thrombin receptor kinetics as described in the work by Vu et al.⁴⁹ The model included most of the major calcium mobilization pathways including CICR, CCE, IP₃ receptor-dependent store Ca²⁺ release, and Ca²⁺ buffering. In agreement with the Wong and Klassen model,^46,47 and the prevalent understanding at that time, CCE replenishes the intracellular store (i.e., endoplasmic reticulum) directly from the extracellular space. The Na⁺/Ca²⁺ exchanger (NCX) and the plasma membrane Ca²⁺ ATPase (PMCA) pump were also included as means of cytosolic Ca²⁺ extrusion. The model was focused on the IP₃ and Ca²⁺ dynamics and included separate mass balances for cytosolic, store and buffered Ca²⁺. The model was able to reproduce the response to thrombin with reasonable accuracy. The model was able to simulate experimental behavior without inclusion of the CICR and CCE mechanisms. Oscillations was also documented after perturbation of parameter values affecting the feedback between Ca²⁺ and IP₃ and the re-sequestration rates of Ca²⁺. The model also suggested a minor role of cytosolic buffers for oscillations.

Schuster and coworkers⁵⁰ developed a model to simulate changes in membrane electrical activity following bradykinin stimulation of coronary artery ECs. Experimental data provided empirical correlations for the cytosolic calcium and IP₃ changes following stimulation. The focus of the model was to predict K⁺ currents and membrane potential changes in the presence and absence of extracellular Ca²⁺. Bradykinin induced transient hyperpolarization mainly via the apamin-sensitive, small-conductance K⁺ channels. Interestingly, the model suggested significant K⁺ accumulation in the intercellular space, following bradykinin stimulation, sufficient enough to activate Na⁺/K⁺-ATPase, or inwardly rectifying K⁺ channels in overlying SMCs. This result is consistent with the proposed role of K⁺ as an EDHF.

In a recent study, we presented a detailed EC model that integrates both EC Ca²⁺ dynamics and plasmalemmal electrical activity to investigate EC responses to various stimulatory conditions and the relationship between Ca²⁺ and membrane potential (V_m).⁵¹ The model describes most of the major membrane channels and pumps present in EC of rat mesenteric arteries (Figure 1d). The plasma membrane includes kinetic descriptions for nonselective cation (NSC) channels, store-operated cation (SOC) channels, small (SK_Ca) and intermediate (IK_Ca) conductance calcium-activated K⁺ channels, inward rectifier K⁺ channels (K_IR), volume-regulated anion channels (VRAC), calcium-activated Cl^– channels (CACCs), NCX and Na⁺-K⁺-Cl^– co-transporter and Na⁺-K⁺-ATPase pump. It also includes intracellular Ca²⁺ handling components such as IP₃ receptor, sarco/endoplasmic reticulum Ca²⁺ ATPase (SERCA), and plasma membrane Ca²⁺ ATPase (PMCA) pumps. Ca²⁺-dependent NO release is also incorporated. For the first time, we integrated balances for the major ionic species (i.e., K⁺, Cl^–, Na⁺) in addition to the balances for cytosolic, store and buffered Ca²⁺ and IP₃, and the Hodgkin–Huxley type formalism for the membrane potential. The model reproduces experimentally observed EC V_m responses to volume-sensitive anion channel inhibitors and to extracellular potassium concentration changes. In addition, simulated Ca²⁺ transients during agonist stimulation agree with experimental data, both under control and Ca²⁺-activated potassium channel blockade conditions. The detailed representation of the cell's electrical activity in addition to the Ca²⁺ dynamics enabled us to investigate important mechanisms involved in the regulation of vascular tone including the ability of the cell to hyperpolarize in response to K⁺ challenge or the controversial role of V_m on transmembrane Ca²⁺ influx.

Up to this date, the majority of the EC models were compartmental in nature. Recently, Hong et al.⁵² developed a 2-D finite element model that incorporated intracellular resolution and spatial concentration gradients. The purpose of the model was to evaluate the effects of spatial segregation of (eNOS) and CCE channels in caveolae, on eNOS activation in response to ATP. The model had circular geometry with endoplasmic reticulum (ER) located at the center of the cell. The model included major Ca²⁺ pathways like CCE modulated by a second messenger molecule (i.e., calcium influx factor), SERCA and PMCA pumps, IP₃-dependent Ca²⁺ release from the ER (Jer) and calcium buffering. The model simulations predicted up to three times higher concentration of Ca²⁺ in the caveolar domain which is absent with even distribution of CCE channels or IP₃-induced fluxes. The ER proximity to the cell membrane with CCE localization was shown to affect the peak caveolar Ca²⁺ concentration in a distance-dependent manner with decreasing transients as distance increased. This study highlights the need for subcellular resolution in future models of EC Ca²⁺ dynamics and signaling.

SMC MODELS

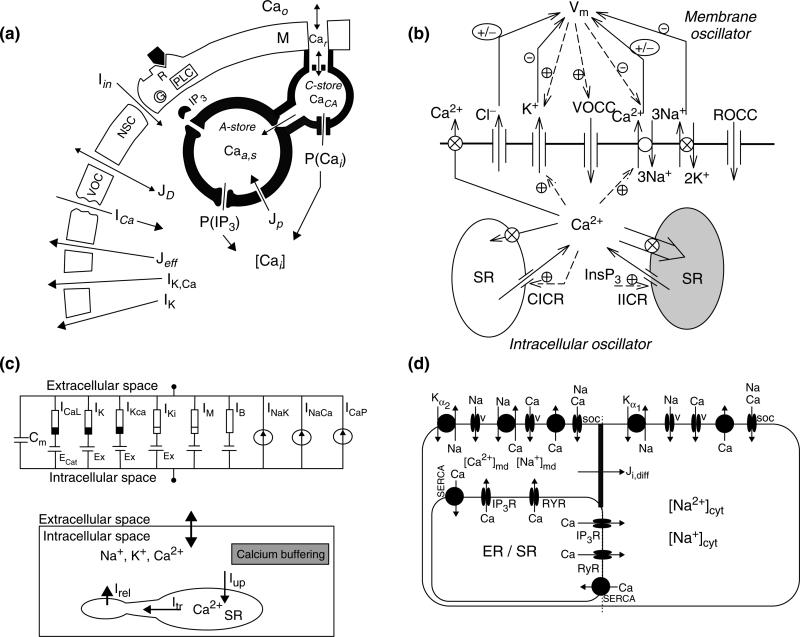
Wong and Klassen⁵³ proposed a generic model of Ca²⁺ regulation in vascular SMCs. It included transmembrane Ca²⁺ fluxes through voltage-operated calcium channels (VOCCs), IP₃- and Ca²⁺-sensitive intracellular stores, and a refilling mechanism for the stores directly from the extracellular space (Figure 2a). The model was able to reproduce Ca²⁺ responses to agonist stimulation, and to membrane depolarization. Later, they extended their original model by incorporation of voltage- and Ca²⁺-dependent K⁺ channels and agonist-activated nonselective channels.⁵⁴ Their new model also accounted for membrane electrical activity in addition to calcium dynamics and presented simulations of endothelin-induced V_m and Ca²⁺ transients and oscillations. Soon after Wong and Klassen's original model, Gonzalez-Fernandez and Ermentrout⁵⁵ formulated an SMC Ca²⁺ dynamics model to investigate Ca²⁺ oscillations in small arteries and the phenomenon of vasomotion. They incorporated Ca²⁺ and K⁺ transmembrane currents and a nonspecific leak current. They also accounted for Ca²⁺ buffering in the cytosol, the Ca²⁺-dependent crossbridge formation of the contractile apparatus, and incorporated the biomechanics description modeling the vessel as a thick-walled cylinder. Regular periodic oscillations of intracellular Ca²⁺ and vessel diameter, were generated by the interaction of voltage-dependent Ca²⁺ current with voltage- and Ca²⁺-dependent K⁺ currents. Increasing pressure decreased vessel diameter (i.e., myogenic tone) through pressure-dependent activation of the Ca²⁺ channels and the subsequent elevation of cytosolic Ca²⁺.

FIGURE 2.

Models of calcium dynamics in SMCs. (a) The Wong and Klassen model of Ca²⁺ dynamics and membrane's electrical behavior in vascular smooth muscle (reproduced with permission from Ref 53. Copyright 1993 Elsevier). The model includes two intracellular stores. A-store is an IP₃-sensitive store. C-store is replenished by extracellular Ca²⁺. J_eff and J_D are the active and passive transmembrane Ca²⁺ efflux; J_p is the Ca²⁺ uptake rate of the A-store; I_Ca is the Ca²⁺ current through the voltage-operated channel; I_in is the inward current through the receptor-operated channel; I_K,Ca and I_K are the calcium and voltage-dependent K⁺ channels. (b) Minimal model reproduced from Parthimos and coworkers.⁵⁸ Model contains two independent internal stores [a ryanodine-sensitive (CICR) and inositol 1,4,5-trisphosphate (InsP3) sensitive]. Membrane component contains descriptions for: transmembrane currents for Cl^–, K⁺ channels; voltage- and receptor-operated Ca²⁺ channels (VOCCs and ROCCs, respectively); Na⁺-K⁺-ATPase, and Ca²⁺-ATPase pumps; NCX. (c) Detailed model reproduced with permission from Ref 62. Copyright 2003 Elsevier. Membrane model (upper panel) describing ionic membrane currents and transmembrane potential. Black and white indicates resistance with voltage-dependent nonlinearity, and the all white resistor indicates linear element. Fluid compartment model (lower panel) describes ionic dynamics, Ca²⁺ buffering, and Ca²⁺ handling by sarcoplasmic reticulum (SR). The SR is divided into a ryonadine-sensitive release compartment and an uptake compartment containing SERCA pumps that communicate. (d) Diagram of the cell model presented and reproduced from Ref 65. Copyright 2007 American Physiological Society. Model contains three intracellular compartments: bulk cytosol (cyt), microdomains (md), and sarcoplasmic reticulum (SR). J_i,diff is the electrodiffusive flux of ion i between the microdomains and the bulk cytosol.

Fink and coworkers⁵⁶ constructed a mathematical model of the IP₃-dependent Ca²⁺ changes in A7r5 cells cultured from rat thoracic aorta SMC line. The authors used physiologically constrained parameter values and their experimental data to describe the kinetics of the IP₃ receptor and the degradation rate of IP₃ in the cytosol. Ca²⁺ buffering in the cytosol and the refilling of the sarcoplasmic reticulum (SR) store via SERCA pumps were also incorporated. The model was able to fit experiments were IP₃ release was stimulated by means of caged-IP₃ or a slowly hydrolysable IP₃ analog. Bennett and coworkers⁵⁷ presented a model of arteriolar SMC contraction following release of NE from perivascular sympathetic nerves. The extracellular NE concentration was calculated as a function of time and radius from 1D reaction-diffusion equation, and used as an input to α1-adrenoceptor. A detailed kinetic model described receptor–transmitter binding, receptor phosphorylation and internalization, G-protein and phospholipase C (PLC) activation, and IP₃ formation. Ca²⁺ was released from the SR through IP₃Rs, and regulated the concentration of actin bound to phosphorylated myosin.

The complexity of Ca²⁺ mobilization and the many components affecting membrane's electrical activity prompted Parthimos and coworkers⁵⁸ to develop a minimal model of an SMC. An attractive feature of their approach was the reduced number of parameters utilized that made this model attractive for subsequent studies of vascular signaling.^12,59,60 The authors utilized their model to investigate chaotic behavior in the irregular contractions of rabbit ear arteries seen during vasomotion. They extended the two-pool model of Goldbeter et al.⁴² by incorporation of various membrane currents such as currents through the VOCC, K⁺, and Cl^– channels, the NCX or the Na⁺-K⁺ pump (Figure 2b). The model generated chaotic behavior as a result of the nonlinear interaction between a membrane oscillator and an intracellular calcium oscillator. By modifying selected parameters, the model could reproduce a wide range of dynamic behavior seen under various experimental conditions and pharmacological interventions.^13,61

In the opposite direction, Yang and coworkers aimed to develop a detailed model that will incorporate all the known significant components of the plasma membrane⁶² in SMCs for rat cerebrovascular arteries. Their study presents perhaps the first attempt for a detailed, tissue-specific vascular model of Ca²⁺ dynamics. Significant effort was spent to obtain current descriptions based on electrophysiological recordings, for VOCC channels, potassium channels (K_v, B_KCa, and Kir), stress-activated NSC channels, Na⁺-K⁺-ATPase, and Ca²⁺-ATPase (Figure 2c). Although experiments from cerebral vessels were given a priority, data from other tissues were also utilized in the absence of a better source. The intracellular compartment included descriptions for Ca²⁺, Na⁺, and K⁺ balance, Ca²⁺ buffering, CICR from the SR, and Ca²⁺ sequestrations through SERCA. The intracellular store representing mostly the SR was adapted from cardiac cell models and included a ryonodine-sensitive release compartment that communicates with the rest of the SR (uptake compartment) where calcium is replenished through the SERCA pump. The Ca²⁺ model was integrated with a mechanical model of cylindrical vessel segment through Ca²⁺-dependent active stress and stress-activated NSC channels. This enabled the authors to simulate vessel contractions and myogenic tone.⁶³ The model was later modified to describe the NO-induced Ca²⁺ concentration reduction and Ca²⁺ desensitization of myosin phosphorylation and force generation.⁶⁴ The ability of this study to simulate macroscale responses, prompted the development of subsequent studies that attempted similar tissue-specific detailed models.^65,66 At the same time, however, it became obvious that such a detailed approach will have to deal with significant obstacles/limitations including the significant number of unknown parameters, the absence of tissue-specific quantitative data (particularly electrophysiological recordings for transmembrane currents), the structure and function of the intracellular stores, and the spatial distribution of receptors, channels, and pumps, to name a few.

We followed a similar approach and we have recently presented a mathematical model of Ca²⁺ and V_m dynamics in SMC based on data mostly from rat mesenteric arterioles (RMAs).⁶⁶ The model incorporates the most significant membrane currents identified in this particular SMC type. It includes IP₃ and Ca²⁺ sensitive overlapping intracellular stores, Ca²⁺ buffering, and descriptions for the α1-adrenoceptor and NO/cGMP signaling pathways. The model accounts for the cytosolic balance of Cl^– in addition to the balance of Na⁺, K⁺, Ca²⁺, and IP₃. Recent experimental evidence suggested the activation of NSC channels (belonging to the TRPC family) by diacylglycerol (DAG) as a mechanism for sustained cell depolarization following adrenoceptor stimulation.⁶⁷ The composition of the sarcoplasmic reticulum, arrangement of IP₃ and ryanodine receptors, and the mechanisms of store replenishment remain up to this date for the most part unknown. Recent data suggest that the stores are not replenished directly by external calcium.⁶⁸ A common ⁶⁹ or at least partially overlapping intracellular Ca²⁺ pools⁷⁰ have been suggested, but evidence also exists for spatially and functionally distinct calcium- and IP₃-sensitive Ca²⁺ stores in SR.⁷¹ In our model we adopted a two-compartment model of the SR similar to that presented in the work by Yang et al.⁶² Values for the majority of the parameters were identified from independent experimental data (although some data were not derived from RMA SMCs). We aimed to limit the number of user-defined parameters and only a reduced number of unknown parameters were optimized to fit integrated cellular responses (i.e., resting ionic concentrations, resting V_m, Ca²⁺ transients in repose to agonist stimulation etc.). The model was validated against a variety of independent observations for whole-cell responses.

The model presented by Edwards and Pallone⁶⁵ investigates the effect of Na⁺ concentration on Ca²⁺ dynamics in the renal microcirculation. One of the main features of this model was the introduction of intracellular subcompartment to account for subcellular heterogeneity and the presence of subplasmalemmal microdomains. Thus, a three-compartment model was constructed and descriptions for model components were derived based on data from descending vasa recta pericytes and other SMCs (Figure 2d). Apart from the major components presented in the SMC model of the work by Yang et al.,⁶² this model also included descriptions for the Na⁺-K⁺-ATPase (NaK)-α2 isoform and the NCX in the microdomain, for Ca²⁺-dependent IP₃ generation and the kinetic behavior of the IP₃ receptor, and accounted for the electrodiffusion of Ca²⁺, Na⁺, and K⁺ between the microdomain and the cytoplasm. The results supported the hypothesis that subplasmalemmal Na⁺ can modulate Ca²⁺ dynamics in SMCs under normal conditions and after blockade of NaK-α2 by ouabain.⁷²

Elements from the minimal model of Parthimos⁵⁸ and the detailed approach of Yang⁶² have been incorporated in an SMC model presented by Jacobsen and coworkers.¹² A significant feature of this model is that it abandons the compartmental approach of the previous modeling attempts and provides a description for cytosolic Ca²⁺ with spatial heterogeneity. This was accomplished by incorporating diffusion of Ca²⁺ within the cytosol in the longitudinal direction of the cell. This one-dimensional transport/Ca²⁺ dynamics model was utilized to examine transition of asynchronous intracellular Ca²⁺ waves to whole-cell Ca²⁺ oscillations often seen during the onset of vasomotion in SMC from RMA. cGMP-dependent Ca²⁺-activated Cl^– channels played a key role in this transition. In the presence of cGMP, the channels depolarize SMC in response to Ca²⁺ release from SR, the depolarizing current synchronize CICR in neighboring cells.

COUPLING CELLS TOGETHER: MULTICELLULAR MODELS OF THE VASCULAR WALL

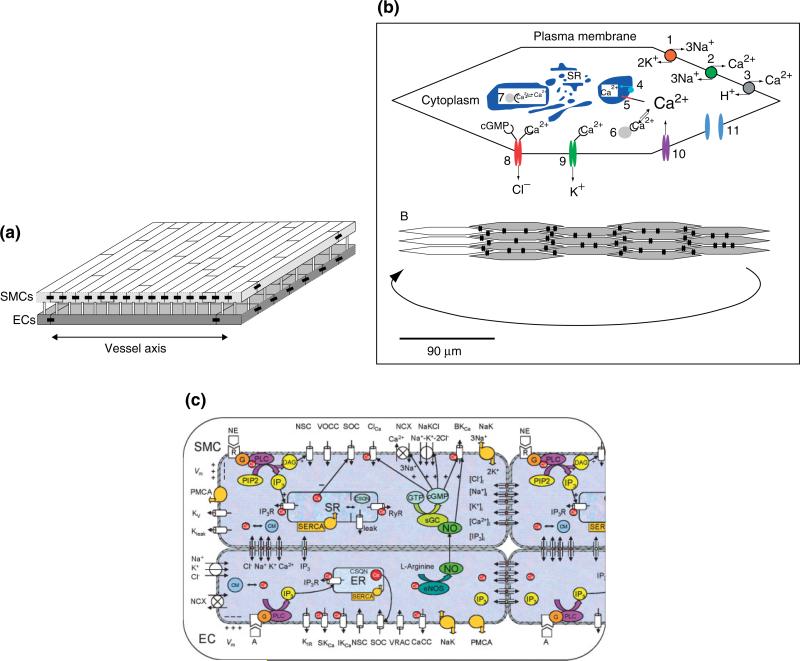
Koenigsberger and coworkers⁵⁹ modified the model of Parthimos et al.⁵⁸ by incorporating agonist- and Ca²⁺- dependent IP₃ formation, modifying selected parameters, and eliminating the membrane oscillator. They used this single-cell model to build a multicellular model of SMCs coupled electrically and through the gap junctional diffusion of Ca²⁺ and IP₃. They investigated with their model the synchronization of intracellular Ca²⁺ oscillators during vasomotion in rat mesenteric resistance vessels. Gap junctions were treated as Ohmic resistances for the electrical coupling, while Ca²⁺ and IP₃ exchange between cells was proportional to their intercellular concentration gradients. In subsequent studies, their multicellular model of the vascular wall was further advanced by incorporating an endothelial layer (Figure 3a). The single EC was based on the Goldbeter⁴² and Schuster⁵⁰ models. In a series of studies the authors examined the effects of endothelium, wall stress, and isotonic, isometric, and isobaric conditions on Ca²⁺ dynamics and vasomotion.^73–75 Simulations suggested among other things that the endothelium can affect vasomotion by moving the SMCs in and out of the oscillatory domain. The existence of multiple stable steady states was shown under some conditions. This multistability may mask the existence of a vasomotion domain in a concentration-response curve. Interestingly, weak calcium coupling and not IP₃ coupling was shown to be crucial to obtain a synchronization of calcium oscillations in vasomotion. A minimum required value was provided for the unknown gap junctional permeability for Ca²⁺ in order for Ca²⁺ diffusion to be able to play such role.

FIGURE 3.

Multicellular models of the vascular wall. (a) The Koenigsberger model integrates on a two-dimensional grid model equations for SMCs superposed on a two-dimensional grid of ECs. ECs are arranged parallel and SMCs perpendicular to the vessel axis (reproduced with permission from Ref 73. Copyright 2005 Elsevier). Cell geometry is approximated by a rectangle. Each cell is connected with its nearest neighbors on the same layer (homocellular connection) and with the cells on the other layer directly superposed on it (hetero-cellular connection). (b) A model of the SMC layer introduced by Jacobsen and coworkers (Reproduced with permission from Ref 76. Copyright 2007 American Physiological Society). Each SMC (upper panel) contains: Na⁺/K⁺-ATPase (1), NCX (2), plasma membrane Ca²⁺-ATPase (3), sarco(endo)plasmic reticulum Ca²⁺-ATPase (4), SR calcium release channel (5), cytoplasmic calcium buffer (6), SR calcium buffer (7), cGMP-sensitive calcium-dependent chloride channel (8), calcium-activated potassium channels (9), voltage-sensitive calcium channel (L-type calcium channel; 10), and gap junction (11). The SMCs are arranged into a single-layered cell plate (lower panel). Each spindle-shaped cell couples to neighboring cells through gap junctions (black double-barrel structures). (c) Multicellular model of a vessel segment presented by Kapela and coworkers.^78,79 ECs and SMCs are placed in appropriate arrangement. Cells are coupled by nitric oxide (NO) and myoendothelial gap junctions permeable to Ca²⁺, Na⁺, K⁺, and Cl^– ions, and IP₃. K_ir—inward rectifier K⁺ channel; VRAC—volume-regulated anion channel; SK_Ca, IK_Ca and BK_Ca—small-, intermediate-, and large-conductance Ca²⁺-activated K⁺ channels; SOC—store-operated channel; NSC—nonselective cation channel, CaCC and Cl_Ca—Ca²⁺-activated chloride channel; NaK—Na⁺-K⁺-ATPase; PMCA—plasma membrane Ca²⁺-ATPase; NCX—Na⁺/Ca²⁺ exchanger; NaKCl—Na⁺-K⁺-Cl^– cotransport; K_v—voltage-dependent K⁺ channel; K_leak—unspecified K⁺ leak current; VOCC—voltage-operated Ca²⁺ channels; SR/ER—sarco/endoplasmic reticulum; IP₃R—IP₃ receptor; RyR—ryanodine receptor; SERCA—SR/ER Ca²⁺-ATPase; CSQN—calsequestrin; CM—calmodulin; R—receptor; G—G-protein; DAG—diacylglycerol; PLC—phospholipase C; sGC—soluble guanylate cyclase; cGMP—cyclic guanosine monophosphate.

Jacobsen and coworkers also integrated their single-cell model¹² into a multicellular model of the smooth muscle layer.⁷⁶ They used this population of SMCs to study the mechanisms of synchronization of Ca²⁺ oscillations in the arterial wall during vasomotion. Intercellular coupling in this model was accomplished by means of an additive electrodiffusion equation. Thus, Ca²⁺ exchange was based on electrochemical gradients and not simply on intercellular concentration differences. The total intercellular current was described as sum of currents carried by individual ions. The gap junctional permeability was similar for each ion and values in the wide range of 0.5–5000 m/s (i.e., permeability per contact surface area) were examined. One of the major outcomes of this study was the central role of cGMP-, dependent CACCs, and of the electrical coupling in cell synchronization and in the initiation of vasomotion in rat small mesenteric arteries. This theoretical prediction agrees with experimental data.⁷⁷ Interestingly, simulations by this model suggested that intercellular diffusion of calcium or another second messenger is not necessary to explain synchronization.

We have also integrated our single-cell models (i.e., the EC model⁵¹ and the SMC model⁶⁶) into a two-cell arrangement to investigate aspects of myoendothelial communication.⁷⁸ In a later study a multicellular model of a vessel segment was constructed⁷⁹ by placing ECs and SMCs in a proper arrangement. ECs and SMCs are coupled through the diffusion of ions and second messengers (i.e., IP₃, NO). The detailed balances for the intracellular ionic concentrations enabled us to partition the total current flow between two cells into currents carried by individual ions. In this way current flow and ionic exchange can be monitored simultaneously. In our model the ionic fluxes through the gap junctions are expressed by four independent Goldman-Hodgkin-Katz (GHK) equations, one for each ionic species (Ca²⁺, Na⁺, K⁺, and Cl^–). Thus, ionic flow is based on electrochemical gradients as predicted by the constant field equation. For low electrochemical gradients, the gap junction coupling described by GHK equations does not differ significantly from the additive electrodiffusion model assumed in the work by Jacobsen et al.⁷⁶ Most importantly, the permeability of a gap junction to an ion (a parameter that has been arbitrarily assigned in previous studies) was estimated from the total gap junction resistance R_gj. R_gj can be determined experimentally and some values exist in the literature for different vascular beds. Diffusion of IP₃ was assumed to be proportional to the concentration difference between neighboring cells. NO availability in SMC was estimated from NO transport models.⁸⁰

The two-cell model⁷⁸ demonstrates the synergistic effect of IK_Ca and SK_Ca blockers in abolishing endothelium-derived NO-independent SM hyperpolarization.⁸¹ The EC exerts a stabilizing effect on CICR-dependent SMC Ca²⁺ oscillations, by increasing the NE concentration window for oscillations. Interestingly the model predicts insufficient myoendothelial Ca²⁺ exchange for inducing global intracellular Ca²⁺ changes in the adjacent cell after stimulation of either layer and a unidirectional effect of IP₃ diffusion (i.e., from SMC to EC) generated as a result of different cellular kinetics. Simulations with the multicellular model⁷⁹ predict SMC Ca²⁺ reduction at distant sites but only a local endothelium Ca²⁺ increase when the endothelial layer is stimulated locally with acetylcholine. Model simulations show electrotonic conduction of membrane potential changes along the endothelial layer as the primary mechanism of spreading vasoreactivity. The model predicts that NE-induced preconstriction can affect the electronic and Ca²⁺ spread along the vessels. This is attributed to changes in radial resistivity and sensitization of the EC layer to IP₃ following stimulation with NE. IP₃, but not Ca²⁺, diffusion through homocellular gap junctions can increase [Ca²⁺]_i in neighboring ECs. This small IP₃-dependent endothelial Ca²⁺ spread can amplify the total current generated at the local site and thus reduces the number of stimulated cells required to induce distant responses.

CHALLENGES IN MODELING VASCULAR CALCIUM SIGNALING

ECs and SMCs regulate Ca²⁺ entry and V_m by expressing an abundant and diverse collection of plasmalemmal ion channels, which are for the most part absent in the available mathematical models. Advancement of the models requires new experimental studies. Incorporation of new electrophysiological data into the models of Ca²⁺ regulation, for example, is essential for increasing their predictive power. Considering the balance of the major intracellular ionic species (i.e., Na⁺, K⁺, Cl^–) in addition to Ca²⁺ is essential for modeling both single-cell electrophysiology and cell-to-cell electrochemical coupling and communication since Ca²⁺ entry is regulated by the membrane potential but also by the intra- and extra-cellular concentrations of Ca²⁺ and the other major ionic species, i.e., K⁺, Cl^–, and Na⁺.^6,82,83 Membrane channels that have not been incorporated in the models may exist that can potentially affect aspects of Ca²⁺ signaling such as the facilitation of Ca²⁺ waves and spreading responses.⁸⁴

Future models need to account for the effect of various microdomains (subplasmalemmal, microprojections), the structure and function of intracellular stores (i.e., SR/ER, mitochondria), the uneven distribution of membrane and store components, and the resulting spatial concentration gradients for ionic species and second messengers. The concentrated presence of IK_Ca channels in EC microprojections⁶ or the differential distribution of RyR and IP₃R in the intracellular stores⁴ can have, for example, a significant effect in cellular function and myoendothelial communication. Although the importance of spatial organization of subcellular components is now appreciated, there is relevant absence of quantitative information for distribution of receptors, channels, pumps and exchangers and the spatial organization of the plasma membrane, the cytosol, or the sarcoplasmic reticulum. Eventually computationally demanding models that will incorporate such information will replace the simpler compartmental models, in order to capture the spatial heterogeneity in the concentration of Ca²⁺ and other ionic species and second messengers.

Finally, future models need to integrate relevant signal-transduction pathways. IP₃-mediated pathways are of special interest since IP₃ balance is important for intracellular and most likely intercellular communication,⁸⁵ but pathways mediated by other second messengers are also emerging.⁸⁶ Modeling vascular tone regulation, in particular, requires integration of signaling pathways with opposing effects on cytosolic Ca²⁺ concentration (e.g., adrenergic pathway versus the EDHF or NO/cGMP pathways). The resulting experimental response depends usually on the balance between such pathways. Modeling attempts have focused mostly on the nitric oxide pathway. However, other vasodilatory agents participate in the regulation of vasomotor control (i.e., EETs, HETES etc.). These signaling pathways could be readily incorporated provided that appropriate quantitative information becomes available for the release, transport, and action of these species in the vessel wall.

Investigations of vascular function should take into account that Ca²⁺ dynamics is a result of a complex, nonlinear system with multiple feedback loops that cannot be properly analyzed using only a reductionist's approach. However, models that are very comprehensive require a large number of parameters, which are often unknown. Therefore, compromises between excessive complexity and oversimplifying reductionism will have to be made at every step in this process.

A SYSTEMS APPROACH FOR INVESTIGATIONS OF VASCULAR FUNCTION

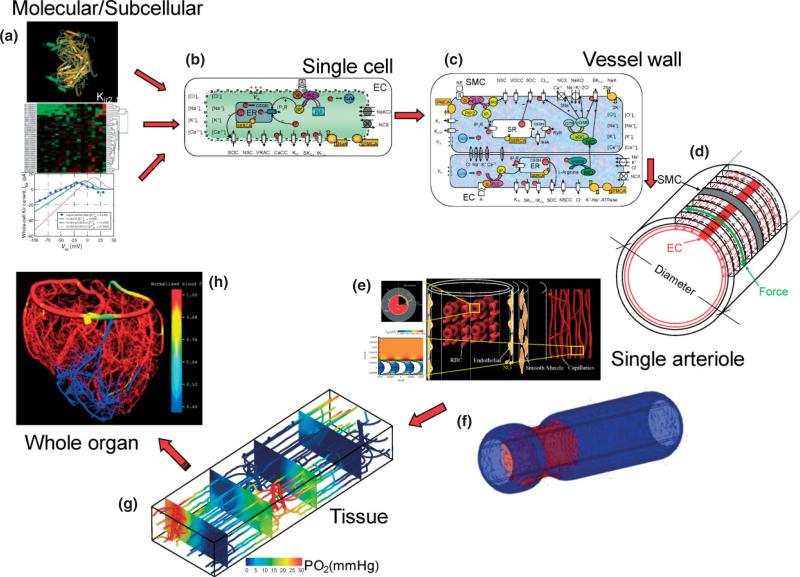
Figure 4 outlines a strategy for integrative modeling of the vasculature and is adapted from a similar strategy outlined for the modeling of the heart.²⁶ The goal is to describe function at a macroscale level by integrating mechanisms at the subcellular/molecular level. Information at the genomic level combined with proteomics and in vitro data such as electrophysiological recordings (Figure 4a) can provide information for the behavior of subcellular components (i.e., a membrane protein forming an ion channel or a signaling pathway). Molecular dynamic simulations can potentially relate, for example, the effect of a mutation to the behavior of a channel,⁸⁷ while gene expression profiling studies can provide information for its increased/decreased presence in a disease state.^88,89 This information can be described through mathematical formulations and these formulations can be integrated to describe single-cell behavior (i.e., Ca²⁺ dynamics and membrane potential responses to stimulation, contractile force development, and release of second messengers and vasoactive species) (Figure 4b). Cells can be coupled (i.e., electrically and through diffusion of species like NO) and multicellular models of the vascular wall will be generated, capable of investigating intercellular communication and signaling (Figure 4c and d).⁹⁰ The detailed EC/SMC Ca²⁺ dynamics and electrophysiology models can be combined with biotransport (Figure 4e)^80,91–93 or biomechanics models (Figure 4f)⁹⁴ to describe function at the vessel level (i.e., diameter responses to agonist, conducted vasomotor responses). Modeling at this level can relate species bioavailability to diameter changes and hemodynamic stress. Models that will describe other aspects of vascular physiology (i.e., angiogenesis, vascular permeability) can also be developed on top of this level. Finally, the description for the regulation of vessel's behavior can be incorporated in detailed computational models of function at the tissue level (i.e., vascular resistance, blood flow, tissue O₂ distribution) (Figure 4g).⁹⁵ Models at this scale can examine short-term network adjustments or long-term structural adaptations in response to metabolic or mechanical stimuli. This approach can be potentially extended to the whole organ level (an example of modeling at this level is presented in (Figure 4h) reproduced from Smith et al.⁹⁶ or whole organism level by incorporating for example predictions for the peripheral vascular resistance to whole-body models of blood pressure regulation). Thus, the outlined multiscale modeling approach can be utilized in different areas of vascular pathophysiology (as a result of the universality of calcium signaling) and can relate pathological responses to the underlying cellular and molecular mechanisms.

FIGURE 4.

Strategy for integrative modeling of the vasculature. (a) Genomic, proteomic and in vitro data such as electrophysiological recordings can be utilized to provide mathematical formulations for subcellular components and signaling pathways. Representative example shows the three-dimensional folding of KIR_2.1 protein and the current–voltage behavior of a K_IR channel in an EC. (b) An EC model⁵¹ that integrates such formulations and incorporates membrane channels, pumps and exchangers, intracellular compartments, and signaling mechanisms. The model can simulate membrane electrophysiology, dynamic behavior of Ca²⁺ and other ions, and the generation of second messengers and signaling factors. (c) EC and SMCs can be coupled through gap junctions and the diffusion of species like NO and IP₃.⁷⁸ (d) Multicellular models of the vascular wall can be constructed by placing EC and SMCs cells in an appropriate arrangement.⁷⁹ (e) Example of a biotransport model investigating the diffusion of species (i.e., NO, O₂) in and around a single arteriole and incorporates RBCs and nearby capillaries.⁸⁰ (f) A biomechanics model of a single arteriole presents the constriction of the vessel at the site of norepinephrine application in the absence of longitudinal signal conduction. (g) Detailed computational model investigating blood flow and O₂ distribution in three-dimensional vascular networks and mesoscale tissue volumes.⁹⁵ (h) Reconstructed whole-organ vessel network and blood flow calculations.(Reprinted with permission from Ref 96. Copyright 2002 Society for Industrial and Applied Mathematics).