Methodological Issues in Measuring Health Disparities

Abstract

Objectives

This report discusses six issues that affect the measurement of disparities in health between groups in a population:

• Selecting a reference point from which to measure disparity

• Measuring disparity in absolute or in relative terms

• Measuring in terms of favorable or adverse events

• Measuring in pair-wise or in summary fashion

• Choosing whether to weight groups according to group size

• Deciding whether to consider any inherent ordering of the groups.

These issues represent choices that are made when disparities are measured.

Methods

Examples are used to highlight how these choices affect specific measures of disparity.

Results

These choices can affect the size and direction of disparities measured at a point in time and conclusions about the size and direction of changes in disparity over time. Eleven guidelines for measuring disparities are presented.

Conclusions

Choices concerning the measurement of disparity should be made deliberately, recognizing that each choice will affect the results. When results are presented, the choices on which the measurements are based should be described clearly and justified appropriately.

Introduction

One of the goals of Healthy People 2010 is “to eliminate health disparities among segments of the population, including differences that occur by gender, race or ethnicity, education or income, disability, geographic location, or sexual orientation”(1). The U.S. Department of Health and Human Services Strategic Plan includes a goal to eliminate disparities in health care (2) and Congress mandated an annual National Healthcare Disparities Report (NHDR) (3). States have also adopted the Healthy People 2010 goal to eliminate disparities for selected indicators of health (4). Each of these initiatives entails an obligation to measure disparities in health and to monitor trends in disparities.

This report discusses six significant issues that should be considered in measuring disparities: first, the selection of a reference point from which to measure disparity (5); second, measurement of disparity in absolute or in relative terms (5); third, measurement of disparity in terms of favorable or adverse events (6,7); fourth, measurement of disparity focusing on individual groups in a pair-wise fashion or focusing on a summary measure for the domain that includes these groups (8,9); fifth, choosing whether to weight component groups when calculating summary measures of disparity; and sixth, choosing whether or not to consider the order inherent in the domains with ordered categories when calculating summary measures of disparity (6). These measurement choices affect the way a disparity is expressed, including the size and direction of the disparity. Furthermore, these choices have implications for conclusions about changes in disparities over time, as well as for conclusions about differences in disparity across different health Indicators, geographic areas, or populations. Different choices can, and frequently do, lead to different conclusions about disparities.

In addition to discussing these issues, this report presents guidelines for making measurement choices. These guidelines provide a consistent framework for describing the size and direction of disparities; promote clear communication about the nature of disparities to policymakers and the general public; and facilitate comparisons of disparities over time and across indicators, geographic areas, or populations. There is no single, best way to measure disparity that is appropriate in all situations. The strengths and limitations of different choices are highlighted, and not all of the guidelines presented here are applicable in every situation.

Measuring Disparity

Indicators of health are measured in terms of rates, percentages, proportions, means, or other quantifiable measures such as life expectancy. These measures can be calculated for each group in a domain of groups. A domain is a set of groups defined in terms of a specific characteristic of persons in a population. Ideally, the set of groups is mutually exclusive and exhaustive (that is, each person in the population is assigned to only one group, and all persons in the population are assigned to a group). For example, the domain of gender consists of males and females.

Disparities become evident when quantitative measures of health (rates, percentages, etc.) are compared between the groups in a domain. These measures permit comparisons between groups regardless of the number of persons in the group. Disparities are frequently measured between groups in a domain; however, disparities can also be measured from other reference points such as the total population. The choice of a reference point from which to measure disparity is one of the critical issues discussed below.

For the purposes of this discussion, the following definition is proposed:

Disparity—The quantity that separates a group from a specified reference point on a particular measure of health that is expressed in terms of a rate, percentage, mean, or some other quantitative measure.

This definition provides the basis for the direct measurement of disparities in indicators of health between groups. It also provides the basis for monitoring changes in disparities over time, and for making comparisons of disparities across health-related indicators and across geographic areas or populations. In the interest of brevity the term “rate” is generally used in the discussion that follows, but the principles discussed apply to rates, proportions, percentages, means, and other quantitative measures of health.

This definition does not presume that membership in a particular group is necessarily the cause of any disparity between groups. For example, the disparity between males and females in breast cancer death rates is largely due to gender-specific genetic differences. However, the gender disparity in cigarette smoking might be due to a variety of cultural, educational, and economic factors related to gender. Identification of the determinants of disparity is beyond the scope of this discussion.

Issues and Choices

Choosing a reference point

Disparities are measured from a reference point.

Reference point—The specific value of a rate, percentage, proportion, mean, or other quantitative measure from which a disparity is measured.

Any one of the groups in a domain could be chosen as a reference point from which to measure disparity. The group that represents the largest proportion of the population might be chosen (3). The rate for the largest group is usually the most stable, but there are frequently groups with rates better than the rate for the largest group. The most favorable group (hereinafter referred to as the “best” group) rate provides a convenient reference point for comparing the disparity status of other group rates because all differences are in the same direction (7). Using the group with the best rate as a reference point has possible disadvantages. For example, this group might change over time or differ from place to place; or it might be a very small population group, thus making this group’s rate the least stable. When there are only two groups in a domain (gender, for example) or only two groups of interest, the rate for either group could be chosen as the reference point. In these cases, the more favorable group rate (the rate reflecting better health status or less risk) is usually chosen as the reference point.

Disparities also can be measured relative to a reference point that is not a specific group. The unweighted arithmetic mean of the rates for the groups in a domain could be employed as a reference point. The mean is employed in measures of variability such as the mean deviation, the variance, the standard deviation, and the coefficient of variation. However, the mean is influenced by outliers—group rates that are substantially different from the rates for most of the groups. Over time, the mean of group rates is affected by substantial changes in the rate for any particular group.

Disparities can be measured relative to the rate for the total population represented by the domain of groups. The rate for the total population is a weighted average of the group rates in a domain (the group rates are weighted by the proportion of persons in each group). The total population rate is also the mean for all individuals in the population. The total population rate is more stable than the other reference points above, and unlike the mean of group rates, it will have the same value across all domains that encompass the same population. However, the total population also has limitations as a reference point when comparisons are made over time or across geographic areas or populations using summary measures. Changes in the total population rate over time are a function of changes in group rates as well as changes in the distribution of persons among groups. It can, therefore, be difficult to distinguish the effects of changes in group rates from changes in group composition.

Disparities can also be measured relative to a standard such as a Healthy People target (1). The target can be fixed for an extended period of time and it has no sampling or other sources of random variation associated with it. Unlike the other reference points discussed above, a target is chosen through a deliberative process that may involve the application of specific criteria. If the targets for health indicators are established using different criteria, this should be taken into consideration when disparities are compared across indicators.

In table A, simple differences between infant mortality rates by race and Hispanic origin of the mother and each of five possible reference points are shown. These rates are based on the 2000 period linked birth/infant death data set (10). For each race/ethnic group the size of the difference depends on the reference point from which it is measured. For infants of Asian or Pacific Islander, Hispanic, and non-Hispanic white mothers, the direction (sign) of the difference also depends on the reference point from which it is measured.

Table A.

Differences between infant mortality rates by race and Hispanic origin of mother and selected reference points: United States, 2000

				Reference point1
Race and Hispanic origin of mother	Number of infant deaths	Number of live births	Infant mortality rate1	Another group rate (Non-Hispanic white) 5.7	Best group rate (Asian or Pacific Islander) 4.9	Mean of group rates 7.6	Total population rate 6.9	Healthy People 2010 target 4.5
				Difference1
American Indian or Alaska Native	346	41,668	8.3	2.6	3.4	0.7	1.4	3.8
Asian or Pacific Islander	977	200,544	4.9	−0.8	0.0	−2.7	−2.0	0.4
Hispanic	4,564	815,883	5.6	−0.1	0.7	−2.0	−1.3	1.1
Non-Hispanic black	8,212	604,367	13.6	7.9	8.7	6.0	6.7	9.1
Non-Hispanic white	13,461	2,362,982	5.7	0.0	0.8	−1.9	−1.2	1.2

¹Infant deaths per 1,000 live births.

SOURCE: National Vital Statistics System, linked birth/infant death data file.

The advantages and disadvantages of each reference point depend on the context in which disparities are being measured. The choice of a reference point also has implications for other issues addressed in this report, such as the measurement of disparities in absolute or relative terms. It is not possible to recommend a single reference point for use in all situations. It is essential to recognize, however, that the choice of a reference point will determine the size and direction of the disparity.

Guidelines 1 and 2

• 1.When disparities are measured, the reference point should be explicitly identified and the rationale for choosing a particular reference point should be provided.
• 2.If comparisons are made between two groups, the more favorable group rate should be used as the reference point. (This would be the lowest rate assuming that rates are expressed in terms of adverse events—see the following text.)

The first guideline is needed because the nature of disparities cannot be understood unless the point relative to which they are measured is clearly identified. The second guideline is a recommendation that will contribute to consistency in the measurement of disparities.

Measuring disparity in absolute and in relative terms

An absolute measure of disparity is a simple arithmetic difference between a group rate and a specified reference point. An absolute measure of disparity is expressed in the same units as the rates themselves.

• Simple difference = rate of interest–reference point = R_i – R_r

In table A the simple difference was calculated between the infant mortality rate for mothers in each of five race or ethnic groups and each of five possible reference points.

A relative measure of disparity expresses the difference between rates in terms of the chosen reference point. The percentage difference expresses the simple difference from the reference point as a percentage of the reference point.

$$\text{Percentage difference}=\frac{\text{rate of interest}-\text{reference point}}{\text{reference point}}•100=\frac{R_i-R_r}{R_r}•100$$

In a relative measure of disparity, the reference point becomes the unit of measurement. As with absolute measures of disparity, the size and direction (sign) of the disparity depends on which reference point is selected.

Measuring disparity at a single point in time

In table B both the simple difference and the percentage difference between the infant mortality rate for mothers in each of four race or ethnic groups and the rate for infants of Asian or Pacific Islander mothers (the best group rate) is shown.

Table B.

Absolute and relative measures of disparity between the mortality rate for infants of mothers in four race and Hispanic origin groups and the rate for infants of Asian or Pacific Islander mothers (the best group rate) : United States, 2000

Race or ethnic group	Infant mortality rate1	Absolute	Relative
		Simple difference1	Percent difference
Asian or Pacific Islander2	4.9	(2)	(2)
American Indian or Alaska Native	8.3	3.4	69.4
Hispanic	5.6	0.7	14.3
Non-Hispanic black	13.6	8.7	177.6
Non-Hispanic white	5.7	0.8	16.3

¹Infant deaths per 1,000 live births.

²The best group rate was used as the reference point.

SOURCE: National Vital Statistics System, linked birth/infant death data file.

When disparity is measured from the same reference point, the simple difference and the percentage difference are perfectly correlated. The essential difference between the two is in terms of how the disparity is expressed. Absolute and relative measures of disparity from the same reference point lead to the same conclusions about disparities between groups. Both the simple difference and the percentage difference indicate that the largest disparity is for infants of non-Hispanic black mothers, and both indicate that the disparity from the reference point for non-Hispanic black mothers is about 2.5 times the disparity for infants of American Indian or Alaska Native mothers.

Measuring change in disparity over time

Absolute and relative measures of disparity can provide contradictory evidence concerning changes in disparity over time. In the upper panel of table C the simple difference between the mortality rate for infants of non-Hispanic black mothers and the reference point declined from 10.3 to 8.7 infant deaths per 1,000 live births between 1990 and 2000. In the lower panel the percentage difference between the mortality rate for infants of non-Hispanic black mothers and the reference point increased from 156.1 to 177.6 percent between 1990 and 2000. Different conclusions about the direction of change are often observed when absolute and relative measures of disparity are compared over time.

Table C.

Changes in the simple difference and the percentage difference between infant mortality rates for each of four race and Hispanic origin groups and the rate for infants of Asian or Pacific Islander mothers (the best group rate): United States, 1990 and 2000

	1990		2000
Race or origin group	Infant mortality rate1	Simple difference1	Infant mortality rate1	Simple difference1	Change 2000–19901
Asian or Pacific Islander2	6.6	(2)	4.9	(2)	(2)
American Indian or Alaska Native	13.1	6.5	8.3	3.4	−3.1
Hispanic	7.5	0.9	5.6	0.7	−0.2
Non-Hispanic black	16.9	10.3	13.6	8.7	−1.6
Non-Hispanic white	7.2	0.6	5.7	0.8	0.2
		Percent difference		Percent difference	Change 2000–19903
American Indian or Alaska Native	13.1	98.5	8.3	69.4	−29.1
Hispanic	7.5	13.6	5.6	14.3	0.7
Non-Hispanic black	16.9	156.1	13.6	177.6	21.5
Non-Hispanic white	7.2	9.1	5.7	16.3	7.2

¹Infant deaths per 1,000 live births.

²The best group rate was used as the reference point.

³Change in percentage points.

SOURCE: National Vital Statistics System, linked birth/infant death data file.

In the example in table C the discrepancy occurs because the relative comparison adjusts for the decline in infant mortality rates that occurred for both non-Hispanic black mothers and Asian or Pacific Islander mothers (the group used as the reference point). Depending on how the underlying rates change, conclusions about changes in disparity over time based on absolute and relative comparisons may differ. If rates were increasing rather than decreasing, a decrease in a relative measure of disparity might correspond to an increase in an absolute measure of disparity.

Expressing a disparity using a relative measure has both advantages and disadvantages that need to be considered when choosing a reference point. On one hand, changes in the underlying rates are automatically adjusted for. On the other hand, information about the size of the change in the underlying rates is not retained in a relative comparison. Based on a relative measure of disparity, for example, the difference between one and four deaths per 100,000 population is the same as the difference between 100 and 400 deaths per 100,000 population—in both cases the second rate is 300 percent greater than the first. In absolute terms, the simple difference between one and four deaths per 100,000 population is the same as the simple difference between 401 and 404 deaths per 100,000 population.

Guideline 3

• 3.Disparities should be measured in both absolute and relative terms in order to understand their magnitude, especially when making comparisons over time or across geographic areas, populations, or indicators.

This guideline promotes a more complete understanding of the magnitude of disparities.

Comparing disparities across geographic areas or populations

The disparity between a group rate and a reference point in one geographic area or population can be compared with the disparity between a comparable group rate and a comparable reference point in another geographic area or population. The disparity between men and women in rates of death caused by diseases of the heart could be compared across two or more States, for example. In such applications, conclusions based on absolute and relative comparisons will also depend on the underlying rates. Comparisons based on both absolute and relative measures are, therefore, indicated.

Comparing disparities across different indicators

The disparity between a group rate and a reference point for one health indicator can also be compared with the disparity between a comparable group rate and a comparable reference point for another health indicator. For example, the disparity between men and women in the rate of cigarette smoking could be compared with the disparity between men and women in rates of death caused by lung cancer. Once again, comparisons based on both absolute and relative measures are indicated because conclusions will depend on the underlying rates. When comparisons are made across indicators, however, it is not possible to take advantage of both absolute and relative measures of disparity in all situations. Absolute measures of disparity cannot be compared across indicators that are based on different units of measurement (or across indicators that cannot be converted to a common unit of measurement). Relative measures, on the other hand, can be used to make comparisons across all indicators regardless of the unit of measurement.

Measuring disparity in terms of adverse events

Most health-related indicators can be expressed either in terms of favorable events or in terms of adverse events. A favorable event or characteristic is considered desirable and is promoted through public health action. An adverse event or characteristic is considered undesirable, and reduction or elimination is promoted through public health action.

The utilization of mammography, for example, can be expressed as a favorable event (the percentage of women who had a mammogram within the past 2 years) or as an adverse event (the percentage of women who did not have a mammogram within the past 2 years).

The size of an absolute disparity between a group and a reference point is the same whether the indicator is expressed in terms of favorable or adverse events (although the sign differs). The magnitude of a relative disparity depends on the magnitude of the reference point from which the disparity is measured. The magnitude of the reference point depends on whether the indicator is expressed in terms of favorable events or in terms of adverse events. Therefore, both the size and direction (sign) of a relative measure of disparity depend on whether the indicator is expressed in terms of favorable or adverse events (6,7).

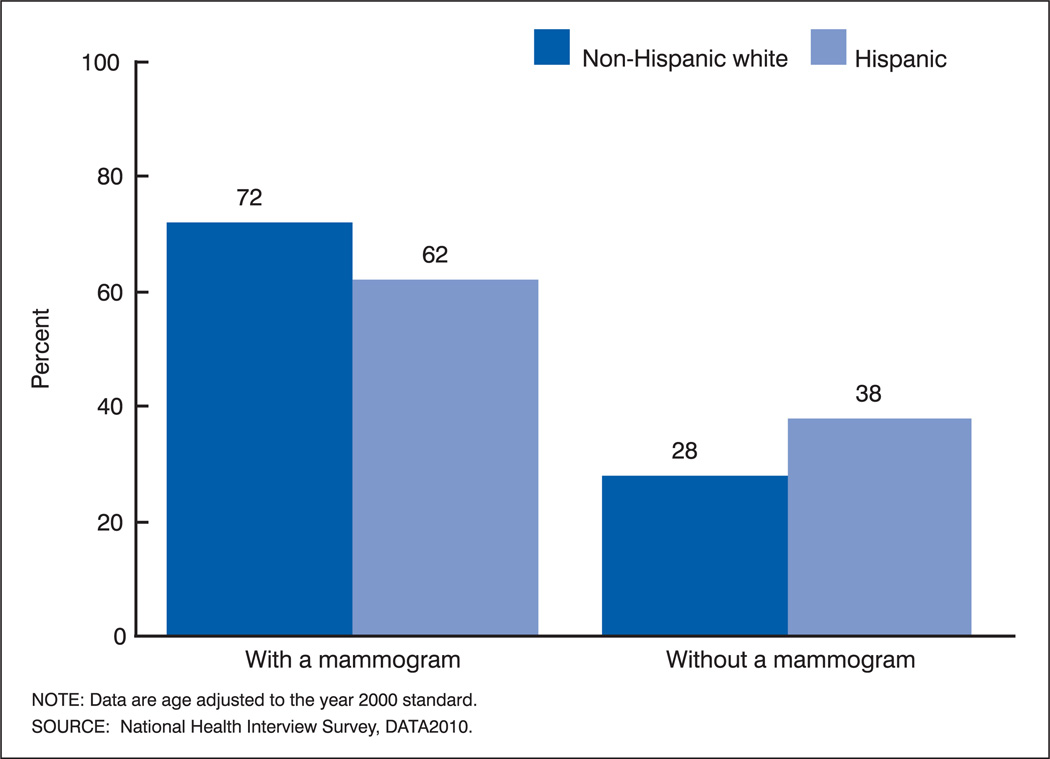
A simple example illustrates the effect of expressing an indicator in terms of favorable or adverse events on absolute and relative measures of disparity. On the left side of figure 1, the percentage of non-Hispanic white and Hispanic women 40 years and over who had a mammogram within the past 2 years is shown based on data from the National Health Interview Survey in 2000 (11). On the right side, the percentage of women who did not have a mammogram within the past 2 years is shown for the same groups. The simple difference between the two groups is 10 percentage points, whether the comparison is based on the percentage with a mammogram or the percentage without a mammogram. As long as the same reference point is used, the sign of the difference changes, but the magnitude of the difference between the percentage of women who had a mammogram and the percentage who did not have a mammogram remains the same.

Figure 1.

Percentages of non-Hispanic white and Hispanic women aged 40 years and over by use of mammography within the past 2 years: United States, 2000

However, when a relative measure of disparity is employed, the magnitude of the measure differs. On the left side of figure 1, the percentage of non-Hispanic white women who had a mammogram is 16.1 percent greater than the percentage of Hispanic women who had a mammogram [(72 – 62) / 62 • 100 = 16.1 percent]. On the right side of figure 1, the percentage of non-Hispanic white women who did not have a mammogram is 26.3 percent less than the percentage of Hispanic women who did not have a mammogram [(28 – 38) / 38 • 100 = −26.3 percent]. Not only the sign (positive or negative) but also the magnitude of the percentage difference depend on whether it is computed based on the percentage of women who had a mammogram or the percentage who did not have a mammogram. This will be true whenever the reference point differs from the exact midpoint of possible values.

Conclusions about changes in disparity over time also depend on whether an indicator is expressed in terms of favorable or adverse events (6). Table D shows the percentage of women who had a mammogram during the past 2 years and the percentage of women who did not have a mammogram during the past 2 years for non-Hispanic white and Hispanic women in 1990 and 1998 (10). The simple difference between the percentage of non-Hispanic white and Hispanic women who had a mammogram during the past 2 years increased from 7.5 percentage points in 1990 to 7.8 percentage points in 1998. The simple difference also increased from −7.5 percentage points to −7.8 percentage points for women who did not have a mammogram during the past 2 years. However, changes in the relative differences between Hispanic and non-Hispanic white women were not the same for both favorable and adverse events. The percentage difference between non-Hispanic white and Hispanic women who had a mammogram within the past 2 years decreased from 16.6 percent in 1990 to 13.0 percent in 1998. A decrease in disparity is indicated because the percentage difference moved closer to 0. The percentage difference between non-Hispanic white and Hispanic women who did not have a mammogram within the past 2 years increased from −13.7 percent in 1990 to −19.6 percent in 1998. The percentage difference moved further from 0, indicating an increase in disparity.

Table D.

Percentages of non-Hispanic white and Hispanic women aged 40 years and over by use of mammography within the past 2 years: United States, 1990 and 1998

	Mammogram				No mammogram
Year	Non-Hispanic white (Nhw)	Hispanic (H)	Simple difference (Nhw–H)	Percent difference (Nhw–H)/H × 100	Non-Hispanic white (Nhw)	Hispanic (H)	Simple difference (Nhw–H)	Percent difference (Nhw–H)/H ×100
	Percent				Percent
1990	52.7	45.2	7.5	16.6	47.3	54.8	−7.5	−13.7
1998	68.0	60.2	7.8	13.0	32.0	39.8	−7.8	−19.6
Percent change	129.0	133.2	24.0	3−21.7	1−32.3	1−27.4	24.0	343.1

¹The percent change in the percent is calculated as follows: ((percent in 1998 – percent in 1990)/percent in 1990 × 100)

²The percent change in the simple difference is calculated as follows: ((simple difference in 1998 – simple difference in 1990)/simple difference in 1990 × 100)

³The percent change in the percent difference is calculated as follows: ((percent difference in 1998 – percent difference in 1990) / percent difference in 1990 × 100)

SOURCE: National Center for Health Statistics. Health, United States, 2004 With Chartbook on Trends in the Health of Americans. Hyattsville, MD: 2004.

In this example, both the magnitude and direction of change in the relative measure of disparity depend on whether the indicator is expressed in terms of favorable or adverse events. The percentage difference between Hispanic and non-Hispanic white women who had a mammogram moved closer to 0 by 21.7 percent, and the percentage difference between Hispanic and non-Hispanic white women who did not have a mammogram moved further from 0 by 43.1 percent. Similar results can occur when comparisons are made across different indicators, geographic areas, or populations.

Several factors might influence the choice to measure disparity in terms of favorable or adverse events. It would not be appropriate to compare the relative disparity in one indicator expressed in terms of favorable events that occur frequently with the relative disparity in a second indicator expressed in terms of adverse events that occur infrequently. In order to make comparisons across different indicators, all of the indicators should be expressed in either adverse or favorable terms. In addition, the results of relative comparisons over time (or across geographic areas or populations) depend on whether differences are measured in terms of favorable or adverse events. Finally, it would be unusual to measure the relative disparity for certain types of health indicators in terms of favorable events. Death rates are a good example. The relative difference in survival rates for some causes of death can become almost negligible.

Expressing relative disparities in terms of adverse events would enhance the consistency and comparability of relative measures of disparity across indicators and over time.

Guideline 4

• 4.When relative measures of disparity are employed to compare disparities across different indicators of health, all indicators should be expressed in terms of adverse events.

This convention would have no effect on absolute measures of disparity, and it is not necessary for purposes of monitoring changes in relative disparity over time for a single indicator. However, confusion concerning the desired direction of change and the meaning of changes in relative measures of disparity over time could be avoided by consistently expressing indicators in terms of adverse events, conditions, or behaviors that are to be reduced or eliminated. In either case, it should be clear whether the indicator is being expressed in terms of favorable or adverse events, and the reference point should be clearly identified (guideline 1). Guideline 4 does not apply to health indicators that are expressed in terms of means (such as mean blood pressure) or other quantitative measures (such as life expectancy) that cannot be expressed in adverse terms.

Measuring disparity in pair-wise or in summary fashion

When there are more than two groups in a domain, one of the first decisions to be made is whether the focus of attention is on individual groups or on the domain to which these groups belong. Ideally, a domain consists of a set of mutually exclusive and exhaustive population groups that are based on one or more characteristics of persons in a population, such as gender, race and ethnicity, urbanization level, education, or income. Focusing on the individual groups implies comparing one group with another or comparing each component group with a single reference point, measuring disparity for each group in the domain. Focusing on the domain implies quantifying the degree of disparity across all groups composing the domain.

Why focus on the domain in addition to the individual groups?

Most policy and programmatic applications of disparity measurement will likely involve measuring disparity for individual groups. Yet, there are instances where focusing on disparity within an entire domain may be not only relevant but also more appropriate than focusing on disparities measured for each component group.

For example, some domains consist of groups that are somewhat arbitrarily defined and therefore not inherently meaningful. Examples include domains where the component categories are ordered and reflect some amount of the underlying dimension being measured, such as education or income. The category “persons with family incomes between 200 and 300 percent of the poverty threshold” may not be inherently interesting as a group but only as they relate to those with less or more income. That is to say, in the absence of a policy-related rationale, few would object to changing this group to “persons with incomes between 200 and 400 percent of poverty” if this definition constituted a more statistically reliable group and the other income groups changed concomitantly.

It may also be desirable to focus on disparity within the domain, in addition to group-specific disparity, for domains where the groups are inherently meaningful but the defining aspect of the domain is also meaningful in a broader sense. This would characterize most domains with unordered categories, such as race and ethnicity. It would also characterize some forms of ordered domains, such as urbanization status, where it could be argued that groups such as “rural,” “suburban,” and “central city” are inherently meaningful. Although we might well want to know the amount of a health disparity of a specific group, such as Asians and Pacific Islanders or persons residing in rural areas, we might also want to know the extent of disparities within the domains of “race” or “urbanization level.”

Drawing conclusions about the amount of disparity within a domain by examining the disparity for each group can be difficult, especially if the domain consists of several groups and the goal is to make comparisons across health indicators, across populations, or over time. In order to measure disparity for a domain, information on disparities for the component groups needs to be combined.

Measures that summarize disparity for a domain

Measures that summarize disparity for a domain reflect adding together the disparities measured for the component groups. Therefore, summary measures for unordered groups are generally analogous to the pair-wise measures discussed in the preceding sections of this report; all the issues discussed in relation to pair-wise measures are equally relevant to summary measures. One critical distinction between summary and pair-wise measures of disparity is that the signs attached to differences of each group from the reference point are ignored when constructing summary measures, either by taking the absolute value or squaring the differences.

In general, summary measures of disparity for unordered groups are similar in concept to traditional measures of variability used in statistics, such as the mean deviation and the variance. If the arithmetic mean is used as the reference point, and the absolute group differences from the mean are added together and divided by the number of groups, the result is the mean deviation. If the differences are squared before adding them together and dividing by the number of groups, the result is the variance; taking the square root of the variance yields the standard deviation.

Other, nontraditional, measures of disparity can be created by using the same procedures but altering the reference point. A mean deviation or standard deviation can be computed using differences from the best rate, the rate for the largest group, the total population rate, or from a predefined target. In each procedure an absolute or squared difference or deviation is computed for each component group in the domain; only the reference point from which the deviation is computed is changed.

Each procedure produces a summary measure that expresses disparity in absolute terms, retaining the original units of measurement. Each absolute summary measure can be converted into a relative measure by dividing by the reference point. When, for example, the standard deviation is divided by the arithmetic mean, the result is the coefficient of variation, a commonly used measure of relative variation.

A summary measure of disparity can be based on absolute or squared deviations. Squared deviations give greater weight to extreme values, and extreme values may be related to sample size as well as reflecting true disparity. On the other hand, squared deviations are easier to handle statistically than are absolute values. An advantage of using the standard deviation and the coefficient of variation as the measures of absolute and relative disparity is that standard errors for these measures can be obtained from standard statistical software.

It is important to bear in mind that all summarization involves a loss of information. So, when summary measures of disparity are used, the implications of the choices made with respect to how to measure disparity will be less transparent to the audience than with pair-wise measures.

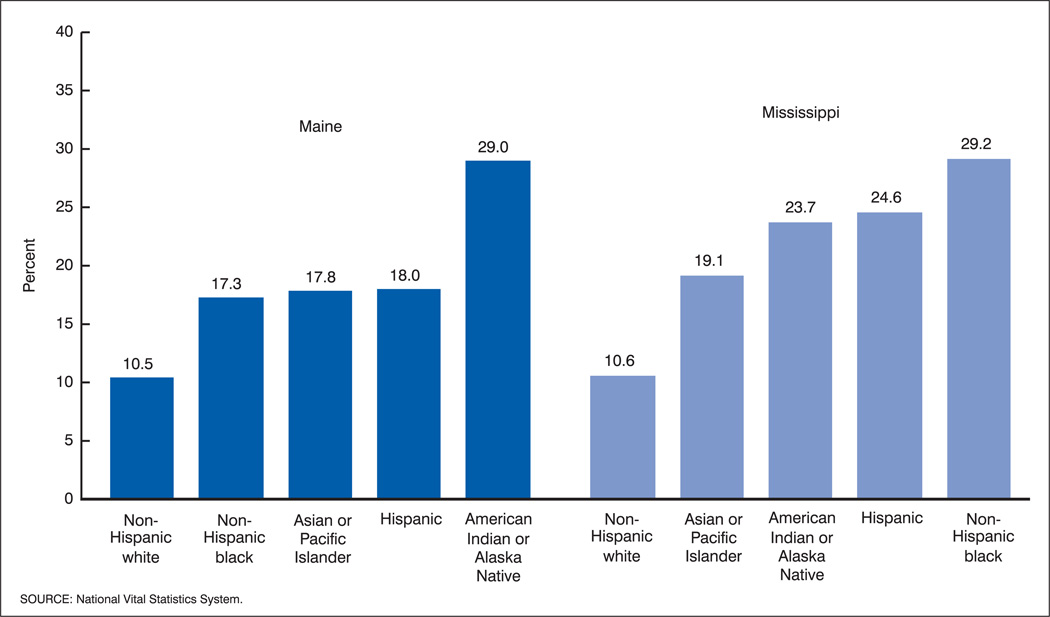
As an example, figure 2 shows the percentage of mothers not receiving prenatal care in the first trimester of pregnancy by race and Hispanic origin in Mississippi and Maine for the years 1997–99. The range in the percentages not receiving first trimester care across race and Hispanic origin groups is nearly identical in the two States. But, in Maine the values for the three groups between the extreme values are more similar than in Mississippi.

Figure 2.

Percentages of mothers with no prenatal care in the first trimester by race and Hispanic origin: Maine and Mississippi, 1997–99

Table E shows the mean absolute deviation of the group rates of no first trimester prenatal care computed from different reference points for Maine and Mississippi. Using absolute deviations from the group with the best rate (which, in this case, is also the largest group—non-Hispanic white women), Mississippi has greater disparity (10.8) than Maine (8.0). This is also true when the mean absolute deviation is computed from the mean of the group rates, although the difference between the two States is not as large (5.3 versus 4.2). But using the percentage of all live births in the State with no first trimester care (the total rate) as the reference point, Maine is shown to have greater racial and ethnic disparity than Mississippi (7.7 versus 5.7). Converting the absolute measure to a relative measure by dividing by the reference point magnifies the differences between these alternative measures of disparity. Using the best group value as the reference point, relative disparity in Mississippi is 26 percentage points higher than in Maine; using the value for the total population as the reference point, relative disparity in Maine is 40 percentage points higher than in Mississippi; and using the mean as the reference point indicates nearly equal levels of disparity for the two States.

Table E.

Mean deviations from alternative reference points in the percentage of mothers without prenatal care during the first trimester by race and Hispanic origin: Maine and Mississippi, 1997–99

	Best rate		Mean rate		Total rate
Alternative values	Maine	Mississippi	Maine	Mississippi	Maine	Mississippi
Reference point	10.5	10.6	18.5	21.4	11.0	19. 3
Mean deviations
Absolute	8.0	10.8	4.2	5.3	7.7	5.7
Relative	76%	102%	23%	25%	70%	30%

SOURCE: National Vital Statistics System.

Why do the results for the summary disparity measures vary so greatly depending on the choice of reference point? Ninety-five percent of all live births in Maine are born to non-Hispanic white women, so Maine’s total rate is only slightly higher than the non-Hispanic white rate, even though lack of prenatal care is lowest for non-Hispanic white births. In Mississippi 53 percent of live births were to non-Hispanic white women, and 43 percent were to non-Hispanic black women; thus, the total rate in Mississippi was 19.3 compared with 11.0 in Maine. As a result, using the total rate as the reference point produces, on average, larger group differences for Maine than for Mississippi. For Maine, the summary disparity measure based on deviations from the best rate (that of non-Hispanic whites) is very similar to the summary measure based on deviations from the total rate because non-Hispanic whites constitute such a large proportion of the total. But for Mississippi, the best rate and the total rate are quite different.

Guidelines 5, 6, and 7

• 5.Pair-wise comparisons are called for when the objective is to measure disparity for each group in a domain.
• 6.Summary measures can be used to quantify the degree of disparity across all groups composing a domain.
• 7.Conclusions based on summary measures always should be interpreted in conjunction with the group-specific rates on which they are based.

Choosing whether to weight component groups when calculating summary measures of disparity

The comparison between Maine and Mississippi highlights another issue to consider when deciding how to summarize disparity across a domain: deciding whether to weight the group values by the proportion of the population they represent. Conceptually, not weighting the group-specific values maintains a perspective that focuses on the individual groups. That is, unweighted values imply that what is important is the group itself, regardless of its share of the population. Weighting, on the other hand, offers a population-based perspective on disparity across a domain. Weighting implies that the way the domain is constituted within the overall population is important. This approach is similar to looking at absolute measures of disparity, in that, weighted measures provide more information about the impact or consequences of disparity for the population as a whole.

The implications of these two approaches can be examined using the example of no first trimester prenatal care in Maine and Mississippi (table F). The first thing to note is that weighting by the proportion of live births occurring in each race and Hispanic origin group eliminates any distinction between the mean and the total value for all live births because the weighted mean equals the total rate. Using either the best group value or the total rate as the reference point, the weighted mean deviations show that racial and ethnic disparity in prenatal care is greater in Mississippi than in Maine. The greater disparity in Mississippi reflects the fact that non-Hispanic whites, with just over 50 percent of live births, have the lowest rate of late or no prenatal care, and non-Hispanic blacks, with just over 40 percent of live births, have the highest rate. Thus, both extremes of the distribution represent large shares of the population of live births. This stands in stark contrast to Maine, where only 5 percent of all live births occur to groups other than non-Hispanic whites.

Table F.

Weighted mean deviations from alternative reference points in the percentage of mothers without prenatal care during the first trimester by race and Hispanic origin: Maine and Mississippi, 1997–99

	Best rate		Mean or total rate
Alternative values	Maine	Mississippi	Maine	Mississippi
Reference point	10.5	10. 6	11.0	19.3
Weighted mean deviations:
Absolute	0.5	8. 4	0.9	9.0
Relative	5%	80%	9%	47%

SOURCE: National Vital Statistics System.

The decision of whether to weight the component groups when summarizing disparity across a domain should take into consideration the reason for computing the summary measure of disparity as well as conceptual considerations. It could be reasoned that, conceptually, examining disparity among unweighted racial and ethnic groups is fairer and, therefore, more appropriate. That is, it shouldn’t matter that the group with the highest rate of inadequate prenatal care in Maine (American Indian or Alaska Native) represents less than 1 percent of all live births. A weighted summary measure will indicate relatively little racial and ethnic disparity in prenatal care in Maine and will therefore obscure the existence of the very high rate of inadequate prenatal care among American Indians, unless this rate is otherwise highlighted. On the other hand, it could be reasoned that, compared with Maine, Mississippi has a much harder task in attempting to eliminate racial and ethnic disparity in prenatal care, and summary measures designed to influence broad policy should reflect this burden aspect of disparity.

The implications of using either unweighted or weighted group values when calculating a summary measure of disparity need to be carefully considered. Not only does this decision need to be evaluated with respect to the purpose and application of the summary measures, but the implications with respect to other types of decisions (such as the choice of a reference point) should be considered. For example, calculating a mean deviation from the total population value produced summary measures that showed Maine as having greater racial and ethnic disparity in prenatal care than Mississippi, despite there being less variation in the unweighted group rates in Maine. Thus, combining unweighted deviations from a weighted mean may be as likely to create confusion as to provide interpretable measures of disparity.

Guidelines 8 and 9

• 8.The choice of whether to weight the component groups when summarizing disparity across a domain should take into consideration the reason for computing the summary measures. In addition, implications with respect to other types of decisions, such as the choice of a reference point, need to be considered.
• 9.The size of the groups and the number of persons affected in each group should be taken into account when assessing the impact of disparities.

Creating summary measures of disparity for domains with ordered categories

Deciding how to create a summary measure of disparity becomes even more complicated when the domain consists of groups that represent ordered categories of the characteristic determining the domain, such as level of income or level of education. With domains consisting of ordered groups, the first decision to be made is whether to consider the order inherent in the domain.

Table G shows two hypothetical populations divided into four income groups. In population 1, the percentage in fair or poor health declines steadily with increasing income. Population 2 has the same set of group values for fair or poor health, but the values are ordered differently across the groups so that the decline in fair or poor health is no longer monotonic with increasing income. The question to consider is whether income-related disparity in this health indicator should be considered the same for both populations. Would we want to indicate that income-related disparity in health is identical if these populations represented geographic areas (such as States) or population subgroups (such as non-Hispanic whites and Hispanics) or if they represented the same population at two different points in time? If the types of summary measures discussed in the previous section are applied to these data, these two populations would appear to have the same amount of income-related disparity in fair or poor health. The major argument for taking the inherent order of the groups into account when measuring disparity for ordered domains (especially domains reflecting socioeconomic status) is that interest generally lies in how health varies with the amount of the characteristic defining the domain, not with the groups themselves.

Table G.

Percentages of two hypothetical populations in fair or poor health by income level

Population	Poor	Near poor	Middle income	High income
1	30	20	15	5
2	30	20	5	15

NOTE: Income levels are defined as a percentage of the poverty threshold. Poor is income less than 100 percent of the poverty threshold. Near poor is 100 to less than 200 percent of the poverty threshold. Middle income is between 200 and less than 400 percent of the poverty threshold. High income is 400 percent or more of the poverty threshold.

Similarly, it can be argued that weighting groups by population size is more appropriate for domains with ordered groups, especially those reflecting socioeconomic status, than for other types of domains. As mentioned above, income and education groups are perhaps more appropriately thought of as categories reflecting the amount of income or education that persons have. Thus, the groups within these domains differ by the amount of the defining characteristic, and categories can be formed by cutting the distribution at any number of points. Weighting the categories by their population size helps compensate for the somewhat arbitrary nature of category formation for these variables. Another argument for weighting summary measures of disparity for socioeconomic domains is that they differ from most other domains when viewed from a policy perspective. Unlike other domains where health disparity is a concern (such as sex and race and ethnicity) the distribution of the population across socioeconomic categories can be influenced by policy. And, although changing the underlying distributions of income and education may not be the intention or focus of public health policy, it may well be important to know how changing socioeconomic distributions influence health disparities. For example, from a policy perspective, it could be important to know if education-related disparity in obesity declines over 10 years as a result of a greater percentage of individuals achieving higher levels of education, even though the obesity rates within education-level remain the same.

Over the last two decades, a considerable amount of work has been done to develop and apply summary measures of socioeconomic disparity in population health that address the unique aspects of these domains. One approach has been to use regression-based measures to summarize disparity (5,12–14). Conceptually, this approach can be viewed as a logical extension of the usual form of graphical presentation of health indicators by categories of education or income.

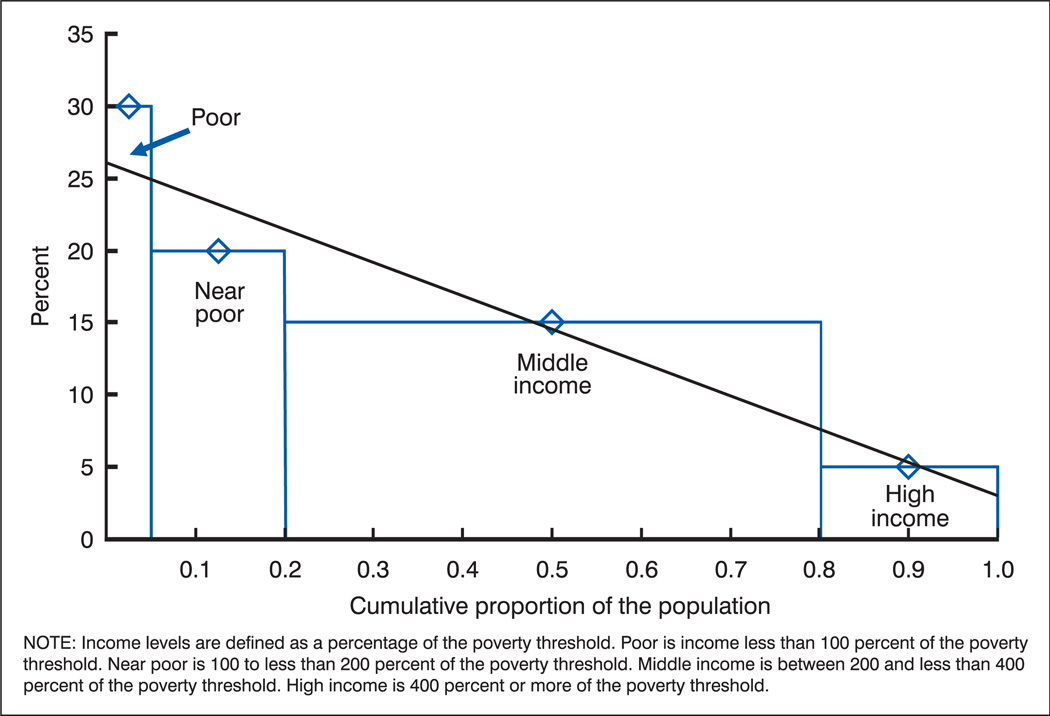
Regression-based measures retain the inherent order of the categories (like the usual graphical presentation), but they incorporate the population weights of the categories. The size of each category is taken into account by placing the groups on an axis that reflects the cumulative proportion of the population represented by the ordered groups. As shown in figure 3, income levels are ordered from lowest to highest level of income, and the width of each bar reflects the proportion of the total population having that level of income. The value of the health indicator—in this case the percentage in fair or poor health—for each income category is plotted at the midpoint of the relevant bar.

Figure 3.

Percentages of hypothetical population in fair or poor health by income level

An absolute summary index of disparity is formed using regression to fit a straight line to these percentages (figure 3). The slope of this line, referred to as the Slope Index of Inequality (SII), can be interpreted as the average change in the percentage in fair or poor health over the entire population ordered by level of income (15,16). Thus, for the hypothetical population 1, the SII of −22 (table H) indicates that the percentage with fair or poor health declines by an average of 22 percentage points over the population ranked from lowest to highest income. With the socioeconomic groups ordered from lowest to highest, the sign of the slope will be negative when the health indicator declines with increasing education or income, positive when it increases as the value of the socioeconomic variable increases, and will go to 0 when there is no consistent relationship with the socioeconomic variable.

Table H.

Percentages in fair or poor health by income level and regression-based summary indices of disparity for three hypothetical populations

	Population 1		Population 2		Population 3
Income level	Percent in fair or poor health	Proportion of population	Percent in fair or poor health	Proportion of population	Percent in fair or poor health	Proportion of population
Poor1	30	0.05	30	0.05	30	0.2
Near poor2	20	0.15	20	0.15	20	0.2
Middle income3	15	0.60	5	0.60	15	0.4
High income4	5	0.20	15	0.20	5	0.2
Regression-based summary index of disparity
SII5	−22		−10		−29
RII6(mean)	−1.54		−0.94		−1.70
RII6(ratio)	7.7		2.8		12.5

¹Poor is income less than 100 percent of the poverty threshold.

²Near poor is 100 to less than 200 percent of the poverty threshold.

³Middle income is between 200 and less than 400 percent of the poverty threshold.

⁴High income is 400 percent or more of the poverty threshold.

⁵SII is Slope Index of Inequality.

⁶RII is Relative Index of Inequality.

Because the x-axis is the cumulative proportion of the population, and therefore goes from 0 to 1, the entire population is the unit over which the slope changes. This means that the slope is the difference between the value of X at 1 (the theoretical highest income individual) and the value of X at 0 (the theoretical lowest income individual). Viewed in this manner, the SII is similar to the most common way of looking at disparity, that is, calculating the excess adverse health in the lowest ranked group compared with the highest ranked group. The advantage of the SII as a summary measure is that it incorporates the health values for all groups and the proportion of the population they reflect.

A relative version of the slope index, referred to as the Relative Index of Inequality (RII), can be formed in one of two ways, denoted as RII(mean) and RII(ratio). The slope index can be divided by the mean of the weighted group values, which is equivalent to dividing by the value of the health indicator for the total population. Thus, the RII(mean) formed by dividing the slope index by the mean is a ratio of the absolute measure of disparity (the SII) to the population value of the health indicator. For population 1, the RII(mean) of –1.54 (table H) means that the SII is just over one and one-half times the percentage in fair or poor health for the population as a whole (14.5 percent). This method of forming the relative index is analogous to the relative versions of summary measures for unordered groups, discussed previously.

A relative measure of disparity can also be formed by dividing the value of Y at the intercept (X = 0) by the value of Y at X = 1. This form of the relative index, the RII(ratio), has intuitive appeal for audiences familiar with health research literature that extensively employs rate ratios and odds ratios when comparing groups. It also forms an intuitive relative complement to the absolute measure of disparity because the slope itself (the SII) is the difference between the predicted value of Y at X = 1 and the predicted value of Y at X = 0 but avoids the negative sign associated with the difference. The RII(ratio) for population 1 (see table H) indicates that the regression-predicted percentage in fair or poor health at the lowest point on the income distribution (27.3) is 7.7 times the predicted value at the highest point (3.3). It should be recognized, however, that the RII(ratio) will tend to amplify differences in disparity between populations compared with the RII(mean).

Because regression analysis can take so many forms, there have been other adaptations of the original formulation (the use of logistic (17, 18) and Poisson regression models (19), for example) that researchers deemed more appropriate to their particular analyses and data. But the underlying conceptual model remains the same over all these various formulations. For the hypothetical examples discussed here, the SII and RII are calculated by fitting a linear regression line to the category-specific values by means of weighted least-squares, with the weights being the proportion of the population in each category.

The implications of using summary measures of disparity that retain the inherent order of the categories are demonstrated by comparing the SIIs and RIIs for population 1 with those for population 2 (table H). This comparison demonstrates what happens in the case of the hypothetical reversal of rates in the two highest income categories. If the percentage in fair or poor health is greater among persons in the highest income category than among persons with middle incomes (as in population 2), the slope decreases, both absolutely and relatively, indicating a reduction in income-related disparity.

Table H also shows the effect of changing the income distribution on these regression-based indices of disparity. Comparing population 3 with population 1 shows that an increase in the proportion of the population that is poor or near poor (with a proportionate reduction in the proportion of the population in the middle income range) raises the SII and RII, even if the income category-specific rates remain the same. The increase in these disparity measures reflects the greater proportion of the population experiencing higher rates of fair or poor health compared with population 1.

An alternative approach to summarizing socioeconomic disparities in health is based on adapting the Lorenz curve approach to measuring income inequality for individuals to the measurement of health disparities across ordered socioeconomic groups.

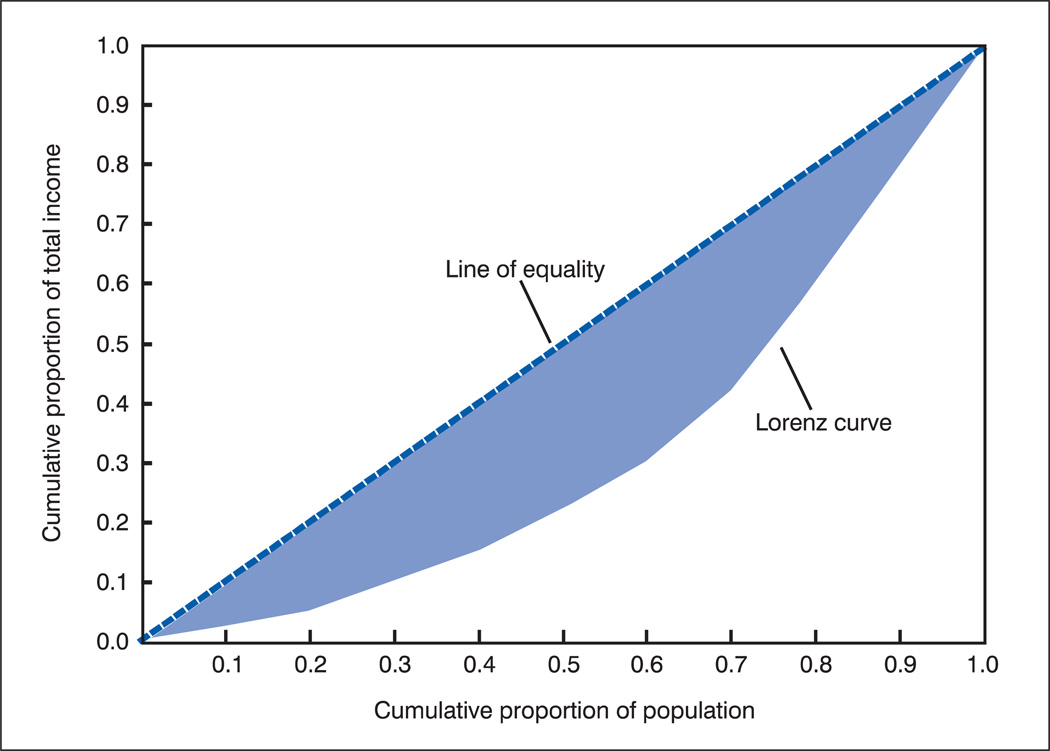
The Lorenz curve plots the cumulative proportion of income received by individuals in a population proceeding from the lowest income individual to the individual with the highest income (see figure 4). By looking at the curve, you can tell what proportion of income is received by each cumulative percentile of the income distribution. Complete income equality would be described by a diagonal line, indicating, for example, that the bottom 20 percent of the population received 20 percent of total income, and the bottom half received 50 percent of total income. The Gini coefficient, the most common summary measure of income inequality, is the area between the Lorenz curve and the diagonal expressed as a proportion of the total area under the diagonal. Values closer to 0 indicate less income inequality, and values closer to 1 indicate high levels of inequality.

Figure 4.

Lorenz curve for a hypothetical population

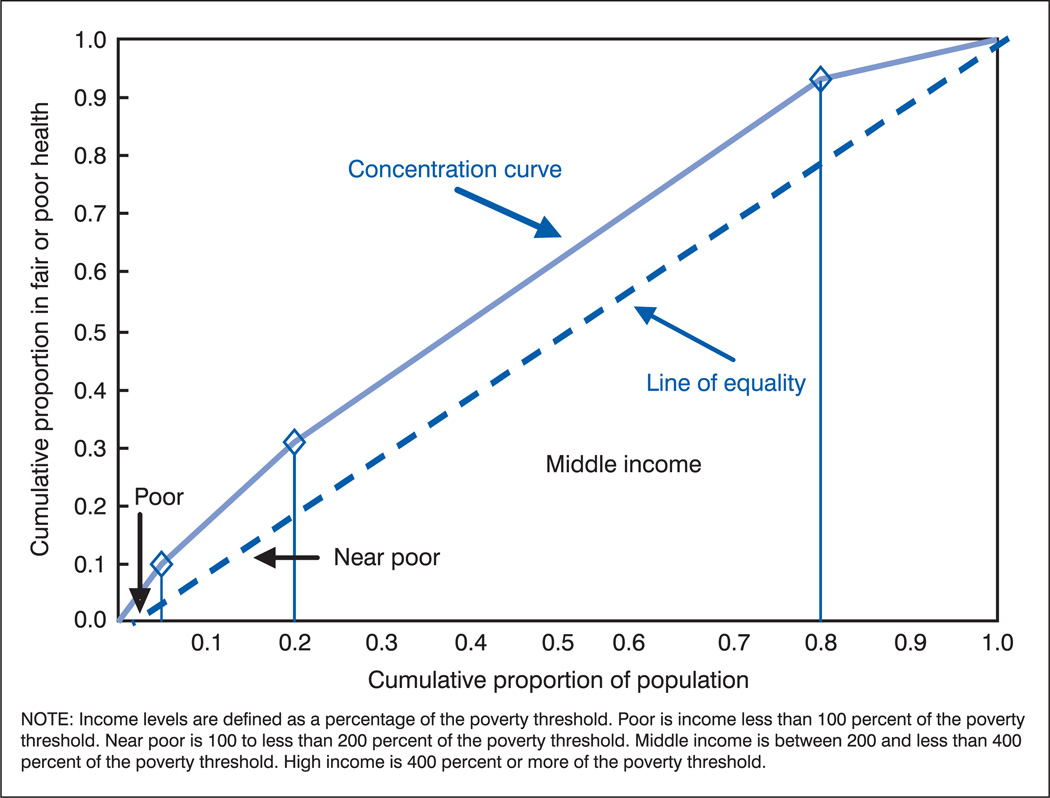
Adapting income inequality measures to apply to socioeconomic health disparities implies using the socioeconomic groups—rather than individuals—and plotting the cumulative proportion of the population obtained when the groups are ordered by socioeconomic level along the X axis. For example, figure 5 shows the income groups for our hypothetical population 1 ordered along the X axis. The Y axis represents the cumulative proportion of the population reflecting the health indicator—in our example, the cumulative proportion of the population in fair or poor health.

Figure 5.

Concentration curve for hypothetical population 1

The curve that is generated by this plot is referred to as the concentration curve (rather than a Lorenz curve), and the summary index of disparity derived from this curve is known as the concentration index (C). The concentration index is 2 times the net area between the curve and the diagonal (13). The concentration index is a measure of relative disparity, but an absolute version can be calculated by using the actual cumulative number of health events rather than their cumulative proportion (13).

If the values of the health indicator decline uniformly with increasing socioeconomic level, all points defining the concentration curve will lie above the diagonal, and C will carry a negative sign. If the values of the health indicator increase uniformly with increasing socioeconomic level, all points defining the concentration curve will lie below the diagonal, and C will have a positive sign. If the health indicator does not change monotonically with increasing socioeconomic level, the curve can cross the diagonal. When this happens, C will move closer to 0 because that portion of the area on the opposite side of the diagonal will be subtracted. Thus, C reflects the net area with a given sign.

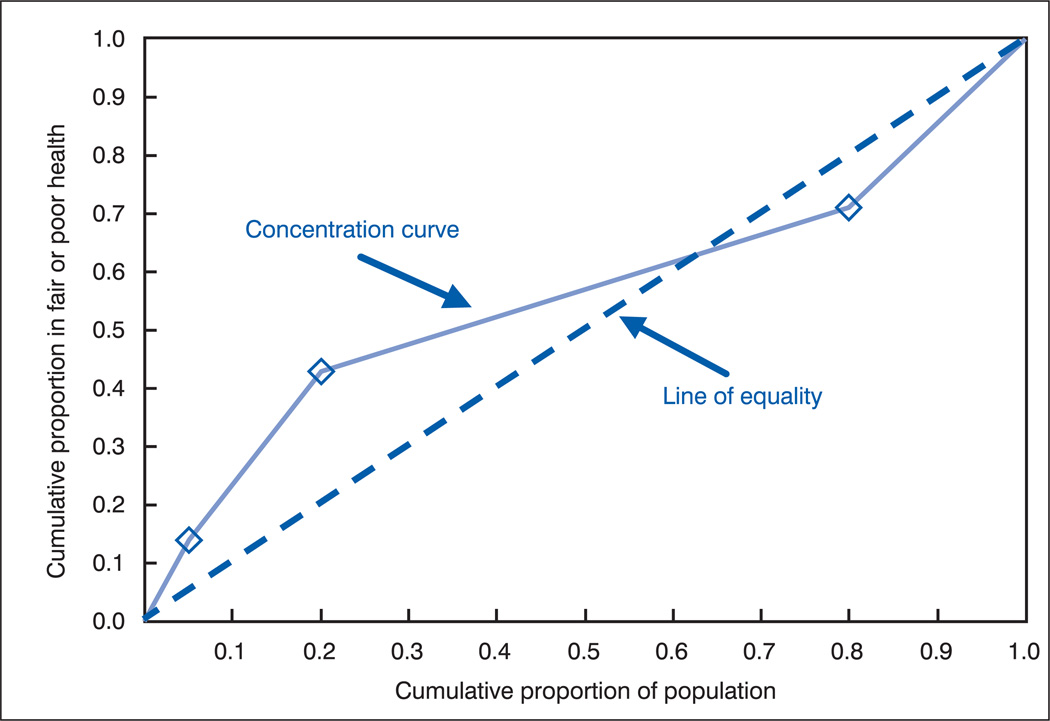
For example, figure 6 shows the concentration curve generated for the hypothetical population 2 and demonstrates what happens in the case of a reversal of rates in the two highest income categories (compared with population 1).

Figure 6.

Concentration curve for hypothetical population 2

Because the percentage in fair or poor health is now greater among persons in the highest income category than among persons with middle incomes, the concentration curve crosses the diagonal and the net area with the negative sign decreases compared with population 1. The value of C is now closer to 0, indicating a reduction in the disparity in fair or poor health across income groups.

Table J shows C and the RII (formed by dividing the SII by the mean) for all three hypothetical populations described previously. Both measures indicate that relative income disparity in fair or poor health is least for population 2 and greatest for population 3, differing from population 1 by similar relative amounts.

Table J.

Summary indices of disparity for three hypothetical populations

Summary index of disparity	population 1	population 2	population 3
Concentration index (C)	−0.20	−0.12	−0.26
RII1 (mean)	−1.54	−0.94	−1.70

¹RII is Relative Index of Inequality.

The similarity between the results obtained from the two measures is not merely fortuitous. Wagstaff and colleagues identified the straightforward mathematical relationship between C and the RII(mean) (13). Both the slope of the regression line and the concentration index are based on the weighted covariance of X and Y, where X is the ranked cumulative population and Y is the health indicator. Multiplying the RII by twice the weighted variance of X produces the concentration index.

Therefore, the choice between the regression-based and the concentration curve-based approaches to summarizing socioeconomic disparity in health depends primarily on practical considerations rather than on conceptual differences. In some instances, the visual comparison of disparity between two or more populations or two or more points in time can be simpler and more intuitive with graphs of concentration curves than with graphs of regression slopes, especially if the actual values of the health indicator are included on the figure as the data points through which the regression line is fitted. On the other hand, regression-based measures are likely to be more intuitively meaningful to persons concerned with public health. This, combined with inclusion of regression procedures in software commonly used by health researchers, probably accounts for the larger number of studies that have used the SII or RII.

Guideline 10

• 10.When the primary interest is in how health varies with the amount of the characteristic defining the domain rather than with the groups themselves, summary measures of disparity that take into account the order of groups should be considered.

Precision of disparity measures

The precision of the statistics used to measure disparity should also be considered when these statistics are interpreted. The precision of a measure of disparity depends on the precision of the estimated rates used to compute the statistic. The precision of the rates depends on sampling error or other sources of random variation in the data used to compute the rates.

Precision is usually expressed in terms of the standard error of a statistic or the width of a confidence interval based on the statistic. The narrower the confidence interval, the more precise the estimate for a given level of confidence will be. A 95-percent confidence interval is frequently employed. The upper and lower limits of a confidence interval can be produced for the statistics used to measure disparity whenever quantitative estimates of variability (standard errors) are available for the rates, percentages, etc. on which these measures of disparity are based.

Guideline 11

• 11.When ever possible, a confidence interval should accompany each measure of disparity.

In general, the upper and lower limits of a 95-percent confidence interval for a statistic are calculated as:

$$\text{Lower limit}=S-(1.96•{\mathrm{S}\mathrm{E}}_{\mathrm{s}})\text{Upper limit}=S+(1.96•{\mathrm{S}\mathrm{E}}_{\mathrm{s}})$$

where S is the point estimate for a statistic, and SE_S is the standard error for the estimate of S. Estimates of precision for summary measures can be produced using a re-sampling or bootstrap procedure whenever standard errors are available for the underlying rates (20). This procedure uses the rate and standard error for each group to re-estimate each group rate many times assuming a random normal distribution. Based on these group rates, the same number of summary measure estimates is generated, and the distribution of these estimates is used to compute a standard error for the summary measure. Confidence limits for the summary measure are then computed as shown above.

Techniques for testing the statistical significance of differences between rates and differences in measures of disparity are described elsewhere (7,8,21,22).

Discussion

The definition of disparity in terms of differences in group rates is consistent with the second goal of Healthy People 2010, “to eliminate health disparities among segments of the population,…”(1). In Healthy People 2010 the following choices have been made concerning the measurement of disparities (7):

• Disparities are measured from the best group rate in each domain to emphasize the potential for improvement.

• Disparities are measured in both absolute and relative terms to emphasize the difference between absolute and relative differences and to understand changes over time more completely.

• Disparities are measured in terms of adverse events in order to facilitate comparisons across Indicators.

• Pair-wise measures are used to monitor progress toward the elimination of disparity for individual groups, and summary measures are used to monitor progress toward the elimination of disparity for each domain of three or more groups (race and ethnicity, education, and income).

• Component groups are not weighted when summarizing disparity across a domain. However, the size of the groups is considered when assessing the impact of disparities.

• In the interest of simplicity and consistency, summary measures are estimated the same way for domains with ordered and unordered groups.

The choices that are appropriate for monitoring progress toward the elimination of disparity in Healthy People 2010 may not be appropriate in other situations. The best group rate cannot be used as a reference point when it is not reliable because of small numbers. Absolute differences in rates cannot be compared across indicators based on different units of measurement. Indicators such as mean blood pressure or life expectancy cannot be expressed in terms of adverse events. And comparison of summary measures of disparity across indicators depends on comparability in the number of groups and in the assignment of persons to groups.

In this report, the words “disparity” and “difference” are used interchangeably. In common usage, however, disparity frequently connotes a negative judgment or inequity. Indeed, judgments are needed to identify disparities that require public health action. The absolute size of a disparity is not a sufficient basis for taking action. The absolute difference between 1 and 4 deaths per 100,000 may not have the same meaning as the difference between 401 and 404 deaths per 100,000. The relative size of a disparity is also not sufficient. A relative difference of 10 percent in the percentage of women who did not have a mammogram may not have the same meaning as a 10 percent difference in infant mortality rates. Nor is the statistical significance of a disparity sufficient. In sample surveys, for example, drawing a larger sample or combining years of data can change a nonsignificant difference into a significant difference. A deliberative process involving a review of what is known about the determinants of the observed disparity is needed to identify disparities that are inequitable (23,24).

Conclusions

In this report disparity is defined as the difference between a group and a reference point—expressed in terms of a rate, percent, proportion, or some other quantifiable measure. The effects of different choices on measures of disparity were examined. Based on this discussion, 11 guidelines concerning the measurement of disparity are proposed. These guidelines do not prescribe a single way to measure disparity, they are not applicable in all situations, and they are not applicable to all of the ways that differences in indicators of health are measured. Nevertheless, these guidelines are intended to bring greater consistency to the examination of disparities as a function of differences between groups in quantifiable indicators of health.

Guidelines for Measuring Disparities in Terms of Differences Between One or More Group Rates and a Reference Point

1. When disparities are measured, the reference point should be explicitly identified and the rationale for choosing a particular reference point should be provided.

2. If comparisons are made between two groups, the more favorable group rate should be used as the reference point. (This would be the lowest rate assuming that rates are expressed in terms of adverse events—see guideline 4 below.)

3. Disparities should be measured in both absolute and relative terms in order to understand their magnitude.

4. When relative measures of disparity are employed to compare disparities across different indicators of health, all indicators should be expressed in terms of adverse events.

5. Pair-wise comparisons are called for when the objective is to describe disparities between one or more individual groups and a specific reference point.

6. Summary measures can be used when disparities are measured for a domain of several groups and comparisons are to be made over time or across indicators, geographic areas, or populations.

7. Conclusions based on summary measures always should be interpreted in conjunction with the group-specific rates on which they are based.

8. The choice of whether to weight the component groups when summarizing disparity across a domain should take into consideration the purpose and application of the summary measures. In addition, implications with respect to other types of decisions, such as the choice of a reference point, need to be considered.

9. The size of the groups and the number of persons affected in each group should be taken into account when assessing the impact of disparities.

10. When the primary interest is in how health varies with the amount of the characteristic defining the domain, rather than with the groups themselves, summary measures of disparity that take into account the order of groups should be considered.

11. Whenever possible, a confidence interval should accompany each measure of disparity.