Spatiotemporal morphometry of adjacent tissue layers with application to the study of sulcal formation

Abstract

The process of brain growth involves the expansion of tissue at different rates at different points within the brain. As the layers within the developing brain evolve they can thicken or increase in area as the brain surface begins to fold. In this work we propose a new spatiotemporal formulation of tensor based volume morphometry that is derived in relation to tissue boundaries. This allows the study of the directional properties of tissue growth by separately characterizing the changes in area and thickness of the adjacent layers. The approach uses temporally weighted, local regression across a population of anatomies with different ages to model changes in components of the growth radial and tangential to the boundary between tissue layers. The formulation is applied to the study of sulcal formation from in-utero MR imaging of human fetal brain anatomy. Results show that the method detects differential growth of tissue layers adjacent to the cortical surface, particularly at sulcal locations, as early as 22 gestational weeks.

1 Introduction

This work is motivated by the study of growth patterns in the developing brain. In particular, there is considerable interest in exploring geometric characteristics of growth that underlie the formation of sulci and gyri. Multiple hypotheses regarding the ontogeny of cortical folding patterns have emerged that consider factors like axonal tension [1], differential cortical expansion [2], mechanical constraints [3] and genetic determination [4] as well as combinations of these factors [e.g. [5], [6]]. A more complete characterization of the local growth patterns associated with cortical folding in the human fetus will provide evidence for the development of theories on gyrogenesis

Tensor based morphometry is a powerful tool that makes use of accurate spatial normalization to study local differences in tissue size across a population, that can be used to study changes in anatomy with age. It has recently been used to study fetal brain growth [7] and brain growth in early childhood [8], [9], [10], [11]. One of the key challenges in TBM analysis is interpreting not just the scalar volume increase with growth, but the directional characteristics that induce the formation of a sulcated brain from a smooth fetal brain. In this paper we describe an approach to examining how tissue growth occurs in adjacent tissue layers as the shape of the boundary between them evolves. We derive a statistical framework to model the components of tissue growth over time in relation to the local coordinate frame of the tissue boundary. We apply this to look at how primary sulci are formed in the developing human fetus in relation to the boundary between the cortical plate and sub-plate, by specifically mapping normal and tangential components of volume increases on either side of the tissue boundary. We make use of temporally weighted, local regression to test whether the rate of area or thickness is increasing or decreasing over time. This allows us to study the pattern of increases in the area of layers in relation to increases in thickness of the layers at specific gestational ages.

2 Methods

For a cross-sectional population of n subject at different ages, we compute a transformation D_i, i = 1, 2, …n for each subject, which captures the geometric changes required to spatially normalize each subject image to a common space. At each voxel p, the local differences size and shape can be derived from the deformation tensor which is defined as the gradient of the transformation ( $D_i^p[x,y,z]$) at that voxel and is given by $(J_i^p)=\left[\frac{\partial D_i^p[x,y,z]}{\partial x\partial y\partial z}\right]$. We form an average brain surface by constructing a triangulated mesh from the cortical surface of the average image. The Jacobian matrices within 4 mm of each surface vertex were averaged (in the log domain [12] and placed onto the surface mesh for surface modeling. For each subject, this then provided a map that summarizes shapes changes on the cortical surface.

2.1 Discriminating shape change into area or thickness changes

Shape changes adjacent to anatomical boundaries occur as a series of changes in local area and thickness of the adjacent tissue layers. At each location on the boundary, change in neighboring tissue area and thickness can be quantified by resolving the Jacobian matrix into its radial and tangential components respectively. We form a surface normal map (N) by computing the surface normal at each vertex of the average surface. Vertex-wise approximation of change in neighboring layer thickness $T_i^p$, is the scalar projection of the Jacobian tensor (( $J_i^p$)) of the tissue location projected onto the corresponding surface normal (n),

$$T_i^p=\mathit{abs}({\mathbf{n}}^T(J_i^p)\mathbf{n})$$ (1)

In order to compute the change in local surface area, we compute maps of vectors tangential to the surface and perpendicular to the surface normal vector. The cross-product of n and an arbitrary, non-colinear vector r results in one possible tangent (t1) to the surface. The other surface tangent (t2) is the cross-product of (t1) and n. Local change in area is the scalar component of the Jacobian tensor onto t1 and t2,

$$A_i^p=\sqrt{(\mathbf{t}{\mathbf{1}}^T(J_i^p)\mathbf{t}\mathbf{1})\times (\mathbf{t}{\mathbf{2}}^T(J_i^p)\mathbf{t}\mathbf{2})}$$ (2)

For each subject, we compute a map of surface area A_i and thickness T_i change which can then be used to analyze local changes in shape.

2.2 Modeling local changes at specific time points

In order to examine the temporal progression of changes in surface shape, we use locally weighted regression (LWR) [13] to examine the relationship between surface area or thickness and a time-variable of interest (e.g. age of subjects). LWR is a non-parametric method that fits a smooth regression model to the data by fitting simple models to localized subsets of the data. For each independent variable of interest (IVOI), a lower degree polynomial is fitted using weighted least squares, giving more weight to points near the IVOI and less weight to points further away. The regression is considered complete when a local model is fit to all independent variables. In order to study age-specific models of surface shape change, we performed LWR with area (or thickness) as the dependent variable and age as the independent variables. Let Y correspond to the vector of dependent variables (at a single vertex), X is the vector of independent variables and and ε are the errors. As shown in Equation 2.2, for each independent variable X_i, a linear model is fit by using weighted least squares where W_i is the weight matrix. A generalized bell-shaped function is usually used to form the weight matrix. (The matrix dimensions of each of the variables are indicated below each variables in Equation 2.2). LWR results in a vector of coefficients (β₁, …, β_n) corresponding to the total number of independent variables.

$$\begin{array}{ccc}\hfill W_{i}Y=\hfill & \hfill W_{i}X{\beta }_i\hfill & \hfill +\epsilon \hfill \\ (n\times 1)\hfill & \hfill (n\times n)(n\times 1)(1\times 1)\hfill & \hfill (n\times 1)\end{array}$$

Hypothesis testing

Resulting regression coefficient (β₁, …, β_n) maps are tested for significance using a standard t-test. Statistical significance was computed and these were corrected multiple comparisons using permutation tests [14].

The β₁, …, β_n values are estimates of increase or decrease in area or thickness at a particular time point and the hypothesis tests estimate statistical significance of these changes.

3 Application – Comparing growth patterns between cortical plate (CP) and subplate (SP) during early fetal development

The following experiments were performed using clinical MR scans of 40 fetal subjects at gestational ages ranging from 20 to 28 weeks. The mothers were referred for fetal MRI due to questionable abnormalities on prenatal ultrasound or a prior abnormal pregnancy. All women had normal fetal MRI and all newborns have had normal postnatal neurodevelopment. Fetal imaging was performed in our institution on a 1.5T scanner (GE Healthcare, Milwaukee, WI) without sedation of the mother or the fetus. For each subject multiple stacks of single-shot fast spin-echo (SSFSE) T2-weighted slice images (pixel size 1 mm × 1 mm, slice thickness ≈ 3 mm) are planned in the approximately axial, sagittal and coronal planes with respect to the fetal brain and are acquired with MR sequence parameters (TR = 4500 ms, TE = 91 ms). High resolution 3D volumes were reconstructed from 2D slice MR images using the slice intersection motion correction (SIMC) technique [15]. The reconstructed volumes were automatically segmented into individual tissue types (developing grey matter, developing white matter, the germinal matrix) using an atlas-based approach with probabilistic atlases generated from a spatiotemporal model of the fetal brain [16]. The tissue label maps for each of the 40 scans were co-aligned using an unbiased groupwise registration algorithm. The algorithm simultaneously estimated an average brain shape and a deformable mapping to each of the anatomies being studied. This average shape was estimated in such a way to ensure that the average distance from each point in that space, when mapped to the individuals in the group, is forced to be zero, forming a so-called minimum deformation anatomy. For each subject, the Jacobian matrix maps were computed, from the resulting deformation fields, to quantify the pattern of deformation required to spatially normalize individual anatomies. The inner surface of the cortical plate in the group average tissue segmentation map was formed into a triangulated mesh using a topology preserving marching cubes algorithm [17].

For each subject, we computed two surface Jacobian maps corresponding to two layers of the cerebral mantle namely the cortical plate (CP) and the subplate (SP). For each layer, we compute a set of maps describing local changes in surface thickness and surface area changes. For each layer and metric, we compute a model of spatial changes from 21 to 28 weeks GA at 1 week intervals.

3.1 Results and discussion

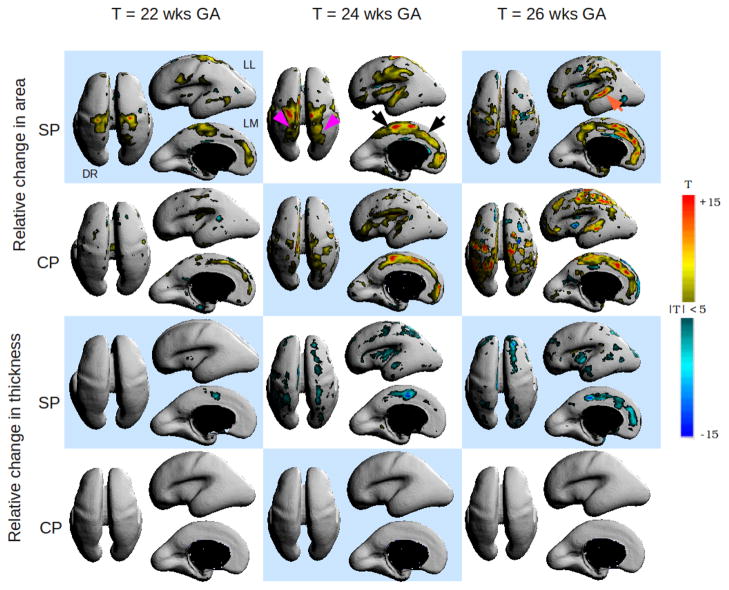
Figure 2 shows a matrix of the statistically significant variations in area and thickness between the CP and the SP. The T Maps were overlaid on the average surface and displayed using the Rview software⁵. Due to space constraints, we have shown growth patterns for 22, 24 and 26 weeks only. Overall, we see distinctly different patterns of area and thickness changes between the two layers. We also see a distinct temporal pattern of area and thickness change from 21 to 28 weeks. On the SP, the medial side of the fronto-parietal region (as indicated by black arrows) shows a progressive, relative increase in area from 21 to 27 weeks which corresponds to relative decrease in the thickness component of growth during this period. We also notice that the emergence of the post-central sulcus (purple arrows) as increase in area of the SP beginning at 23 weeks which is correlated with a increase in area on the CP plate at the corresponding location after 24 weeks. We observe in the lateral views that the operculization process manifests as changes in area and volume both on the SP and CP. Local area increases in the SP begin at the operculum at 22 weeks. By 24 weeks, the increase in area has shifted to accommodate the emergence of the superior temporal gyrus and by 26 weeks area increases also occurs at the location of the superior temporal sulcus (orange arrow). A similar pattern of area increase is also visible on the CP although the process seems to be delayed by 1 week. During this period, the local thickness component of growth on the SP decreases as expected. Local area increases at the presumptive location of the fronto-parietal gyrus is visible in both the SP and the CP between 21–24 weeks. The lack of change in thickness of the CP is supported by the findings of Rakic et al. [18], who postulate that the CP enlarges primarily by tangential expansion as a uniform surface and not by increase in thickness.

Fig. 2.

Spatiotemporal patterns of variational growth between the cortical plate (CP) and subplate (SP) during early fetal development. Warm colors indicate significant, relative increase in area or thickness component of growth with time and cool colors indicate statistically significant reductions in area or thickness component. DR = Dorsal view, LL = left lateral view and LM = left medial view. Changes are bilateral unless noted otherwise.

We see a distinct difference in the directional growth of the CP and SP. In regions of cortical folding, the CP and SP expanded in overlapping areas. Moreover, where SP expanded in the tangential direction, SP also significantly grew in the normal direction. In contrast, the CP did not increase in the normal direction, from which we infer there is no detectable change in thickness at our image resolution. The total expansion of SP underlying developing gryi is in agreement with the histological observation in gyrencephalic animals of large visible SP at gyri and very thin SP at sulci [19], [20]. Coincident expansion of the CP and SP, which is primarily composed of axonal fibers held at transient contacts prior to reaching final targets in the CP [20], may support cortical folding hypotheses that suggest that connectivity is a major driver of cortical folding patterns [1], [21].

4 Conclusion

In this paper, we have introduced descriptors that allow us to characterize growth in adjacent tissue layers in terms of changes in area and thickness. Also for the first time, we use temporally weighted, local regression to create spatiotemporal models of tissue growth along an evolving tissue boundary between the adjacent layers. The two methods are incorporated into the TBM framework to model differential patterns of tissue growth between two adjacent anatomical layers. Using the proposed spatiotemporal morphometry framework, we modeled variational growth patterns between the CP and SP which underly the mechanism of sulcation in a fetal brain. The spatiotemporal method allowed us to precisely stage growth patterns of various tissue layers corresponding to the emergence of the primary sulci. Future work will include extending this analysis to other tissue boundaries within the fetal brain and examining the correlation between changes across the boundary (e.g volume increases in SP vs area increases in CP). The general framework of spatiotemporal morphometry can be adapted to other applications.

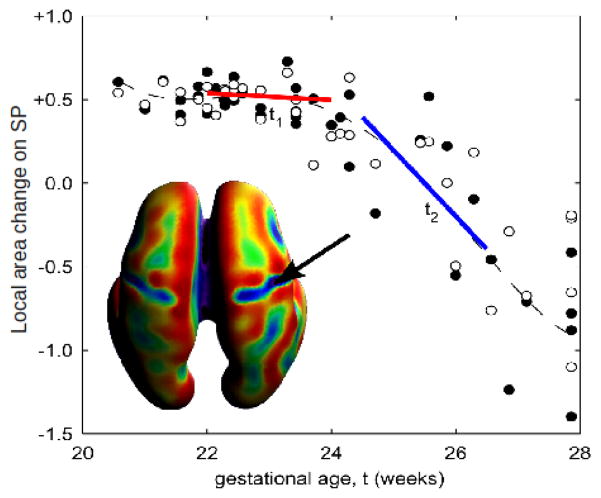
Fig. 1.

Example of using LWR to model area changes at a particular location on the subplate (SP). A smooth function is fit to the entire time interval by fitting linear models to smaller subsets of data. For each subset of data, the independent variables closest to the independent variable of interest are weighted higher than those further away.