Reconstruction of Scattered Data in Fetal Diffusion MRI

Abstract

In this paper we present a method for reconstructing diffusion-weighted MRI data on regular grids from scattered data. The proposed method has the advantage that no specific diffusion model needs to be assumed. Previous work assume the tensor model, but this is not suitable under certain conditions like intravoxel orientational heterogeneity (IVOH). Data reconstruction is particularly important when studying the fetal brain in utero, since registration methods applied for movement and distortion correction produce scattered data in spatial and diffusion domains. We propose the use of a groupwise registration method, and a dual spatio-angular interpolation by using radial basis functions (RBF). Leave-one-out experiments performed on adult data showed a high accuracy of the method. The application to fetal data showed an improvement in the quality of the sequences according to objective criteria based on fractional anisotropy (FA) maps, and differences in the tractography results.

1 Introduction

Diffusion Magnetic Resonance Imaging (dMRI) is an imaging modality that has been used for studying the normal (Dubois et al., 2008; Mukherjee et al., 2002; Prayer and Prayer, 2003) and pathological (Anjari et al., 2007) development of the brain in pediatrics. Advances in pulse sequences (Kim et al., 2008; Turner et al., 1990), parallel imaging (Bammer et al., 2001), and coil design have reduced the acquisition problems associated to fetal motion and mother’s breathing, which allowed the study of the brain in utero (Baldoli et al., 2002; Bui et al., 2006; Kim et al., 2008; Righini et al., 2003). Because of the limited sensitivity of fetal ultrasound to detect and depict the maturational processes of the developing white matter, dMRI can be considered as one of the most promising modalities for studying in vivo the natural course of human white matter development. A dMRI study consists of the acquisition of a reference image with no sensitivity to diffusion and a set of diffusion-weighted (DW) images in non-collinear directions that allow the estimation of the local diffusion properties according to a specific diffusion model. In the simplest case, the local diffusion is modeled as a rank-2 tensor (Minati and Weglarz, 2007), which requires at least 6 DW images besides the reference. The methods for diffusion estimation from dMRI sequences assume that the gathered diffusion-sensitized signals come from the same physical point, but this condition is difficult to accomplish in practice. Figure 1 shows an example of the sequences used in this paper.

Figure 1.

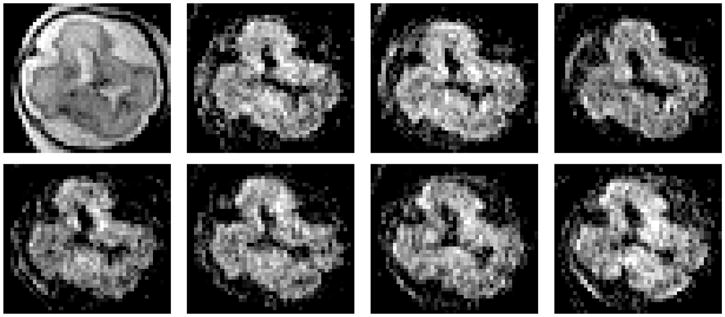
Example of a fetal brain dMRI sequence. From left to right the image of reference ( $T_2^{\mathit{epi}}$) and the first 7 DW images.

In adults, eddy current-induced image distortions and rigid patient motion during prolonged acquisitions cause image misalignment in dMRI sequences, invalidating the assumption of a consistent relationship between image space and anatomy. Several methods have been developed to correct such distortions directly during image acquisition (Andersson et al., 2003; Chen and Wyrwicz, 2001; Roemer and Hickey, 1988) or by applying image registration techniques (Andersson and Skare, 2002; Jezzard et al., 1998; Nielsen et al., 2004; Rohde et al., 2004). However, such methods may fail when applied to fetal dMRI, requiring the development of specific image processing methods. Unpredictable fetal movements coupled to the mother’s breathing result in a set of slices of variable orientation in the space, which hinders the use of 2D affine transformations for modeling distortions. If the image acquisition is fast enough, the fetal motion can be neglected for each slice, and the transformations can be considered as affine for each slice independently (Rousseau et al., 2006; Jiang et al., 2009; Kim et al., 2010). Besides this increase in the complexity of the transform, image registration methods encounter problems related primarily to echo-planar imaging with inherently low resolution and noisy sequences that can be sensitive to subject motion.

After registration, the corrected sequence is usually obtained by using resulting transformations to interpolate diffusion-sensitized values on a regular spatial grid. However, this approach disregards changes in gradient directions associated to spatial transformations, which introduce a bias in diffusion measurements and fiber orientation estimates (Leemans and Jones, 2009). Recently, (Jiang et al., 2009) have presented a reconstruction method from scattered data assuming that the local diffusion properties can be represented by a rank-2 tensor model. The main drawback of this method is that such diffusion model cannot describe voxels containing multiple fibers with different orientations, a condition found in a considerable number of points in the normal brain and referred to as intravoxel orientational heterogeneity (IVOH) (Tuch et al., 2002). The fitting of a rank-2 tensor model to measurements coming from regions presenting fiber crossing results in oblate-shaped ellipsoids, whose principal eigenvector provides no accurate information about orientation and their derived anisotropy indexes are no longer valid indicators of the axonal density.

In this paper, we present a reconstruction method of dMRI sequences from scattered data independent of the diffusion model, which can be used with more complex diffusion models like Gaussian mixture models or high-order diffusion tensors. After observing that standard registration methods may fail when applied for distortion correction of fetal dMRI sequences, we have developed a novel registration technique that first registers jointly the DW images and then uses a derived image for registration with the T2-weighted reference image. The application of the resulting transformations to the original sequence results in scattered data in the spatial and gradient domains, and a dual RBF-based interpolation was used to reconstruct the entire sequence on regular grids. The method was validated by using adult data acquired under controlled motion conditions and a set of four fetal dMRI sequences.

2 Method

2.1 Origin of scattered data

Typically, a dMRI sequence consists of a set of N + 1 regularly sampled images S = {S₀, S₁, ··· S_N } where S₀ is the image obtained without diffusion weighting, and S_i=1:N are diffusion-weighted (DW) images obtained with diffusion-sensitizing gradients G_i of direction U_i and strength b. Under ideal conditions, S₀ and S_i at the same spatial point X are related by the Stejskal-Tanner equation (Stejskal and Tanner, 1965):

$$ln\left(\frac{S_i(X)}{S_0(X)}\right)=-{\gamma }^2{D}_i{\delta }^2\left(\mathrm{\Delta }-\frac{\delta }{3}\right)\left|\right|G_i\left|\right|$$ (1)

where γ is the gyromagnetic ratio of proton, D_i is the diffusion in direction U_i, δ is the gradient duration, and Δ is the time between two pulses. However, distortions caused by eddy currents and fetal motion invalidate this relationship since voxels with the same image coordinates may not correspond to the same physical point.

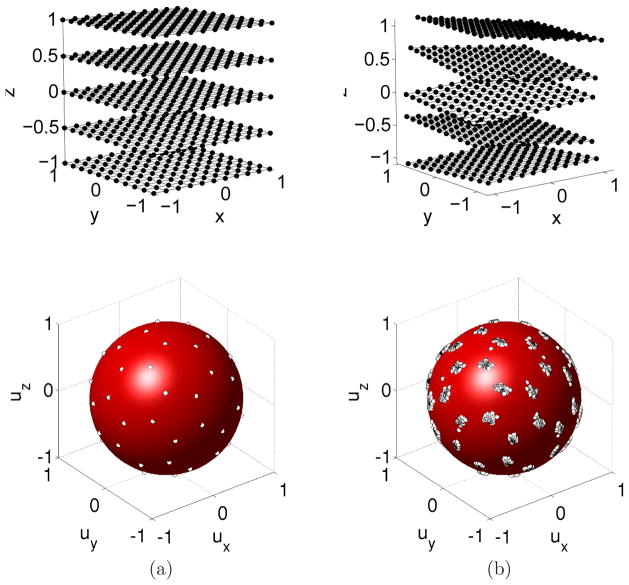
Image registration techniques can be applied to restore the lost spatial correspondence between S₀ and S_i. As explained later, in our case, each slice is transformed with a specific affine transformation. When applying this transformation to the original data, we obtain a set of slices with different spatial positions, orientations, and associated diffusion directions (Figure 3). The resulting measurements we have about water diffusion direction and strength are then scattered over the fetal anatomy, both with respect to their intended location and their intended orientation. Thus, unlike a non-motion corrupted study where we have measurements of different diffusion directions at the same spatial location, we now have different directional measurements acquired from inconsistent spatial locations. In addition, the specific directions in which diffusion is being measured are also rotationally scattered from their intended regular angular distribution by the motion of the fetus. The origin of scattered data can also be explained in terms of sampling grids. Under the assumption of constant b values, a dMRI sequence results from the sampling of diffusion-sensitized signals over a regular spatial (Ω_spa) and spherical (Ω_sph) grid. Ω_sph provides the directions for diffusion sampling, and usually consists of a set of equally spaced points in the unit sphere (Jones et al., 1999). Figure 2 shows two examples of the spherical grids used in this paper. Making use of sampling grids, the original sequence can be written as

Figure 3.

Scattered data resulting from the registration process. Data in spatial and gradient spaces before (a) and after (b) registration. Multiple gradient directions are generated for each original direction since the transformation is different for each component slice (and the corrected gradient direction depends on the transformation).

Figure 2.

Examples of spherical grids used in this paper. (a) 20-directions Ω_sph (b) 30-directions Ω_sph.

$$\mathcal{S}=\{(X,\mathrm{\Theta },S(X,\mathrm{\Theta })):(X,\mathrm{\Theta })\in {\mathrm{\Omega }}_{\mathit{spa}}\times {\mathrm{\Omega }}_{\mathit{sph}}\}$$ (2)

After correction, becomes

$${\mathcal{S}}^{\prime }=\{(X^{\prime },{\mathrm{\Theta }}^{\prime },S(X^{\prime },{\mathrm{\Theta }}^{\prime })):(X^{\prime },{\mathrm{\Theta }}^{\prime })\in {\mathrm{\Omega }}^{\prime }\}$$ (3)

where X′ and Θ′ are the transformed physical points and gradient directions respectively, and Ω′ is a transformation of the domain Ω_spa × Ω_sph. As the transformed coordinates (X′, Θ′) are no longer elements of a regular grid, results scattered. This is illustrated in figure 3.

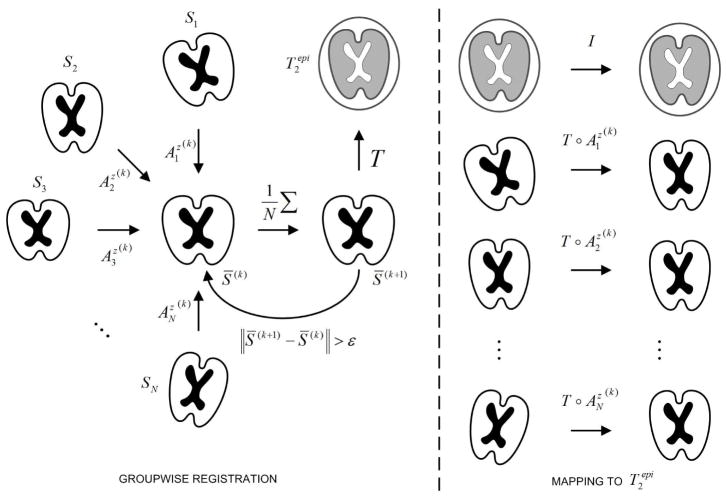
2.2 Registration approach

Distortion correction methods relying on the registration of S_i to S₀ may fail when applied to fetal dMRI, even when good results are obtained with adult data (Jiang et al., 2009). This can be understood by comparing the joint histograms built from S₀ and S₁ by using sequences where these images were considerably aligned. Figure 5 shows that for the fetal sequence, the intensities of S₀ and S₁ are very independent and the relation between intensities cannot be guaranteed. This could explain the misregistration obtained even when using information-theoretic similarity measures, since the dependency of intensities is necessary for intensity-based image registration. Figure 5 also shows that there exists a correlation between DW-images of the fetal sequence, which could make possible the registration of these images. Based on the previous observations, we have implemented a method that takes advantage of the intensity dependence between DW images to first obtain their joint alignment (Figure 4). To this end, we first register the images S_i to an arbitrary chosen reference (S_r) by using a transformation model (A^z) consisting of a set of full affine transformations applied to each slice independently (denoted by the superscript z), and mutual information (MI) (Maes et al., 1997; Wells et al., 1996) as similarity metric. The spatial transformation $A_{ri}^z$ from S_i to S_r is defined as

Figure 5.

Dependence of intensities between components of a dMRI sequence illustrated by means of joint histograms between (a) S₀ and S₁, adult; (b) S₀ and S₁, fetus; (c) S₁ and S₁, adult; (d) S₁ and S₁, fetus.

Figure 4.

Groupwise registration method. Initially all images S_i are registered to an arbitrary DW image S^* taken as reference. Then, all images are resampled and averaged to obtain a first average S̄⁽¹⁾, which becomes the new reference. At iteration k, the images S_i are registered to the mean S̄^(k) to obtain the transforms $A_i^{(k)}$. After convergence, S̄^(k) is registered to $T_2^{\mathit{epi}}$, and the composition of transformations $T\circ A_i^{z(k)}$ is applied to map all images S_i into the coordinate system of $T_2^{\mathit{epi}}$.

$$A_{ri}^z(X)=M(X)·X+O(X)$$ (4)

where M(X) is a 3 × 3 matrix and O(X) is the offset. Differently from a global affine transform, M and O depend on the spatial position X, more specifically on the k-component of the corresponding image coordinates. Then, a new reference S̄⁽¹⁾ is computed by averaging the transformed images S_i and the process is repeated until the mean squared error (MSE) between S̄^(k−1) and S̄^(k) for consecutive iterations k − 1 and k is lower than a given threshold ε. Finally, S̄^(k) is registered to S₀ and the resulting transformation A_0r is composed with $A_{ri}^z$ to obtain the final transformation between S_i and S₀:

$$A_{0i}^z(X)=(A_{0r}\circ A_{ri}^z)(X)$$ (5)

The image S̄^(k) is characterized by a higher signal-to-noise ratio (SNR) than images S_i, and provides a better depiction of the anatomical structure of the brain (Figure 6). These properties allow an accurate registration to S₀, necessary to map all the sequence in its space of coordinates. In order to find the optimum value of $A_{0i}^z(X)$ we have used an iterative gradient ascent method, and the optimization of parameters was performed independently for each slice. If the parameters of $A_{0i}^z(X)$ are represented by

Figure 6.

Average DW image S̄^(k) (a) compared to S₁ (b) and S₀ (c).

$$P=\{P^0,P^1,\cdots ,P^Z\}$$ (6)

where P^z is a vector containing the transformation parameters for the slice z, and Z is the number of slices in the volume, the estimate of P^z is updated at iteration k as

$$P^{z(k)}=P^{z(k-1)}+\lambda \nabla MI(P^{z(k-1)})$$ (7)

The initial value of λ was set experimentally to 0.2 and reduced by a 0.8 factor when MI(P^z(k−1)) < MI(P^z(k)).

2.3 Scattered interpolation

To interpolate values on a regular grid from scattered data, we have used radial basis functions (RBF) since it is one of the most widely used general methods for interpolation of scattered data in multidimensions (Press et al., 2007). RBFs have already been applied for interpolation on spherical geodesic grids in the context of numerical weather prediction, outperforming linear interpolation strategies (Carfora, 2007). In dMRI, the complexity is increased since an interpolation in the spatial domain is also required. The idea behind RBF interpolation is that every point has an influence on a neighborhood according to some functional φ(r), where r is the distance from such point. Then, the value of the function at a general point P is given by a linear combination of the φ’s centered at points P_i as:

$$y(P)=\sum _{i=0}^{N-1}{w}_i\phi (||P-P_i||)$$ (8)

where the weights w_i are calculated by solving a linear system of equations for the function to agree with the observations at points P_i.

In this paper, we have used a Gaussian function as RBF, which is one of the most commonly used functions for RBF-based interpolation. As this function tends to zero for high r, and the influence of points P_i distant from P can be neglected. This allows considering only points in a neighborhood (P) of P for interpolation, which reduces the computational complexity of the method. 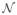(P) was formed by points P_i falling inside the support region of the Gaussian function, defined in the context of this paper as the interval [−s_φ, +s_φ] so that φ(s_φ) = 0.01 × φ(0).

In our case, each point contains spatial and angular coordinates that must be considered separately because of the difference in scale between both types of coordinates. This situation is different from the problem addressed in (Carfora, 2007) where only an interpolation in the sphere is required. To take into account these differences, we propose to modify Equation 8 by replacing the single RBF with the product of a spatial (φ) and an angular (ψ) RBF:

$$y((X,\mathrm{\Theta }))=\sum _{i=0}^{N-1}{w}_i\phi (\mid X-X_i^{\prime }\mid )\psi (\mid \mathrm{\Theta }-{\mathrm{\Theta }}_i^{\prime }\mid )$$ (9)

where X = (x, y, z) are the spatial coordinates, and Θ = (φ, θ) the spherical coordinates of the sampling vector U_i. Differently from Equation 8, Equation 9 allows a dual interpolation in two different unrelated spaces. In Equation 9, $\mid X-X_i^{\prime }\mid$ represents the Euclidean distance, whereas $\mid \mathrm{\Theta }-{\mathrm{\Theta }}_i^{\prime }\mid$ is the geodesic distance over the unit sphere:

$$\mid \mathrm{\Theta }-{\mathrm{\Theta }}_i^{\prime }\mid =\mathit{arccos}(\mathit{sin}(\theta )\mathit{sin}({\theta }_i)\mathit{cos}(\phi -{\phi }_i)+\mathit{cos}(\theta )\mathit{cos}({\theta }_i))$$ (10)

Note that both distances are not mixed directly, but through functions φ (·) and ψ (·), which are different for euclidean and geodesic distances. The domain of definition of these functions is not the same, but the codomains (i.e. the set of output values) are comparable.

3 Materials and experiments

3.1 Image data

Fetal MRI was performed on a 1.5 T Siemens Avanto MRI Scanner (SIEMENS, Erlangen, Germany) at the Hautepierre Hospital (Strasbourg, France) using an 6-channel phased array coil combined to the spine array positioned around the mother abdomen. An axial spin echo single-shot echo-planar sequence was acquired in free breathing along 30 non-collinear diffusion gradient encoding directions with a b value of 700s/mm². The following pulse sequence parameters were used: TR=6800 ms; TE=99 ms; FOV=250×250 mm²; matrix = 128×128; 41 contiguous axial slices of 3.5 mm thickness covering the whole fetal brain; no gap; number of excitations = 2. The total imaging time was 7.2 minutes. Pregnant women were briefed before the exam and signed informed consent. To reduce motion artifacts, fetal sedation was obtained with 1 mg of flunitrazepam given orally to the mother 30 mi before the exam. The study was approved by the local ethics committee.

For validation purposes, three dMRI sequences of the brain were acquired for an adult healthy subject in the following conditions: (i) static in supine position ( 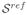, the reference), (ii) static with the head rotated by a fixed angle with respect to the reference ( 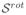), and (iii) dynamic with subject motion during the acquisition ( ).

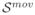3.2 Slice-to-volume registration accuracy

Initially we want to explore the ability to recover slice to volume alignment for typical but known motion, on typical anatomical structures. Fetal data are not suitable for assessing accuracy since motion artifacts are always present to some degree. Therefore, only the adult dataset 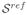was used to this aim. The fetal motion was simulated by applying a random motion to each slice, and then we applied the method described in section 2.2 to recover this simulated motion. The displacements were chosen from a uniform distribution with a varying range of [−8, +8]mm for translations in each direction, and between [−10, +10]° for each rotation. These ranges of variation represent movements observed in real fetal data, and they are similar to those used in the context of anatomical reconstruction of the fetal brain (Rousseau et al., 2006; Gholipour-Baboli et al., 2010; Kim et al., 2010).

The accuracy was assessed by computing a registration error measured on a set of 4 points P_i within every slices as follows: $\mathit{RMS}={(\frac{1}{N}{\sum }_{i=1}^N{\mathit{TRE}}_i)}^{\frac{1}{2}}$, where TRE is the target registration error defined as TRE = ||P_i − T̂^−l (T*(P_i))||². T^* denotes the known applied motion transformation, and T̂ is the estimated geometric transformation. P_i are the corners of the intersection between the bounding box containing the brain, and each slice. The error previously defined provides thus a maximum bound of the registration error for the region of interest.

3.3 Evaluation of RBF interpolation

3.3.1 Leave-one-out test

A leave-one-out test by using the adult data 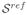was performed for evaluating the capability of recovering non-acquired DW images from the available measurements. This test estimates the image $S_j^{\mathit{ref}}$ at a point (X_j, Θ_j) from ${\mathcal{S}}^{\mathit{ref}}\backslash {\mathcal{S}}_j^{\mathit{ref}}$ and 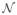(X_j)\X_j, which in terms of RBF interpolation can be expressed as:

$${\widehat{\mathcal{S}}}^{\mathit{ref}}(X_j,{\mathrm{\Theta }}_j)=\sum _{i=0,i\ne j}^{N-1}{w}_i\phi (\mid X_j-X_i\mid )\psi (\mid {\mathrm{\Theta }}_j-{\mathrm{\Theta }}_i\mid )$$ (11)

We have then computed the RMS error between 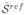(X_j, Θ_j) and 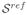(X_j, Θ_j) for a set of spatial points distributed randomly over the brain according to an uniform probability density function.

3.3.2 Estimation from rotated sequences

In this experiment, S^ref was estimated from 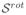. For the same physical point, the diffusion measurements should be the same since the diffusion properties of the tissue do not change with the patient orientation. However, the diffusion signals are gathered for different points and directions in the patient’s local coordinate system, since the gradient directions are fixed in the coordinate system of the scanner. Therefore, the estimation of S^ref from 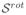requires an interpolation in the space and in the sphere, and the resulting sequence Ŝ^ref should be ideally equal to 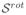. The error is thus an index of performance of the reconstruction method. Differently from the leave-one-out experiment, here all DW images of 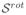at all spatial positions are employed for estimation.

3.3.3 Estimation in presence of motion

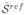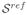We have increased the complexity of the estimation problem by adding the influence of the patient’s motion. The idea here was to explore if fiber bundles could be missed in sequences spoiled by severe motion artifacts, and to what extend they could be recovered by using the reconstructed sequence. To this end, an estimation ( ) of from 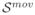was computed. A visual comparison was then performed between the tractographies for 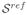, , 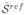and .

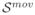3.4 Diffusion descriptors

To evaluate the performance of the registration method, we have also considered three criteria for quality assessment.

3.4.1 Mean FA in the CSF

One of the most widely used indexes of anisotropy is the fractional anisotropy (FA), defined as

$$FA=\sqrt{\frac{{({\lambda }_1-{\lambda }_2)}^2+{({\lambda }_2-{\lambda }_3)}^2+{({\lambda }_3-{\lambda }_1)}^2}{2({\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2)}}$$ (12)

where λ₁, λ₂, and λ₃ are the eigenvalues of the diffusion tensor. The mean value of FA over the cerebrospinal fluid (CSF) is expected to be close to zero because of the isotropic diffusion properties of the CSF. Registration errors may induce an increase of this measure, since voxels belonging to the CSF in some DW images may be matched with voxels belonging to the gray or white matter in others.

3.4.2 Entropy of FA in the brain

The second considered criterion was the entropy of the FA image (H_FA) over the brain. At level of the tensor estimation method, the effect of a misalignment between DW images is perceived as noisy measurements of the diffusion signal. This perturbs the parameters of the estimated tensors in a random fashion, producing noisy FA measurements characterized by higher H_FA values. (Nielsen et al., 2004) have compared polynomial and affine distortion correction, and observed a reduction in erroneous regions of FA maps along with a more spiky FA distribution in favor of the polynomial registration. (Netsch and van Muiswinkel, 2004) have reported an increase in the sharpness of FA maps after distortion correction. In both cases, the observations are in agreement with the lower H_FA values expected.

3.4.3 Standard deviation of the diffusion signal

The third considered criterion was the normalized standard deviation of the diffusion signal over the CSF. For the same reasons explained in the previous paragraph, this value is also expected to be lower after applying distortion correction methods.

4 Results

The test for assessing the slice-to-volume registration accuracy described in Section 3.2 was applied to $S_0^{\mathit{ref}}$ and $S_1^{\mathit{ref}}$. RMS values higher than 0.2 mm were considered as registration failures, and discarded for analysis. Under this criterion, successful registrations were obtained in 95% of the applied transformations. The obtained RMS errors were 0.162 ± 0.004 mm for $S_0^{\mathit{ref}}$, and 0.105 ± 0.011 mm for $S_1^{\mathit{ref}}$, which means that the registration method provides results with subvoxel accuracy for adult data. Figure 7(a) shows the distribution of this error.

Figure 7.

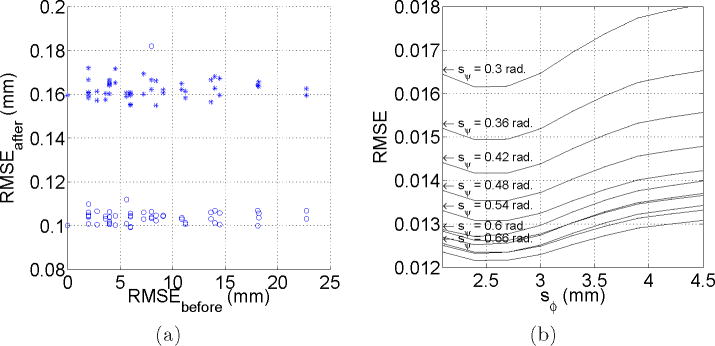
(a) Slice-to-volume registration accuracy. This figure shows the RMS error before and after registration for $S_0^{\mathit{ref}}$ (○) and $S_1^{\mathit{ref}}$ (+). Each point corresponds to a specific applied transformation. (b) Estimation of 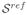from 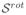. The figure shows the normalized RMS error for different support regions of the RBF functions φ and ψ.

The RMS error between the original sequence 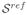and its leave-one-out estimation 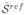was lower than 0.001 for s_φ ∈ [2.0, 4.5] mm, and s_ψ ∈ [0.6, 0.9] rad. The minimum error value was obtained for s_φ 4.0 mm (twice the inter-plane resolution for the adult data), suggesting that the inclusion of points from adjacent slices is important for interpolation purposes. Higher values of s_φ make the interpolated value dependent of distant points that could present quite different diffusion properties, and the error starts increasing. No dependence of s_ψ was found in this experiment. This could owe to the fact that the gradient table remains unchanged in this experiment, and after a threshold value (0.54 rad for adult data) all the 5 nearest gradient directions are included in the interpolation. Further increases s_ψ in the considered range does not modify the included directions.

Figure 7(b) shows the results when estimating 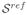from 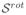. Differently from the leave-one-out experiment, in this case the error does depends on s_ψ, being lower for higher s_ψ values. In this experiment, the gradient table is changed to take into account the spatial rotations resulting from registration, and the gradient directions used for interpolation are not equidistant from the interpolated direction (Figure 8). Now, as s_ψ increases, gradient directions are incorporated gradually and the error decreases in the same manner. After a given value (0.72 in our case) the error starts increasing again, because of the influence of distant gradient directions.

Figure 8.

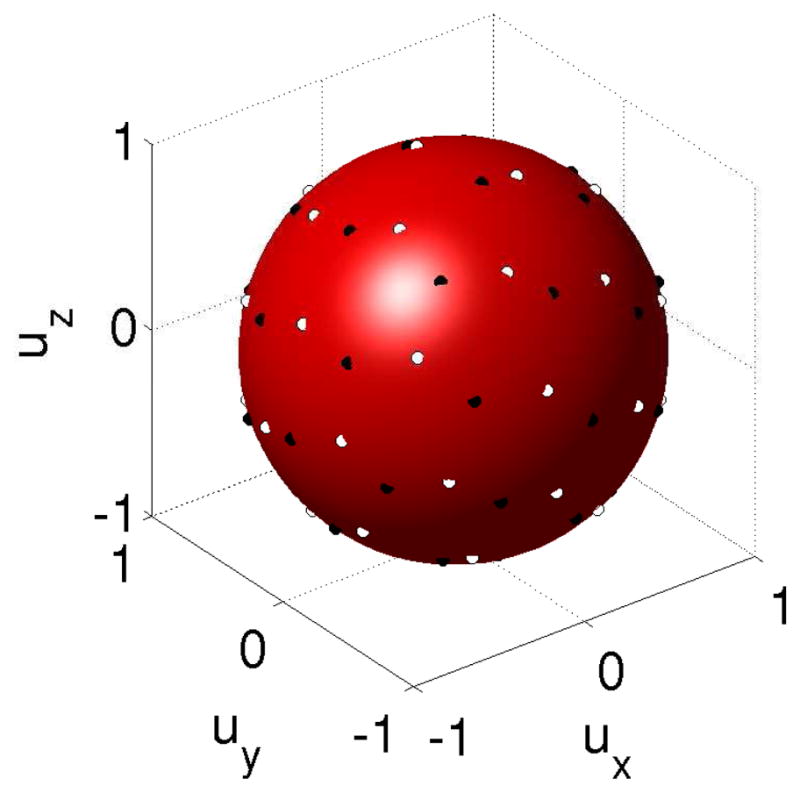
Original sampling vectors for sequence 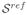(white circles) and corrected vectors of 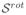(black circles) after registration to 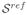. Black circles are not equidistant from white circles because of the rotation introduced by the registration.

Figure 9 shows the results of the experiment described with sequences acquired in presence of motion (section 3.3.3). This figure shows that a sequence spoiled by severe motion artifacts needs to be reconstructed before applying diffusion estimation methods, and that the interpolation method presented in this paper enables estimates approaching the quality of the gold standard.

Figure 9.

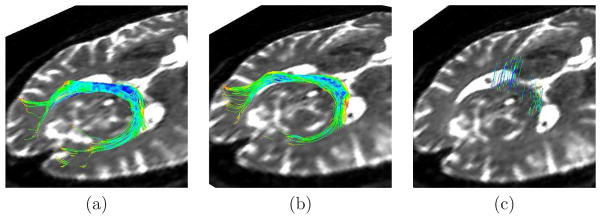
Tractographies of the splenium of the corpus callosum in an adult subject for (a) 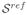, (b) 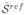, the estimation of 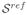from 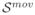, and (c)

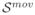
Table 1 compares the diffusion descriptors defined in section 3.4 and computed for the original and post-processed sequences. Besides the reconstruction method presented in this paper, we have applied the method for correction of distortions produced by eddy currents and patient motion available in FSL¹, a library widely used for the analysis of DTI brain imaging data. In all cases, the diffusion descriptors obtained after application of the proposed method are lower than those corresponding to the original sequences. These results are in agreement with the underlying idea that the proposed indexes effectively quantify the quality of the reconstructed sequences. However, table 1 shows that in some cases the FSL provides the lowest (i.e. better) values even when visual quality is diminished with respect to the original (motion increased). This could be explained by considering the tensor estimation from randomly distributed diffusion signals, which provides no preferential diffusion directions and low FA values. In cases of severe misregistration, the standard deviation of the diffusion signal is not affected in the same way as FA-based indexes, since its value will also tend to increase in these cases.

Table 1.

Diffusion descriptors used to quantify the goodness of the correction methods. None means that any method was applied. FSL is the eddy current correction method provided by this library (S₀ was used as reference). RBF is the reconstruction method presented in this paper. H_fa = Entropy of FA over the brain, ${\overline{FA}}_{\mathit{csf}}$ = mean FA over the CSF, and σ_csf = normalized standard deviation of the diffusion signal over the CSF.

Method	Fetus #1			Fetus #2			Fetus #3			Fetus#4
	Hfa	${\overline{FA}}_{\mathit{csf}}$	σcsf	Hfa	${\overline{FA}}_{\mathit{csf}}$	σcsf	Hfa	${\overline{FA}}_{\mathit{csf}}$	σcsf	Hfa	${\overline{FA}}_{\mathit{csf}}$	σcsf
None	1.52	0.18	0.12	1.35	0.25	0.15	1.43	0.27	0.17	1.40	0.22	0.18
FSL	1.59	0.14	0.14	1.19	0.19	0.15	1.18	0.19	0.16	1.20	0.20	0.17
RBF	1.46	0.13	0.12	1.21	0.20	0.13	1.25	0.20	0.15	1.19	0.20	0.14

To perform the tractography, an expert radiologist traced regions containing the splenium and genu of the corpus callosum (CC), and both pyramidal tracts (PR and PL) on the $T_2^{se}$ images. These regions were used for seeding the tractography after propagation to the $T_2^{\mathit{epi}}$ image by using affine registration, and to assess the presence/absence of these specific bundles in the analyzed cases. Tensors were estimated by using a standard least squares method, and the tractography was performed by applying a streamline method. In both cases we have used the algorithms implemented in Slicer². In all the analyzed fetuses the three bundles (CC, PR, and PL) were identified, with shape and localization consistent with previous anatomical knowledge as assessed by the expert radiologist. Figure 11 shows an example of the obtained results.

Figure 11.

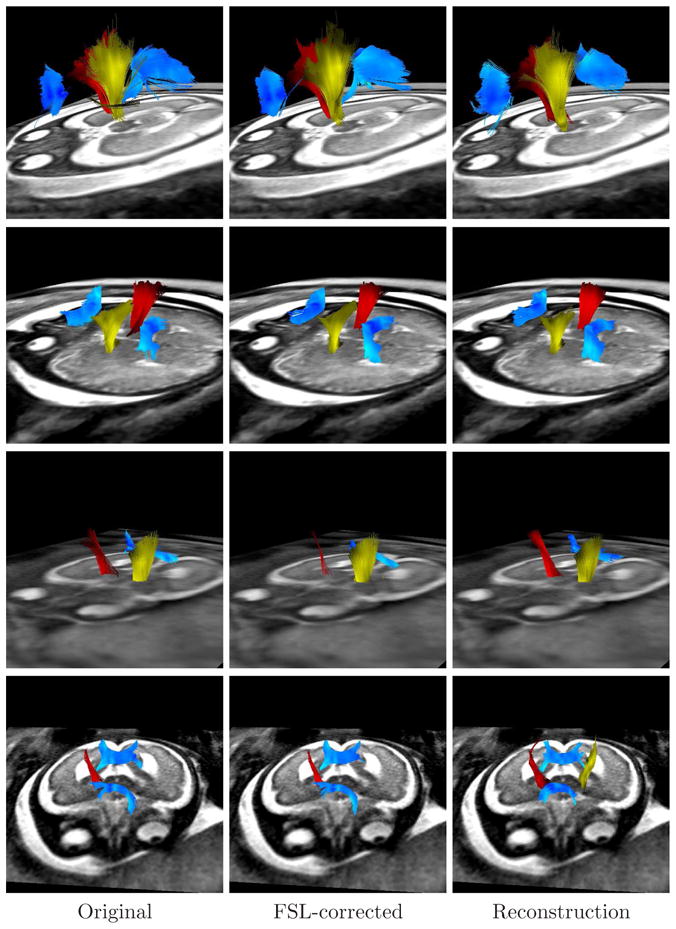
Tractographies performed on the sequences used in this paper, showing the corpus callosum (blue), the right pyramidal tract (red), and the left pyramidal tract (yellow). Each row corresponds to a different fetus, and each column to a different method. Absent tracts mean that such tracts could not be detected (for example the genu of the CC in the third fetus).

5 Discussion

In this paper, we have presented a novel method for reconstructing fetal dMRI sequences from scattered data. The advantage over previously proposed methods (Jiang et al., 2009) is the independence of the diffusion model, which allows its use for studying diffusion patterns even in IVOH conditions. The method consists of a groupwise registration method for correction of motion and eddy-current distortions, followed by a spatio-angular interpolation based on RBFs used to estimate signal values on regular sampling grids.

Even when in adults the image registration of DW images with $T_2^{\mathit{epi}}$ provide acceptable results for distortion correction, its application to fetal images may fail. Based on this observation, we adopted a registration strategy that takes advantage of the correlation between DW images and that provides good visual results. The final mapping to $T_2^{\mathit{epi}}$ was performed by registering this image with the averaged diffusion signal. At the b-values used in this paper (b = 700) the SNR of DW images is relatively high. However, the SNR degrades for acquisitions at high b-values (Akazawa et al., 2010), and further experiments should be done to know the effects on the registration accuracy.

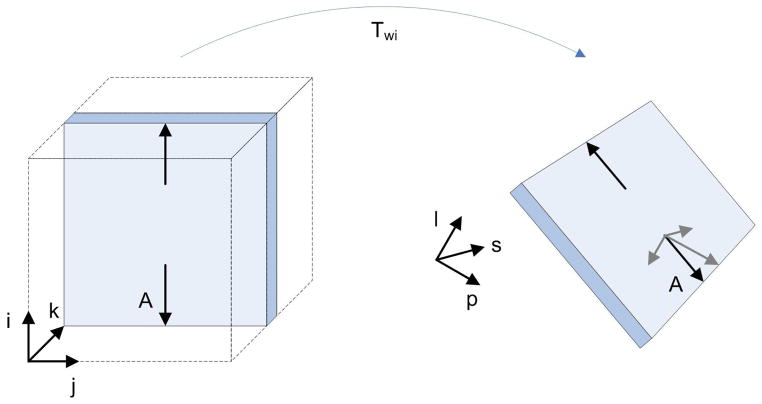
In the bibliography, distortions caused by eddy currents are assumed to occur in the image plane along the diffusion encoding direction (Haselgrove and Moore, 1996; Jezzard et al., 1998), and consist of in-plane magnification, shear, and translation. This distortion model has been used on adult data by assuming absence of rotations, and a spatial correspondence of slices between the T2-weighted image and the DW images (Mangin et al., 2002; Nielsen et al., 2004). In fetal data, these assumptions are not valid any longer because of the fetal movement. Another difference of fetal sequences with respect to adult sequences is that the transformation from image to world coordinates (IC and WC respectively) is not the identity. This transformation extracted from the DICOM header provides the mapping from each voxel to the WC defined with respect to the mother, but the fetus can be in an arbitrary position with respect to her. Therefore, an in-plane distortion in IC becomes a spatial distortion in WC as shown in figure 10. As the transformation defined in 5 is defined in WC, the choice of a full affine transformation allows to take into account the 3D rotations and distortions. For simplicity, we have not constrained the shear and scaling in the direction perpendicular to the image acquisition plane (which should remain constant), and the method relies on the metric for guiding the registration process accurately.

Figure 10.

Distortions in WC. At left, a magnification in the phase encoding direction is represented by arrows parallel to i (arrows are much longer than in real cases for representation purposes). After transforming the slice into WC, the arrow A has components along each one of the directions defining the WC system (l = left, p = posterior, s = superior). Therefore, a magnification along a single direction in IC becomes a magnification along all directions in WC. The same concept is applicable to shearing and translation.

In the context of reconstruction of fetal anatomical images, a motion model has been used for regularization (Kim et al., 2010; Rousseau et al., 2006). This model is based on an interleaved acquisition protocol that assumes that anatomical locations of slices are temporally correlated due to smooth motion of the fetus in relation to the imaging time. In this paper, no motion model was employed since image acquisition was performed in a standard manner, which is a worse case situation in the sense that no assumption is made with respect to the fetal motion and this is considered as random.

The quantitative assessment of different registration results is difficult since a gold standard for validation is not available in dMRI. The assessment of improvement is mainly performed by visual comparison of images before and after correction (Haselgrove and Moore, 1996; Nielsen et al., 2004; Rohde et al., 2004). Quantitative approaches have been proposed like the values of the affine transformation parameters as a function of the slice number (Mangin et al., 2002), and the transformation consistency (Netsch and van Muiswinkel, 2004). In this paper we have investigated the use of alternative indexes based on the diffusion signal and the FA maps. Table 1 suggests that σ_csf is the one that best corresponds to the visual inspection, since it is higher for the original and the FSL-corrected sequences, which present distortions completely removed with the proposed method. FA-based descriptors like H_fa and ${\overline{FA}}_{\mathit{csf}}$ are not robust to situations of severe misregistration and can provide good values in cases of completely misaligned sequences.

One of the main limitations found during the experimental design was the impossibility of acquiring fetal sequences under controlled conditions, constraining the validation to the use of adult data. This is a consequence of the fetal motion and the respiration artifacts introduced by the mother. Even when the obtained results cannot be extrapolated directly to fetal sequences, they help understand the responses of the method to changes in parameters, which is important to optimize its performance. For example, s_ψ and s_φ cannot be set to arbitrarily high values, since distant points start influencing local diffusion properties that are not necessary shared with the intended location. The previous knowledge of the expected fetal motion plays an important role for setting these values.

The tractography in fetal dMRI sequences is a challenging task since the incomplete myelinization necessary for detecting fibers, and the absence of a ground truth to compare the results. In adults, the correction of distortions has been shown to have an important influence on the tractography results (Aksoy et al., 2010; Merhof et al., 2007). This was confirmed by the results shown in Figure 9, which shows how completely missed tracts in a sequence corrupted by motion can be recovered after reconstruction. In fetal dMRI, we have also found such differences, but their significances are unknown. The assessment of significance would require the design of a comparative study based on objective measurements, which is out of the scope of this paper. To our knowledge, the only previous work on fetal tractography in vivo was carried out by (Kasprian et al., 2008), but unfortunately no distortion correction was performed and therefore no differences in tractography are shown.

Another interesting aspect to discuss is the intersubject variability with respect to the extension, shape, and location of the detected tracts. Even when the images analyzed in Figure 11 correspond all to the third trimester of GA, there are some differences in the tract features. These differences could correspond to changes occurring during the normal developing of the brain (Bui et al., 2006; Kostovic and Vasung, 2009; Prayer et al., 2006).

One additional problem that can occur more frequently in fetal studies is the presence of dark slices due to within slice motion. Typically, the slice acquisition time is short enough to gather the diffusion signal without perturbations, but in situations of fast fetal motion the image is completely lost. This creates registration problems, and introduces spurious data into the interpolation. In the sequences analyzed in this paper this artifact was absent, and therefore it was not considered in the current implementation of the method. The automatic detection and removal of slices without diffusion signal is an open problem and constitutes a work in progress.

The reconstruction of fetal dMRI sequences is a key step in the image processing pipeline necessary for the study of the human brain development, and influences all the subsequent steps. The method presented in this paper allows the formation of an estimate of diffusion properties across the fetal brain, without priors about diffusion properties of the tissue that could bias the tractography results, and the clinical conclusions extracted from them.

6 Conclusions

In this paper, we have presented a method for reconstructing fetal dMRI sequences from scattered data. A groupwise registration method based on slice-by-slice affine transformations was applied to compensate motion and eddy-current distortions, and a dual spatio-angular interpolation based on RBFs was used to estimate signal values on regular sampling grids. The advantage over previously proposed methods (Jiang et al., 2009) is the independence of the diffusion model, which allows its use for studying diffusion patterns even in IVOH. Experiments with adult data showed subvoxel accuracy for the slice-to-volume registration, and high accuracy for recovering non-acquired DW images from available measurements. In fetuses, the method improved the quality of the sequences as evidenced by the lower values of ${\overline{FA}}_{\mathit{cfs}}$, H_fa, and σ_csf with respect to the original sequences. The tractography provided different results for the original and reconstructed sequences, but they must be quantified and compared with objective criteria in order to assess their clinical significance. This is the current line of research.

A Registration method

The algorithm 1 provides the pseudocode corresponding to the registration method presented in section 2.2.

Algorithm 1.

Distortion correction method. S₀: T₂-weighted image; S_i: Diffusion-weighted image with gradient i; $A_i^z$: affine slice by slice transformation between S_i and S̄^(k). The circle symbol (○) represents a function composition. The function resample (S_i, $A_{ri}^z$) performs a RBF interpolation of $A_{ri}^z(S_i)$ since data are scattered and standard interpolation algorithms cannot be applied.