Mapping the Spread of Methamphetamine Abuse in California From 1995 to 2008

Abstract

Objectives. From 1983 to 2008, the incidence of methamphetamine abuse and dependence (MA) presenting at hospitals in California increased 13-fold. We assessed whether this growth could be characterized as a drug epidemic.

Methods. We geocoded MA discharges to residential zip codes from 1995 through 2008. We related discharges to population and environmental characteristics using Bayesian Poisson conditional autoregressive models, correcting for small area effects and spatial misalignment and enabling an assessment of contagion between areas.

Results. MA incidence increased exponentially in 3 phases interrupted by implementation of laws limiting access to methamphetamine precursors. MA growth from 1999 through 2008 was 17% per year. MA was greatest in areas with larger White or Hispanic low-income populations, small household sizes, and good connections to highway systems. Spatial misalignment was a source of bias in estimated effects. Spatial autocorrelation was substantial, accounting for approximately 80% of error variance in the model.

Conclusions. From 1995 through 2008, MA exhibited signs of growth and spatial spread characteristic of drug epidemics, spreading most rapidly through low-income White and Hispanic populations living outside dense urban areas.

Methamphetamine abuse and dependence (MA) arises as one consequence of successive courses of heavy use and chronic relapse that characterize addiction to this drug. Although methamphetamine appears to be no more addictive than other drugs such as cocaine and heroin, MA has been related to a broad range of risks and associated outcomes, including assault, suicide and homicide, hyperthermia, cardiovascular problems, dental problems, burns, sexually transmitted diseases, affective psychoses, schizophrenic disorders, and depression.¹ Rates of MA have increased substantially in Western and Midwestern states of the United States, Mexico, Oceania, and countries in West and Central Europe over the past 30 years.² Within the United States, rates of MA are spatially heterogeneous, varying substantially from one geographic region to another and reflecting local demand and historical trends in production and distribution through national and international drug cartels.³ Increases in MA rates in Pacific and Southwestern states in the 1980s were followed by dramatic increases in Midwestern and Southern states in the 1990s and early 2000s.

Within California, a state that has been the focus of considerable research on MA, restrictions on sales of chemical precursors used to make methamphetamine transiently reduced arrests⁴ and hospitalizations related to MA.⁵ However, each restriction was followed by adaptation of drug production and distribution systems and resumed growth.⁶ Methamphetamine is unique in that sales of specific chemical precursors required for production, particularly ephedrine and pseudoephedrine, can be controlled through legislation and enforcement. Major federal laws restricting precursor chemicals took effect in August 1989 (Chemical Diversion and Trafficking Act, restricting bulk sales of ephedrine in powder form), August 1995 (Domestic Chemical Diversion Control Act, restricting sales of some ephedrine products), October 1996 and 1997 (Comprehensive Methamphetamine Control Act, further restricting sales of ephedrine products immediately and pseudoephedrine products 1 year later), and April 2006 (Combat Methamphetamine Epidemic Act, adding restrictions on over-the-counter sales of related pseudoephedrine and ephedrine products).⁷

The evident rapid growth and continued spread of MA and related problems have led some researchers to identify methamphetamine use and abuse as the latest “drug epidemic” in the United States, a label that refers to either the magnitude or perceived significance of MA as a social problem, not to the analysis of MA as a contagious epidemic per se.⁸ Analyzed as a contagious disease epidemic, susceptible populations would begin to use methamphetamine through exposure to other users or other vectors of transmission (e.g., an active drug market). Early growth of the epidemic would be exponential in form, focused in particular at-risk subpopulations, and would exhibit signs of contagious spread.⁹

Although overall growth in incidence rates of a contagious disease can be assessed with highly aggregated population data, detailed assessments of growth associated with population subgroups and spatial patterns of contagious spread require consistently collected and geographically well-resolved space-time data. Spatial units must be small relative to the velocity of disease spread and periods of observation must be small relative to change in incidence rates. US drug abuse monitoring systems are designed to provide consistent estimates of incidence and prevalence rates, but these data are either unresolved at state and local levels (e.g., National Survey of Drug Use and Health¹⁰) or resolved to a handful of communities across the nation (e.g., the Drug Abuse Warning Network¹¹). On the other hand, publically available hospital discharge data from states in the United States may provide a consistently collected, relatively well-resolved source of diagnostic information that can be used to assess the incidence and prevalence of MA. These data are collected and available at the zip code level in California and provide an indication of spatially heterogeneous growth in MA across the state over time.

METHODS

We characterized the general historical pattern of MA growth from 1983 to 2008 through descriptive analyses of aggregate data for the state. In addition, we undertook an analysis of MA discharges for all zip codes across the state from 1995 through 2008. The spatial resolution of zip codes is better than that of cities or counties, but it comes at the cost of working with units that differ greatly in size (e.g., 1 zip code is larger than the state of Rhode Island) and change shape over time.¹² Postal codes for US addresses are frequently redefined to improve the efficiency of local mail delivery. As a result, 18% of California zip codes were misaligned in the 1995 through 2008 period (i.e., their number, size, and boundaries changed from year to year). We used a hierarchical Bayesian Poisson space-time analysis to relate MA discharges to population and environmental characteristics; the analysis provided an assessment of spatial correlation caused by contagion as a Gaussian conditional autoregressive (CAR) process.^13,14 We used a statistical approach that enabled estimation of year-specific CAR effects with differently dimensioned adjacency matrices and incorporated measures of the impacts of misalignment based on population demographics.¹⁵ These measures indexed change in population characteristics attributable to redefinition of zip code areas.

Outcome Measure

We obtained annual zip code–level counts of hospital discharges related to MA for the years 1995 through 2008 from patient-level records provided by the California Office of Statewide Health Planning and Development. These records identify all hospitalizations that result in at least 1 overnight stay, and include up to 24 diagnostic codes from the International Classification of Diseases, Ninth Revision, Clinical Modification (ICD-9-CM).¹⁶ We selected discharges that included either a primary or secondary diagnosis of amphetamine dependence (code 304.4) or amphetamine abuse (code 305.7).¹⁶ These diagnostic classifications include other psychostimulants but are dominated by MA. Among nationwide drug treatment episodes listing stimulants as the primary drug of abuse, methamphetamine’s share grew from 75% in 1995 to 94% in 2008, whereas the absolute number of treatment episodes for nonmethamphetamine stimulants declined slightly during this time.¹⁷ However, MA was the primary diagnosis for only a minority of hospital discharges in California (e.g., 1.8% in 2005). Secondary diagnoses were most commonly associated with psychoses, schizophrenia or depressive disorders (38.4%), cellulitis and abscesses commonly associated with MA (3.3%), other drug dependence (3.2%), and congestive heart failure (2.7%). A total of 83.9% (SD = 8.71%) of hospitalizations represented cases that had not been admitted earlier in each year, providing a good connection between annual incidence and prevalence estimates. Excluding hospitalizations among the homeless without zip codes (less than 4.8% in any year) and zip codes masked to 3 digits (< 2.9%), 97.8% of records with 5-digit zip codes were geocoded to patients’ residential zip codes in each year.

Fixed-Effect Explanatory Variables

With the restriction that measures must be available at the zip code level over time, we selected population-level fixed effects variables to represent well-understood correlates of MA from previous cross-sectional studies.² The set provided here constitutes all those available for the state at the time of this study. We obtained annual intercensus estimates of zip code demographics from Sourcebook America.^18,19 These included population proportions of Whites and Hispanics (we examined proportions of Blacks and Asians in preliminary analyses, but they were unrelated to MA), population density (quintiles calculated per unit area and coded to reduce the influence of outliers that arose in estimates for small population sizes), median household income (thousands of 2007 inflation-adjusted dollars), and average household size. Environmental and population measures included a zip code indicator of connectedness to high-speed roadway systems (presence of class 1 or 2 highways) and county-level measures of unemployment²⁰ as well as arrests for drug manufacturing and “dangerous drug” sales or distribution (arrest categories strongly dominated by methamphetamine).²¹ We included rates of total hospitalization in each zip code as a covariate to account for differences in access to hospital care. Year-specific intercepts represented temporal changes in statewide MA hospitalizations. We also included covariates representing the proportion of misaligned population and its interaction with selected demographic characteristics.

Hierarchical Bayesian Space-Time Model

We used a hierarchical Bayesian approach to analyzing these space-time data that enabled us to (1) address small-area effects (e.g., extreme outliers estimated among small populations in sparsely settled zip codes), (2) estimate the extent of spatial autocorrelation in MA ostensibly related to spatial contagion (similarity of rates between adjacent geographic units), (3) include data from nested geographic units (zip codes within counties), and (4) provide posterior estimates of changing distributions of MA over space and time (model-based predicted values from the Bayesian analysis). Hierarchical Bayesian models provide great flexibility in estimating correlated effects between adjacent spatial units—that is, the tendency of adjacent spatial areas to exhibit similar rates of abuse over time, reflected in the estimate of spatial autocorrelation. For this purpose, we assumed that a CAR process related rates of MA between adjacent places and represented connections between places by a binary connection matrix labeling adjacent zip codes in each year (our measure of spatial contagion). Thus, the CAR process assumes that the priors for the distribution of autoregressive effects are Gaussian and that adjacent units are not statistically independent (the Bayesian model thus providing a statistical correction for these correlated effects).²² In addition to the CAR random effect, we included an additional random effect to model residual overdispersion in rates that was not spatially autocorrelated.²³ Finally, since we used both zip code–level and county-level data in these analyses, we included county-level random effects. We considered zip codes to be nested within counties on the basis of centroid membership. More than 80% of zip codes in any year were wholly contained within county areas. More than 98% of zip codes had 95% or more of their populations wholly included within county boundaries.

Spatial Misalignment Model

Standard Bayesian hierarchical models assume that geographic units are defined consistently across time. This is not the case for zip codes. The statewide count of California zip codes increased from 1605 in 1995 to 1693 in 2008, and approximately 4% of zip codes in each year had boundary changes affecting at least 1% of their population (as estimated with year 2000 census block–level data). We used a “spatial misalignment” variant of the standard Bayesian hierarchical model that allows the use of zip code data for longitudinal analysis despite frequent changes in these geographic units.¹⁵ This misalignment approach introduces separate CAR random effects for each time period, each with prior mean zero and a common standard deviation. The model also allows for a separate random effect that is not spatially autocorrelated and accounts for overdispersion.²⁴

Model Specification and Estimation

Given that the outcome measure was the count of hospitalizations in a given zip code in each year, we used a Poisson regression model:

where Y_i,t represents the count of amphetamine-related hospital discharges in zip code i during year t and E_i,t denotes the expected number of the hospitalizations under the assumption that statewide discharges were distributed across zip codes in direct proportion to population. Hence, exp(μ_i,t) may be interpreted as the relative rate of hospitalization among those residing in spatial unit i in year t: regions with exp(μ_i,t) > 1 will have greater counts than expected on the basis of their population, and regions with exp(μ_i,t) < 1 will have fewer than expected. Following standard generalized linear models, the log-relative rate, μ_i,t, was modeled linearly as

This is a linear combination of fixed covariate effects and random effects that may take account of spatial or temporal correlation. Vector α_i is a set of year-specific intercepts that control for statewide changes in amphetamine hospitalization that are not explained by other covariates. X′_i,t is a matrix containing space- and time-specific covariates and β is a vector of fixed-effects estimates of the impacts of those covariates. θ_i,t and φ_i,t denote the pair of random effects capturing spatially unstructured heterogeneity and CAR spatial dependence, respectively. Finally, γ_c is a county-specific random effect that accounts for hierarchical effects related to the fact that the unemployment and arrest covariates were available only for counties rather than at the zip code level. We estimated the model using WinBUGS 1.4.3 software.²⁵ Uninformative or weakly informative priors were specified on all fixed and random effects. We allowed the model to burn in for 80 000 Markov Chain Monte Carlo (MCMC) iterations, by which point all model estimates had converged between 2 chains with different initial values. We then sampled posterior estimates over an additional 40 000 MCMC iterations to provide model results.

RESULTS

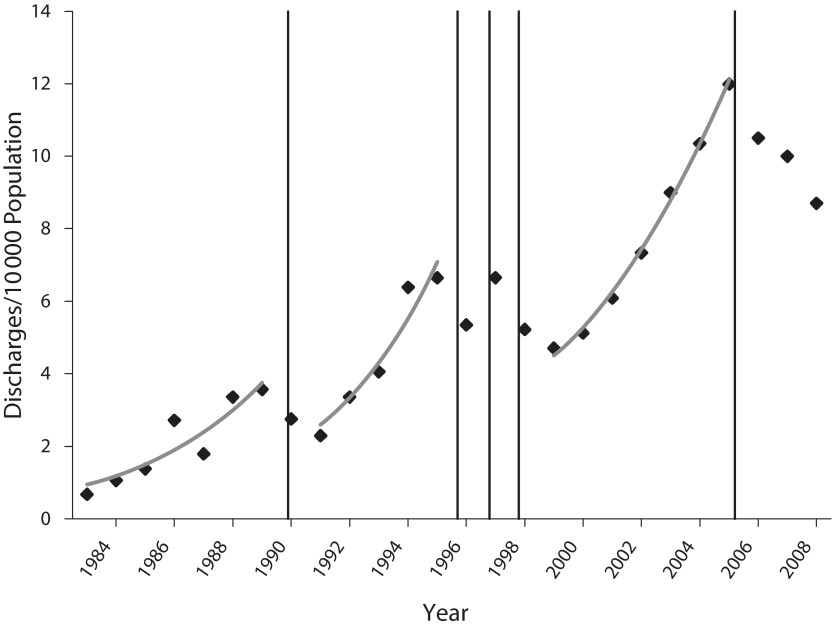
Figure 1 presents a plot of the growth of MA from 1983 through 2008. The vertical lines indicate years in which each precursor law went into effect. Although some subjective judgment as to the duration of impacts of each law is required, a scalloped pattern of interrupted exponential growth appeared over 3 intervals during this time. Growth was 26% per year from 1983 through 1989, 29% per year from 1991 through 1995, and 18% per year from 1999 through 2005. During this time, methamphetamine production for California markets shifted away from illegal domestic laboratories to importation through Mexican cartels. Reductions in supply restrained but did not stop growth.⁵ Figure 2 displays a spatially smoothed map of rates of MA per 10 000 persons over zip codes for the years 1995, 2005 (the most recent peak), and 2008. The 1995 map reflects the largely rural distribution of MA during early phases of growth, with a characteristic “bloom” along the central coast noted at that time. The rural character of MA continues through the peak in 2005, with very high rates in northern and southern areas of the state and greater use in urban areas. Note, however, that the bloom along the central coast has declined. The most recent wave retreats by 2008 and leaves behind somewhat greater rates in different geographic areas, with the coastal bloom increased once again.

FIGURE 1—

Methamphetamine abuse and dependence (MA) discharges in California, per 10 000 persons in 1983 through 2008.

Note. Fitted exponentials for 3 successive growth phases are as follows: MA = 0.749e0.230t, MA = 2.014e0.252t, MA = 3.824e0.165t; entire period: MA = 1.889e0.069t.

FIGURE 2—

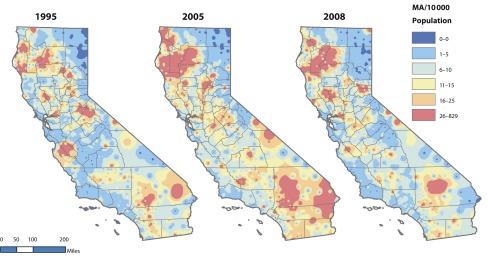
Methamphetamine abuse and dependence (MA) discharges in California by geographic distribution for selected years.

Note. Geographic distribution years chosen as first year of available zip code data (1995), recent peak of epidemic (2005), and most recent year (2008). Edge corrected inverse distance weights using zip code centroids and a variable search radius of 25 points.

Most of these general features of MA are reflected in the results of the more detailed and highly resolved Bayesian Poisson space-time analysis for the period 1995 through 2008 provided in Table 1. The top portion of the table presents fixed effects for demographic, environmental, county, and control covariates, showing the mean effect estimate (log relative rate), its standard deviation, the Monte Carlo error in estimate (an assessment of the computational accuracy of the mean; a Monte Carlo error less than 1/20th the standard deviation is the usual criterion), the 95% credible interval around the median, and transformed relative rate at the median. The middle portion of the table presents the same information for misalignment measures. Those effects for which the credible interval did not include zero are marked by asterisks. Finally, the bottom portion of the table presents variance components for the model, the standard deviations of random effects related to nesting of zip codes within counties, spatial autoregression (represented by the CAR process), and residual error. Alpha (α) is an index of the contribution of spatial autoregression relative to all variance components in the model; it may vary from zero to 1, and the estimated value of 0.8830 indicates that some 88% of residual error is related to the CAR process.

TABLE 1—

Bayesian Poisson Space-Time Regression of Incidence of Methamphetamine Abuse and Dependence: California, 1995–2008

Parameter	Mean (SD)	MC Error	Median (95% Credible Interval)	Relative Rate
Demographic characteristics
Average household size	−0.3686 (0.0178)	0.0009	−0.3661 (−0.4067, −0.3382)a	0.6917
Household income × 1000	−0.0144 (0.0004)	0.0000	−0.0144 (−0.0151, −0.0136)a	0.9857
Proportion White	0.3129 (0.0433)	0.0021	0.3118 (0.2340, 0.3983)a	1.3674
Proportion Hispanic	0.8751 (0.0485)	0.0023	0.8750 (0.7839, 0.9725)a	2.3991
Population density quintile 2	0.0474 (0.0243)	0.0010	0.0475 (0.0007, 0.0958)a	1.0486
Population density quintile 3	0.0966 (0.0265)	0.0012	0.0960 (0.0468, 0.1513)a	1.1015
Population density quintile 4	0.0870 (0.0286)	0.0013	0.0860 (0.0326, 0.1460)a	1.0909
Population density quintile 5	0.0531 (0.0315)	0.0015	0.0525 (−0.0089, 0.1194)	1.0545
Environmental characteristic: highway class 1 or 2	0.0479 (0.0117)	0.0005	0.0477 (0.0256, 0.0719)a	1.0490
County-level covariates
Dangerous drug arrests/100	0.4113 (0.1986)	0.0098	0.4180 (0.0139, 0.7863)a	1.5088
Meth manufacture arrests/100	−0.9595 (1.1170)	0.0526	−0.9479 (−3.2150, 1.2140)	0.3831
% unemployed	−0.0200 (0.0076)	0.0004	−0.0195 (−0.0391, −0.0079)a	0.9802
Control covariate: total hospital discharges	−0.0010 (0.0003)	0.0000	−0.0010 (−0.0016, −0.0003)a	0.9990
Misalignment and interactions
% population misaligned	−0.0633 (0.0209)	0.0010	−0.0618 (−0.1050, −0.0281)a	0.9387
Average household size	0.0020 (0.0049)	0.0002	0.0022 (−0.0080, 0.0110)	1.0020
Household income × 1000	0.0002 (0.0001)	0.0000	0.0002 (0.0001, 0.0003)a	1.0002
Proportion White	0.0518 (0.0165)	0.0008	0.0514 (0.0211, 0.0842)a	1.0532
Proportion Hispanic	0.0219 (0.0165)	0.0007	0.0219 (−0.0103, 0.0538)	1.0221
Random effects
County	0.4159 (0.0216)	0.0007	0.4154 (0.3752, 0.4597)
Spatial	0.6130 (0.0132)	0.0006	0.6128 (0.5889, 0.6402)
Noise	0.2234 (0.0105)	0.0005	0.2235 (0.2032, 0.2441)
α = spatial/(spatial + noise)	0.8824 (0.0117)	0.0005	0.8830 (0.8579, 0.9034)a

Note. MC error = Monte Carlo error. Credible intervals are expressed as log relative rates. Relative rates estimated for the median are shown in the last column to the right. The model included zip code–level and county-level covariates with separate random effects, with the conditional autoregressive process specified at the zip code level. α represents an approximation of the proportion. error attributable to spatial dependence (see Methods). Year-specific fixed-effect intercepts are not shown.

^aCredible interval has < 5% chance of including zero.

We observed well-supported effects relating populations with smaller households, lower incomes, greater proportions of White and Hispanic populations, and proximity to highway systems to greater rates of MA. Greater rates of MA were also seen in areas with medium population densities (neither extremely rural nor urban), although credible intervals for these effects substantially overlapped. Among county-level covariates, greater dangerous drug arrests and less unemployment were related to greater rates of MA. Effects related to misalignment indicated that larger misaligned populations were related to lower estimates of MA, a general downward bias that affected estimates in those zip code areas that were redefined to include different population groups. However, larger misaligned proportions of high-income White populations were related to higher estimates of MA (Table 1), an upward bias that affected estimates in those zip code areas that were redefined to include larger numbers of this subpopulation. Importantly, the range of relative rates affected by the impact of misalignment (specific to units and years) was .093 to 16.68, a factor of 179.

The ratios of proportional change in MA rates to proportional change in the exogenous measures give a sense of the effect sizes observed in the study (arc elasticities estimated at the mean for all other measures). These fall into 3 natural groups. Effects related to income and household size indicated roughly proportional change with regard to MA (0.8 and 1.0, respectively). Each 1% increase in income was associated with 0.8% fewer MA incidents, and each 1% increase in household size was associated with 1.0% fewer MA incidents. Effects related to proportions of Whites and Hispanics were less elastic (0.2 in each case), and effects related to unemployment (0.08), highway access (0.03), and all population density quintiles (about 0.02) were inelastic. These effects, however, must be viewed against the background of very substantial differences in the ranges of these measures across geographic areas.

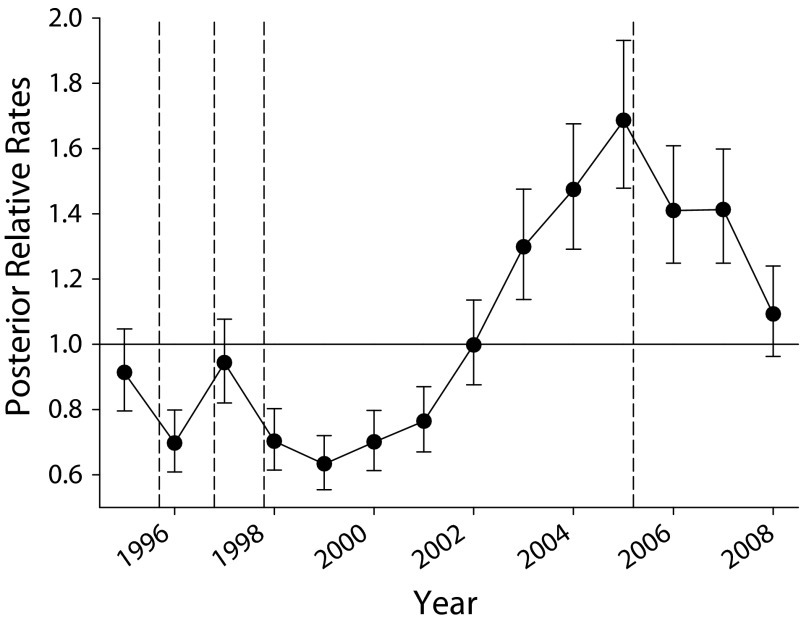
When we controlled for effects related to all covariates in the model, overall MA growth averaged 17% per year from 1999 through 2008 (Figure 3). There was little growth in the middle to late 1990s, a period that coincided with the introduction of a series of precursor laws. This was followed by a period of rapid growth of 25% per year from 2001 through 2005, which came to an end in 2006 following the enactment of the Combat Methamphetamine Epidemic Act in 2005. When we examined posteriors related to these effects (Figure 4a), it was evident that some growth in MA took place in urban cores, but it was also substantial in suburban and rural areas outside these settings. By 2008, substantial reductions appeared in many areas, with high levels remaining in rural and exurban areas to the northeast of San Francisco Bay and dense suburban areas in the south San Francisco Bay Area to the north of San Jose. Relative growth from 1995 to 2008 is shown in Figure 4b, with most substantial increases seen in suburban areas on the San Francisco peninsula and in the northern, largely suburban, areas of San Jose.

FIGURE 3—

Posterior estimated growth of relative incidence rates of methamphetamine abuse and dependence.

Note. Relative rates across zip codes are scaled to state average and bracketed by 2.5%–97.5% credible intervals.

FIGURE 4—

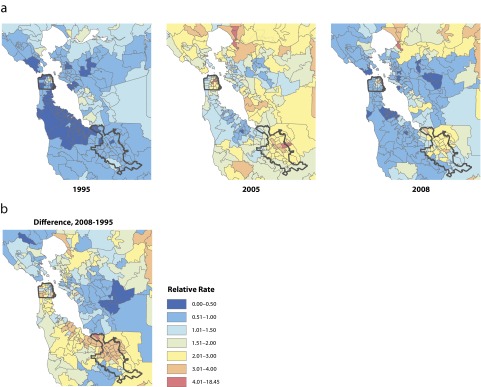
Posterior estimated growth of relative incidence rates of methamphetamine abuse and dependence, (a) geographic distribution for selected years and (b) geographic distribution of overall change: San Francisco Bay Area, 1995–2008.

Note. Bay area maps show pattern of positive spatial autocorrelation.

The patterns of growth indicated in these figures suggest spatial contagion. This observation is supported by the substantial value obtained for α indicated in Table 1. A further examination of posteriors for the CAR effects in the model across years shows spatial autocorrelation, estimated by Moran’s I to be positive and very substantial (Moran’s I = 0.7359; 95% credible interval = 0.7039, 0.7679). Moran’s I can conveniently be interpreted as a Pearson correlation coefficient, suggesting that about 54% of the residual variance in rates of MA in zip code areas was correlated with those in surrounding adjacent areas. Overlaid on these effects were different patterns of growth associated with demographic characteristics. A sampling of these showed strong effects associated with income (greater MA in poor suburban and rural areas; Figure 5), modest effects associated with population density (greater MA in suburban and exurban areas; Figure 5), and substantial effects associated with household size (greater MA in areas with many single households like San Francisco; Figure 5) and racial/ethnic composition (greater MA in areas with large Hispanic or White populations; Figure 5). In combination, these effects reflect those that characterize human populations at high risk for MA: predominant White and Hispanic low-income populations living in suburban and exurban areas. The major exception is MA in central San Francisco, a locale where MA has been prevalent since the 1970s.

FIGURE 5—

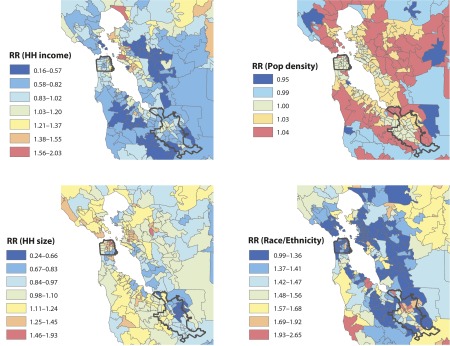
Posterior relative incidence rates of methamphetamine abuse and dependence for 4 model covariates, household income, population density, household size, and race/ethnicity: San Francisco Bay Area, 2008.

Note. HH = household; Pop = population; RR = relative rate. HH income range = $6640 (RR = 2.03) to $181 180 (RR = 0.16); population density quintiles = 0–7.72 (RR = 1.04) to 2356–20 120 (RR = 0.95) persons/km²; HH size = 1.00 (RR = 0.24) to 6.74 (RR = 1.93) persons/HH; racial/ethnic group composition = no Whites or Hispanics (RR = 0.99) to 41.8% White and 97.6% Hispanic (RR = 2.65).

DISCUSSION

This statistical model of the growth of MA in California demonstrates that well-resolved space-time data can be used to assess population and environmental features associated with abuse spread, to examine growth when effects related to these characteristics are statistically controlled, and to assess spatial correlated growth over time. To accomplish this, we also addressed some of the problems associated with space-time misalignment among zip code units and their effects on the estimation of MA in the state. We found that MA growth was greatest in suburban and exurban areas with larger White and Hispanic low-income populations, small household sizes, access to highway systems, active drug markets, and less unemployment at the county level. Historical change in MA across the state appears to follow a pattern of interrupted exponential growth, suggesting adaptation of the methamphetamine market to each precursor law. After 2008, growth in MA increased once again in California, rising from 8.3 to 9.7 incidents per 10 000 persons in 2009, then to 11.2 incidents per 10 000 persons in 2010. Conservatively assuming a growth rate of about 12% per year (the average from 1983 through 2008), we expect that incidents increased to 12.5 cases per 10 000 persons in 2011. (An observed value of 12.1 cases per 10 000 persons appeared during preparation of this article.) As indicated in Figures 2 and 5, heterogeneity in relative rates for MA related to these measures across areas of the state was very substantial.

From these observations, we believe it is reasonable to suggest that growth of MA may be usefully treated as one outcome of a socially contagious epidemic of use, as if an opportunistic infection (an active drug market) was spreading through populations at risk for abuse (e.g., low-income suburban and exurban groups) and increasing risks for related sequelae (e.g., comorbid health and psychiatric disorders).²⁶ This is a popular view among disease modelers, but not one well supported by statistical epidemiology.⁹ The current study does provide additional statistical support for this argument by demonstrating substantial spatial autocorrelation in MA growth over time, growth that is presumably associated with market spread (e.g., along highway systems). But the current approach only considers spatial effects within years, leaving dynamic modeling of cross-lagged space-time effects to future work. Spatial statistical models in epidemiology and biological geography now provide the ability to assess velocities of the spread of biological infections, identify boundaries to spread, and provide statistical support for mathematical infectious disease models.^27,28 These methods may be applicable to the long-term prevention of the spread of MA using a mixture of prevention, enforcement, and treatment resources.²⁹

Illicit drug markets can be usefully studied and modeled within an economic framework, providing valuable insights into the impacts of supply reductions and enforcement efforts on drug demand and use.^30,31 However, these models are not well suited to estimating the rate and direction of disease spread (equating MA to a disease process), population characteristics associated with spread, or spatial limits to the spread of MA. For these purposes, spatial epidemiological models of disease spread and spatial ecological models for boundary analysis provide useful tools. Although the representation of MA as a “disease” may be construed as a metaphor for otherwise unobserved spatial economic processes, the scientific question is whether it is a practically useful metaphor for analyses of the spread of drug-using behaviors. Illicit drug markets are, indeed, economic markets with their own unique dynamics,³² but they also represent unique social processes by which related problem behaviors spread through human populations. We expect that these complementary approaches have much to provide the field.

Ultimately, the goal of this work is to suggest efficient environmental controls that can constrain the rapid growth of MA in the future.³³ Treatment, prevention, and enforcement efforts are often brought to bear on drug markets long after they have formed and the chronic relapsing disease processes that characterize addiction are well under way. Delays in identifying expanding drug epidemics limit the ability of treatment, prevention, and enforcement efforts to reduce or eliminate abuse and may be a prime determinant of the failure of these programs.³⁴ Mated to formal population models of a disease process, statistical disease models can identify characteristics and locations of at-risk populations, provide opportunities to inoculate at-risk groups, assess critical population sizes required for the development of a drug market, enable focused enforcement efforts, and provide for the fair allocation of treatment resources for populations most exposed to MA.