Abstract
Studies of incidental category learning support the hypothesis of an implicit prototype-extraction system which is distinct from explicit memory (Smith, 2008). In those studies, patients with explicit-memory impairments due to damage to the medial-temporal lobe performed normally in implicit categorization tasks (Bozoki, Grossman, & Smith, 2006; Knowlton & Squire, 1993). However, alternative interpretations are that: i) even people with impairments to a single memory system have sufficient resources to succeed on the particular categorization tasks that have been tested (Nosofsky & Zaki, 1998; Zaki & Nosofsky, 2001); and ii) working memory can be used at time of test to learn the categories (Palmeri & Flanery, 1999). In the present experiments, patients with amnestic mild cognitive impairment or early Alzheimer’s disease were tested in prototype-extraction tasks to examine these possibilities. In a categorization task involving discrete-feature stimuli, the majority of subjects relied on memories for exceedingly few features, even when the task structure strongly encouraged reliance on broad-based prototypes. In a dot-pattern categorization task, even the memory-impaired patients were able to use working memory at time of test to extract the category structure (at least for the stimulus set used in past work). We argue that the results weaken the past case made in favor of a separate system of implicit-prototype extraction.
Keywords: categorization, implicit learning, explicit memory, amnesia
An interesting debate in cognitive neuroscience concerns the issue of whether an implicit memory system, which is distinct from the explicit memory system that governs tasks such as old-new recognition and recall, is responsible for certain forms of category learning (Ashby & O’Brien, 2005; Newell, Dunn, & Kalish, 2011; Poldrack & Foerde, 2008; E.E. Smith, 2008; Smith, Patalano, & Jonides, 1998). Following E.E. Smith (2008), in the present article we focus on a particular type of implicit category learning termed the prototype-extraction task, in which participants induce a category structure via incidental exposure to statistical distortions of a single category prototype.
As reviewed in more detail below, there are various intriguing demonstrations of implicit category learning in prototype-extraction tasks (e.g., Bozoki, Grossman, & Smith, 2006; Knowlton & Squire, 1993; Keri, 2003; Kolodny, 1994; Reed, Squire, Patalano, et al., 1999; Squire & Knowlton, 1995). In general, in these demonstrations, patients are tested who have damage to the hippocampus and medial temporal lobe. Such patients show severe deficits in a variety of explicit memory tasks (e.g., Squire, Clark, & Bayley, 2004). However, the same patients perform as well as matched controls in tasks of implicit prototype extraction. Such behavioral dissociations are directly predicted by the view that a separate implicit system governs category learning and that this implicit system is intact in these patient groups. [Based on brain-imaging work, some researchers have suggested in particular that implicit learning in single-category prototype-extraction tasks recruits neural mechanisms from posterior occipital cortex and/or striatum (e.g., Reber, Gitelman, Parrish, & Mesulam, 2003; Reber, Stark & Squire, 1998a,b; Zeithamova, Maddox, & Schnyer, 2008). We consider some of this brain-imaging work in our General Discussion.]
Nevertheless, other researchers have questioned the interpretation of the behavioral dissociations and suggested that they are consistent with models that do not distinguish between explicit and implicit memory systems (e.g., Love & Gureckis, 2007; Newell et al., 2011; Nosofsky & Zaki, 1998; Palmeri & Flanery, 2002; Shanks & St. John, 1994; Zaki, 2004). There are two main concerns that have been advanced. First, it may simply be that whereas normal performance in, say, a recognition task requires a high-functioning long-term memory system, normal performance in a categorization task can be achieved with that same system even if it is impaired. Intuitively, for example, an impaired observer may still have sufficiently good memories for her past experiences of “trees” to make the kinds of gross-level similarity judgments required to classify a test object as a “tree”. By contrast, it would require an extremely good memory for that same observer to determine whether that specific tree is an exact match to some single previously experienced one.
Second, in some of the categorization tasks from the cognitive-neuroscience literature, it appears that working memory can be used, at least to some degree, as a basis for learning the categories at time of test, without any involvement of long-term memory (Bozoki et al., 2006; Palmeri & Flanery, 1999, 2002; Zaki & Nosofsky, 2001, 2007). For example, suppose that one is presented with a list of objects and is told that the goal is to discover a category of objects that is embedded in the list. Suppose further that half the objects in the list are trees and the remaining half are random objects. It seems clear in this example that an observer could use his or her working memory for recently presented, repeated trees on the test list to infer that embedded category. Thus, good categorization performance could be achieved without long-term memories for any study items. This possibility is a reasonable one, because patients with impaired long-term explicit memory often have normal working memory.
In a recent critical review of the literature, E.E. Smith (2008) considered carefully the evidence for these alternative possibilities and made a good case that a separate implicit system does govern performance in prototype-extraction tasks. At the same time, his review pointed to important unresolved questions in need of further research. The present work was motivated by Smith’s (2008) review, with the goal of further investigating some of these open questions. We start by briefly reviewing some of the specific forms of evidence that Smith (2008) considered and that we pursued further in the present research.
Implicit Learning in the Dot-Pattern Prototype-Extraction Task
Knowlton and Squire (1993) presented both amnesic patients and normal controls with a set of 40 statistical distortions of a dot-pattern prototype. The subjects studied the patterns under incidental training conditions. Following study, the subjects were informed of the existence of the category and were presented with a set of test patterns. Some patterns were new members of the category (new patterns at varying levels of distortion from the prototype), whereas others were randomly generated non-members. Interestingly, the patients performed as accurately as did the controls on the categorization task, despite performing much worse on a test of recognition memory that involved the same kinds of dot patterns. This dramatic dissociation in performance led Knowlton and Squire (1993) to posit that category learning was mediated by an implicit system, separate from the explicit system that governs old-new recognition memory.
Nosofsky and Zaki (1998) proposed an alternative single-memory-system account of these results. According to their account, both the amnesics and controls stored the study patterns as individual exemplars in memory. However, because their memory system was impaired, the amnesics had less ability to discriminate among the distinct exemplar traces. Nosofsky and Zaki (1998) fitted a well-known exemplar model [Nosofsky’s (1986, 1988) generalized context model] to Knowlton and Squire’s (1993) categorization and recognition data. The model assumes that both categorization and recognition decisions are based on similarity comparisons of the test items to the stored exemplars. The amnesics’ reduced ability to discriminate among exemplars was represented in terms of a lower setting of an overall sensitivity parameter in the model. In a nutshell, this single-memory-system model provided a good quantitative account of the full set of categorization and recognition data reported by Knowlton and Squire (1993). Furthermore, the dissociation between categorization and recognition across the amnesic and normal groups was easily predicted by the model. The intuition is that whereas a reduced level of sensitivity is particularly detrimental to making judgments about whether a test item is an exact match to some single exemplar, it is sufficient to support near-normal categorization judgments, which require only gross-level assessments of similarity to be made.
The exemplar model failed to account adequately, however, for results from another study conducted by Squire and Knowlton (1995). Using the same dot-pattern prototype-extraction task, they demonstrated that a severe amnesic (E.P.) could also learn the dot-pattern categories, despite having zero ability to make old-new discriminations in the recognition task. Because the Nosofsky-Zaki (1998) model requires that there be at least some ability to discriminate between distinct memory traces in order to predict above-chance categorization, those results posed a considerable challenge to the model.
This challenge was addressed in a study conducted by Palmeri and Flanery (1999). Remarkably, these researchers demonstrated that normal subjects could learn the Knowlton-Squire categories at time of test, without any exposure to the initial study patterns. That is, as described earlier in our introduction (see our “trees” vs. “random objects” example), given the number of highly similar category members included in the test, Palmeri and Flanery’s subjects were apparently able to induce the category structure embedded in that list. (A complete exemplar-model account of performance in the task would most likely involve an integration of weak memories for the study instances and more recent memories for the test items – for a formal example, see Zaki & Nosofsky, 2007.) This issue of the extent to which subjects can accomplish category-learning at time of test is one of the central questions that we will pursue further in the present research.
Implicit Category Learning Using Objects Composed of Discrete Features
A second major demonstration of implicit category learning in prototype-extraction tasks comes from a paradigm introduced by Reed, Squire, Patalano, Smith, and Jonides (1999) and pursued by Bozoki, Grossman, and Smith (2006). In this task, a different class of stimulus materials is used than in the dot-pattern tasks. Whereas the dot patterns are composed of fuzzy, difficult-to-describe dimensions, the stimuli in the Reed et al. task are cartoon animals composed of a set of highly separable, binary-valued discrete dimensions (or features). For example, the cartoon animals varied along dimensions such as long or short neck, striped or dotted body marking, round or pointed ears, and so forth. A category of such animals was defined around a single prototype that had a typical feature value along each of its dimensions. Various low-level distortions of the prototype were then constructed by randomly switching the value of one or two features. Subjects studied these distortions of the prototype in an incidental training task. Then, subjects were presented with new members of the category at varying levels of distortion from the prototype, as well as with patterns that were very dissimilar to the prototype (i.e., the majority of feature values had been switched).
Analogous to the results reported by Knowlton and Squire (1993), Reed et al. (1999) and Bozoki et al. (2006) found that patients with impaired explicit memory performed normally in the categorization task. Thus, the evidence for forms of implicit prototype extraction is quite general, as it was found for both the difficult-to-describe dot patterns used by Knowlton and Squire and for the easy-to-describe feature-based stimuli of Reed et al. and Bozoki et al.
Furthermore, Bozoki et al. (2006) and Smith (2008) noted that, although Palmeri and Flanery (1999) had demonstrated category learning at time of test, this demonstration was provided only for young, normal undergraduates. It is an open question whether or not memory-impaired patients can rely on similar forms of learning-during-test. To begin to examine this question, Bozoki et al. tested their patient groups in two conditions. One had initial exposure to the set of training items, whereas the second received no training and attempted to learn the categories at time of test. Bozoki et al. demonstrated clearly that, although some learning during test occurred, overall performance was far better for the group that had received the initial incidental training. Therefore, the results supported the hypothesis of implicit category learning from the study instances.
Motivation for the Present Study: 1. How Many Features?
The results from Bozoki et al. (2006) along with the review of those results by Smith (2008) served as the point of departure for the present study. There were two main issues that we wished to investigate. First, although Reed et al. (1999) and Bozoki et al.’s (2006) results are consistent with the hypothesis that a separate implicit system mediates prototype extraction, the interpretation of those behavioral data has been questioned in past work. The central concern is that subjects can perform extremely well on the cartoon-animal categorization test even if they remember and use just a single feature or two from the study items. For example, according to calculations from Zaki and Nosofsky (2001), subjects could achieve approximately 87% correct categorizations in the Reed et al. task if they relied solely and consistently on the presence of any single feature in the set of test animals. Thus, the concern is analogous to the one described previously for the Knowlton-Squire dot-pattern studies. The good categorization performance of the memory-impaired patients may not reflect the operation of a separate implicit memory system. Instead, even a patient with impairments to some single long-term memory system may have the capacity to remember just a couple of typical features from the study phase.
In their original study, Reed et al. (1999) had considered this possibility that subjects used just a few features to perform the task. Their preferred interpretation, however, was that their patients had instead formed a broad-based prototype for the study animals, which included memories for almost all of the typical features. For example, they concluded that “…the pattern of endorsement rates…indicates that participants had learned about the prototypical category in a broad sense by learning something about each of the nine features” (Reed et al., 1999, p. 415). Reed et al. reported several analyses to bolster their interpretation. For example, in one analysis, they found that, averaged across subjects, the most frequently endorsed feature was endorsed only 77% of the time, suggesting that subjects were not relying on the value of some single feature as a basis for making their judgments.
Nevertheless, in a replication of Reed et al.’s task that involved only normal undergraduates, Zaki and Nosofsky (2001) conducted extended formal modeling analyses of the individual-subject categorization data. Those analyses indicated that the categorization behavior of virtually all of the subjects could be explained if they had remembered and used exceedingly few features. (The formal model presumed that there was some noise in the decision process because of the use of probabilistic decision rules. For example, if some single feature had occurred in 80% of the study instances, then a subject might endorse a test pattern with that feature on 80% of the test trials.) In addition to providing excellent quantitative accounts of the categorization choice probabilities, the model provided results consistent with the feature-endorsement analyses reported previously by Reed et al. (see Zaki & Nosofsky, 2001, pp. 351-353 for details).
The primary goal of Experiment 1 in the present article was to pursue further the issues reviewed above. Do patients with impaired explicit memory rely on a separate implicit learning system to extract broad-based prototypes as a basis for categorization in the Reed et al. and Bozoki et al. tasks? Or are the previous results due to both patients and normal controls relying on just a small subset of remembered features? We will argue that, if the latter is the case, then such results do not constitute evidence in favor of a separate implicit learning system. To investigate the issue, we conducted a modified version of the Reed et al. task that involved the use of forced-choice judgments between candidate members of the categories. As will be explained in Experiment 1, the use of forced-choice judgments should strongly motivate subjects to make use of a broad-based prototype, if such a prototype had indeed been abstracted implicitly from the study instances.
Motivation for the Present Study: 2. The Role of Learning During Test
In this research we also address a second main issue, namely the extent to which learning-during-test may account for the good performance sometimes observed for patients with impaired explicit memory. As noted above, Bozoki et al. found that their memory-impaired patients who did not receive initial training in a study phase performed much worse in the categorization test than those who did receive training. This result provides good evidence that memories for the study-item materials contribute substantially to performance on that task. However, a careful reading of the literature will indicate that single-memory-system theorists have never claimed that performance in the Reed et al. and Bozoki et al. tasks is primarily mediated by learning at time of test. A claim that has been made is that performance in the Knowlton-Squire dot-pattern task may be mediated by this form of learning (Palmeri & Flanery, 1999). In our view, there is a crucial conceptual difference between the Reed et al. task and the Knowlton and Squire one. This difference forces caution in making generalizations from the results of one task to the other. In particular, in the test phase of the Knowlton and Squire task, subjects are presented with a high proportion of patterns that are very similar to the prototype and are also presented with a high proportion of random patterns with little resemblance to the category members or to each other. It is under such conditions that it seems plausible for the embedded category to be discovered through use of working memory at time of test. By contrast, an analogous test structure of high-similarity versus random patterns is not present (or is not as transparent) in the Reed et al. paradigm. Thus, in that paradigm, there is much less structure in the test-phase materials to guide category learning at time of test.
In our view, therefore, it remains important to examine the extent to which learning-during-test takes place in the Knowlton-Squire paradigm. Although Palmeri and Flanery (1999) have already reported substantial learning-during-test in that paradigm (see also Zaki & Nosofsky, 2007), their demonstrations involved only high-functioning undergraduates with no memory impairments. As noted by Smith (2008, p. 6), it remains a wide open question to what extent patients with memory impairments may also use working memory as a basis for performance in the Knowlton-Squire task. We investigate this question directly in the present research.
Structure of Article
In sum, this research addresses two separate but inter-related issues pertaining to the interpretation of results from the prototype-extraction paradigm. The first main issue is the extent to which observers abstract and make use of a broad-based prototype in the discrete-feature version of the task. The second issue is the extent to which even memory-impaired patients may rely on working memory and learning-during-test in the dot-pattern version of the paradigm. The results from both versions of the task stand as the major pieces of behavioral evidence to which Smith (2008) pointed in making the case for implicit category learning, so continued progress demands that these issues be carefully investigated.
In the to-be-reported experiments, we tested memory-impaired patient groups and matched normal controls on a battery of category-learning tasks. Because of limits in our ability to recruit large numbers of the memory-impaired patients, the battery was administered in a within-subjects fashion, with the ordering of testing the tasks always the same. For simplicity in the presentation, we report the results in the form of two separate experiments. We consider issues related to possible transfer effects across tasks in our Experiment-2 Discussion section and suggest that they are probably minor.
We decided to test several groups of subjects in the experimental battery. In their recent study, Bozoki et al. (2006) tested patients at early stages of Alzheimer’s disease (AD). A major characteristic of early AD patients is impairment of explicit, hippocampally mediated memory, similar to the deficits seen in the amnesics tested in the studies of Knowlton and Squire (1993) and Reed et al. (1999). Therefore, Bozoki et al. suggested that such patients might serve as a reasonable model system for testing hypotheses about implicit categorization in groups with impaired explicit memory. Nevertheless, past results involving implicit category learning in AD patients have been mixed (e.g., Keri, Kalman, & Keleman, 2001; Keri, Kalman, & Rapcsak, et al., 1999). Furthermore, such patients generally exhibit impairments that go beyond deficits in just long-term explicit memory, including impairments in semantic memory, working memory, attention/executive functions, and visuospatial skills (e.g., Perry & Hodges, 1999). Therefore, we decided to test patients with amnestic mild cognitive impairment (MCI) as well, where there are more focused deficits related to explicit memory (Petersen, 2004). For such patients, damage to neural mechanisms that are hypothesized to mediate implicit prototype abstraction, such as POC and striatum, is likely to be minimal or absent. Of course, we also tested a group of elderly normal controls who were matched to the AD and MCI groups on age and education level. Finally, following completion of the main study we also tested a large group of college undergraduates, mainly for purposes of validating a formal model of category judgment that we will use to help analyze the data.
Experiment 1
The purpose of Experiment 1 was to investigate the basis for the good performance of memory-impaired subjects on the discrete-feature prototype-abstraction tasks conducted by Reed et al. (1999) and Bozoki et al. (2006). Is the good performance due to their use of a broad-based implicit prototype, or are subjects relying instead on memories for just a few features? If the latter is the case, then there may be no need to posit the operation of some separate implicit-learning system. Instead, even if there is a single long-term memory system, a patient with impairment to that system may still be able to remember and use just a few salient features.
To investigate these alternatives, we designed a modified version of the Reed et al. (1999) task. The study phase was essentially the same as in Reed et al.’s paradigm. We used the same study phase because we wished to ensure that subjects learned under the same types of incidental training conditions as in previous demonstrations of implicit learning (for further discussion, see Smith, 2008). The new wrinkle in our task involved the nature of the test phase. Note that in the Reed et al. paradigm, subjects are presented on each trial with a single test item, and simply respond “Yes” or “No” as to whether the test item is a member of the category. Under such conditions, it is easy to rely on just a single feature or two to make one’s judgments. Furthermore, as we noted earlier in our article, Zaki and Nosofsky (2001), showed that extremely good performance can be achieved in the Reed et al. yes-no task by applying a single-feature or two-feature strategy. In an attempt to avoid this difficulty, in our paradigm subjects were instead presented on each trial with a pair of test items, and were asked to judge which member of the pair was a better example of the category that they had experienced during training.
The use of forced-choice paired-comparisons is a common method of assessing implicit memory and category knowledge (e.g., Voss, Baym, & Paller, 2008; Westerberg, Paller, et al., 2006). For the present paradigm, we judged that such a procedure might be highly diagnostic. The reason is that there would be numerous paired-comparison trials in which the two members of a pair would have identical feature values on various dimensions. Thus, the procedure might prevent sole reliance on just one or two remembered feature values from the study phase. For example, suppose that some observer found Dimension 1 of the cartoon animals to be highly salient and would have relied solely on that feature in a Yes-No task. In the present paired-comparison task, there would be numerous test trials in which the value on Dimension 1 is identical across the members of the pair, so its value could not be used as a basis for deciding the better example of the category. Thus, there would be strong motivation for the observer to make use of a broader-based prototype, if such a prototype had indeed been abstracted from the study instances.
If the single-memory-system hypothesis is correct, then a reasonable hypothesis is that normal control subjects will perform better than the memory-impaired subjects on the paired-comparison task. Presumably, they will have remembered more of the typical features that were trained during the study phase, and should be able to put those remembered features to use in making their paired-comparison judgments. Alternatively, if subjects rely on a separate implicit memory system to form a broad-based prototype for the category, and if this system is intact in the patient groups, then the memory-impaired patients might continue to exhibit excellent performance. Still another possibility is that, despite the strong motivation for making use of a broad-based prototype, both the amnesic and control groups will continue to rely on a small number of features for performing the task. To examine these possibilities, we conducted extended formal modeling analyses at the individual-subject level to reveal the feature-use strategies of the participants. As will be seen, these modeling analyses provide a powerful complement to the overall performance data observed across the different groups.
Methods
Subjects
The memory-impaired and elderly control subjects were drawn from the Indiana Alzheimer Disease Center (IADC) at Indiana University School of Medicine. Inclusion criteria were age 60 years and older, and IADC consensus panel diagnosis of dementia due to probable Alzheimer’s disease (AD), amnestic mild cognitive impairment (MCI), or Normal Cognition. Subjects were excluded if there was history of dementia due to cause other than AD, presence of significant neurologic disease or psychiatric illness, current substance abuse, or cancer diagnosis or treatment in the last three years other than skin cancer. Subjects were also excluded who had Mini-mental State Examination (MMSE) score less than 15/30, corrected vision less than 20/70, or Geriatric Depression Scale score greater than 7/15. Two sets of memory-impaired patients were recruited for the project. There were 12 subjects who met NINCDS/ADRDA criteria for dementia due to probable AD (McKhann et al., 1984). (One of these subjects withdrew from the study during the testing because of perceived difficulty in performing the first task.) There were 14 subjects who met criteria for amnestic MCI (Petersen, 2004). There were 28 healthy elderly controls also recruited from the IADC. The three groups were matched in age and education level, but each group differed significantly from one another in their MMSE scores (see Table 1).
Table 1.
Baseline and demographic characteristics by diagnostic group.
| Healthy Control (n = 28) |
MCI (n = 14) |
AD (n = 11) |
|
|---|---|---|---|
| Age | 71.9±9.3 | 73.8±5.2 | 76.3±6.6 |
| Female | 17 (60.7%) | 7 (50%) | 5 (45.5%) |
| Race | |||
| Black | 1 (3.6%) | 0 (0%) | 0 (0%) |
| Asian | 0 (0%) | 0 (0%) | 1 (9.1%) |
| White | 27 (96.4%) | 14 (100%) | 10 (90.9%) |
| Education, years | 15.5±2.0 | 15.6±2.8 | 15.8±3.5 |
| CDR, stage (range 0-3) | 0.0±0.0 | 0.5±0.0*** | 1.1±0.5*** |
| CDR sum of boxes (range 0-15) | 0.0±0.0 | 0.93±0.43*** | 4.82±3.01*** |
| MMSE (range 0-30) | 29.3±1.0 | 26.9±1.8*** | 23.5±3.2*** |
| Boston Naming (range 0-60) | 57.0±3.1 | 53.1±4.2** | 46.5±8.3*** |
| Animal Fluency | 20.5±5.6 | 18.7±5.2 | 12.4±3.3*** |
| AVLT, sum recall (range 0-75) | 52.5±7.9 | 31.6±6.5*** | 25.3±6.5*** |
| AVLT, delay recall (range 0-15) | 10.8±2.6 | 1.8±2.0*** | 1.2±2.0*** |
| Constructional Praxis (range 0-11) | 10.0±1.2 | 9.6±1.1 | 9.2±1.3 |
| CP, delayed recall (range 0-11) | 8.4±2.1 | 5.3±2.2*** | 2.8±3.2*** |
| COWA | 41.1±10.2 | 37.9±9.6 | 27.5±14.8** |
| Trail Making Part A | 31.0±10.5 | 40.2±17.4* | 53.8±24.5*** |
| Trail Making Part B | 75.8±43.2 | 118.8±66.1* | 202.8±106.2*** |
Notes: MCI = Mild Cognitive Impairment, AD = Alzheimer disease, MMSE = Mini-mental State Examination, CDR = Clinical Dementia Rating, AVLT = Auditory Verbal Learning Test, CP = constructional Praxis. Data entries are means and plus-or-minus one standard deviation. Asterisks denote outcomes of t-tests comparing the results of each of the MCI and AD groups to the control group.
p < .05,
p < .01,
p < .001
Additional details regarding demographic characteristics of the groups are provided in Table 1. Importantly, the table reveals that both the AD patients and the MCI patients performed significantly worse than did the controls on several tests of explicit memory, including AVLT sum, AVLT delay, and CP delay.1 Thus, if these groups perform well on the prototype extraction task, it would provide evidence in favor of a separate implicit category-learning system that is intact in these groups.
Finally, there were 110 undergraduate students from Indiana University Bloomington who participated in a parallel version of the task battery.
The project was approved by the Indiana University institutional review board. All patients and all elderly controls gave written informed consent, were paid a small honorarium, and were tested by a trained research associate from the Department of Psychiatry at the Indiana University School of Medicine, Indianapolis. The undergraduate students also gave written informed consent, participated in partial fulfillment of an introductory psychology course requirement, and were tested in an experimental psychology laboratory at Indiana University Bloomington.
Stimuli
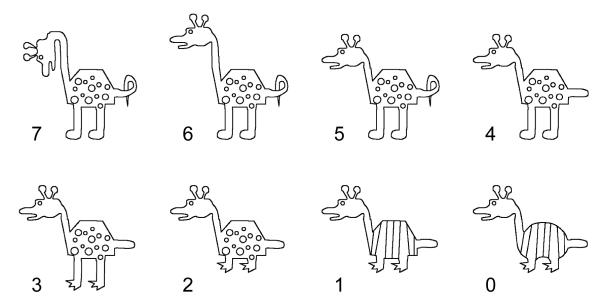
The stimuli were line drawings of 512 different cartoon animals, adapted from the stimuli used previously by Reed et al. (1999) and Bozoki et al. (2006) – for illustrations, see Figure 1. The cartoon animals were constructed by varying 9 binary features (see Figure 1 for details). The stimuli were presented on a standard computer screen within a 500 pixel square and subtended a visual angle of less than 12 degrees.
Figure 1.
Examples of the cartoon-animal stimuli used in Experiment 1. The animal at the top-left is a randomly chosen prototype stimulus. Its randomly chosen features would be the typical features for a given subject. The remaining stimuli in the figure show cartoon animals with decreasing numbers of features in common with the prototype. (Each animal is labeled in terms of the number of variable features that it has in common with the prototype.) Moving from left to right and then from the top to the bottom row, the features switched from their typical to their atypical value are: head direction, neck length, tail shape, feet shape, leg length, body markings, and body shape. The animal at the bottom right is the anti-prototype. In the present example, the feature values of ear shape and face type are held fixed across all animals. Those features might be variable features for another subject.
For each subject, one of the 512 stimuli was randomly selected as a prototype. Two of the 9 features were chosen at random to be fixed. All cartoon animals that were presented to the subject had those same two fixed values. Thus, the stimulus set for any given subject was chosen from among 128 animals that varied along the remaining 7 binary dimensions. These remaining 128 stimuli were sorted according to the number of features that they shared with the prototype (not including the fixed features). This measure of feature similarity to the prototype ranged from 7 (the prototype itself) to 0 (the animal that shared none of the 7 features with the prototype). We refer to the animal that shared no features with the prototype as the “antiprototype”. We used the number of features shared with the prototype to label each main type of animal. An example of each main stimulus type is depicted in Figure 1.
A set of 20 study animals was randomly selected from among those that had high similarity to the prototype. To create this set of 20 study items, 5 animals were randomly chosen from among those that had 6 features in common with the prototype, and 15 animals were chosen from among those that had 5 features in common with the prototype.
Procedure
The task began with a study phase. Subjects were told that they would see a set of cartoon animals and were instructed to carefully observe each animal to get an idea of what the animals are like. These orienting instructions were essentially identical to the ones used in the closely related studies of Reed et al. (1999) and Bozoki et al. (2001). A series of 40 animals was then presented to each subject. As in the previous investigations, these 40 trials consisted of 2 blocks of the 20 study animals presented in a random order. Each trial began with a fixation cross presented for 750ms in the center of the screen followed by a study item that appeared for 7 seconds, also centered on the screen. The next trial began immediately. No responses were required as training was strictly observational.
After study, subjects were informed that all the cartoon animals that they had just seen belonged to a single category called “peggles”. They were then told that on each trial in the next phase of the experiment they would be presented with a pair of cartoon animals, and that they should choose the animal that they judged to be a better example of a “peggle”. Furthermore, they were instructed that they should base their responses on the overall appearance of each animal and not rely on the value of just a single feature. (These latter instructions were intended to be biased in favor of the broad-based implicit-prototype hypothesis.)
The test phase consisted of 56 trials in which a pair of animals was presented on the screen, one centered on the left half of the screen and the second centered on the right. The two items within each pair were different stimulus types, varying in the number of features they shared with the prototype. There are 28 possible pairwise combinations of distinct stimulus types (e.g., 7-6, 7-5… 7-0, 6-5… 1-0) and each appeared once in a random order in each of 2 test blocks. For each main stimulus type, the actual animal token that was presented was chosen at random (with replacement) from the set of cartoon animals that shared the requisite number of features with the prototype. (It should be noted that the structure of the test phase makes it logically impossible for subjects to extract the category structure at time of test, because all stimulus types are presented with equal frequency.)
Participants selected the left cartoon animal by pressing ‘F’ on a standard keyboard and selected the right by pressing the ‘J’ key. Participants were advised that there was a correct answer on each trial; however, no feedback was provided. The locations of the stimulus types (left or right side of the screen) were randomized. Test trials were response terminated and the participant pressed the space bar to begin the next trial.
Results
Categorization Accuracy
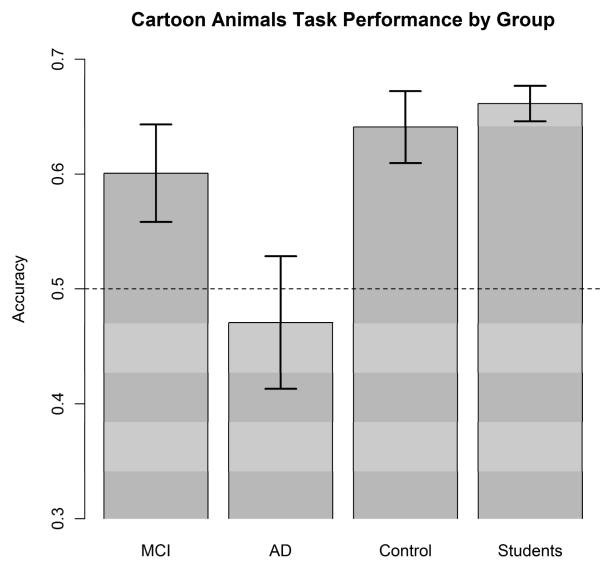
We defined a “correct” response in the paired-comparison task to be one in which the observer endorsed the member of the pair with the larger number of typical features in common with the prototype. The mean proportion of correct responses for the four groups of subjects is shown in Figure 2. Our initial analyses will focus on the two patient groups and the matched elderly controls, with results from the undergraduate-student group considered separately. There are numerous factors that distinguish the student group from the others, so it seems best to not consider them as another “condition” within the same experiment. Besides differences in age and education level, the students were tested in a separate location and by different experimenters. We suspect that their overall motivation level was also different from the patient groups and the elderly controls.
Figure 2.
Experiment 1: Mean proportion of correct responses for each of the groups in the paired-comparison task. MCI = mild cognitive impairment; AD = Alzheimer’s disease.
Inspection of Figure 2 reveals that the MCI and control groups had the same overall performance levels on the task, whereas the AD group performed much more poorly. Indeed, the performance of the AD group was slightly worse than chance. Focused t-tests on these overall performance data revealed that the AD patients performed significantly worse than did the controls, t(37) = −2.77, p = .009. However, there was no performance difference between the MCI group and the controls, t(40) = 0.75, p = .46.
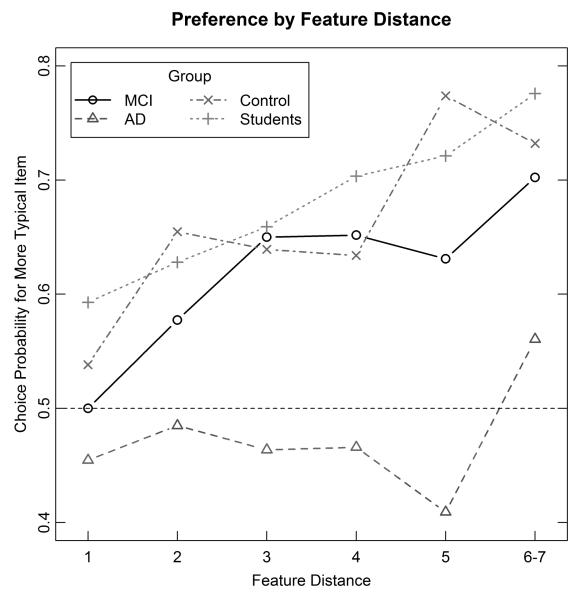
A more fine-grained breakdown of the results is provided in Figure 3. This figure plots, for each of the groups, the probability of a correct response as a function of the “feature distance” between the members of a pair. The feature distance is defined as the difference between the number of typical features in the better versus the worse category-member of each pair. For example, if test-item 1 had 6 typical features and test-item 2 had 2 typical features then the feature-distance would be equal to 4. (Because of small sample sizes, the data are averaged across feature-distances of 6 and 7, where only a few types of pairs contribute any observations.) These functions are important, because they reveal how responding varied with the relative typicality of the instances. Inspection of the figure reveals that, for both the MCI and control groups, the proportion of correct responses increases systematically as the feature-distance increases. Furthermore, there is little overall difference between the feature-distance functions of the MCI and control groups, suggesting that both groups engaged in very similar behavior. By contrast, the AD group shows little effect of feature distance, with responding almost always near chance. These descriptions are corroborated by statistical test. For example, we conducted a 2 × 6 ANOVA comparing the MCI and control groups, using group and feature-distance as factors. There was a significant main effect of feature-distance, F(5,200)=10.17, MSE=.022, p<.001, reflecting the improved category judgments as feature-distance increased. However, there was no main effect of group (F<1) and the group × feature-distance interaction did not approach statistical significance, F(5,200)=1.50, MSE=.022, p=.19. These null effects suggest very similar behavior patterns for the MCI and control groups. By contrast, a 2 × 6 ANOVA comparing the AD and control groups revealed both a main effect of group, F(1,37)=7.85, MSE=.215, p=.008; and a group × feature-distance interaction, F(5,185)=2.96, MSE=.023, p=.014, reflecting the obvious poor performance of the AD group.
Figure 3.
Experiment 1: Mean proportion of correct choices for each of the groups plotted as a function of the feature-distance between the members in each pair. MCI = mild cognitive impairment; AD = Alzheimer’s disease.
Preliminary Discussion
We were surprised to observe the very poor performance of the AD group on the paired-comparison task. In the Yes-No version of the same experiment, Bozoki et al. (2006) found that their AD group performed as well as the matched normal controls. As will be seen, the present group of AD subjects also performed poorly in a Yes-No version of the Knowlton-Squire dot-pattern task (see Experiment 2), so the poor performance does not seem to be solely attributable to some type of confusion regarding paired-comparison judgments. As noted in our introduction to this experiment, other investigators have also sometimes observed patterns of performance in which early-AD patients show some deficits in implicit category learning. The factors that lead to such variability in overall levels of performance among early-AD patients remain as an issue for future research.2
On the other hand, our finding that the performance of the MCI patients was as good as that of the matched elderly controls provides some initial support for the hypothesis of a separate, implicit category-learning system that is intact in that group. Nevertheless, a cause for concern is that the overall performance levels of both the MCI and control groups (as well as the undergraduate student group) seem relatively poor. An ideal-observer that uses a broad-based prototype for the paired-comparison judgments can achieve perfect performance for the task. Therefore, to help further interpret these results, we conducted formal modeling analyses of the individual-subject paired-comparison data.
Formal Modeling Analyses
We analyzed the results by fitting different versions of a minor extension of Tversky’s (1972) elimination-by-aspects (EBA) model to the data of the individual subjects. The EBA model is a classic process model for how observers make choices among multiple alternatives and it is straightforward to apply it to the case of paired-comparison choices. In application to the present paradigm, the process-based interpretation for the EBA model is that the observer samples the individual features of the members of a pair in a probabilistic order until a feature is located that discriminates between the members of the pair. If Alternative A has the “typical” value of the feature, i.e., the feature value that matches the prototype, then the observer chooses Alternative A; otherwise, the observer chooses Alternative B. Another process-based interpretation for the same descriptive model is that the observer makes probabilistic decisions based on the overall match of the distinctive features of the alternative objects to the prototype.
We fitted three different versions of the EBA model to the data – for details of the models, see Appendix A. The versions differed only in terms of assumptions regarding the amount of “weight” that observers gave to the individual features of the objects in making their categorization judgments. In the most general version of the model, a separate weight was estimated for each of the individual seven features of the objects, yielding an extremely general and flexible account of performance. More interesting are the special-case versions of the model. One special case formalized the idea that the observer had formed a veridical broad-based prototype from the training instances. In this special-case version, the 7 dimension weights were set equal to one another. This version is intended to provide an approximation to the implicit-prototype process that Reed et al. and Bozoki et al. hypothesized. At the opposite extreme, in a second special-case version of the model, only two of the seven weights were allowed to take on non-zero values, formalizing the idea that the subject used an extremely small number of features in order to make his or her paired-comparison judgments. Of course, the two non-zero dimension weights were allowed to differ across the individual observers, because there is no reason to expect that all subjects would use the same two dimensions for making their judgments.
We evaluated the models by using a well-known fit statistic known as the Bayesian Information Criterion (BIC; Schwarz, 1978) – for details, see Appendix A. For present purposes, the important point is that the BIC penalizes the absolute fit that is achieved by a model by adding a term related to its number of free parameters and the size of the data sample. (In the present application, the most general version of the EBA model uses 7 free parameters; the broad-based prototype version uses 1 free parameter; and the 2-weight version uses 2 free parameters.) All other things equal, the larger the number of free parameters, the less parsimonious is the model. The basic idea is to choose the model that achieves a balance of good fit and parsimony.
The results of the modeling analyses are summarized in Tables 2 and 3. In Table 2 we report, for each of the groups, the proportion of subjects for which the 2-weight model yielded a better BIC fit than did either the broad-based prototype model or the full 7-weight EBA model. These model-based analyses suggest strongly that, regardless of group, subjects relied on just a small number of remembered features for making their paired-comparison judgments. Inspection of Table 2 indicates that the behavior of the vast majority of the patients and elderly controls is better characterized by the 2-weight model than by the broad-based prototype model [MCI: sign(14)=14, p=.0001; AD: sign(11)=9, p=.07; Control: sign(28)=21, p=.013]. Furthermore, although only .66 of the student group is better characterized by the 2-weight model, this result is misleading. In particular, many members of the student group are best characterized by a 1-weight model, which assumes reliance on only a single feature rather than two features. Among the students, either a 1-weight or a 2-weight model yielded a better BIC fit than did the broad-based prototype model in .82 of the cases [sign(110)=90, p<.0001].
Table 2.
Proportion of Cases in which the 2-Weight Model Yielded a Better BIC than did the Competing Model.
| Group | ||||
|---|---|---|---|---|
| Competing Model |
MCI | AD | Control | Student |
| Broad-Based Prototype |
1.00 | .82 | .75 | .66 |
| Full 7-Weight EBA |
0.93 | 1.00 | .96 | .96 |
Note. MCI = Mild Cognitive Impairment; AD = Alzheimer disease; EBA = elimination-by-aspects; BIC = Bayesian Information Criterion.
Table 3.
Mean BIC Values for the Alternative Models.
| Group | ||||
|---|---|---|---|---|
| Model | MCI | AD | Control | Student |
| 2-Weight EBA |
62.2 | 66.8 | 61.9 | 62.4 |
| Broad-Based Prototype |
73.3 | 78.9 | 68.8 | 67.9 |
| Full 7-Weight EBA |
72.4 | 78.9 | 74.3 | 75.1 |
Note. MCI = Mild Cognitive Impairment; AD = Alzheimer disease; EBA = elimination-by-aspects; BIC = Bayesian Information Criterion.
The same conclusion is reached if one compares the fits of the 2-weight model to those of the full, 7-weight EBA model. Although the 7-weight EBA model is guaranteed to provide at least as good an absolute fit to the data as does the 2-weight model (because the 7-weight model generalizes the 2-weight version), the BIC comparisons indicate that its extra free parameters are generally wasted. Almost always, the 2-weight model is the preferred model in terms of its balance of fit and parsimony.
The Table-2 comparisons are mirrored by results that compare the mean BIC yielded by each of the models. As shown in Table 3, for each group, the mean BIC yielded by the 2-weight model is superior to the one yielded by either the broad-based prototype model or the 7-weight EBA model. (The smaller the BIC, the better is the fit.) In all cases, these fit differences were statistically significant at roughly the p=.001 level.
In another analysis, we fitted the EBA model to each subject’s data in iterative fashion, with the number of non-zero weights varied from 1 to 7. For each subject, we then determined the number of non-zero weights that yielded the best BIC fit of the model to that subject’s data. The results of that analysis are summarized in Table 4. As can be seen in the table, for all four groups of subjects, in roughly 70% of the cases the best BIC fit was achieved by a model that assumed use of either 1 or 2 dimensions of the objects.
Table 4.
Estimated Dimension-Use Distributions for each Group.
| # of Non-Zero Dimension Weights | |||||||
|---|---|---|---|---|---|---|---|
| Group | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| MCI | .21 | .43 | .00 | .36 | .00 | .00 | .00 |
| AD | .27 | .45 | .09 | .09 | .09 | .00 | .00 |
| Control | .36 | .36 | .14 | .11 | .04 | .00 | .00 |
| Student | .41 | .29 | .17 | .07 | .05 | .01 | .00 |
Note. MCI = Mild Cognitive Impairment; AD = Alzheimer disease.
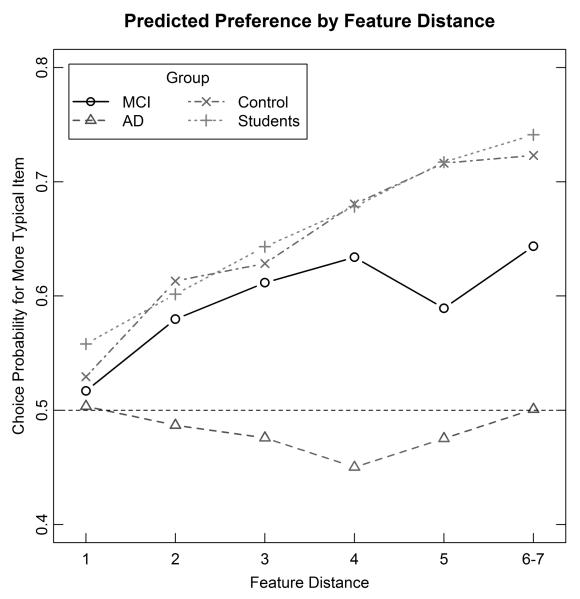
In Figure 4, we plot the predictions from the 2-weight model for each of the four main groups of subjects. These predictions are aggregated across the individual subjects in each of the groups. The main point of displaying this figure is simply to confirm that, at least at the aggregate level of analysis, the 2-weight model captures quite well the main performance patterns as a function of the variables of group and feature distance (compare to Figure 3).
Figure 4.
Experiment 1: Predicted proportion of correct choices from the 2-weight EBA model plotted as a function of group and feature-distance between the members in each pair. EBA = elimination-by-aspect, MCI = mild cognitive impairment; AD = Alzheimer’s disease.
Discussion
The early-AD patients performed very poorly on the paired-comparison forced-choice version of the cartoon-animal categorization task. As will be seen in Experiment 2, these same patients also performed very poorly on the classic dot-pattern paradigm of Knowlton and Squire (1993). Past research has demonstrated repeatedly that even severe amnesics perform well on the Knowlton-Squire dot-pattern task. In our view, the very poor performance of our early-AD patients on both tasks suggests caution in whether such patients serve as an appropriate model system for groups with focused deficits in hippocampally-mediated explicit memory. Instead, such patients may have more generalized deficits. As noted in our introduction, Bozoki et al. found that a similar group of early-AD patients performed normally on the Yes-No version of the cartoon-animals task. Future research is needed to determine whether the difference in results is due to the task difference (Yes-No vs. paired-comparison), some aspect of the experimental-testing environments, or to some characteristic that distinguishes the groups of early-AD patients that were tested across the two studies.
The more interesting result from the present experiment is that the MCI patients’ overall performance was as good as that of the controls. Moreover, the MCI’s typicality gradient (plot of performance against feature distance) was also virtually identical to the one observed for the controls. These overall-performance results lend support to the hypothesis of a spared implicit category-learning system in that group.
Nevertheless, a deeper analysis suggests continued caution regarding the separate-systems hypothesis. First, the overall performance levels of both the MCIs and controls were relatively poor compared to what could reasonably be achieved by the consistent use of a broad-based prototype. Second, the results from the formal modeling analyses were consistent with the view that the vast majority of subjects in the task relied on only one or two features for making their judgments.
One possibility is that, given the incidental-training conditions of the study phase (the same ones as used by Reed et al, 1999, and Bozoki et al., 2006), neither the patient groups nor the control group were cognizant of a very large number of the typical features of the category members. A second possibility is that subjects chose decision rules that focused on only a small subset of the features, rather than engaging in an attempt to make global-similarity comparisons to the prototype or the training instances. Future research will be required to disentangle these possibilities.
Regardless of which possibility is correct, in our view these modeling results weaken the case for a separate implicit category-learning system. Even in the present paired-comparison version of the cartoon-animals task, which should strongly motivate the use of a broad-based prototype, there is little evidence that subjects are relying on very many features from the training instances.
Separate-systems theorists might argue that subjects’ apparent focus on a small number of features is not incompatible with an implicit memory system. Indeed, in work conducted concurrently with the present study, Glass, Chotibut, Pacheco, Schnyer, and Maddox (in press) found that normal older adults performed slightly better than did younger adults in a yes-no, single-category prototype extraction task similar to the one conducted by Reed et al. (1999) and Bozoki et al. (2006). Furthermore, they conducted modeling analyses similar to the ones reported previously by Zaki and Nosofsky (2001) for the yes-no task. Like Zaki and Nosofsky (2001), they found that most individuals attended to relatively few features in making their categorization judgments. Glass et al. interpreted their results in terms of an implicit perceptual-representation learning system that was intact in the older adults. However, they acknowledged that future research was needed to sharply distinguish their interpretation from single-system accounts.
Clearly, formal modeling results such as those of Zaki et al. (2001) and Glass et al. (in press) for the yes-no task, as well as the present modeling results for the more diagnostic forced-choice task, do not rule out the possible presence of a separate implicit category-learning system. Instead, our key point is that such results suggest that there may be no need to posit the operation of the separate system. That is, because even patients with impairments to some single memory system may be able to remember and make use of just a couple of salient features, there may be no need to posit the role of a separate, implicit category-learning system to explain their performance. 3
In our view, our appeal to parsimony in generating this argument is reasonable and important. As currently expressed, the multiple-system accounts offered by Reed et al. (1999), Bozoki et al. (2006), and Glass et al. (in press) are quite general and they subsume the alternative type of single-system account suggested here. A guiding principle of scientific theorizing is that simpler models (e.g., ones involving a single memory system) are to be preferred to more complex models (e.g., ones involving multiple memory systems) unless the greater complexity is clearly warranted by the data. The results from the cartoon-animals version of the prototype-extraction task do not seem to warrant the more complex model.
Experiment 2
In Experiment 2 we switch from the cartoon-animals task to the other major implicit prototype-extraction task, namely the Knowlton and Squire (1993) dot-pattern paradigm. Recall that the main purpose of the experiment is to investigate the potential contribution of learning-during-test to performance in this task. Although Palmeri and Flanery (1999) documented learning-during-test in this paradigm for normal college undergraduates, there is little information regarding the extent to which elderly, memory-impaired patients can also learn the Knowlton-Squire dot-pattern category at time of test.
In Experiment 2, we tested the memory-impaired patients, elderly controls, and students in both a training version and no-training version of the Knowlton-Squire task. For reasons explained in our introduction, each subject participated in both versions of the task. The no-training version of the task was always preceded by the training version. As we argue below, although the design confounds the order of testing with the training variable, we believe it is a sensible procedure in the present case. Furthermore, based on the observed pattern of results, we will argue that any influences of transfer effects across the tasks were likely very minor.
To conduct the study as a within-subjects design, we constructed two separate sets of dot-pattern categories. Half the subjects received training on Set 1 and half received training on Set 2 (and vice-versa for the subsequent no-training condition). For the first set, we used the same stimuli as had been used previously by Knowlton and Squire (1993). The second set was constructed by randomly permuting the x-y coordinates of the original patterns (see Method section for details) to produce a new set with extremely similar statistical properties as the original.
Our intent was to produce two dot-pattern sets that were conceptual replications of one another. Furthermore, in pilot work, we found that undergraduate students showed nearly identical results for the two sets in the standard training version of the task. Despite our intention, as will be seen, the variable of dot set unexpectedly turned out to have a major and extremely interesting impact on the full pattern of results.
Methods
Subjects
The subjects were the same as in Experiment 1.
Stimuli
The stimuli were the classic types of dot-pattern stimuli used in numerous previous studies of prototype learning (Posner, Goldsmith, & Welton, 1967). The patterns consisted of nine black dots displayed in a dispersed fashion on the computer screen. Each pattern appeared within a 500 pixel square in the center of the computer screen and subtended a visual angle of less than 12 degrees.
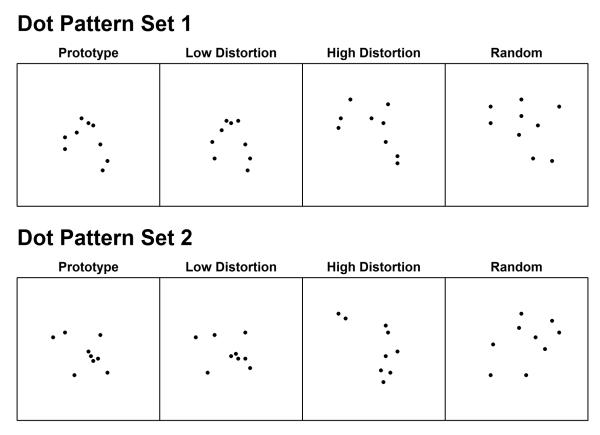
Dot Set 1 was the same set of patterns as used in Knowlton and Squire (1993). This set consists of 40 study items that are all high distortions of a single prototype and also consists of 84 test patterns. The 84 test patterns are made up of 4 repetitions of the prototype pattern itself, 20 low distortions of the prototype, 20 new high distortions of the prototype, and 40 random dot patterns (see Knowlton & Squire, 1993, for further details). An example of each of these types of patterns is shown in the top row of Figure 5. Dot Set 2 was generated by randomly permuting the 18 coordinates that specify the location of the nine dots in each pattern in a consistent manner for all study and test items. An example of each of the main types of patterns from Dot Set 2 is shown in the bottom row of Figure 5.
Figure 5.
Experiment 2: Representative examples of the main stimulus types in the dot-pattern experiment. The top row provides examples from Dot Set 1 and the bottom row provides examples from Dot Set 2.
Procedure
Training Version of Dot-Pattern Task
Following a rest break from the cartoon-animals task of Experiment 1, subjects engaged in the standard training version of the dot-pattern categorization task. The task consists of a study phase and a test phase. In the study phase, each of the 40 study patterns was presented in a random order for 5 seconds, with a 750 ms inter-stimulus interval. We used the incidental-training manipulation of Knowlton and Squire (1993), in which participants were instructed to mentally point to the dot that appeared to lie closest to the center of each pattern.
Following the study phase, subjects were told that the 40 patterns they just viewed all belonged to the same category. They were then instructed that they would be shown novel dot patterns and that they would need to indicate whether or not each pattern was a member of the category. Subjects were instructed to press the ‘J’ key if they believed the dot pattern was a member of the category and the ‘F’ key if they believed that it was not. Additionally, they were told that roughly half of the patterns would be members of the category. Trials were response terminated, and the next trial began when the participant pressed the space bar.
The 84 test-phase patterns were presented in a random order. Subjects were told that although there was a correct answer for each pattern, no feedback would be provided. In this training version of the task, roughly half the subjects in each group were assigned Dot-Set 1 and roughly half were assigned Dot-Set 2. Each subject’s dot-set assignment was reversed in the subsequent no-training version of the task.
No-Training Version of Dot-Pattern Task
Following a rest break from the training version of the task, subjects engaged in the no-training version. This condition was the same as the training version, except there was no study phase. Again, the test phase consisted of 84 randomly ordered trials involving 4 presentations of the prototype, 20 low distortions, 20 high distortions, and 40 random patterns. It was explained to subjects that they would need to classify a set of new dot patterns in a manner similar to what they had just done in the previous task, even though they had received no training regarding the category. It was made clear to subjects that the new category had no relation to the one learned previously. Subjects were told that although the task may seem strange at first, there was a good chance that they could discover the category as they viewed the test patterns.4 Furthermore, they were told that roughly half of the patterns would be members of the category. In all other respects, the task was the same as the training version.
Dot-Pattern Recognition
During the course of conducting the experiment, we decided that it would be useful to also collect data in an explicit memory task involving old-new recognition of a separate set of dot patterns. For some subjects, a final old-new recognition task was conducted at the end of the test battery. Other subjects were invited to return for a supplementary session. The Method and Results for this supplementary recognition task are reported in Appendix B. The purpose was simply to verify that the subjects diagnosed with MCI did indeed display significantly worse recognition memory for the present types of stimuli than did the group of matched elderly controls.
Results
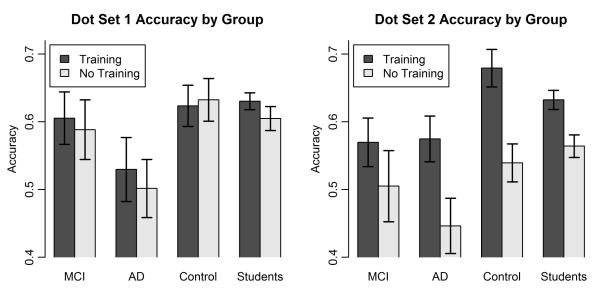
The overall mean proportion of correct categorizations is shown as a function of group, training, and dot set in Figure 6. Among the most salient results is that, whereas the training variable had little influence for any of the groups for Dot-Set 1, it had a major influence for all of the groups for Dot-Set 2, with those subjects who received training performing much better than those who did not receive training. This observation is confirmed by statistical test. We conducted a 3 × 2 × 2 mixed-model ANOVA on the proportion-correct scores, using group (MCI, AD, and control), training, and dot set as factors. (Although the students showed the same pattern as did the patients and elderly controls, we again treat that group separately.) The most important result is that the analysis revealed an interaction of the variables of training and dot set, F(1,47)=6.68, MSE=.012, p=.013, reflecting the near-absent effect of training in the context of Dot-Set 1, but the big effect of training in the context of Dot-Set 2. The same interaction effect is obtained if the analysis is restricted to just the MCI and control groups. Given this interaction effect, we decided to analyze separately the results for Dot-Sets 1 and 2.
Figure 6.
Experiment 2: Mean proportion of correct categorization decisions plotted as a function of group, training, and dot set. MCI = mild cognitive impairment; AD = Alzheimer’s disease.
Regarding Dot-Set 1 (see Figure 6, left panel), note first that the AD group performed worse than did the MCIs and the controls. The near-chance performance of the AD group in this task is reminiscent of their performance in the paired-comparison task of Experiment 1. Again, it appears that this group of subjects has generalized deficits that extend beyond just impaired explicit memory.
More interesting is that, for Dot Set 1, there is little difference in performance across the MCI and controls groups and little effect of whether subjects received training. (Furthermore, the overall performance scores on the standard training version of the task are virtually identical to what other researchers have reported in past work.) We conducted a 2×2 ANOVA on the proportion-correct scores using group (MCI vs. control) and training as factors. The main effect of group did not approach significance, F < 1; there was no effect of training, F < 1; and no interaction between group and training, F < 1. This lack of any main effect or interaction effect involving training is also obtained if the AD group is included in the analysis. As can be seen, there was also little or no effect of training for the student group, t(108)=1.17, p=.24.
These results for Dot-Set 1 both replicate and make important extensions to previous results in the literature. First, the finding that overall categorization performance for the MCIs is nearly as good as that for the elderly controls replicates previous results that show that memory-impaired patients perform at near-normal levels in the Knowlton-Squire task. Second, the finding that the undergraduate students performed essentially as well in the no-training version of the task as in the training version replicates Palmeri and Flanery’s (1999) influential finding. The significant contribution to new knowledge is that we now find that even the MCIs and the elderly controls perform as well in the no-training as in the training version of the task. Apparently, at least when the Knowlton-Squire (1993) stimuli are used, even memory-impaired patients and elderly controls can rely on working memory to extract the category structure at time of test. This important finding addresses one of the key open questions motivated by Smith’s (2008) review.
To our surprise, however, markedly different patterns of results were obtained for the Dot-Set-2 materials. Clearly, for these materials, there is now a big effect of training. Moreover, and equally interesting, the MCIs now perform worse overall than do the elderly controls in both the no-training and training versions of the task. We conducted a 2×2 ANOVA on the Dot-Set-2 results using group (MCI vs. control) and training as factors. The analysis revealed a significant main effect of group, F(1,38) = 4.63, MSE=.012, p=.038; and a significant main effect of training, F(1,38)=11.56, MSE=.012, p=.002. The interaction was not significant, F(1,38)=1.11, MSE=.012, p=.30. (The same pattern of statistical results is obtained if the AD group is included in the analysis.) Note that the undergraduate students also performed significantly worse in the no-training condition than in the training condition for the Dot-Set-2 materials, t(108)=3.13, p=.002, attesting to the robustness of the effect.
A more detailed picture of the results is provided in Figure 7, which plots the gradient of endorsement probabilities for the individual types of patterns as a function of group, training, and dot set. In general, the steeper the gradient, the better is performance, with the key issue being the extent to which endorsement probabilities for the prototype and the low and high distortions exceed the endorsement probabilities for the random patterns. Inspection of the figure reveals that the steepness of the gradients mirrors the overall performance patterns already described above. For example, for Dot-Set-1 (top row panels), the MCIs and controls show similar gradients that do not vary much across the training and no-training conditions. By contrast, for Dot-Set-2 (bottom row panels), the gradient for the controls is steeper than that of the MCIs in the training condition, and the gradients for both groups flatten out in the no-training condition.
Figure 7.
Experiment 2: Mean proportion of category endorsements plotted as a function of group, training, dot set, and stimulus type. MCI = mild cognitive impairment; AD = Alzheimer’s disease. Proto = prototype, low = low distortion, high = high distortion.
Discussion
In addition to replicating important previous results, the present study provided several major new contributions. First, using the original Knowlton-Squire (1993) materials, we found that both a group of MCI patients and a group of matched elderly controls performed as well in the no-training version of the prototype-extraction task as in the training version. Whereas such a result had been observed previously by Palmeri and Flanery (1999) for high-functioning undergraduate students, the present results show that it holds more generally for both memory-impaired and elderly populations. In our view, these results again weaken the case for the existence of a separate, implicit category-learning system. Previous findings that memory-impaired patients perform as well as do normal subjects on the categorization task (using the Knowlton-Squire stimuli) have been interpreted as evidence that a spared implicit system abstracts the prototype that defines the study instances. The case is weakened because such populations can apparently rely solely on working memory at time of test to extract the category structure.
A second major new contribution is the finding that the pattern of results is dependent on the precise form of the stimulus materials that are used. When we used the original Knowlton-Squire dot-pattern set, we replicated the previously reported patterns of performance that have been observed. Unexpectedly, however, use of a second dot-pattern set, which had similar statistical properties as the original, led to a different pattern of results. First, the memory-impaired group no longer performed as well as the matched controls on the training-version of the task, breaking the classic dissociation between explicit memory and implicit categorization. Even considered on its own, this result provides a major new contribution to knowledge, because it indicates that past results involving spared implicit prototype extraction may be limited in generality. Second, all groups showed marked deficits in performance in the no-training version of the task compared to the training version. Thus, the extent to which observers can rely solely on working memory to extract the category structure also depends on the dot set.
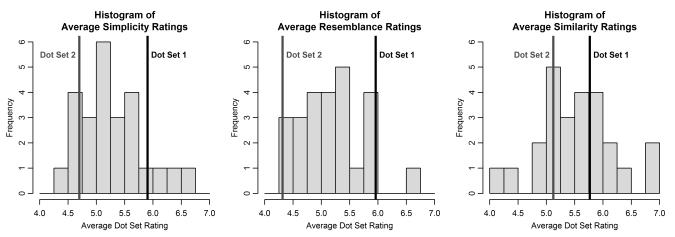
Future research is needed to test for the generality and detailed basis of these findings. In hindsight, our impression is that the Knowlton-Squire (1993) prototype and low distortions (see Figure 5 of the present article) have a particularly simple and regular structure. To verify this impression, we conducted a follow-up study with new undergraduate participants who rated 25 different low-distortion dot-pattern sets on several different attributes (details are provided in Appendix C). Each dot-pattern set was generated by a consistent, random permutation of the coordinates of the members of Dot-Set 1. Included among the 25 sets were Dot Sets 1 and 2 from the present experiment. One rating scale assessed the extent to which the patterns in each set had a simple and regular structure. A second scale assessed the extent to which the patterns resembled or reminded the observers of some object or form that they had experienced in the real world. And a third scale assessed the extent to which the patterns within each set were similar to one another. The ratings for Dot-Set 1 were at the upper extreme of the distribution on both the simplicity and resemblance scales. As it turned out, the ratings for Dot-Set 2 were towards the lower end of the distribution on both scales. The within-class similarity ratings showed these same patterns of results but were not as extreme.
It seems likely that properties such as simplicity of structure may influence the ability of observers to extract the category structure at time of test and may contribute to the ability of memory-impaired patients to perform at near-normal levels in the categorization task. Future research is needed to systematically investigate the role of such factors. In any case, in our view, our finding that use of a slightly modified dot set led to breaking the classic dissociation between prototype extraction and explicit memory further weakens the past case for a separate implicit category-learning system.
As acknowledged at the outset, a possible concern regarding the present results is that they were obtained in a within-subjects design that used a fixed order of testing of the tasks. For example, the training version of the dot-pattern task always occurred after the paired-comparison cartoon-animals task, so various transfer effects may have arisen. Note, however, that the overall performance levels and category-endorsement gradients in our replication of the training version of the Knowlton-Squire task were virtually identical to what has been reported numerous times in the past. Therefore, any influence of the cartoon-animals task on the subsequent dot-pattern performance would appear to be minimal.
Likewise, the no-training version of the dot-pattern task always occurred after the training version. Clearly, it would not have been sensible to test the no-training version before the training version. The reason is that the category-learning aspect of the dot-pattern task would then have been revealed, so the study phase of the training version would no longer be incidental in character. By contrast, for the no-training version, there is no need to disguise the study phase as an incidental task because there is no study phase.
We acknowledge the possibility that unknown and complex transfer effects could in principle have influenced the patterns of performance on the no-training version of the dot-pattern task. In our judgment, however, any such effects were probably minor. Perhaps most convincing is that in our replications using the Knowlton-Squire (1993) materials (Dot Set 1), our results for the student group were virtually identical to those reported previously by Palmeri and Flanery (1999), who used a between-subjects design.
General Discussion
Summary, Implications, and Future Research Directions
The purpose of this research was to pursue two open questions regarding the nature of implicit prototype extraction in memory-impaired groups. First, as demonstrated by Reed et al. (1999) and Bozoki et al. (2006), memory-impaired patients perform at normal levels in a yes-no prototype-extraction task involving incidental category learning of discrete feature-based (cartoon-animal) stimuli. A concern that has been raised is that performance in this task may be mediated by reliance on a very small number of remembered features from the training phase (Zaki & Nosofsky, 2001). In the present Experiment 1, we made efforts to address this difficulty by conducting a paired-comparison version of the task that should strongly motivate subjects to use a broader sample of remembered prototypical features, if such a broad-based prototype were indeed available. On the one hand, our MCI patients’ overall performance levels on the task were the same as those of the matched elderly controls, which provides preliminary evidence in favor of a spared implicit category-learning system. Nevertheless, despite the strong motivation provided by our paired-comparison task, our model-based analyses continue to suggest that most subjects relied on exceedingly few features to make their judgments. There is no evidence that subjects made use of a broad-based prototype. Thus, because even patients with impairments to a single memory system may be able to remember and make use of a couple of features, there may be no need to posit the role of a separate, implicit learning system.
In our view, the paired-comparison task remains an excellent route to disentangling these competing interpretations of the near-normal performance of the memory-impaired patients. Future work might pursue the issue in a variety of ways. For example, in the study phase of the task, instead of providing subjects with instructions to get a general impression of what the animals are like, more focused incidental training instructions might be provided that would enable participants to notice more individual typical features of the category. Likewise, implicit learning of a broad-based prototype might also occur with a greater number of training trials. Still another possibility is to provide stronger motivation to subjects to retrieve as many remembered features as possible, such as by using payoffs for correct paired-comparison choices. Should clear-cut evidence be found that memory-impaired patients perform as well as controls in cases in which both groups perform at high levels by making use of a broad-based prototype, it would provide a more convincing case for a separate implicit category-learning system.
The second goal of our research was to pursue the question of the extent to which learning-during-test may contribute to the performance of memory-impaired patients in the classic Knowlton-Squire (1993) dot-pattern prototype-extraction task. This aspect of the research made several significant contributions. First, we found that, when using the original Knowlton-Squire stimuli, even memory-impaired subjects (as well as matched elderly controls) were able to use learning-during-test to extract the category structure embedded in the test list. This result weakens the past case made for implicit category learning, because implicit memory of the study instances is apparently not needed in order for such subjects to achieve near-normal performance on the task. Furthermore, because the vast majority of studies that have conducted the Knowlton-Squire task have used these original materials, these results involving the Knowlton-Squire stimuli are crucial.
Second, unexpectedly, we found that with a modified set of dot patterns (that had a very similar statistical structure as the original set), a much different pattern of results was obtained. Not only was learning-during-test greatly reduced, but the classic dissociation between explicit memory and implicit categorization disappeared. That is, the memory-impaired patients performed significantly worse on even the training version of the categorization task than did the matched controls.
Even this latter result on its own makes an important new contribution to knowledge in this field. As reviewed in our introduction, the general pattern of “dissociation” between categorization and recognition in amnesic and control subjects is as predicted by a single-system exemplar model. However, the exemplar model does predict some deficit in categorization performance for the amnesics compared to the controls. Within individual studies, the amnesic deficit rarely approaches statistical significance, which is the basis for the reported dissociation effect. However, in a meta-analysis, Zaki (2004) found that when the results were considered across studies, a statistically significant deficit emerged. Using a slightly modified set of materials, we now find statistically significant evidence for the predicted amnesic deficit even within a single study. The result points to the potential importance of specific properties of individual stimulus sets in yielding statistical dissociations between explicit memory and implicit categorization performance.
Future research that examines these issues might benefit by formalizing constrained versions of both multiple-memory-system and single-memory-system categorization models and comparing them qualitatively and quantitatively across multiple simultaneous data sets (Wills & Pothos, 2012). In our view, the present results challenge “strong” versions of multiple-system models that posit highly efficient forms of implicit category learning in the prototype-extraction tasks. For example, such models would seem to predict that our memory-impaired patients should abstract a broad-based prototype in the cartoon-animals task of Experiment 1, and that details of the dot set should not have exerted such a prominent role in Experiment 2. By contrast, “weak” versions of multiple-system models could also be formulated. For the cartoon-animals task, such models might posit the abstraction of implicit prototypes composed of a very limited number of features. And for the dot-pattern task, such models might posit that ability to abstract a prototype depends crucially on the simplicity and regularity of the patterns. If the detailed nature of the implicit category-learning process and its interactions with explicit memory are not specified, then weak versions of the multiple-system models would seem to subsume single-system models. In this case, we would need to rely on the criterion of parsimony as a basis for making model comparisons. In recent work, Berry, Shanks, Speekenbrink, and Henson (2012) developed a statistical approach to comparing both strong and weak multiple-system models to single-system models in the domains of perceptual priming and recognition. Possibly, such an approach could also be developed for comparing such models in the present domain of category prototype extraction.
Brain-Imaging Evidence
Finally, whereas the evidence considered in the present research focused on past behavioral dissociations, another major source of evidence for a separate implicit prototype-extraction system comes from brain-imaging research. In a seminal series of studies, Reber and his colleagues (Reber et al., 2003; Reber, Stark, & Squire, 1998a,b) conducted brain imaging under conditions in which subjects engaged in either the dot-pattern prototype-extraction task or else in an old-new recognition task. (In the recognition task, subjects studied five random dot patterns, and then were tested on these five old patterns and new random patterns.) Dramatically different patterns of brain activity were observed across the two tasks. In the prototype-extraction task, category members were associated with decreased activity in posterior occipital cortex (POC). By contrast, in the recognition task, old patterns led to increased activity in POC and to increased activity in brain regions associated with explicit memory, including hippocampus. Reber et al. (2003) and Smith (2008) have theorized that the categorization-based POC deactivation represents a category fluency effect that allows patients with explicit memory disorders to perform prototype extraction..
Despite this rather direct brain-imaging evidence for separate neural systems mediating implicit prototype extraction and explicit recognition, alternative possibilities need to be considered. First, note that in the prototype-extraction task, the to-be-endorsed patterns were novel patterns that were all similar to a single prototype. By contrast, in the recognition task, the to-be-endorsed patterns were highly distinct items that were exact matches to unrelated, old study items. Thus, rather than reflecting differences between categorization versus recognition per se, the brain-imaging results could have been reflecting these stimulus differences (for closely related arguments, see Gureckis, James, and Nosofsky, 2011). Second, as argued by Nosofsky, Little, and James (2012), one would also expect observers to vary parameter settings across the tasks in order to satisfy the different task goals. For example, an observer would likely establish a stricter criterion for similarity matching in a recognition task than in a categorization task. The reason is that judging an item to be “old” suggests that it provides an “exact match” to some study item; whereas judging that an item belongs to a category suggests only that it has some sufficient degree of “family resemblance” to the study items. Thus, the differing brain-activation results observed across categorization and recognition could also have been reflecting adaptive changes in parameter settings. In a recent brain-imaging study, Nosofsky et al. (2012) found clear evidence that changes in parameter settings do lead to robust changes in patterns of brain activation across categorization and recognition tasks involving the same types of stimuli. Furthermore, Nosofsky et al. (2012) found that once one controls for both stimulus-related and parameter-related differences, there is little evidence that categorization and recognition recruit separate neural memory systems.
Neural Machinery and Single-System Models
Formal “single-system” approaches to modeling categorization and recognition, such as the exemplar-based GCM, are framed at an abstract, cognitive level of analysis. Those approaches do not deny that the neural machinery that instantiates the cognitive computations may be composed of multiple, interacting components. However, they do assume that the same multi-component, interactive neural system governs both categorization and recognition. We are far from the point of specifying the detailed manner in which a single-system cognitive model of categorization and recognition might be instantiated in the brain. Nevertheless, in concluding our article, we point to some parallels between past single-system cognitive approaches and to influential approaches framed at a neuro-computational level.
As reviewed in our introduction, according to Nosofsky’s (1986, 1988) GCM, categorization and recognition decisions are based on the “summed similarity” of a test item to exemplars stored in memory. Conceivably, many brain regions may contribute to this summed-similarity computation. Presumably, included among these regions are hippocampus and medial temporal lobe cortex (MTLC), which are strongly implicated in varieties of explicit memory. Hippocampus and MTLC have also been implicated in rule-based category learning tasks (e.g., Nomura & Reber, 2008); tasks that require learning exceptions to category rules (e.g., Davis, Love, & Preston, 2012); tasks that require learning of multiple prototypes (e.g., Glass et al., in press; Zeithamova, Maddox, & Schnyer, 2008); and tasks that involve explicit learning of single prototypes (Reber et al., 2003). We believe that it is highly plausible that these regions play some role in the current implicit prototype-extraction tasks as well. According to Norman and O’Reilly’s (2003) influential complementary learning systems (CLS) approach, both hippocampus and MTLC contribute to recognition memory. In their model, structures in MTLC compute a summed-similarity signal, and targets and similar lures create similar neural representations in these structures. By contrast, hippocampus is presumed to implement pattern separation, whereby even fairly similar input patterns may give rise to quite distinct neural representations. However, as emphasized by Norman (2010), there are boundary conditions on this function, such that when the inputs are highly similar, “pattern-separation failure” may occur. Under these conditions, the properties of the hippocampal memory signal tend to resemble the properties of the cortical memory signal. Possibly, depending on parameter settings, the distributions of summed similarity produced by hippocampus under such conditions may still be sharper than those produced by the cortical structures.
There is clear evidence that volumes of the hippocampus and entorhinal cortex (ERC) are significantly reduced in patients with amnestic MCI (e.g., Pennanen et al., 2004). (Note that ERC is a structure in MTLC that mediates directly with hippocampus.) The dot-pattern stimuli tested in the classic designs that demonstrate dissociations between categorization and recognition all tend to be highly similar to one another. Thus, according to the CLS approach, the memory signals produced by hippocampus should resemble the cortical signals in both amnesics and controls. However, if hippocampus and ERC are damaged in patients with amnestic MCI, then these structures may fail to produce sharper summed-similarity signals for discriminating between targets and lures. Recall that the GCM’s account of the categorization-recognition dissociations observed in amnesic and normal individuals is based on the idea that amnesics have reduced sensitivity in discriminating between the summed-similarity signals of targets and lures. Thus, the CLS approach may provide a neural basis for the cognitive-level explanation proposed within the GCM.
This explanation does not provide a complete story, however. Instead, as demonstrated in the present research, a full explanation of amnesic and control performance in tasks of prototype extraction will also need to specify the role of working memory in category-learning at time of test. Note that the multiple neural networks involved in working memory appear to be largely intact in patients with amnestic MCI. Therefore, our finding that those patients performed similarly to the controls in the no-training condition of the dot-pattern prototype-extraction task (using the Knowlton-Squire stimuli) seems sensible as well. Overall, our results suggest that developing a complete neural-level account of performance in prototype-extraction tasks will involve contributions from both long-term-memory and working-memory networks. Thus, although our results weaken the past case that completely separate neural memory systems underlie categorization and recognition, the “single system” that may mediate performance on these tasks is likely to be composed of multiple, highly interacting neural components.
Acknowledgements
This work was supported by grants MH48494 from the National Institute of Mental Health and FA9550-08-1-0486 from the Air Force Office of Scientific Research to Robert Nosofsky.
Appendix A. Paired-Comparison Models and Model-Evaluation Method
Formal Models
In the EBA model, each dimension j of a set of multidimensional objects is assigned a weight, wj (0 ≤ wj). In choosing between two objects, on any given step of the process, the observer probabilistically samples (without replacement) a dimension in proportion to its weight. In particular, on any given step of the process, the probability that the observer samples some dimension j is given by
| (A1) |
where the sum in the denominator of Equation A1 is over all dimensions that have not yet been sampled. If the two objects have distinct values on the sampled dimension j, then the observer chooses the alternative with the preferred feature value. In application to the present paradigm, that feature value would be the one that is in common with the category prototype. By contrast, if the two objects have identical values on dimension j, then a new dimension is probabilistically sampled from among those dimensions that remain. The process continues until one of the alternatives is chosen. It should be noted that the model can represent what is essentially a deterministic order of inspecting dimensions by assigning weights with extremely large differences in relative magnitude.
As noted by Tversky (1972, p. 287, Equation 7), according to this process model, it turns out that the probability that the observer selects alternative A over alternative B is given by
| (A2) |
where the sums are over all features that are unique to alternatives A and B, respectively. Note that an alternative process interpretation for the Equation-A2 response rule is that the observer makes decisions based on weighted matches of the objects to the prototype (Bergert & Nosofsky, 2007). That is, the term ∑k∈A–Bwk represents the weighted match of the unique features of object A to the prototype, and likewise for the term ∑k∈B–Awk. The observer then chooses alternative A with probability that is proportional to its relative weighted match.
In the present application, we use a minor extension of Tversky’s EBA model, given by
| (A3) |
where b (b>0) is a “background” constant. The interpretation is that, on each step of the process, the observer stops sampling dimensions with probability b/[∑wk + b], and then chooses randomly between the two alternatives. If b is very small relative to the magnitude of the dimension weights, then the observer tends to exhaustively sample all of the dimensions until a choice is made. By contrast, if b is very large relative to some of the dimension weights, then random guessing may occur fairly often.
As noted in the text, we fitted different members of the class of models defined by Equation 3 to the choice-probability data of each of the individual subjects. The most general version of the model served as a general framework for analyzing the data. In this most general version, all of the dimension weights and the background-constant b were allowed to vary as free parameters. (Without loss of generality, the dimension weights can be constrained to sum to one, so this full model uses 7 free parameters.) In one special-case version of the model, which formalized use of a broad-based prototype, the 7 dimension weights were set equal to one another and only the background-constant b was allowed to vary as a free parameter. At the opposite extreme, in a second special-case version of the model, only two of the seven weights were allowed to take on non-zero values, formalizing the idea that the subject used an extremely small number of features in order to make his or her paired-comparison judgments. As explained in the text, the two non-zero dimension weights were allowed to differ across the individual observers.
Model fits
The fits of the models were evaluated by using the Bayesian Information Criterion (BIC), defined as
| (A4) |
where ln L is the maximum log-likelihood of the data given the parameters in the model, p is the number of free parameters used by the model, and N is the number of observations in the data set. The preferred model is the one that achieves the smallest BIC. As noted in the text, the BIC penalizes the log-likelihood fit that is achieved by a model by adding a term related to its number of free parameters. All other things equal, the larger the number of free parameters, the less parsimonious is the model, so the larger is its BIC.5
Appendix B. Old-New Recognition Task
During the course of conducting the experiment, we decided that it might be useful to collect old-new recognition data from the MCI and control subjects, simply to verify an explicit memory impairment for the MCI group using the present kinds of materials. For some subjects, the recognition task was added to the battery as a final task; other subjects were invited back to participate in a supplementary session in which only the recognition task was tested. We collected recognition data from a total of 13 MCI subjects and 14 elderly controls.
In the recognition task, a set of 40 high-distortion dot patterns was randomly generated for each participant. To construct the set, 40 different prototypes were first randomly generated, and then a high distortion of each individual prototype was generated. Five of the high distortions were randomly selected to serve as “old” study items, and the remaining 35 patterns served as lures. In an initial study phase, each of the old items was presented 8 times each (8 blocks of 5 randomly ordered presentations of the items). In a subsequent test phase, there were 7 blocks of 10 trials each. Within each test block, each of the 5 old items was presented once, and there were also 5 presentations of novel lures. The order of presentation within each block was randomized. Subjects were provided with explicit memory instructions prior to viewing the patterns in the study phase. In the test phase, subjects were instructed to respond “old” only if a test pattern was an exact match to one of the items presented during study. All other aspects of the stimulus materials, timing of the displays, and so forth, were the same as already described for the dot-pattern categorization tasks.
Across the 7 blocks of recognition testing, the mean proportion of correct recognition decisions was significantly higher for the controls (.82) than for the MCI subjects (.68), t(25) = 2.24, p = .034. An analysis restricted to just the first block of recognition testing yielded extremely similar results: control mean = .82, MCI mean = .65, t(25) = 2.28, p = .031.
Appendix C. Dot-Pattern Ratings Experiment
Method
Subjects
The subjects were 73 undergraduates from Indiana University who participated in partial fulfillment of an introductory psychology course requirement.
Stimuli
The stimuli were 25 sets of 20 low distortions of dot pattern prototypes. The patterns of each set were constructed by using consistent, random permutations of the coordinates of the low distortions of Dot-Set 1. Included among the 25 sets were the low distortions of Dot-Sets 1 and 2.
Procedure
Subjects provided ratings on three scales. One scale assessed the extent to which the patterns in each set had a simple and regular structure. A second scale assessed the extent to which the patterns resembled or reminded the observers of some object or form that they had experienced in the real world. A third scale assessed the extent to which the patterns within each set were similar to one another. Subjects provided ratings on a scale from 1 through 9 and were urged to use the full range of the scale. The ratings were provided during blocks of 25 trials (one rating scale per block) and the ordering of the three rating blocks was randomized for each subject. On each trial, the full set of 20 low distortions of a given dot set was displayed simultaneously on the screen in a 5 × 4 grid. The assignment of each dot pattern within a set to each location in the grid was chosen randomly on each trial for each subject. The order of presentation of the 25 dot sets was randomized anew for each subject in each rating block.
Results
The distributions of mean ratings for the 25 dots sets are shown for each of the ratings scales in Figure A3. As can be seen in the figure, the mean ratings for Dot-Set 1 were towards the upper end of the distribution on the simplicity and resemblance scales, whereas the mean ratings for Dot-Set 2 were at the lower end of each of these scales. We will refer to the 23 dot sets not including Dot-Sets 1 and 2 as the remaining dot sets. Dot-Set 1 had a significantly higher mean rating on the simplicity scale than did the remaining dot sets, t(72) = 2.64, p = .01; whereas Dot-Set 2 had a significantly lower rating, t(72) = −2.02, p < .05. Likewise, Dot-Set 1 had a significantly higher mean rating on the resemblance scale than did the remaining dot sets, t(72) = 3.35, p < .01, whereas Dot-Set 2 had a significantly lower rating, t(72) = −3.18, p < .01. The patterns of results went in the same direction on the similarity scale but were not statistically significant.
Figure A3.
Distribution of mean ratings on each of the three scales for the 25 dot sets. The ratings for Dot-Sets 1 and 2 are indicated by the vertical lines in each panel.
Footnotes
Bozoki et al. (2006, p. 822-823) used the same type of evidence to document explicit-memory deficits in the patient groups that they tested. In addition, as reported in our Experiment 2, we conducted a recognition-memory task involving the dot-pattern stimuli used in subsequent tasks in the complete battery. As reported in Appendix B, the MCI subjects performed significantly worse than did the controls on this recognition task, providing another source of evidence of the explicit-memory deficits of our MCI group.
Bozoki et al. (2006, p. 818) report that their AD subjects had mean age 73.9, mean education 14.7, and mean MMSE score 20.6. Our AD subjects had mean age 76.3, mean education 15.8, and mean MMSE score 23.6.
An ardent implicit-prototype theorist might argue that our MCI subjects would have been unable to explicitly recognize even one or two of the typical features from the training set. Such a concern is mitigated by two considerations. First, Reed et al. (1999) tested amnesic subjects with explicit-memory deficits at least as great as those of our MCI subjects. Using a study procedure and cartoon animals that were essentially identical to the present ones, these investigators found that their subjects could recall in a cued-recall task roughly 9 of the 18 features that had composed the training items. (Given this clear-cut result, Bozoki et al. (2006) did not collect explicit memory judgments for the individual features in their follow-up study. Given our already long task battery, we decided to omit such a task as well.) Second, we tested our MCI subjects in an explicit recognition task involving the dot-pattern stimuli from Experiment 2 (see Appendix B). Although the MCIs performed significantly worse on the recognition task than did the controls, their overall performance (68% correct) was far better than chance (50% correct).
Palmeri and Flanery (1999) used a more elaborate manipulation in which subjects were led to believe that they had experienced a “subliminal” study phase. Although this manipulation is an ingenious one, we worried that some of our memory-impaired subjects might not fully engage in the task if the instructions failed to convince them of their ability to categorize from subliminally presented patterns. Thus, because of limits in the number of available MCI subjects, we decided to investigate these issues involving learning-during-test in the present more straightforward manner.
The BIC penalty term provides only an approximation to the overall flexibility of formal models. In the present case, for example, the 2-weight model has additional flexibility because the dimensions that receive non-zero weights are not chosen a priori. We do not believe that our main conclusions would be altered if more complex model-selection techniques were used, but further research would be needed to confirm this assertion.
References
- Ashby FG, O’Brien JB. Category learning and multiple memory systems. Trends in Cognitive Sciences. 2005;9:83–89. doi: 10.1016/j.tics.2004.12.003. [DOI] [PubMed] [Google Scholar]
- Bergert FB, Nosofsky RM. A response-time approach to comparing generalized rational and take-the-best models of decision making. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2007;33:107–129. doi: 10.1037/0278-7393.33.1.107. [DOI] [PubMed] [Google Scholar]
- Berry CJ, Shanks DR, Speekenbrink M, Henson RNA. Models of recognition, repetition priming, and fluency: Exploring a new framework. Psychological Review. 2012;119:40–79. doi: 10.1037/a0025464. [DOI] [PubMed] [Google Scholar]
- Bozoki A, Grossman M, Smith EE. Can patients with Alzheimer’s disease learn a category implicitly? Neuropsychologia. 2006;44:816–827. doi: 10.1016/j.neuropsychologia.2005.08.001. [DOI] [PubMed] [Google Scholar]
- Davis T, Love BC, Preston AR. Learning the exception to the rule: Model-based fMRI reveals specialized representations for surprising category members. Cerebral Cortex. 2012 doi: 10.1093/cercor/bhr036. [DOI] [PubMed] [Google Scholar]
- Glass BD, Chotibut T, Pacheco J, Schnyer DM, Maddox WT. Normal aging and the dissociable prototype learning systems. Psychology and Aging. doi: 10.1037/a0024971. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gureckis TM, James TW, Nosofsky RM. Re-evaluating dissociations between implicit and explicit category learning: An event-related fMRI study. Journal of Cognitive Neuroscience. 2011;23:1697–1709. doi: 10.1162/jocn.2010.21538. [DOI] [PubMed] [Google Scholar]
- Keri S. The cognitive neuroscience of category learning. Brain Research Reviews. 2003;43:85–109. doi: 10.1016/s0165-0173(03)00204-2. [DOI] [PubMed] [Google Scholar]
- Keri S, Kalman J, Keleman O, Benedek G, Janka Z. Are Alzheimer’s disease patients able to learn visual prototypes? Neuropsychologia. 2001;39:1218–1223. doi: 10.1016/s0028-3932(01)00046-x. [DOI] [PubMed] [Google Scholar]
- Keri S, Kalman J, Rapcsak SZ, Antal A, Benedek G, Janka Z. Classification learning in Alzheimer’s disease. Brain. 1999;122:1063–1068. doi: 10.1093/brain/122.6.1063. [DOI] [PubMed] [Google Scholar]
- Knowlton B, Squire L. The learning of categories: Parallel brain systems for item memory and category knowledge. Science. 1993;262(5140):1747–1749. doi: 10.1126/science.8259522. [DOI] [PubMed] [Google Scholar]
- Kolodny J. Memory processes in classification learning: An investigation of amnesic performance in categorization of dot patterns and artistic styles. Psychological Science. 1994;5:164–169. [Google Scholar]
- Love B, Gureckis T. Models in search of the brain. Cognitive, Affective, and Behavioral Neuroscience. 2007;7(2):90–108. doi: 10.3758/cabn.7.2.90. [DOI] [PubMed] [Google Scholar]
- McKhann G, Drachman D, Folstein M, Katzman R, Price D, Stadlan EM. Clinical diagnosis of Alzheimer’s disease: report of the NINCDS-ADRDA Work Group under the auspices of Department of Health and Human Services Task Force on Alzheimer’s Disease. Neurology. 1984;34:939–944. doi: 10.1212/wnl.34.7.939. [DOI] [PubMed] [Google Scholar]
- Newell BR, Dunn JC, Kalish M. Ross BH, editor. Systems of category learning: Fact or fantasy? The Psychology of Learning and Motivation. 2011;54:167–215. [Google Scholar]
- Nomura EM, Reber PJ. A review of medial temporal lobe and caudate contributions to visual category learning. Neuroscience and Biobehavioral Reviews. 2008;32:279–291. doi: 10.1016/j.neubiorev.2007.07.006. [DOI] [PubMed] [Google Scholar]
- Norman KA. How hippocampus and cortex contribute to recognition memory: Revisiting the complementary learning systems model. Hippocampus. 2010 doi: 10.1002/hipo.20855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norman KA, O’Reilly RC. Modeling hippocampal and neocortical contributions to recognition memory: A complementary-learning-systems approach. Psychological Review. 2003;110:611–646. doi: 10.1037/0033-295X.110.4.611. [DOI] [PubMed] [Google Scholar]
- Nosofsky RM. Attention, similarity, and the identification-categorization relationship. Journal of Experimental Psychology: General. 1986;115:39–57. doi: 10.1037//0096-3445.115.1.39. [DOI] [PubMed] [Google Scholar]
- Nosofsky RM. Exemplar-based accounts of relations between classification, recognition, and typicality. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1988;14:700–708. [Google Scholar]
- Nosofsky RM, Little DR, James TW. Activation in the neural network responsible for categorization and recognition reflects parameter changes. Proceedings of the National Academy of Sciences. 2012;109:333–338. doi: 10.1073/pnas.1111304109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nosofsky RM, Zaki SR. Dissociations between categorization and recognition in amnesic and normal individuals: An exemplar-based interpretation. Psychological Science. 1998;9(4):247–255. [Google Scholar]
- Palmeri TJ, Flanery MA. Learning about categories in the absence of training. Psychological Science. 1999;10(6):526–530. [Google Scholar]
- Palmeri TJ, Flanery MA. Memory systems and perceptual categorization. In: Ross BH, editor. The psychology of learning and motivation: Advances in research and theory. Vol. 41. Academic Press; San Diego: 2002. pp. 141–189. [Google Scholar]
- Pennanen C, Kivipelto M, et al. Hippocampus and entorhinal cortex in mild cognitive impairment and early AD. Neurobiology of Aging. 2004;25:303–310. doi: 10.1016/S0197-4580(03)00084-8. [DOI] [PubMed] [Google Scholar]
- Perry RJ, Hodges JR. Attention and executive deficits in Alzheimer’s disease: A critical review. Brain. 1999;122:383–404. doi: 10.1093/brain/122.3.383. [DOI] [PubMed] [Google Scholar]
- Petersen RC. Mild cognitive impairment as a diagnostic entity. Journal of Internal Medicine. 2004;256(3):183–194. doi: 10.1111/j.1365-2796.2004.01388.x. [DOI] [PubMed] [Google Scholar]
- Poldrack R, Foerde K. Category learning and the memory systems debate. Neuroscience and Biobehavioral Reviews. 2008;32:197–205. doi: 10.1016/j.neubiorev.2007.07.007. [DOI] [PubMed] [Google Scholar]
- Posner MI, Goldsmith R, Welton KE., Jr. Perceived distance and the classification of distorted patterns. Journal of Experimental Psychology. 1967;73:28–38. doi: 10.1037/h0024135. [DOI] [PubMed] [Google Scholar]
- Reber P, Gitelman D, Parrish T, Mesulam M. Dissociating explicit and implicit category knowledge with fMRI. Journal of Cognitive Neuroscience. 2003;15(4):574–583. doi: 10.1162/089892903321662958. [DOI] [PubMed] [Google Scholar]
- Reber PJ, Stark CEL, Squire LR. Cortical areas supporting category learning identified using fMRI. Proceedings of the National Academy of Sciences. 1998a;95:747–750. doi: 10.1073/pnas.95.2.747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reber PJ, Stark CEL, Squire LR. Contrasting cortical activity associated with category memory and recognition memory. Learning and Memory. 1998b;5:420–428. [PMC free article] [PubMed] [Google Scholar]
- Reed JM, Squire LR, Patalano AL, Smith EE, Jonides JJ. Learning about categories that are defined by object-like stimuli despite impaired declarative memory. Behavioral Neuroscience. 1999;113:411–419. doi: 10.1037//0735-7044.113.3.411. [DOI] [PubMed] [Google Scholar]
- Schwarz G. Estimating the dimension of a model. The Annals of Statistics. 1978;6:461–464. [Google Scholar]
- Shanks DR, St. John M. Characteristics of dissociable human learning systems. Behavioral and Brain Sciences. 1994;17:367–447. [Google Scholar]
- Smith EE. The case for implicit category learning. Cognitive, Affective, and Behavioral Neuroscience. 2008;8:3–16. doi: 10.3758/cabn.8.1.3. [DOI] [PubMed] [Google Scholar]
- Smith EE, Patalano A, Jonides J. Alternative strategies of categorization. Cognition. 1998;65(2-3):167–196. doi: 10.1016/s0010-0277(97)00043-7. [DOI] [PubMed] [Google Scholar]
- Squire LR, Clark RE, Bayley PJ. Medial temporal lobe function and memory. In: Gazzaniga M, editor. The cognitive neurosciences. 3rd ed MIT Press; Cambridge, MA: 2004. pp. 691–708. [Google Scholar]
- Squire L, Knowlton B. Learning about categories in the absence of memory. Proceedings of the National Academy of Sciences of the United States of America. 1995;92(26):12470–12474. doi: 10.1073/pnas.92.26.12470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tversky A. Elimination by aspects: A theory of choice. Psychological Review. 1972;79:281–299. [Google Scholar]
- Voss JL, Baym CL, Paller KA. Accurate forced-choice recognition without awareness of memory retrieval. Learning and Memory. 2008;15:454–459. doi: 10.1101/lm.971208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westerberg CE, Paller KA, et al. When memory does not fail: Familiarity-based recognition in mild cognitive impairment and Alzheimer’s disease. Neuropsychology. 2006;20:193–205. doi: 10.1037/0894-4105.20.2.193. [DOI] [PubMed] [Google Scholar]
- Wills AJ, Pothos EM. On the adequacy of current empirical evaluations of formal models of categorization. Psychological Bulletin. 2012;138:102–125. doi: 10.1037/a0025715. [DOI] [PubMed] [Google Scholar]
- Zaki SR. Is categorization performance really intact in amnesia? A meta-analysis. Psychonomic Bulletin and Review. 2004;11(6):1048–1054. doi: 10.3758/bf03196735. [DOI] [PubMed] [Google Scholar]
- Zaki SR, Nosofsky R. A single-system interpretation of dissociations between recognition and categorization in a task involving object-like stimuli. Cognitive, Affective, & Behavioral Neuroscience. 2001;1(4):344–359. doi: 10.3758/cabn.1.4.344. [DOI] [PubMed] [Google Scholar]
- Zaki SR, Nosofsky R. A high-distortion enhancement effect in the prototype learning paradigm: Dramatic effects of category learning during test. Memory & Cognition. 2007;35(8):2088–2096. doi: 10.3758/bf03192940. [DOI] [PubMed] [Google Scholar]
- Zeithamova D, Maddox WT, Schnyer DM. Dissociable prototype learning systems: Evidence from brain imaging and behavior. The Journal of Neuroscience. 2008;28:13194–13201. doi: 10.1523/JNEUROSCI.2915-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]