Determining the calibration of confidence estimation procedures for unique peptides in shotgun proteomics

Abstract

The analysis of a shotgun proteomics experiment results in a list of peptide-spectrum matches (PSMs) in which each fragmentation spectrum has been matched to a peptide in a database. Subsequently, most protein inference algorithms rank peptides according to the best-scoring PSM for each peptide. However, there is disagreement in the scientific literature on the best method to assess the statistical significance of the resulting peptide identifications. Here, we use a previously described calibration protocol to evaluate the accuracy of three different peptide-level statistical confidence estimation procedures: the classical Fisher’s method, and two complementary procedures that estimate significance, respectively, before and after selecting the top-scoring PSM for each spectrum. Our experiments show that the latter method, which is employed by MaxQuant and Percolator, produces the most accurate, well-calibrated results.

1. Introduction

In a typical shotgun proteomics experiment, a database search procedure assigns to each of the tens of thousands of observed fragmentation spectra a peptide from a given database [1, 2, 3]. The resulting peptide-spectrum matches (PSMs) are then ranked by a match quality score that, ideally, places the correctly matched spectra near the top of the ranked list. Because many spectra are incorrectly matched, however, a key challenge in this setting is the assignment of accurate statistical confidence estimates to the resulting identified spectra [4]. Such estimates are essential for setting appropriate score thresholds to control the error rates and for the downstream interpretation of the results.

The confidence assigned to a PSM may be reported using various measures, but all of them rely fundamentally on the notion of a p value. Roughly speaking, the p value assigned to a match between spectrum S and peptide P with score x is the probability that we would observe a score greater than or equal to x, assuming that P is not actually responsible for generating S. Statisticians refer to the situation that we are not interested in—in this case, that peptide P did not generate spectrum S—as the null hypothesis. Thus, a small p value indicates high confidence, because it is extremely unlikely that we would observe such a high score from data generated under the null hypothesis.

Before conclusions can be drawn from the results, the p values must be corrected for multiple testing, because thousands of spectra are matched to the thousands of peptides in the database. This correction can be done using a false discovery rate (FDR) analysis [5, 6, 7], which estimates the expected fraction of false positives among the identifications accepted by a given score threshold x, i.e., identifications with scores greater than or equal to x. To describe the confidence of a specific identification, the q value is defined as the minimal FDR required to accept the identification, after having considered all possible thresholds. For PSMs, the confidence is routinely estimated using one of several different approaches, including target-decoy analysis [8, 9], parametric curve fitting procedures [10, 11], maximum likelihood methods [12] or exact dynamic programming methods [13].

In this work, we focus on methods for assigning statistical confidence estimates to peptides, rather than to PSMs. Although the definition of a unique peptide can vary, for example depending on how alternative post-translational modifications are considered, this study deals with any reduction of PSMs to peptides. Regardless of the peptide definition, peptide confidence estimates are interesting for two reasons. First, in peptidomics [14], the peptides themselves are the entity of interest and the need for peptide-level confidence estimates is obvious. Second, even in experiments in which proteins are of primary interest, many existing protein confidence estimation procedures require accurate peptide-level confidence estimates as an intermediate step. Such procedures include commonly used algorithms such as ProteinProphet [15], MaxQuant [16] and Fido [17]. It should be noted, however, that protein confidence is sometimes estimated directly from PSMs [18, 19].

A priori, it may not be immediately obvious that confidence estimates assigned to PSMs cannot be transferred directly to peptides. To see that such an approach is problematic, consider an example in which 1000 PSMs are deemed significant with an FDR of 0.01. This set of selected PSMs should contain approximately 99% correct matches and 1% incorrect matches [6, 7]. To produce a list of unique peptides, it is tempting to take the list of confident PSMs, make a corresponding list of all the peptides therein, and then claim that 99% of these peptides were correctly identified. This claim, however, is likely to be incorrect. The reason is illustrated in Figure 1 and demonstrated below. The essence of the problem is that a truly present peptide will be matched by a higher number of PSMs, on average, than an absent peptide. This asymmetry arises because the incorrect PSMs are distributed across the entire peptide database, whereas the correct PSMs are distributed across only the set of present peptides. As a consequence, the peptide-level FDR is often higher than for the corresponding set of PSMs.

Figure 1. False discovery rate increases when we move from PSMs to peptides.

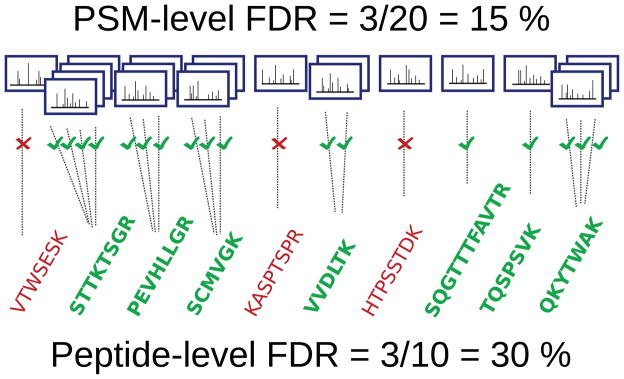
The figure illustrates how the FDR associated with a collection of 20 PSMs might double when we consider FDR calculated at the peptide-level for the same spectra.

Given that PSM-level statistical confidence estimates cannot be used as peptide-level confidence estimates, we need a reliable method to convert from one to the other. An intuitive approach could be to combine the evidence from many PSMs mapping to the same peptide to produce a single confidence estimate for the given peptide. However, previous studies have pointed out that multiple PSMs cannot be considered independent evidence of the peptide’s presence in the mixture [15]. Due to this dependence between spectra that map to the same peptide, many procedures weed out redundant PSMs, discarding all but the highest scoring PSM for each peptide. Indeed, to our knowledge, this principle is used by all fully probabilistic protein level inference methods described in the literature [20, 21, 16, 22, 23].

However, once the redundant PSMs have been eliminated, the literature is split between two different ways to assign confidence measures to the remaining PSMs, the so called peptide-level statistics. Some authors suggest that one should use the PSM-level statistics of the remaining peptides [24, 15]. We will refer to this procedure as Estimate then Weed-Out (ETWO). Other authors suggest that one should first weed out the redundant PSMs and then calculate peptide-level measures using target-decoy analysis. We refer to this procedure as Weed-Out Then Estimate (WOTE). WOTE is employed for instance in MaxQuant [16] and Percolator [21].

In this work, we systematically evaluate the statistical calibration of ETWO and WOTE. We apply a previously described calibration protocol [25] to three datasets using three different scoring functions. We demonstrate that WOTE yields better calibrated statistics than ETWO in each of our analyses, an effect that becomes quite pronounced when using multiple hypothesis corrected statistics, such as FDRs, q values and posterior error probabilities (PEPs) of the unique peptides. Furthermore, similar to a negative control, we empirically confirm the dependence between multiple PSMs mapping to the peptide by also testing the calibration of Fisher’s method to combine p values.

2. Methods

2.1. Estimating peptide-level p values

The input to a statistical confidence estimation procedure is a collection of fragmentation spectra, each of which is associated with a single target peptide and a single decoy peptide. Each target or decoy PSM is assigned a score.

We consider three methods for estimating peptide-level p values. The first procedure, WOTE, proceeds as follows. Separately for the target and the decoy matches, we identify peptides that appear multiple times in this list of PSMs, and from each set of redundant PSMs, we eliminate all but the highest-scoring PSM. The result is two lists of peptides—targets and decoys—ranked by score. From here, the procedure is identical to what has been described previously [26]: we treat the decoy scores as a null distribution, and we use them to compute p values for the target scores. Specifically, for an observed score x associated with a given target PSM, the corresponding p value is estimated as the fraction of decoys with scores better than x. Assuming that the score function is defined such that large scores are better, then the p value of x is estimated as in Equation 1, where X₀ is the set of scores of the decoy PSMs of interest:

$$\widehat{p(x)}=\frac{\mid \{x_0\in X_0:x_0\ge x\}\mid +1}{\mid X_0\mid +1},$$ (1)

In this setting, we interpret X₀ as the unique decoy peptides remaining after we have removed PSMs with redundant peptide matches. The addition of 1 to the numerator and denominator yields a p value estimate with the correct type 1 error rate [27]. The above equation can be roughly understood by reasoning that the target PSM itself, with score x, is also drawn from the null distribution when the null hypothesis is true. Subsequently, the resulting collection of peptide p values can be adjusted for multiple testing using standard methods [6, 28, 29]. Thus, the output of the procedure is a list of peptides, each associated with a PEP or a q-value.

The second procedure, ETWO, is similar to WOTE; however, in this case, we calculate all statistics with respect to PSMs rather than peptides. Hence, we instead interpret X₀ in Equation 1 as the set of decoy PSMs before we have removed redundancy. We also perform all the multiple hypothesis corrections based on all PSMs. We subsequently use the PSM-level PEPs and q values as peptide-level statistics.

The third strategy is the classical Fisher’s method to combine independent p values. This approach combines a set of PSM-level p values into a peptide-level p value, under the null hypothesis that all PSMs are incorrect. First, p values are calculated according to Equation 1 and, just like in the ETWO method, peptides that appear multiple times are not filtered out before the p value calculation; hence, X₀ in this case is the set of all decoy PSMs. This procedure thus yields PSM-level p values. Subsequently, the p values p_i, …, p_k of the k PSMs matching a given peptide are combined into a χ² test statistic:

$${\chi }^2=-2\sum _{i=1}^{k}ln(p_i)$$ (2)

Assuming that the peptides were identified independently, this statistic follows a χ² distribution with 2k degrees of freedom, thereby allowing us to calculate a p value corresponding to the observed χ². Finally, the peptide-level p values are converted to q values, as described above.

2.2. Assessing the calibration of estimated p values

To determine whether the estimated peptide-level p values are accurate, we employ a previously described semi-labeled calibration test [25]. This test involves searching spectra derived from a purified sample of known protein content with respect to a bipartite target database containing a sample partition and an entrapment partition. The sample partition includes amino acid sequences of the known proteins and likely contaminants in the sample. The entrapment partition is larger, and contains repeatedly shuffled versions of the sample sequences. Considering only the highest scoring PSM of each spectrum, most uninterpretable spectra will match to the entrapment sequences of the bipartite database. These matches are then labeled as incorrect, and are used as a null model, while the other PSMs are discarded. Hence, using an additional decoy database, p values can be assigned to entrapment PSMs (or peptides), to obtain a set of null p values. By definition, null p values follow a uniform distribution; hence, we can test our p value estimation procedure by examining the distribution of p values assigned to entrapment PSM. The entrapment partition differs from a decoy database in the sense that the matches are not used to estimate error rates; instead, the entrapment partition serves to “trap” as many of the uninterpretable spectra as possible. The decoy databases used here are reversed versions of the bipartite target databases.

2.3. Datasets

To test the calibration of p values, we used fragmentation spectra from three different samples of known protein content [30, 31, 32] (Table 1). The sequences of the proteins and the known contaminants of the sample make up the sample partition of the bipartite database. Each protein sequence was then shuffled 25 times to generate an entrapment partition 25 times the size of the sample partition. This number was chosen to obtain an entrapment partition sufficiently larger than the sample partition. The sample and entrapment sequences were concatenated for each dataset to form the bipartite databases used in the calibration protocol.

Table 1. Datasets used for the calibration test of the p values.

Three datasets generated from purified protein samples were used in this study. The table lists the names we assign to each dataset, a short description, and how we form a database for the expected identifications (the sample database).

Name	Description	Sample database
ISB18 mix	Ten Orbitrap runs from the Seattle Proteome Center’s Standard Protein Mix Database mix 7 [30].	Provided with the data (110 proteins including contaminants).
Sigma 49 mix	Three replicate LTQ analyses of human proteins from the Mass Spectrometry Research Center at Vanderbilt University [31].	Universal Proteomics Standard FASTA file (Sigma Aldrich, 49 proteins).
OMICS 2002	14 runs of control mixture A reported in OMICS 2002 and obtained from the Institute for Systems Biology (Seattle, WA, USA) [32].	Provided with the data (107 proteins).

The spectra were searched and scored using Crux version 1.37 [33] in sequest-search mode and MSGF+ version 8806 [13]. The negative logarithm of the MSGF+ E value was used as the MSGF+ score. The Crux searches were followed by analysis via Percolator version 2.03 [21]. Non-enzymatic searches were used, with a 10 ppm precursor mass tolerance for the ISB18 dataset, and 3 Da for the Sigma 49 and OMICS 2002 datasets. We calculate the p value as explained above, according to Equation 1. The distribution of entrapment p values was evaluated by the distance, D_KS, reported from a Kolmogorov-Smirnov (K-S) test. The smaller the value of D_KS, the closer to uniform the p value distribution. Finally, quantile-quantile (Q-Q) plots were made to compare the empirical distribution of null p values with a uniform distribution.

In experiments involving complex mixtures from full cell lysates, a yeast dataset described previously [21] was used. Here, we searched the data with Crux and Percolator as described above, but using tryptic searches with any number of missed cleavages and a 3 Da mass tolerance window.

3. Results

3.1. The WOTE method yields well calibrated peptide-level p values

When comparing different methods to compute peptide-level p values, our main concern is that the p values are well calibrated, meaning that the statistical scores accurately indicate our confidence in the correctness of the peptide identification. Therefore, as described above, we compare the null distribution of reported p values to an ideal uniform distribution using a Q-Q plot, in which a uniform p value distribution lies close to the y = x diagonal.

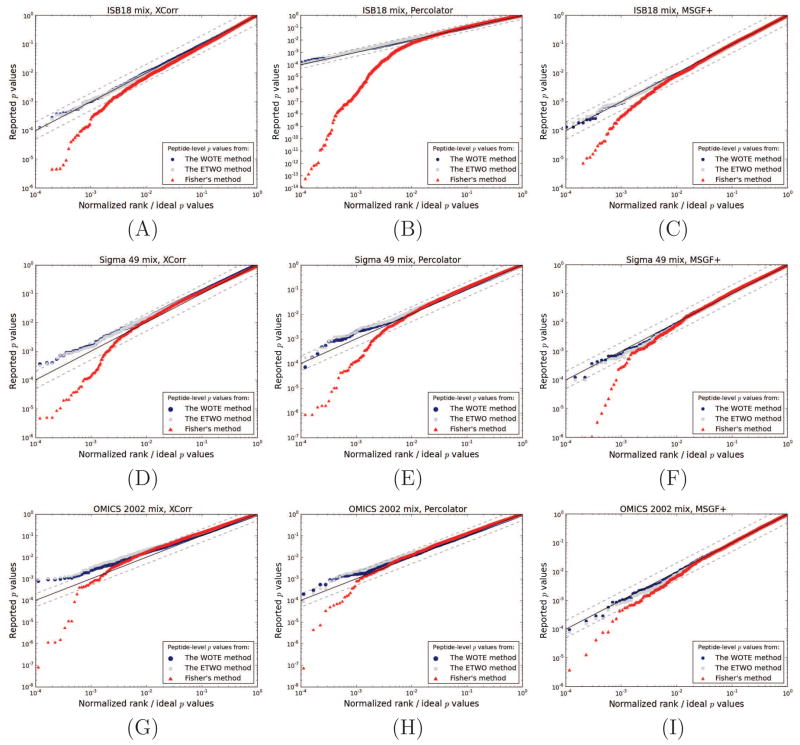
We tested the calibration of the peptide-level p values reported from the WOTE, ETWO and Fisher’s methods using three scoring schemes—the SEQUEST XCorr [34], the MSGF+ score [13] and the Percolator score [21]—on three different datasets of known protein mixtures. The results are shown in Figure 2. Regardless of the scoring scheme or dataset used, the WOTE and the ETWO method yields entrapment peptide p values that distribute nearly uniformly. Fisher’s method, on the other hand, clearly produces p values that lie further from the uniform distribution. The mean Kolmogorov-Smirnov D_KS values of the three scores across the datasets (ISB18 mix, Sigma 49 and OMICS, respectively) were 0.014, 0.025, 0.022 for WOTE, 0.028, 0.041, 0.037 for ETWO and 0.047, 0.048, 0.046 for Fisher’s method. Although the figures indicate no large differences between WOTE and ETWO, the D_KS values suggest that WOTE is better calibrated. The D_KS value quantifies the deviance of all p values from the uniform distribution, and does not emphasize the importance of small p values, as the log-scaled plot does. However, the peptides assigned low p values are generally of more interest than others; thus, the calibration of these p values is more important.

Figure 2. The calibration of peptide-level p values from WOTE, ETWO and Fisher’s method.

Three different datasets of known protein mixtures were scored against a bipartite target and a reversed decoy database using Crux, MSGF+ and Percolator. Subsequently, p values were estimated using either the SEQUEST’s XCorr (left side panels), the Percolator score (middle panels) or scores from MSGF+ (right side panels). Entrapment peptide p values are plotted relative to an ideal, uniform distribution of p values. The y = x diagonal is indicated by a black line, and y = 2x and y = x/2 are shown by dashed lines. Panels (A), (B) and (C) show results from the ISB18 mix. Panels (D), (E) and (F) represent the Sigma 49 mix, and panels (G), (H) and (I) represent the OMICS 2002 mix.

For independent tests, Fisher’s method outputs uniformly distributed p values under the null hypothesis. Therefore, the poor empirical calibration of the p values produced by Fisher’s method’s is due to dependencies between peptide sequences and peptide scores. This phenomenon is illustrated in Figure 3(A), which shows the correlation between scores assigned to the same entrapment peptide with respect to two different spectra. In general, such a dependence is expected for peptides that are present in the sample, but not for peptides that are absent. This observed covariation leads us to suspect that peptide sequences have some inherent sequence property that repeatedly causes similar scores. This is analogous to spectral covariation, seen for raw score functions such as XCorr [11, 4], but with respect to the peptide sequence rather than the spectrum. To test whether peptide sequence properties such as peptide length (Figure 3 B), mass or m/z (data not shown) influenced this correlation, we plotted the Percolator score as a function of these properties; however, no correlation was observed for these features. One plausible, alternative explanation for this phenomenon is that the theoretical fragment masses of the peptide sequence by chance closely resemble the fragmentation spectrum of a common modified peptide in the sample, which is not found in the protein database [15].

Figure 3. Covariation of entrapment peptides’ p values.

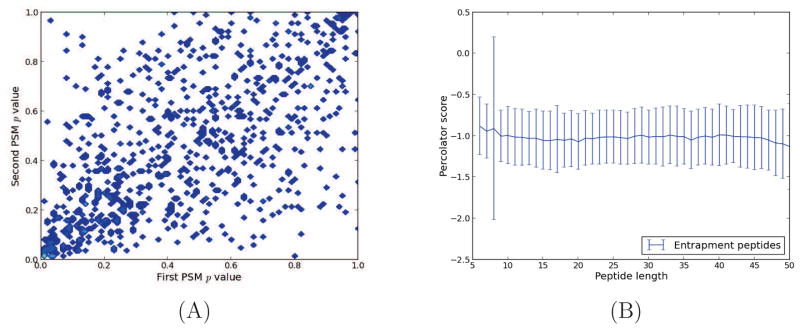
Orbitrap spectra from 10 runs of the ISB18 mix 7 were searched against a bipartite database. For each of the 10 runs, we collected only the entrapment peptides that had been identified twice. (A) Based on their Percolator score, we plotted the two PSM-level p values for each identified peptide (Pearson correlation coefficient = 0.60). Similar covariation was seen for p values estimated using Crux and MSGF+, as well as for the two other standard datasets. (B) The mean Percolator score of entrapment PSMs as a function of peptide length (number of amino acids in peptide sequence). The error bars represent one standard deviation.

3.2. The difference between WOTE and ETWO becomes more pronounced at the level of multiple-hypothesis corrected statistics

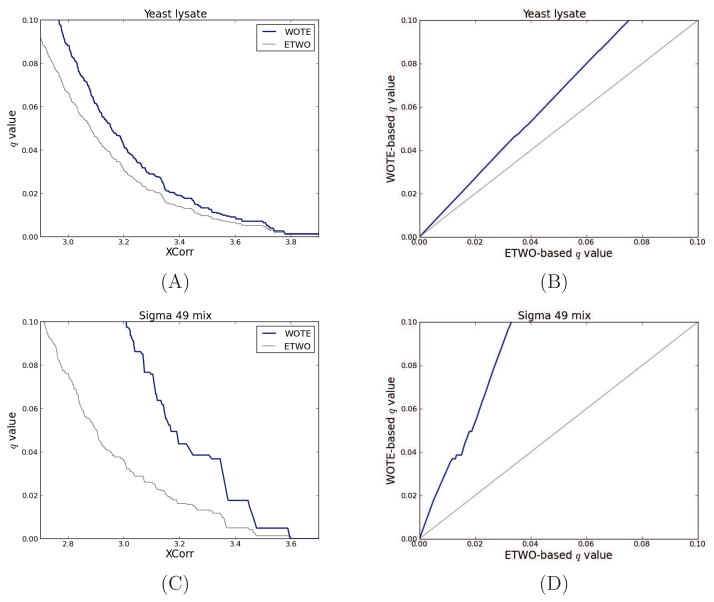
A striking difference between ETWO and WOTE lies in the sets to which the multiple-hypothesis correction is applied. With ETWO, multiple-hypothesis corrected statistics are calculated for PSMs, while they are calculated for unique peptides with WOTE. From a theoretical perspective, it is clear that multiple-hypothesis corrections should be applied to the set of hypothesis that are tested, and not to another set. For this reason, we expect that WOTE will give more accurate results because it performs its multiple hypothesis corrections on the same level as we report our statistics. To demonstrate this difference, we applied the WOTE and ETWO method to two different datasets (Figure 4). The left panels illustrate the relationship between WOTE and ETWO peptide-level q values as a function of the underlying score, and the right panels show the direct relationship between the two types of q values. For example, in panel B, which corresponds to a collection of spectra from a yeast whole cell lysate, an ETWO-based q value threshold of 1% corresponds to a WOTE-level q value threshold of 1.35%. In terms of the number of identifications, ETWO and WOTE identifies 1661 and 1516 unique peptides, respectively, for a 1% q value threshold.

Figure 4. Varying data complexity: Comparison between WOTE and ETWO peptide-level q values.

The left two panels plot the WOTE and ETWO peptide-level q values as a function of XCorr threshold; the right panels plot peptide-level q values as a function of PSM-level q values. Panels (A) and (B) correspond to a high complexity set of 35,108 target and 35,108 decoy PSMs derived from a yeast whole cell lysate [21]. Panels (C) and (D) correspond to a low complexity set of 34,816 target and 34,816 decoy PSMs from the Sigma 49 dataset. All q values were estimated using qvality [37] considering their XCorr score. Two-sided K-S tests of the similarity between q values from WOTE and ETWO produced highly significant p values (< 10⁻¹⁰⁰), indicating their difference. Similar results were obtained when using the Percolator score and MSGF+ (data not shown).

A more pronounced difference between these two types of q values can be seen for highly purified mixtures (panels C and D). For all datasets we analyzed, the line representing peptide-level versus PSM-level q values was consistently above y = x, regardless of the score and mass tolerance window used. These results clearly illustrate that the false discovery rate associated with a fixed score threshold is larger at the peptide-level than at the PSM-level.

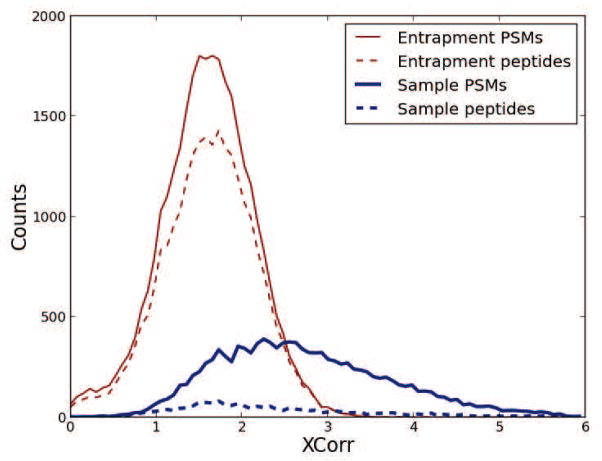
As mentioned previously, the explanation for the higher false discovery rate on the peptide-level than on the PSM-level is that the average number of PSMs that match present peptides is higher than the average number of PSMs that match absent peptides. To illustrate this phenomenon, we made histograms of the distribution of the ISB18 PSMs matching the sample and entrapment part of the target database (Figure 5). From the histogram we can see the dramatic effect produced by present peptides amassing more PSMs than absent peptides. This effect explains the large deviations in multiple hypothesis corrected statistics between WOTE and ETWO: q values and false discovery rates are proportional to the ratios of the areas under the curve between incorrect and all identifications with scores over a threshold, fractions that we easily can spot as different for peptides and PSMs. Similarly, posterior probabilities are proportional to the ratio of the “heights of the curves” of the incorrect and all identifications, ratios that we again can spot as different between PSMs and peptides.

Figure 5. Entrapment and sample distribution for PSMs and peptides.

Using the ISB18 mix dataset, we divided our findings into entrapment and sample PSMs, depending on what sequence in the bipartite database they were matched to. We further weeded-out redundant PSMs to create a list of unique peptides, for the entrapment and sample matches. The histogram shows the effect of the weeding-out procedure for the two groups.

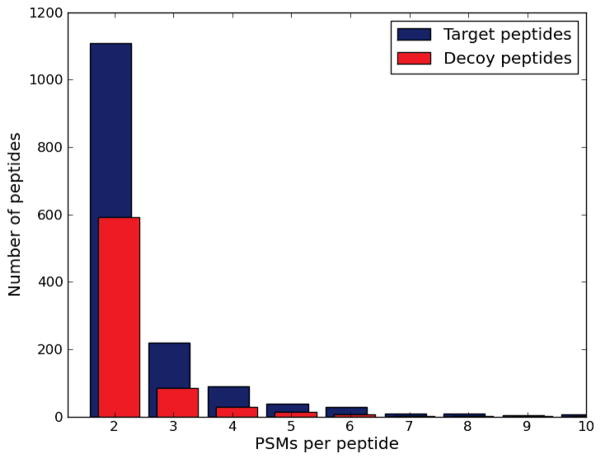
To assure that this phenomenon is not an artifact of the low complexity of the runs, we compared the number of PSMs per peptide for all peptides identified when matching 35,108 yeast spectra against a target database and a decoy database. The distribution in Figure 6 shows that target peptides are identified by more PSMs than decoy peptides.

Figure 6. The average number of PSMs per peptide is higher for matches against the target database than against the decoy database.

We scored 35,108 spectra derived from a yeast lysate against a target and a decoy database. We then compared the number of PSMs per peptide for peptides having two or more PSMs per peptide. 30,669 target peptides and 33,252 decoy peptides had one PSM each.

4. Discussion

We have employed a semi-labeled calibration test using known protein samples to assess three methods for estimating peptide-level confidence estimates. We found that WOTE and ETWO are well calibrated in the sense that they produce p values that are uniform under the null hypothesis. On the other hand, we find a large discrepancy between the q values produced by WOTE and ETWO, a discrepancy attributed to the fact that the multiple hypothesis correction is erroneously performed on the PSM-level when using ETWO.

Some use of the ETWO method is likely the result of confusion regarding the difference between PSM- and peptide-level statistics. We would like to emphasize the distinction between PSMs and unique peptides, as they comprise of two disparate sets of identifications. Hence, their error rates must be evaluated separately.

Previous research has concluded that multiple PSMs involving the same peptide should not imply increased peptide confidence because observed spectra cannot be considered independent evidence for a single peptide [15]. Bern et al. go further and claim that the number of PSMs might not differ between present and absent peptides [22]. In their observation, almost as many decoy PSMs as target PSMs (22% and 24%) redundantly identify a peptide. We confirm the non-independence of peptides by showing the extent to which p values of PSMs to the same peptide correlate, even for incorrect matches (see Figure 3(A)). On the other hand, in contrast to what Bern et al. report, but in agreement with Shteynberg et al., we show that peptides that are present in the sample do obtain more matches than absent peptides (Figure 5 and 6). This result indicates that the number of spectra matched to a peptide is indeed an important indication of the peptide confidence. Most likely, this effect did not show up for Bern et al. because a majority of the PSMs map uniquely to a peptide; thus, the average number of PSMs per target and decoy peptide does not clearly differ. However, we look closer at the redundant PSMs, and we consequently find that there is indeed a difference between target and decoy peptides. In fact, this effect is frequently used for quantifying proteins using spectral counting [35, 36].

Although we have demonstrated that WOTE is the desired method for estimating peptide level statistical confidence measures, an apparent drawback of this procedure is its failure to make use of multiple spectra matching the same peptide. Based on the above reasoning, the ideal method would estimate peptide-level statistics using information from all PSMs, without assuming independence, to improve the discrimination between present and absent peptides. This, in turn, would yield more confident protein identifications. Bern et al. introduce the principle of combining p values of PSMs mapping to the same peptide sequence, but with different post-translational modifications. The same idea could be extended to combine PSMs of peptides identified with different charge states. Such PSMs are more likely to be independent; hence, this method is probably the most accurate current approach for combining p values of multiple PSMs.

As stated earlier, the accuracy of the peptide-level confidence estimates influences the reliability of the confidence estimates for proteins. Given an unbiased and efficient protein inference algorithm, well calibrated peptide level statistics from the WOTE procedure, are expected to generate well calibrated protein level statistics. ETWO, on the other hand, is anti-conservative, and expected to generate more protein identifications, but with an inflated error rate. However, it is important to note that although the statistics of PSMs and peptides might be well calibrated, the subsequent protein inference algorithm also risks introducing biases. For completely reliable proteomics results, protein inference procedures should therefore be calibrated as well, an issue not addressed in this study.

Researchers aiming at estimating the statistical confidence of results from proteomics experiments generally make assumptions about how to model the data. The target-decoy analysis, for instance, requires such assumptions. In practice, it is difficult to know whether these assumptions are reasonable, without empirically validating the results. Thus, we encourage users and developers of new procedures for estimating peptide-level confidence, to test the accuracy of the results, for instance by using the semi-labeled calibration test.

Well-calibrated p values are a prerequisite, but no guarantee, for accurate statistics. The largest discrepancy between WOTE and ETWO is manifested on the level of multiple testing corrected statistics such as PEPs and q values. Hence, it is less of an error to use p values generated by ETWO, as Combyne [22] does, than to use multiple testing corrected posterior probabilities. As a conclusion, multiple hypothesis corrections should be carried out for the set of hypothesis that we are testing. Multiple hypothesis-corrected statistics cannot easily be transferred from one set to a subset or superset of the tested hypothesis without corrections.

Highlights.

1. Confidence estimates for unique peptides and peptide-spectrum matches (PSMs) differ.

2. Methods for transfering estimates from PSMs to peptides have not been validated.

3. Here, we evaluate the statistical accuracy, or calibration, of three such procedures.

4. One of the procedures tested (here denoted WOTE) produces well calibrated results.