Bayesian Analysis on Meta-analysis of Case-control Studies Accounting for Within-study Correlation

Abstract

In retrospective studies, odds ratio is often used as the measure of association. Under independent beta prior assumption, the exact posterior distribution of odds ratio given a single 2 × 2 table has been derived in the literature. However, independence between risks within the same study may be an oversimplified assumption because cases and controls in the same study are likely to share some common factors and thus to be correlated. Furthermore, in a meta-analysis of case-control studies, investigators usually have multiple 2×2 tables. In this paper, we first extend the published results on a single 2×2 table to allow within study prior correlation while retaining the advantage of closed form posterior formula, and then extend the results to multiple 2 × 2 tables and regression setting. The hyperparameters, including within study correlation, are estimated via an empirical Bayes approach. The overall odds ratio and the exact posterior distribution of the study-specific odds ratio are inferred based on the estimated hyperparameters. We conduct simulation studies to verify our exact posterior distribution formulas and investigate the finite sample properties of the inference for the overall odds ratio. The results are illustrated through a twin study for genetic heritability and a meta-analysis for the association between the N-acetyltransferase 2 (NAT2) acetylation status and colorectal cancer.

1 Introduction

Very often epidemiological studies involve comparison between two populations with binary outcomes. Data from these studies are usually summarized by a single or multiple 2 × 2 tables. Inference on the comparative measures between two probabilities of an adverse event, or risks, by using 2 × 2 tables has been investigated by many statisticians. The confidence intervals derived from conventional large sample theory often have poor coverage probabilities when the risk is rare or the sample size is small¹. Sometimes one could encounter the “zero cell” problem, which further impairs the use of conventional confidence intervals. A quick remedy for the “zero cell” problem is to add an arbitrary positive number to the cells^2,3,4. However, this arbitrary positive number makes the interpretation of results difficult and contradicting conclusions could be made with choices of numbers⁵. For the confidence intervals of odds ratios, the most commonly used exact method in practice is obtained by inverting the Fisher’s exact test^6,7. This method, with coverage probabilities always greater than nominal levels, has been criticized for being too conservative due to the discreteness of the test statistic^8,9,10. Consequently the loss of power would diminish the practical utility of this method.

Alternative methods have been proposed for studies with rare events or small sample sizes. In this regard, at least two general statistical approaches have been suggested. One is the frequentist approach where various confidence intervals have been proposed with the primary goal being to obtain the actual coverage probability close to the nominal level^{11,12,13,14,15,16}. Instead of inverting two separate one-sided tests as in Cornfield¹¹, Baptista and Pike¹² and Agresti and Min¹³ suggested inverting a single two-sided test. Aitkin et al.¹⁴ constructed the confidence intervals based on inverting the likelihood ratio test. More recently, Agresti and Min¹⁵ proposed the unconditional method where they found that the proposed confidence intervals tend to be shorter and have coverage probability closer to the nominal level compared to the intervals based on the conditional method.

The second general approach is the Bayesian approach where the main objective of inference is to obtain the posterior distribution of odds ratios that reflects the evidence from the data and the available prior knowledge. The Bayesian approach does not suffer from the “zero cell” problem because a prior distribution of risk is assumed and the inference is solely based on the posterior distribution of the risk or the comparative measures of risks. Conjugate beta prior distributions for risks are often used because its simplicity and flexibility to incorporate prior knowledge. Efforts have been made to obtain the posterior distribution of odds ratios. Under independent beta priors, Zelen and Parker¹⁷ and Ashby et al.¹⁸ suggested two normal approximations for the posterior distribution of log odds ratio. The exact cumulative posterior distribution of odds ratios has been derived by Numinen and Mutanen¹⁹ with the assumption of hyperparameters being positive integers. Marshall²⁰ extended the results to allow hyperparameters being any positive numbers. Given the important contributions on the exact Bayesian inference of odds ratio under independent prior risk assumption, to our best knowledge, the exact Bayesian inference under dependent beta prior risks has never been considered. In some situations, independence between risks within the same study may be an oversimplified assumption because cases and controls in the same study are likely to share some common factors and thus to be correlated. One such example is given in the following.

Our motivating example is a meta-analysis of the N-acetyltransferase 2 acetylation status and colorectal cancer risk. N-acetyltransferase 2 (NAT2) is a low-penetrance gene that regulates metabolizing enzymes. The activity of the enzymes is classified as rapid and slow acetylators. To investigate the association between rapid NAT2 acetylator status and colorectal cancer, Ye and Parry²¹ conducted a meta-analysis based on twenty published case-control studies from January 1985 to October 2001. The twenty studies were conducted at very different locations including Australia, Japan, Spain, UK and USA. Consequently, the environment and genetic background of different studies can be very different. On the other hand, cases and controls in the same study are likely to share some common, but possibly unmeasured, factors such as ancestors. The probabilities of exposures (i.e., rapid NAT2 acetylator) in cases and controls within the same study were likely to be correlated. To test this hypothesis empirically, we calculated the correlation coefficient between the proportions of having rapid NAT2 acetylator in cases and controls within the same study. A preliminary data analysis has indicated a strong within study correlations (see details in Section 4.2). Therefore, it is important to consider the consequence of ignoring within study correlation, and extend the current results under independent prior risk assumption to dependent prior assumption.

In this paper, we first extend the results in Marshall²⁰ to incorporate within study prior correlation by using the Sarmanov family²². We then extend our results to multiple 2 × 2 tables and regression setting, which are common in meta-analysis and meta-regression analysis²³. We also evaluate the performance of the models with independent and correlated priors through simulation studies. We note that the Sarmanov models for bivariate binary outcomes have been introduced to the applications of marketing innovatively by Danaher and Hardie²⁴, where the focus is on predicting one outcome given the other. In contrast, the focus of this paper is on meta-analysis, where we are more interested in estimating both the overall and study-specific odds ratios.

This article is organized as follows. Section 2 states the main results, where we first extend the current results for a single 2 × 2 table with independent priors to correlated priors, and then extend to multiple 2 × 2 tables and regression setting. In Section 3, we conduct simulation studies to verify our formulas and evaluate the finite sample performance of the estimation procedure. We illustrate our methods in Section 4 with two examples: an analysis on a single 2 × 2 table and a meta-analysis for the association between the N-acetyltransferase 2 (NAT2) acetylation status and colorectal cancer. We summarize our results and discuss possible extensions in Section 5.

2 Statistical Methodology

In this section, we will first restate the results on the exact posterior distribution of odds ratio for a single 2 × 2 table under independent prior, and then extend it to a bivariate correlated prior. Furthermore, we will extend the results to multiple 2×2 tables and discuss the estimation procedure.

2.1 Single 2 × 2 table

Let n_j, y_j and p_j (j=1,2 for case and control groups respectively) be the number of subjects, number of exposed subjects, and risk of being exposed in the jth group, respectively. Assume that the prior risks p₁ and p₂ are beta random variables with hyperparameters (a₁, b₁) and (a₂, b₂) respectively, where a_j, b_j > 0. The posterior distributions of p₁ and p₂ are beta distributions with parameters (α₁, β₁) and (α₂, β₂) respectively, where α_j = y_j + a_j and β_j = n_j − y_j + b_j (j = 1, 2). Denote the odds ratio of risks comparing the second group with the first group by θ = {p₂/(1 − p₂)}/{p₁/(1 − p₁)}. If the prior risks p₁ and p₂ are assumed independent, the posterior risks p₁ and p₂ given data are independent and the corresponding posterior distribution of odds ratio θ has been derived by Marshall²⁰ as follows

$$f_{\theta }(\theta ;{\alpha }_1,{\beta }_1,{\alpha }_2,{\beta }_2)={\theta }^{-1-{\beta }_2}{\left\{B({\alpha }_1,{\beta }_1)B({\alpha }_2,{\beta }_2)\right\}}^{-1}B({\alpha }_1+{\alpha }_2,{\beta }_1+{\beta }_2)\times F({\alpha }_2+{\beta }_2,{\beta }_1+{\beta }_2;{\alpha }_1+{\alpha }_2+{\beta }_1+{\beta }_2;1-\frac{1}{\theta }),\text{for}\theta >0,$$ (1)

where B(α, β) denotes the beta function defined by ${\int }_0^1{t}^{\alpha -1}{(1-t)}^{\beta -1}dt$ and F (·, ·; ·; ·) denotes the hypergeometric function²⁵ defined by

$$F(\alpha ,\beta ;\gamma ;z)=\frac{1}{B(\beta ,\gamma -\beta )}{\int }_0^1{t}^{\beta -1}{(1-t)}^{\gamma -\beta -1}{(1-tz)}^{\alpha }dt,\text{for}\gamma >\beta >0.$$

However, in many situations, independent priors between risks in cases and controls may be an over-simplified assumption because cases and controls within the same study are likely to share some common factors. One such example is in genetic association studies where people in same study are likely to share similar environmental factors or similar ancestors²⁶. Another example is in multivariate meta-analysis where multiple correlated outcomes of interests were provided in each study^24,27,28,29.

Sarmanov²² first proposed and studied a family of bivariate distributions constructed from marginal distributions. This framework was re-discovered and studied by Cole et al.³⁰, Lee²⁶ and Shubina and Lee³¹. The general form of the Sarmanov bivariate distribution for a pair of random variables (p₁, p₂) with the specified marginal distributions f₁(p₁) and f₂(p₂) is given by

$$g(p_1,p_2)=f_1(p_1)f_2(p_2)\{1+\rho {\psi }_1(p_1){\psi }_2(p_2)\},$$ (2)

where ψ_j(·) are bounded integrable nonconstant functions that satisfy ∫ ψ_j(t)f_j(t)dt = 0 for j = 1, 2, and 1 + ρψ₁(p₁) ψ₂(p₂) ≥ 0 to ensure a nonnegative distribution²⁶. When beta marginals for p₁ and p₂ are assumed, i.e. f_j(p_j) = B(α_j, β_j), the function ψ_j(p_j) can be ψ_j(p_j) = (p_j − μ_j)/δ_j, where μ_j = a_j/(a_j + b_j) is the mean of p_j and ${\delta }_j=\sqrt{{\mu }_j(1-{\mu }_j)/(a_j+b_j+1)}$ is the square root of variance of p_j (j = 1, 2). An advantage of choosing this function ψ_j(p_j) is that the parameter ρ has an intuitive interpretation of correlation coefficient, i.e., ρ = corr(p₁, p₂). Note that when ρ = 0, equation (2) reduces to independent bivariate beta distribution, i.e., the product of two independent beta distributions.

When beta marginals are assumed, Sarmanov family in equation (2) (referred to as Sarmanov beta priors) has the following advantage in modeling. First, it allows for both positive and negative correlations; second, it only needs specification of marginal distributions and correlation parameter, which has important advantage in Bayesian inference because it is often easier to specify and interpret univariate prior comparing to bivariate prior; third, it is pseudo-conjugate for binomial distribution, i.e., equation (2) can be expressed as linear combinations of independent bivariate beta distributions²⁶. Here we derived the exact posterior distribution of odds ratio under Sarmanov beta priors as follows (see Appendix Section A for the proof),

$$f_{\theta }^{\ast }(\theta ;{\alpha }_1,{\beta }_1,{\alpha }_2,{\beta }_2,\rho )={\omega }_1{f}_{\theta }(\theta ;{\alpha }_1,{\beta }_1,{\alpha }_2,{\beta }_2)+{\omega }_2{f}_{\theta }(\theta ;{\alpha }_1+1,{\beta }_1,{\alpha }_2,{\beta }_2)+{\omega }_3{f}_{\theta }(\theta ;{\alpha }_1,{\beta }_1,{\alpha }_2+1,{\beta }_2)+{\omega }_4{f}_{\theta }(\theta ;{\alpha }_1+1,{\beta }_1,{\alpha }_2+1,{\beta }_2),$$ (3)

where f_θ (θ; α₁, β₁, α₂, β₂) is the posterior density function of odds ratio under independent beta priors, defined in equation (1), ω_k (k = 1, …, 4) are functions of a₁, b₁, a₂, b₂, ρ given in Appendix Section A.

When within study correlation is zero, i.e., ρ = 0, in which the weights are ω₁ = 1 and ω₂ = ω₃ = ω₄ = 0, the results in equation (3) reduce to the previous results in equation (1). When within study correlation is nonzero, the prior correlation is introduced to the posterior distribution of odds ratio through the weights ω_k. Note that in order to ensure a nonnegative Sarmanov beta prior distribution, i.e., 1 + ρφ₁(p₁)φ₂(p₂) ≥ 0, the correlation ρ must subject to the constraint

$$-c/max(a_1{a}_2,b_1{b}_2)\le \rho \le c/max(a_1{b}_2,a_2{b}_1),$$

where $c=\sqrt{a_1{a}_2{b}_1{b}_2}/\sqrt{(a_1+b_1+1)(a_2+b_2+1)}$. It is easy to see that the range is narrower than [−1, 1]. For example, the constraint is [−0.5, 0.5] with Jeffreys prior (a₁ = b₁ = a₂ = b₂ = 0.5). This is a common problem for non-normal bivariate distributions such as the Farlie-Gumbel-Morgenstern distribution whose correlation coefficients are limited to the interval [−1/3, 1/3]³².

2.2 Multiple 2 × 2 tables and regression extensions

The rapid growth of evidence-based medicine has lead to a dramatic increasing attention to meta-analysis which combines statistical evidence from multiple studies. When the primary scientific interest is in comparing risks between two populations, data are often summarized by multiple 2×2 tables.

For the i-th study, let n_ji, y_ji and p_ji (j=1,2 for case and control groups respectively) be the number of subjects, number of exposed subjects, and risk of being exposed in the jth group, respectively. The study-specific risks, or the random effects, (p_1i, p_2i) are often assumed to be independent across studies, following a common distribution. To allow for heterogeneity in risks across studies and prior correlations in risks within the same study, a Bayesian hierarchical model can be assumed as follows,

$$\begin{array}{l}(p_{1i},p_{2i})\mid (a_1,b_1,a_2,b_2,\rho )\stackrel{i.id.}{\sim }g(p_1,p_2;a_1,b_1,a_2,b_2,\rho ),\hfill \\ (y_{1i},y_{2i})\mid (n_{1i},n_{2i},p_{1i},p_{2i})\stackrel{\mathit{ind}.}{\sim }\text{Binomial}(y_{1i}\mid n_{1i},p_{1i})\times \text{Binomial}(y_{2i}\mid n_{2i},p_{2i}),\hfill \end{array}$$ (4)

where the distribution g(p₁, p₂; a₁, b₁, a₂, b₂, ρ) is the Sarmanov beta prior with hyperparameters (a₁, b₁, a₂, b₂, ρ) as in model (2). Denote the dispersion parameter φ_j = 1/(a_j + b_j +1). The model (4) allows for two types of correlations: the correlation between the exposure status for two subjects from the same study and the same group, φ_j, and the correlation between the exposure status for two subjects from the same study but different groups, $\rho \sqrt{{\phi }_1{\phi }_2}$. One interesting property of the model (4) is the linear regression relationship between p_1i and p_2i. Specifically, the conditional expectation can be calculated from the equation (2) as E[p₂|p₁] = μ₁ + ρδ₂/δ₁(p₁ − μ₁), which takes the same form as in bivariate normal distribution.

These hyperparameters (a₁, b₁, a₂, b₂, ρ) are often unknown. One way is to impose another level of hierarchy by assuming the prior distributions for these parameters. Alternatively, with abundant data, the hyperparameters can be well estimated from the data. Such approaches are called empirical Bayes methods^33,34,35,36. The hyperparameters can be obtained by maximizing the log marginal likelihood combining all studies as considered in Danaher and Hardie²⁴

$$logL(a_1,b_1,a_2,b_2,\rho )=\sum _{i=1}^{n}log\left[P_{BB}(y_{1i};n_{1i},a_1,b_1)P_{BB}(y_{2i};n_{2i},a_2,b_2)\left\{1+\frac{\rho }{{\delta }_1{\delta }_2}\frac{(y_{1i}-n_{1i}{\mu }_1)(y_{2i}-n_{2i}{\mu }_2)}{(a_1+b_1+n_{1i})(a_2+b_2+n_{2i})}\right\}\right],$$ (5)

where P_Bin(y_ji; n_ji, p_ji) and P_BB(y_ji; n_ji, a_j, b_j) are the probability mass function of binomial distribution and beta-binomial distribution, respectively. The model (5) can be referred to as Sarmanov beta-binomial. When ρ = 0, the Sarmanov beta-binomial reduces to the independent beta-binomial model, i.e., product of two beta-binomial distributions. This model can be fitted using commonly used statistical software such as SAS, SPLUS/R and STATA. We implement it through R (R Development Core Team, Version 2.11.1) with the optim function, which uses a quasi-Newton method with box constraints on the ranges of parameters. Furthermore, we use delta method to get the variance of log odds ratio. The Wald intervals for log odds ratio is then calculated and transformed to the Wald intervals for odds ratio. A SPLUS/R program to fit this model (with a working example) is attached in Appendix Section B.

Denote (â₁, b̂₁, â₂, b̂₂, ρ̂) the maxima of the log marginal likelihood function (5). The quantity of primary interest, overall odds ratio, defined by θ = {μ₂/(1−μ₂)}/{μ₁/(1−μ₁)} with μ_j = a_j/(a_j +b_j) can be estimated by plugging in the estimates of hyperparameters. On the other hand, the study-specific odds ratio in the ith study, θ_i, has posterior distribution $f_{{\theta }_i}^{\ast }({\theta }_i;y_{1i}+a_1,n_{1i}-y_{1i}+b_1,y_{2i}+a_2,n_{2i}-y_{2i}+b_2,\rho )$ if the hyperparameters were known. In practice, we can simply replace the hyperparameters by their estimates. Note that the inference based on $f_{{\theta }_i}^{\ast }({\theta }_i;y_{1i}+\widehat{a_1},n_{1i}-y_{1i}+\widehat{b_1},y_{2i}+\widehat{a_2},n_{2i}-y_{2i}+\widehat{b_2},\widehat{\rho })$ ignores the uncertainty on the hyperparameter estimates, hence may leads to credible intervals that are liberal. To obtain confidence intervals that close to the nominal level, one can use the bias correction method or the bootstrap method^37,38.

To adjust for study level covariates, the model (4) can be extended to the regression setting. Specifically, we assume that the study-specific risk p_ji for j = 1, 2 have Beta distributions with mean parameters μ_ji and dispersion parameters φ_j, respectively,

$$p_{ji}\mid ({\phi }_j,{\mu }_{ji})~\text{Beta}\{p_{ji};{\mu }_{ji}/(1/{\phi }_j-1),(1-{\mu }_{ji})/(1/{\phi }_j-1)\}\text{for}j=1,2,$$

where Beta(p; α, β) is the beta distribution defined by B(α, β)⁻¹p^α−1(1−p)^β−1. Then E[p_ji|φ_j, μ_ji] = μ_ji and $var(p_{ji}\mid {\phi }_j,{\mu }_{ji})={\delta }_{ji}^2={\phi }_j{\mu }_{ji}(1-{\mu }_{ji})$. The mean of each Beta distribution is a function of covariates

$${\mu }_{ji}=h^{-1}(X_i{\eta }_j)\text{for}j=1,2,$$

where h(·) is some link function and X_i are the study-specific covariates related to study-specific risks. To allow for the correlation between risks, we assume the paired study-specific risks (p_1i, p_2i) follow the Sarmanov beta prior distribution, i.e.,

$$\begin{array}{l}(p_{1i},p_{2i})\mid ({\phi }_1,{\mu }_{1i},{\phi }_2,{\mu }_{2i})~\text{Beta}\{p_{1i};{\mu }_{1i}/(1/{\phi }_1-1),(1-{\mu }_{1i})/(1/{\phi }_1-1)\}\\ \times \text{Beta}\{p_{2i};{\mu }_{2i}/(1/{\phi }_2-1),(1-{\mu }_{2i})/(1/{\phi }_2-1)\}\left\{1+\rho \frac{(p_{1i}-{\mu }_{1i})}{{\delta }_{1i}}\frac{(p_{2i}-{\mu }_{2i})}{{\delta }_{2i}}\right\}\end{array}$$

This model allows different dispersion parameter φ_j across different groups. Similarly to the estimation procedure for model (4), this bivariate beta-binomial regression model can be fitted by maximizing the log marginal likelihood function.

3 Simulation Study

3.1 A Single case-control study

To verify the results in formulas (1) and (3) empirically, we conducted simulation studies using Monte Carlo methods. For concreteness, we used the twin study dataset considered in Fisher⁶. More details of this dataset will be introduced in Section 4.1. Two settings were considered. In the first setting, independent Jeffreys prior on p₁ and p₂ (i.e., a₁ = b₁ = a₂ = b₂ = 0.5) was assumed. We drew 5, 000 samples of p₁ and p₂ independently from f₁(p₁) = Beta(p₁; 10.5, 3.5) and f₂(p₂) = Beta(p₂; 2.5, 15.5), respectively. For each pair of samples p₁ and p₂, we calculated the odds ratio θ = {p₂/(1 − p₂)}/{p₁/(1 − p₁)} and plotted the histogram. We then calculated the density function using the formula (1) and overlaid the density curve on top of the histogram. In the second setting of correlated priors, p₁ and p₂ were assumed to follow Samarnov prior with ρ = 0.5, a₁ = b₁ = a₂ = b₂ = 0.5. The samples were jointly drawn using rejection sampling techniques in the following steps:

1. Sample p₁ and p₂ independently from f₁(p₁) and f₂(p₂);

2. Simulate u from Uniform distribution over (0, 1);

3. Accept (p₁, p₂) as one pair of samples if u ≤ g(p₁, p₂)/[M · f₁(p₁)f₂(p₂)], where g(·) is density function (2), M is an upper bound of importance ratio g(p₁, p₂)/[f₁(p₁)f₂(p₂)]. Specifically, we let M = 1 + |ρ|/(δ₁δ₂), where δ_j is the square root of variance of p_j (for j = 1, 2) as defined in Section 2.1;

4. Repeat steps 1 to 3 until sufficient pairs of samples are obtained.

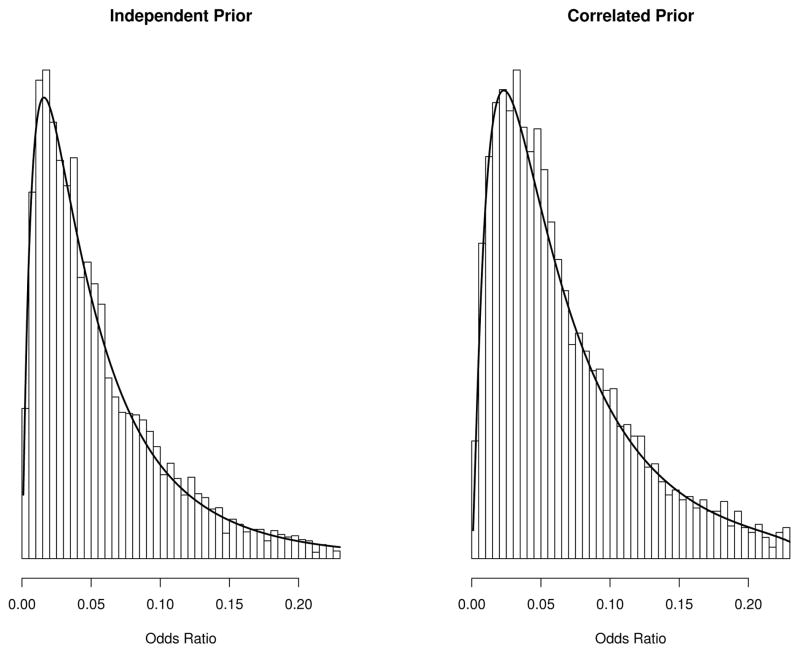
Figure 1 shows the histograms based on random samples and the overlaid density functions based on formulas (1) and (3). The empirical results suggested that the posterior density functions of odds ratio are correct.

Figure 1.

Histograms of 5, 000 odds ratio samples overlaid on density functions calculated by formulas (1) and (3) under independent prior (left panel) and correlated prior (right panel)

3.2 Meta-analysis of case-control studies with binary exposure

When multiple 2 × 2 tables are available, the hyperparameters can be estimated using the empirical Bayes method illustrated in Section 2.2. Then the overall odds ratio and the within study correlation can be obtained. In this subsection, we conducted simulation studies to evaluate the finite sample performance of the maximum likelihood estimator for the overall log odds ratio (OR). We set the true values of hyperparameters a₁ = b₁ = a₂ = b₂ = 0.5, with within study correlation ρ = 0, 0.2, 0.4, and the number of studies being 20, 40, and 60. The configuration of sample sizes for the studies were set as the same as that in the meta-analysis conducted by Ye and Parry²¹. Table 1 compares the bias, true standard error (computed as the standard deviation of the overall log OR estimates and labeled as “SD”), model based standard error (labeled as “SE”), and coverage probability (labeled as “CP”) of the Wald confidence interval for the log OR estimated from Sarmanov beta-binomial model (5) and independent beta-binomial model. Note that the model based SE is the square root of the average of the overall log OR variance estimated via Delta method. When ρ = 0, the independent model gives unbiased estimates, model based SE close to true SE, and coverage probabilities close to nominal levels while the Sarmanov model performs equally well in terms of bias, true SE, and model based SE, only with coverage probabilities negligibly worse. When ρ = 0.2 or 0.4, the Sarmanov model can still provide unbiased estimates, model based SE close to true SE, and coverage probabilities close to 0.95. Although the log OR estimates from independent model are also unbiased, the model based SEs deviate from the true SEs and the coverage property of the confidence intervals deteriorates. These simulation results indicate that Sarmanov model can provide valid inference and is robust to the within study correlation with moderate number of studies. In contrast, although the independent model could obtain consistent estimates for odds ratio, the estimated variability for these estimates would be inadequate; hence confidence intervals and statistical tests are not feasible.

Table 1.

Estimates of the bias, true standard error (SD), model based standard error (SE), coverage probability (CP) and relative efficiency (RE) of common odds ratio estimated from all studies (in log scale) in 5000 simulations based on Sarmanov beta-binomial model and independent beta-binomial model, with different number of studies n, for different within study correlations ρ. (a₁, b₁, a₂, b₂) = (0.5, 0.5, 0.5, 0.5).

		Sarmanov model					Independent model
n	ρ	Bias	SD	SE	CP (%)	RE	Bias	SD	SE	CP (%)	RE
20	0	−0.005	0.439	0.415	92.6	1.000	−0.005	0.438	0.416	93.4	0.995
	0.2	0.003	0.388	0.378	94.4	1.000	0.003	0.395	0.416	96.0	0.826
	0.4	0.003	0.321	0.336	96.8	1.000	0.004	0.352	0.416	97.7	0.652
40	0	−0.001	0.302	0.294	93.8	1.000	−0.001	0.302	0.295	94.4	0.993
	0.2	0.005	0.271	0.268	94.5	1.000	−0.006	0.272	0.295	96.7	0.825
	0.4	0.002	0.228	0.233	96.1	1.000	0.002	0.247	0.295	98.2	0.624
60	0	0.000	0.250	0.240	93.7	1.000	0.000	0.250	0.241	94.0	0.992
	0.2	0.004	0.222	0.219	94.4	1.000	0.004	0.222	0.241	96.7	0.826
	0.4	0.005	0.185	0.188	95.5	1.000	0.006	0.201	0.241	98.1	0.609

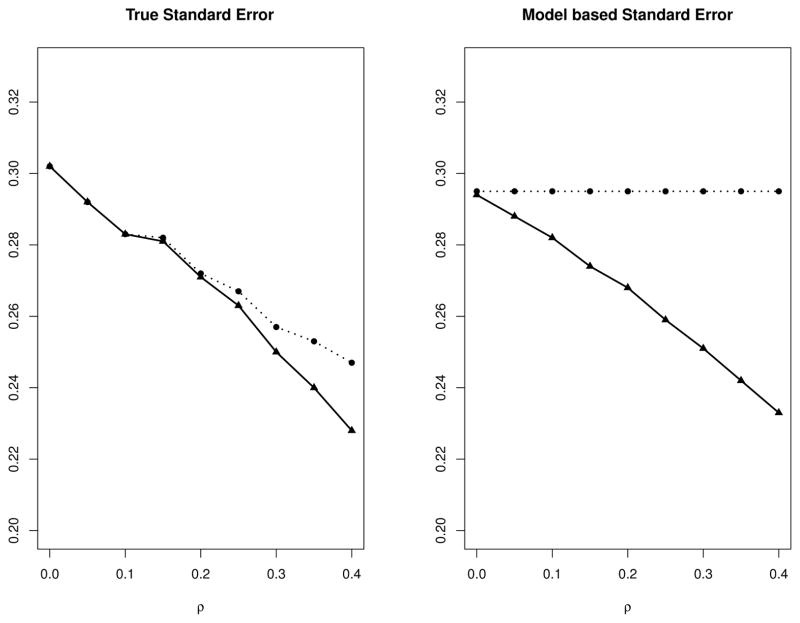
One interesting phenomena shown in Table 1 is that the true SE decreases as the within study correlation ρ increases. To visually display this pattern, we compare in Figure 2 the true SE (left panel) and the model based SE (right panel) from the Sarmanov model and the independent model under various ρ with number of studies n being 40. The left panel of Figure 2 shows that, when ρ increases, the true SEs of both models decrease due to “borrowing strength” across groups²⁷ but the Sarmanov model always provides smaller true SEs because the log OR is estimated by the maximum likelihood estimator. In contrast, as shown by the right panel of Figure 2, the model based SE from the independent model remains unchanged, because the likelihood function of the independent model fails to incorporate the within study correlation. The model based SEs from the Sarmanov model are close to the true SEs. Figure 2 suggests that inference based on the Sarmanov model can take advantage of the within study correlation by “borrowing strength” across groups, while the independent model produces confidence intervals that are over-conservative. The relative efficiency, comparing the estimator based on independent beta-binomial model to Sarmanov beta-binomial model, is also calculated in Table 1. The relative efficiency decreases dramatically as the correlation increases and the efficiency gain by using the Sarmanov model can be as large as 39%. Another interesting phenomena in Table 1 is that the true SE of the Sarmanov model when n = 40 and ρ = 0.4 is even smaller than the true SE from the independent model when n = 60 and ρ = 0. This indicates that by “borrowing strength” across groups, the required number of studies to achieve certain efficiency can be significantly reduced.

Figure 2.

Variance estimates under different correlation coefficients from Sarmanov beta-binomial model (solid lines) and independent beta-binomial model (dotted lines). True standard error (left panel). Model based standard error (right panel). Number of studies is 40.

4 Applications

4.1 Application to a twin study for genetic heritability

In the landmark paper by Fisher⁶, a small study of criminal twins of same gender was considered with the objective to quantify the evidence of heritability of criminality. The frequencies of convictions of monozygotic and dizygotic twins of criminals can be summarized by a single 2 × 2 table. Specifically, 10 out of 13 monozygotic twins of criminals were convicted with crime, while only 2 out of 17 dizygotic twins of criminals were convicted. In our notation, y₁ = 10, n₁ = 13, y₂ = 2 and n₂ = 17.

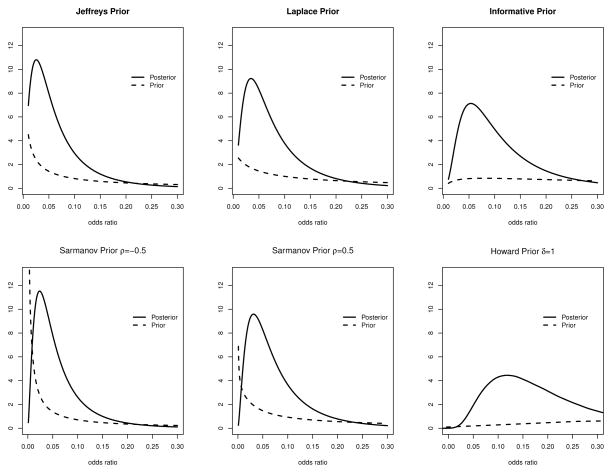
Of interest is the association between the criminal conviction and genomic sharing of criminal twins. This can be measured by the odds ratio of conviction comparing dizygotic twins with monozygotic twins. Although the primary objective in Fisher⁶ is testing rather than estimation, we consider it as a good example to illustrate the exact Bayesian inference and sensitivity analysis. We considered six different priors, which include three independent beta priors, i.e., Jeffreys Prior, Laplace prior and an informative prior with ρ = 0 and all other hyperparameters being 0.5, 1 and 2 respectively, two Sarmanov correlated priors (i.e., a₁ = b₁ = a₂ = b₂ = 0.5, ρ = −0.5, 0.5) and one prior suggested by Kass and Raftery³⁹ and Howard⁴⁰ (i.e., a₁ = b₁ = a₂ = b₂ = 0.5, δ = 1 in Section 7 of Howard⁴⁰). The corresponding prior and posterior distributions of odds ratio under the six prior distributions are plotted in Figure 3. As shown in Figure 3, the posterior distributions under all three independent priors and two Sarmanov correlated priors share similar pattern of having most of weights on small values of odds ratio, whereas the posterior distribution based on Howard’s prior is much flatter. This leads to similar credible intervals under independent priors and Sarmanov correlated priors, while much more conservative credible interval (i.e., credible interval closer to 1) under Howard’s prior. The parameter settings for the priors and posterior, along with the corresponding 95% equal tail credible intervals and 95% highest posterior density regions for odds ratio, are summarized in Table 2. Specifically, if Jeffreys prior is assumed, the credible intervals for odds ratio under independent model (i.e. ρ = 0) are very close to the credible intervals derived from the correlated models with ρ = −0.5 or ρ = 0.5, suggesting that the Bayesian inference of odds ratio based on this dataset is fairly robust to the prior independence assumption.

Figure 3.

Prior and posterior distributions of odds ratio under Jeffreys prior, Laplace prior and informative prior (upper panels) and Sarmanov priors (ρ = −0.5 and ρ = 0.5) and Howard prior (lower panels). Odds ratios are defined as the ratio of odds of conviction comparing dizygotic twins to monozygotic twins.

Table 2.

Bayesian Inference under Independent and Correlated Priors. HDR: highest posterior density region.

Priors	Posterior Mean	Posterior Median	95% equal tail credible interval	95% HDR credible interval
Independent Jeffreys Prior (a1 = a2 = b1 = b2 = 0.5)	0.064	0.043	[0.005, 0.245]	[0.000, 0.189]
Independent Laplace Prior (a1 = a2 = b1 = b2 = 1)	0.080	0.057	[0.008, 0.291]	[0.001, 0.227]
Independent informative Prior (a1 = a2 = b1 = b2 = 2)	0.114	0.086	[0.016, 0.374]	[0.005, 0.300]
Sarmanov Prior ρ = −0.5 (a1 = a2 = b1 = b2 = 0.5)	0.057	0.038	[0.004, 0.222]	[0.000, 0.170]
Sarmanov Prior ρ = 0.5 (a1 = a2 = b1 = b2 = 0.5)	0.078	0.054	[0.007, 0.284]	[0.001, 0.222]
Correlated Prior proposed by Howard (δ = 1, a1 = a2 = b1 = b2 = 0.5)	0.207	0.172	[0.048, 0.571]	[0.027, 0.478]

4.2 Application to a meta-analysis of the N-acetyltransferase 2 acetylation status and colorectal cancer risk

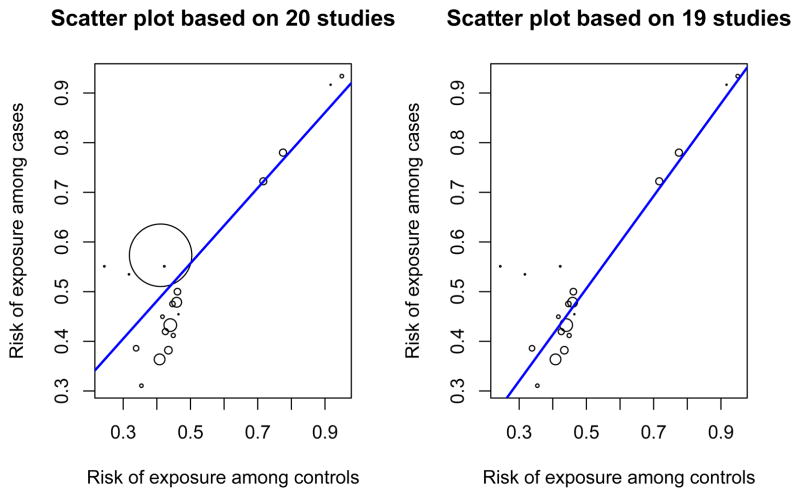
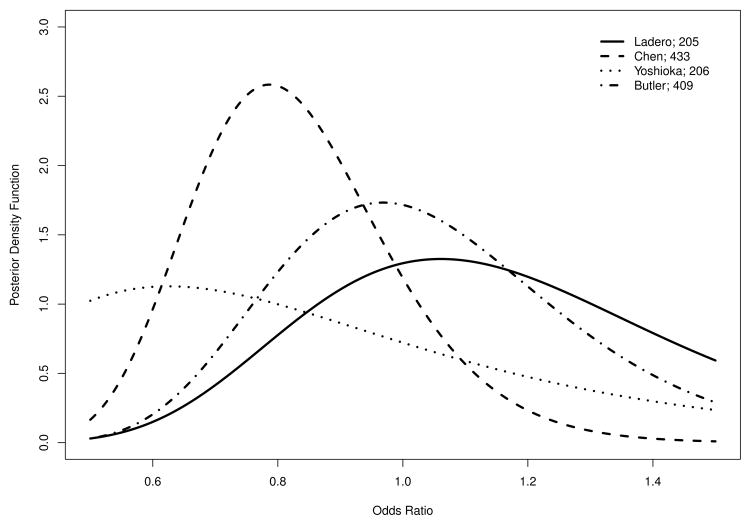
N-acetyltransferase 2 (NAT2) gene is critical to the metabolism of a wide range of hydrophobic compounds including carcinogens. Rapid NAT2 acetylation status has been considered as a risk factor for colorectal cancer in many studies. Because of the inconsistent results of the studies with respect to the presence and magnitude of the association, Ye and Parry²¹ conducted a meta-analysis based on twenty published case-control studies from January 1985 to October 2001. Twenty studies were included in the meta-analysis with 4, 471 colorectal cancer cases and 4, 885 controls among which 2, 361 and 2, 238 subjects had rapid NAT2 acetylator status. The data are summarized in Table C.1 of the Appendix Section C. A strong within study correlation between probabilities of exposure in cases and controls is found, with Pearson’s correlation, Spearman’s rank correlation, and Kendall’s tau equal to 0.872, 0.493, and 0.396, respectively, and all p-values less than 0.03. To visualize this pattern, a scatter plot of probability of exposure among cases and controls was displayed in the left panel in Figure 4. It displays strong positive within study correlation. As suggested by simulation studies in Section 3.2, the within study has to be accounted for to ensure valid inference on odds ratio. Here we define the odds ratio as the ratio of odds of having rapid NAT2 acetylator status comparing those with colorectal cancer to those without. We fit both independent beta-binomial model and Sarmanov beta-binomial model. The likelihood ratio test yields a p-value of 0.075, suggesting moderate evidence of correlation. We then obtained the estimates of hyperparameters (â₁, b̂₁, â₂, b̂₂, ρ̂) = (3.108, 2.914, 3.942, 3.361, 0.125), and the exact posterior distribution of each study-specific odds ratio using formula (3). Figure 5 presents the posterior density functions of four randomly selected study-specific odds ratios.

Figure 4.

Scatter plot of risks of exposure among cases and controls for Ye and Parry²¹ dataset. The area of each circle is proportional to the total sample size of the study. A regression line is overlaid with coefficients estimated by weighted least squared (weights proportional to the total sample size of the study). Left: scatter plot based on all twenty studies. Right: scatter plot based on dataset with the largest study removed.

Figure 5.

Posterior distributions of study-specific odds ratios for four studies: Ladero et al.⁴¹, Chen et al.⁴², Yoshioka et al.⁴³, and Butler et al.⁴⁴. The numbers in the legend are the total sample sizes of the studies. Odds ratios are defined as the ratio of odds of having rapid N-acetyltransferase 2 (NAT2) acetylator status comparing those with colorectal cancer to those without.

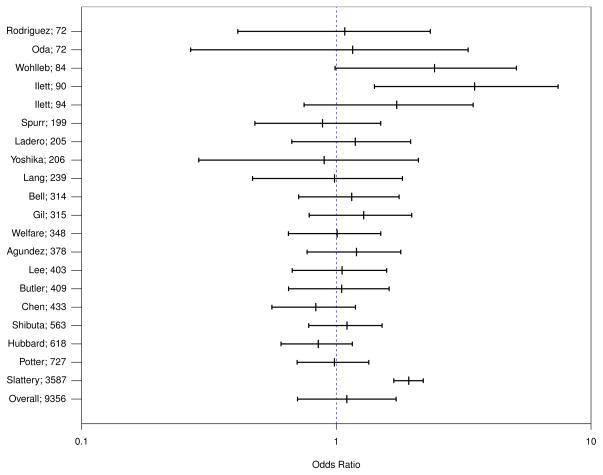
By applying Bisection root-finding method to compute the 2.5% and 97.5% quantiles, we constructed the 95% equal-tail credible intervals of each study-specific odds ratio. The overall odds ratio is estimated by (â₂b̂₁)/(â₁b̂₂) and the 95% confidence interval is constructed by exponentiating the Wald’s intervals of overall log odds ratio. Figure 6 presents the forest plot with credible intervals of study-specific odds ratios and confidence interval of overall odds ratio. The overall odds ratio for rapid NAT2 acetylator status and colorectal cancer risk is 1.100 (95% CI: 0.704, 1.718). In contrast, the overall odds ratio estimated from the independent beta-binomial model is 1.138 (95% CI: 0.717, 1.806). Although the odds ratio estimates from both models are not statistically significant, Sarmanov beta-binomial model provides sizable efficiency gain compared to independent beta-binomial model due to its ability of accounting for correlation within studies (relative efficiency is 0.867). In general, the larger the within study correlation, the larger efficiency gain by using Sarmanov beta-binomial model, as shown in Section 3.2. Notice that one large study could be the most influential on the analysis (3587 out of total of 9356 subjects). To evaluate the sensitivity of the results on this large study, we conduct the analysis with this study removed. The corresponding estimates for odds ratio are 1.066 (95% CI: 0.668, 1.702) under Sarmanov beta-binomial model and 1.110 (95% CI: 0.683, 1.803) under independent beta-binomial model. In summary, the analysis with the largest study removed suggests similar conclusions.

Figure 6.

Forest plot of 20 study-specific and the overall odds ratios with 95% credible intervals. The numbers on the y-axis are the total sample sizes of the studies. Odds ratios are defined as the ratio of odds of having rapid N-acetyltransferase 2 (NAT2) acetylator status comparing those with colorectal cancer to those without.

5 Discussion

Recently, multivariate random effect models for meta-analysis have become increasingly popular in biomedical research. The major advantages of these models are the ability of accounting for heterogeneity between studies, similarly to the univariate random effect model proposed by DerSimonian and Laird⁴⁵, and the ability to allow for within study correlation^27,28,29. In this paper, we considered exact Bayesian inference of a single or multiple 2×2 tables under a class of independent or correlated priors. This type of prior distributions have the advantage of having closed form formulas for the posterior distributions of odds ratio, and allowing for between studies heterogeneity and within study correlations. We evaluated the finite sample performance of the estimation procedure of the overall log odds ratio through simulation studies. The Sarmanov model can provide valid inference and is robust to the within study correlation, while the independent model can only give valid inference when the within study correlation is zero. Moreover, we found that the Sarmanov model can utilize the within study correlation by “borrowing strength” across groups, which significantly reduces the required number of studies to achieve certain efficiency. The simulation studies suggest that the efficiency gain by using the Sarmanov models can be as large as 39%. In addition, the posterior distribution of the study-specific odds ratio can be easily calculated and displayed due to our exact formulas of the posterior density functions. We also discussed the regression extension when the study-specific covariates are available. The computation in this paper was performed in R (R Development Core Team, Version 2.11.1). Codes are available from the corresponding author upon request.

One important application of the Sarmanov beta binomial models can be meta analyses in genome-wide association studies (GWAS). In the last decade, genome-wide association studies have made considerable progress in identifying gene variants that are associated with susceptibility of diseases. The genetic effects are mostly moderate or small in magnitude. Single studies are often underpowered to detect associated gene variants. Meta-analysis of many GWAS is a promising approach to detect associations with greater power and to study the consistency of these finding across studies⁴⁶. Traditional approaches include Fisher’s method of combining p-values, and inverse variance weighting methods under univariate fix-effects or random effect models. The Sarmanov beta binomial model can improve the performance over the traditional approaches in meta-analyses of GWAS because it can not only allow for heterogeneity between studies due to real population differences such as ethnic ancestry, study design, or phenotypic differences, but also utilize the within study correlation such as population substructure or cryptic relatedness⁴⁷.

We want to mention a related bivariate random effect model that was originally proposed in the context of bivariate meta-analysis^48,49 and diagnostic test^50,51. This model assumes a hierarchical model, similarly to the Sarmanov beta binomial model, with the transformed probabilities (e.g. after logit-transformation) following a bivariate normal distribution. This model is often referred as bivariate generalized linear mixed model (BGLMM). The Sarmanov beta binomial model considered in this paper is different with the BGLMM in at least two aspects. First, the BGLMM implicitly assumes the linear regression relationship between p₁ and p₂ in the transformed scale, while the Sarmanov beta binomial model assumes the linear regression relationship in the original scale as illustrated in Section 2.2. Secondly, the BGLMM models the correlation in a transformed scale, hence the interpretation of correlation is transformation dependent and less intuitive. Instead, the Sarmanov beta binomial model directly models the correlation between p₁ and p₂, which has an easier interpretation. The price to pay for the Sarmanov beta binomial model is that the possible range for the correlation is often smaller than [−1, 1], which is a common problem for non-normal bivariate distributions³².

As pointed out by an anonymous reviewer, in the meta-analysis example in Section 4.2, much of the correlation between cases and controls within the same study could be explained by study-level covariates such as race and country. It would be of interest to explore the performance of the regression extension of the models considered, which can be a future research direction.

Appendix

Section A: Derivation of equation (3) and some results on the moments of odds ratio

proof

With beta marginals and mixing functions φ_i = (p_i − μ_i)/δ_i, the Sarmanov prior distribution of p₁ and p₂ can be written as linear combination of products of independent beta distributions as follows,

$$\begin{array}{l}g(p_1,p_2;a_1,b_1,a_2,b_2,\rho )=v_1\text{beta}(p_1;a_1,b_1)\text{beta}(p_2;a_2,b_2)+v_2\text{beta}(p_1;a_1+b_1)\text{beta}(p_2;a_2,b_2)\\ +v_3\text{beta}(p_1;a_1,b_1)\text{beta}(p_2;a+1,b_2)+v_4\text{beta}(p_1;a_1+b_1)\text{beta}(p_2;a_2+1,b_2),\end{array}$$

where beta(·; a_j, b_j) is the beta distribution, v_k (k = 1, …, 4) are weights, defined by, v₁ = 1 + ρd, v₂ = v₃ = −ρd, v₄ = ρd, d = (μ₁μ₂)/(δ₁δ₂). After some algebra, the posterior distribution of p₁ and p₂ given data is also a linear combination of products of independent beta distributions,

$$\begin{array}{l}Pr(p_1,p_2\mid y_1,y_2,a_1,b_1,a_2,b_2,\rho )={\omega }_1\text{beta}(p_1;{\alpha }_1,{\beta }_1)\text{beta}(p_2;{\alpha }_2,{\beta }_2)+{\omega }_2\text{beta}(p_1;{\alpha }_1+1,{\beta }_1)\text{beta}(p_2;{\alpha }_2,{\beta }_2)\\ +{\omega }_3\text{beta}(p_1;{\alpha }_1,{\beta }_1)\text{beta}(p_2;{\alpha }_2+1,{\beta }_2)+{\omega }_4\text{beta}(p_1;{\alpha }_1+1,{\beta }_1)\text{beta}(p_2;{\alpha }_2+1,{\beta }_2),\end{array}$$

where the weights ω_k (k = 1, …, 4) are defined by,

$$\begin{array}{c}{\omega }_1=\frac{v_{1}B({\alpha }_1,{\beta }_1)B({\alpha }_2,{\beta }_2)}{CB(a_1,b_1)B(a_2,b_2)},{\omega }_2=\frac{v_{2}B({\alpha }_1+1,{\beta }_1)B({\alpha }_2,{\beta }_2)}{CB(a_1+1,b_1)B(a_2,b_2)},\\ {\omega }_3=\frac{v_{3}B({\alpha }_1,{\beta }_1)B({\alpha }_2+1,{\beta }_2)}{CB({\alpha }_1,b_1)B(a_2+1,b_2)},\text{and}{\omega }_4=\frac{v_{4}B({\alpha }_1+1,{\beta }_1)B({\alpha }_2+1,{\beta }_2)}{CB({\alpha }_1+1,b_1)B(a_2+1,b_2)},\end{array}$$

and C, the normalizing constant, is calculated as

$$C=\frac{v_{1}B({\alpha }_1,{\beta }_1)B({\alpha }_2,{\beta }_2)}{B(a_1,b_1)B(a_2,b_2)}+\frac{v_{2}B({\alpha }_1+1,{\beta }_1)B({\alpha }_2,{\beta }_2)}{B(a_1+1,b_1)B(a_2,b_2)}+\frac{v_{3}B({\alpha }_1,{\beta }_1)B({\alpha }_2+1,{\beta }_2)}{B(a_1,b_1)B(a_2+1,b_2)}+\frac{v_{1}B({\alpha }_1+1,{\beta }_1)B({\alpha }_2+1,{\beta }_2)}{B(a_1+1,b_1)B(a_2+1,b_2)}.$$

The proof is completed following the derivation of equation (1).

Under independent beta priors, the k-th posterior moment of odds ratio exists for k < min(α₁, β₂) and is given by

$$E[{\theta }^k;{\alpha }_1,{\beta }_1,{\alpha }_2,{\beta }_2]=\frac{B({\alpha }_1-k,{\beta }_1+k)B({\alpha }_2+k,{\beta }_2-k)}{B({\alpha }_1,{\beta }_1)B({\alpha }_2,{\beta }_2)}.$$ (6)

Specifically, the mean and variance are given by E[θ; α₁, β₁, α₂, β₂] = β₁α₂/{(α₁ −1)(β₂ − 1)} and

$$\mathit{var}(\theta ;{\alpha }_1,{\beta }_1,{\alpha }_2,{\beta }_2)=\frac{{\beta }_1({\beta }_1+1){\alpha }_2({\alpha }_2+1)}{({\alpha }_1-1)({\alpha }_1-2)({\beta }_2-1)({\beta }_2-2)}-{\left\{\frac{{\beta }_1{\alpha }_2}{({\alpha }_1-1)({\beta }_2-1)}\right\}}^2.$$

Under correlated beta priors, the k-th posterior moment of odds ratio exists for k < min(α₁, β₂) and is given by

$$E[{\theta }^k;{\alpha }_1,{\beta }_1,{\alpha }_2,{\beta }_2,\rho ]={\omega }_{1}E[{\theta }^k;{\alpha }_1,{\beta }_1,{\alpha }_2,{\beta }_2]+{\omega }_{2}E[{\theta }^k;{\alpha }_1+1,{\beta }_1,{\alpha }_2,{\beta }_2]+{\omega }_{3}E[{\theta }^k;{\alpha }_1,{\beta }_1,{\alpha }_2+1,{\beta }_2]+{\omega }_{4}E[{\theta }^k;{\alpha }_1+1,{\beta }_1,{\alpha }_2+1,{\beta }_2],$$ (7)

where E[θ^k; α₁, β₁, α₂, β₂] is the k-th posterior moment of odds ratio under independent beta priors, defined in equation (6).

Section B: SPLUS/R program to fit model (4) and a working example

# function to compute the log-likelihood in 


equation (5)


myLik <- function(mypar, mydat) {
   par <- par.cal(mypar); a1 <- par[1]; b1 <- par[2]; a2 <- par[3]; b2 <- par[4]
   temp1 <- (lgamma(a1+mydat$y1) + lgamma(b1+mydat$n1-mydat$y1)+ lgamma(a2+mydat$y2) + lgamma(b2+mydat$n2-mydat$y2)
          + lgamma(a1+b1) + lgamma(a2+b2))
   temp2 <- (lgamma(a1) + lgamma(b1) + lgamma(a2) + lgamma(b2)+ lgamma(a1+b1+mydat$n1) + lgamma(a2+b2+mydat$n2))
   if (flag == 0) myLogLik <- sum(temp1 - temp2) # if independent beta-binomial model
   if (flag == 1) { # if Sarmanov beta-binomial model
    rho <- par[5]
    mu1 <- a1/(a1+b1); mu2 <- a2/(a2+b2)
    delta1 <- sqrt(mu1*(1-mu1)/(a1+b1+1)); delta2 <- sqrt(mu2*(1-mu2)/(a2+b2+1))
    temp3 <- (log(1+rho/delta1/delta2*(mydat$y1-mydat$n1*mu1)*(mydat$y2-mydat$n2*mu2)/(a1+b1+mydat$n1)/(a2+b2+mydat$n2)))
    myLogLik <- sum(temp1 - temp2 + temp3)}
   return(myLogLik)
}
# Back-transform the parameters (a1,b1,a2,b2,rho) to original scale
par.cal <- function(mypar) {
  a1 <- exp(mypar[1]); b1 <- exp(mypar[2]); a2 <- exp(mypar[3]); b2 <- exp(mypar[4])
  if (flag == 0) return(c(a1,b1,a2,b2))
  if (flag == 1) {
   eta <- mypar[5]; cc <- sqrt(a1*a2*b1*b2)/sqrt((a1+b1+1)*(a2+b2+1))
   upper.bound <- cc/max(a1*b2, a2*b1); lower.bound <- -cc/max(a1*a2, b1*b2)
   rho <- (upper.bound-lower.bound)*exp(eta)/(1+exp(eta)) + lower.bound
   return(c(a1,b1,a2,b2,rho))}
}
# function to calculate Wald confidence interval of OR using Delta method
OR.comp.log <- function(par, hessian) {
  a1 <- par[1]; b1 <- par[2]; a2 <- par[3]; b2 <- par[4]
  myOR.overall <- log(a2/b2/(a1/b1))
  myVar <- solve(-hessian)
  if (flag == 0) myD <- matrix(c(-1, 1, 1, -1), nrow=1)
  if (flag == 1) myD <- matrix(c(-1, 1, 1, -1, 0), nrow=1)
  myOR.overall.Var <- as.numeric(myD %*% myVar %*% t(myD)); myOR.overall.sd <- sqrt(myOR.overall.Var)
  myOR.left.bound <- myOR.overall-1.96*sqrt(myOR.overall.Var); myOR.right.bound <- myOR.overall+1.96*sqrt(myOR.overall.Var)
  return(list(OR=exp(myOR.overall), OR.left=exp(myOR.left.bound), OR.right=exp(myOR.right.bound)))
}
# Example 2 in Section 4.2: dataset from Ye and Parry (2002) Med Sci Monit
y1 <- c(10,19,13,40,13,92,33,151,50,34,140,74,68,96,134,95,88,807,119,162)
n1 <- c(41,45,41,96,28,205,36,329,112,96,343,174,201,221,187,100,200,1963,258,209)
y2 <- c(27,27,23,49,20,14,33,112,96,32,100,73,44,81,156,99,228,931,60,156)
n2 <- c(49,49,43,109,44,34,36,234,202,103,275,174,114,212,216,106,527,1624,120,200)
init.val <- rep(0, 5)
# fit independent beta-binomial model
flag <- 0 # flag = 0: independent beta-binomial model
results.indep <- optim(init.val[1:4], myLik, method = “L-BFGS-B”, lower=rep(-20,4), upper=rep(20,4),
          control = list(fnscale=-1,maxit=1000), hessian = T, mydat=list(y1=y1,n1=n1,y2=y2,n2=n2))
OR.comp.log(par.cal(results.indep$par), results.indep$hessian)
# fit Sarmanov beta-binomial model
flag <- 1 # flag = 1: Sarmanov beta-binomial model
results <- optim(init.val, myLik, method = “L-BFGS-B”, lower=rep(-20,5), upper=rep(20,5),
                control = list(fnscale=-1,maxit=1000), hessian=T, mydat=list(y1=y1,n1=n1,y2=y2,n2=n2))
OR.comp.log(par.cal(results$par), results$hessian)
# Likelihood ratio test for within-study correlation
pchisq(q=-2*(results.indep$value-results$value), df=1, ncp=0, lower.tail = FALSE, log.p = FALSE)

Section C: Table C.1

Table C.1.

Data from a Meta-analysis of Studies on the association between rapid N-acetyltransferase 2 (NAT2) acetylator status (event) and colorectal cancer risk (cases)²¹

Author	Cases		Control
	no. events	no. observations	no. events	no. observations
Ilett	27	49	10	41
Ilett	27	49	19	45
Wohlleb	23	43	13	41
Ladero	49	109	40	96
Rodriguez	20	44	13	28
Lang	14	34	92	205
Oda	33	36	33	36
Shibuta	112	234	151	329
Bell	96	202	50	112
Spurr	32	103	34	96
Hubbard	100	275	140	343
Welfare	73	174	74	174
Gil	44	114	68	201
Chen	81	212	96	221
Lee	156	216	134	187
Yoshika	99	106	95	100
Potter	228	527	88	200
Slattery	931	1624	807	1963
Agundez	60	120	119	258
Butler	156	200	162	209