Abstract
Unsupervised multi-layered (“deep”) models are considered for general data, with a particular focus on imagery. The model is represented using a hierarchical convolutional factor-analysis construction, with sparse factor loadings and scores. The computation of layer-dependent model parameters is implemented within a Bayesian setting, employing a Gibbs sampler and variational Bayesian (VB) analysis, that explicitly exploit the convolutional nature of the expansion. In order to address large-scale and streaming data, an online version of VB is also developed. The number of basis functions or dictionary elements at each layer is inferred from the data, based on a beta-Bernoulli implementation of the Indian buffet process. Example results are presented for several image-processing applications, with comparisons to related models in the literature.
I. Introduction
There has been significant recent interest in multi-layered or “deep” models for representation of general data, with a particular focus on imagery and audio signals. These models are typically implemented in a hierarchical manner, by first learning a data representation at one scale, and using the model weights or parameters learned at that scale as inputs for the next level in the hierarchy. Researchers have studied deconvolutional networks [1], convolutional networks [2], deep belief networks (DBNs) [3], hierarchies of sparse auto-encoders [4], [5], [6], and convolutional restricted Boltzmann machines (RBMs) [7], [8], [9]. The key to many of these algorithms is that they exploit the convolution operator, which plays an important role in addressing large-scale problems, as one must typically consider all possible shifts of canonical bases or filters. In such analyses one must learn the form of the basis, as well as the associated coefficients. Concerning the latter, it has been recognized that a preference for sparse coefficients is desirable [1], [8], [9], [10].
When using the outputs of layer l as inputs for layer l+1, researchers have investigated several processing steps that improve computational efficiency and can also improve model performance. Specifically, researchers have pooled and processed proximate parameters from layer l before using them as inputs to layer l + 1. One successful strategy is to keep the maximum-amplitude coefficient within each pooled region, this termed “max-pooling” [7], [8]. Max-pooling has two desirable effects: (i) as one moves to higher levels, the number of input coefficients diminishes, aiding computational speed; and (ii) it has been found to improve inference tasks, such as classification [11], [12], [13].
Some of the multi-layered models have close connections to over-complete dictionary learning [14], in which image patches are expanded in terms of a sparse set of dictionary elements. The deconvolutional and convolutional networks in [1], [7], [9] similarly represent each level of the hierarchical model in terms of a sparse set of dictionary elements; however, rather than separately considering distinct patches as in [14], the work in [1], [7] allows all possible shifts of dictionary elements or basis functions for representation of the entire image at once (not separate patches). In the context of over-complete dictionary learning, researchers have also considered multi-layered or hierarchical models, but again in terms of image patches [15], [16] (the model and motivation in [15], [16] is distinct from the deep-learning focus of this and related deep-learning papers).
All of the methods discussed above, for “deep” models and for sparse dictionary learning for image patches, require one to specify a priori the number of basis functions or dictionary elements employed within each layer of the model. In many applications it may be desirable to infer the number of required basis functions based on the data itself. Within the deep models, for example, the basis-function coefficients at layer l are used (perhaps after pooling) as input features for layer l + 1; this corresponds to a problem of inferring the proper number of features for the data of interest, while allowing for all possible shifts of the basis functions, as in the various convolutional models discussed above. The idea of learning an appropriate number and composition of features has motivated the Indian buffet process (IBP) [17], as well as the beta-Bernoulli process to which it is closely connected [18], [19]. Such methods have been applied recently to (single-layer) dictionary learning in the context of image patches [20]. Further, the IBP has recently been employed for design of “deep” graphical models [21], although the problem considered in [21] is distinct from that associated with the deep models discussed above.
In this paper we demonstrate that the idea of building an unsupervised deep model may be cast in terms of a hierarchy of factor-analysis models, with the factor scores from layer l serving as the input (potentially after pooling) to layer l + 1. Of the various unsupervised deep models discussed above, the factor analysis view of hierarchical and unsupervised feature learning is most connected to [1], where an ℓ1 sparseness constraint is imposed within a convolution-based basis expansion (equivalent to a sparseness constraint on the factor scores). In this paper we consider four differences with previous deep unsupervised models: (i) the form of our model at each layer is different from that in [1], particularly how we leverage convolution properties; (ii) the number of canonical dictionary elements or factor loadings at each layer is inferred from the data by an IBP/beta-Bernoulli construction; (iii) sparseness on the basis-function coefficients (factor scores) at each layer is imposed with a Bayesian generalization of the ℓ1 regularizer; (iv) fast computations are performed using Gibbs sampling and variational Bayesian (VB) analysis, where the convolution operation is exploited directly within the update equations. Furthermore, in order to address large-scale data sets, including those arriving in a stream, online VB inference is also developed.
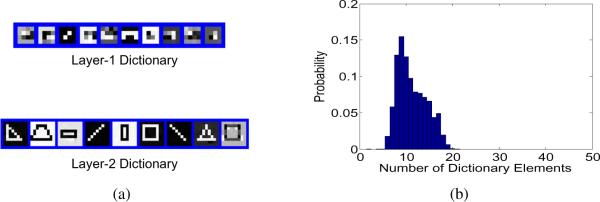
While the form of the proposed model is most related to [1], the characteristics of our results are more related to [7]. Specifically, when designing the model for particular image classes, the higher-layer dictionary elements have a form that is often highly intuitive visually. To illustrate this, and to also highlight unique contributions of the proposed model, consider Figure 1, which will be described in further detail in Section V; these results are computed with a Gibbs sampler, and similar results are found with batch and online VB analysis. In this example we consider images from the “car” portion of the Caltech 101 image database. In Figure 1(a) we plot inferred dictionary elements at layer two in the model, and in Figure 1(d) we do the same for dictionary elements at layer three (there are a total of three layers, and the layer-one dictionary elements are simple “primitives”, as discussed in detail in Section V). All possible shifts of these dictionary elements are efficiently employed, via convolution, at the respective layer in the model. Note that at layer two the dictionary elements often capture localized details on cars, while at layer three the dictionary elements often look like complete cars (“sketches” of cars). To the authors' knowledge, only the (very distinct) model in [7] achieved such physically interpretable dictionary elements at the higher layers in the model. A unique aspect of the proposed model is that we infer a posterior distribution on the required number of dictionary elements, based on Gibbs sampling, with the numerical histograms for these numbers shown in Figures 1(c) and (f), for layers two and three, respectively. Finally, the Gibbs sampler infers which dictionary elements are needed for expanding each layer, and in Figures 1(b) and (e) the use of dictionary elements is shown for one Gibbs collection sample, highlighting the sparse expansion in terms of a small subset of the potential set of dictionary elements. These results give a sense of the characteristics of the proposed model, which is discussed in detail in the subsequent discussion.
Fig. 1.
Dictionary learned from Car dataset. (a) frequently used dictionary elements at the second layer, organized left-to-right and top-down by their frequency of usage; (b) dictionary usage at layer two, based on typical collection sample, for each of the images under analysis (white means used, black means not used); (c) approximate posterior distribution on the number of dictionary elements needed for layer two, based upon Gibbs collection samples; (d) third-layer dictionary elements, ; (e) usage of layer-three dictionary elements for a typical Gibbs collection sample (white means used, black means not used); (f) approximate posterior distribution on the number of dictionary elements needed at layer three. All dictionary elements and are shown in the image plane.
The remainder of the paper is organized as follows. In Section II we develop the multi-layer factor analysis viewpoint of deep models. The detailed form of the Bayesian model is discussed in Section III, and methods for Gibbs, VB and on-line VB analysis are discussed in Section IV. A particular focus is placed on explaining how the convolution operation is exploited in the update equations of these iterative computational methods. Several example results are presented in Section V, with conclusions provided in Section VI. An early version of the work presented here was published in a conference paper [22], which focused on a distinct hierarchical beta process construction, and in which the batch and online VB computational methods were not developed.
II. Multilayered Sparse Factor Analysis
A. Single layer
The nth, image to be analyzed is , where Kc is the number of color channels (e.g., for gray-scale images Kc = 1, while for RGB images Kc = 3). We consider N images {Xn}n=1,N, and each image Xn is expanded in terms of a dictionary, with the dictionary defined by compact canonical elements , with and . The dictionary elements are designed to capture local structure within Xn, and all possible two-dimensional (spatial) shifts of the dictionary elements are considered for representation of Xn. For K canonical dictionary elements the cumulative dictionary is {dk}k=1,K. In practice the number of dictionary elements K is made large, and we wish to infer the subset of dictionary elements needed to sparsely render Xn as
| (1) |
where ∗ is the convolution operator and bnk ∈ {0, 1} indicates whether dk is used to represent Xn, and represents the residual. The matrix Wnk represents the weights of dictionary k for image Xn, and the support of Wnk is , allowing for all possible shifts, as in a typical convolutional model [7]. Let represent the components of Wnk, where the set contains all possible indexes for dictionary shifts. We impose within the model that most wnki are sufficiently small to be discarded without significantly affecting the reconstruction of Xn. A similar sparseness constraint was imposed in [1], [9], [10].
The construction in (1) may be viewed as a special class of factor models. Specifically, we can rewrite (1) as
| (2) |
where dki represents a shifted version of dk, shifted such that the center of dk is situated at , and dki is zero-padded outside the support of dk. The dki represent factor loadings, and as designed these loadings are sparse with respect to the support of an image Xn (since the dki have significant zero-padded extent). This is closely related to sparse factor analysis applied in gene analysis, in which the factor loadings are also sparse [23], [24]. Here, however, the factor loadings have a special structure: the sparse set of factor loadings correspond to the same zero-padded dictionary element dk, with the nonzero-components shifted to all possible locations in the set . Details on the learning of model parameters is discussed in Section III, after first developing the complete hierarchical model.
B. Decimation and Max-Pooling
For the nth image Xn and dictionary element dk, we have a set of coefficients , corresponding to all possible shifts in the set . A “max-pooling” step is applied to each Wnk, with this employed previously in deep models [7] and in recent related image-processing analysis [11], [12]. In max-pooling, each matrix Wnk is divided into a contiguous set of blocks (see Figure 2), with each such block of size nMP,y × nMP,x. The matrix Wnk is mapped to with the mth value in corresponding to the largest-magnitude component of Wnk within the mth max-pooling region. Since Wnk is of size , each is a matrix of size , assuming integer divisions.
Fig. 2.
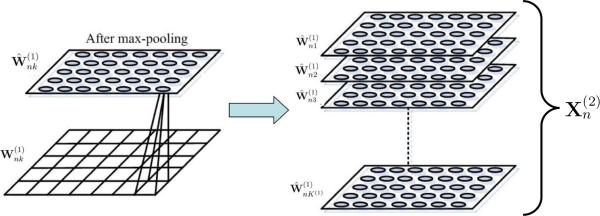
Explanation of max pooling and collecting of coefficients from layer one, for analysis at layer two (a similar procedure is implemented when transiting between any two consecutive layers in the hierarchical model). The matrix defines the shift-dependent coefficients for all two-dimensional shifts of dictionary element , for image n (this same max-pooling is performed for all images n ∈ {1, …, N}). The matrix of these coefficients are partitioned with spatially contiguous blocks (bottom-left). To perform max pooling, the maximum-amplitude coefficient within each block is retained, and is used to define the matrix (top-left). This max-pooling process is performed for all dictionary elements , k ∈ {1, …, K(1)}, and the set of max-pooled matrices are stacked to define the tensor at right. The second-layer data for image n is , defined by a tensor like that at right. In practice, when performing stacking (right), we only retain the layers for which at least one , corresponding to those dictionary elements used in the expansion of the N images.
To go to the second layer in the deep model, let denote the number of k ∈ {1, …, K} for which bnk ≠ 0 for at least one n ∈ {1, …, N}. The corresponding max-pooled images from are stacked to constitute a datacube or tensor (see Figure 2), with the tensor associated with image n now becoming the input image at the next level of the model. The max-pooling and stacking is performed for all N images, and then the same form of factor-modeling is applied to them (the original Kc color bands are now converted to effective spectral bands at the next level). Model fitting at the second layer is performed analogous to that in (1).
After fitting the model at the second layer, to move to layer three, max-pooling is again performed, yielding a level-three tensor for each image, with which factor analysis is again performed. Note that, because of the max-pooling step, the number of spatial positions in such images decreases as one moves to higher levels. Therefore, the basic computational complexity decreases with increasing layer within the hierarchy. This process may be continued for additional layers; in the experiments we consider up to three layers.
C. Model features and visualization
Assume the hierarchical factor-analysis model discussed above is performed for L layers, and therefore after max-pooling the original image Xn is represented in terms of L tensors (with layers or “spectral” bands at layer l, and correspond to the original nth image, for which ). The max-pooled factor weights may be employed as features in a multi-scale (“deep”) classifier, analogous to [11], [12]. We consider this in detail when presenting results in Section V.
In addition to performing classification based on the factor weights, it is of interest to examine the physical meaning of the associated dictionary elements (like shown in Figure 1, for Layer 1 and Layer 2 dictionary elements). Specifically, for l > 1, we wish to examine the representation of in layer one, i.e., in the image plane. Dictionary element is an tensor, representing shifted to the point indexed by i, and used in the expansion of represents the number of spatial pixels in . Let denote the pth pixel in , where for l > 1 vector p identifies a two-dimensional spatial shift as well as a layer level within the tensor (layer of the tensor to the right in Figure 2); i.e., p is a three-dimensional vector, with the first two coordinates defining a spatial location in the tensor, and the third coordinate identifying a level k in the tensor.
Recall that the tensor of factor scores at layer l for image n is manifested by “stacking” the matrices. The (zero-padded) basis function therefore represents one special class of tensors of this form (one used for expanding ), and each non-zero coefficient in corresponds to a weight on a basis function (factor loading) from layer l − 1. The expression simply identifies the pth pixel value in the basis , and this pixel corresponds to a coefficient for a basis function at layer l − 1. Therefore, to observe at layer l − 1, each basis-function coefficient in the tensor is multiplied by the corresponding shifted basis functions at layer l − 1, and then all of the weighted basis functions at layer l − 1 are superimposed.
For l > 1, the observation of at level l − 1 is represented as
| (3) |
where represents a shifted version of one of the dictionary elements at layer l − 1, corresponding to pixel p in . The set , for three-dimensional indices p, serve as weights for the associated dictionary elements at the layer below. Specifically, when considering for p = (ix, iy, k), we are considering the weight on basis function , which corresponds to the weight on when it is shifted to (ix, iy).
Because of the max-pool step, when performing such a synthesis a coefficient at layer l must be associated with a location within the respective max-pool sub-region at layer l − 1. When synthesizing examples in Section V of dictionary elements projected onto the image plane, the coefficients are arbitrarily situated in the center of each max-pool subregion. This is only for visualization purposes, for illustration of the form of example dictionary elements; when analyzing a given image, the location of the maximum pixel within a max-pool subregion is not necessarily in the center.
Continuing this process, we may visualize at layer l − 2, assuming l − 1 > 1. Let represent the pth pixel of the tensor . The dictionary element may be represented in the l − 2 plane as
| (4) |
This process may be considered to lower layers, if desired, but in practice we will typically consider up to l = 3 layers; for l = 3 the mapping represents in the image plane.
III. Hierarchical Bayesian Analysis
We now consider a statistical framework whereby we may perform the model fitting desired in (1), which is repeated at the multiple levels of the “deep” model. We wish to do this in a manner with which the number of required dictionary elements at each level may be inferred during the learning. Toward this end we propose a Bayesian model based on an Indian buffet process (IBP) [17] implementation of factor analysis, executed with a truncated beta-Bernoulli process [18], [19].
A. Hierarchical model
We employ a model of the form
| (5) |
where J denotes the number of pixels in the dictionary elements dk and dkj is the jth component of dk. Since the same basic model is used at each layer of the hierarchy, in (5) we do not employ model-layer superscripts, for generality. The integer P denotes the number of pixels in Xn, and IP represents a P × P identity matrix. The hyperparameters (e, f) and (g, h) are set to favor large αnki and βj, thereby imposing that the set of wnki will be compressible or approximately sparse, with the same found useful for the dictionary elements dk (which yields dictionary elements that look like sparse “sketches” of images, as shown in Figure 1).
The IBP construction may be used to infer the number of dictionary elements appropriate for representation of , while also inferring the dictionary composition. In practice we truncate K, and infer the subset of dictionary elements actually needed to represent the data. This procedure has been found to be computationally efficient in practice. One could alternatively directly employ the IBP construction [17], in which the number of dictionary elements is treated as unbounded in the analysis.
B. Computations
Recalling that indexes the set of all possible shifts within the image of any dictionary element dk, an important aspect of this model construction is that, when implementing a Gibbs sampler or variational Bayesian (VB) analysis, all coefficients may be updated efficiently using the convolution operator (convolving dk with Xn), which may be implemented efficiently via the FFT. Therefore, while the model appears computationally expensive to implement, because all possible dictionary shifts must be considered, efficient implementations are possible; this is discussed in detail in Section IV, where both of Gibbs sampler and variational Bayesian implementations are summarized.
C. Utilizing the Bayesian outputs
The collection samples manifested by a Gibbs sampler yield an ensemble of models, and VB yields a factorized approximation to the posterior of all model parameters. When performing max-pooling, moving from layer l to layer l + 1, a single model must be selected, and here we have selected the maximum-likelihood (ML) sample among the collection samples, or the MAP point from the VB analysis. In future research it is of interest to examine fuller exploitation of the Bayesian model. The main utility of the Bayesian formulation in the applications presented here is that it allows us to use the data to infer the number of dictionary elements, with related ideas applied previously in a distinct class of deep models [25] (that did not consider shifted dictionary elements).
D. Relationship to previous models
In (5), recall that upon marginalizing out the precisions αnki we are imposing a Student-t prior on the weights wnki [26]. Hence, with appropriate settings of hyperparameters (e, f), the Student-t imposes that the factor scores wnki should be (nearly) sparse. This is closely connected to the model in [1], [8], [9], [10], in which an ℓ1 regularization is imposed on wnki, and a single (point) estimate is inferred on all model parameters. In [1] the authors also effectively imposed a Gaussian prior on εn, as we have in (5). Hence, there are two principal differences between the proposed model and that in [1]: (i) here the beta-Bernoulli/IBP construction allows one to infer the number of dictionary elements (factor loadings) needed to represent the data at a given layer in the hierarchy, while in [1] this number is set; (ii) we infer the model parameters using both of Gibbs sampling and variational Bayesian, which yield an ensemble of models at each layer rather than a point estimate. As discussed above, here the main advantage of (ii) is as a means to achieve (i), since in most of our results we are not yet exploiting the full potential of the ensemble of solutions manifested by the approximate posterior; (iii) sparseness is imposed on the filter coefficients and filters themselves, via a Bayesian generalization of the ℓ1 regularizer; and (iv) in order to handle massive data collections, including those arriving in a stream, we develop online variational Bayes.
IV. Exploiting Convolution in Inference
In this section, we introduce two ways to infer the parameters in the multilayered model, Gibbs sampling and variational Bayesian. Furthermore, an online version of variational Bayesian inference is also developed to allow the model to scale.
A. Gibbs Sampler
We may implement the posterior computation by a Markov chain Monte Carlo (MCMC) method based on Gibbs sampling. Samples are constituted by iteratively drawing each random variable (model parameters and latent variables) from its conditional posterior distribution given the most recent values of all the other random variables. The full likelihood is represented as
| (6) |
In the proposed model all conditional distributions used to draw samples are analytic, and relatively standard in Bayesian analysis. Therefore, for conciseness, all conditional update equations are presented in Supplementary Material.
B. Variational Bayesian Inference
We have described Gibbs sampling for each layer's model. We now describe variational inference, replacing sampling with optimization. For layer l of the model, in variational Bayesian inference [27], [28] we seek a distribution Q(Θl; Γl) to approximate the exact posterior p(Θl|Xl), where Θl ≡ {bl, Wl, dl, πl, γl, αl, βl. Our objective is to optimize the parameters Γl in the approximation Q(Θl; Γl).
Toward that end, consider the lower bound of the marginal log likelihood of the observed data
| (7) |
Note that the term p(Xl) is a constant with respect to Γl, and therefore is maximized when the Kullback-Leibler divergence KL(q(Θl; Γl)∥p(Θl|Xl)) is minimized. However, we cannot explicitly compute the KL divergence, since p(Θl|Xl) is unknown. Fortunately, the numerator term in may be computed, since p(Xl)p(Θl|Xl) = p(Xl|Θl)p(Θl), and the prior p(Θl) and likelihood function p(Xl|Θl) are available. To make computation of tractable, we assume q(Θl|Γl) has a factorized form . With appropriate choice of qm, the variational expression may be evaluated analytically. The VB update equations are provided in Supplementary Material.
C. Online Variational Bayesian Analysis
Since the above variational Bayesian requires a full pass through all the images each iteration, it can be slow to apply to very large datasets, and is not naturally suited to settings where new data is constantly arriving. Therefore, we develop online variational inference for the multi-layered convolutional factor analysis model, building upon a recent online implementation of latent Dirichlet allocation [29]. In online variational inference, stochastic optimization is applied to the variational objective. We subsample the data (in this case, images), compute an approximation of the gradient based on the subsample, and follow that gradient with a decreasing step-size. The key insight behind efficient online variational inference is that coordinate ascent updates applied in parallel precisely form the natural gradient of the variational objective function. Although the online VB converges much faster for large datasets, the practical algorithm is nearly as simple as the batch VB algorithm. The difference is only the update of global parameters, i.e., πk and dk in convolutional factor analysis. Suppose we randomly subsample one image each iteration and the total number of sampled images is D, the lower bound of image n is defined as
| (8) |
where H(·) is the entropy term for the variational distribution. Now, our goal is to maximize the lower bound
| (9) |
where the expectation is taken over the empirical distribution of the data set. The expression is the variational lower bound evaluated with D duplicate copies of image n. Then, take the gradient of global parameters (ξl, Λl, , ) of as follows
| (10) |
| (11) |
| (12) |
| (13) |
Similar with the natural gradient algorithm, an appropriate learning rate ρt is also needed to ensure the parameters to converge to a stationary point in online inference. Then the updates of ξl, Λl, and become
| (14) |
In our experiments, we use ρt = (τ0+t)−κ, where κ ∈ (0.5, 1] and τ0 > 0. The overall learning procedure is summarized in Algorithm 1.
|
|
|
Algorithm 1 Online Variational Bayesian Inference for Multilayered Convolutional Factor Analysis |
Initialize  and and  randomly. randomly. |
| for t = 0 to ∞ do |
| Sample an image n randomly from the dataset. |
| for l = 1 to L do |
Initialize  and and 
|
| if l > 1 then max-pool Xl from layer l − 1 |
| repeat |
| for k = 1 to Kl do |
Compute  and and  (see Supplementary Material for details). (see Supplementary Material for details). |
| end for |
| until Stopping criterion is met |
| end for |
| Set ρt = (τ0 + t)−κ |
| for l = 1 to L do |
| for k = 1 to Kl do |
Compute the natural gradients  and and 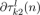 using (10), (11) , (12) and (13). using (10), (11) , (12) and (13). |
Update 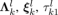 and and 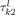 by (14). by (14). |
| end for |
| end for |
| end for |
|
|
V. Experimental Results
A. Parameter settings
While the hierarchical Bayesian construction in (5) may appear relatively complex, the number of parameters that need be set is not particularly large, and they are set in a “standard” way [19], [20], [26]. Specifically, for the beta-Bernoulli model b = 1, and for the gamma distributions c = d = h = 10−6, e = g = 1, and f = 10−3. The same parameters are used in all examples and in all layers of the “deep” model. The values of P, J and K depend on the specific images under test (i.e., the image size), and these parameters are specified for the specific examples. In all examples we consider gray-scale images, and therefore Kc = 1. For online VB, we set the learning rate parameters as τ0 = 1 and κ = 0.5.
In the examples below, we consider various sizes for at a given layer l, as well as different settings for the truncation levels K(l) and the max-pooling ratio. These parameters are selected as examples, and no tuning or optimization has been performed. Many related settings yield highly similar results, and the model was found to be robust to (“reasonable”) variation in these parameters.
B. Synthesized and MNIST examples
To demonstrate the characteristics of the model, we first consider synthesized data. In Figure 3 we show eight canonical shapes, with shifted versions of these basic shapes used to constitute ten example images (the latter are manifested in each case by selecting four of the eight canonical shapes, and situating them arbitrarily). The eight canonical shapes are binary, and are of size 8 × 8; the ten synthesized images are also binary, of size 32 × 32 (i.e., P = 1024).
Fig. 3.
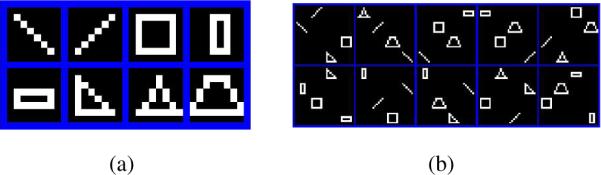
(a) The eight 8 × 8 images at top are used as building blocks for generation of synthesized images. (b) 10 generated images are manifested by arbitrarily selecting four of the 8 canonical elements, and situating them arbitrarily. The images are 32 × 32, and in all cases black is zero and white is one (binary images).
We consider a two-layer model, with the canonical dictionary elements of size 4 × 4 (J = 16) at layer l = 1, and of spatial size 3 × 3 (J = 9) at layer l = 2. As demonstrated below, a two-layer model is sufficient to capture the (simple) structure in these synthesized images. In all examples below we simply set the number of dictionary elements at layer one to a relatively small value, as at this layer the objective is to constitute simple primitives [3], [4], [5], [6], [7], [8]; here K = 10 at layer one. For all higher-level layers we set K to a relatively large value, and allow the IBP construction to infer the number of dictionary elements needed; in this example K = 100 at layer two. When performing max-pooling, upon going from the output of layer one to the input of layer two, and also when considering the output of layer two, the down-sample ratio is two (i.e., the contiguous regions in which max-pooling is performed are 2 × 2; see the left of Figure 2). The dictionary elements inferred at layers one and two are depicted in Figure 4; in both cases the dictionary elements are projected down to the image plane. Note that the dictionary elements from layer one constitute basic elements, such as corners, horizontal, vertical and diagonal segments. However, at layer two the dictionary elements , when viewed on the image plane, look like the fundamental shapes in Figure 3(a) used to constitute the synthesized images. As an example of how the beta-Bernoulli distribution infers dictionary usage and number, from Figure 4(b) we note that at layer 2 the posterior distribution on the number of dictionary elements is peaked at 9, with the 9 elements from the maximum-likelihood sample shown in Figure 4(a), while as discussed above eight basic shapes were employed to design the toy images. In these examples we employed Gibbs sampler with 30,000 burn-in iterations, and the histogram is based upon 20,000 collection samples.
Fig. 4.
The inferred dictionary for the synthesized data in Figure 3(b). (a) dictionary elements at layer one, and layer two, ; (b) estimated posterior distribution on the number of needed dictionary elements at level two, based upon the Gibbs collection samples. In (a) the images are viewed in the image plane. The layer one dictionary images are 4 × 4, and the layer one dictionary images are 9 × 9 (in the image plane, as shown). In all cases white represents one and black represents zero.
We next consider the widely studied MNIST data1, which has a total of 60,000 training and 10,000 testing images, each 28 × 28, for digits 0 through 9. We perform analysis on 10,000 randomly selected images for Gibbs and batch variational Bayesian (VB) analysis. We also examine online variational Bayesian inference on the whole training set; this an example of the utility of online-VB for scaling to large problem sizes.
A two-layer model is considered, as these images are again relatively simple. In this analysis the dictionary elements at layer one, , are 7 × 7, while the second-layer, , are 6 × 6. At layer one a max-pooling ratio of three is employed and K = 24, and at layer two a max-pooling ratio of two is used, and K = 64.
In Figure 5 we present the at Layer 2, as inferred by Gibbs, batch VB and online VB, in each case viewed in the image plane. Layer 1 dictionary are basic elements, and they look similar for all three computational methods, and are omitted for brevity. Additional (and similar) Layer 1 dictionary elements are presented below. We note at layer two the take on forms characteristic of digits, and parts of digits.
Fig. 5.

The inferred dictionary for MNIST data. (a) Layer 2 dictionary elements inferred by Gibbs sampler from 10,000 images; (b) Layer 2 dictionary elements inferred by batch variational Bayesian from 10,000 images; (c) Layer 2 dictionary elements inferred by online variational Bayesian from 60,000 images. In all cases white represents one and black represents zero.
For the classification task, we construct feature vectors by concatenating the first and second (pooling) layer activations based on the 24 Layer 1 and 64 Layer 2 dictionary elements; results are considered based on Gibbs, batch VB and online VB computations. The feature vectors are utilized within a nonlinear support vector machine (SVM) [30] with Gaussian kernel, in a one-vs-all multi-class classifier. The parameters in the SVM are tuned by 5-fold cross-validation. The Gibbs sampler obtained an error rate of 0.89%, online VB 0.96%, and batch VB 0.95%. The results from this experiment are summarized in Table I, with comparison to several recent results on this problem. The results are competitive with the very best in the field, and are deemed encouraging, because they are based on features learned by a general purpose, unsupervised model.
TABLE I.
Classification performance for the MNIST dataset of the proposed model (denoted cFA, for convolutional factor analysis) using three inference methods, with comparisons to approaches from the literature.
We now examine the computational costs of the batch and online VB methods, relative to the quality of the model fit. As a metric, we use normalized reconstruct mean square error (RMSE) on held-out data, considering 200 test images each for digits 0 to 9 (2000 test images in total). In Figure 6 we plot the RMSE at Layers 1 and 2, as a function of computation time for batch VB and online VB, with different mini-batch sizes. For the batch VB solution all 10,000 training images are processed at once for model learning, and the computation time is directly linked to the number of VB iterations that are employed (all computations are on the same data). In the online VB solutions, batches of size 50, 100 or 200 are processed at a time (from the full 60,000 training images), with the images within a batch selected at random; for online VB the increased time reflected in Figure 6 corresponds to the processing of more data, while increasing time for the batch results corresponds to more VB iterations. All computations were run on a desktop computer with Intel Core i7 920 2.26GHz and 6GB RAM, with the software written in Matlab. While none of the code has been carefully optimized, these results reflect relative computational costs of batch and online VB, and relative fit performance.
Fig. 6.
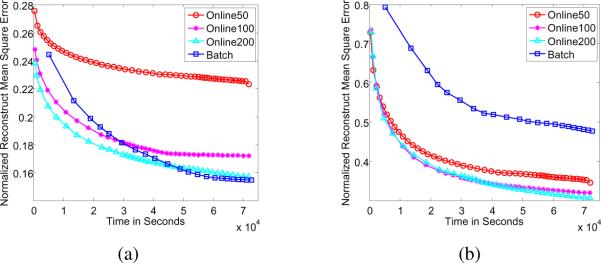
Held-out RMSE for batch VB and online VB with different sizes of mini-batches on MNIST data. Here we use 10,000 images to train batch VB. (a) Layer 1, (b) layer 2
Concerning Figure 6, the largest batch size (200) yields best model fit, and at very modest additional computational cost, relative to smaller batches. At Layer 2 there is a substantial improvement in the model fit of the online VB methods relative to batch (recalling that the fit is measured on held-out data). We attribute that to the fact that online VB has the opportunity to sample (randomly) more of the training set, by the sequential sampling of different batches. The size of the batch training set is fixed and smaller, for computational reasons, and this apparently leads to Layer 2 dictionary elements that are well matched to the training data, but not as well matched and generalizable to held-out data. This difference between Layer 1 and Layer 2 relative batch vs. online VB model fit is attributed to the fact that the Layer 2 dictionary elements capture more structural detail than the simple Layer 1 dictionary elements, and therefore Layer 2 dictionary elements are more susceptible to over-training.
C. Caltech 101 data
The Caltech 101 dataset2 is considered next. We rescale and zero-pad each image to 100 × 100, maintaining the aspect ratio, and then use local contrast normalization to preprocess the images. Layer 1 dictionary elements are of size 11 × 11, and the max-pooling ratio is 5. We consider 4 × 4 dictionary elements , and 6 × 6 dictionary elements . The max-pooling ratio at Layers 2 and 3 is set as 2. The beta-Bernoulli truncation level was set as K = 200. We first consider modeling each class of images separately, with a three-level model considered, as in [7]; because all of the images within a given class are similar, interesting and distinctive structure is manifested in the factor loadings, up to the third layer, as discussed below. In these experiments, the first set of results are based upon Gibbs sampling.
There are 102 image classes in the Caltech 101 data set, and for conciseness we present results here for one (typical) class, revisiting Figure 1; we then provide a summary exposition on several other image classes. The Layer 1 dictionary elements are depicted in Figure 7, and we only focus on and , from layers two and three, respectively. Considering the (in Figure 1(a)), one observes several parts of cars, and for (Figure 1(d)) cars are often clearly visible. It is also of interest to examine the binary variable , which defines which of the candidate dictionary elements are used to represent a given image. In Figure 1(b) we present the usage of the (white indicates being used, and black not used, and the dictionary elements are organized from most probable to least probable to be used). From Figures 1(c) and 1(f), one notes that of the 200 candidate dictionary elements, roughly 134 of them are used frequently at layer two, and 34 are frequently used at layer three. The Layer 1 dictionary elements for these data (typical of all Layer 1 dictionary elements for natural images) are depicted in Figure 7.
Fig. 7.

Layer 1 dictionary elements learned by a Gibbs sampler, for the Caltech 101 dataset.
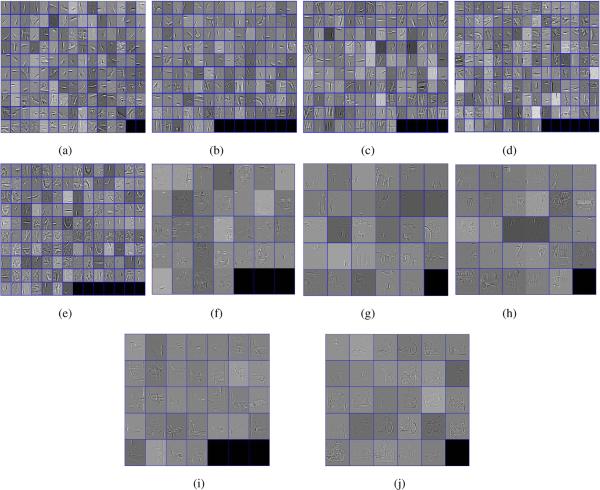
In Figure 8 we show Layer 2 and Layer 3 dictionary elements from five additional classes of the Caltech 101 dataset (the data from each class are analyzed separately). Note that these dictionary elements take on a form well matched to the associated image class. Similar class-specific Layer 2 and object-specific Layer 3 dictionary elements were found when each of the Caltech 101 data classes was analyzed in isolation. Finally, Figure 9 shows Layer 2 and Layer 3 dictionary elements, viewed in the image plane, when the model trains simultaneously on five images from each of four classes (20 total images), where the four classes are faces, cars, planes, and motorcycle. We see in Figure 9 that the Layer 2 dictionary elements seem to capture general characteristics of all of the classes, while at Layer 3 one observes specialized dictionary elements, specific to particular classes.
Fig. 8.
Analysis of five datasets from Caltech 101, based upon Gibbs sampling. (a)–(e) Inferred layer-two dictionary elements, , respectively for the following data sets: face, elephant, chair, airplane, motorcycle; (f)–(j) inferred layer-three dictionary elements, , for the same respective data sets. All of images are viewed in the image plane, and each of the classes of images were analyzed separately.
Fig. 9.

Joint analysis of four image classes from Caltech 101, based on Gibbs sampling. (a) Original images; (b) layer-two dictionary elements , (c) layer-three dictionary elements . All figures in (b) and (c) are shown in the image plane.
The total Caltech 101 dataset contains 9,144 images, and we next consider online VB analysis on these images; batch VB is applied to a subset of these data. A held-out data set of 510 images is selected at random, and we use these images to test the quality of the learned model to fit new data, as viewed by the model fit at Layers 1 and 2. Batch VB is trained on 1,020 images (the largest number for which reasonable computational cost could be achieved on the available computer), and online VB was considered using mini-batch sizes of 10, 20 and 50. The inferred Layer 1 and Layer 2 dictionaries are shown in Figure 10. Figure 11 demonstrates model fit to the held-out data, for the batch and online VB analysis, as a function of computation, in the same manner as performed in Figure 6. For this case the limitations (potential over-training) of batch VB is evident at both Layers 1 and 2, which is attributed to the fact that the Caltech 101 data are more complicated than the MNIST data.
Fig. 10.

The inferred Layer 1 (top) and Layer 2 (bottom) dictionary for Caltech 101 data. (a) Layer 1 and Layer 2 dictionary elements inferred by batch variational Bayesian on 1,020 images; (b) Layer 1 and Layer 2 dictionary elements inferred by online variational Bayes on the whole data set (9,144 images).
Fig. 11.

Held-out RMSE for batch VB and online VB with different sizes of mini-batches on Caltech101 data, as in Figure 6. (a) Layer 1, (b) Layer 2
D. Layer-dependent activation
It is of interest to examine the coefficients at each of the levels of the hierarchy, here for l = 1, 2, 3. In Figure 12 we show one example from the face data set, using Gibbs sampling and depicting the maximum likelihood collection sample. Note that the set of weights becomes increasingly sparse with increasing model layer l, underscoring that at layer l = 1 the dictionary elements are fundamental (primitive), while with increasing l the dictionary elements become more specialized and therefore sparsely utilized. The corresponding reconstructions of the image in Figure 12, as manifested via the three layers, are depicted in Figure 13 (in all cases viewed in the image plane).
Fig. 12.
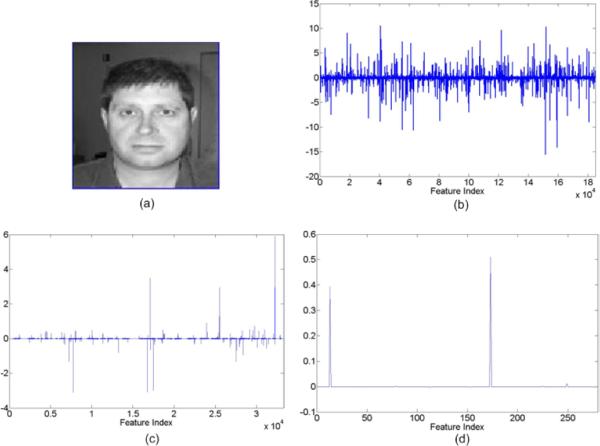
Strength of coefficients for all of three layers. (a) image considered; (b) layers one; (c) layer two; (d) layer three.
Fig. 13.

The reconstructed images at each layer for Figure 9(a). (a) image after local contrast normalization; (b) reconstructed image at Layer 1; (c) reconstructed image at Layer 2; (d) reconstructed image at Layer 3.
E. Sparseness
The role of sparseness in dictionary learning has been discussed in recent papers, especially in the context of structured or part-based dictionary learning [33], [34]. In deep networks, the ℓ1-penalty parameter has been utilized to impose sparseness on hidden units [1], [7]. However, a detailed examination of the impact of sparseness on various terms of such models has received limited quantitative attention. In this section, we employ the Gibbs sampler and provide a detailed analysis on the effects of hyperparameters on model sparseness.
As indicated at the beginning of this section, parameter b controls sparseness on the number of filters employed (via the probability of usage, defined by {πk}). The normal-gamma prior on the wnki constitutes a Student-t prior, and with e = 1, parameter f controls the degree of sparseness imposed on the filter usage (sparseness on the weights Wnk). Finally, the components of the filter dk are also drawn from a Student-t prior, and with g = 1, h controls the sparsity of each dk. Below we focus on the impact of sparseness parameters b, d and f on sparseness, and model performance, again showing Gibbs results (with very similar results manifested via batch and online VB).
In Figure 14 we present variation of MSE with these hyperparameters, varying one at a time, and keeping the other fixed as discussed above. These computations were performed on the face Caltech 101 data using Gibbs computations, averaging 1000 collection samples; 20 face images were considered and averaged over, and similar results were observed using other image classes. A wide range of these parameters yield similar good results, all favoring sparsity (note the axes are on a log scale). Note that as parameter b increases, a more-parsimonious (sparse) use of filters is encouraged, and as b increases the number of inferred dictionary elements (at Layer 2 in Figure 15) decreases.
Fig. 14.

Average MSE calculated from last 1,000 Gibbs samples, considering BP analysis on the Caltech 101 faces data (averaged across 20 face images considered).
Fig. 15.
Considering 20 face images from Caltech 101, we examine setting of sparseness parameters; unless otherwise stated, b = 102, f = 10−5 and h = 10−5. Parameters h and f are varied in (a) and (b), respectively. In (c), we set e = 10−6 and f = 10−6 and make hidden units unconstrained to test the influence of parameter b on the model's sparseness. In all of cases, we show the Layer-2 filters (ordered as above) and an example reconstruction.
F. Classification on Caltech 101
We consider the same classification problem considered by [1], [7], [35], [4], [36], considering Caltech 101 data [1], [7], [8]. The analysis is performed in the same manner these authors have considered previously, and therefore our objective is to demonstrate that the proposed new model construction yields similar results. Results are based upon a Gibbs, batch VB and online VB (mini-batch size 20).
We consider a two-layer model, and for Gibbs, batch VB and online VB 1,020 images are used for training (such that the size of the training set is the same for all cases). We consider classifier design similar to that in [7], in which we perform classification based on layer-one coefficients, or based on both layers one and two. We use a max-pooling step like that advocated in [11], [12], and we consider the image broken up into subregions as originally suggested in [35]. Therefore, with 21 regions in the image [35], and F features on a given level, the max-pooling step yields a 21 · F feature vector for a given image and model layer (42 · F features when using coefficients from two layers). Using these feature vectors, we train an SVM as in [7], with results summarized in Table II (this table is from [1], now with inclusion of results corresponding to the method proposed here). It is observed that each of these methods yields comparable results, suggesting that the proposed method yields highly competitive performance; our classification results are most similar to the deep model considered in [7] (and, as indicated above, the descriptive form of our learned dictionary elements are also most similar to [7], which is based on an entirely different means of modeling each layer). Note of course that contrary to previous models, critical parameters such as dictionary size are automatically learned form the data in our model.
TABLE II.
Classification performance of the proposed model (denoted cFA, for convolutional factor analysis) with several methods from the literature. Results are for the Caltech 101 dataset.
| # Training / Testing Examples | 15/15 | 30/30 |
|---|---|---|
| DN-1 [1] | 57.7 ± 1.0% | 65.8 ± 1.3% |
| DN-2 [1] | 57.0 ± 0.8% | 65.5 ± 1.0% |
| DN-(1+2) [1] | 58.6 ± 0.7% | 66.9 ± 1.1% |
| Lazebnik et al. [35] | 56.4 | 64.6 ± 0.7% |
| Jarret et al. [4] | – | 65.6 ± 1.0% |
| Lee et al. Layer-1 [7] | 53.2 ± 1.2% | 60.5 ± 1.1% |
| Lee et al. Layers-1+2 [7] | 57.7 ± 1.5% | 65.4 ± 0.5% |
| Zhang et al. [36] | 59.1 ± 0.6% | 66.2 ± 0.5% |
| cFA Layer-1 Gibbs sampler | 53.5 ± 1.3% | 62.5 ± 0.9% |
| cFA Layers-1+2 Gibbs sampler | 58.0 ± 1.1% | 65.7 ± 0.8% |
| cFA Layer-1 Batch VB | 52.1 ± 1.5% | 61.2 ± 1.2% |
| cFA Layers-1+2 Batch VB | 56.8 ± 1.3% | 64.5 ± 0.9% |
| cFA Layer-1 Online VB | 52.6 ± 1.2% | 61.5 ± 1.1% |
| cFA Layers-1+2 Online VB | 57.0 ± 1.1% | 64.9 ± 0.9% |
Concerning performance comparisons between the different computational methods, the results based upon Gibbs sampling are consistently better than those based on VB, and the online VB results seem to generalize to held-out data slightly better than batch VB. The significant advantage of VB comes in the context of dictionary learning times. On 1,020 images for each layer, the Gibbs results (1,500 samples) required about 20 hours, while the batch VB on 1,020 images required about 11 hours. By contrast, when analyzing all 9,144 Caltech 101 images, online VB required less than 3 hours. All computations were performed in Matlab, on an Intel Core i7 920 2.26GHz and 6GB RAM computer (as considered in all experiments).
G. Online VB and Van Gogh painting analysis
Our final experiment is on a set of high-resolution scans of paintings by Vincent van Gogh. This data includes 101 high resolution paintings with various sizes (e.g., 5000 × 5000). Art historians typically analyze the paintings locally, focusing them into sub-images; we follow the same procedure, dividing each image into several 128 × 128 smaller images (each painting ranged from 16 to 2000 small images) [37]. The total data set size is 40,000 sub-images.
One issue with these paintings is that often significant portions of the image do not include any brushstrokes, and this portion of the data is mostly insignificant background, including cracks of paint due to aging or artifacts from the canvas. This can be observed in Figure 16. Batch deep learning (Gibbs and batch VB) cannot handle this dataset, due to its huge size. The online VB algorithm provides a way to train the dictionary by going over the entire data set, iteratively sampling several portions from paintings. This mechanism also provides robustness to the regions of paintings with artifacts – even if some sub-images are from such a region, the ability to go over the entire data set eliminates over-fitting to artifacts.
Fig. 16.

Analysis of Van Gogh Paintings with online VB. (a) The original image, (b) pre-processing highlights the brushstrokes (best viewed by electronic zooming), (c) Layer 1 (top) and Layer 2 (bottom) layer dictionaries learned via online VB by processing 20,000 sub-images.
For Layers 1 and 2, we use respective dictionary element sizes of 9 × 9 and 3 × 3, and corresponding max-pooling ratios of 5 and 2. The mini-batch size is 6 (recall from above the advantages found in small mini-batch sizes). The truncation level K is set to 25 for the first layer and 50 for the second layer. The learning rate parameters are ρ0 = 1 and κ = 0.5. We analyzed 20,000 sub-images and the learned dictionary is shown in Figure 16. The Layer 2 dictionary elements, when viewed on the image plane, look similar to the basic vision “tokens” discussed by [38] and [39]. This is consistent with our observation in Figure 10(a) and one of the key findings of [22]: when the diversity in the dataset is high (e.g., analyzing all classes of Caltech 101 together), learned convolutional dictionaries tend to look like primitive edges (Gabor basis functions). We observe that similar type of tokens are extracted by analyzing diverse brushstrokes of Van Gogh which have different thicknesses and directions. The learning of this observation, and the effects of scaling to large data sizes, is a product provided by the online VB computational method. It is interesting that the types of learned dictionary elements associated with data as complicated as paintings are similar to those inferred for simpler images like in Caltech 101 (Figure 10(a)), suggesting a universality of such for natural imagery. Further research is needed for use of the learned convolutional features in painting clustering and classification (the types of methods used for relatively simple data, like Caltech 101 and MNIST, are not appropriate for the scale and diversity of data considered in these paintings).
VI. CONCLUSIONS
The development of deep unsupervised models has been cast in the form of hierarchical factor analysis, where the factor loadings are sparse and characterized by a unique convolutional form. The factor scores from layer l serve as the inputs to layer l + 1, with a max-pooling step. By framing the problem in this manner, we can leverage significant previous research with factor analysis [40]. Specifically, a truncated beta-Bernoulli process [18], [19], motivated by the Indian buffet process (IBP) [17], has been used on the number of dictionary elements needed at each layer in the hierarchy (with a particular focus on inferring the number of dictionary elements at higher levels, while at layer one we typically set the model with a relatively small number of primitive dictionary elements). We also employ a hierarchical construction of the Student-t distribution [26] to impose sparseness on the factor scores, with this related to previous sparseness constraints imposed via ℓ1 regularization [1]. The inferred dictionary elements, particularly at higher levels, typically have descriptive characteristics when viewed in the image plane.
Summarizing observations, when the model was employed on a specific class of images (e.g., cars, planes, seats, motorcycles, etc.) the layer-three dictionary elements when viewed in the image plane looked very similar to the associated class of images (see Figure 8), with similar (but less fully formed) structure seen for layer-two dictionary elements. Further, for such single-class studies the beta-Bernoulli construction typically only used a relatively small subset of the total possible number of dictionary elements at layers two and three, as defined by the truncation level. However, when considering a wide class of “natural” images at once, while the higher-level dictionary elements were descriptive of localized structure within imagery, they looked less like any specific entity (see Figure 10); this is to be expected by the increased heterogenity of the imagery under analysis. Additionally, for the dictionary-element truncation considered, as the diversity in the images increased it was more likely that all of the possible dictionary elements within the truncation level were used by at least one image. Nevertheless, as expected from the IBP, there was a relatively small subset of dictionary elements at each level that were “popular”, or widely used (see Section III-A).
The proposed construction also offers significant potential for future research. Specifically, we are not fully exploiting the potential of the Gibbs and VB inference. To be consistent with many previous deep models, we have performed max-pooling at each layer. Therefore, we have selected one (maximum-likelihood) collection sample of model parameters when moving between layers. This somewhat defeats the utility of the multiple collection samples that are available. Further, the model parameters (particularly the dictionary elements) at layer l are inferred without knowledge of how they will be employed at layer l + 1. In future research we will seek to more-fully exploit the utility of the fully Bayesian construction. This suggests inferring all layers of the model simultaneously. This can be done with a small modification of the existing model. For example, if the max-pooling step is replaced with average pooling. Alternatively, the model in [1] did not perform pooling at all. By removing the max-pooling step in either manner, we have the opportunity to infer all model parameters jointly at all layers, learning a joint ensemble of models, manifested by the Gibbs collection samples, for example. One may wish to perform max-pooling on the inferred parameters in a subsequent classification task, since this has proven to be quite effective in practice [11], [12], but the multiple layers of the generative model may first be learned without max pooling.
By jointly learning all layers in a self-consistent Bayesian manner, one has the potential to integrate this formulation with other related problems. For example, one may envision employing this framework within the context of topic models [41], applied for inferring inter-relationships between multiple images or other forms of data (e.g., audio). Further, if one has additional meta-data about the data under analysis, one may impose further structure by removing the exchangeability assumption inherent to the IBP, encouraging meta-data-consistent dictionary-element sharing, e.g, via a dependent IBP [42], or related construction. It is anticipated that there are many other ways in which the Bayesian form of the model may be more-fully exploited and leveraged in future research.
Footnotes
References
- [1].Zeiler M, Krishnan D, Taylor G, Fergus R. Deconvolution networks. Conf. Computer Vision Pattern Recognition (CVPR) 2010 [Google Scholar]
- [2].LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proc. IEEE. 1998;86:2278–2324. [Google Scholar]
- [3].Hinton G, Salakhutdinov R. Reducing the dimensionality of data with neural networks. Science. 2006;313(5786):504–507. doi: 10.1126/science.1127647. [DOI] [PubMed] [Google Scholar]
- [4].Jarrett K, Kavukcuoglu K, Ranzato M, LeCun Y. What is the best multi-stage architecture for object recognition? Int. Conf. Comp. Vision (ICCV) 2009 [Google Scholar]
- [5].Ranzato M, Poultney C, Chopra S, LeCun Y. Efficient learning of sparse representations with an energy-based model. Neural Inf. Proc. Systems (NIPS) 2006 [Google Scholar]
- [6].Vincent P, Larochelle H, Bengio Y, Manzagol P. Extracting and composing robust features with denoising autoencoders. Proc. Int. Conf. Mach. Learning (ICML) 2008 [Google Scholar]
- [7].Lee H, Grosse R, Ranganath R, Ng AY. Convolutional deep belief networks for scalable unsupervised learning of hierarchical representations. Proc. Int. Conf. Mach. Learning (ICML) 2009 [Google Scholar]
- [8].Lee H, Largman Y, Pham P, Ng A. Unsupervised feature learning for audio classification using convolutional deep belief networks. Neural Info. Processing Systems (NIPS) 2009 [Google Scholar]
- [9].Norouzi M, Ranjbar M, Mori G. Stacks of convolutional restricted boltzmann machines for shift-invariant feature learning. IEEE Conference on Computer Vision and Pattern Recognition (CVPR).2009. [Google Scholar]
- [10].Lee H, Ekanadham C, Ng AY. Sparse deep belief network model for visual area V2. Neural Info. Processing Systems (NIPS) 2008 [Google Scholar]
- [11].Boureau Y, Bach YLF, Ponce J. Learning mid-level features for recognition. Proc. Computer Vision Pattern Recognition. 2010 [Google Scholar]
- [12].Wang J, Yang J, Yu K, Lv F, Huang T, Gong Y. Locality-constrained linear coding for image classification. Proc. Computer Vision Pattern Recognition. 2010 [Google Scholar]
- [13].Boureau Y, Ponce J, LeCun Y. A theoretical analysis of feature pooling in vision algorithms. Proc. Int. Conf. Mach. Learning (ICML) 2010 [Google Scholar]
- [14].Mairal J, Bach F, Ponce J, Sapiro G. Online dictionary learning for sparse coding. Proceedings of the International Conference on Machine Learning.2009. [Google Scholar]
- [15].Jenatton R, Mairal J, Obozinski G, Bach F. Proximal methods for sparse hierarchical dictionary learning. Proceedings of the International Conference on Machine Learning.2010. [Google Scholar]
- [16].Zhang X, Dunson D, Carin L. Tree-structured infinite sparse factor model. Proc. Int. Conf. Machine Learning. 2011 [PMC free article] [PubMed] [Google Scholar]
- [17].Griffiths TL, Ghahramani Z. Infinite latent feature models and the indian buffet process. Advances in Neural Information Processing Systems. 2005:475–482. [Google Scholar]
- [18].Thibaux R, Jordan M. Hierarchical beta processes and the Indian buffet process. International Conference on Artificial Intelligence and Statistics.2007. [Google Scholar]
- [19].Paisley J, Carin L. Nonparametric factor analysis with beta process priors. Proc. Int. Conf. Machine Learning. 2009 [Google Scholar]
- [20].Zhou M, Chen H, Paisley J, Ren L, Sapiro G, Carin L. Non-parametric bayesian dictionary learning for sparse image representations. Proc. Neural Information Processing Systems. 2009 [Google Scholar]
- [21].Adams R, Wallach H, Ghahramani Z. Learning the structure of deep sparse graphical models. AISTATS. 2010 [Google Scholar]
- [22].Chen B, Polatkan G, Sapiro G, Dunson D, Carin L. The hierarchical beta process for convolutional factor analysis and deep learning. Proc. Int. Conf. Machine Learning (ICML) 2011 doi: 10.1109/TPAMI.2013.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].West M. Bayesian factor regression models in the “large p, small n” paradigm. In: Bernardo JM, Bayarri M, Berger J, Dawid A, Heckerman D, Smith A, West M, editors. Bayesian Statistics 7. Oxford University Press; 2003. pp. 723–732. [Google Scholar]
- [24].Carvalho C, Chang J, Lucas J, Nevins JR, Wang Q, West M. High-dimensional sparse factor modelling: Applications in gene expression genomics. Journal of the American Statistical Association. 2008;103:1438–1456. doi: 10.1198/016214508000000869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Adams R, Wallach H, Ghahramani Z. Learning the structure of deep sparse graphical models. International Conference on Artificial Intelligence and Statistics.2010. [Google Scholar]
- [26].Tipping M. Sparse Bayesian learning and the relevance vector machine. Journal of Machine Learning Research. 2001;1:211–244. [Google Scholar]
- [27].Wainwright M, Jordan M. Graphical models, exponential families, and variational inference. Foundations and Trends in Machine Learning. 2008;1(1–2):1–305. [Google Scholar]
- [28].Jordan M, Ghahramani Z, Jaakkola T, Saul L. Introduction to variational methods for graphical models. Machine Learning. 1999;37:183–233. [Google Scholar]
- [29].Hoffman M, Blei D, Bach F. Online learning for latent Dirichlet allocation. Advances in Neural Information Processing Systems. 2010 [Google Scholar]
- [30].Cristianini N, Shawe-Taylor J. An Introduction to Support Vector Machines. Cambridge University Press; 2000. [Google Scholar]
- [31].Weston RCJ, Ratle F. Deep learning via semi-supervised embedding. Proc. Int. Conf. Mach. Learning (ICML) 2008 [Google Scholar]
- [32].Ranzato M, Huang F-J, Boureau Y-L. Unsupervised learning of invariant feature hierarchies with applications to object recognition. IEEE Conference on Computer Vision and Pattern Recognition (CVPR).2007. [Google Scholar]
- [33].Hoyer PO. Non-negative matrix factorization with sparseness constraints. J. Machine Learning Research. 2004;5:1457–1469. [Google Scholar]
- [34].Lee DD, Seung HS. Learning the parts of objects by non-negative matrix factorization. Nature. 1999;401(6755):788–791. doi: 10.1038/44565. [DOI] [PubMed] [Google Scholar]
- [35].Lazebnik S, Schmid C, Ponce J. Beyond bags of features: Spatial pyramid matching for recognizing natural scene categories. Proc. Computer Vision Pattern Recognition (CVPR) 2006 [Google Scholar]
- [36].Zhang H, Berg AC, Maire M, Malik J. SVM-KNN: Discriminative nearest neighbor classification for visual category recognition. Computer Vision Pattern Recognition (CVPR) 2006 [Google Scholar]
- [37].Johnson CR, Hendriks E, Berezhnoy I, Brevdo E, Hughes SM, Daubechies I, Li J, Postma E, Wang JZ. Image processing for artist identification: Computerized analysis of Vincent van Gogh's brushstrokes. IEEE Signal Processing Magazine. 2008 [Google Scholar]
- [38].Marr D. Vision. Freeman, San Francisco. 1982 [Google Scholar]
- [39].Donoho DL. Nature vs. Math: Interpreting Independent Component Analysis in Light of Recent work in Harmonic Analysis. Proc Int Workshop on Independent Component Analysis and Blind Signal Separation ICA2000. 2000:459–470. [Google Scholar]
- [40].Knowles D, Ghahramani Z. Infinite sparse factor analysis and infinite independent components analysis. 7th International Conference on Independent Component Analysis and Signal Separation.2007. [Google Scholar]
- [41].Blei D, Ng A, Jordan M. Latent Dirichlet allocation. J. Machine Learning Research. 2003;3:993–1022. [Google Scholar]
- [42].Williamson S, Orbanz P, Ghahramani Z. Dependent indian buffet processes. Proc. Int. Conf. Artificial Intell. Stat. (AISTATS) 2010 [Google Scholar]