Sodium Along With Low-Threshold Potassium Currents Enhance Coincidence Detection of Subthreshold Noisy Signals in MSO Neurons

Abstract

Voltage-dependent membrane conductances support specific neurophysiological properties. To investigate the mechanisms of coincidence detection, we activated gerbil medial superior olivary (MSO) neurons with dynamic current-clamp stimuli in vitro. Spike-triggered reverse-correlation analysis for injected current was used to evaluate the integration of subthreshold noisy signals. Consistent with previous reports, the partial blockade of low-threshold potassium channels (I_KLT) reduced coincidence detection by slowing the rise of current needed on average to evoke a spike. However, two factors point toward the involvement of a second mechanism. First, the reverse correlation currents revealed that spike generation was associated with a preceding hyperpolarization. Second, rebound action potentials are 45% larger compared to depolarization-evoked spikes in the presence of an I_KLT antagonist. These observations suggest that the sodium current (I_Na) was substantially inactivated at rest. To test this idea, I_Na was enhanced by increasing extracellular sodium concentration. This manipulation reduced coincidence detection, as reflected by slower spike-triggering current, and diminished the hyperpolarization phase in the reverse-correlation currents. As expected, a small outward bias current decreased the pre-spike hyperpolarization phase, and TTX blockade of I_Na nearly eliminated the hyperpolarization phase in the reverse correlation current. A computer model including Hodgkin-Huxley type conductances for spike generation and for I_KLT showed reduction in coincidence detection when I_KLT was reduced or when I_Na was increased. We hypothesize that desirable synaptic signals first remove some inactivation of I_Na and reduce activation of I_KLT to create a brief temporal window for coincidence detection of subthreshold noisy signals.

INTRODUCTION

Interaural time difference (ITD) of acoustic signals is encoded with great accuracy by neurons in many vertebrates (Bernstein 2001; Goldberg and Brown 1969; Moiseff and Konishi 1981; Spitzer and Semple 1995; Yin and Chan 1990). This accuracy, which greatly exceeds the temporal precision observed in other parts of the brain, is based on several specializations. Anatomical features, such as axonal delay lines (Jeffress 1948), permit ITD determination by coincidence detection. Electrophysiological mechanisms also play an important role, including rapid, adapting synaptic currents (Gardner et al. 1999; Raman and Trussell 1992; Smith et al. 2000), fast low-threshold potassium currents (I_KLT) (Manis and Marx 1991; Rathouz and Trussell 1998; Reyes et al. 1994) and circuitry to provide fast and precisely timed inhibition (Brand et al. 2002; Grothe and Sanes 1994). Experimental and modeling studies suggest that such biophysical properties enhance the ability of auditory neurons to preserve temporal fidelity of signals by synchronizing (phase locking) to strong sinusoidal stimuli (Oertel 1983; Reyes et al. 1996; Rothman and Young 1996). In our previous study, we focused on integration of subthreshold inputs, finding an increased signal-to-noise ratio for small signal detection due to activation of I_KLT (Svirskis et al. 2002; Svirskis and Rinzel 2003). The present study extends previous findings to consider how I_Na kinetics act in concert with I_KLT to enhance coincidence detection for subthreshold noisy signals.

Brain stem auditory neurons commonly receive a high level of spontaneous afferent activity. Even in the absence of an acoustic stimulation, this random firing can reach rates of 100 Hz (Liberman 1978, 1982). Primary afferent fibers with different spontaneous rates have different projection patterns within the cochlear nucleus (Liberman 1991, 1993) suggesting a specific role for such “random” activity. For the purposes of the present study, it is notable that MSO cells can also display spontaneous firing in vivo, suggesting a significant amount of random spontaneous excitatory input (Carr and Konishi 1990; Goldberg and Brown 1969; Young and Rubel 1986). Our previous (Svirskis et al. 2002) and present study are motivated by the observation that noise can facilitate the detection of weak signals in diverse natural and artificial systems (Russell et al. 1999; Wiesenfeld and Moss 1995). Therefore, it is possible that neuronal spontaneous random activity could serve a similar function in MSO neurons during coincidence detection because it increases in lower auditory brain stem centers during performance (Ryan et al. 1984). The detection of small signals is particularly important for animal survival, and the membrane properties that participate in shaping integration of such signals are of great interest.

Stochastic inputs have been used extensively to investigate how neuronal and input properties influence temporal processing characteristics (Bryant and Segundo 1976; Gauck and Jaeger 2000; Hunter et al. 1998; Longtin and Laniel 1997; Mainen and Sejnowski 1995; Softky and Koch 1993). Here, we explore the influence of I_Na and I_KLT gating properties on the integration of subthreshold noisy signals in coincidence detection by recording from gerbil MSO neurons in vitro, stimulated with computer-generated currents that mimic transient random weak synaptic conductances. The use of random stimuli allowed us to employ spike-triggered reverse correlation to study integration of small signals in coincidence detection. Reverse correlation for injected current calculates the mean current preceding spike generation and provides a possibility to monitor how membrane properties shape pre-spike integration (Bryant and Segundo 1976). For example, it has been shown that the rate of change of membrane potential before spike generation defines integration precision (Kisley and Gerstein 1999) and spike-generation threshold (Azouz and Gray 2003) in coincidence detection.

We found that I_Na in addition to I_KLT and hyperpolarization-activated current, I_h, influence the precision of coincidence detection of subthreshold signals and their effects on the reverse-correlation current support this conclusion. The partial inactivation of I_Na and partial activation of I_KLT at rest requires on average a transient priming hyperpolarization followed by fast depolarization to trigger spike generation. The brief subthreshold excitatory inputs for this fast rise in voltage toward threshold must be precisely coincident to outrace the inactivation I_Na and reactivation of I_KLT. I_h depolarizes the resting membrane enough to partially inactivate I_Na and activate I_KLT. Computer simulations demonstrated similar effects of inactivation of I_Na and activation of I_KLT on coincidence detection of subthreshold signals.

METHODS

Experimental

Gerbils (Meriones unguiculatus) aged postnatal (P) days 17–20 were used to make 200 µm MSO brain slices oriented intermediate between the coronal and the horizontal plane. The artificial cerebrospinal fluid (ACSF) contained (in mM) 125 NaCl, 4 KCl, 1.2 KH₂PO₄, 1.3 MgSO₄, 26 NaHCO₃, 15 glucose, 2.4 CaCl₂, and 0.4 l-ascorbic acid (pH 7.3 when bubbled with 95% O₂-5% CO₂). The ACSF was continuously superfused in the recording chamber at 4–5 ml/min at room temperature (22–24°C). Although we were able to obtain recordings at higher temperature (35°C) to corroborate our findings (Figs. 2D, inset, and 3A, inset), the state of neurons deteriorated much faster. Whole cell current-clamp recordings were obtained mostly from medial and dorsal MSO neurons (Axoclamp2A). The neurons were visually identified using IR-DIC microscopy (Olympus). The internal patch solution contained (in mM) 127.5 potassium gluconate, 0.6 EGTA, 10 HEPES, 2 MgCl₂, 5 KCl, 2 ATP, 10 phosphocreatinine (Tris salt), and 0.3 GTP (pH 7.2). The following drugs were added to the ACSF as specified in results: 20 nM dendrotoxin K (DTXK, Alomone Labs, Israel), a concentration that would block all homogeneous Kv1.1 channels (Robertson et al. 1996), 20 nM dendrotoxin I (DTXI, Alomone Labs, Israel), 2 µM ZD7288 (SIGMA), and 1 µM tetrodotoxin (TTX, Alomone Labs, Israel). Recording electrodes were fabricated from borosilicate glass micro-capillaries (1.5 mm OD), and their resistance ranged from 6 to 8 MΩ.

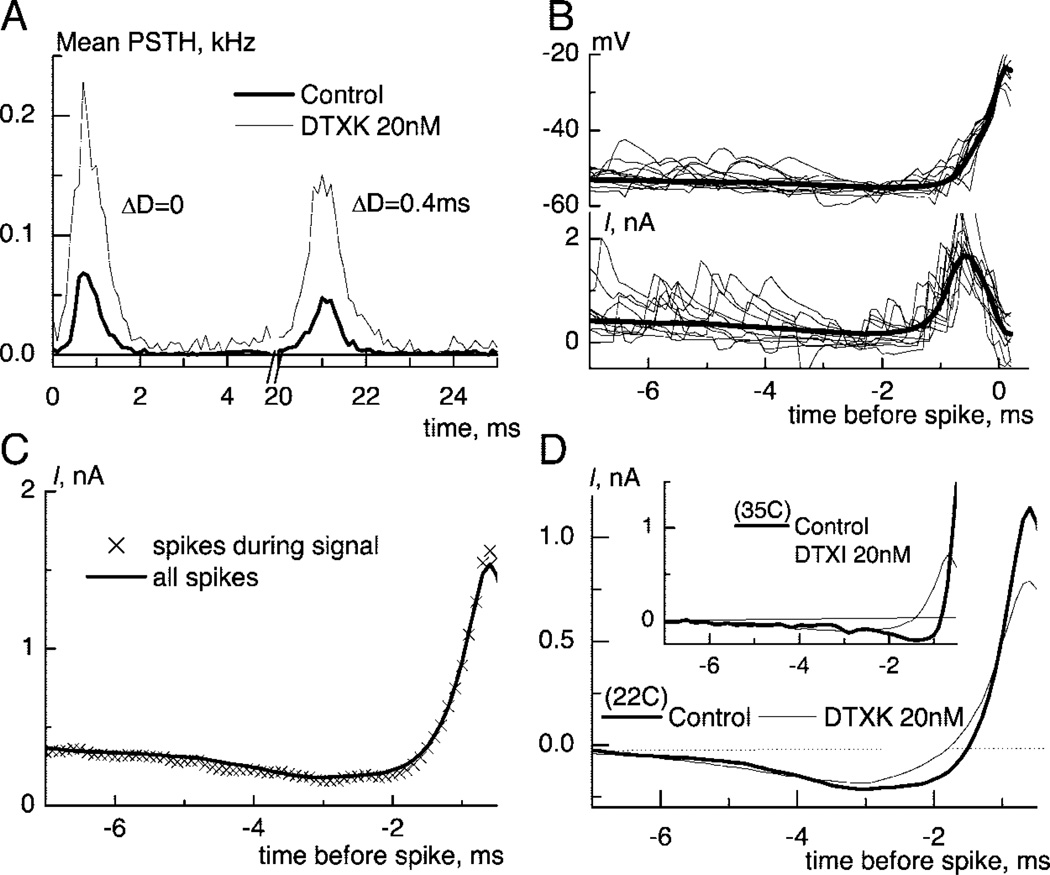
FIG. 2.

I_KLT reduces the integration time for noisy spike-preceding inputs. A: post stimulus time histograms in response to noise and 2 “signal” excitatory PSGs (EPSGs) delivered simultaneously and with a delay of 0.4 ms before and after DTXK (population means, n= 10). B: 10 consecutive traces of membrane potential (top) and injected current (bottom) preceding spike generation. The thick curves are the mean traces i.e. spike triggered reverse correlations. Note that even raw traces show reduced excitation just before spike-triggering depolarization. C: traces of reverse correlation for all spikes and for spikes evoked during 1 ms after injection of signal EPSGs in normal conditions (average for 10 neurons). D: change in reverse correlation currents after DTXK. The dip was relatively unchanged, but the maximum rate of rise was strongly reduced (offsets were subtracted). Inset: The change of temporal shape at 35C. Note much faster rising slope at this temperature.

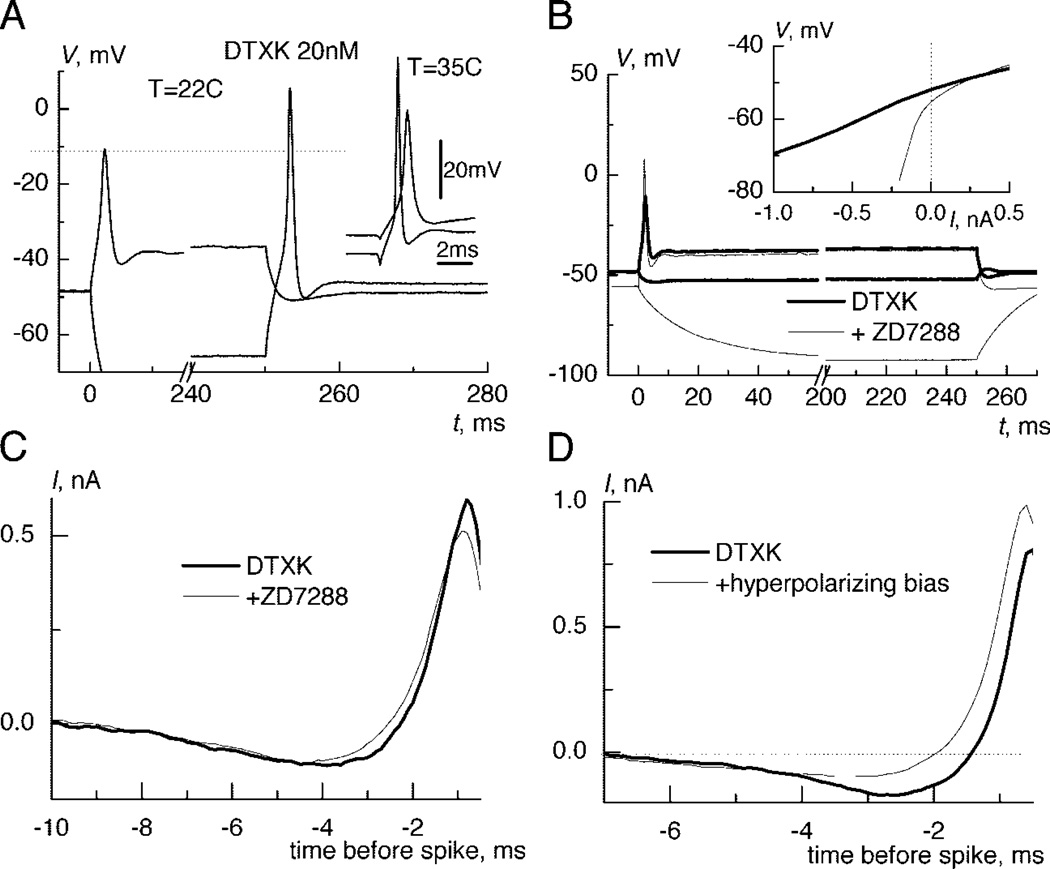
FIG. 3.

Influence of I_h on response properties and the integration of small signals. A: the amplitude of rebound spikes after hyperpolarizing injection of −1 nA are larger than that of spikes evoked by depolarizing injection of 0.8 nA even after application of DTXK. Inset: the same was true for spikes evoked by threshold current injections (0.4 and 1 nA) from rest or during hyperpolarization by −0.75 nA at 35°C. B: an I_h antagonist (ZD7288) hyperpolarized neurons but did not change the response to a depolarizing current step. Inset: steady current-voltage relation shows that ZD7288 blocked a large portion of the hyperpolarization activated current. C: spike-triggered reverse-correlation current changed very little after ZD7288 because the integration was defined by remaining I_KLT an I_NaD: injection of hyperpolarizing bias current reduced the dip. Offsets were subtracted in D and C.

Data acquisition and stimulus generation was carried out under computer control at 10 kHz. We used the board PCI-MIO-16E-1 (NI 6070E) providing ≤1.5-MHz input sampling and 400-kHz output generation in non-FIFO mode and the programming package Lab-View (National Instruments), which allows setting real-time priority thereby suspending other parts of the operating system. The Lab View program interfaced a module written in the C++ programming language for computing stimulus and response statistics. We used the dynamic-clamp method for stimulus generation. The dynamic clamp’s stability was assured by monitoring for skipped data points and inspecting saved traces of raw data (Fig. 2B). Because the dynamic clamp critically depends on how fast the potential in the electrode equilibrates, we compensated the electrode capacitance while monitoring the decay of the electrode potential in discontinuous current-clamp mode provided by the Axoclamp amplifier. The response always settled down in <0.1 ms.

The program determined in real time the time-varying current that was injected into the neuron according to the calculated conductance value and the measured instantaneous membrane potential (Reyes et al. 1996; Sharp et al. 1993). The program also saved spike times, defined as the time points when the membrane potential crossed —20 mV from below. The time course of injected current preceding each spike (Fig 2B) by 20 ms was stored in the computer memory buffer and was used to calculate the spike-triggering current by reverse correlation.

To study the coincidence detection of weak random signals, we employed two stimulus paradigms. Each stimulus had features, although different, that could be related to MSO neurons in vivo. One stimulus was reminiscent of more realistic sound-evoked synaptic input and consisted of random (simulated) postsynaptic conductance transients (PSGs) with a periodically modulated delivery rate. The probability, P, for a PSG to occur in the time interval dt was equal to dt • R • (M • (sin[2π(t — D — ΔD)/T]— 1) + 1) if the value of the expression was greater than 0, and P = 0 otherwise. Here, R was the maximal rate, M was the modulation depth, T was the period, D was the delay for inhibition, and ΔD was the delay between signals for coincidence detection. Two sets of excitatory and inhibitory trains, one with zero delay and the other with a particular value of ΔD, were used for coincidence detection. R was equal to 2 kHz for both excitation and inhibition; M = 1; D = 1 ms for inhibition; T = 2 ms; and dt = 0.1 ms. We used this idealized description of input to simplify calculations performed in real time. The stimulus was applied for 25 ms with rest intervals of 25 ms. The PSGs had exponentially distributed random amplitudes that were chosen so that each 25-ms presentation generated no more than two spikes (see following text). Because of the weakness of our stimulus and the presence of inhibitory PSGs, the spikes could be evoked at anytime during the stimulus, and there were no onset transients in the post stimulus time histogram (not shown). The stimulation regimen lasted 180 s. Several thousand events were collected for computing probability to observe a spike.

The second type of stimulus paradigm was chosen to reflect the fact that MSO neurons receive spontaneous random synaptic input. This stimulus was used to explore signal integration preceding spike generation by using reverse correlation and coincidence detection of individual excitatory PSGs (EPSGs). It contained two subthreshold “signal” synaptic conductances, EPSGs, in the presence of noise representing spontaneous input. Each EPSG was generated as a simple exponential decay from a step onset and time constant of 1 ms. This signal EPSG was to represent the coincident arrival of a few much smaller unitary-like EPSGs, such as would occur in the case of a weak auditory signal. For coincidence detection, the delay between the pair of signal EPSGs was absent or equal to 0.4 ms. This pair was generated each 20 ms while two trains of random smaller (on average) transient EPSGs and IPSGs (1-ms decay time constants) were delivered continuously, representing the “noise.” Each of the excitatory and inhibitory trains had exponentially distributed inter-event times (independent Poisson trains) with a mean rate of 2 kHz.

For random excitation, the reversal potential was 0 mV, and for inhibition it was —70 mV. The amplitude of synaptic conductance had an exponential distribution with the same mean for excitation and inhibition and was 10 times smaller that the amplitude of the EPSG required for triggering an action potential. The resulting mean injected current was inward, and <0.5 nA and mean membrane potential was 2–4 mV above rest. The resulting spontaneous firing rate was equal to several tens of hertz, in agreement with in vivo studies in the MSO (Goldberg and Brown 1969). The amplitude for the signal EPSGs and PSGs in periodically modulated trains was two times larger. After the application of pharmacological agents, the stimuli were delivered with the same amplitudes in order to define drug effects. Thereafter the amplitudes were reduced so that firing rate would remain below several tens of hertz. The stimulation lasted 180 s in order to gather several thousand events to calculate statistics.

Computational

We formulated and used a single-compartment (lumped neuron) model with Hodgkin-Huxley-type Na⁺ and K⁺ (delayed rectifier) conductances for spike generation, and a low-threshold potassium conductance (Svirskis et al. 2002). The parameters for spike generation were taken from Lytton and Sejnowski (1991), and parameters for I_KLT from Rathouz and Trussell (1998). The dependence on voltage of activation and inactivation gating was changed for the Na⁺ conductance and I_KLT to achieve better resemblance to the observed responses of MSO neurons (Svirskis et al. 2002). The currents were calculated by using the general equation: I = g • A_cell • m^p • h^q (V – E); where g is specific conductance, A_cell is membrane area, p and q represent the numbers of gating subunits, V is membrane potential, E is reversal potential for the current. Activation and inactivation gating variables, m and h, respectively, were governed by equations of the form: du/dt = [u_∞(V) – u)]/τ_u(V). The “steady-state” value for the gating variable, u, was u_∞ = α/(α + β), and the “time constant” τ_u = 1/(α + β); both u_∞ and τ_u were voltage dependent: α = A₀exp[–0.0393zγ(V_0.5 – V)], β = B₀exp[0.0393z(1 – γ)(V_0.5 – V)], where z is the effective gating charge. The fast-activating sodium current had a reversal potential E = 50 mV; its activation was described by the parametersP = 3, z = 3.3, γ = 0.7, A₀ = 4.2 ms⁻¹, B₀ = 4.2 ms⁻¹, V_0.5 = −29.5 mV; inactivation had the following parameters: q = 1, z = −3.0, γ = 0.27, A₀ = 0.09 ms⁻¹, B₀ = 0.09 ms⁻¹, V_0.5 = −60 mV. The time constants for activation and inactivation had limits to their minimal values set to 0.05 and 0.25 ms, respectively, to avoid exponents from occasional overflowing. The delayed rectifier conductance had only an activation gating variable, described by the parameters: E = −90 mV, p = 4, z = 3, γ = 0.8, A₀ = 0.3 ms⁻¹, B₀ = 0.3 ms⁻¹, V_0.5 = −30 mV, and the minimal time constant for activation of 1 ms. The conductance of the low-threshold potassium current, I_LKT, was described by the parameters: E = −90 mV, p = 1, z = 2.88, γ = 0.39, A₀ = 0.2 ms⁻¹, B₀ = 0.17 ms⁻¹, V_0.5 = −45 mV. This current did not inactivate. A constant bias current of 2.5 nA, mimicking the depolarizing effect of I_h current, was injected.

The specific conductances, g, were 0.2, 0.01, and 0.02 nS/µm² for I_Na, the delayed rectifier, and I_KLT, respectively. The area of the compartment, A_cell, was 10⁴ µm²; specific conductance for membrane leakage was 3.333*10⁻³ nS/µm²; specific capacitance was 10⁻⁵ nF/µm² with the resulting time constant τ_m of 3 ms. The model’s resting membrane potential was about −50 mV (similar to that measured in vitro), and the spike threshold was ~20 mV above rest.

The stimuli for the computational neuron were the same as those used in experiments, except for the conductance amplitudes of the PSGs. For the signal EPSG the amplitude, A, was 18 nS. For the random PSGs the mean amplitude, a, was 9 nS. For the periodically modulated stimulus, the mean amplitude of PSGs was 18 nS. The numerical integration was performed with a fixed step-size second-order Crank-Nicholson scheme (Press et al. 1992), using a time step of 40 µs.

RESULTS

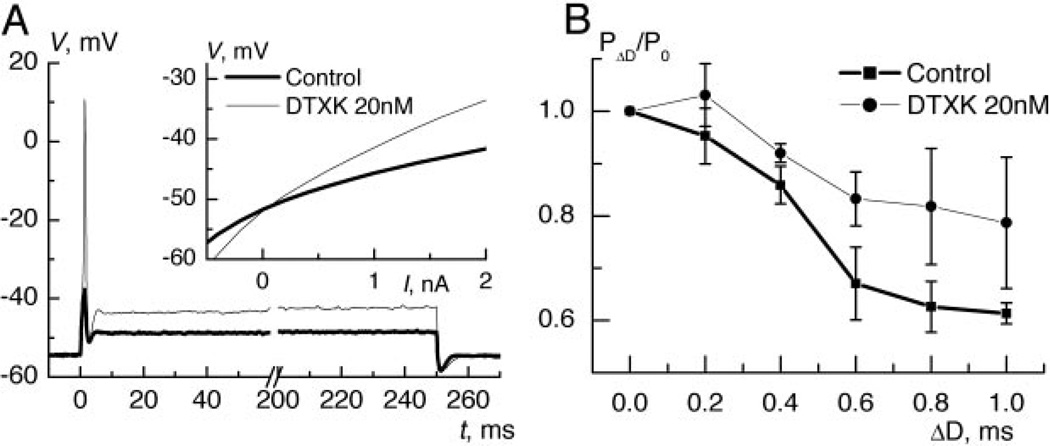
We recorded from gerbil MSO P17–P20 neurons to investigate how membrane properties shape coincidence detection of small noisy signals. The mean resting membrane potential (RMP) was −50.6 ± 2.9 (SD) mV (n = 45). All neurons responded to any depolarizing suprathreshold step stimulus with just a single spike with amplitude of 49.2 ± 17 mV (n = 45). The MSO neurons were stimulated using the dynamic-clamp procedure to simulate synaptic conductances. Two sets of input excitation and input inhibition trains of random stimuli, generated according to a periodically modulated probability, were applied to evaluate the sensitivity to coincidence (described in methods). The probability, P_ΔD, to generate a spike during a stimulus with a particular delay, ΔD, between the two sets of trains was normalized by the probability when ΔD = 0ms. To test how the low-threshold potassium current shaped coincidence detection, we applied DTXK (20 nM), which is a specific blocker of Kv1.1 channels (Robertson et al. 1996). Within this age range, the toxin did not convert neurons to tonic firing (Fig. 1A) but reduced spike threshold and blocked ~50% of the outward current as seen from the steady current-voltage plot (Fig. 1A, inset, average for 6 neurons). Application of the nonspecific blocker of low-threshold potassium channels, DTXI(20 nM), at temperature of 35° C also did not induce tonic firing (n = 3, not shown). As expected (Kuba et al. 2002; Reyes et al. 1996), such changes of membrane properties reduced sensitivity to the delay (Fig. 1B, average for 4 neurons).

FIG. 1.

Role of I_KLT in response properties and coincidence detection of periodically modulated random input. A: response of medial superior olivary (MSO) neuron to a depolarizing step current injection of 0.6 nA. After application of dendrototin K (DTXK) the same strength of injected current evoked a spike. Inset: an average for 6 neurons of steady current-voltage relation before and after application of DTXK. B: sensitivity to delay for periodically modulated random trains before and after DTXK (average for 4 neurons).

A different stimulus protocol was used to apply reverse-correlation techniques to analyze how membrane currents enable coincidence detection of small signals. Two subthreshold signal EPSGs were imbedded in noise composed of random trains of smaller excitatory and inhibitory EPSGs. Coincidence detection of such signals was similar to periodically modulated trains and was also significantly reduced from P_0.4/P₀ = 0.72 to 0.87 (mean, P < 0.02, n = 10) by the partial block of I_KLT. The similarity between the measures of coincidence detection indicates that integration of this type of stimulus also reflects system sensitivity to coincidence for the more natural periodically modulated inputs. Post stimulus time histograms, PSTH, (Fig. 2A, average for 10 neurons), showed that application of DTXK broadened the response half-widths, thus reducing the temporal precision of integration.

The mean injected current preceding spike generation was calculated as the spike triggered reverse correlation (Fig 2B, see methods). Although the spike trains in response to random stimuli contained spikes evoked by signals and by noise, we calculated the reverse correlation for all spikes together to reduce the duration of data gathering. In our case of small signal stimulation, the signal EPSGs were only two times larger than the “spontaneous” EPSGs in the generated noisy input. Even a fully coincident pair of signal EPSGs was two times smaller that the threshold for spike generation, and randomly occuring smaller EPSGs had to be added for a pair of signal EPSGs to generate the spike. For these reasons, reverse-correlation currents were identical to those for spikes evoked only during 1 ms after injection of signal EPSGs (Fig. 2C, average for 10 neurons).

The reverse-correlation time courses contained a characteristic shape with a dip, reflecting a tendency for the advantageous input to hyperpolarize the membrane potential before spike generation, followed by a sharp rise of injected depolarizing current responsible for spike generation (Fig. 2D). After DTXK, the dip was not much reduced, but the maximum slope of rise was reduced significantly from 1.8 to 1.1 nA/ms (Fig. 2D, population mean, n = 10, P < 0.05). The reverse correlation was changed similarly when the bathing solution temperature was 35°C (n = 3, Fig. 2D, inset), although the rising slope was much steeper. Thus we view this reduced sensitivity to signal coincidence after DTXK as due to slower temporal integration by the cell. Indeed, the delay between signal EPSGs is equivalent to a slower rate of rise for the total injected current. For this reason, the reverse correlation’s reduced rate of rise in DTXK shows that the pair of signal EPSGs has a higher probability to evoke a spike because spike generation can occur with slower rising inputs and, hence, the sensitivity to coincidence is reduced.

After application of DTXK, all neurons continued to respond with a single spike to a depolarizing current step and also displayed a rebound spike after termination of a hyperpolarizing step (Fig. 3A). We previously reported that, before P15, such phasic responses are converted to sustained firing during blockade of I_KLT(Svirskis et al. 2002), indicating that additional biophysical features are required to explain phasic firing in mature neurons. In the present study, we found that the amplitude of the rebound spike (measured from the peak to the minimum of the after hyperpolarization) was 45% larger than the amplitude of depolarization evoked spike (63.4 ± 15 vs. 43.8 ± 12.1 mV, n = 7). The amplitude of the spike-evoked after hyperpolarization was also higher when the bath solution was at 35°C (n = 3, Fig. 3A, inset). This finding in the presence of DTXK indicates that a substantial portion of spike-generating sodium conductance is inactivated at rest (see following text). Moreover, it suggests a mechanism, other than I_KLT, that could contribute to coincidence detection in MSO neurons.

Brain stem auditory neurons have a prominent hyperpolarization activated current, I_h (Bal and Oertel 2000). To test its role in MSO neurons, we applied a specific I_h blocker ZD7288 (2µM) in addition to the DTXK. This treatment led to membrane hyperpolarization from −51.6 ± 2.9 to −55.3 ± 1.9 mV (n = 6; Fig. 3B). In addition, there was a very strong reduction of membrane conductance below resting potential, resulting in a larger spike amplitude (Fig. 3B). However, the response and the shape of the steady current-voltage relation was little affected above the resting membrane potential (Fig. 3B, inset, average for 4 neurons). The small remaining conductance at hyperpolarized potentials indicates that the leak conductance is relatively small and that the membrane properties near rest are shaped by potential sensitive conductances.

The overall shape of the reverse correlation current changed little after ZD7288 (Fig. 3C), although the maximal rate of rise of injected current was reduced from 0.73n to 0.53 nA/ms (mean, n = 6). Apparently, the generated noisy stimulus caused the mean membrane potential to depolarize in the range where the dynamics of the partially blocked I_KLT and I_Na shape the integration.

Presumably, one role for I_h is to depolarize the membrane potential, which causes stronger I_KLT activation and inactivation of sodium conductance. To test this idea, we hyperpolarized the neurons with injection of bias current. Hyperpolarization of the mean membrane potential by −9 mV during noisy stimulation led to both a reduction of the maximal rate of rise of the reverse correlation current (1.2–0.95 nA/ms; n = 5) and a reduction in its hyperpolarizing dip (Fig. 3D). Hyperpolarization by the bias current apparently reduces sodium inactivation and increases the availability of sodium channels, making unnecessary the transient dip in membrane potential prior to a spike.

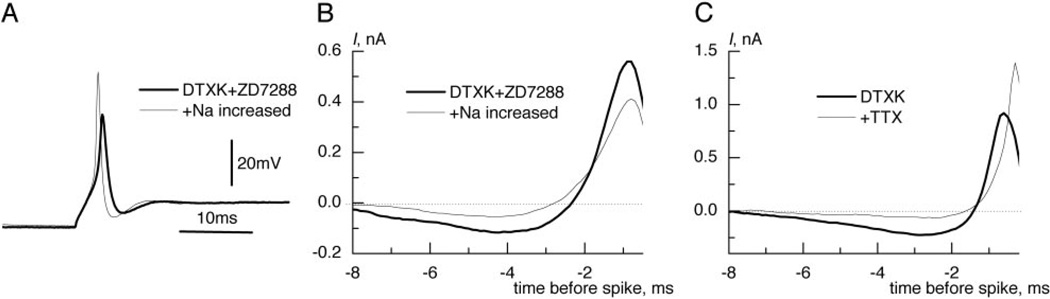
To test further how the sodium current’s strength affects integration, we increased the extracellular sodium concentration by 30%. Under such conditions, the spike amplitude increased (Fig. 4A) from 48.2 ± 12.8 to 67.3 ± 7.3 mV (n = 5). When stimulated with two signal EPSGs on a noisy background input, the reverse correlation of injected current had a much reduced dip, and the maximal slope was reduced almost twofold (Fig. 4B, average for 7 neurons) from 0.61 ± 0.15 to 0.35 ± 0.1 nA/ms (n = 7, P< 0.001 t-test for paired samples). The sensitivity for coincidence was measured for the delay of 1.4 ms and found to be reduced, as estimated by the drop in P_1.4/P₀, from 0.6 to 0.7. We used ΔD = 1.4 ms between signal EPSGs because after partial blockage of I_KLT and full block of I_h, the neurons became rather poor coincidence detectors and temporal integration was much slower.

FIG. 4.

Sodium current strongly influenced integration of small signals. A: increase of extracellular sodium concentration by 30%, in addition to DTXK and ZD7288, made inward current stronger and enlarged the spike. B: strengthening of sodium current reduced the dip and slowed the rise of the reverse-correlation current. C: after addition of TTX, reverse correlation was triggered by crossings of depolarized potential level. Note that the dip almost disappeared, suggesting that it was needed to reduce inactivation. Offsets were subtracted in B and C.

Exploring further how I_Na influences temporal integration, we blocked sodium channels with TTX after, application of DTXK. In this case, the reverse correlation was triggered by the crossings at an arbitrary depolarized membrane potential level. The level was chosen so that the rate of crossings was similar to the firing rate before application of TTX. Under such conditions, the dip in the reverse correlation current was almost completely absent (Fig. 4C), confirming that it was required on average as a precondition for I_Na activation. We hesitate, however, to compare the maximal rise rates of the reverse-correlation current in this condition with those in the control case because here the depolarizing membrane potential, as it rises toward the defined level, was being driven by injected current only without any account for the dynamics of I_Na activation, as in the control case.

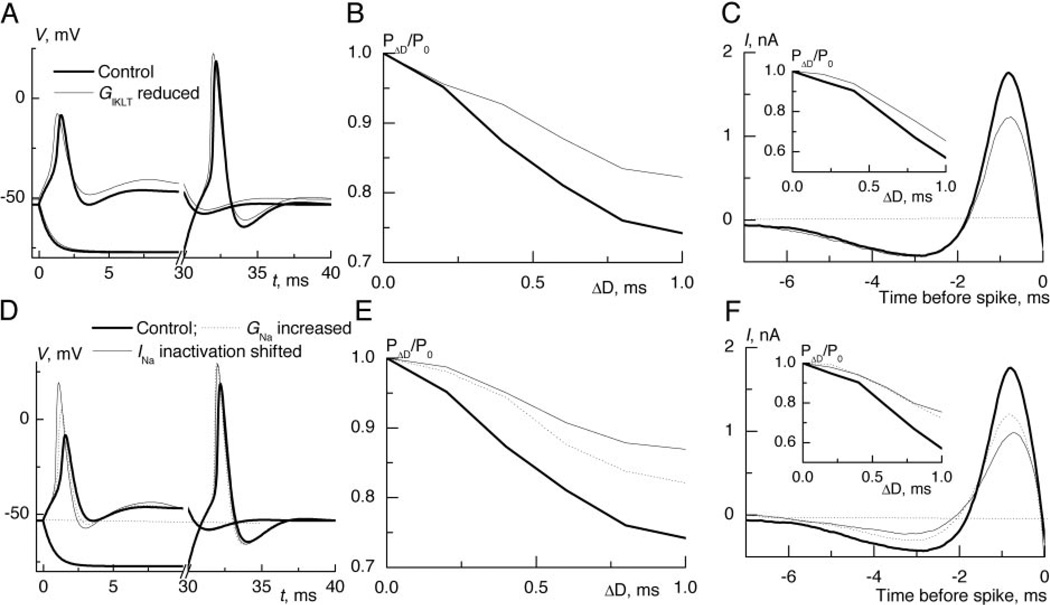
Our experimental findings on the mechanisms of coincidence detection for small noisy signals are supported by the computational results obtained with our biophysical Hodgkin-Huxley-like model. We used our previously developed model (Svirskis et al. 2002), but for this study, we shifted by −15 mV the inactivation voltage sensitivity for sodium channels to mimic better the rebound spikes (Fig. 5A) as seen in these more developed neurons that were not observed in neurons <P17. Our model neuron fires phasically (Fig. 5A). After a 25% reduction of I_KLT current, the sensitivity to coincidence was reduced for both periodically modulated random trains (Fig. 5B) and for signal EPSGs (Fig. 5C, inset). The spike-triggered reverse correlation of the inward current had the same shape as observed for MSO neurons, including a characteristic dip before the rise of the mean injected current. Also in agreement with experimental data, the reduction of I_KLT conductance did not change the overall shape, but the slope of maximal rise was reduced from 2.1 to 1.5nA/ms, confirming that the fast rise of the input current is needed to avoid activation of I_KLT and facilitate spike generation.

FIG. 5.

In the model, reduction of I_KLT or strengthening of I_Na weakens coincidence detection. A: model neuron fired phasically before and after 25% reduction of I_KLT conductance. Note that spike amplitude was almost unaffected. The reduction of I_KLT weakened sensitivity to coincidence for periodically modulated input (B) and for signal EPSGs (C, inset). C: slower rising currents could trigger spike generation as evident from reverse-correlation traces. D: the amplitude of depolarization evoked spike was enlarged more by the 10-mV shift of inactivation than by 50% increase of maximal sodium conductance. E: increased strength of I_Na at rest reduced sensitivity to coincidence for periodically modulated inputs (E) and signal EPSGs (F, inset). F: the shift of inactivation to depolarized potentials resulted in a strongest reduction of the dip and rising rate of mean spike evoking current.

Two strategies were used to then increase the strength of sodium conductance for spike generation: the maximal conductance was increased by 50% or the inactivation at rest was reduced by shifting the inactivation voltage dependence by 10 mV toward depolarized potentials. In both cases, the increased availability of sodium current resulted in larger spikes, although the shift of inactivation had a stronger effect (Fig. 5D). Coincidence detection of periodically modulated random trains (Fig. 5E) and of signal EPSGs (Fig. 5F, inset) was strongly reduced by such changes in the sodium conductance (Fig. 5E). Again the shift of inactivation had a relatively stronger influence. In agreement with experimental findings, the spike-triggered reverse correlation showed reduced maximal rates of rise from 2.1 to 1.28 nA/ms for increased conductance, and to 0.96 nA/ms for shifted inactivation (Fig. 5F). The dip, showing how strongly the advantageous input signals tended to hyperpolarize the cell before spike generation, was also reduced in both cases (Fig. 5F).

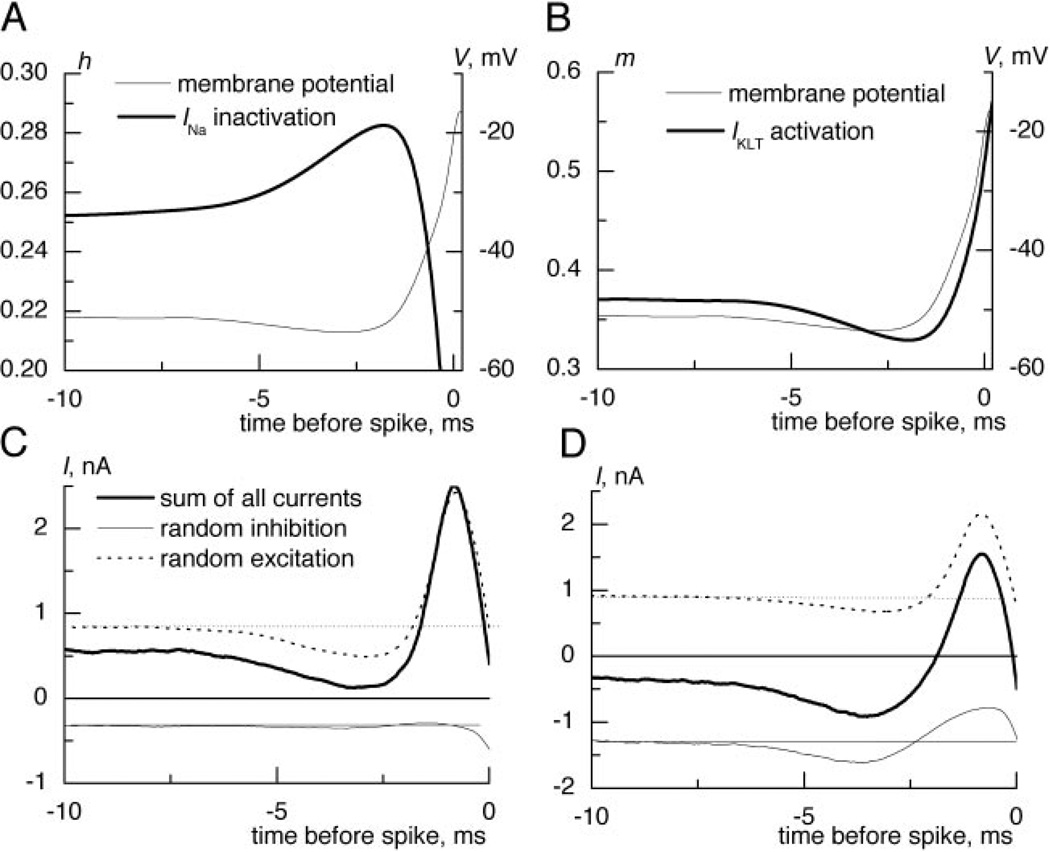
The reverse correlation in the model simulations allowed us to calculate the mean changes in I_Na inactivation and I_KLT activation taking place before spike generation. As expected, I_Na inactivation (Fig. 6A) and I_KLT activation (Fig. 6B) were reduced by the spike-preceding hyperpolarization. Experimental and modeling data suggest that in MSO neurons, high temporal precision in coincidence detection is achieved by input combinations that avoid activation of low-threshold potassium channels and inactivation of sodium channels and that prime the spike generator by even relieving beforehand some I_KLT activation and I_Na inactivation.

FIG. 6.

Changes in membrane currents and input components before spike generation. The inactivation variable, h (A), and I_KLT activation variable, m, (B) reached their minimal values when membrane potential started to depolarize for spike generation. For the synaptic input with excitation and inhibition with equal mean conductances, the hypepolarizing dip was mostly generated by the reduction of excitatory component (C). D: when inhibition was strengthened several times, it also participated in shaping the dip and the spike-generating current.

DISCUSSION

Detection of weak noisy signals in nonoptimal sensory settings is important for early identification of prey and predators and generally for an organism’s survival. A noise imposed on a signal, while intuitively a nuisance, may actually facilitate recognition (Chatterjee and Robert 2001; Russell et al. 1999). At the neural computational level, it is therefore of interest to understand how cellular mechanisms might be specialized and utilized for the integration of subthreshold inputs in a noisy background, be it internally or externally generated. So motivated, we have studied MSO neurons in vitro to investigate how subthreshold voltage-dependent currents shape coincidence detection of small random signals in noise. Spike-triggered reverse-correlation analysis showed that the input current preceding spike generation reflects the necessity on average for synaptic input transients to first remove inactivation of sodium conductance and reduce the resting activation of low-threshold potassium currents and then, with a rapid depolarizing combination, to bring the cell to spike threshold. A model incorporating a Hodgkin-Huxley description of voltage-dependent conductance shows similar dependence of coincidence detection on the availability of sodium currents and I_KLT. We have used independent manipulations to demonstrate that gating properties of both I_Na and I_KLT contribute to the extraordinary precision of MSO neurons as coincidence detectors. Nevertheless, other mechanisms, including other potassium currents, may also participate.

We used the dynamic-clamp method to generate random postsynaptic conductances. Because the simulated conductances decayed exponentially in time the temporal profile of the spike-triggered reverse correlation for injected current could be influenced by such temporal structure of the injected current. However, the shape of the reverse correlation was strongly affected by manipulations on membrane properties. This suggests that the dip and the rate of rise of the average spike preceding current was mostly determined by voltage-dependent membrane currents.

The majority of results were obtained at room temperature. Because kinetics of ionic channel gating could be very sensitive to temperature we repeated some experiments at 35°C. Unfortunately, the faster deterioration of neuronal state at 35°C precluded us from obtaining all results at such temperature. Although the response properties of neurons became much faster, the qualitative features were the same. The reduction of I_KLT resulted in slower rising reverse-correlation traces while the dip was preserved (Fig 2D, inset). The spike amplitude was also higher when it was evoked from hyperpolarized potentials (Fig 3A, inset). This suggest that the findings are applicable for neurons operating in natural conditions.

The observed sensitivity of neurons to the delay between generated signals was on the order of 0.5ms (Fig 1B). This delay is several times larger than the physiological range of ITDs that can occur in the gerbil auditory system (Brand et al. 2002). This discrepancy can be resolved by the much faster response properties at higher temperatures (compare Fig 2D and its inset). It is possible that in natural conditions the voltage gating of currents is fast enough to be sensitive to delays in the physiological range.

Spike-triggered reverse correlation for the input current had a particular shape with a hyperpolarizing dip before the sharp depolarizing rise of the injected current in experiments (Figs. 2D, 3 C and D, and 4B) and in the model (Fig. 5 C and F). In our previous report (Svirskis et al. 2002), we considered the possibility that the dip removed some I_KLT conductance. However, the dip remains in the presence of DTXK. Furthermore, the ability of DTXK to convert MSO neurons from phasic to tonic is age dependent. By P17, there is clearly a second biophysical mechanism that supports phasic response properties. The present results reflect a tendency for the input to precondition I_KLT and I_Na by hyperpolarizing the membrane a few micro seconds before the sudden and stronger depolarizing component that triggers a spike (Fig. 6A and B).

Either reduced excitation or increased inhibition could underlie the dip generation in the neurons and in the model. However, it is tempting to relate the hyperpolarizing dip to preceding inhibition which influences ITD processing in MSO (Brand et al. 2002; Grothe and Sanes 1994; Grothe et al. 1997; Kapfer et al. 2002) and nucleus laminaris, (NL) (Funabiki et al. 1998; Takahashi and Konishi 2002). To assess these different possibilities, one should consider if the inhibitory input is strong enough to hyperpolarize the membrane sufficiently. In our calculations, we used similar mean conductance amplitudes for both excitatory and inhibitory inputs. In this case, the dip is created by the reduction of excitatory input (Fig. 6C) as it is the dominant input current to the neuron model due to its larger driving force. However, when the inhibitory current was made as strong as the excitatory current, by shifting the reversal potential to −80 mV and increasing the mean conductance amplitude three times, the dip was generated by both a reduction of excitation and an increase of inhibition (Fig. 6D).

The low availability of partially inactivated sodium current in MSO neurons contributes to the preference for spike generation of synaptic input combinations that remove some inactivation of sodium channels, and leads to the characteristic “dip-and-fast-rise” shape of the reverse correlation. This observation led us to increase the strength of the sodium current by raising extracellular sodium concentration. This manipulation augmented the spike amplitude by 40%. The most obvious explanation for the increased I_Na is the larger driving force. However, a 30% increase in extracellular concentration translates, according to the Nernst equation, to a mere 6% increase in driving force for sodium ions at room temperature. A second possible explanation for the larger spikes is a shift of inactivation to depolarizing potentials similar to that observed in dissociated hippocampal neurons (Kuo and Liao 2000). It was suggested that increased extracellular sodium concentration could facilitate the deinactivation of sodium channels by directly knocking-off inactivating peptide (Kuo and Liao 2000). We explored both possibilities in our computational model: an increased sodium current and a shifted inactivation. The increased I_Na resulted in reduced sensitivity to coincidence for both mechanisms suggesting that the overall strength of available I_Na for spike generation is of importance.

For octopus cells in the auditory brain stem, it was suggested that the hyperpolarization-activated inward I_h current depolarizes neurons and counteracts activated I_KLT current at rest (Bal and Oertel 2000; Oertel et al. 2000). This combination of active conductances also reduces the time constant for integration (Oertel et al. 2000). In agreement with these findings, we found that I_h depolarizes the membrane and partially activates I_KLT at rest in MSO neurons. In addition, spike-triggered reverse correlation suggests that the depolarization of the membrane potential by I_h also inactivates more sodium channels and makes availability of this current a critical factor in selecting coincident inputs for spike generation.

Together, our results suggest that advantageous subthreshold synaptic input combinations will on average have a particular temporal structure if it is to generate a spike with high probability. Such favored synaptic currents should first, by hyper-polarizing the neuron, reduce sodium channel inactivation and partially deactivate I_KLT, which are present at rest. Then the input should very rapidly depolarize the cell, to avoid reactivating I_KLT and inactivating I_Na, and bring the potential to threshold. Such preference for temporal structure with a fast rise is responsible for high temporal sensitivity in coincidence detection of small signals in a noisy background.