Abstract
Success in many decision-making scenarios depends on the ability to maximize gains and minimize losses. Even if an agent knows which cues lead to gains and which lead to losses, that agent could still make choices yielding suboptimal rewards. Here, by analyzing event-related potentials (ERPs) recorded in humans during a probabilistic gambling task, we show that individuals' behavioral tendencies to maximize gains and to minimize losses are associated with their ERP responses to the receipt of those gains and losses, respectively. We focused our analyses on ERP signals that predict behavioral adjustment: the frontocentral feedback-related negativity (FRN) and two P300 (P3) subcomponents, the frontocentral P3a and the parietal P3b. We found that, across participants, gain maximization was predicted by differences in amplitude of the P3b for suboptimal versus optimal gains (i.e., P3b amplitude difference between the least good and the best gains). Conversely, loss minimization was predicted by differences in the P3b amplitude to suboptimal versus optimal losses (i.e., difference between the worst and the least bad losses). Finally, we observed that the P3a and P3b, but not the FRN, predicted behavioral adjustment on subsequent trials, suggesting a specific adaptive mechanism by which prior experience may alter ensuing behavior. These findings indicate that individual differences in gain maximization and loss minimization are linked to individual differences in rapid neural responses to monetary outcomes.
Introduction
In the last decade, individual differences in decision behavior have been linked to neural responses to positive and negative feedback (Frank et al., 2004; Klein et al., 2007). A common method for probing these behavioral effects has been the analysis of two hallmark event-related potentials (ERPs): the frontocentral feedback-related negativity (FRN) and the P300 (P3). The FRN is elicited by worse-than-expected outcomes (Holroyd and Coles, 2002), and its magnitude after losing has been found to predict whether participants will switch their choice on the subsequent trial (Cohen and Ranganath, 2007). In contrast, the P3 is thought to reflect attentional processes involved in stimulus evaluation and memory updating (Donchin and Coles, 1988; Nieuwenhuis et al., 2005), and is composed of two distinguishable subcomponents: the early, frontally distributed P3a and the late, parietally distributed P3b (Polich, 2007).
Across a number of studies, participants' relative propensities to learn to avoid losses versus learning to achieve gains are correlated with the FRN amplitude difference between losses and gains (Frank et al., 2005, Eppinger et al., 2008, Cavanagh et al., 2011). However, loss avoidance and gain seeking do not necessarily imply optimal behavior in complex scenarios. For example, online poker players tend to adopt strategies that increase the frequency of gains versus losses, although this results in decreased profits overall since the average magnitude of their losses significatively exceeds the average magnitude of their gains (Siler, 2010). Rather than relying on a simple, binary distinction between gains and losses, optimal decision-making probably relies on brain's ability to distinguish the best (optimal) gain from all other gains, and similarly for losses. Although we hypothesized that this neural discrimination is reflected in the FRN, we also analyzed the P3 since it has also been found to predict behavioral adjustment (Chase et al., 2011). A previous study (Venkatraman et al., 2009) reported brain activity associated with a strategy that maximized gains and minimized losses versus a strategy that increased the probability of winning, but no study has so far has reported brain activity that independently predicts gain maximization and loss minimization.
Participants performed a decision-making task in which they selected the magnitude of their wager in response to a pair of probabilistic outcome-predicting cues on each trial. Gain maximization was defined as the ability to choose the large bet on trials with >50% probability of winning, and loss minimization as the ability to choose the small bet on trials with <50% probability of winning. We predicted that gain maximization would correlate, across participants, with the difference between the FRN elicited by the smallest (worst) and largest (best) gains, whereas loss minimization would correlate with the difference between the FRN elicited by the largest (worst) and smallest (best) losses. Finally, to further advance our understanding of the mechanisms underlying individual differences in choice behavior, FRN and P3 responses were assessed in terms of their ability to directly predict trial-to-trial behavioral adjustment.
Materials and Methods
Participants.
Forty-five healthy, right-handed, adult volunteers (22 male) participated in this study (ages, 18–31 years; mean, 23.05). Participants gave written informed consent and were financially compensated for their time ($15/h). They received an extra bonus (mean, $12.21; SD, $7.75) proportional to the points earned during the experimental session. All procedures were approved by the Duke University Health System Institutional Review Board. Four participants were excluded from further data analysis due to technical difficulties during their experimental sessions, leaving a final sample of 41 participants (20 male).
Stimuli and task.
We designed a probabilistic decision-making task using elements from the experimental designs of Gehring and Willoughby (2002) and Frank et al. (2004). Participants sat in front of a computer screen and performed 800 trials over the course of a single experimental session divided into 40 ∼1.7 min blocks. Subjects were told that each trial would start with the presentation of two symbols, and that some symbols tended to precede losses and other symbols tended to precede gains. They were instructed to try to learn which symbols were associated with which outcomes and to use that information to bet either two points or eight points on each trial. Also, they were told that the probabilistic relationship between symbols and gains/losses would remain constant during the entire task. Subjects were also informed that although a monetary bonus proportional to the points earned during the session would be given, no information regarding the conversion from points to money would be provided until the end of the experiment. Before data collection, participants completed a 20-trial practice session using a set of symbols different from that used during data collection.
The temporal sequence of the task as it unfolded over a single trial is shown in Figure 1A. Each trial started with the presentation of a pair of symbols (Higrana characters) and a fixation cross, which were displayed for 1500 ms. The pair of symbols presented on each trial was randomly selected, without replacement, from the set of 20 possible pairings of five unique symbols (Fig. 1B). Considering that these were right–left counterbalanced, these 20 pairs actually corresponded to 10 unique (nonmatching) combinations of symbols, so that each unique combination was presented twice per block.
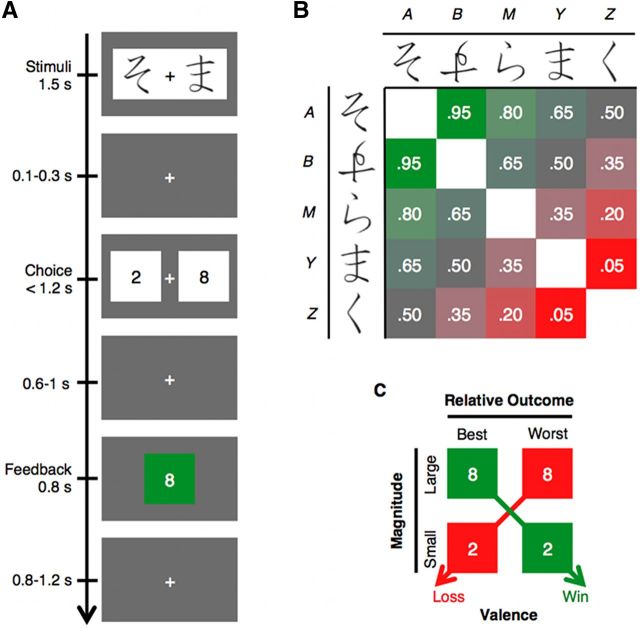
Figure 1.
Experimental design. A, In each trial, participants viewed a stimulus pair providing information about the probability of winning [p(win)] on that trial. Then they chose between a large (8 points) and a small bet (2 points) by pressing a button corresponding to the side of the screen containing their preference. Feedback was provided as a green box surrounding the wager amount if the participants won the bet, and as a red box if the participant lost. B, The stimulus pair to be presented on each trial was randomly selected from a set of 20 possible pairs formed from five different novel symbols, which are labeled A, B, M, Y, and Z here, and which are referred to by these labels throughout the text. Each stimulus pair was associated with a probability of winning [p(win)] for that trial as annotated and color coded in the figure, ranging from red to green as p(win) increases. The p(win) associated with each pair was calculated as an adjustment from 50% determined by each symbol (+0.3, +0.15, 0, −0.15, and −0.3 for A, B, M, Y, and Z, respectively; for details, see Materials and Methods). Over the course of a block of 20 trials, each symbol was paired twice with each one of the other symbols, and symbols were never paired with themselves. C, As result of the design, feedback conveyed information about the valence (gain vs loss) and magnitude (large vs small) of the outcome on the current trial. Feedback also conveyed information about value of the feedback compared to the outcome that “would have been” if the alternative decision had been made (relative outcome, worst vs best).
After an interstimulus interval (ISI) jittered between 100 and 300 ms, two white squares with the numerals “8” and “2” depicting the wager amount choices appeared randomly on the right and left of the fixation cross. Participants chose their wager amount for the trial by pressing a button with the hand corresponding to the side of the screen containing their wager preference. Feedback concerning the outcome of the trial was presented after an ISI jittered between 600 and 1000 ms and appeared as a green box around the chosen number if the participant won on that trial (i.e., gained that number of points) or as a red box around the chosen number if the participant lost that number of points. If no response was made within 1200 ms, the words “no response” and a box corresponding to losing eight points were presented on the screen. The next trial started after an intertrial interval jittered between 800 and 1200 ms. Participants were instructed to maintain fixation on the fixation cross throughout the experimental runs.
The outcome's valence (win or loss) on each trial was probabilistically determined according to the probability of winning [p(win)] associated with the presented stimulus pair (Fig. 1B). The p(win) associated with each pair was calculated as an adjustment from 50% determined by each symbol: p(win) = 0.5 + pL + pR, where pL and pR are the adjustments associated with the symbol presented to the left and right of the screen, respectively (Symbol labeled: A = +0.3, B = +0.15, M = 0, Y = −0.15, and Z = −0.3). For example, the stimulus pair presented in Figure 1A corresponds to symbol labels A and Y, and following Figure 1B, p(win)AY = chance + p(win)A + p(win)Y = 0.5 + 0.3 − 0.15 = 0.65.
Most importantly for our research questions, participants could make a choice that would influence the magnitude of outcomes, but they had no control over the valence of the result. Optimal behavior entailed betting eight points each time that a likely winning pair [i.e., p(win) > 0.5] was presented, and betting two points each time that a likely losing pair [i.e., p(win) < 0.5] was presented.
Besides magnitude (small or large) and valence (win or loss), feedback in the task also conveyed information about the relative value of the feedback compared to the outcome that “would have been” if the alternative wager amount had been selected. This variable, which accords roughly with intuitions of “rejoice” or “regret,” was labeled as “relative outcome.” This can be seen in Figure 1C. Thus, the +8 and −2 outcomes reflect the best possible gain and the best possible loss, respectively, given that in each case the alternative outcome would be six points worse (i.e., +2 and −8, respectively).
Electroencephalogram recording and preprocessing.
The electroencephalogram (EEG) was recorded continuously from 64 channels mounted in a customized, extended coverage, elastic cap (Electro-Cap International; www.electro-cap.com) using a bandpass filter of 0.01–100 Hz at a sampling rate of 500 Hz (SynAmps; Neuroscan). All channels were referenced to the right mastoid during recording. The positions of all 64 channels were equally spaced across the customized cap and covered the whole head from slightly above the eyebrows in front to below the inion posteriorly (Woldorff et al., 2002). Impedances of all channels were kept below 5 kΩ, and fixation was monitored with electrooculogram recordings. Recordings took place in an electrically shielded, sound-attenuated, dimly lit, experimental chamber.
Offline, EEG data were exported to MATLAB (MathWorks) and processed using the EEGLAB software suite (Delorme and Makeig, 2004) and custom scripts. The data were low-pass filtered at 40 Hz using linear finite impulse response filtering, downsampled to 250 Hz, and rereferenced to the algebraic average of the left and right mastoid electrodes. For each participant, we implemented a procedure for artifact removal based on independent component analysis (ICA). This approach has been used in a number of studies (Debener et al., 2005; Eichele et al., 2005; Scheibe et al., 2010) to obtain EEG data with diminished contribution of ocular/biophysical artifacts. First, we visually rejected unsuitable portions of the continuous EEG data. This procedure resulted in the exclusion of 20 trials on average (±SD, 8.36 trials) from the original 800-trial-long data set for each participant. Second, we separated the data into 1200 ms feedback-locked epochs, spanning from 400 ms before to 800 ms after the onset of the feedback stimulus, with a prestimulus baseline period of 200 ms. Third, we performed a temporal infomax ICA (Bell and Sejnowski, 1995). With this analysis, independent components with scalp topographies and signals that could be assigned to known stereotyped artifacts (e.g., blinks) based on their distribution across trials, their component waveform, and/or their spectral morphologies were removed from the data (Jung et al., 2000a,b; Delorme et al., 2007). The remaining components were back-projected to the scalp to create an artifact-corrected data set.
Previous studies have consistently found that the FRN has a frontocentral distribution with a peak of amplitude over the standard 10–20 FCz location at ∼250 ms after feedback onset (Miltner et al., 1997; Gehring and Willoughby, 2002; Nieuwenhuis et al., 2004). On the other hand, the P3 has been conceptualized as being formed by two subcomponents: the P3a with a frontocentral distribution and a maximum amplitude between 300 and 400 ms following stimulus presentation, and the P3b with a parietocentral distribution and a peak of amplitude occurring between 60 and 120 ms later (Nieuwenhuis et al., 2005; Polich, 2007). To assess the FRN and the P3a we used a region of interest (ROI) cluster of seven sensors centered on the canonical channel FCz as a frontal ROI. To assess the P3b we used a parietal ROI cluster of seven sensors centered on channel Pz.
On frontal sites, the FRN appears superimposed on the P3a, and as several studies have noted, the FRN peak can be shifted depending on the amplitude of this frontal P3 (Yeung and Sanfey, 2004; San Martín et al., 2010; Chase et al., 2011). This is consistent with the idea that scalp-recorded neuroelectrical activity corresponds to the linear sum of the activity of a discrete set of neural sources (Baillet et al., 2001). Thus, to more effectively quantify the FRN amplitude accounting for differences in the P3-induced baseline, we used a mean amplitude to mean amplitude approach. More specifically, the FRN amplitude for each trial was calculated in the frontal ROI as the average potential across a 204–272 ms window after feedback (i.e., relative to the feedback stimulus onset) minus the average voltage potential from a short 188–200 ms window preceding it. (Note that the effective sampling rate was 250 Hz, and thus these window lengths were all multiples of 4 ms.) This approach accounts in part for the overlap between the FRN and P3 (cf. Yeung and Sanfey, 2004; Frank et al., 2005; Bellebaum et al., 2010; Chase et al., 2011).
In addition, given that differences between conditions were in fact observed before the onset of the FRN, we decided to also include an earlier window into our analyses. We refer to this activity as the P2, noting that it may represent an early stage of the slower-wave P3a. We measured the P2 amplitude on the frontal ROI as the average ERP voltage potentials from a 152–184 ms postfeedback window. The P3a was quantified as the average potential from a 284–412 ms window in the frontal ROI, and the P3b as the average potential from a 416–796 ms window in the parietal ROI, both relative to the prestimulus baseline.
Overview of the data analysis.
Through our analyses we wished to explore the relationship between individual differences in feedback-elicited brain activity and individual differences in choice behavior, particularly in gain maximization and loss minimization. However, our paradigm has learning and choice components that are difficult to distinguish from each other during the initial part of the experiment. To focus on the choice components of the processing, we excluded from our analyses the trials from the first quarter of the experimental session, using only the last three-quarters of the session, which we took as representative of stable learned behavior (Fig. 2A; see below, Results, Behavioral results).
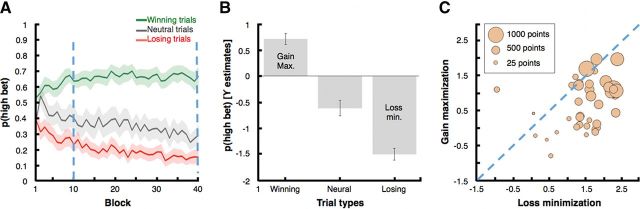
Figure 2.
Behavioral results. A, Choice behavior for likely winning, neutral, and likely losing trials across blocks. All the analyses were restricted to the last three-quarters of the trials, indicated here as the area between the vertical dashed lines (shaded areas indicate SEM for each trace). B, The presentation of likely winning pairs was positively associated with the probability of betting high. Gain maximization was defined as the strength of this association for each participant. The presentation of neutral pairs was negatively associated with the probability of betting high. The presentation of likely losing pairs was also negatively associated with the probability of betting high. Across participants, loss minimization scores corresponded to the strength of this association multiplied by −1 (i.e., or, equivalently to the strength of the association between likely losing pairs and the probability of betting low). Error bars indicate SEM. C, Gain-maximization and loss-minimization scores were positively correlated with each other and independently with the amount of points earned by each participant during the session. Earnings are coded by the size of each bubble. Participants with low gain-maximization and low loss-minimization scores tend to be represented by smaller bubbles than participants with high scores in such dimensions. The dashed line distinguishes between participants that were better in gain maximization than in loss minimization (above the line) and those who showed the opposite tendency (below).
Using behavioral metrics derived from subjects' choices, we tested the hypothesis that neural differences between the worst gain (i.e., +2) and the best gain (i.e., +8) would scale with gain maximization, while the neural differences between the worst loss (i.e., −8) and the best loss (i.e., −2) would scale with loss minimization. In addition, we assessed the association between the amplitude of ERP components and trial-to-trial behavioral adjustment.
Behavioral data analysis.
To extract individual scores in gain maximization and loss minimization, we characterized each subject by his/her observed probability to bet the larger amount on likely winning trials [p(win) > 0.5], neutral trials [p(win) = 0.5], and likely losing trials [p(win) < 0.5]. We then expressed these probabilities on a logit-function scale, γ = log(p/1 − p), where p is the probability to bet the larger amount on a given trial. This logit transform allows for better characterizations of differences in probability at the low and high ends of the scale. The γ coefficients were estimated for each of the three types of trials for each participant. For all of our subsequent analyses, the strength of gain maximization was measured by the γ estimate for likely winning pairs: the more positive that value was for a participant, the more likely the participant was to bet high on likely winning trials. On the other hand, the strength of loss minimization was measured by the γ estimate for likely losing pairs multiplied by −1, such that the more positive this value was for a participant, the more likely the participant was to bet low on likely losing trials.
Gain maximization, loss minimization, and ERPs for worst versus best outcomes.
Our first ERP data analysis tested the hypothesis that the difference between the neural responses elicited by feedback stimuli indicating the worst (+2) versus best (+8) gains would scale with gain maximization, and that the difference between the neural responses elicited by feedback stimuli indicating the worst (−8) versus best (−2) losses would scale with loss minimization. As such, we computed four ERPs for each participant, each ERP corresponding to averaged EEG activity time locked to the presentation of each of the four feedback stimulus types. After removing the first quarter of the data to minimize the effect of learning (see above, Overview of the data analysis), 154 trials on average went into the ERP for +8 (SD, 32.70), 139 into the ERP for +2 (SD, 39.18), 207 trials into the ERP for −2 (SD, 40.01), and 84 trials into the ERP for −8 (SD, 35.45). Then we computed the difference in the ERP signal for conditions +2 minus +8 and −8 minus −2 for each participant. Finally, we performed a multiple linear regression using gain-maximization and loss-minimization scores for each participant (i.e., γgain-max and γloss-min) as explanatory variables for such ERP differences, according to the following equations: ERP difference (+2 > +8) = constant + βgain-max * γgain-max + βloss-min * γloss-min + ε, and ERP difference (−8 > −2) = constant + βgain-max * γgain-max + βloss-min * γloss-min + ε, where ε is a vector of error terms.
We performed this analysis separately for the P2, FRN, P3a, and P3b components. For correction of multiple comparisons, we applied the stepdown method described by Holm (1979).
ERPs correlates of behavioral adjustment.
The last analysis was intended to assess directly the association between each ERP component and the behavioral adjustment on subsequent trials. We considered each trial t in terms of the two cue symbols that were presented (S1t and S2t) and the bet that was wagered. We then asked whether the wager choice (high or low) was the same or different on the next trial that presented S1t and/or S2t. This analysis was done separately for the next appearance of each one of these symbols, regardless of whether they appeared paired together or individually with other symbols; that is, a trial on which symbols labeled A and Y were presented was compared both with the next trial to present A and the next trial to present Y (which may have been the same trial). We defined a switch variable that assumed the value 0 if the same bet was chosen on each of these trials, 1 if the trial with one of the two cue symbols involved the same bet and the other the opposite, and 2 if neither trial resulted in the same bet. Note that this particular scoring ignores the temporal delay between subsequent presentations of the stimuli and precludes any interaction between the elements of each pair.
Evoked responses corresponding to the P2, FRN, P3a, and P3b components were each entered as dependent variables to fit a linear mixed model using different levels of outcome and adjustment level as fixed effects and a participant's identifier (μ) as a random effect: ERP = constant + βoutcome * χoutcome + βadjustment * χadjustment + μ + ε, where outcome was a categorical variable with three levels (+2, −2, and −8), and adjustment level was likewise a categorical variable with two levels (1, switching for one symbol; 2, switching for both symbols). We used the +8 outcome and the not-switching condition as constants for the model. In other words, the β estimates that we report below for the fixed effects reflect expected deviations from the ERP components elicited by the best gain (i.e., +8), when such a result was followed by the same choice (i.e., a large bet) on the immediately next trial(s) wherein the same cue symbols were presented. For correction of multiple comparisons, we applied the method described by Holm (1979).
After removing the data from the first quarter of the trials, 49 trials went into each of these 12 ERPs on average for each subject (SD, 27.64). The condition with the maximum number of trials across participants was “not switching after −2” (mean, 93.23; SD, 38.85; range, 11–167), and the condition with the minimum number of trials was “not switching after −8” (mean, 20.51; SD, 19.31; range, 8–109). No condition was associated with fewer than seven trials for any of the 41 participants included in the analysis.
Results
Behavioral results
A visual inspection of choice behavior across blocks (Fig. 2A) suggests that the participants quickly learned the contingencies of the task. Indeed, an ANOVA on the probability of high bets on the first block showed that, overall, participants' choices already distinguished between trial types within this block (F(2,80) = 5.3993, p < 0.01), with a greater proportion of high bets on positive trials compared to both neutral (p = 0.02, Tukey's range post hoc tests) and negative trials (p = 0.01). However, to minimize the effect of the early stages of learning, and to instead focus on the choice behavior effects, all the analyses that we report below were restricted to the last three-quarters of the experimental session (blocks 11 to 40), when learning had roughly converged on a stable pattern of choice behavior (Fig. 2A, marking lines).
Gain maximization and loss minimization
As expected, γ estimates for the tendency to bet high on likely winning trials were positive (t(40) = 6.60, p < 0.0001; i.e., subjects overall chose to bet high on likely winning trials), and γ estimates for the tendency to bet high on likely losing trials were negative (t(40) = −13.37, p < 0.0001; i.e., subjects overall chose to bet low on likely losing trials). Estimates of γ reflecting the tendency to bet high on neutral trials were also negative (t(40) = −4.11, p < 0.0005), revealing that subjects generally chose to bet low on neutral trials (Fig. 2B).
Hereafter, values of the γ estimate for the probability of betting high on likely winning trials will be referred as gain-maximization scores for each participant. Similarly, the additive inverse of the γ estimates that reflect the probability of betting high on likely losing trials (i.e., −γ), will be referred to as loss-minimization scores. Note that most of the participants were better at loss minimization than gain maximization (Fig. 2C, 35 of the 41 below the dashed line).
By definition, high gain-maximization and high loss-minimization scores should predict high earnings in our task, and their net effects on earnings should not differ significantly. As expected, we found that both gain maximization (r = 0.67, p < 0.0001) and loss minimization (r = 0.70, p < 0.0001) were correlated with participant's earnings. We also found a positive correlation between gain-maximization and loss-minimization values across subjects (r = 0.37, p = 0.02). Importantly, the last correlation suggests that we had success in differentiating our behavioral measures from participants' overall risk preferences. Specifically, if gain maximization were referring to risk seeking and loss minimization were referring to risk aversion, we should have found a negative correlation between these measures, but instead we observed a positive correlation.
Finally, to confirm that there was no difference between the effects of gain maximization and loss minimization in earnings, we compared the points earned by two groups of participants identified through a median split procedure. The first group consisted of those participants that had high gain-maximization and low loss-minimization scores (n = 8), and the second groups consisted of those participants (n = 8) who showed the opposite pattern (i.e., low gain-maximization and high loss-minimization scores). A t test revealed no significant difference in earnings between these two groups (p = 0.69).
ERP results
ERP responses to monetary feedback independently predict gain maximization and loss minimization across participants
Figure 3 presents the grand-average ERP waveforms extracted for the four possible outcomes on each trial. We asked whether individual differences in neural responses to different possible outcomes might correlate with individuals' gain-maximization and loss-minimization scores. Indeed, gain maximization was positively associated across subjects with the difference between the P3b elicited by the worst gains (+2) and that elicited by the best gains (+8; for statistics, see Table 1). On the other hand, loss-minimization scores were positively associated with the differences between the amplitudes for the P2, the P3a, and the P3b elicited by the worst (−8) and best (−2) losses. In contrast, the amplitude of the FRN did not significantly correlate with any of these behavioral measures.
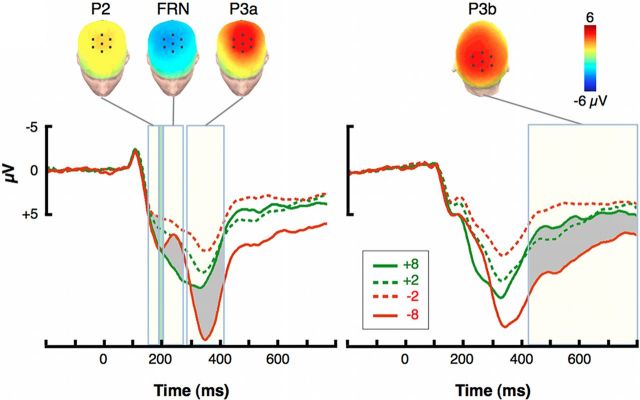
Figure 3.
Feedback-locked ERPs and their distribution over the scalp. Left, ERP traces, Grand averages for each outcome from a frontal ROI of seven electrodes centered on FCz and located over frontocentral cortex. Cream-colored rectangles show the time windows defined for each of the ERP components. The thin rectangle in light green, immediately preceding the FRN time window, represents the reference latencies for quantifying the FRN amplitude. Shadowed areas correspond to the contrasts presented in the topographies above. Left, ERP topographies, Distribution of key effects for each ERP component over the scalp and location of the frontal ROI. The topography of the P2 effect is presented in terms of the −8 minus −2 contrast, whereas the FRN and P3a are presented in terms of the −8 minus +8 contrast. The topographies were constructed subtracting the average activity for the two contrast conditions over the specified time window defined for each component. Right, ERP traces, Grand averages from each outcome from a parietal ROI of seven electrodes centered on Pz and located over the parietal cortex. Right, ERP topographies, Distribution of key effects for each ERP component over the scalp and location of the parietal ROI. The topography of the P3b effects is presented in terms of the −8 minus +8 contrast.
Table 1.
Association between ERP contrasts and the variables of gain maximization and loss minimization
| ERP contrasts |
||||||||
|---|---|---|---|---|---|---|---|---|
| P2 |
FRN |
P3a |
P3b |
|||||
| +2 > +8 | −8 > −2 | +2 > +8 | −8 > −2 | +2 > +8 | −8 > −2 | +2 > +8 | −8 > −2 | |
| R2 | 0.15 | 0.31 | 0.19 | 0.11 | 0.24 | 0.37 | 0.38 | 0.37 |
| Model predictors | β, p | β, p | β, p | β, p | β, p | β, p | β, p | β, p |
| Constants | −0.08, 0.90 | −0.65, 0.40 | 0.23, 0.69 | −0.35, 0.67 | −0.06, 0.96 | 0.53, 0.75 | −0.89, 0.22 | 0.12, 0.92 |
| Gain max. | 0.52, 0.23 | −0.53, 0.30 | 0.49, 0.21 | −0.95, 0.09 | 2.54, 0.01 | −0.66, 0.57 | 2.34, 2 (10−5)a | −0.74, 0.38 |
| Loss min. | −1.05, 0.01 | 2.00, 2 (10−4)a | −1.1, 0.01 | −0.32, 0.54 | −2.29, 0.01 | 4.94, 5 (10−5)a | −0.56, 0.24 | 3.66, 4 (10−5)a |
a Significant with a Holm's corrected alpha level set at 0.05 (for 24 tests).
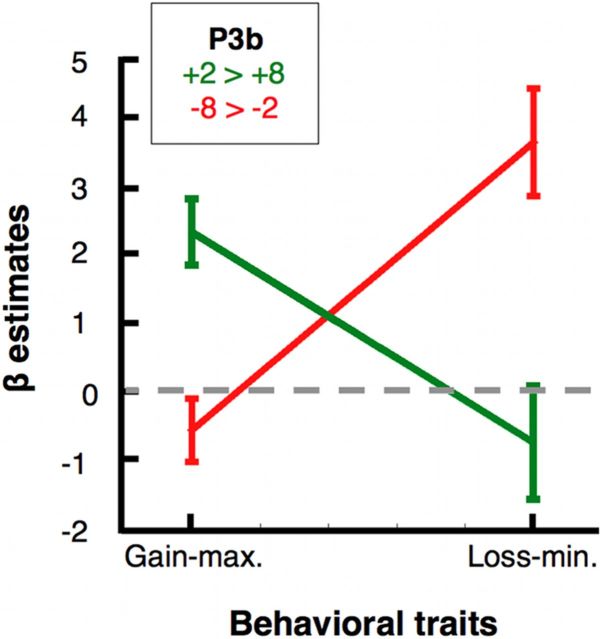
Strikingly, these results show that gain maximization and loss minimization have different patterns of association with the P3b (Fig. 4). The contrast “worst > best” between the two types of gains was significantly associated with gain maximization (β = 2.34, p < 0.0001) but not with loss minimization (β = −0.56, p = 0.24). The contrast “worst > best” between the two types of losses was significantly associated with loss minimization (β = 3.66, p < 0.0001), but not with gain maximization (β = −0.74, p = 0.38). To further support this finding, we performed a stepwise regression procedure. First, we removed loss minimization as a predictor from our original model to predict the +2 > +8 P3b differences across participants. We found that the performance of this new model (which included only gain maximization and constant) was not statistically different from the performance of the original one (F(1, 38) = 1.45, p > 0.1). However, when we removed gain maximization as a predictor from the original model, the new model (which included only loss minimization and a constant) was significantly outperformed by the original one (F(1, 38) = 27.14, p < 0.00001). Then, we performed the same procedure to evaluate the association between loss minimization and the −8 > −2 P3b. We found the opposite pattern of results. The performance of a model that excluded gain maximization was not statistically different from the performance of the original model (F(1, 38) = 0.79, p > 0.1), but the original model significantly outperformed a model that excluded only loss minimization (F(1, 38) = 21.46, p < 0.00005).
Figure 4.
Neural differentiation between gain maximization and loss minimization. Across participants, the differential P3b amplitude derived from the contrast between feedback of worst (least good) versus best gains was associated with the gain maximization scores but not significatively with the loss minimization. In contrast, the differential P3b signal for worst versus best (least bad) losses was associated with loss minimization, but not significantly with gain maximization. This last effect was also found for the P2 and P3a (Table 1). Error bars correspond to the SE of the β estimates.
In sum, although gain maximization and loss minimization were correlated at the behavioral level, gain maximization and loss minimization were associated with different contrasts at the neural level. Specifically, gain maximization was associated with the differences in P3b amplitude between the worst (+2) and the best gain (+8) across participants, while loss minimization was associated with the differences in P3b amplitude between the worst (−8) and the best loss (−2).
The results from our original models also suggest a temporal difference between the neural processing associated with these two types of choices, since the neural processing associated with loss minimization was also found in earlier latencies (i.e., P2 and P3a time windows), while the first index of neural processing associated with gain maximization was found much later, in the 416–796 ms postfeedback window (i.e., P3b).
ERP predictors of behavioral adjustment
Given the previously reported associations between the P3 and behavioral adjustment (Chase et al., 2011), we asked whether neural responses in our task predicted changes in behavior on a trial-to-trial basis. Finding such a relationship would strengthen the argument that the P3 activity reflects adjustment processes aimed toward gain maximization and loss minimization. To test this, we designed a linear mixed model (see Materials and Methods) using different levels of outcome (−8, −2, +2, +8) and adjustment level (0, not switching; 1, switching for one symbol; 2, switching for both symbols) as predictors of neural responses corresponding to the P2, FRN, P3a, and P3b components.
We found that the P2 elicited by the −8 feedback stimuli was statistically indistinguishable from the P2 elicited by the outcome stimuli coded in the constant condition (i.e., +8). On the other hand, the P2 for −2 and +2 was smaller than the constant P2 (Fig. 3; for statistics, see Table 2). This result is consistent with a previous study by Goyer et al. (2008), who found that, compared to small-magnitude outcomes, large-magnitude monetary outcomes elicited a greater positive potential in pre-FRN latencies (starting at ∼150 ms in their case). The FRN was larger (i.e., more negative) for −8, −2, and +2, compared to the best possible outcome (+8), which is consistent with previous studies showing that the FRN responds to feedback along a general good–bad dimension (for review, see San Martín, 2012). P3a and P3b amplitudes showed similar modulations as a function of outcome, with larger responses to −8 and smaller responses to −2 compared to +8, although the P3a was also smaller for +2 compared with +8. Overall, these P3 results are consistent with previous studies showing that the P3 is greater both for large- versus small-magnitude outcomes, and for suboptimal versus optimal outcomes (Yeung and Sanfey, 2004; Chase et al., 2011).
Table 2.
Association between ERP components and the variables outcome and behavioral adjustment
| ERP components |
||||
|---|---|---|---|---|
| P2 | FRN | P3a | P3b | |
| R2 | 0.05 | 0.11 | 0.15 | 0.18 |
| Model predictors | β, p | β, p | β, p | β, p |
| Constants | 6.81, 4 (10−47)a | 1.95, 3 (10−11)a | 11.3, 1 (10−35)a | 5.90, 6 (10−31)a |
| Outcome +2 | −1.37, 7 (10−8)a | −1.16, 9 (10−7)a | −1.61, 5 (10−5)a | 0.18, 0.24 |
| Outcome −2 | −1.9, 3 (10−13)a | −1.53, 2 (10−10)a | −3.36, 1 (10−15)a | −1.51, 1 (10−8)a |
| Outcome −8 | 0.01, 0.49 | −2.70, 2 (10−16)a | 3.88, 1 (10−17)a | 3.29, 1 (10−14)a |
| Adjustment 1 | 0.42, 0.0302 | 0.19, 0.18 | 0.75, 0.02 | 0.27, 0.12 |
| Adjustment 2 | 0.32, 0.09 | −0.10, 0.31 | 1.02, 0.002a | 0.42, 0.03 |
a Significant with a Holm's corrected alpha level set at 0.05 for 24 tests.
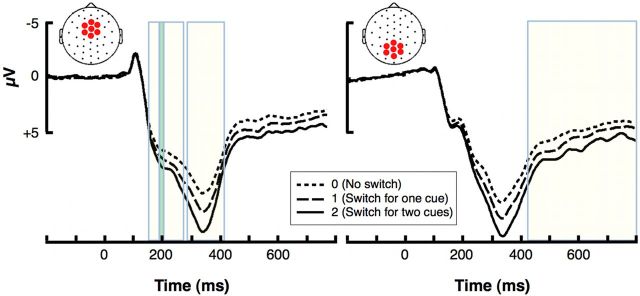
Most importantly, both the P3a and P3b amplitudes scaled with adjustment level (Fig. 5). However, only the relationship between P3a and the largest adjustment (2, switching for both symbols) survived our rather conservative approach to multiple comparisons (Table 2). Importantly, the FRN showed no significant association with behavioral adjustment, not even according to uncorrected p values. In sum, the larger the P3a was on a given trial, the more likely the subjects were to change their choice behavior on the next appearance of the same symbols.
Figure 5.
Feedback-locked ERPs as a function sequential behavioral adjustment. The ERP traces show the effect of (future) behavioral adjustment on the P2, FRN, and P3a (left) and P3b (right) amplitudes. The P3a subcomponent significantly predicted whether participants would switch choice behavior on the subsequent trial(s) presenting the same symbols. For example, if the current trial presented the symbols M and Z and the participant chose 8 as the wager amount, then the larger the P3a, the larger the probability of choosing 2 on the next presentation of M and Z, either if M and Z are presented paired or unpaired on their subsequent occurrences.
Discussion
When confronted by choices from among competing options, simply avoiding losses and seeking gains may be an insufficient strategy for generating optimal behavior. In other words, to achieve long-term positive outcomes, decision makers must not only be concerned with the relative frequency of gains and losses, but also with the relative magnitude of gains and losses. Previous behavioral studies have found that deficits in gain maximization and loss minimization are associated with negative life outcomes in gambling (Siler, 2010) and depression (Maddox et al., 2012). Here, we contribute to the identification and functional characterization of the neural mechanisms that may underlie such effects by showing that the amplitude of two P3 subcomponents predicted individual differences in gain maximization and loss minimization (P3b) and the subsequent behavioral adjustment (P3a). These findings suggest the P3 may reflect brain activity involved in adjusting choice behavior in support of maximizing gains and minimizing losses.
Different neural signatures for gain maximization and loss minimization
Previous studies (Frank et al., 2005; Eppinger et al., 2008; Cavanagh et al., 2011) have suggested that the ability to learn to avoid negative outcomes scales with the sensitivity of the FRN to losses. We used a task in which losses could not be avoided, but could be minimized, and in which gains could not be ensured, but could be maximized. From this, we expected to find a dissociation between gain maximization and loss minimization involving the FRN: gain maximization would be associated with the neural differentiation of gains, whereas loss minimization would be associated with the neural differentiation of losses. We did indeed find this pattern of results in the ERP activity, but in the P3b rather than in the FRN. A possible reason for the discrepancy between our results and those of the previous studies is that in those studies, valence and relative outcome information (i.e., best vs worst outcome relative to the outcome that “would have been” if the alternative decision had been made) were always correlated, and the FRN is known to be primarily sensitive to valence (Yeung and Sanfey, 2004). In contrast, our task distinguished outcome valence from relative outcome. Accordingly, this manipulation was able to decouple valence evaluation from relative outcome information, which thereby allowed us to distinguish the functional processes reflected by the FRN and the P3b.
The differentiation between gain maximization and loss minimization that we found in the P3b is in many ways consistent with the context-updating hypothesis for the P3 (Donchin, 1981; Donchin and Coles, 1988), which proposes that the P3 reflects the amount of cognitive resources used during the revision of an internal model of the environment. Such a model would be revised whenever discrepancies between a stimulus and model-derived predictions bring the validity of the model into question. This hypothesis is complemented by the context-updating/locus coeruleus (LC)–P3 hypothesis (Nieuwenhuis et al., 2005; Nieuwenhuis, 2011), which builds on the similarities between the context-updating hypothesis and the role of the LC–norepinephrine (NE) system in learning (Aston-Jones and Cohen, 2005; Yu and Dayan, 2005; Dayan and Yu, 2006), to propose that the P3 reflects cortical activity resulting from phasic modulation by the LC–NE system.
In considering the application of this model to the present study, it indeed seems likely that the participants would have been dynamically updating an internal model of the association between various symbols and the probability of winning [p(win)] that informed decisions on each trial. In this scenario, high gain-maximization scores would be associated with a strong tendency to modify representations leading to future choices likely to produce suboptimal gains while maintaining representations leading to choices that maximize gains. According to the context-updating/LC–P3 hypothesis, this would be reflected in a large P3b for suboptimal compared to optimal gains (i.e., +2 > +8), as was the case. On the other hand, high loss-minimization scores would be associated with a tendency to modify representations leading to choices likely to produce suboptimal losses, while maintaining representations leading to choices that minimize losses. According to the context-updating/LC–P3 hypothesis, this would be associated with a large P3b for suboptimal compared to optimal losses (i.e., −8 > −2), as was also the case. Below we discuss the additional analyses that advance a mechanistic explanation of these results.
P3 sensitivity to large magnitude and choice bias
The P3 response has been found previously to be an index of attentional allocation (Schupp et al., 2004; Gao et al., 2011). In our study, the findings of positive-polarity feedback-magnitude effects starting rather early (P2) and lasting for a long period (P3a and P3b, where large-magnitude outcomes were, overall, associated with large ERP amplitudes) suggests that people pay more attention to large outcomes. Large outcomes probably induce greater arousal than small ones because they have a greater impact on cumulative earnings in economic scenarios. Neuroimaging studies have identified a number of regions that are sensitive to outcome magnitude, including the orbitofrontal cortex, insula, and ventral striatum (Elliott et al., 2000; Knutson et al., 2000; Breiter et al., 2001; Delgado et al., 2003). Although these frontal and subcortical regions may not directly contribute to the outcome-sensitive P3 subcomponents reported here (i.e., as generators), some of these regions may be involved in allocating additional cognitive resources to the processing of large outcomes, which may in turn be reflected by the P3 activity.
This additional allocation of attention to large-magnitude outcomes may explain why participants were overall better at loss minimization than gain maximization. Specifically, an increased amount of cognitive resources marshaled in response to large outcomes might benefit loss minimization by selectively enhancing the processing of large-magnitude outcomes that indicate the need for behavioral adjustment (i.e., −8 is not just a negative outcome but also a large-magnitude one). On the other hand, gain maximization requires adjusting behavior after a small-magnitude outcome (i.e., +2, the suboptimal gain) and thus would not benefit from an attentional bias toward large-magnitude outcomes.
P3 subcomponents predict behavioral adjustment
We found that the P3a, rather than the FRN, predicted behavioral adjustment between trial occurrences in the trial sequence in which the same symbols were presented. The P3b also tended to distinguish between the absence of adjustment and the largest adjustments, but such difference did not survive our conservative method of correcting for multiple comparisons. We propose an interpretation of these results that is also consistent with the context-updating/LC–P3 hypothesis, namely, that decisions on each trial were informed by an internal model of the symbol/p(win) contingencies, and the P3 amplitude reflects the extent of the feedback-triggered revision of such a model.
With respect to the roles of the FRN and the P3 in feedback-guided decision making, our results suggest that the P3 is involved in using outcome-predicting cues to adjust behavior when the goal is maximizing gains and minimizing losses, whereas the FRN might be involved in using such cues when the goal is approaching gains and avoiding losses (Frank et al., 2005). An issue for future research will be to determine how the behavioral goals and context of the task affect the relative involvement of different brain signals in feedback-guided decision making.
Time course of feedback processing
The temporal resolution of ERPs allows us to propose a time course of feedback processing. According to its distribution over the scalp, and in line with previous studies (Yeung and Sanfey, 2004; Goyer et al., 2008; San Martín et al., 2010), we interpret the P2 activity (∼180 ms after feedback onset) as an early stage of the P3, probably preceding stimulus awareness (Sergent et al., 2005; Del Cul et al., 2007) and related to an implicit appreciation of the task relevance of the stimulus (Potts et al., 2006). As our results suggest, such appreciation can be biased (e.g., greater attentional sensitivity toward large-magnitude outcomes), and according to our interpretation it can selectively enhance later stages of feedback processing. The FRN (∼250 ms) seems to index the evaluation of outcome value (“how much value was acquired/lost”), presumably in terms of a reward prediction error (Holroyd and Coles, 2002). Such a mechanism might not directly adjust behavior, but might rather inform subsequent processes that update the representation of probabilistic contingencies. We interpret the P3 amplitude as reflecting such revisions. Interestingly, recent work has been able to accurately simulate the P3 under the assumption that it is driven, in part, by precomputed prediction errors (Feldman and Friston, 2010). In line with the context-updating/LC–P3 hypothesis, the P3 amplitude may reflect the amount of attention engaged during the feedback-induced revision of an internal model of the environment that informs choice behavior. During the course of the P3, the P3a (∼350 ms) may serve as a link between a stimulus-driven attentional process that recruits a frontal circuit initially indexed by the P2/early P3 and a memory updating process that recruits a temporoparietal circuit and that is indexed by the P3b (∼450 ms) (Polich, 2007).
Overall, our results suggest that the P3 response to monetary outcomes reflect an adaptive mechanism by which prior experience may alter ensuing choice behavior. Moreover, our results suggest that individual differences in this process, as reflected in the P3, are linked to individual differences in gain maximization and loss minimization during economic decision making.
Footnotes
This work was supported by a Fulbright scholarship and a CONICYT grant to R.S.M., and by NIMH Grant R01-MH060415 to M.G.W. We thank Kenneth C. Roberts for helpful assistance during the preparation of the experiment, Stevan Budi for assistance with data collection, and R. McKell Carter for helpful assistance and comments during data analysis.
The authors declare no competing financial interests.
References
- Aston-Jones G, Cohen JD. An integrative theory of locus coeruleus-norepinephrine function: adaptive gain and optimal performance. Annu Rev Neurosci. 2005;28:403–450. doi: 10.1146/annurev.neuro.28.061604.135709. [DOI] [PubMed] [Google Scholar]
- Baillet S, Mosher JC, Leahy RM. Electromagnetic brain mapping. IEEE Signal Process Mag. 2001;18:14–30. doi: 10.1109/79.962275. [DOI] [Google Scholar]
- Bell AJ, Sejnowski TJ. An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 1995;7:1129–1159. doi: 10.1162/neco.1995.7.6.1129. [DOI] [PubMed] [Google Scholar]
- Bellebaum C, Polezzi D, Daum I. It is less than you expected: the feedback-related negativity reflects violations of reward magnitude expectations. Neuropsychologia. 2010;48:3343–3350. doi: 10.1016/j.neuropsychologia.2010.07.023. [DOI] [PubMed] [Google Scholar]
- Breiter HC, Aharon I, Kahneman D, Dale A, Shizgal P. Functional imaging of neural responses to expectancy and experience of monetary gains and losses. Neuron. 2001;30:619–639. doi: 10.1016/S0896-6273(01)00303-8. [DOI] [PubMed] [Google Scholar]
- Cavanagh JF, Bismark AJ, Frank MJ, Allen JJ. Larger error signals in major depression are associated with better avoidance learning. Front Psychol. 2011;2:331. doi: 10.3389/fpsyg.2011.00331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chase HW, Swainson R, Durham L, Benham L, Cools R. Feedback-related negativity codes prediction error but not behavioral adjustment during probabilistic reversal learning. J Cogn Neurosci. 2011;23:936–946. doi: 10.1162/jocn.2010.21456. [DOI] [PubMed] [Google Scholar]
- Cohen MX, Ranganath C. Reinforcement learning signals predict future decisions. J Neurosci. 2007;27:371–378. doi: 10.1523/JNEUROSCI.4421-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dayan P, Yu AJ. Phasic norepinephrine: a neural interrupt signal for unexpected events. Network. 2006;17:335–350. doi: 10.1080/09548980601004024. [DOI] [PubMed] [Google Scholar]
- Debener S, Ullsperger M, Siegel M, Fiehler K, von Cramon DY, Engel AK. Trial-by-trial coupling of concurrent electroencephalogram and functional magnetic resonance imaging identifies the dynamics of performance monitoring. J Neurosci. 2005;25:11730–11737. doi: 10.1523/JNEUROSCI.3286-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Del Cul A, Baillet S, Dehaene S. Brain dynamics underlying the nonlinear threshold for access to consciousness. PloS Biology. 2007;5:2408–2423. doi: 10.1371/journal.pbio.0050260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delgado MR, Locke HM, Stenger VA, Fiez JA. Dorsal striatum responses to reward and punishment: effects of valence and magnitude manipulations. Cogn Affect Behav Neurosci. 2003;3:27–38. doi: 10.3758/CABN.3.1.27. [DOI] [PubMed] [Google Scholar]
- Delorme A, Makeig S. EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J Neurosci Methods. 2004;134:9–21. doi: 10.1016/j.jneumeth.2003.10.009. [DOI] [PubMed] [Google Scholar]
- Delorme A, Sejnowski T, Makeig S. Enhanced detection of artifacts in EEG data using higher-order statistics and independent component analysis. Neuroimage. 2007;34:1443–1449. doi: 10.1016/j.neuroimage.2006.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donchin E. Surprise!.Surprise? Psychophysiology. 1981;18:493–513. doi: 10.1111/j.1469-8986.1981.tb01815.x. [DOI] [PubMed] [Google Scholar]
- Donchin E, Coles MGH. Is the P300 component a manifestation of context updating? Behav Brain Sci. 1988;11:357–374. doi: 10.1017/S0140525X00058027. [DOI] [Google Scholar]
- Eichele T, Specht K, Moosmann M, Jongsma ML, Quiroga RQ, Nordby H, Hugdahl K. Assessing the spatiotemporal evolution of neuronal activation with single-trial event-related potentials and functional MRI. Proc Natl Acad Sci U S A. 2005;102:17798–17803. doi: 10.1073/pnas.0505508102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elliott R, Friston KJ, Dolan RJ. Dissociable neural responses in human reward systems. J Neurosci. 2000;20:6159–6165. doi: 10.1523/JNEUROSCI.20-16-06159.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eppinger B, Kray J, Mock B, Mecklinger A. Better or worse than expected? Aging, learning, and the ERN. Neuropsychologia. 2008;46:521–539. doi: 10.1016/j.neuropsychologia.2007.09.001. [DOI] [PubMed] [Google Scholar]
- Feldman H, Friston KJ. Attention, uncertainty, and free-energy. Front Hum Neurosci. 2010;4:215. doi: 10.3389/fnhum.2010.00215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank MJ, Seeberger LC, O'Reilly RC. By carrot or by stick: cognitive reinforcement learning in parkinsonism. Science. 2004;306:1940–1943. doi: 10.1126/science.1102941. [DOI] [PubMed] [Google Scholar]
- Frank MJ, Woroch BS, Curran T. Error-related negativity predicts reinforcement learning and conflict biases. Neuron. 2005;47:495–501. doi: 10.1016/j.neuron.2005.06.020. [DOI] [PubMed] [Google Scholar]
- Gao X, Deng X, Chen N, Luo W, Hu L, Jackson T, Chen H. Attentional biases among body-dissatisfied young women: an ERP study with rapid serial visual presentation. Int J Psychophysiol. 2011;82:133–142. doi: 10.1016/j.ijpsycho.2011.07.015. [DOI] [PubMed] [Google Scholar]
- Gehring WJ, Willoughby AR. The medial frontal cortex and the rapid processing of monetary gains and losses. Science. 2002;295:2279–2282. doi: 10.1126/science.1066893. [DOI] [PubMed] [Google Scholar]
- Goyer JP, Woldorff MG, Huettel SA. Rapid electrophysiological brain responses are influenced by both valence and magnitude of monetary rewards. J Cogn Neurosci. 2008;20:2058–2069. doi: 10.1162/jocn.2008.20134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holm S. A simple sequentially rejective multiple test procedure. Scandinavian J Stat. 1979;6:65–70. [Google Scholar]
- Holroyd CB, Coles MG. The neural basis of human error processing: reinforcement learning, dopamine, and the error-related negativity. Psychol Rev. 2002;109:679–709. doi: 10.1037/0033-295X.109.4.679. [DOI] [PubMed] [Google Scholar]
- Jung TP, Makeig S, Humphries C, Lee TW, McKeown MJ, Iragui V, Sejnowski TJ. Removing electroencephalographic artifacts by blind source separation. Psychophysiology. 2000a;37:163–178. doi: 10.1111/1469-8986.3720163. [DOI] [PubMed] [Google Scholar]
- Jung TP, Makeig S, Westerfield M, Townsend J, Courchesne E, Sejnowski TJ. Removal of eye activity artifacts from visual event-related potentials in normal and clinical subjects. Clin Neurophysiol. 2000b;111:1745–1758. doi: 10.1016/S1388-2457(00)00386-2. [DOI] [PubMed] [Google Scholar]
- Klein TA, Neumann J, Reuter M, Hennig J, von Cramon DY, Ullsperger M. Genetically determined differences in learning from errors. Science. 2007;318:1642–1645. doi: 10.1126/science.1145044. [DOI] [PubMed] [Google Scholar]
- Knutson B, Westdorp A, Kaiser E, Hommer D. FMRI visualization of brain activity during a monetary incentive delay task. Neuroimage. 2000;12:20–27. doi: 10.1006/nimg.2000.0593. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Gorlick MA, Worthy DA, Beevers CG. Depressive symptoms enhance loss-minimization, but attenuate gain-maximization in history-dependent decision-making. Cognition. 2012;125:118–124. doi: 10.1016/j.cognition.2012.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miltner W, Braun C, Coles M. Event-related potentials following incorrect feedback in a time-estimation task: evidence for a “generic” neural system for error detection. J Cogn Neurosci. 1997;9:788–798. doi: 10.1162/jocn.1997.9.6.788. [DOI] [PubMed] [Google Scholar]
- Nieuwenhuis S. Learning, the P3, and the locus coeruleus-norepinephrine system. In: Mars R, Sallet J, Rushworth M, Yeung N, editors. Neural basis of motivational and cognitive control. Cambridge, MA: MIT; 2011. pp. 209–222. [Google Scholar]
- Nieuwenhuis S, Yeung N, Holroyd CB, Schurger A, Cohen JD. Sensitivity of electrophysiological activity from medial frontal cortex to utilitarian and performance feedback. Cereb Cortex. 2004;14:741–747. doi: 10.1093/cercor/bhh034. [DOI] [PubMed] [Google Scholar]
- Nieuwenhuis S, Aston-Jones G, Cohen JD. Decision making, the P3, and the locus coeruleus-norepinephrine system. Psychol Bull. 2005;131:510–532. doi: 10.1037/0033-2909.131.4.510. [DOI] [PubMed] [Google Scholar]
- Polich J. Updating P300: an integrative theory of P3a and P3b. Clin Neurophysiol. 2007;118:2128–2148. doi: 10.1016/j.clinph.2007.04.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Potts GF, Martin LE, Burton P, Montague PR. When things are better or worse than expected: the medial frontal cortex and the allocation of processing resources. J Cogn Neurosci. 2006;18:1112–1119. doi: 10.1162/jocn.2006.18.7.1112. [DOI] [PubMed] [Google Scholar]
- San Martín R. Event-related potential studies of outcome processing and feedback-guided learning. Front Hum Neurosci. 2012;6:304. doi: 10.3389/fnhum.2012.00304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- San Martín R, Manes F, Hurtado E, Isla P, Ibañez A. Size and probability of rewards modulate the feedback error-related negativity associated with wins but not losses in a monetarily rewarded gambling task. Neuroimage. 2010;51:1194–1204. doi: 10.1016/j.neuroimage.2010.03.031. [DOI] [PubMed] [Google Scholar]
- Scheibe C, Ullsperger M, Sommer W, Heekeren HR. Effects of parametrical and trial-to-trial variation in prior probability processing revealed by simultaneous electroencephalogram/functional magnetic resonance imaging. J Neurosci. 2010;30:16709–16717. doi: 10.1523/JNEUROSCI.3949-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schupp HT, Junghöfer M, Weike AI, Hamm AO. The selective processing of briefly presented affective pictures: an ERP analysis. Psychophysiology. 2004;41:441–449. doi: 10.1111/j.1469-8986.2004.00174.x. [DOI] [PubMed] [Google Scholar]
- Sergent C, Baillet S, Dehaene S. Timing of the brain events underlying access to consciousness during the attentional blink. Nat Neurosci. 2005;8:1391–1400. doi: 10.1038/nn1549. [DOI] [PubMed] [Google Scholar]
- Siler K. Social and psychological challenges of poker. J Gambl Stud. 2010;26:401–420. doi: 10.1007/s10899-009-9168-2. [DOI] [PubMed] [Google Scholar]
- Venkatraman V, Payne JW, Bettman JR, Luce MF, Huettel SA. Separate neural mechanisms underlie choices and strategic preferences in risky decision making. Neuron. 2009;62:593–602. doi: 10.1016/j.neuron.2009.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woldorff MG, Liotti M, Seabolt M, Busse L, Lancaster JL, Fox PT. The temporal dynamics of the effects in occipital cortex of visual-spatial selective attention. Brain Res Cogn Brain Res. 2002;15:1–15. doi: 10.1016/S0926-6410(02)00212-4. [DOI] [PubMed] [Google Scholar]
- Yeung N, Sanfey AG. Independent coding of reward magnitude and valence in the human brain. J Neurosci. 2004;24:6258–6264. doi: 10.1523/JNEUROSCI.4537-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu AJ, Dayan P. Uncertainty, neuromodulation, and attention. Neuron. 2005;46:681–692. doi: 10.1016/j.neuron.2005.04.026. [DOI] [PubMed] [Google Scholar]