Linking Outcomes from Peabody Picture Vocabulary Test Forms using Item Response Models

Abstract

Purpose

The present work describes how vocabulary ability as assessed by three different forms of the Peabody Picture Vocabulary Test (PPVT) can be placed on a common latent metric through item response theory (IRT) modeling, by which valid comparisons of ability between samples or over time can then be made.

Method

Responses from 2,625 cases in a longitudinal study of 697 persons for 459 unique PPVT items (175 items from PPVT-R Form M, 201 items from PPVT-3 Form A, and 83 items from PPVT-3 Form B) were analyzed using a two-parameter logistic IRT model.

Results

The test forms each covered approximately ±3 standard deviations of vocabulary ability with high reliability. Some differences between item sets in item difficulty and discrimination were found between the PPVT-3 Forms A and B.

Conclusions

Comparable estimates of vocabulary ability obtained from different test forms can be created via IRT modeling. The authors have also written a freely available SAS program that uses the obtained item parameters to provide IRT ability estimates given item responses to any of the three forms. This scoring resource will allow others with existing PPVT data to benefit from this work as well.

Accurate measurement of individual differences is critical for testing theories about cognition and its development, as well as for making critical real-world decisions about the ability of a given individual. Maintaining reliability of measurement within longitudinal studies can be especially challenging, given that test items may need to be added or removed over time in order to preserve sensitivity of measurement across developmental stages. Such necessary modifications, as well as revision of existing instruments over time or use of alternative test forms, can threaten comparability of the resulting test scores. Without comparable measurement across occasions of study, one cannot determine whether any observed change in test scores over time is due to real growth or is simply an artifact of differing procedures of measurement.

The current paper focuses on the changing test forms over time of the Peabody Picture Vocabulary Test (PPVT), a widely-used instrument used for assessing vocabulary knowledge in children and adults. It is well suited to the assessment of children’s vocabulary acquisition and for identification of children with language impairments (c.f., Rice & Watkins, 1996). A recent study identified the PPVT as one of the diagnostic instruments frequently used by speech language pathologists in clinical practice to diagnose Specific Language Impairment (SLI) in children (Eickhoff, Betz, & Ristow, 2010). PPVT scores serve as estimates of vocabulary growth as a consequence of language intervention (c.f., Rice & Hadley, 1995), as a description of growth in vocabulary in early childhood (c.f., Rice, 2009), and as a validity comparison for growth in other indicators of language acquisition, such as the mean length of utterance (Rice, Redmond, & Hoffman, 2006). Various versions of the PPVT continue to be used by researchers and clinicians within and outside the field of speech pathology to document children’s language acquisition (c.f., Snow et al., 2007, for use of the PPVT-3). More recently, PPVT scores have served as phenotypes in genetic investigations (Rice, Smith, & Gayán, 2009).

The PPVT measure of vocabulary features multiple-choice items in which four pictures are shown for each vocabulary word (including verbs, nouns, and adjectives). The respondent is instructed to select the picture that best illustrates the definition of the word (read aloud by an examiner, who then scores the response as correct or incorrect). The PPVT was originally developed in 1959 and a revised version including two alternate forms was developed in 1981 (PPVT-R Forms L and M; Dunn & Dunn, 1981). A third version, also with two alternate forms, was developed in 1997 (PPVT-3 Forms A and B; Dunn & Dunn, 1997). A fourth version with two alternate forms was developed in 2007 (PPVT-4 Forms A and B).

Perhaps more than any other test, there has been extensive discussion of potential differences with clinical implications across test versions, especially for PPVT-R vs. PPVT-3, in which higher scores on the PPVT-3 have raised concern. Ukrainetz and Duncan (2000) noted that Washington and Craig (1992, 1999) found higher mean levels of performance on PPVT-3 for a sample of children very similar demographically to a previous sample, although no children received both forms of the tests, thereby weakening the comparison. Ukrainetz and Duncan (2000) reported an analysis of publisher test data for 193 children who received PPVT-3 and Form L of the PPVT-R. They found test scores approximately 10 standard score points higher on PPVT-3 in the 7–10 year age range, and about 4 points higher for older children. Gray, Plante, Vance, and Henrichsen (1999) compared 31 children ages 4–5 years with SLI and 31 age-matched control children and reported high validity but weak sensitivity for SLI for PPVT-3. Pankratz, Morrison, and Plante (2004) administered PPVT-R and PPVT-3 to 76 adults with differing levels of language ability. They found fewer individuals identified as having low levels of vocabulary on the PPVT-3. Peña, Spaulding, and Plante (2006) suggest that the inclusion of language impaired persons in the norming sample could lessen sensitivity to vocabulary deficits. Although the publishers of the PPVT have offered a conversion table for the PPVT-3 to use with the PPVT-R, a similar conversion table has not been made available for the current version, PPVT-4. As a result, the PPVT-3, even with lessened sensitivity to language impairments, may remain the better option for a number of research studies.

One potential consequence of such continually evolving instruments is that the use of different PPVT forms across time may create problems in measuring growth in vocabulary ability in longitudinal studies. Standard scores cannot be used to assess absolute growth (i.e., a child of average ability who increases in vocabulary at an expected rate relative to his or her age peers will retain a PPVT standard score of 100 over time), and so raw scores may be used as an alternative. However, raw scores from different test forms cannot be meaningfully compared if the number of items differs across test forms. Consider an example study in which the PPVT-Rm (with 175 items) is used at the first occasion, but the PPVT-3a (with 204 items) is used at the second occasion. Even if both forms measure the same ability, direct comparisons of their raw scores to assess growth will be compromised by their incompatible ranges of possible scores. Comparison of raw scores even across test forms with the same number of items could still be problematic, in that differences across forms in the difficulty of the individual items or item sets could lead to artifactual differences in raw scores across forms. Although we focus on the PPVT specifically in this study, it is important to recognize the relevance of these problems of comparability to any instrument in which growth is assessed using different forms over time.

Fortunately, these comparability problems can be resolved through item response theory (or IRT), a family of psychometric models that describe how observed item responses are predicted by the continuous latent ability they measure (i.e., vocabulary ability measured by the PPVT items). The use of IRT models to create comparable measures of ability across test forms has a long-standing tradition in educational testing (e.g., Kim & Cohen, 1998), as well as in psychology (e.g., Curran et al., 2008). IRT models use statistical techniques that rely on overlapping items in multiple test forms to anchor the ability scores produced by the analysis.

Accordingly, the purpose of the current longitudinal study is to use an IRT model to create comparable measures of vocabulary ability over time as obtained from three different PPVT forms: PPVT-Rm, PPVT-3a, and PPVT-3b. In addition to using the common items from these forms to anchor the analyses, we also used person linking data, in which multiple test forms were administered to the same person at the same occasion, creating what is called a common items (e.g., Hanson & Béguin, 2002) and common persons linking design (e.g. Masters, 1985). Through IRT modeling all persons and items are placed onto the same latent metric, providing a common measurement scale with which to make valid comparisons between persons or over time, even if their data were obtained from different test forms. In contrast to the aforementioned research, the current IRT calibration sample was much larger and featured much more variability in age and ability, which are important considerations in ensuring sufficient information for all test items. Consequently, the results provided by the present IRT modeling are likely to be more stable, robust, and replicable than any comparisons of more restricted samples. More importantly, though, the present IRT modeling also provides a means through which the results of these form comparisons can be utilized directly by other investigators. To that end, we have provided a freely available SAS program that creates IRT scores of vocabulary ability for use instead of raw scores given responses to one or more of these three PPVT forms. Through this resource other researchers and practitioners will also be able to translate their existing PPVT data from different forms onto a common latent metric for making valid comparisons between persons or over time.

Method

Participants

PPVT data for the current study were collected over 15 years within a series of ongoing longitudinal studies (see Rice, Smolik, Perpich, Thompson, Rytting, & Blossom, 2010, and Rice, Smith, & Gayán, 2009, for details). The sample was part of a study of children with Specific Language Impairment (SLI), their parents and siblings, and control children and families. A total of 2,625 cases from 697 unique persons were analyzed, of which 51% were male. In this sample, 22.6% were children ascertained as having SLI, 47.8% were other children, and 29.6% were adults. The race/ethnicity percentages were: White, 85.8%; Multi-racial, 6.5%; American Indian, 3.3%; Black, 1%; Asian, <1%; Not reported, 3.4%. Hispanic ethnicity was reported by 5.3% of the sample. The number of occasions of measurement per person ranged from 1 to 16 (M = 3.8, SD = 3.9). Respondent ages in years ranged from 2.5 to 59.6 (M = 11.7, SD = 8.6). PPVT-3a data were obtained from 1,992 cases from 595 persons, PPVT-Rm data were obtained from 2,073 cases from 537 persons, and PPVT-3b data were obtained from 377 cases from 377 persons. The mean standard score for the full sample was 96.9 (SD = 14.4).

Test Forms and Linking Data

Linking data (needed for a concurrent analysis of three test forms) was available across both persons and items. With regard to linking across forms by common persons, the PPVT-3a and PPVT-Rm forms were linked using 1,440 cases from 432 persons who completed both forms at approximately the same occasion (i.e., an age difference between occasions of 0 to 0.34 years, M = 0.02, SD = 0.04). The PPVT-Rm and PPVT-3b forms were linked using 377 cases from 377 persons who completed both forms at approximately the same occasion (i.e., an age difference between occasions of 0 to 0.17 years, M = 0.01, SD = 0.02). With regard to linking across forms by common items, the PPVT-3a and PPVT-3b forms each contain 204 items, none of which are shared. The PPVT-Rm form contains 175 items, 3 of which are shared with the PPVT-3a form, and 121 of which are shared with the PPVT-3b form. Because only the PPVT-Rm had items in common with the other forms, its item responses were used for any shared items. Thus, a total 459 unique items were analyzed, including 201 PPVT-3a items, 175 PPVT-Rm items, and 83 PPVT-3b items. The number of item responses from each case (i.e., for one person at one occasion) ranged from 11 to 218 (M = 97.0, SD = 37.1). The number of unique responses for each item (i.e., across cases) ranged from 22 to 1165 (M = 554.8, SD = 357.8).

Test Procedure

The PPVT-3a and PPVT-3b tests were administered as instructed in their test manual (Dunn & Dunn, 1997). The 204 items in each test are ordered in difficulty and grouped into sets, such that each respondent only completes the items likely to be most relevant to him or her (e.g., items that would be too easy or too difficult are not administered). The test begins with the set of 12 recommended items based on the respondent’s age. If the respondent makes 1 or fewer errors on that initial 12-item set, that item set becomes the basal item set. Alternatively, if 2 or more items are missed in the initial item set, the preceding (easier) 12-item set is administered, continuing until the criterion of 1 or fewer errors is created. Once this basal item set has been established, additional 12-item sets in ascending difficulty are administered until 8 or more errors is made in an item set, which becomes the ceiling item set, the last item of which is the ceiling item. The PPVT-3a or PPVT-3b raw score is then calculated by subtracting the total number of errors made between the basal and ceiling item sets from the ceiling item.

The 175 items in the PPVT-Rm (Dunn & Dunn, 1981) are also ordered in difficulty, but they are not grouped into 12-item sets. Instead, a starting item is recommended based on the respondent’s age, and administration continues until 8 consecutive correct responses are given. The 8^th item answered correctly is the basal item. From there, administration continues with sequential items in ascending difficulty until 6 errors are made in 8 consecutive responses. The last item administered is the ceiling item. The PPVT-Rm raw score is then calculated by subtracting from the ceiling item the total number of errors made between the basal item and the ceiling item. The procedures for exceptions due to inconsistent responses are detailed in the test manuals. The scoring processes assume that all items (administered or not) below the basal item would have been correct and that all items above the ceiling item would have been incorrect.

Results

Psychometric Model

The 459 unique PPVT items were analyzed using item response theory (IRT) models, a family of psychometric models that predict individual item responses from the characteristics of each item and the latent ability of each respondent (see Embretson & Reise, 2000). IRT models are closely related to confirmatory factor analysis (CFA) models, in that a continuous latent trait (here, vocabulary ability) is thought to cause the observed item responses, such that the relation between item responses is due only to the ability of the person responding (or multiple abilities in multidimensional models). The primary difference between CFA and IRT models is that CFA models continuous item responses directly, whereas IRT models the probability of categorical (i.e., binary or ordinal) item responses via link functions (i.e., transformations of probability).

The basic form of the IRT model to be used for the PPVT items is shown in Equation 1:

$$\text{probability}({\text{y}}_{\text{ip}}=1\mid {\text{Ability}}_{\text{p}})=\frac{exp\left[1.7{\text{a}}_{\text{i}}({\text{Ability}}_{\text{p}}-{\text{b}}_{\text{i}})\right]}{1+exp\left[1.7{\text{a}}_{\text{i}}({\text{Ability}}_{\text{p}}-{\text{b}}_{\text{i}})\right]},$$ (1)

in which the probability of a correct response to item i for person p (y_ip = 1) depends on three model parameters: the person vocabulary ability (Ability_p), the item difficulty (b_i), and the item discrimination (a_i). The constant 1.7 is used to maintain comparability across other IRT models (e.g., normal ogive). The IRT model in Equation 1 is known as the 2-parameter logistic model because it has two estimated parameters per item (a_i and b_i) and because it can be specified to predict the log-odds (logit) of the response instead. Other IRT models for binary responses (such as incorrect or correct response here) include the 1-parameter logistic (or Rasch) model, in which the item discrimination parameter (a) is held constant across items, or the 3-parameter logistic model, which includes an additional parameter for each item (c_i) of a lower asymptote for the probability of a correct response (i.e., due to guessing).

The key concept in an IRT model is that there is a common latent metric on which all persons (based on their ability) and all items (based on their difficulty) can be located. Because this common metric is unobserved, we must set its scale by fixing the mean and the variance of the latent ability variable to known values (or by fixing the a_i and b_i parameters for one item, similar to model identification in CFA models). For convenience, we can give the latent ability metric a mean = 0 and variance = 1, such that the ability estimates can be interpreted like z-scores. These ability estimates are interpreted using the items on their common latent continuum, such that a person’s ability is the item difficulty level (b_i) at which the probability of a correct response is 50%. Likewise, item difficulty (b_i) is the amount of ability needed for a probability of a correct item response of 50%. To illustrate, we substitute hypothetical values for person ability, item difficulty, and item discrimination into Equation 1, as shown in Equation 2:

$$\begin{array}{l}\text{Item}1:\text{probability}({\text{y}}_{1\text{p}}=1\mid {\text{Ability}}_{\text{p}})=\frac{exp\left[1.7(1)(0--1)\right]}{1+exp\left[1.7(1)(0--1)\right]}=.85\hfill \\ \text{Item}2:\text{probability}({\text{y}}_{\text{2p}}=1\mid {\text{Ability}}_{\text{p}})=\frac{exp\left[1.7(1)(0-1)\right]}{1+exp\left[1.7(1)(0-1)\right]}=.15\hfill \end{array},$$ (2)

in which we specify the predicted probability of a correct item response assuming average ability (Ability_p = 0) and an item discrimination of a_i = 1 (as will be explained next). In Equation 2, if ability exceeds item difficulty (as in Item 1, b₁ = 1), the probability of a correct response will be > .50. If item difficulty exceeds ability instead (as in Item 2, b₂ = 1), the probability will be < .50.

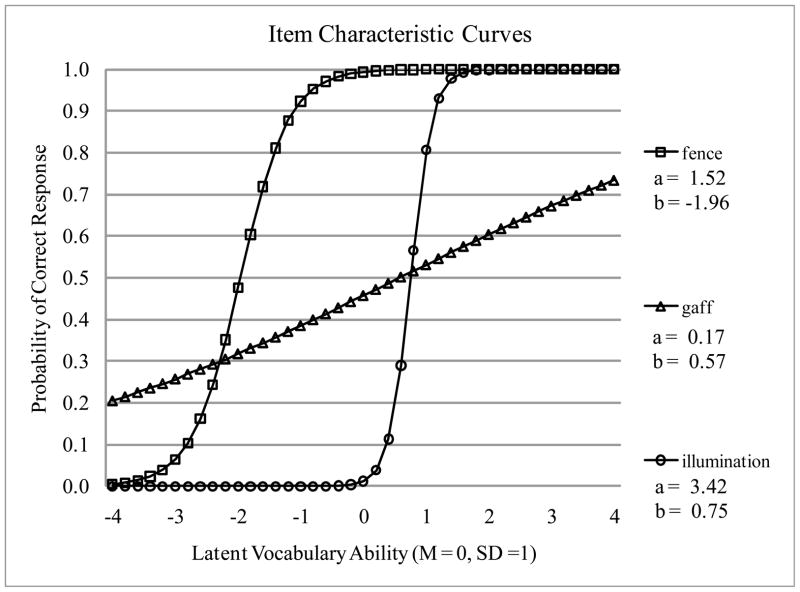
To differentiate item difficulty (b_i) from item discrimination (a_i), we can examine Figure 1, in which item characteristic curves are shown for the probability of a correct response across person ability (scaled with M = 0 and VAR = 1) for three of the PPVT items: fence and gaff (from PPVT-3a), and illumination (from both the PPVT-Rm and PPVT-3b). As shown in Figure 1, fence is the easiest item of the three, with an item difficulty of b = −1.96, whereas the other two items have higher levels of difficulty (gaff: b = 0.57, illumination: b = 0.75). Thus, 0.75 ability or greater is needed to have more than a 50% chance of answering gaff and illumination correctly, but only −1.96 ability or greater is needed to have more than a 50% chance of answering fence correctly. However, these three items vary widely in item discrimination (a_i), which is the strength of relationship between the item response and person ability, as shown by the slope of the item characteristic curve at the item difficulty (b_i) location. Gaff has low item discrimination (a = 0.17), as indicated by its shallow slope across ability. This means relative to the steeper slope of illumination (a = 3.42), the probability of a correct response to gaff does not increase as rapidly across person ability. Highly discriminating items like illumination are valuable, in that they provide greater information about person ability, but only at their corresponding level of difficulty. Thus, fence will be informative for persons of low ability (≈ −1.96), illumination will be informative for persons of average to high ability (≈ 0.75), but gaff will be less informative than the other items (but will be most informative for ability ≈ 0.57).

Figure 1.

Item Characteristic Curves for 3 PPVT Items.

Because they include separate item and person parameters, IRT models offer important advantages for obtaining comparable measurement using different test forms across samples or occasions. Rather than assuming that all items are interchangeable, differences between items (i.e., in their difficulty and discrimination) are explicitly considered. Likewise, the IRT model estimates the most likely latent ability given the pattern of item responses, rather than indexing ability by the number of correct items. Such raw scores offer limited comparability across forms because they are inherently tied to the specific items given and to the specific sample in which the items were administered. In contrast, given a one-time linking of items from different test forms onto the same latent metric, the resulting IRT ability estimates can then be compared directly because they do not depend on the specific items, forms, or persons used. This advantage is particularly relevant in calibrating the items from different forms of the PPVT given the aforementioned controversy regarding the differences in the norming samples used across PPVT forms – such differences become moot in IRT modeling, in which any differences in the ability of the persons in the sample and difficulty in the items are explicitly taken into account.

Further, rather than making an unreasonable assumption of equivalent precision of measurement at all levels of ability (as is assumed when using raw scores), precision of measurement in IRT (known as test information) differs explicitly across the range of ability based on the discrimination and number of items corresponding to each level of ability. Thus, a test can be strategically modified to maintain optimal sensitivity of measurement across samples with different levels of ability or across time, such as by employing more difficult items at later occasions in order to “grow” the ability range over which a test can measure reliably (a strategy employed explicitly in the current administration of the PPVT).

We now describe the IRT model estimation and results for the concurrent analysis of the 459 unique items from the PPVT-Rm, PPVT-3a, and PPVT-3b in our longitudinal sample.

Model Estimation

The item difficulty and discrimination parameters for the 459 PPVT items were obtained simultaneously via a Markov Chain Monte Carlo (MCMC) estimation algorithm, as implemented by the program IRTMCMC, available in the electronic appendix online. MCMC estimation was chosen because of its ability to provide detailed information about each estimated parameter, which was especially important given the differing number of responses across items. Mirroring estimation in the IRT program BILOG (Mislevy & Bock, 1983) and the algorithm by Patz and Junker (1999), we specified prior distributions as follows: standard normal distribution for item difficulty (M = 0, VAR = 1), log-normal distribution for item discrimination (M = 0, VAR = 0.5), and standard normal distribution for person ability (M = 0, VAR = 0.5). Following Patz and Junker (1999), ability estimates were generated after the item parameters were calibrated by fixing the item parameters to their estimated values. The item calibration used a single chain with a burn-in phase of 3,000 iterations. Following the burn-in phase, a sample of 400 draws, spaced 5 iterations apart, was used to generate estimates of the item parameters. Convergence was judged by an additional 4 chains of the same length, allowing for the use of the Gelman and Rubin (1992) diagnostic statistic (R) given in the CODA library (Plummer, Best, Cowles, & Vines, 2009) in R (2009). Convergence for the item parameters was indicated by R being close to 1.0 (the optimal value). The largest R for item difficulty was 1.13 and the largest R for item discrimination was 1.18. The average autocorrelation of the MCMC at lag 20 was near 0, indicating convergence was achieved.

Item discrimination (a_i) varied across items, as indicated by the preferred fit of the 2-parameter logistic model (with a_i and b_i per item) over the 1-parameter (or Rasch) logistic model (with b_i per item but a common a across items). Given our use of MCMC to estimate the IRT model parameters, the comparison of the 2-parameter model to the 1-parameter model was conducted using the deviance information criterion (or DIC; Spiegelhalter, Best, Carlin, & Van der Linde, 2002; ΔDIC =3,635,427.4), a standard index used for comparing Bayesian models in which smaller values indicate a better model. Estimation of a 3-parameter logistic model (with a_i, b_i, and c_i per item) resulted in severe convergence problems for the c_i lower asymptote parameters (that reflect the lowest possible probability of a correct response). This is most likely because of the administration procedure of the PPVT. That is, because of the influence of person ability on which items get administered, most items will generally not be administered to persons of lower ability. Thus, for many items there was little to no information at the lower end of the ability spectrum that would be needed to determine its lower asymptote. Accordingly, the 2-parameter logistic model was used as the final model.

Finally, although the data were longitudinal, the IRT model treated cases as independent. Although problematic in other contexts, the dependency from sampling multiple occasions from the same person is not problematic here given that dependency generally affects the standard errors of model estimates, but not the model estimates themselves. Thus, the longitudinal dependency will not impact the item parameter estimates needed to generate person ability estimates (c.f., Mislevy & Chang, 2000). When using person ability estimates in subsequent analyses, however, any dependency in estimates from the same person should be modeled (e.g., as can be done via mixed effects growth models).

Item Parameter Estimates and Test Information

Table 1 lists the item difficulty (b_i) and item discrimination (a_i) estimates and their standard errors (SE) for each test form (PPVT 3a, PPVT-Rm, and PPVT-3b). The range of the item difficulty estimates (b_i) indicates that the items can measure up to approximately ±3 SD around the mean, although the PPVT-Rm has slightly easier items, whereas the PPVT-3a has more difficult items. The range of the item discrimination estimates (a_i) indicates variability in the strength of the relationship between the item response and vocabulary ability across items. The range of item discrimination estimates is fairly constant across test forms, although the PPVT-3a items have lower minimum and maximum item discrimination values.

Table 1.

Item Parameter Estimates and Standard Errors across PPVT Test Forms

Item Parameter	Mean	SD	Minimum	Maximum
Difficulty (b) Estimate
PPVT-3a (204 items)	−0.32	1.35	−2.97	3.65
PPVT-Rm (175 items)	−0.28	1.37	−3.09	3.03
PPVT-3b (204 items)	−0.38	1.34	−2.78	3.03
Difficulty (b) Standard Error
PPVT-3a (204 items)	0.08	0.07	0.02	0.37
PPVT-Rm (175 items)	0.09	0.08	0.02	0.46
PPVT-3b (204 items)	0.13	0.09	0.02	0.46
Discrimination (a) Estimate
PPVT-3a (204 items)	1.52	0.65	0.17	3.39
PPVT-Rm (175 items)	1.67	0.64	0.45	3.58
PPVT-3b (204 items)	1.53	0.60	0.39	3.54
Discrimination (a) Standard Error
PPVT-3a (204 items)	0.18	0.10	0.04	0.59
PPVT-Rm (175 items)	0.22	0.09	0.08	0.44
PPVT-3b (204 items)	0.27	0.14	0.08	0.93

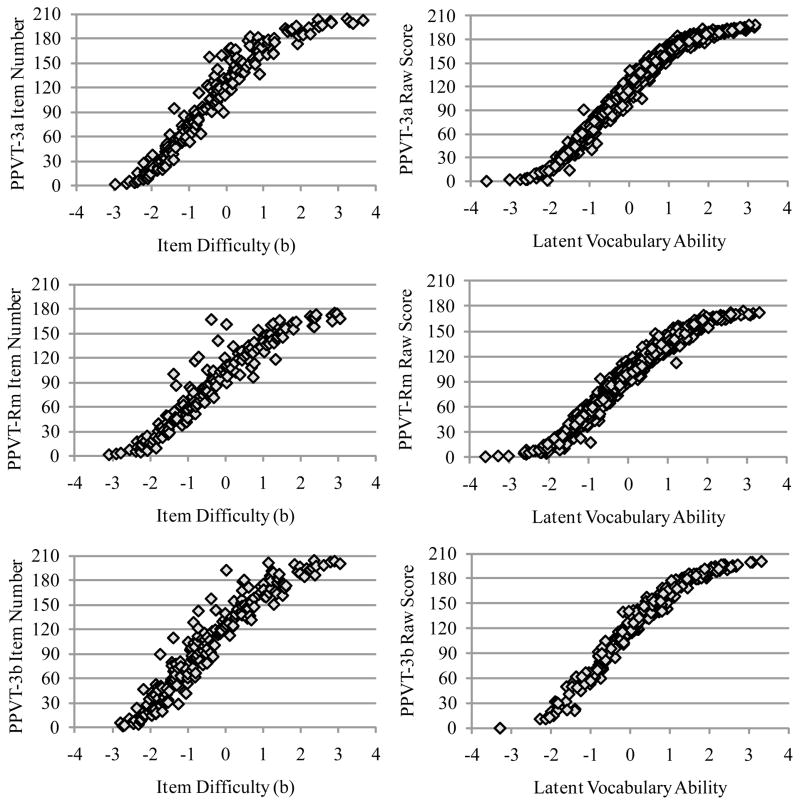
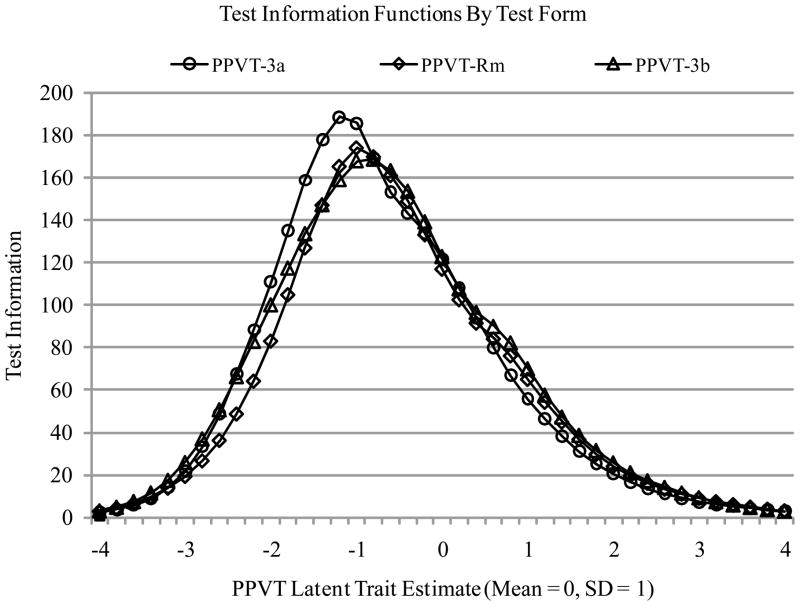
The left side of Figure 2 plots the PPVT item numbers (on the y-axes) against their item difficulty values (on the x-axis). As expected given that the PPVT items ascend in difficulty, there is a strong positive relationship between item number and item difficulty in each form, although there appears to be more dispersion in the item difficulty values for the highest items. Further, as stated earlier, in IRT the reliability of measurement is not assumed constant, but instead varies across ability as a function of the number of and discrimination of items that are targeted to each level of ability. Accordingly, Figure 3 shows the precision of measurement achieved across ability levels via test information functions, as calculated from the estimated item parameters (see Embretson & Reise, 2000). Test information can be converted to reliability as (information/[information + 1]), such that a test information value of 9 corresponds to 90% reliability. Given this conversion of information to reliability, Figure 3 shows the PPVT-Rm and PPVT-3b achieve 90% reliability for persons between −3.4 and 3.0 SD of ability, whereas the PPVT-3a achieves 90% reliability for persons between −3.4 and 2.8 SD of ability. Thus, the test forms are comparable in how precisely they measure vocabulary across the range of ability.

Figure 2.

PPVT Test Form Item Numbers by Item Difficulty (left) and PPVT Raw Scores by Latent Ability Estimates (right).

Figure 3.

Test Information Functions across PPVT Test Forms (in which information > 9 indicates reliability > .90).

Comparability of Item Sets in the PPVT-3 Forms

The PPVT-3a and PPVT-3b were created as parallel forms with identical administration procedures (e.g., 17 sets of 12 items in ascending difficulty) and no common items. Although Table 1 suggests that the forms are largely comparable in difficulty and discrimination overall, given that the items are administered in 17 fixed item sets, we also evaluated their comparability across these item sets by calculating the mean and standard deviation (SD) for item difficulty (b) and item discrimination (a) within each of the 12-item sets, as shown in Table 2.

Table 2.

PPVT Item Difficulty and Discrimination by Item Set for PPVT-3a and PPVT-3b

Item Set	Difficulty (b)				Discrimination (a)
	Mean		SD		Mean		SD
	3a	3b	3a	3b	3a	3b	3a	3b
1	−2.35	−2.44	0.28	0.20	1.63	1.48	0.36	0.33
2	−1.94	−1.96	0.23	0.18	1.80	1.57	0.37	0.21
3	−1.75	−1.71	0.23	0.25	1.98	1.73	0.38	0.47
4	−1.57	−1.67	0.16	0.34	1.92	1.77	0.53	0.74
5	−1.25	−1.39	0.16	0.29	2.20	1.84	0.64	0.47
6	−1.04	−1.10	0.21	0.21	2.08	1.80	0.79	0.53
7	−0.88	−0.97	0.12	0.32	1.91	1.93	0.66	0.84
8	−0.69	−0.75	0.37	0.37	1.46	1.62	0.54	0.31
9	−0.34	−0.63	0.10	0.23	1.70	1.73	0.49	0.70
10	−0.25	−0.37	0.22	0.39	1.58	1.70	0.52	0.66
11	−0.03	−0.03	0.25	0.40	1.53	1.57	0.47	0.59
12	0.21	0.21	0.31	0.38	1.33	1.37	0.41	0.40
13	0.46	0.60	0.22	0.26	1.38	1.55	0.41	0.47
14	0.52	0.92	0.57	0.50	0.98	1.38	0.46	0.70
15	1.07	1.12	0.35	0.42	1.12	1.13	0.42	0.56
16	1.67	1.45	0.48	0.60	0.68	1.00	0.31	0.35
17	2.76	2.31	0.53	0.52	0.60	0.78	0.25	0.21

First, the mean item difficulty was monotonically increasing across item sets for each test as expected. The difference between forms in the within-set mean item difficulty was 0.06 (SD = 0.18), ranging from −0.40 to 0.45, with the largest differences between forms in item sets 9, 16, 17 (in which PPVT-3a was more difficult), and 14 (in which PPVT-3b was more difficult). The difference between forms in the within-set SD for item difficulty was −0.06 (SD = 0.09), ranging from −0.19 to 0.08, with the largest differences between forms in item sets 4, 7, 10, and 11 (in which PPVT-3b showed more variability in difficulty). Second, the difference between forms in the within-set mean item discrimination was −0.002 (SD = 0.21), ranging from −0.40 to 0.36, with the largest differences between forms in item sets 14 and 16 (in which PPVT-3b was more discriminating), and 2, 3, 5, and 6 (in which PPVT-3a was more discriminating). Finally, the difference between forms in the within-set SD for item discrimination was −0.03 (SD = 0.16), ranging from −0.24 to 0.26, with the largest differences between forms in item sets 4, 7, 9, 14 (in which PPVT-3b showed more variability in discrimination), and 6 and 8 (in which PPVT-3a showed more variability in discrimination). This examination reiterates one of the benefits of an IRT analysis – because responses to each item are modeled rather than the sum across items, any differences in item difficulty and discrimination across test forms (such as those found within the PPVT-3 item sets here) can be taken into account explicitly in the model, avoiding potential biases in person ability estimates that could result from an invalid assumption of parallel forms.

Person Ability Estimates

So far we have focused on the item difficulty and discrimination parameters, but the IRT model also provides estimates of the most likely vocabulary ability for each person at each occasion. These IRT ability estimates ranged from −3.61 to 3.32 (M = 0.06, SD = 1.01) and were symmetric around 0 as expected. As shown on the right side of Figure 2, the IRT ability estimates and their corresponding PPVT raw scores were strongly related, with r = .97 or greater for each test form. However, the raw scores appeared somewhat compressed at the extremes of the scale, such that the IRT ability estimates continued to distinguish among persons at extreme ability levels (who were near the floor or ceiling of the raw scores). In addition, the IRT ability estimates were correlated r = 0 .78 with age of assessment, whereas the correlations of age with each raw score were slightly smaller (PPVT-3a: r = .71, PPVT-Rm: r = .74, PPVT-3b: r = .72).

Finally, because we wish for others to benefit from our IRT modeling of the PPVT forms, we have provided a freely available SAS program in the electronic appendix online. This SAS program uses PROC MCMC and the item parameters from the 2-parameter logistic model to create estimates of vocabulary ability on a common IRT latent metric given responses to any items from one or more of the PPVT-Rm, PPVT-3a, or PPVT3b test forms. The IRT ability estimates and their standard errors are then saved for use in further analyses in place of the form-dependent raw scores. These IRT ability estimates can then be used to make comparisons across persons or time (e.g., growth curve analyses) regardless of which form the person received, and thus will be a more robust representation of ability than will a form-dependent raw score. Because the item parameters have already been estimated, even researchers with small samples can utilize this resource to obtain form-independent IRT ability estimates from the PPVT.

Discussion

The present study illustrated how comparable measurement of vocabulary ability across PPVT test forms can be obtained through item response theory (IRT) modeling. IRT models predict the probability of a correct response from each person to each item as a function of the characteristics of the item and of the ability of the person being measured. In this study, a longitudinal sample ranging from early childhood to adulthood was used to concurrently model responses to the PPVT-Rm, PPVT-3a, and PPVT-3b forms (linked via common items and persons), creating a common latent continuum of ability by which valid comparisons of ability can then be made, even when obtained using different forms across samples or over time.

The same cannot be said for raw scores from different forms, in which different total numbers of items (e.g., 175 items in the PPVT-Rm versus 204 items in the PPVT-3a/b) will render raw scores incomparable. Although the PPVT-3 manual includes a table for converting raw scores from the PPVT-R to the PPVT-3, this conversion was based on a 1-parameter logistic model that assumes all items are equally discriminating. Given this assumption that did not hold in the present work (in which a 2-parameter model that allows differences in discrimination across items fit better), this conversion table will provide a coarser translation of ability across forms than will the present IRT calibration (and author-provided program for ability scores).

But even comparison of raw scores from test forms with the same number of items could still be problematic, in that differences between forms in the difficulty of the individual items or item sets could lead to artificial differences in the raw scores between forms. For instance, in the current study (as reported in Table 2), for two persons of equal ability, a person who receives item set 9 from the PPVT-3b (rather than the PPVT-3a) is likely to have more correct answers (and thus a higher raw score) because item set 9 is systematically easier (with greater variability in easiness) in the PPVT-3b than in the PPVT-3a. Even if comparable item difficulty is obtained overall (e.g., as shown in Table 1), differences in difficulty at the item level or item set level are inevitable. Such non-parallel items are problematic when ability is indexed using raw scores, but not when ability scores are obtained from psychometric models (e.g., IRT or CFA models) that explicitly account for such differences between items. This is especially relevant given the systematic differences between the norming samples for the PPVT-3 and the PPVT-R – by modeling the item response as the unit of analysis rather than raw or standard summary scores, such norming differences become moot.

An IRT ability scoring approach also encourages the strategic use of alternate forms. That is, because the respondents may remember the words administered, using the same items over time may bias ability estimates. Using alternate forms of comparable difficulty can be very useful in reducing such retest effects – but an IRT scoring approach allows one to maintain such benefits while avoiding the detriments associated with not exactly parallel forms. Further, given prior knowledge of the difficulty and discrimination of each possible item, efficiency and precision of measurement can be optimized by administering targeted items whose difficulty is most appropriate for the ability to be measured. This idea is already implemented in the PPVT, in which different starting items are recommended based on age. However, the calculation of PPVT raw scores assumes that all items below the starting item would be correct (and that all items above the ceiling item would be incorrect), whereas these untested assumptions are unnecessary for obtaining ability estimates via IRT modeling, yet another benefit of this approach.

Although IRT modeling is a flexible and powerful means by which valid comparisons of vocabulary ability obtained from different PPVT test forms can be made, it is important to recognize our assumptions in doing so. First, we have assumed that a single ability underlies the responses to all PPVT items. Although a multidimensional IRT model could have been used if multiple abilities were postulated instead, we had no reason to pursue this in the current study given considerable existing research with the PPVT as a measure of a single vocabulary ability. Second, although differences in vocabulary ability are part of the IRT model, the item characteristics (e.g., difficulty and discrimination) that relate each item response to vocabulary ability are assumed to be invariant across all persons and ages. Unfortunately, this assumption of equivalent item functioning is not testable given the administration of the PPVT, in which only items appropriate for a respondent’s age or level of ability are given (resulting in little overlap of item responses for persons of different ages or ability). However, it is important to acknowledge that this assumption of invariant measurement is always invoked in any research study using PPVT raw or standard scores, and thus is not unique to our IRT modeling.

Finally, given the existence of two new PPVT-4 forms, an important next step will be to pursue concurrent IRT modeling of the items from the PPVT-R, PPVT-3, and PPVT-4 forms simultaneously using additional linking data from the PPVT-4. Given that only 25% of the 228 items on each of the two PPVT-4 forms are unique (with the remaining 75% already in the PPVT-3 forms), the items in common could be used to link responses to the PPVT-4 to those from the other forms. Additional linking could be achieved by administering the PPVT-3 and PPVT-4 to persons at the same occasion (i.e., as we had done with the PPVT-Rm and PPVT-3 forms here). In either case, though, a wide range of ages (i.e., a sample of young children through adults, as in the current study) would be needed in order to obtain sufficient responses to all items, given that PPVT items are administered selectively to persons based on age and ability.

In conclusion, the use of multiple test forms can create problems in comparing the resulting indices of ability across different samples or over time. Many of these problems can be resolved through the use of psychometric models (such as IRT) that provide a common latent metric by which such comparisons can be made. We hope this application of IRT modeling of existing PPVT data (and the IRT scoring program we have provided) will not only be useful to others who wish to examine differences in vocabulary ability between persons or over time, but that it illustrates the potential of these methods for other tests with multiple forms as well.