High Efficiency Electrodes for Deep Brain Stimulation

Abstract

Deep brain stimulators are powered with primary cell batteries and require surgical replacement when they are depleted. We sought to decrease power consumption, and thereby increase device lifetime by increasing neuronal stimulating efficiency with novel electrode designs. Our hypothesis was that high-perimeter electrodes that increase the variation of current density on their surface will generate larger activating functions for surrounding neurons, hence increasing stimulation efficiency. We implemented finite element models of cylindrical DBS electrodes with conventional circular perimeters, with serpentine perimeters, and with segmented contacts. The high-perimeter electrodes significantly increased the variation of current density on the electrode surface. We randomly positioned a population of 100 model axons around the electrodes and quantified neural activation with 100 μs cathodic stimuli. Input-output curves of percentage axons activated as a function of stimulation intensity indicated that the novel electrode geometries decreased power consumption by up to ~20% for axons parallel to the electrode and up to ~35% for axons perpendicular to the electrode. Reduced power consumption achieved with these designs will reduce the costs and risks associated with surgeries to replace depleted stimulators.

I. Introduction

Deep brain stimulation (DBS) is an FDA-approved, clinically effective treatment for symptoms of essential tremor, Parkinson’s disease and dystonia, and shows promise in the treatment of other disorders including epilepsy, obsessive-compulsive disorder, and depression. Deep brain stimulators are powered with primary cell batteries and require surgical replacement when they are depleted. The median life span of the implant is approximately 4 years [1, 2] and in applications requiring high charge injection implants may last less than 1 year [3]. Surgical replacement is expensive and carries substantial risk. For example, the complication rate is three times higher for replacement of cardiac pacemakers than for original device placement [4], and replacement of implanted defibrillators has an 8.1% complication rate [5]. We sought to reduce power consumption and thus increase implant lifetimes by alterations in the electrode geometry.

The proposed approach to increase the efficiency of neural excitation by alterations in the electrode geometry is based on the fundamentals of extracellular neural stimulation. Neural excitation by extracellular sources can be qualitatively predicted with the activating function (ƒ), which is proportional to the second spatial derivative of the extracellular potential (V_e) (i.e., the activating function, ƒ_x ∝ Δ²V_e/Δx2) [6]. Our design ideas were motivated by geometries that generate higher activating function in the tissue than conventional DBS electrodes. Rewriting the activating function in terms of the current density J indicates that the activating function is proportional to the spatial derivative of current density in the tissue, ΔJ_x/Δx. Therefore, our hypothesis was that electrode geometries that increase the variation of current density over the electrode surface would generate larger activating function for surrounding neurons, thereby decreasing thresholds and increasing neuronal stimulating efficiency. The objective of this project was to design novel high-perimeter cylindrical electrode intended to increase the efficiency of deep brain stimulation.

Based on our previous work, which demonstrated that increasing electrode perimeter by segmenting increased the magnitude of the activating function [7], we designed prototype cylindrical electrodes with high-perimeters achieved by using a serpentine edge and segmentation. Electrical finite element models were combined with cable models of a population of neurons to test the hypothesis that increasing the electrode perimeter increases stimulation efficiency. The results show that by proper selection of geometrical parameters the high-perimeter electrodes will decrease power consumption by up to ~20% for parallel axons and ~35% for perpendicular axons at DBS-relevant fiber diameters and distances.

II. Methods

We used computational models to quantify the efficiency of neural excitation of prototype high-perimeter cylindrical electrodes. The potentials generated in a modeled tissue medium were calculated using the finite element method. The potentials were coupled to a population of model myelinated nerve fibers to calculate input-output curves of the proportion of nerve fibers activated as a function of the stimulation voltage and stimulation power.

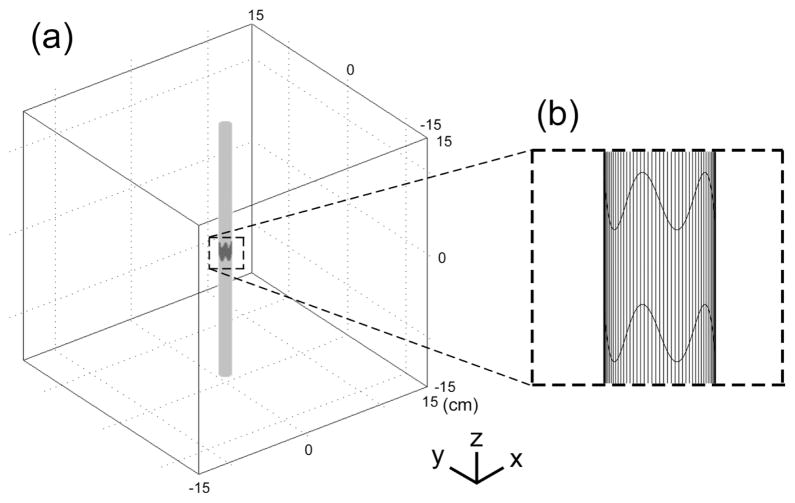
Three dimensional finite element models of cylindrical electrodes positioned in a homogenous isotropic tissue medium were implemented in COMSOL Multiphysics (Figure 1). The model included an electrode surface with a potential of 1 V, surfaces of the insulating shafts on both sides of the electrode, and a homogenous volume conductor representative of CNS tissue (σ = 0.2 S/m [8]). The tissue medium was modeled as a box with a side length of 30 cm and all the outer boundaries set to ground (V = 0). The 3D models were partitioned into 398,232 to 1,722,879 tetrahedral elements. The conjugate gradient method with preconditioning (incomplete Cholesky factorization) was used to solve the models. The total current delivered by the electrode at 1 V was calculated by integrating of the current density along the electrode surface. The sizes of the tissue volume and element mesh were set such that doubling the volume of the tissue or reducing the mesh size resulted in <3% change in the total current delivered by the electrode. The simulations calculated the distributions of current density and of potentials (V_e) in the modeled region for each electrode configuration.

Figure 1.

Geometry of the finite element model of a cylindrical electrode positioned in a homogenous isotropic volume of modeled tissue, with the boundary conditions of 1 V on the electrode, and 0 V at the outer boundary. The tissue medium was modeled as a 30cm-by-30cm box with a conductivity of 0.2 S/m.

Populations of 100 myelinated nerve fibers were randomly positioned within a 6mm × 6mm × 6mm box surrounding the electrode, and were oriented either parallel or perpendicular to the cylindrical electrode. The model nerve fibers had mammalian membrane dynamics [9] and were 4 μm in diameter. The models were implemented in NEURON version 6.1 [10] and solved using backward Euler implicit integration with a time step of 0.001 ms. The threshold voltages were calculated with binary search algorithm with a tolerance of 1 μV. The extracellular potential at each node of Ranvier was determined by spline interpolation from the potentials solved by the finite element models. Input-output (recruitment) curves of percentage of activated nerve fibers as a function of the stimulation voltage were generated by applying a monophasic cathodic voltage pulse with pulse width of 100 μs to the electrode. Input-output curves of the percentage of activated axons as a function of the stimulation power were also generated by multiplying the threshold voltage by the delivered current at the threshold voltage.

III. Results

We used finite element models to calculate current density distribution on the surface of serpentine- and circular-perimeter cylindrical electrodes, as well as the potentials generated in a modeled tissue volume around the electrodes. Subsequently, we used populations of model myelinated nerve fibers to calculate input-output curves of nerve fiber activation as a function of stimulation magnitude and stimulation power. We compared a conventional circular-perimeter electrode (electrode #1), an electrode with a serpentine perimeter (electrode #5), and a segmented electrode with a serpentine perimeter (electrode #6).

A. Distributions of Current Density

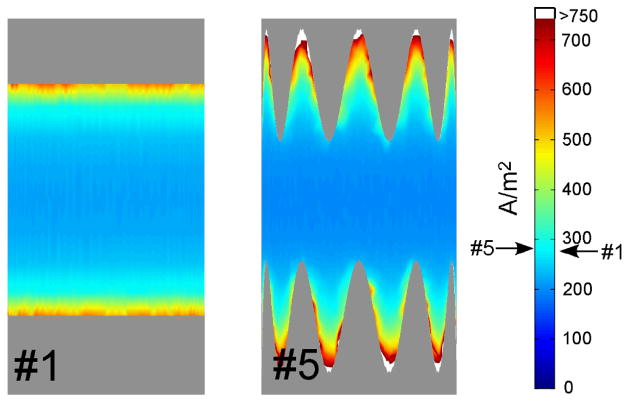
The current density distributions on the surface of electrodes #1 and #5 when a constant voltage of 1V was applied are shown in Figure 2. The current density increased towards the perimeter of the electrodes. The current density was uniform along the circular perimeter, while the current density was highly non-uniform along the serpentine perimeter, and was highest at the crests and lowest in the troughs of the sinusoid. These results supported with hypothesis that the serpentine perimeter would increase the spatial variation of the current density, and thereby the magnitude of the activating function.

Figure 2.

Distributions of current density on the surface of electrodes #1 and #5. The arrows on scale indicate the average current densities.

B. Input-Output Curves of Neural Activation and Power Efficiency

We quantified activation of a population of 4 μm diameter model myelinated fibers randomly positioned within ~2.5 mm of the electrode. This diameter is representative of axons in the CNS, for example axons in the STN (subthalamic nucleus) have diameters of 1–2 μm, and axons in the internal capsule have diameters of 4–6 μm [11]. The spatial extent of activation in thalamic deep brain stimulation was predicted to have a radius of 2.0–3.9 mm for stimulation amplitudes of 1–3.5 V [12].

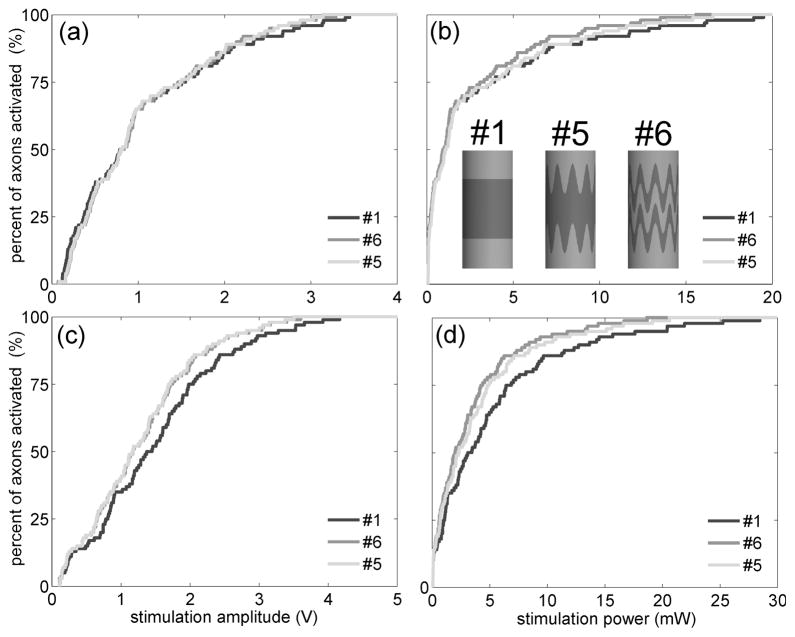
With 100 axons positioned parallel to the electrode, the average threshold voltage with the serpentine-perimeter electrode (#5) was 2.2% lower (Figure 3a) and the average power consumption was 7.7% lower (Figure 3b) than with the circular-perimeter electrode (#1). The serpentine-perimeter electrode generated a larger maximum activating function than the circular-perimeter electrode in only 34 out of 100 axons. The input-output curves as a function of stimulus voltage for the two electrodes crossed at approximately 60% activation, indicating that the serpentine-perimeter electrode recruited the last (farther) ~40 axons at lower thresholds than the circular-perimeter electrode, but not the first (closer) ~60 axons.

Figure 3.

Input-output curves of the percentage of activated axons as a function of the stimulation amplitude and stimulation power for electrodes #1, #5 and #6. (a)(b) Percent of axons activated as a function of stimulation voltage (a) and stimulation power (b) when 100 axons were positioned parallel to the electrode. (c)(d) Percent of axons activated as a function of stimulation voltage (c) and stimulation power (d) when 100 axons were positioned perpendicular to the electrode.

With 100 axons positioned perpendicular to the electrode, the serpentine-perimeter electrode (#5) decreased the average threshold voltage by 15% (Figure 3c) and decreased the average power consumption by 26% (Figure 3d), as compared to the circular-perimeter electrode (#1). The serpentine-perimeter electrode generated a larger maximum activating function than the circular-perimeter electrode in 88 out of 100 axons. The input-output curves as a function of stimulus voltage for the two electrodes crossed at 7% activation, indicating that the serpentine-perimeter electrode recruited the last (farther) ~93 axons at lower thresholds than the circular-perimeter electrode, but not the first (closer) ~7 axons.

The serpentine perimeter increased stimulation efficiency, and our previous results suggested that segmentation may also increase stimulation efficiency [7]. We designed an electrode (#6) that combined segmentation and a serpentine perimeter. Electrode #6 required smaller average threshold voltage to activate fibers in either orientation (Figure 3a,c). Electrode #6 was also highly efficient in activating both parallel fibers (power decreased by 20%) and perpendicular fibers (power decreased by 35%) (Figure 3b,d).

IV. Discussion

Deep brain stimulators are powered with primary cell batteries with a medium lifetime of less than 4 years. When the batteries are depleted, the stimulator must be replaced, and surgical replacement is expensive and carries significant risk. The objective of this study was to increase stimulation efficiency through design of novel high-perimeter designs. Increases in stimulation efficiency will reduce the power requirements of implantable neural stimulators, thereby increasing device lifetime and reducing the risks and costs of stimulator replacement.

We constructed 3D finite element models DBS electrodes with conventional circular perimeters, with serpentine perimeters, and with segmented contacts. The potentials calculated with the FEM models were coupled with cable models of myelinated nerve fibers to calculate neuronal stimulation thresholds. Input-output curves of activation of a population of randomly distributed nerve fibers with electrodes of different geometries were compared to quantify stimulation efficiency. Stimulating efficiency was increased with the novel high-perimeter electrode designs. The effects of increasing electrode perimeter on stimulating efficiency were dependent not only on the electrode geometry, but also on the orientation of the fibers and the distance of the fibers from the electrode. Thus, novel electrode geometries provide a means to reduce power consumption by implantable pulse generators, and may provide a means to enhance the threshold differences between differently oriented fibers (i.e., selectivity).

The relative efficiency of stimulation with different electrode designs was dependent on the orientation of the fibers and the distance of the fibers from the electrode. For axons parallel to the electrode, the input-output curve generated by the serpentine-perimeter electrodes often crossed with the input-output curve generated by the circular-perimeter electrode, indicating that the circular-perimeter electrode activated axons close to the electrode at lower thresholds while serpentine-perimeter electrodes activated mode distant axons at lower thresholds. When the curves crossed at small percentages of activation, the serpentine-perimeter electrodes significantly increased the stimulating efficiency of parallel axons. On the other hand, for axons perpendicular to the electrode, the input-output curves generated by serpentine-perimeter electrodes were always to the left of the input-output curves generated by the circular-perimeter electrode, indicating that the serpentine-perimeter electrodes activated perpendicular axons with lower thresholds regardless of the distance of the fibers to the electrode.

Because the effects of increasing electrode perimeter on stimulating efficiency were dependent on the fiber orientation relative to the axis of the electrode, it is important to consider the orientation of the fibers targeted during deep brain stimulation. Both subthalamic nucleus (STN) projection neurons and globus pallidus internus (GPi) fibers of passage represent possible therapeutic targets of DBS in the treatment of Parkinson’s disease [13,14]. Internal capsule (IC) fibers of passage also pass in close proximity to STN DBS electrode, and are often related to the side effects of DBS. Axonal tracing experiments [15] have revealed that STN projection neurons course either dorsally along the ventral border of the thalamus or ventrally along the lateral border of the STN on their way to the globus pallidus, which results in a more perpendicular orientation to the electrode. The direction of GPi fibers turns to run along the border of the STN [14,16,17], thus GPi fibers have portions both parallel and perpendicular to the electrode. The IC fibers define the lateral border of the STN and course ventrally approximately parallel to the electrode [16]. Therefore, to account for this anatomical variability of fiber orientations and the therapeutic or side effects caused by stimulating different fiber groups, it seems more desirable that our novel electrode designs increase stimulating efficiency of perpendicular axons than that of parallel axons. Indeed, our model study indicated a consistent increase of stimulation efficiency of perpendicular axons across various serpentine electrode geometries.

Finite element models of electrodes and the surrounding volume conductor were coupled with compartmental cable models of a population of neurons to study the effects of increasing the perimeter of the DBS electrode on stimulation efficiency. The electrical potentials were calculated using the FEM based on the assumption that the tissue medium was homogenous and isotropic. Although the true biological volume conductor is inhomogeneous and anisotropic, a recent study of deep brain stimulation indicated that a homogenous isotropic model provided predictions of voltage distributions remarkably similar to a more detailed inhomogenous and anisotropic model for the expected region of stimulation around the electrode [18]. Further, the current study did not focus on the absolute stimulation efficiency of an electrode, but rather the comparative stimulation efficiency between electrodes with various geometries. The population of model neurons did not include cell bodies, dendrites, or synaptic inputs. Although both experiment studies [19] and computational models [20] indicate that during extracellular stimulation action potential initiation occurs in the axon, the impact of changes in geometry on the efficiency of activating other neural elements may differ from those for the axons considered here.