Diffusion MRI at 25: Exploring brain tissue structure and function

Abstract

Diffusion MRI (or dMRI) came into existence in the mid-1980s. During the last 25 years, diffusion MRI has been extraordinarily successful (with more than 300,000 entries on Google Scholar for diffusion MRI). Its main clinical domain of application has been neurological disorders, especially for the management of patients with acute stroke. It is also rapidly becoming a standard for white matter disorders, as diffusion tensor imaging (DTI) can reveal abnormalities in white matter fiber structure and provide outstanding maps of brain connectivity. The ability to visualize anatomical connections between different parts of the brain, non-invasively and on an individual basis, has emerged as a major breakthrough for neurosciences. The driving force of dMRI is to monitor microscopic, natural displacements of water molecules that occur in brain tissues as part of the physical diffusion process. Water molecules are thus used as a probe that can reveal microscopic details about tissue architecture, either normal or in a diseased state.

Introduction

The first images of water diffusion in the human brain came to live 25 years ago. Since then important methodological and conceptual developments have been made and diffusion MRI has become a pillar of modern neuroimaging. For the last 20 years diffusion MRI has been used clinically to investigate neurological disorders, especially for the management of patients with acute stroke. But it has also rapidly become a standard for white matter disorders. The idea that white matter organisation and microstructure is important for understanding cognition and disease came to prominence through the work of nineteenth century anatomists such as Meynert and Dejerine. Their careful dissections, and studies of patients after brain damage, helped to shape our current thinking on how connections, and disconnections, influence brain function. The advent of diffusion MRI in the late twentieth century opened up possibilities for studying white matter anatomy and brain connections in living patients and normal subjects. In addition to providing new insights into neuroanatomy, the technique has even greater potential in the understanding of psychiatric or functional disorders in the future.

In this review, we will provide a background to the principles of diffusion MRI and its interpretation, discuss use of diffusion MRI for connectomics, and summarise applications of the method in health and disease. We will highlight current challenges and opportunities for future research.

Diffusion MRI principles

The concept behind diffusion MRI

Molecular diffusion refers to the random translational motion of molecules (also called Brownian motion), which results from the thermal energy carried by these molecules, a physical process which was well characterized by Einstein (Einstein, 1905). In a free medium, during a given time interval, molecular displacements obey a three-dimensional Gaussian distribution: Molecules travel randomly in space over a distance that is statistically well described by a “diffusion coefficient”, D. This coefficient depends only on the size (mass) of the molecules, the temperature and the nature (viscosity) of the medium. On a statistical basis, diffusion is reflected by the mean-squared distance traveled by molecules in a given interval of time: (1)

$$<X^2>=2\mathit{DTd}$$

where < X² > is the average mean-squared diffusion distance along one direction and T_d is the diffusion time. For example, in the case of “free” water molecules diffusing in water at 37 °C, the diffusion coefficient is 3.10⁻³ mm². s⁻¹. This means that about 32% of the molecules have reached at least 17 μm during 50 ms, while only 5% of them have traveled over distances greater than 34 μm. In practice, however, the actual diffusion distance is reduced in biological tissues compared to free water, and the displacement distribution is no longer Gaussian, as water molecules move in tissues bouncing, crossing, contouring or interacting with many tissue components, such as cell membranes, fibers or macromolecules. In other words, while over very short times diffusion mainly reflects the local intrinsic viscosity, at longer diffusion times (such as those used with dMRI) the effects of the obstacles become predominant. Hence, dMRI is deeply rooted in the concept that, during their diffusion-driven displacements, molecules probe tissue structure at a micrometer scale well beyond the usual millimetric image resolution. The non-invasive observation of the water diffusion-driven displacement distributions in vivo thus provides unique clues to the fine structural features and geometric organization of neural tissues, and to changes in those features with physiological or pathological states.

How diffusion MRI images are obtained

Diffusion MRI monitors the diffusion process itself, or in other words, the actual molecular random walks. Currently, it is the only method available to provide such information in vivo noninvasively. Early water diffusion measurements were made in (excised) biological tissues using Nuclear Magnetic Resonance (NMR) in the 1960s and 70s, based on the pioneering works of Carr and Purcell (1954) and Hahn (1950), and, most importantly, Stejskal and Tanner (1965), who introduced a specific diffusion encoding technique using magnetic gradient pulses. But it was not until the mid 1980s that the basic principles of diffusion MRI were laid out. The problem was to mix such pulses with those used in MRI for spatial encoding. While the problem might look trivial, it was not, and there are still many technical outstanding issues (as a matter of fact, many at that time thought diffusion MRI was not even possible). The potential was to localize the diffusion measurements, that is, to obtain maps of the diffusion coefficients in tissues, which had never been done before, especially in vivo.

Although Mansfield (Mansfield and Morris, 1982) suggested that the combination of diffusion magnetic pulse gradients experiments and MRI was theoretically feasible, he did not actually implement it. Some preliminary work was done by Wesbey et al. (1984) to determine whether diffusion had a detectable effect in conventional MRI scans and whether modifying the acquisition parameters could possibly increase the effect. At the same time and independently, several researchers were able to achieve a full-scale implementation of diffusion MRI and generate diffusion maps of inanimate objects (Le Bihan and Breton, 1985, Merboldt et al., 1985 and Taylor and Bushell, 1985). The first dMRI images of the human brain were obtained in 1985 and published thereafter (Le Bihan et al., 1986), along with the key concepts underlying dMRI as we know it today, such as the “Apparent Diffusion Coefficient” or the “b factor” (see below).

Almost any MR imaging sequence can be designed to be sensitive to diffusion by adding magnetic field gradients (the built-in magnetic field gradient pulses in all MRI imaging sequences for spatial encoding are usually way too small to induce significant diffusion effects). Most diffusion MRI studies have been based on the pulsed field gradient (PFG) method. Basically, the role of those field gradient pulses is to label space along one direction and for a finite time interval, and to encode any displacement of hydrogen nuclei carried by water molecules along that direction. Given the large number of water molecules in each image voxel the distribution of the random, diffusion-driven displacements produces a destructive interference effect which results in an attenuation of the MRI signal (Fig. 1). This signal attenuation, A, is precisely and quantitatively linked to the diffusion coefficient, D: (2)

$$A=\exp (-b\mathrm{D})$$

where b is the so-called “b factor” (Le Bihan and Breton, 1985 and Le Bihan et al., 1986): The attenuation obviously first depends on the magnetic field gradient pulses used for diffusion encoding (square of amplitude and time course), as well as the gradient pulses used for MRI spatial encoding. With modern MRI scanners the degree of diffusion-weighting of the images is set by fixing the b factor to a given value (often 1000 s/m², which gives approximately 65% signal attenuation in the brain from water diffusion).

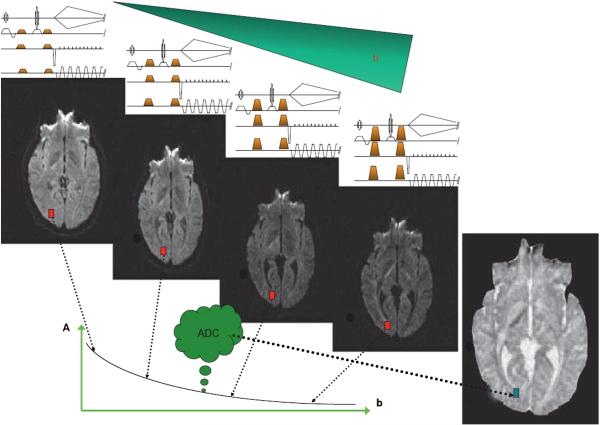
Fig. 1.

Diffusion-weighted and diffusion-calculated (ADC) images. The set of diffusion-weighted images is obtained using different b-values, by changing the intensity of the diffusion gradient pulses (gold trapezoids) in the MRI sequence. In diffusion-weighted images, the overall signal intensity in each voxel decreases with the b-value. Tissues with high diffusion (such as ventricles) get darker more rapidly when the b-value is increased and become black. Tissues with low diffusion remain with a higher signal. As diffusion-weighted images also contain T₁ and T₂ contrast, one may want to calculate pure diffusion (or ADC) images. To do so, the variation of the signal intensity, A(x, y, z), of each voxel (red boxes) with the b-value is fitted using Eq. (3) to estimate the ADC for each voxel (green box). In the resulting image, the contrast is inverted: bright corresponds to fast diffusion and dark to low diffusion.

To save on acquisition and processing time, some investigators, often clinicians, limit their diffusion studies to the analysis of such “diffusion-weighted” images. One must be aware, however, that their content is affected by many other parameters than diffusion, mainly the basic MRI relaxation times T₁ and T₂. As these parameters may not have the same behavior as diffusion during different physiological or pathological conditions, variations in image intensity may be difficult to interpret (Burdette et al., 1999). While diffusion-weighted images may be convenient to use in clinical practice, whenever possible, quantitative diffusion images are preferred. In theory, it is possible to get rid of T₁ and T₂ contrast and obtain pure maps of the diffusion coefficient by acquiring two images with different b-values, b and b₀, and reversing Eq. (2) on a voxel-by-voxel basis: (3)

$$\mathit{Dx},y,z=\mathit{ln}[\mathit{Ax},y,z(\mathit{bo})∕\mathit{Ax},y,z(b\left)\right]∕(b-b_0).$$

On these “calculated diffusion maps”, diffusion values are displayed using quantitative grayscale, where brightness corresponds to high, fast diffusion and darkness to low, slow diffusion. Color-coded images have also been proposed.

Pitfalls and limitations

Although the first diffusion images of the brain were obtained in the mid 1980s (Le Bihan et al., 1986), it was not until the mid 1990s that diffusion MRI really took off. Initially, the specifications of the clinical MRI scanners made it difficult to obtain reliable diffusion images, as acquisition times were long (10 to 20 min) and the presence of the large gradient pulses required for diffusion also made the images very sensitive to macroscopic motion artifacts, such as those induced by head motion, breathing or even cardiac related brain pulsation (Anderson and Gore, 1994). Therefore, although diffusion MRI was shown to be potentially useful in the clinic, demonstrative clinical studies started only later, when better MRI scanners, equipped with echo-planar imaging (EPI) became available. Because EPI is a “single-shot” acquisition technique motion artifacts are virtually eliminated (Avram and Crooks, 1988, McKinstry et al., 1990 and Turner et al., 1990). Recently developed “parallel” acquisition techniques, which allow signals to be collected simultaneously using an array of several radiofrequency coils, further reduces residual artifacts, such as geometric distortion due to magnetic inhomogeneities (Bammer et al., 2001 and Bammer et al., 2002).

Another approach is to divide the acquisition in multiple shots (segmented EPI), which decreases the sensitivity to susceptibility artifacts and allow a better spatial resolution to be reached (Porter and Heidemann, 2009). Alternative fast acquisition schemes, such as spiral MRI (Li et al., 2005), and PROPELLER (Pipe, 1999), have been proposed to overcome some specific EPI limitations, or else so-called “steady-state free precession” (SSFP) (Le Bihan, 1988 and Merboldt et al., 1989). Unfortunately, the effects of diffusion and relaxation are intrinsically mingled, so that diffusion measurements are always contaminated to some degree by relaxation effects, which precludes any accurate diffusion measurement (Le Bihan et al., 1989 and Wu and Buxton, 1990). Nonetheless, SSFP may remain a fast way of performing diffusion MRI with high SNR and contrast-to-noise ratio (CNR), with only modest gradient strengths, which makes it appealing for some applications in which accurate quantification is not an issue (McNab and Miller, 2008). Another alternative to reduce the diffusion time is to use of sinusoidal pulses, as was suggested long ago with NMR (Gross and Kosfeld, 1969): Pulses are placed next to each other and have inversed polarities, becoming part of an “oscillating” gradient. The diffusion time is then greatly reduced, determined by the period of the oscillation, and can be potentially very short. Unfortunately, the diffusion sensitivity is also drastically reduced. A remedy is to use a train of oscillating gradients (OGSE). This approach, which requires powerful gradients, has the potential to give clues to the nature of the obstacles of diffusion in tissues (Does et al., 2003).

Indeed, the maximum strength of the gradient hardware available (often below 40 mT/m) on clinical MRI scanner remains an important limitation. Large b values cannot be reached, which is a problem for tissues with very low diffusion. Also, long TEs (which lead to reduced signal intensities) are necessary to allow sufficient diffusion times and sufficient diffusion encoding. Water diffusion displacements then become relatively large, loosely defined, and precise inference of tissue structure (such as cell size or membrane permeability) from diffusion measurements becomes very difficult to realize.

It is important to notice that only the displacement (diffusion) component along the gradient direction is detectable. However, diffusion is truly a three-dimensional process, therefore, water molecular mobility in tissues is not necessarily the same in all directions. This diffusion anisotropy may result from the presence of obstacles that limit molecular movement in some directions more than others. Slight anisotropic diffusion effects were observed in biological tissues very early on, especially in tissues with strongly oriented components, such as excised rat skeletal muscles (Cleveland et al., 1976 and Hansen, 1971). However, it is not until the advent of diffusion MRI that anisotropy was detected for the first time in vivo, at the end of the 1980s, in spinal cord and brain white matter ( Chenevert et al., 1990 and Moseley et al., 1990b). Diffusion anisotropy in white matter grossly originates from its specific organization in bundles of more or less myelinated axonal fibers running in parallel: Diffusion in the direction of the fibers (whatever the species or the fiber type) is about 3–6 times faster than in the perpendicular direction (Fig. 2). Special treatment is required for dMRI in the presence of diffusion anisotropy, but we should first take a closer look at the actual content of dMRI images.

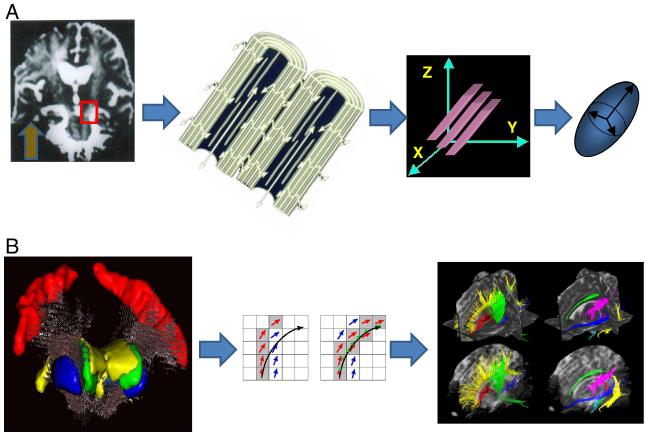
Fig. 2.

Diffusion anisotropy and diffusion tensor imaging. In the presence of anisotropic diffusion the ADC, as in white matter, depends on the measurement direction. A left to right: Measurement direction was vertical (yellow arrow). Vertical tracts (such as pyramidal tract) have high ADC, while horizontal tracts (as in corpus callosum) are dark. This results from the fact that diffusion is reduced perpendicularly to the white matter fibers due the presence of plasma membranes and myelin. With Diffusion Tensor Imaging it becomes possible to characterize diffusion in all 3 dimensions and to determine the direction of fastest diffusion. For each image voxel an ellipsoid can be produced the nature of which is related to key DTI parameters: overall ellipsoid volume and mean diffusivity, the shape (oblong) to the degree of fractional anisotropy and the orientation to the fiber main direction. B left to right: After the ellipsoids have been obtained for all voxels of the image (here for the cortico-spinal tract out of the motor cortex in red) an algorithm is used to determine whether adjacent voxels are likely to be connected (here with the FACT algorithm from Mori et al., 1999). Connected voxels within putative tracts are then displayed using pseudo-colors. It should be noticed that such color tracks are purely the results of a software and do not represent genuine anatomical structures.

Interpretation of diffusion MRI images

The ADC concept: a scaling issue

One has to keep in mind that the overall signal observed in a dMRI images at a millimetric resolution, results from the integration, on a statistical basis, of all the microscopic displacement distributions of the water molecules present in this voxel. As a departure from earlier diffusion studies in biological studies where efforts were made to depict the true diffusion process ( Cooper et al., 1974, Tanner, 1978 and Tanner, 1979), it was suggested (Le Bihan et al., 1986) to portray the complex diffusion processes that occur in a biological tissue on a voxel scale using the microscopic, free diffusion physical model (on which is based Eq. (2)), but replacing the physical diffusion coefficient, D, with a global, statistical parameter, the Apparent Diffusion Coefficient (ADC). The ADC concept has been largely used since then in the literature. This parameterization of the diffusion process by a global ADC is intended to represent those physical processes that occur at scales smaller than the scales resolved by the method: The large scale is imposed by technical limitations (e.g., hardware), while the actual “theater” scale of the biophysical elementary processes is, of course, determined by physical phenomena at molecular scale. Parameterization somewhat allows us to bridge the gap between the two scales. It was used, for instance, by Einstein to indirectly demonstrate the existence of atoms through the identification of diffusion with Brownian motion in the framework of the molecular theory of heat (Einstein, 1956). With most current systems, especially those developed for human applications, the voxel size remains large (a few mm³). The averaging, smoothing effect resulting from this scaling presumes some homogeneity in the voxel and makes a direct physical interpretation out of the global parameter somewhat difficult, unless some assumptions can be made. The ADC now depends not only on the actual diffusion coefficients of the water molecular populations present in the voxel, but also on experimental, technical parameters, such as the voxel size and the diffusion time. The reverse problem consisting in retrieving specific information on tissue microscopic features from ADC measurements is somehow ill-posed and the object of intense research, as outlined below.

Water diffusion in brain tissue is not free

The ADC in the brain is 2 to 10 times smaller than free water diffusion in an aqueous solution (which is 3.10⁻³ mm² . s⁻¹ at 37 °C). Furthermore, many studies have experimentally established that the water diffusion-sensitized MRI signal attenuation in brain tissue (and other tissues as well) as a function of the sensitization (b-value) could not be well described by a single exponential decay, as would have been expected (Eq. (2)) in an unrestricted, homogenous medium (free brownian diffusion) (Niendorf et al., 1996). High viscosity, macromolecular crowding and restriction effects have been proposed to explain the water diffusion reduction in the intracellular space (Hazlewood et al., 1991), and tortuosity effects for water diffusion in the extracellular space ( Chen and Nicholson, 2000 and Nicholson and Philipps, 1981) (Fig. 3). With restricted diffusion, for instance, the displacements of the molecules become limited when they reach the boundaries of close spaces and the ADC goes down with longer diffusion times. However, no clear restriction behavior has been observed in vivo for water in the brain, as the diffusion distance seems to increase well beyond cell dimensions with long diffusion times ( Le Bihan et al., 1993 and Moonen et al., 1991). Furthermore, studies have established long ago that the overall low diffusivity of water in cells could not be well explained by true compartmentation (restriction) effects from cell membranes nor by scattering or obstruction (tortuosity) effects from cellular macromolecules ( Chang et al., 1973, Colsenet et al., 2005 and Rorschach et al., 1973). This strongly suggests that the cellular components responsible for the reduced diffusion coefficient in biological tissues are much smaller than the diffusion length currently used with MRI. Indeed, there is growing evidence that membranes, even if they are permeable, are likely the main actor which “hinders” the water diffusion process (see Le Bihan, 2007 for a review).

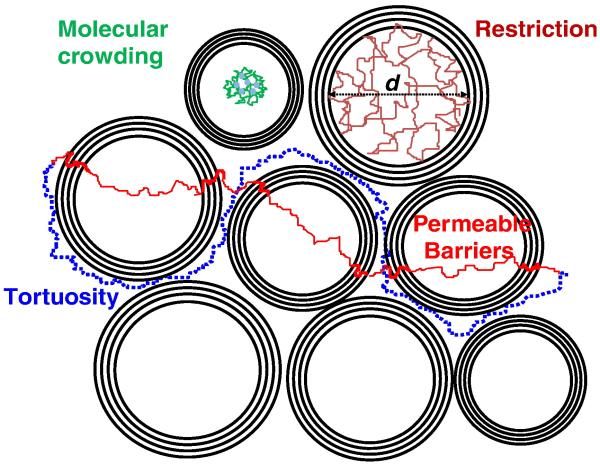
Fig. 3.

Elementary mechanisms of hindered diffusion. For free diffusion, the diffusion distance increases linearly with the square root of the diffusion distance with the diffusion coefficient as a constant slope. In the presence of obstacles, such as cell membranes, diffusion is not free and the diffusion distance increases less with the diffusion time. For diffusion restricted in a space of dimension d, the diffusion distance plateaus at d. For tortuous diffusion or diffusion through permeable barriers, the diffusion distance first increases as for free diffusion for very short diffusion times (usually not reachable with MRI) and stabilizes at a slower rate for long diffusion times. This reduced diffusion coefficient depends on the geometry of the tissue (tortuosity factor) and the membrane permeability constant. Bulk diffusion may also be reduced compared to free water because of the molecular crowding (proteins, macromolecules) within the cellular environment.

Phenomenologically, however, the dMRI signal attenuation as a function of the b-value is often very well fitted, however, with a biexponential function corresponding to two water diffusion pools or phases in slow exchange, with a fast and a slow diffusion coefficient ( Assaf and Cohen, 1998 and Niendorf et al., 1996): (4)

$$A=\mathit{fslowexp}(-\mathit{bDslow})+\mathit{ffastexp}(-\mathit{bDfast})$$

f and D are the volume fraction and the diffusion coefficient associated to the slow and fast diffusion phases (SDP and FDP, respectively), with f_slow + f_fast = 1 (in this simple model differences in T2 relaxation are not taken into account). Studies performed by Niendorf et al. (1996) in the rat brain in vivo (with b factors up to 10,000 s mm⁻²) using this model yielded ADC_fast = (8.24 ± 0.30) × 10⁻⁴ mm²/s and ADC_slow = (1.68 ± 0.10) × 10⁻⁴ mm²/s with f_fast = (0.80 ± 0.02) and f_slow = (0.17 ± 0.02). Similar measurements have been made in the human brain using b factors up to 6000 s mm⁻². The estimates for those diffusion coefficients and the respective volume fractions of those pools have been strikingly consistent across literature ( Clark and Le Bihan, 2000, Maier et al., 2001 and Mulkern et al., 1999); Le Bihan et al., 2006 6552/id.

The problem with this biexponential model is that the nature of the two diffusion pools has remained elusive. It has been often considered that the extracellular compartment might correspond to the FDP, as water would be expected to diffuse more rapidly there than in the intracellular, more viscous compartment. However, the volume fractions of the two water phases obtained using the biexponential model do not agree with those known for the intra- and extracellular water fractions (F_intra > = 0.80 and F_extra < = 0.20 (Nicholson and Sykova, 1998 and LeBihan and vanZijl, 2002). Furthermore, some careful studies have shown that such biexponential diffusion behavior could also be seen solely within the intracellular compartment, pointing out that both the SDP and FDP probably coexist within the intracellular compartment. Theoretical models have shown that restriction caused by cylindrical membranes can also give rise to a pseudo-biexponential diffusion behavior in nerves (Stanisz et al., 1997). Other models have been introduced, for instance based on a combination of extraaxonal water undergoing hindered diffusion and intraaxonal water undergoing restricted diffusion (so-called CHARMED model Assaf et al., 2004). Although such models could account for a pseudo-biexponential diffusion behavior and diffusion anisotropy in white matter, with the potential to estimate white matter fiber average diameter (Assaf et al., 2008), it remains to be seen how it could be applied to the brain cortex, given that true restricted diffusion effects have not been really observed for water in the brain. Several groups have also underlined the important role of dynamic parameters, such as membrane permeability and density (Novikov et al., 2011), water exchange (Chin et al., 2004, Karger et al., 1988 and Novikov et al., 1998), and geometrical features, such as cell size distribution or axons/dendrite directional distribution (Chin et al., 2004, Kroenke et al., 2004, vanderWeerd et al., 2002 and Yablonskiy et al., 2003). Noticeably, however, those distinct models lead to a diffusion signal decay which is nevertheless well approximated by a biexponential fit (Chin et al., 2004, Sukstanskii et al., 2004 and Yablonskiy et al., 2003).

This biexponential shape of the diffusion attenuation would also remain valid in the presence of 2 water pools when the exchange regime becomes ‘intermediate’, but one has to replace the values for f_slow,fast and D_slow,fast in Eq. (4) by more complex parameters taking also into account the residence time of the molecules in the fast and slow compartments relative to the measurement time in a more realistic manner (Karger et al., 1988). Unfortunately, in this condition, the parameters in Eq. (4) no longer represent the volume fractions and diffusion coefficients of two genuine physical compartments, but become complex mathematical expressions mixing the intrinsic diffusion coefficients, the volume fractions and the acquisition parameters. Other pertinent mathematical models have been introduced (see Yablonskiy and Sukstanskii, 2010 for a review) with associated parameters, such as the kurtosis (Jensen and Helpern, 2010a), which quantifies the deviation from a Gaussian process. But again, the relationship of those parameters with actual tissue parameters is not straightforward, unless strong and often unrealistic hypotheses are made about tissue structure or measurement conditions (Jensen and Helpern, 2010b).

Variations of ADC with cell size, importance of cell membranes

A second ensemble of experimental findings has demonstrated that the changes of the volume fractions of the intra- and extracellular spaces which result from cell swelling and shrinking in different physiological, pathological or experimental conditions always lead to variations of the ADC. The drop of ADC which is observed during acute brain ischemia has been clearly correlated with the cell swelling associated with cytotoxic edema ( Sotak, 2004 and Van Der Toorn et al., 1996), for instance. Furthermore, earlier work on animal models has also shown that a decrease in water diffusivity could be visualized using MRI during intense neuronal activation, such as during status epilepticus induced by bicucculine (Zhong et al., 1993) or cortical electroshocks (Zhong et al., 1997). This diffusivity drop propagates along the cortex at a speed of about 1–3 mm/min, consistent with spreading depression ( Busch et al., 1996, Hasegawa et al., 1995, Latour et al., 1994, Mancuso et al., 1999 and Röther et al., 1996). Here also the diffusion drop ( Hasegawa et al., 1995, Latour et al., 1994, Mancuso et al., 1999 and Röther et al., 1996) has been correlated to cell swelling ( Dietzel et al., 1980, Hansen and Olsen, 1980 and Phillips and Nicholson, 1979). More recently ADC decrease has also been observed in rat brain hippocampus slices upon activation of NMDA receptors by kainate acid (Flint et al., 2009).

The mechanisms underlying those changes remain, however, speculative. Several studies have established that the variations in size of the intra and extracellular compartments correlate well with the observed changes in the fraction of the slow and fast diffusion pools of the biexponential model (Benveniste et al., 1992, Dijkhuizen et al., 1999, Hasegawa et al., 1996, Niendorf et al., 1996, OShea et al., 2000 and Van Der Toorn et al., 1996). For instance, the ADC decrease which results from cell swelling in perfused rat hippocampal slices induced by ouabain (Buckley et al., 1999) has been shown to result in an increase of the SDP fraction, but the SDP and FDP diffusion coefficients do not change. These results suggest that the global water ADC decrease does not result from the increase in extracellular tortuosity induced by the shrinking of the extracellular space caused by cell swelling, nor by an increase in intracellular restriction effects, but rather from a shift of balance from the fast to the more hindered slow diffusion water pool. In light of those results it is becoming clear that the slow and fast diffusion pools, if they exist, likely do not correspond to physical compartments, but rather to different functional diffusion behaviors (Le Bihan, 2007). Simulation of the diffusion process shows that water molecules near tissue boundaries (e.g. cell membranes) seem to “stick” to these boundaries which artificially results in a decreased diffusion coefficient. Overall it seems that it is the density and the spatial arrangement of the membranes, and the time given to water molecules to interact with membranes, which plays a determinant role in the ADC values measured by dMRI (Le Bihan, 2007). Given the important surface/volume ratio of most cells, the amount of water molecules interacting with cell membranes is important. In these conditions it might not be so surprising that any fluctuation in cell size, whether swelling or shrinking, would induce a large variation in ADC (the total cell membrane surface scales with the square of its radius), making dMRI very sensitive to cell size variations, whether physiological or pathological. According to this view, large b values and long diffusion times should thus be chosen to maximize such interaction effects on the dMRI images, while very short diffusion times could be aimed to dissect the mechanisms leading to dMRI contrast.

Diffusion anisotropy in white matter: towards brain connectivity studies

The concepts of restriction, hindrance or tortuous displacements around multiple physical compartments are particularly useful in understanding diffusion findings in brain white matter (Le Bihan, 1995). The facts are that: 1/ Water diffusion is highly anisotropic in white matter (Chenevert et al., 1990, Moseley et al., 1990a and Turner et al., 1990); 2/ Such anisotropy has been observed even before fibers are myelinated, though to a lesser degree (Baratti et al., 1999, Beaulieu et al., 1998, Neil et al., 1998, Prayer et al., 1997, Rutherford et al., 1991b, Takeda et al., 1997, Toft et al., 1996 and Vorisek and Sykova, 1997); 3/ The ADCs measured in parallel and perpendicularly to the fibers do not seem to depend on the diffusion time (Le Bihan et al., 1993, Moonen et al., 1991 and Clark and Le Bihan, 2000) at least for diffusion times longer than 20 ms.

Initial reports suggested that the anisotropic water diffusion could be explained on the basis that water molecules were restricted in the axons (anisotropically restricted diffusion) due to the presence of the myelin sheath (Hajnal et al., 1991 and Rutherford et al., 1991a). Restricted diffusion has been observed for intra-axonal metabolites (see box 1), such as N-acetylaspartate, or for truly intra-axonal water (Assaf and Cohen, 1996). However this effect probably accounts for only a limited part of the whole picture, as “true” restriction patterns have not been observed for water diffusion in white matter in vivo except perhaps in very dense and compact bundles, such as the corpus callosum. Extracellular water may also contribute to the anisotropy effect: Perpendicularly to the fibers, water molecules must diffuse along tortuous pathways around fibers, which “slow” them down (Le Bihan et al., 1993). Also, the packed, parallel arrangement of the fibers may be sufficient to explain the presence of anisotropy before myelination, although to a lesser degree. As for the axonal transport it is unlikely that it could significantly contribute the water diffusion anisotropy considering its very low velocity. Neurofilaments within the axons do not seem to play any role either. At this stage experimental evidence points toward the importance of the spatial organization of the membranes. Myelin is not required for diffusion anisotropy, but it modulates the degree of anisotropy.

Although the exact mechanism for the anisotropy has remained not completely understood, it became apparent at a very early stage in the early 1990s, that this anisotropy effect could be exploited to map out the orientation in space of the white matter tracks in the brain, assuming that the direction of the fastest diffusion would indicate the overall orientation of the fibers, as shown first by Douek et al. (1991). However, the work on diffusion anisotropy really took off with the introduction in the field of diffusion MRI of the more rigorous formalism of the Diffusion Tensor, by Basser et al., 1994a and Basser et al., 1994b.

The diffusion tensor

The proper way to address anisotropic diffusion is to consider the diffusion tensor (Jost, 1960 and Stejskal and Tanner, 1965). Diffusion is no longer characterized by a single scalar coefficient but by a symmetric tensor, D, which fully describes molecular mobility along each axis and correlation between displacements along these axes: (5)

$$\underset{¯}{\mathbf{D}}=\begin{array}{ccc}\hfill {\mathit{D}}_{\mathit{xx}}\hfill & \hfill {\mathit{D}}_{\mathit{xy}}\hfill & \hfill {\mathit{D}}_{\mathit{xz}}\hfill \\ \hfill {\mathit{D}}_{\mathit{xy}}\hfill & \hfill {\mathit{D}}_{\mathit{yy}}\hfill & \hfill {\mathit{D}}_{\mathit{yz}}\hfill \\ \hfill {\mathit{D}}_{\mathit{xz}}\hfill & \hfill {\mathit{D}}_{\mathit{yz}}\hfill & \hfill {\mathit{D}}_{\mathit{zz}}\hfill \end{array}.$$

In theory it is possible to obtain all the components of the diffusion tensor with dMRI by acquiring images sensitized to 6 different diffusion directions, which is obtained by combining the magnetic gradient pulses along the X, Y and Z axes, as shown by Basser et al., 1994a and Basser et al., 1994b. The signal attenuation then becomes: (6)

$$A=\exp \left(-\sum _{i=x,y,z}\sum _{j=x,y,z}{\underset{¯}{\mathbf{b}}}_{\mathit{ij}}{\underset{¯}{\mathbf{D}}}_{\mathit{ij}}\right)$$

where b_ji are the elements of the b matrix (which now replaces the b-factor). One must also consider the coupling of the nondiagonal elements from different axes, b_ij, of the b-matrix with the nondiagonal terms, D_ij, (i ≠ j), of the diffusion tensor, which reflect correlation between molecular displacements in perpendicular directions. Calculation of b may quickly become complex when many gradient pulses are used (Mattiello et al., 1994), but full determination of the b-matrix and the diffusion tensor is necessary to properly and fully assess anisotropic diffusion.

As it is difficult to display tensor data, the concept of ‘diffusion ellipsoids’ has been conveniently proposed (Basser et al., 1994a and Basser et al., 1994b): An ellipsoid is a three-dimensional representation of the diffusion distance covered in space by molecules in a given diffusion time. It is obtained by “diagonalizing” the diffusion tensor, (a mathematical operation which provides orthogonal directions coinciding with the main diffusion directions, that is directions along which diffusion is the fastest) for each image voxel (Fig. 2). In the case of isotropic diffusion, the ellipsoid is simply a sphere, the size of which is proportional to the diffusion coefficient. In the case of anisotropic diffusion the ellipsoid becomes elongated (cigar-shape) if one diffusion direction predominates or flat (pancake-shape) if one direction contributes less than the others.

With diffusion tensor imaging (DTI) diffusion data can be analyzed in three ways to provide information on tissue microstructure and architecture for each voxel (Basser, 1997 and Le Bihan, 1995): 1/ The mean diffusivity, which characterizes the overall mean-squared displacement of molecules (average ellipsoid size) and the overall presence of obstacles to diffusion; 2/ the degree of anisotropy, which describes how much molecular displacements vary in space (ellipsoid eccentricity) and is related to the presence and coherence of oriented structures; 3/ the main direction of diffusivities (main ellipsoid axes), which is linked to the orientation in space of the structures (Fig. 2). These three DTI ‘meta-parameters’ can all be derived from the complete knowledge of the diffusion tensor or some of its components. For instance, it has been pointed out that in stroke the average diffusion and the diffusion anisotropy in white matter had different time courses, potentially enhancing the use of D-MRI for the accurate diagnosis and prognosis of stroke (Sotak, 2002).

Another possible scenario can occur when anisotropy is present at a microscopic level (because of the presence of oriented structures, such as dendrites in brain cortex), but not at a voxel level due to the averaging effect over the many different directions present in the voxel. It is becoming possible to unravel the presence of such microscopic anisotropic structures using appropriate dMRI sequences encoding coupling between multiple diffusion directions (Ozarslan and Basser, 2008).

Diffusion MRI and fiber tracking, towards connectomics

Studies of neuronal connectivity are important to interpret functional MRI data and establish the networks underlying cognitive processes. A detailed knowledge of the anatomical connections (in terms of length and size of the fibers, as obtained from the diffusion tensor measurements) might also give in the future some information on the propagation times between activated foci and, thus, indirectly provide clues on the timing of the activation of each node of the network. This kind of information would be particularly useful to explore synchronizations between cortical regions.

Basic DTI provides a means to determine the overall orientation of white matter bundles in each voxel, assuming that only one direction is present or predominant in each voxel, and that diffusivity is the highest along this direction. Three-dimensional vector field maps representing fiber orientation in each voxel can then be obtained back from the dMRI data. A second step after this “inverse problem” is solved consists in “connecting” subsequent voxels on the basis of their respective fiber orientation to infer some continuity in the fibers.

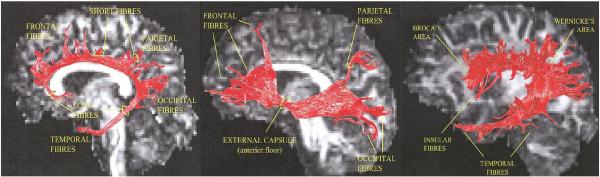
The first such approaches were published in 1999 by multiple groups, working independently (Conturo et al., 1999, Jones et al., 1999b and Mori et al., 1999). They used simple propagation techniques to follow the estimates of principle diffusion direction derived from a diffusion tensor fit to generate ‘streamlines’ that were hypothesized to correspond to the trajectories of underlying fiber pathways. Such methods allowed for beautiful reconstructions of some of the major fiber bundles of the living human brain for the first time (Fig. 2 and Fig. 5). Another approach has been based on regional energy minimization (minimal bending) to select the most likely trajectory among several possible (Poupon et al., 2000) or use “spin glasses models” (Mangin et al., 2002).

Fig. 5.

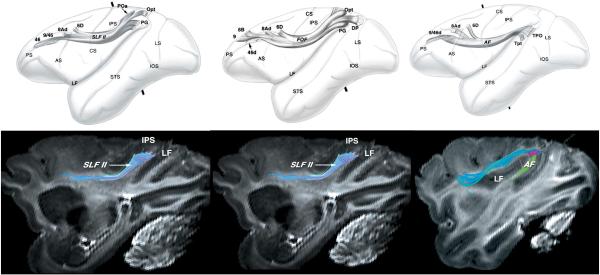
Tractography allows for ‘virtual dissection’ of major fiber bundles from the human brain. Illustrated here, from left to right, are the corpus callosum, inferior frontal occipital fasciculus, and superior longitudinal fasciculus.

Images taken from Catani et al. Neuroimage (2002), with permission.

One limitation of such approaches is that they can only operate when anisotropy is high and so confidence in the estimates of the principle diffusion direction is high. In practice, this means that such approaches typically use an anisotropy threshold (of e.g., 0.2) and terminate pathways when anisotropy drops below this level. Hence, while it is possible to track major fiber bundles within the white matter, it is not possible to continue to trace fibers to their destinations in gray matter nor to trace through regions of fiber complexity or crossing.

An alternative group of techniques was developed a few years later that use probabilistic, rather than deterministic, models of diffusion (Behrens et al., 2003b, Hagmann et al., 2003, Lazar and Alexander, 2005 and Parker et al., 2003). Such schemes take into account the uncertainty in estimates of the principle diffusion direction and represent this explicitly. When operating within such a probabilistic framework, it is no longer necessary to impose an anisotropy threshold on tracking, and it becomes possible to trace pathways all the way to their gray matter targets, building up a representation of the probabilities of different pathways from a given seed. This opened up new possibilities for inferring patterns of cortico-cortical connectivity.

The earliest such models, however, still suffered from the limitation of only estimating a single principle diffusion direction at each voxel. This is a poor model for the many white matter voxels containing multiple fiber populations at different orientations. In this case the diffusion tensor model which assumes only 1 direction per voxel starts to fail, and the acquisition of dMRI images sensitized to many diffusion directions (instead of 6) are necessary to appropriately depict the orientation distribution. Many of the probabilistic methods have now been extended, to allow for estimation of more than one diffusion direction at each voxel (Behrens et al., 2007, Hosey et al., 2005 and Parker and Alexander, 2005), providing that sufficient data is acquired to allow for such estimates to be reliably made. Tractography algorithms working on data modeled in this way can then make use of information about the relative strength of the fiber populations, as well as the orientation at which samples approach a given voxel. The ability to model crossing offered significant advantages for tractography, allowing for previously untracable pathways, such as the lateral portions of the corticospinal tract, to be reliably tracked (Fig. 5).

Indeed; other alternatives to the tensor model include approaches such as q-ball imaging (Tuch, 2004) or diffusion spectrum imaging (Wedeen et al., 2005), that aim to directly estimate the orientation distribution function, without the need to impose a particular distribution, such as a gaussian, on the data. Such approaches can resolve multiple fiber orientations within a voxel and have provided powerful insights into orientation structure at high angular and spatial resolution — for example allowing for visualization of intrinsic structure in the cortical gray matter (Tuch et al., 2003) (Fig. 6) or modeling of fiber crossings. Such models can be used to perform tractography (Wedeen et al., 2008) and have enabled, for example, high resolution delineation of cerebellar circuits (Granziera et al., 2009).

Fig. 6.

Tractography algorithms that can model more than one fiber population allow for tracking through regions of fiber crossing. One the left hand side of this image are results for tracking the corticospinal tract in 9 individual brains using a single fiber probabilistic model; typically, only the medial portions of the tract can be followed. On the right hand side the same data is modeled using two fiber orientations and the more lateral portions of the tract can now be seen.

Images taken from Behrens et al. Neuroimage (2007), with permission.

The ability to track to and from gray matter opened up the possibility of using tractography to provide information on cortical and subcortical parcellation (Behrens and Johansen-Berg, 2005 and Knosche and Tittgemeyer, 2011). Classically, subregions within cortical or cortical gray matter are defined based on differences in cytoarchitecture (Brodmann, 1909), but such differences are not usually visible using MRI. Instead, we typically rely on gross landmarks, such as sulci and gyri, to define approximate borders between regions. In some cases, however, there is limited correspondence between microstructural borders and gross anatomical landmarks (Amunts et al., 1999), and so there has been interest in using other types of information to define functional–anatomical boundaries in the living human brain.

Information on anatomical connectivity, provided by diffusion tractography, is a compelling candidate for this purpose. Each brain region has a unique connectivity fingerprint (Passingham et al., 2002), so it has been proposed that differences in anatomical connectivity patterns could be used to pin-point underlying microstructural boundaries (Behrens and Johansen-Berg, 2005 and Knosche and Tittgemeyer, 2011). Some of the earliest attempts to do this were carried out in the thalamus, a deep gray matter structure consisting of cytoarchitectonically distinct nuclei which project to different regions of cortex. By performing tractography between thalamus and cortex (Behrens et al., 2003a), or even by simply considering local estimates of principle diffusion directions within the thalamus (Wiegell et al., 2003), it is possible to define clusters of thalamic voxels with similar connection patterns; these clusters are consistent across individuals (Johansen-Berg et al., 2005), and likely correspond to nuclei or nuclear groups. In the cortex, it has been possible to apply similar logic to simply identify points where there is a sudden change in connectivity, based on the assumption that such points are likely to correspond to borders between cortical regions (Anwander et al., 2007 and Johansen-Berg et al., 2004). Connectivity-based parcellation raises multiple challenges that are beginning to be addressed including, for example, how to robustly define parcels (Nanetti et al., 2009), determining the level of parcellation (how many clusters to define?) (Jbabdi et al., 2009) and determining correspondence of parcels across individuals (Jbabdi et al., 2009 and Roca et al., 2010). The majority of connectivity-based parcellation studies have focussed on a discrete area of cortex and have aimed to define just a few brain regions within it. However, the same logic could, at least in theory, be applied across the whole brain, and some such attempts have recently been made (Clarkson et al., 2010, Perrin et al., 2008 and Roca et al., 2009).

An important trend has been to match functional connectivity, as obtained with fMRI, and anatomical connectivity inferred from DTI (Koch et al., 2002). This can be done using either task-based or resting fMRI data. While task-based functional connectivity measures will be highly context dependent, covariation in resting functional connectivity are thought to reflect patterns of (direct or indirect) anatomical connectivity to a large extent (Honey et al., 2009). Resting fMRI data, as well as diffusion tractography, have recently been used to derive estimates of the human ‘connectome’, whole brain maps of cortico-cortical connectivity (Biswal et al., 2010 and Gong et al., 2009). Large scale population projects, such as the Human Connectome Project (humanconnectome.org), promise to provide the community with comprehensive maps of systems level cortico-cortical connectivity, enabling the study of structure–function relationships and their interaction with genotype.

When comparing functional and structural maps of connectivity, one has to keep in mind that it is the large white matter bundles (rather than smaller intracortical connections) that dominate tractography estimates, and that there is no indication on the directional and functional status of the information flow along the tracts. Whether MRI will someday be able to provide such crucial knowledge remains to be established.

Validation of these virtual bundles is an important challenge for tractography (Hubbard and Parker, 2009). One attractive approach is to compare tractography performance to known ground truth by using a physical phantom (Perrin et al., 2005). Such studies have provided useful data comparing performance with different tract geometries, for example. However, it has not yet been possible to build a phantom with dimensions and geometry comparable to a real brain fiber bundle and so it remains unclear whether the conclusions of phantom studies apply to real brain data. Therefore, validation of tractography against anatomical data is an important endeavor (Fig. 7).

Fig. 7.

Validation of tractography is an important challenge. Here, results from autoradiographic tracing of fibers in postmortem monkey brains (top row) are compared to results using diffusion spectrum tractography (bottom row) obtained postmortem in different monkeys. Qualitatively, good agreement is found between the course of the third portion of the superior longitudinal fasciculus (left), fronto-occipital fasciulus (middle), and arcuate fasciculus (right).

Images taken from Schmahmann et al. Brain (2007) with permission.

Classical post-mortem dissection methods in humans show reasonable qualitative agreement with tractography (Lawes et al., 2008) but such comparisons are necessarily between subjects and limited to major bundles. More direct anatomical connectivity information can be provided by histological or MR-visible tracers. Between subject comparisons of such data have been carried out in macaque monkey based on autoradiography results, which allow for the trajectory, as well as the termination points, of pathways to be determined (Schmahmann et al., 2007). An important challenge is to make these comparisons within the same animal. One such study used both histological and MR-visible tracers in comparison to diffusion tractography in the brains of three minipigs (Dyrby et al., 2007). Overlaps between techniques was typically around 70–90% but some tracts that were identified using one of the tracers could not be found using tractography. In addition, some presumably spurious pathways were identified using tractography but not found with either tracer; such findings were often in regions of high fiber complexity, where tractography algorithms are susceptible to following erroneous routes. Importantly, this study also found incidences of disagreement between the two tracers used, likely reflecting the fact that the MR-visible tracer (manganese) is transported across synapses, whereas the histological tracer used (biotinylated dextran amine) is not. This highlights the fact that it is not straightforward to identify a ‘gold standard’ for comparison to tractography.

Applications

Acute brain ischemia

The most successful application of diffusion MRI since the early 1990s has been in acute brain ischemia (Baird and Warach, 1998). The application of diffusion MRI to patients with chronic infarct lesions was suggested early on (Chien et al., 1992 and Le Bihan et al., 1986). However, a significant discovery was made later by Moseley et al. (Mintorovitch et al., 1991 and Moseley et al., 1990c) who demonstrated that water diffusion significantly drops (by 30 to 50%) in ischemic brain tissue within several minutes of the occlusion of the middle cerebral artery in the cat. This finding was soon confirmed by many groups using other animal models (see Hossmann and Hoehn Berlage, 1995 and Sotak, 2002 for extensive reviews) and later in human patients with stroke (Sorensen et al., 1996, Sorensen et al., 1999 and Warach et al., 1992) (Fig. 4). In contrast, T2-weighted images of ischemic tissue remain normal for several hours. An increase in T2 will actually occur much later when vasogenic edema develops (Knight et al., 1991). Given the increase in stroke treatments that can be effective, but only if applied during a specific acute stage, it is increasingly important to have imaging modalities which help to determine the likelihood of treatment success. Diffusion MRI today is the imaging modality of choice to manage stroke patients (Chalela et al., 2007 and Schellinger et al., 2007), providing one of the few clear examples of translation to the clinic from MRI methods developed over the past few decades.

Fig. 4.

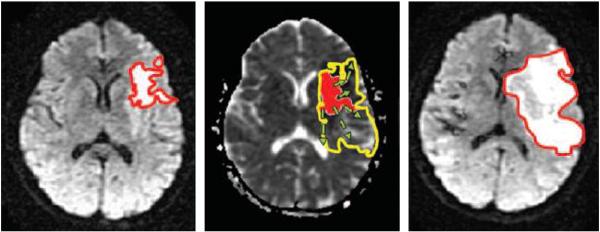
Left: dMRI image obtained at early admission of a patient with middle cerebral artery trunk occlusion. The initial infarct lesion is outlined in red. Middle: On ADC map obtained at admission, the lesion is shaded red, while the predicted outcome volume from a growing model is outlined in yellow. Right: On follow-up dMRI image, the final measured infarct volume, outlined in red, is visible as a hyperintense region, even larger than expected from model. The development of such models will be very useful to predict outcome and orient initial treatment, depending on the expected volume and more importantly the territory which will be affected.

Images taken from Rosso et al. Radiology (2009), with permission.

However, although the decrease in water diffusion right after the ischemic injury has been clearly established, and is used in clinical decision making, its interpretation is still not fully understood, and its relationship with the severity of the ischemic damage and the clinical outcome remains a subject of study (Sotak, 2002). The diffusion drop is linked in some way to the cellular change in energy metabolism that ultimately leads to the decreased activity and then failure of the Na⁺/K⁺ pumps resulting in cytotoxic edema (Hossmann and Hoehn Berlage, 1995). The basic mechanism underlying the drop in diffusion remains unclear. Different hypotheses have been evaluated, such as a possible decrease in the extra- and intracellular water mobility, a shift of water from extracellular to intracellular space, an increase in the intracellular diffusion restriction due to changes in membrane permeability, or an increased tortuosity in the extracellular space due to cell swelling (Norris et al., 1994). Still, diffusion imaging offers great potential in the disease management of stroke patients: First, the development of pharmaceuticals for the treatment of stroke can be greatly facilitated, as drug effects can be assessed objectively and very quickly compared with long and costly clinical trials or animal model studies. With diffusion MRI used in combination with perfusion MRI, which outlines regions with decreased blood flow or increased blood mean transit times (Rohl et al., 2001), and MR “angiography” (which provides images of the vasculature, showing occluded vessels), clinicians have in their hands invaluable tools to help them, at a very early stage when tissue is still salvageable, to assess lesion severity and extension, and to customize a therapeutic approach (pharmacological or interventional) to individual patients (Warach et al., 1997b), as well as to monitor patient progress on an objective basis, both in the acute and the chronic phase (Warach et al., 1996), and to predict clinical outcome (Dreher et al., 1998, Gonzalez et al., 1999, Lovblad et al., 1997, Rosso et al., 2009 and Warach et al., 1997a).

White matter diseases

The potential of “plain” diffusion MRI in neurology has also been studied in brain tumor grading (Sun et al., 2001, Ikezaki et al., 1997 and Krabbe et al., 1997), trauma (Barzo et al., 1997), hypertensive hydrocephalus (Schwartz et al., 1998), AIDS (Chang and Ernst, 1997), eclampsia (Schaefer et al., 1997), leukoaraiosis (Jones et al., 1999a and Okada et al., 1999), migraine (Chabriat et al., 2000) and diseases of the spinal cord in animals (Dreher et al., 1998, Ford et al., 1998, Gulani et al., 1997 and Inglis et al., 1997) and humans (Clark et al., 1999 and Ries et al., 2000). These clinical studies have been motivated by the very high sensitivity of D-MRI to microstructural changes in tissues, so that anomalies can be detected before changes in more conventional images contrasted by the T1 or T2 relaxation times. In some cases, specific (though often speculative) mechanisms underlying physiopathology (edema, Wallerian degeneration, neurotoxicity, swelling, and so on) could be put forward, but a clear association between ADC findings and those microstructural tissue alterations remains difficult to demonstrate. Animal models, tissue modeling and computer simulations may help.

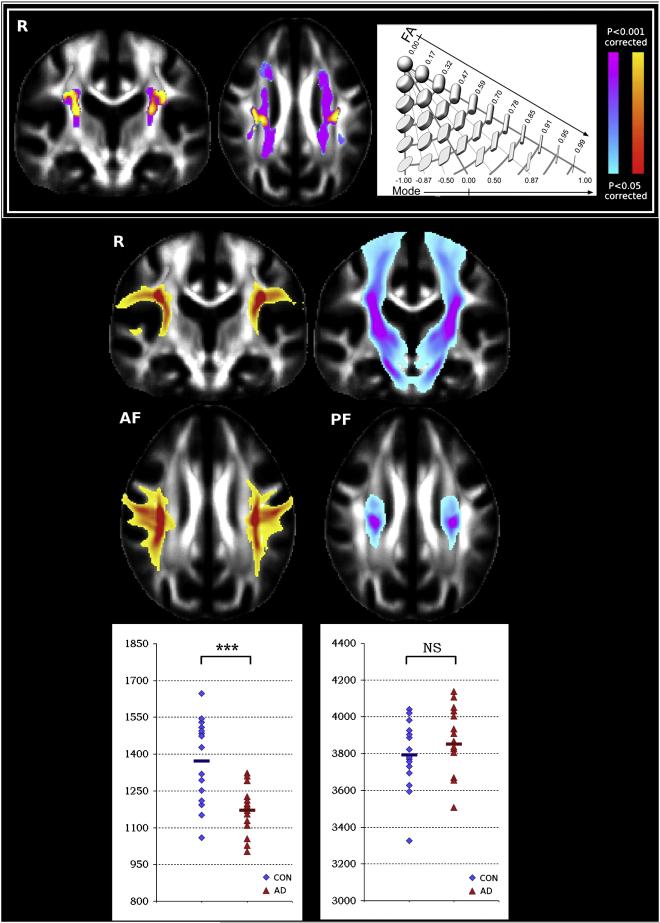
In white matter, any change in tissue orientation patterns inside the MRI voxel would probably result in a change in the degree of anisotropy. There is a growing literature body supporting this assumption: Many clinical studies carried on patients with white matter diseases have shown the exquisite sensitivity of DTI to detect abnormalities at an early stage or to characterize them in terms of white matter fiber integrity. In the white matter, diffusion MRI has already shown its potential in diseases such as multiple sclerosis (Ono et al., 1997). However, DTI offers more through the separation of mean diffusivity indices, such as the trace of the diffusion tensor, which reflects overall water content, and anisotropy indices, which point towards myelin fiber integrity. Examples include multiple sclerosis (Horsfield et al., 1998, Iwasawa et al., 1997, Tievsky et al., 1999 and Werring et al., 1999), leukoencephalopathies (Ay et al., 1998 and Eichler et al., 2002), Wallerian degeneration, HIV-1 infection (Filippi et al., 2001), Alzheimer disease (Hanyu et al., 1997 and Hanyu et al., 1998), or CADASIL (Chabriat et al., 1999). Complimentary indices such as dispersion of the principle diffusion direction (Douaud et al., 2009), or mode of anisotropy (Douaud et al., 2011), can potentially offer even greater insights into underlying pathology (Fig. 8).

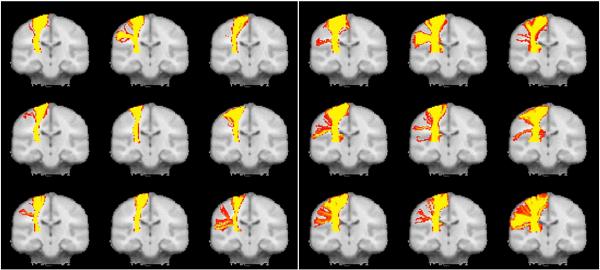
Fig. 8.

Considering multiple diffusion parameters, as well as findings based on tractography, can shed light on complex pathology. In this example, diffusion images were acquired in patients with Alzheimer’s Disease, Mild Cognitive Impairment, and Healthy Controls. In addition to calculating fractional anisotropy (FA), the authors also calculated the mode of anisotropy, which quantifies the degree to which the tensor is planar (disc-shaped) or linear (cigar-shaped), as shown in the schematic in the top right (taken from Ennis and Kindlmann, MRM, 2006). Mode was more sensitive than FA to differences between MCI and controls. The top left figure illustrates that patients showed a counter-intuitive increase in mode (shown in pink), along with an increase in fractional anisotropy (shown in yellow), specifically in a region where association fibers cross with projection fibers. Closer interrogation of this crossing fiber region using tractography (bottom panel), revealed that patients had a decrease in tractography particles in the association fibers (AF), with no change in particles in the projection fibers (PF).

Images taken from Douaud et al. Neuroimage (2011), with permission.

However, D-MRI could also unravel more subtle, functional disorders that do not necessarily translate into anatomical anomalies. For instance, anisotropy measurements may highlight subtle anomalies in the organization of white matter tracks otherwise not visible with plain, anatomical MRI. The potential is enormous for patients with functional symptoms linked to disconnectivity, for instance, in patients with psychiatric disorders (see Lim and Helpern, 2002 for a review). Links between cognitive impairments and abnormal connectivity in white matter based on DTI MRI data have also been reported in frontal regions in schizophrenic patients (Buchsbaum et al., 1998 and Lim et al., 1999), in the corpus callosum and the centrum semiovale in chronic alcoholic patients (Pfefferbaum et al., 2000), in left temporo-parietal regions in dyslexic adults (Klingberg et al., 2000), and in specific disconnection syndromes (Molko et al., 2002).

Anatomical connectivity studies

The ability of diffusion MRI to provide information on anatomical connectivity is important for cognitive neuroscience as defining the inputs and outputs of a brain region offers insights into its functional specialization (Passingham et al., 2002). There is a vast literature on brain connectivity patterns derived from the macaque monkey (Stephan et al., 2001) and this has proved invaluable for study of the human brain in health and disease. However, there are brain regions in which homologies between human and macaque are not clear and therefore extrapolation from the monkey to human are not always possible. In addition, even for regions whose gross anatomy and functional specialization appears comparable across species, it is important to establish connection patterns in human brains specifically, in order to relate this to behavior, physiology, or clinical features, and for comparisons in connectivity across species. This need is particularly marked for the study of functions such as language, which can be more readily tackled in human than in non-human brains.

Croxson and colleagues provided one of the first detailed studies of inter-species patterns of brain connectivity using tractography in both humans and macaques (Croxson et al., 2005). While connection patterns of prefrontal cortex were broadly comparable between human and macaque, some important species-specific questions could be addressed. For example, the inferior frontal gyrus in the human brain plays an important role in language and contains a number of distinct subregions; it is debatable whether these regions should be thought of as premotor or prefrontal areas. By comparing anatomical connection patterns of the human and macaque brain using tractography, Croxson et al showed that the connections of the human anterior inferior frontal gyrus closely resembled macaque prefrontal cortex, whereas the human posterior inferior frontal gyrus appeared more like macaque premotor cortex. This finding supports the idea that parts of the human language system have evolved from the motor system. Other human studies focussed specifically on this inferior frontal region to characterize these pathways in detail using tractography ( Catani et al., 2005 and Frey et al., 2008) and relate this anatomical variation to difference in the distinct functional roles played by the two regions (Friederici et al., 2006). Tractography studies in human have also shown that individual differences in the organization of language pathways linking the inferior frontal and superior temporal lobe have functional relevance: people with a more symmetrical pattern of connections have better recall of semantically associated words (Catani et al., 2007).

As mentioned previously, the ability to track fiber pathways has also been exploited for parcellation of cortical and subcortical structures. Subcortically, tractography has been successfully used to segment subregions within the thalamus (Behrens et al., 2003a, Devlin et al., 2006, Johansen-Berg et al., 2005, Klein et al., 2010, O’Muircheartaigh et al., 2011 and Traynor et al., 2010), amygdalae (Bach et al., 2011) and basal ganglia (Draganski et al., 2008) substantia nigra (Menke et al., 2010). In the cortex, this approach has allowed for definition of boundaries in a large number of human brain regions including the supplementary motor area (SMA) and pre-SMA (Johansen-Berg et al., 2004); putative Brodmann’s areas 44, 45 and 47 in the inferior frontal gyrus (Anwander et al., 2007 and Klein et al., 2007); dorsal and ventral premotor cortex (Schubotz et al., 2010 and Tomassini et al., 2007); regions within the lateral posterior parietal cortex (Mars et al., 2011), as well as regions within the cingulate (Beckmann et al., 2009 and Johansen-Berg et al., 2008). Comparisons with resting state (Mars et al., 2011) or with task-based fMRI data (Johansen-Berg et al., 2004, Johansen-Berg et al., 2005, Schubotz et al., 2010 and Tomassini et al., 2007) underline the functional significance of these parcellations.

Brain development, aging and plasticity

Over the course of life, white matter matures and declines. Effects of aging on white matter ordering can now be studied (Moseley, 2002 and Pfefferbaum et al., 2000), but DTI can also be used to monitor the myelination process in fetuses, babies and during childhood (Schmithorst et al., 2002 and Dubois et al., 2006). DTI has clearly an important potential for the pediatric population (Neil et al., 2002). It has been shown that the degree of diffusion anisotropy in white matter increases during the myelination process (Baratti et al., 1999, Neil et al., 1998 and Takahashi et al., 2000), so that diffusion MRI could be used to assess brain maturation in children (Zimmerman et al., 1998), newborns or premature babies (Huppi et al., 1998 and Neil et al., 1998), as well as to characterize white matter disorders in children (Engelbrecht et al., 2002). Research on brain development has been exploding recently. Advances in neuroimaging have certainly contributed to this expansion, as data can now be obtained non-invasively in newborns or even before birth. Of particular interest is the observation with DTI that water diffusion in white matter in the brain changes dramatically during development, both in terms of average and anisotropic diffusion. As for gray matter, although water diffusion appears isotropic in the adult brain cortex to some extent, there is a short time window when anisotropy can definitely be found. This transient anisotropy effect probably reflects the migration and organization process of glial cells and neurons (e.g. dendritic architecture of pyramidal cells) in the cortex layers (Mori et al., 2001 and Neil et al., 1998). For white matter during postnatal development, the degree of water diffusion anisotropy follows the myelination process (Neil et al., 2002), but the effect is small compared with the prenatal stage where large anisotropy is observed even before axons get myelinated (Beaulieu et al., 1998). The combined effects of the axon packing in the fiber bundles and the thickness of the myelin sheath on the degree of anisotropy have still to be described in detail, but DTI already represents an outstanding tool to study brain development in animals and humans (Dubois et al., 2008). Gray matter migration disorders may also be assessed (Eriksson et al., 2001 and Eriksson et al., 2002).

Although the bulk of developmental changes happen in the first few years of life (Hermoye et al., 2006 and Huang et al., 2006), white matter continues to show slow maturation, particularly in prefrontal pathways, through adolescence (Barnea-Goraly et al., 2005, Ben Bashat et al., 2005, Giorgio et al., 2008, Giorgio et al., 2010b and Schmithorst et al., 2005) and even into early adulthood (Giorgio et al., 2008 and Snook et al., 2005). At the other end of the lifespan, diffusion MRI is sensitive to age-related degeneration in brain structure. Diffusion indices begin to alter, with reducing anisotropy and increasing diffusivity, from middle age (Giorgio et al., 2010a, Pfefferbaum et al., 2000 and Salat et al., 2005).

These developmental and age-related changes have functional consequences. Maturation of prefrontal pathways in children, for example, is associated with development of the cognitive process of ‘delay discounting’ — the tendency to devalue future rewards relative to immediate rewards (Olson et al., 2009), while development of inferior-parietal–prefrontal pathways correlates with improvements in mental arithmetic skills (Tsang et al., 2009). In aging populations, slowing of response times is associated with declining fractional anisotropy in the internal capsule (Madden et al., 2004). These relationships highlight the phenomenon that variation in brain structure is associated with variation in behavior within the context of development or aging. Recently, such individual differences have been a focus of attention in young and middle aged adults, in whom significant age-related change would not be expected.

It has consistently been found that inter-individual variation in behavioral performance of a specific cognitive task is correlated with variation in diffusion indices in pathways thought to mediate task performance (Johansen-Berg, 2010). So, for example, variation in bimanual co-ordination skills correlates with variation in anisotropy within the body of the corpus callosum (Johansen-Berg et al., 2007), a region including transcallosal pathways important for bimanual motor control. By contrast, variation in spatial visualization skills, thought to involve parietal cortex, correlates with variation in anisotropy in white matter underlying the anterior intraparietal sulcus (Wolbers et al., 2006). These associations make sense; we would expect that individual differences in structural features of white matter, such as myelination, axon density or axon diameter, would have consequences for the physiological properties of an axon bundle — affecting properties such as conduction times or synchronization (Fields, 2008). Demonstrations of associations between diffusion measures and physiological measures of pathway integrity, such as those provided by transcranial magnetic simulation (Boorman et al., 2007 and Wahl et al., 2007), provide an empirical demonstration of this mediating link between structure and physiology. Physiological variations would in turn be expected to influence behavior.

What is the basis of individual differences in white matter microstructure? It is possible that the variations reflect innate differences, whereby those whose genetic make-up provides them with particularly well-connected corpus callosum, for example, are destined to perform well in tasks requiring interhemispheric transfer. Another possibility is that these individual differences arise in part through variation in experience throughout life. In this way, training as a pianist, for example, could both strengthen pathways involved in piano-playing and also improve performance on tasks that rely on the processes involved in piano-playing. It has been shown, for instance, that diffusion MRI images acquired in adult pianists reveal that anisotropy of different parts of the white matter bundles was correlated to the number of hours of practice performed at different developmental stages (infancy, teen age period, adulthood), but at decreasing rates with age (Bengtsson et al., 2005). This ability of perform “neuroarcheology” in individual subjects, revealing ones brain history through imaging, is clearly another amazing feature of diffusion MRI.

There is evidence that both genetic and environmental factors influence diffusion measures of white matter structure. Heritability studies suggest that as much as 75–90% of variation in anisotropy is genetic, particularly in parietal and frontal lobes (Chiang et al., 2009). However, this leaves room for influence of the environment, and longitudinal training studies provide further evidence for experience-dependent changes in white matter structure. Juggling (Scholz et al., 2009), working memory training (Takeuchi et al., 2010), and balance training (Taubert et al., 2010), have all been shown to alter white matter diffusion measures in healthy adults over a time period of weeks to months.

Potential of diffusion MRI for functional neuroimaging

Although functional magnetic resonance imaging (fMRI) using the blood oxygen-level dependent (BOLD) effect (Bandettini et al., 1992, Kwong et al., 1992 and Ogawa et al., 1992) has been extremely successful for studying the human brain, it has well-known limitations. The extent, dynamics, and underlying mechanisms of this neurovascular coupling are not yet fully understood (Iadecola and Nedergaard, 2007 and Magistretti and Pellerin, 1999) and the BOLD signal depends on several parameters, so its biophysical link with neuronal activation is not straightforward (Buxton et al., 1998, Buxton et al., 2004, Malonek et al., 1997, Sirotin and Das, 2009 and Van Zijl et al., 1998). Although the coupling between neuronal activation, cell metabolism, and hemodynamic changes has been shown for BOLD fMRI (Logothetis et al., 2001), it may fail in some pathological conditions (Lehericy et al., 2002). Also, the spatial localization of the BOLD signal can be distant from the actual site of neural activity, because the signal source includes various vascular networks ranging from small capillaries to large draining veins (Turner, 2002). Similarly, the physiological delay necessary for the mechanisms triggering the vascular response to work intrinsically limits the temporal resolution of BOLD fMRI.

Recent work has suggested that water diffusion MRI could also be used to visualize changes in tissue microstructure which might arise during neuronal activation: A transient decrease in the ADC of water has been reported in the human brain visual cortex during activation by a black and white flickering checkerboard (Darquie et al., 2001). This diffusion slowdown occurs several seconds before the hemodynamic response detected by BOLD fMRI (Aso et al., 2009 and Kohno et al., 2009). Changes in the water apparent diffusion coefficient (ADC) during neuronal activation would likely reflect transient microstructural changes of the neurons or the glial cells during activation, although this hypothesis has sometimes been challenged (Jin and Kim, 2008, Miller et al., 2007 and Yacoub et al., 2008). Observing such effects would have a tremendous impact, since they would be directly linked to neuronal events, in contrast to blood flow effects which are indirect and remote. Based on the known sensitivity of diffusion MRI to cell size in tissues ( Buckley et al., 1999 and Flint et al., 2009) and on optical imaging studies that have revealed changes in the shape (in particular swelling) of neurons and glial cells during brain activation ( Andrew and Macvicar, 1994, Le Bihan, 2007 and Tasaki, 1999), the observed ADC findings have been tentatively ascribed to a transient swelling of cortical cells. It is also worth noting that contractile proteins associated with dendritic spines (where the majority of synapses are located in the cerebral cortex) could allow these spines to change rapidly in shape during neuronal activity (Fig. 4) ( Crick, 1982 and Halpain, 2000). However, these spines occupy a very small volume fraction and so might not be expected to have an observable effect on the diffusion signal. In any case, these results suggest that dMRI might provide a new approach to produce images of brain activation from signals directly associated with neuronal activation and not through changes in local blood flow.

Conclusion

In summary, it is important to remember that diffusion imaging is a truly quantitative method that gives direct insight into the voxel-averaged microscopic physical properties of tissues (e.g., cell size and shape, geometric packing, and so on) through the observation of the random translational molecular movement. Many theoretical and experimental analyses on the effect of restriction, membrane permeability, hindrance or tissue inhomogeneity have underlined how much care is necessary, however, to properly interpret DTI data and infer accurate information on microstructure and microdynamics of biological systems. With these difficulties in mind, it remains that even at its current stage of development, DTI is the only approach available today to track brain white matter fibers non-invasively in the human brain and to assess anatomical connectivity. In combination with fMRI, which identifies co-activated brain networks and may provides clues to functional connectivity, DTI should thus have a tremendous impact on brain function studies, from animal models to human neuroscience. With the advent of very high field magnets (above 10 T) and powerful gradient hardware (above 100 mT/m), which will push current limits of MRI, one may expect to reach new levels and break new ground in the already flourishing field of diffusion imaging.