Multiple-gate time domain diffuse fluorescence tomography allows more sparse tissue sampling without compromising image quality

Abstract

Diffuse fluorescence tomography systems that employ highly sensitive photo-multiplier tubes for single-photon detection are pushing the sensitivity limits of the field. However, each of these detectors only offers a single data projection to be collected, implying these imaging systems either require many detectors or long scan times to collect full data sets for image reconstruction. This study presents a method of utilizing the time-resolved collection capabilities of time-correlated single-photon counting techniques to increase spatial resolution and to reduce the number of data projections to produce reliable fluorescence reconstructions. Experimental tissue phantom results demonstrate that using data at 10 time gates in the fluorescence reconstructions for only 40 data projections provided superior image accuracy when compared to reconstructions on 320 continuous-wave data projections.

Current diffuse fluorescence tomography (FT) methods have significant tradeoffs between imaging time and quantitative inaccuracies due to model-data mismatch (e.g., shot noise, modeling errors). Fluorescence systems using charged coupled devices (CCDs) provide high imaging throughput by recording many laser projection measurements simultaneously. However, systems using photomultiplier tubes (PMTs) are favored to minimize shot noise contributions through increased photon sensitivity, albeit at the cost of significantly increased imaging time because they are only capable of measuring one optical projection per detector. An FT reconstruction scheme is presented that uses time gates from a temporal point spread function (TPSF) [Fig. 1(a)] to exploit the low noise characteristics and subnanosecond time resolution of PMT-based time-correlated single photon counting (TCSPC). Experimental results collected in tissue phantoms demonstrated a substantial improvement in the accuracy of time-domain (TD) reconstructed fluorescence images compared to continuous-wave (CW) reconstructions, which is the data type most commonly used in CCD-based FT applications. In fact, it is demonstrated that discrepancies are so substantial that a 40 data-projection TD dataset outperformed a 320 data-projection CW dataset in terms of reconstructed image quality and quantitative figures of merit such as contrast recovery and centroid localization error. This demonstrates, for the first time, that FT using highly sensitive time-resolved single-photon detection [1] can be used with 1 order of magnitude fewer optical projections when compared with CW imaging without any compromise in terms of image fidelity. The dramatic decrease in required imaging time that results from using time gates is important because it hints to the possibility that single-photon counting TD FT could be amenable to high throughput imaging of animal models of disease.

Fig. 1.

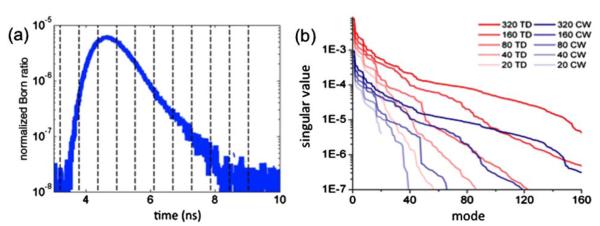
(Color online) (a) Sample experimental TPSF, to be binned into the 10 time gates shown by dotted lines bounding each time gate, (b) singular value spectra for the time domain (TD, blue) and continuous wave (CW, red) Jacobians. Shown are 320, 160, 80, 40, and 20 optical projection Jacobian spectra in order of decreasing opacity.

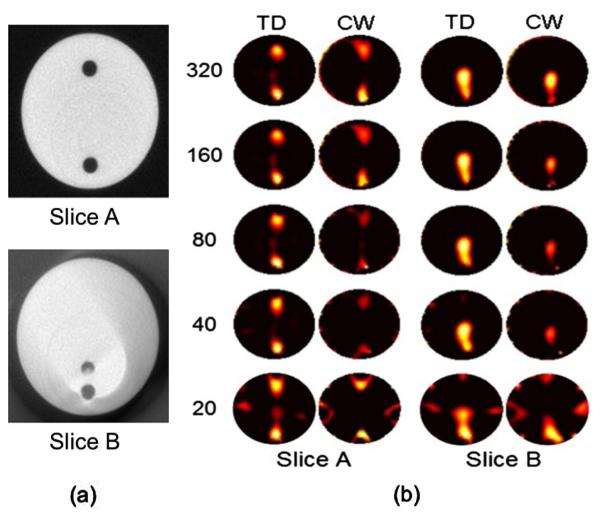
A microcomputed tomography (micro-CT) guided, noncontact, TCSPC PMT-based imaging system [2] was used to collect the TD fluorescence and transmittance normalization data about a 30 mm-diameter cylindrical phantom with two fluorescent inclusions. The polymer structure of the phantom had an absorption coefficient, μ_a = 0.018 mm⁻¹, a reduced scattering coefficient, ${\mu }_s^{\prime }$ = 1.07 mm⁻¹, and a refractive index, n = 1.4, at the excitation wavelength of imaging (760 nm). These values were computed using a TD phantom characterization system by fitting TPSFs against a light transport solution computed using Monte Carlo simulations (INO, Quebec City, Canada). To create fluorescent inclusions in the phantom, two 3 mm-diameter cylindrical holes were drilled in the circular face of the phantom. One inclusion was drilled parallel to the axis of the cylinder, 4.5 mm from its closest edge. The other hole was drilled at an angle of 12° away from the axis of the cylinder starting from a position symmetrically opposite to the first hole, and therefore approaching the first hole allowing the spatial resolution of the imaging system to be tested [Fig. 2(a) depicts two computed-tomography (CT) images of the holes at different axial positions of the phantom]. Each hole was filled with a 100 nM concentration of IRDye-800CW (LI-COR Biosciences, Lincoln, NE) in 1% Intralipid and water. As depicted in Fig. 2(a), the phantom was imaged at two axial slices with edge-to-edge inclusion separations of 16.0 mm (slice A) and 1.6 mm (slice B). For each slice, fluorescence and transmittance TD data was collected simultaneously for 320 optical projections.

Fig. 2.

(Color online) (a) X-ray CT image slices of the phantom showing the domain imaged with FT, (b) FT image reconstructions of the tissue phantom for slices A and B, with increasing numbers of projections (listed at left).

All TPSFs (fluorescence and transmittance) were intensity-calibrated to account for interdetector sensitivity variations and time-referenced with respect to the system impulse response functions (IRFs) [2]. The fluorescence curves were then binned into 10 time gates from 4 to 9 ns, each with a temporal length of 0.5 ns, as shown in Fig. 1(a). Ten equally spaced time gates were used here because this provided optimal inverse problem solutions for the level of signal-to-noise present in the data. Each fluorescence time-gate was normalized through division by the area under the transmittance TPSF collected at the corresponding data projection (i.e., Born-normalization with respect the total transmitted photon count [3]) to mitigate forward model-data mismatch in the reconstruction process. In order for the comparison between TD and CW reconstructions to be as fair as possible, the comparative CW dataset was formed by integrating each TD signal into a single intensity value that was subsequently Born-normalized by the total transmitted photon count.

The forward model was constructed from a TD implementation of a finite-elements model (FEM) diffusion approximation algorithm [4]. Briefly, the Born-normalized data vector, d, was equated to the forward model by the following expression:

$$Jx=d,$$ (1)

where x is the vector of interest (fluorescence image) and J is built from the time-gated sensitivity functions approximated by the forward model (also known as the FT Jacobian). The parameter of interest in this study was the vector x = ημ_af, where η is the quantum efficiency and μ_af is the local optical absorption due to the fluorophores, and the vector is comprised of the product of these parameters at every FEM node. Each TPSF simulated using Eq. (1) was convolved with a lifetime exponential decay curve of the form exp(−t/τ), where τ = 0.3 ns is the average lifetime computed by fitting the late gates of all TPFS curves with a single exponential curve. The expression in Eq. (1) was solved using a modified Levenberg-Marquardt algorithm with a regularization parameter λ = 30 and nonnegative projection of the form presented in [5] at each iteration, with the goal of minimizing the two-norm objective function ${\mid \mid Jx-d\mid \mid }_2^2$. This resulted in the iterative update scheme: Step 1

$$\Delta x={(J^{T}J+\lambda I)}^{-1}\times (Jx-d).$$

Step 2 x = ⟨x + Δx⟩₊, where ⟨·⟩₊ is defined by

$${\left({\langle a\rangle }_{+}\right)}_i=\{\begin{array}{cc}{a}_i,\hfill & a_i\ge 0\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}.$$

An objective criterion had to be used in order to automatically find the optimal number of iterations. In order to compare TD and CW methods in the best-case scenario and avoid bias to either method in the choice of stopping criterion, the reported result [Fig. 2(b)] was the iteration that minimized the spatial error of the reconstruction with respect to the known fluorescence distribution. The spatial error was evaluated by iteratively computing the overlap between the reconstructed image (at each iteration) and the CT-derived target image [Fig. 2(a)].

A detailed analysis is provided comparing TD and CW methods to determine the extent to which parsing the TPSFs into individual time gates can—because of the different tissue information they convey—alleviate the need for a large number of laser projections in FT and, therefore, increase the imaging throughput of single photon detection tomography techniques. The analysis was based on down-sampling the original dataset (composed of 320 TPSFs acquired in 90 minutes) in order to mimic datasets that would have been acquired with reduced scan times. Five data signals were created: from every second projection for the 160 projection dataset, from every fourth projection for the 80 projection data set, and so on down to 20 projections. The TD and CW results of these experimental data reconstructions are shown in Fig. 2(b). The stopping criterion described above was used in all cases except for the 20 projection images of slice B, where the number of iterations was determined to be that leading to the smallest number of image artifacts. Inspection of Fig. 2(b) revealed that TD reconstructions outperformed CW for all source-detector configurations when the imaging time was kept constant for both methods. Slice B in particular showed that the spatial resolution capability for the system was significantly improved by the use of TD methods. This was evidenced by the fact that the two inclusions in slice B could not be discriminated using CW but could be using TD data.

A quantitative comparison analysis of TD and CW reconstructions was performed using four figures of merit. The first one, with a target value of 100%, was the percentage of the total reconstructed fluorescence that was found within the confines of the known locations of the fluorescent inclusions. The second figure of merit was the contrast recovery (target value of 1), namely the ratio of the mean recovered fluorescence in the top inclusion divided by the mean recovered fluorescence in the bottom inclusion. The third figure of merit was the recovered centroid error (target value of 0 mm), corresponding to the distance between the center of mass of each recovered fluorescent inclusion and the position of the corresponding known location of the inclusion. Finally, a receiver operating characteristic (ROC) analysis was applied to each reconstruction based on a variable binary threshold of the image reconstruction compared to the known spatial distribution of the fluorophores. For each image, 100 fluorescence intensity thresholds were considered (between zero and the maximum pixel value) corresponding to different points on the ROC curve. For each threshold, every pixel was categorized as one of the following: a true positive (value was larger than the threshold and within an inclusion), a false positive (value was larger than the threshold and outside an inclusion), a true negative (value was less than the threshold and outside an inclusion), or a false negative (value was less than the threshold and within an inclusion). The area-under-the-curve (AUC) of each ROC curve was used to estimate the accuracy of each reconstruction. The optimal value, for a perfect imaging system, is AUC = 1, corresponding to both sensitivity and specificity being 100%. The results of these figures of merit are displayed in Table 1 for images reconstructed associated with slice A of the tissue phantom. As shown in Table 1, the figures of merit for slice A showed a clear and distinct trend confirming the qualitative observation derived from the images in Fig. 2(b): the TD method offered significant improvements in every category. In other words, FT reconstructions using time gates afford significant benefits compared to the CW technique when the number of optical projections is kept constant. Perhaps the most striking conclusion derived from Table 1 is that the 20- and 40-projection TD reconstructions were generally superior to the 320-projection CW reconstructions. However, only in the case of 40 projections or more were the results independent of which symmetric measurements subset (out of the 320 detected TPSF) was used, thereby illustrating that there is a limit associated with decreasing spatial tissue sampling. These results suggest that it is possible to truncate the number of optical projections in TD by about 1 order of magnitude and still retain the same analytical power associated with using conventional CW methods. The same conclusion was reached qualitatively by inspection of Fig. 2(b).

Table 1. Figures of Merit Used to Compare the Performance of TD and CW Image Reconstructions for Slice A of the Phantom Shown in Fig. 2(a).

Number of Projections		Image Overlap (%)		Centroid Error (mm)
	Data Type		Contrast Recovery	Target #1	Target #2	AUC
320	TD	31.6	1.13	0.884	0.987	0.986
	CW	15.2	1.35	1.07	1.07	0.909
160	TD	31.1	1.14	0.855	0.990	0.986
	CW	15.4	1.36	1.05	1.06	0.911
80	TD	31.6	1.11	0.912	0.937	0.988
	CW	12.1	1.43	1.50	1.35	0.861
40	TD	28.9	0.986	0.898	0.921	0.984
	CW	10.7	1.01	1.37	1.41	0.818
20	TD	28.7	0.808	0.857	1.22	0.945
	CW	16.9	0.92	1.28	1.31	0.874

The reconstruction results were supported by a singular value analysis (SVA). The singular value spectrum of the matrix J governing the forward model of an inverse problem can be used to gauge the conditioning of the inverse problem (e.g., relative amount of linear dependencies, sensitivity to shot noise propagation in the images) [6]. Figure 1(b) shows the singular value spectra for several Jacobians representing both TD and CW formulations for a various number of optical projections. The figure demonstrates that the use of TD information provides a significant improvement over CW for a given imaging geometry. In fact, the figure shows that for comparable levels of signal-to-noise (corresponding, as shown in [6], to a fixed singular value threshold), the TD Jacobians typically allow the inclusion of as much as twice as many singular modes in a reconstructed image.

Significant quantitative improvements have been demonstrated using TD methods over CW. In fact, all qualitative and quantitative figures of merit in this study show that TD methods are superior to CW. This TD method can be exploited to improve spatial resolution in a manner that is akin to early-photon imaging, but it can also be used to lower scan time with little loss in image quality (if any) because fewer optical projections are required due to the improved conditioning of the corresponding inverse problem. This can be useful for high throughput specimen imaging, and simultaneously has the potential to reduce motion-based imaging artifacts.