Structural Refinement from Restrained-Ensemble Simulations Based on EPR/DEER Data: Application to T4 Lysozyme

Abstract

DEER (Double Electron Electron Resonance) is a powerful pulsed ESR (electron spin resonance) technique allowing the determination of distance histograms between pairs of nitroxide spin-labels linked to a protein in a native-like solution environment. However, exploiting the huge amount of information provided by ESR/DEER histograms to refine structural models is extremely challenging. In this study, a restrained ensemble (RE) molecular dynamics (MD) simulation methodology is developed to address this issue. In RE simulation, the spin-spin distance distribution histograms calculated from a multiple-copy MD simulation are enforced, via a global ensemble-based energy restraint, to match those obtained from ESR/DEER experiments. The RE simulation is applied to 51 ESR/DEER distance histogram data from spin-labels inserted at 37 different positions in T4 lysozyme (T4L). The rotamer population distribution along the five dihedral angles connecting the nitroxide ring to the protein backbone is determined and shown to be consistent with available information from X-ray crystallography. For the purpose of structural refinement, the concept of a simplified nitroxide dummy spin-label is designed and parameterized on the basis of these all-atom RE simulations with explicit solvent. It is demonstrated that RE simulations with the dummy nitroxide spin-labels imposing the ESR/DEER experimental distance distribution data are able to systematically correct and refine a series of distorted T4L structures, while simple harmonic distance restraints are unsuccessful. This computationally efficient approach allows experimental restraints from DEER experiments to be incorporated into RE simulations for efficient structural refinement.

INTRODUCTION

Structural information is critical to understand the function of proteins. While X-ray crystallography is the best technique to obtain high-resolution structural information, it is also necessary to examine the protein in its native environment, free from the constraints imposed by the crystal lattice, to achieve a complete picture of its function. Two important spectroscopic approaches occupy a central role in these efforts, nuclear magnetic resonance (NMR) and electron spin resonance (ESR). One advantage of NMR is that it can report directly on the protein conformation through the nuclei in the system. In contrast, ESR requires the introduction of spectroscopic probes into the system via site-directed spin-labeling (SDSL) techniques, with the possible drawback that these could introduce unwanted perturbations. On the other hand, NMR investigations are limited by the size of the protein system, whereas the strong signal from the spin-label unpaired electron confers a sensitivity advantage to ESR even in the case of extremely large macromolecular complexes. Of particular interest, DEER (Double Electron-Electron Resonance) is a powerful ESR technique that makes it possible to measure the distance histogram between a pair of spin-labels inserted in a macromolecule.^1-3 While the experimental distance histograms between pairs of spin-labels contain a lot of information, designing a structural refinement strategy able to exploit the huge amount of data available from ESR/DEER is confronted with a number of challenges.

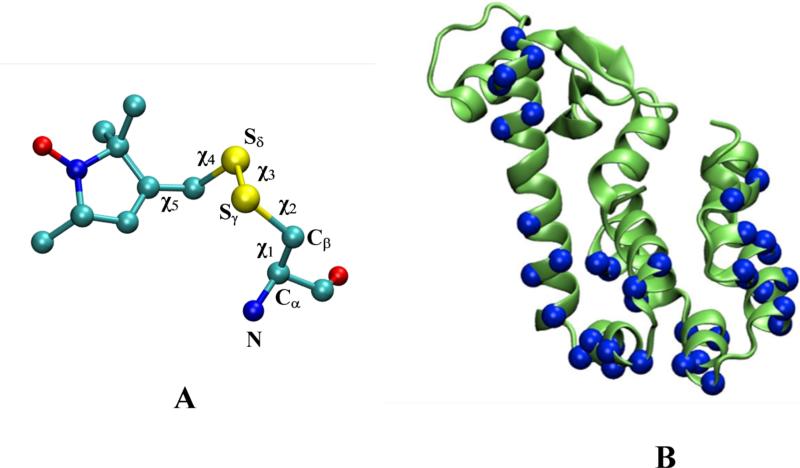
Any probe-based spectroscopic technique requires one to translate experimental measurements into valid information about the protein structure. In the case of ESR spectroscopy, such an operation is complicated by the internal dynamics of the spin-labels, rendering the extraction of detailed structural and dynamic information of the protein difficult. The most commonly used nitroxide spin-label used in ESR is MTSSL (1-oxyl-2,2,5,5-tetramethylpyrroline-3-methyl-methanethiosulfonate), which is typically linked to a cysteine residue in the protein through a disulphide bond (Figure 1A). The MTSSL moiety has five dihedral bonds, resulting in a highly flexible side-chain once it is linked to a protein. A reliable characterization of the dynamical properties of the spin-label is essential to fully exploit the available structural information from ESR/DEER spectra. The well-characterized soluble protein, T4 lysozyme (T4L, Figure 1B), has provided an important model system in the characterization of the conformational properties of MTSSL. Structural and spectroscopic analyses revealed general properties regarding the spin-label motion in protein capture in the “χ⁴/χ⁵ model” for solvent exposed helix surface (SEHS) sites in T4L.⁴ According to this model, internal motion of the spin-label side chain is essentially restricted to rotations about the dihedrals χ⁴ and χ⁵ and the remaining dihedrals are effectively “locked” on the ESR time scale. The χ³ disulphide torsion is opposed by a large energy barrier,⁵ while the χ¹ and χ² torsions are hindered by the formation of a hydrogen bond between the sulfur atom of the spin-label and the backbone amide⁶ and Cα.⁷ Such sulfur-backbone contacts are indeed observed in a number of X-ray crystal structures of T4L with spin-labels^8-15 in support of the χ⁴/χ⁵ model. Despite these efforts, there remains a paucity of data on the population of accessible rotamers of the MTSSL spin-label.

Figure 1.

(A) Side-chain resulting from linking MTSSL (1-oxyl-2,2,5,5-tetramethylpyrroline-3-methyl-methanethiosulfonate) to a cysteine through a disulfide bond. (B) Cartoon representation of T4 lysozyme with the 37 spin-labeled sites (colored in blue).

Computations can provide a “virtual route” to link the atomic structures to the experimental ESR observations. In principle, quantum mechanical ab initio methods offer the most accurate approaches to characterize the energy and conformations of the spin-labels.^16-18 However, these methods are too generally onerous to treat large protein systems and account for thermal fluctuations. Molecular dynamics (MD) simulations based on molecular mechanical force fields offer a realistic alternative strategy to calculate ESR observables.^19,20 For example, MD simulations were able to quantitatively reproduce multi-frequency spectra of spin-labels attached to T4 lysozyme with remarkable accuracy.²¹ Furthermore, the distance distributions from ESR/DEER experiments have been used to ascertain the validity and accuracy of MD simulations and structural models.^2,3,22-27 Computational modeling methods, such as the Multiscale Modeling of Macromolecular systems (MMM) software package of Yevhen Polyhach and Gunnar Jeschke ^28,29, and the PRONOX algorithm of Hatmal et al,³⁰ have been developed to determine the inter-label distances distributions based on the analysis of spin-label rotamers. Attempts were also made to build structural models based on elastic network model and MD simulations that satisfies ESR/DEER distance restraints. ²³ In spite of these efforts, there remains a need to develop a robust and effective computational method for making best use of ESR/DEER data in structural refinement.

Translating the ESR/DEER distance histograms into constraints that can be utilized in structural refinement is not straightforward. All the previous computational simulation studies^22-26 and modeling methods^28,30 use the ESR/DEER distance histogram in post-analysis, to assess the correctness of models that were generated independently from the experimental data. In other words, none of the existing methods “drive” the structural model toward a 3D conformation that satisfies the ESR/DEER data. The standard approach to incorporate experimental knowledge of any average property, 〈q(x)〉=Q, consists in simulating the system in the presence of an artificial energy restraint, k(q(x)-Q)², that biases the configuration x of the system toward the desired outcome.³¹ For example, this is how NOE (nuclear Overhauser effect) distances are imposed in NMR refinement. This approach, however, is not applicable in the case of ESR/DEER data; the measurements report distance histograms and trying to ascribe a single average distance between any pair of atoms (e.g., backbone Cα) is not a valid approximation. A more sophisticated strategy is based on the notion of “restrained-ensemble” (RE) molecular dynamics (MD) simulations introduced by Vendruscolo and co-workers,^32-36 and exploited by Im and co-workers to determine the structure of membrane-bound peptides on the basis of solid state NMR observables.^37-40 Such restrained-ensemble MD simulation scheme consists in carrying out parallel MD simulations of N replicas of the basic system in the presence of a biasing potential that enforces the ensemble-average of a given property toward its known experimental value. Recently, the formal equivalence between the results from restrained-ensemble MD simulation scheme and the maximum entropy method for biasing thermodynamics ensembles⁴¹ was established.⁴² This analysis led to the development of a novel method to incorporate ESR/DEER distance histogram data into multiple-copy restrained-ensemble MD simulations.⁴³ In the RE simulations, distributions of the spin-spin distances are constrained by the spin pair distance histograms obtained from ESR/DEER experiments. While the methodology based on RE simulations is designed to enforce a given set of real-space distance histograms for the purpose of structural refinement, in practice, such distance histograms are obtained by post-processing the measured time-dependent ESR/DEER signal.²⁹ The construction of distance histograms from DEER measurements is a challenging inverse problem that necessitates the utilization of specialized regulation procedures. While our main focus is to enable structural refinement based on experimental data, it is important to keep in mind that the distance histograms can be sensitive to the treatment of the inverse problem.

In the present study, detailed RE simulations based on ESR/DEER data for 51 spin-label pairs inserted at 37 positions in T4L are used to provide a rich source of detailed information about the rotameric states of the MTSSL spin-labels. Using this unprecedented new information from RE simulations and ESR/DEER data, a simplified nitroxide dummy spin-label is then parameterized for the purpose of structural refinement. Finally, the usefulness of the method is illustrated by showing that RE simulations with the dummy nitroxide spin-labels imposing the ESR/DEER experimental distance distribution data are able to systematically correct a series of distorted T4L structures.

METHODS

a) ESR experiments

Nitroxide spin-labels were inserted at 37 different positions in T4 lysozyme (T4L), for a total of 51 different pairs for DEER experiments. The position of the spin-labels in the T4L structure and their relationship to secondary structure elements is summarized in Table 1. All double mutants of T4L used in this study are shown in Supplemental Table S1. Cysteine mutants generated for this study were introduced into the cysteine-free T4L DNA by site-directed mutagenesis.³ Protein expression, purification, and labeling with MTSSL were carried out as previously described.^1,3,6 DEER measurements were preformed on a Bruker 580 pulsed ESR spectrometer operating at either X- (9.6 GHz) or Q- (33.4 GHz) band using a standard four pulse protocol.⁴⁴ Data was collected with the samples at 83 K with 23% (v/v) glycerol as cryoprotectant. Analysis of the DEER data to determine the distance distributions was carried in DeerAnalysis2010 or DeerAnalysis2011.⁴⁵ The data was fit with Tikhonov regularization and L-curve determination of the optimal regularization parameter.⁴⁶ The distance distributions were subsequently converted to 1 Å bins and normalized for use in the RE simulations using a script implemented in MATLAB.

Table 1.

Spin-label positions in T4 Lysozyme, number of spin-spin distance distributions and spin-label rotameric states obtained from RE simulation.

Secondary structures	Number of spin-labels	Number of ESR/DEER histograms	Labeled residues	χ1/χ2rotamer
				χ3 =+90°(p)	χ3 =-90° (m)
Turn (59)	1	1	59	tp	-
H1 (60-80)	9	25	60	-	mm
			61	-	mm
			62	mm	mm
			64	mt	-
			65*	-	mm
			72*	mm, mt	-
			75	mt	-
			76*	-	mm, tm
			79	mt	-
H2 (82-90)	6	8	82*	-	mm
			83	-	mm
			85	-	mm
			86	mt	-
			89	-	mm
			90	-	tt
H3 (93-106)	2	6	93	-	mm
			94	mt	-
H4 (108-113)	3	6	108	-	mt, mm
			109	-	mm
			112	mt	-
H5 (115-123)	5	13	115*	mt	-
			116	mt	-
			119*	mt	-
			122	mt	-
			123	pp1	pt1, pp1
H6 (126-134)	5	15	127	-	mm
			128	mt	-
			131*	-	mm
			132	mt	mm
			134	mt	-
Turn (135)	1	2	135	-	mm
H7 (137-141)	1	1	140	-	mm
H8 (143-155)	3	13	151*	mt	mm
			154	mt	-
			155	-	mm
Turn (159)	1	1	159	mt	-

¹these rotameric states were populated by less than 30%

^*A crystallographic X-ray structure is available for a spin-label at this position (Table 5)

b) Computational details

Molecular dynamic simulations of spin-labeled T4L were carried out with the CHARMM⁴⁷ and NAMD⁴⁸ programs, using the all-atom CHARMM27 protein force field⁴⁹ with the CMAP corrections.⁵⁰ The force field parameters for the nitroxide spin-label developed by Sezer et al.¹⁹, which were found to provide very accurate multi-frequency ESR spectrum in previous studies,^19-21 were employed for the description of the nitroxide spin-labels. The crystal structure of native T4L (2LZM)⁵¹ was used to construct the initial geometry of the T4L system with its spin-labels. Since 37 sites in total were experimentally labelled, it is not possible to introduce all of the nitroxide spin-labels simultaneously into a single protein without extensive steric clashes. To avoid this problem, four copies of the protein (A, B, C, D) were included in the simulation cell (Figure 2) and the 37 spin-labels were distributed among the four copies to ensure that they do not interact with each other. Each copy comprises 9, 9, 9 and 10 spin-labels, respectively. The labeled residues are: [59, 64, 76, 83, 89, 108, 128, 135, 140, 154] in A, [60, 65, 85, 90, 115, 123, 127, 131, 151] in B, [62, 72, 79, 86, 93, 112, 119, 132, 155] in C, and [61, 75, 82, 94, 109, 116, 122, 134, 159] in D. All spin-labels are separated by at least a distance of 10-15Å. To ensure that the four proteins do not interact with each other, the center of mass of each adjacent T4L were separated by 80Å. The whole system thus constructed has a total of 11349 atoms, and is solvated by 41547 TIP3P water molecules within a 160 × 60 × 130 Å rectangular box. The salt concentration was maintained at 0.15 mM/mol by adding 44 potassium and 117 chloride ions. For all the simulations, a weak positional harmonic restraint with a force constant of 1 (kcal/mol)/Ų was applied to the protein backbone to avoid any large displacement. Three different simulation methodologies were utilized in this study: conventional molecular dynamics (MD), locally enhanced sampling (LES)^52-54 and restrained-ensemble (RE) simulations.⁴³

Figure 2.

The simulation set up consisting of 37 spin-labeled side chains distributed in four T4L systems. The distance between the center of mass of each T4L are 80Å from each other; thereby, they are far enough to cause any interaction. Similarly, the spin-label side chains were also kept at least four residues apart with a distance of about 10-15Å from each other; therefore, the interaction between the spin-labels are also minimum. The copies of the spin-labels were generated with CHARMM using the command REPLICA.

Conventional MD Simulation Protocol

Prior to LES and RE simulations, the simulation box was minimized, equilibrated and a 140 ns MD simulation was performed with NAMD⁴⁸. Both equilibration and production simulations were performed under NPT conditions where the temperature was kept at 300 K and the pressure at 1 atm to remain consistent with experimental conditions. The simulations were performed with Langevin⁵⁵ thermostat to control the temperature of the simulation box. A collision frequency, γ, of 5.0 ps^-1 was used for the Langevin thermostat. A dielectric constant of 1.0 was used during the simulation. Bonds involving hydrogen atoms in water were constrained to their equilibrium values using the SHAKE⁵⁶ algorithm. Periodic boundary conditions (PBC) were imposed and a cutoff of 10Å was used for nonbonded interactions with a switch distance of 8Å and pairlist distance of 12Å. Long-range electrostatic behaviour was controlled with the particle mesh Ewald (PME) method.^57,58 First, the conjugate gradient energy minimization was performed for 1000 steps to eliminate initial bad contacts between various atoms. This was then followed by a short equilibration run of 5ns. Then the production MD simulation was performed for 140ns from which the ensemble averaged properties of the spin-labels were calculated. Even with such a long trajectory, it is possible that these ensemble average properties are weighted to the starting rotamers due to the lower probability of the interconversion of the disulfide bond.⁵

Locally Enhanced Sampling Simulation Protocol

The Locally Enhanced Sampling (LES) method,^52-54,59 aims at increasing the sampling efficacy of conformational space of selected groups of atoms relative to conventional MD simulations. LES consists in introducing N non-interacting copies (replicas) of selected groups of atoms, which then interact with the rest of the system with forces that are scaled down by a factor of 1/N. According to an approximate mean-field argument, the statistical distribution of the configurations resulting from LES is expected to be representative of the single-copy conventional MD. To try improving the sampling efficacy of the nitroxide spin-labels conformations using the LES method, all 37 labeled residues were replicated 25 times including their backbone atoms. The multiple copies were generated using the psfgen module of vmd (Visual Molecular Dynamics)⁶⁰ visualization program. The temperature of the replicated atoms was scaled by a factor of 1/N and the masses of the enhanced atoms were also reduced by the same factor to restore the normal velocity distribution. The temperature of the rest of the molecule was kept at 300 K. The last frame from the 140 ns MD simulation was used to start the LES simulation; therefore the system is already well equilibrated. The simulation was performed with NAMD⁴⁸ keeping the backbone atoms of the T4L restrained to their X-ray structure by applying positional restraints with a harmonic force constant of 1 (kcal/mol)/Ų. The production LES simulation was performed for 7ns after an initial 1000 steps of minimization and 1ns of equilibration. All the other simulation parameters were kept the same to those used in the conventional MD simulation.

Restrained Ensemble Simulation Protocol

The restrained ensemble (RE) method was recently developed to exploit the information from experimental distance histograms obtained from ESR/DEER experiments.⁴³ The RE ensemble as implemented here builds on the framework provided by the multiple-copy LES simulation method. As in LES, an ensemble of N non-interacting replicas was created for each spin-label side chain of the basis system (Figure 2). The multiple replicas yield a total of N² distances for each pair of spin-labels. Based on these distances, an energy restraint was implemented in CHARMM⁴⁷ so that at every step of the simulation the histogram obtained from the N² spin-spin distances would be forced to match the experimental distance histogram obtained from the DEER experiment. The possibility of restraining the simulations from the time-dependent DEER signal rather than the post-processed distance histograms was discussed previously.⁴³ To avoid discontinuities between the bins, a smooth Gaussian of width σ is used in the construction of the histograms. Let h̄^ij(n) be the ensemble-averaged “instantaneous” histogram produced by the multiple replica and H^ij(n) be the target experimental histogram. We introduce the energy restraint on all the spin-label i-j pairs, in the system,

$$U_{RE}=\frac{1}{2}K\sum _{\left\{\text{pair}ij\right\}}\sum _{\left\{\mathrm{bin}n\right\}}{\left({\stackrel{‒}{h}}^{ij}\left(n\right)-H^{ij}\left(n\right)\right)}^2$$ (1)

where K is a large harmonic force constant used to enforce the restraint. The ensemble-average histogram h̄^ij(n) is calculated as,

$${\stackrel{‒}{h}}^{ij}\left(n\right)=\frac{1}{N^2}\sum _{s=1}^N\sum _{s^{\prime }=1}^N\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left[\frac{\left(n\Delta r-\mid {\mathbf{r}}_i^s-{\mathbf{r}}_j^{s^{\prime }}\mid \right)}{2{\sigma }^2}\right]$$ (2)

where $\mid {\mathbf{r}}_i^s-{\mathbf{r}}_j^{s^{\prime }}\mid$ is the distance between the spin-label i and spin-label j. Both the experimental and the calculated histograms are recorded with the same bin size Δr of 1 Å, and are normalized to 1 (the distributions h̄^ij(n) and H^ij(n) have dimension of inverse length, and the units of the force constant K is (kcal/mol)/Ų. For details about the implementation of the RE method, see Ref. ⁴³.

All the spin-labels were replicated 25 times using the command REPLICA in CHARMM. Interactions between the replicas and the rest of the system were scaled by 1/25 using the BLOCK command; interactions within each replica were not scaled. A harmonic force constant K of 10000 (kcal/mol)/Ų was used to impose the energy restraint to match the calculated distributions h̄^ij(n) with those of the experiment H^ij(n), and the natural spread σ of the Gaussian was set to 1.7Å. A total of 51 spin-spin distance histograms obtained from ESR/DEER experiments are used simultaneously in the RE simulations of the system. Large displacements of the protein backbone atoms were prevented by applying positional restraints with a harmonic force constant of 1 (kcal/mol)/Ų relative to the X-ray structure. At each time-step, the distance histogram between any selected pair of spin-labels was calculated from Cartesian coordinates of the four protein translated to a unique reference frame. For example, there is an experimental DEER histogram for spin-labels at positions 62 and 109 even though they are located in protein C and D, respectively. To calculate the instantaneous ensemble-average histogram of the pair h̄^62,109(n), the C and D protein systems are translated to a unique reference frame and then the distance between the spin-label at position 62 and the spin-label at position 109 is calculated.

To reduce the size of the simulated system, only the water molecules within 35Šfrom the center of mass of each T4L system were kept, for a total of 19479. A spherical half-harmonic containing restraint with a force constant of 0.5 (kcal/mol)/Ų was used to keep the waters near the proteins. Both equilibration and production simulations were performed under NVT conditions where the temperature for both replica spin-label atoms and normal atoms were kept at 300 K. The rest of the simulation parameters were kept the same to those used in the conventional single-copy MD and LES simulations. To increase the efficiency, five realization of the RE ensemble were simulated simultaneously. They were initiated from the frames at 60, 80, 100, 120 and 140 ns of the single-copy MD simulation after energy minimization and equilibration for 1 ns; 8ns RE simulation was performed for each of the five systems, providing a total of 40ns RE simulation.

Data Analysis Protocol

Spin pair distances and dihedral angles were collected every 10 ps from 140 ns conventional single-copy MD simulation. Thus a total of 14000 data points were obtained for each spin pair distances and dihedral angles. These data were used to calculate the spin pair distance distributions and the rotamer population distributions along five dihedral angles of a particular spin-label. A total of 518000 data points for every dihedral angle were obtained from 37 spin-labels. This enormous amount of data was used to calculate the global rotameric states of the spin-label side chain. For both LES and RE simulations, a total of 625 spin pair distances were obtained from a single simulation step since each spin-label is replicated to 25 copies. The spin pair distances were collected every 10 ps from the last 1ns of the trajectory providing a total of 625000 distances from the simulations, which were then used to calculate the distance distributions. Data for the dihedral angles were collected every 10 ps from the 7ns LES and the 40 ns RE simulations. Since for every spin-label there are 25 copies, a total of 17500 data points were obtained for every spin-label yielding a total of 647500 data points from LES simulation. Following the same procedure, the 40 ns RE simulation provided a total of 987500 data points for every spin-label and a total of 3695375 data points from all spin-labels. These data were used to calculate the dihedral angle distributions. The potential of mean force (PMF) or the change in free energy along the dihedral angles was also calculated by integrating the rotamer population distributions.

RESULTS AND DISCUSSION

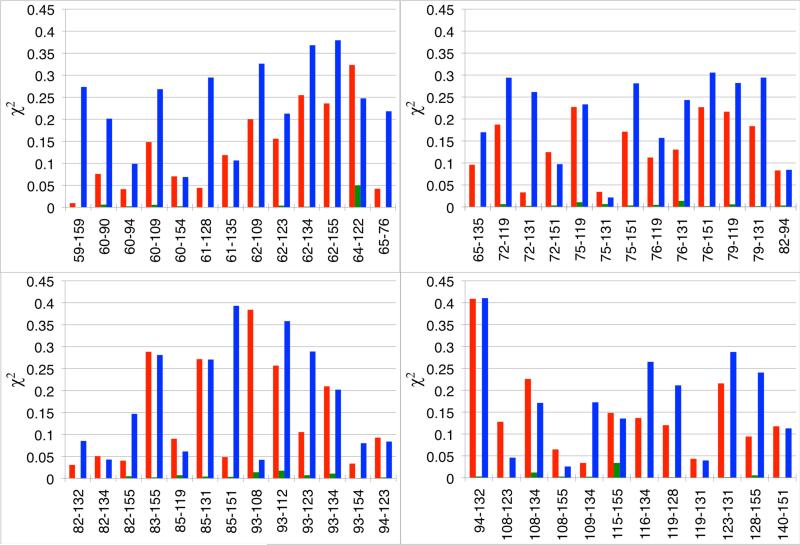
As expected, the 51 spin-label distance histograms obtained from the multiple-copy restrained-ensemble (RE) simulation are very similar to those obtained from ESR/DEER data. It is, however, worth emphasizing that satisfying all the distance histograms simultaneously did not generate any unacceptable distortions of the spin-labels, which are attached to protein backbone restrained near the X-ray structure. This is strongly suggestive that the set of 51 distance histograms generated from the post-processing of the time-dependent DEER signal is broadly consistent with the X-ray structure of T4L and the chemically-acceptable range of conformational flexibility of the MTSSL spin-label. In contrast, the distance histograms obtained from conventional MD and the locally enhanced sampling (LES) differ considerably from experiment (see Figure S6 in the supporting information for all 51 distance distributions). It is possible to rapidly quantify differences in the 51 distance distributions obtain from MD, LES and RE simulation from the total mean-square deviation relative to the DEER data,

$${\chi }^2=\sum _{\left\{\text{pair}ij\right\}}\sum _{\left\{\mathrm{bin}n\right\}}{\left({\stackrel{‒}{h}}^{ij}\left(n\right)-H^{ij}\left(n\right)\right)}^2$$ (3)

As shown in Figure 3, the values of χ² for most of the spin-spin distance histograms are large for MD and LES, while they are very small for RE. In most cases, χ² from LES is slightly larger than from MD, which is perhaps explained by the approximate nature of the multiple-copy mean-field argument underlying the method. Because the protein backbone was restrained to remain near the X-ray structure, these differences can be directly traced back to the conformations of the flexible spin-labels themselves. Clearly, the unbiased sampling from MD and LES produces spin-label conformations that are in fairly substantial disagreement with experimental data. The discrepancy may, in part, reflect inaccuracies in the molecular mechanical force field used in the simulations. However, it is also important to recall that the samples for ESR/DEER experiments are fast-frozen, and the conformational probability of the flexible spin-labels would reflect the proper Boltzmann distribution at room temperature only if the freezing process was infinitely fast (quenching). On the other hand, if the freezing is slow on the timescale of some molecular motions, the conformational distribution will partly drift toward lower temperature population distributions during the process (annealing). Ultimately, it is likely that some slow degrees of freedom are truly quenched while fast degrees of freedom such as side-chain rotamers are partly annealed to local energy conformations.⁶¹ The implication is that the information from the distance histograms imposed via the RE simulations significantly restricts the conformation of the spin-labels, which provides a unique opportunity to determine the conformational propensity of MTSSL nitroxide spin-labels in multiple positions of a soluble protein under the conditions of ESR/DEER experiments.

Figure 3.

Difference in spin-spin distance histograms between experiment and conventional MD (red line), locally enhanced sampling (blue line) and restrained ensemble (green line) simulations.

a) Analysis of the T4L simulations and rotameric distributions of MTSSL

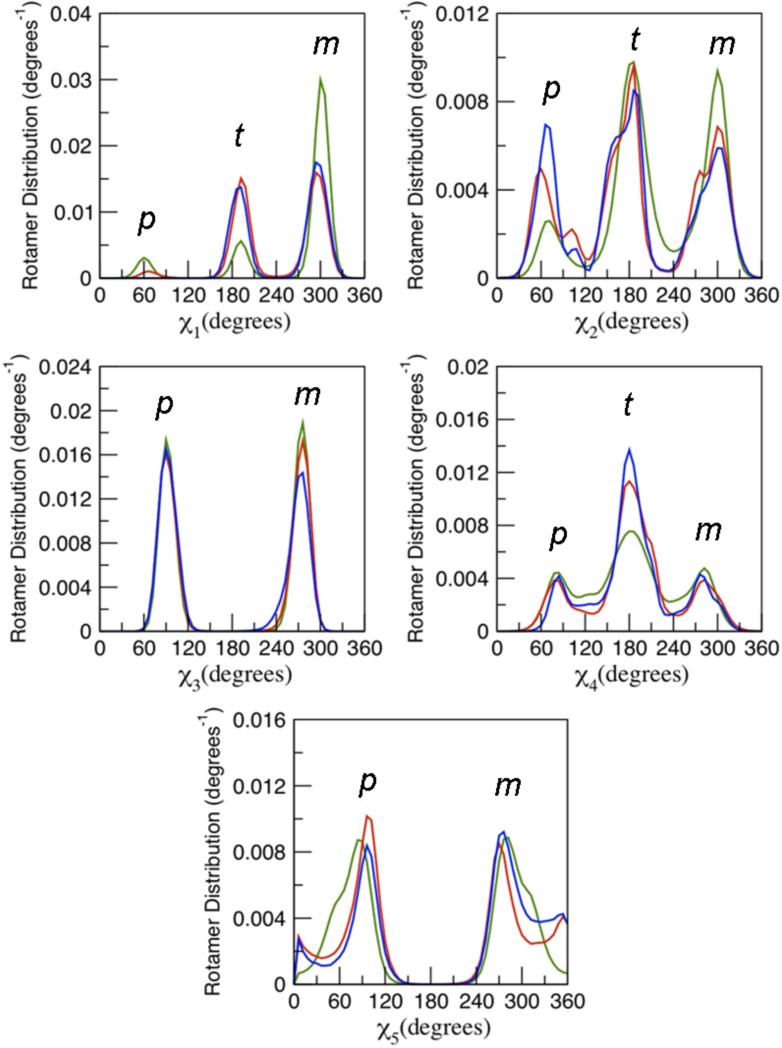
The conformation of the MTSSL nitroxide spin-label is completely characterized by the five dihedral angles, χ¹, χ², χ³, χ⁴ and χ⁵ along the flexible side-chain Cα-Cβ-Sγ-Sδ-Cη-Cζ (Figure 1A). The distribution about the χ¹, χ², χ³, χ⁴ and χ⁵ of all the spin-labels obtained from MD, LES, and RE simulations is shown in Figure 4. For the sake of simplicity, it will be useful to adopt the following convention in the following discussion. The dihedral angles χ¹, χ², and χ⁴ can adopt 3-fold conformations, +60° (or gauche⁺), 180°(or trans), and –60° (or gauche^-), which will be denoted by p, t and m, respectively. According to the RE simulations, the m rotamer for χ¹ is the most populated, while the rotamers from the conventional MD and LES simulations are more broadly distributed. Similarly, the m rotamer for χ² is also the most populated according to the RE simulations, with again a broader distribution from the conventional MD and LES simulations. The distributions of the dihedral angle χ³ of the slowly converting Sγ-Sδ disulfide bond are similar for all three simulations. Essentially, χ³ can adopt only two stable positions, around +90° and -90° (=270°), which will be denoted as p and m, respectively. The last dihedral angle, χ⁵, between the chain and the ring is broadly distributed, with two positions slightly more populated around +90° and -90°, which will be denoted as p and m, respectively. The p and m states were visited for 22 spin-labels in the RE simulation, but only for 11 spin-labels in the conventional MD simulation (Figure S7). Lastly, the rotamer distributions for χ⁴ and χ⁵ obtained from all simulation methods are very similar (Figure 4), suggesting that considerable fluctuations around these two dihedrals are consistent with the ESR/DEER data.

Figure 4.

Rotamer population distribution of the dihedral angle χ¹, χ², χ³, χ⁴ and χ⁵ of the MTSSL spin-label obtained from the conventional MD (red line), locally enhanced sampling (blue line) and restraint ensemble (green line) simulations. All the data from all the spin-labels attached to T4L were combined together to produce the distributions.

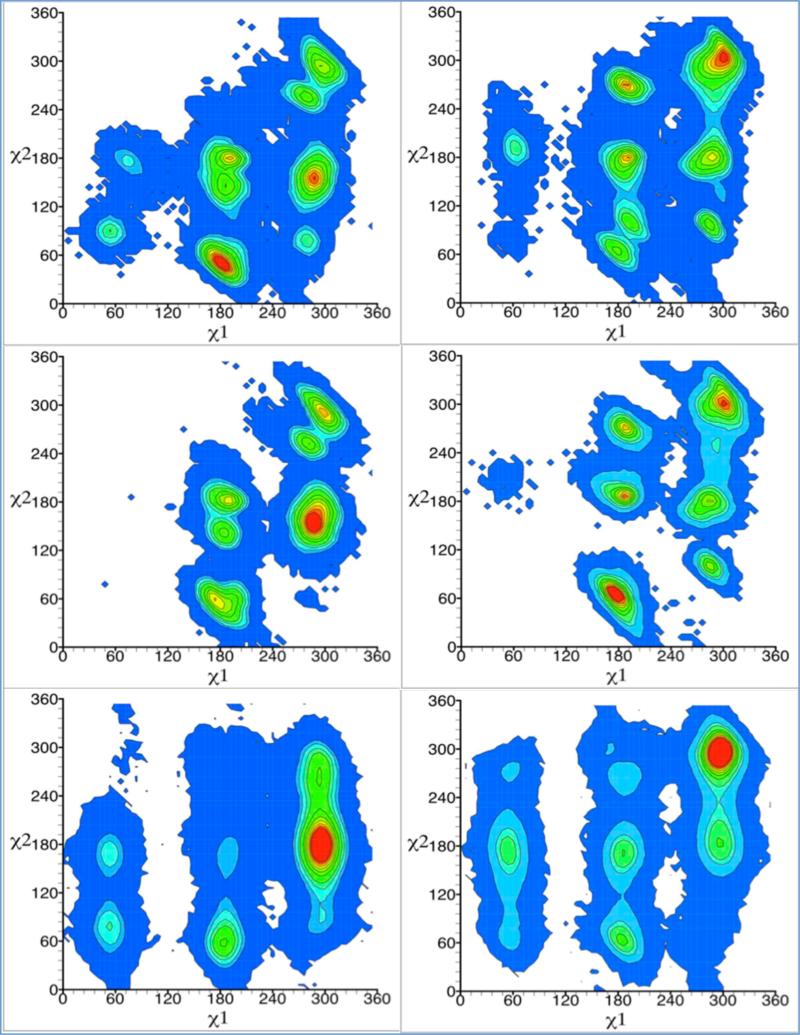
The joint 2D distributions along χ¹ and χ² for prescribed values of χ³ obtained from the MD, LES and RE simulations are shown in Figure 5. The populations of the χ¹/χ² rotameric states are given in Table 2. According to all simulation methods, it is clear that the χ¹/χ² rotamer distribution is strongly affected by the χ³ dihedral angle of the Sγ-Sδ bond. This is consistent with previous studies that have highlighted the correlations between the various dihedrals.^19,28 Only two predominant χ¹/χ²/χ³ joint rotameric states are observed with the RE simulation, mtp (33%) and mmm (32%), whereas several are observed in the LES and MD simulations. This shows that sampling of the conformational space while restraining the spin-label pair via the ESR/DEER distance histograms leads to a considerable reduction in the observed rotameric states. The 2D PMF calculated from the distributions reveal that the free energy barrier between the mt and mm states is only about 1-2 kcal/mol (Figure S8) suggesting the possibility of rapid inter-conversion rates for these dihedral angles. The 2D rotamer population distribution along χ⁴ and χ⁵ shows that they are only weakly correlated. Regardless of the simulation methods, the distribution along χ⁴ and χ⁵ are very similar and fairly independent of the value of χ³ (Figure S9). The populations of the χ⁴/χ⁵ rotameric states are given in Table 3. The results are consistent with the notion that the χ⁴ and χ⁵ dihedral are very mobile, an underlying hypothesis of the so-called χ⁴/χ⁵ model ^4,7, which assumes that the internal motion of the spin-label is largely limited to rotations about the last two dihedrals. Nonetheless, as observed previously²¹, the χ⁴ and χ⁵ dihedral display some intrinsic rotameric preferences. Overall, the LES method appears to produce distributions that cover somewhat less rotameric space than the conventional MD simulation. This might indicate that there are differences in the amount of sampling. Alternatively, it is possible that the results are adversely affected by the mean-field approximation that underlies the LES method.^52,59 Nevertheless, the differences are not sufficiently large to cause concerns, which is reassuring given that the same mean-field approximation is also used in the multiple-copy RE ensemble implementation based on ESR/DEER distance histograms.⁴³

Figure 5.

Rotamer population distribution along χ¹ and χ² of spin-label attached to T4 Lysozyme at χ³ ≈ 90° (left panel) and 270° (right panel) obtained from conventional MD (upper panel), locally enhanced sampling (middle panel) and restraint ensemble ((lower panel) simulations. The units of the angles χ¹ and χ² are in degrees. Population densities are indicated with contour lines with densities increasing from blue to red color.

Table 2.

Rotamer population (%) along χ¹ and χ² of the spin-label attached to T4 Lysozyme at χ³ ≈ 90° and 270° obtained from conventional MD (MD), locally enhanced sampling (LES) and restraint ensemble (RE) simulations.

χ 3	χ1/χ2	MD	LES	RE	χ 3	χ1/χ2	MD	LES	RE
	pp	1.10	0.00	1.51		pp	0.03	0.00	0.66
	tp	13.33	10.00	4.17		tp	5.04	12.95	3.89
	mp	1.20	0.09	0.90		mp	2.58	2.66	0.16
	pt	0.72	0.00	1.18		pt	1.25	0.02	4.23
p (+90°)	tt	11.31	8.35	1.10	m (270°)	tt	7.71	5.80	4.16
	mt	12.20	22.09	33.00		mt	8.44	7.20	6.13
	pm	0.0	0.00	0.01		pm	0.02	0.00	0.34
	tm	0.12	0.04	0.19		tm	6.74	5.27	1.10
	mm	9.25	10.89	5.63		mm	18.96	14.66	31.64
	Total	49.23	51.46	47.48		Total	50.77	48.56	52.31

Table 3.

Rotamer population (%) along χ⁴ and χ⁵ of the spin-label attached to T4 Lysozyme at χ³ ≈ 90° and 270° obtained from conventional MD (MD), locally enhanced sampling (LES) and restraint ensemble (RE) simulations.

χ 3	χ4/χ5	MD	LES	RE	χ 3	χ4/χ5	MD	LES	RE
	pp	1.62	1.11	4.13		pp	1.33	0.27	5.59
	tp	16.44	15.65	12.65		tp	15.26	8.92	14.63
	mp	8.06	10.09	6.21		mp	5.89	2.46	5.31
	pt	0.62	0.47	0.07		pt	0.09	0.07	0.11
p (+90°)	tt	0.61	0.68	0.25	m (270°)	tt	0.72	0.36	0.30
	mt	0.20	0.18	0.09		mt	0.33	0.11	0.10
	pm	6.10	8.26	3.79		pm	7.71	5.45	8.20
	tm	12.71	9.71	14.16		tm	17.78	30.20	13.48
	mm	2.85	5.30	6.31		mm	1.68	0.70	4.60
	Total	49.21	51.45	47.67		Total	50.79	48.54	52.33

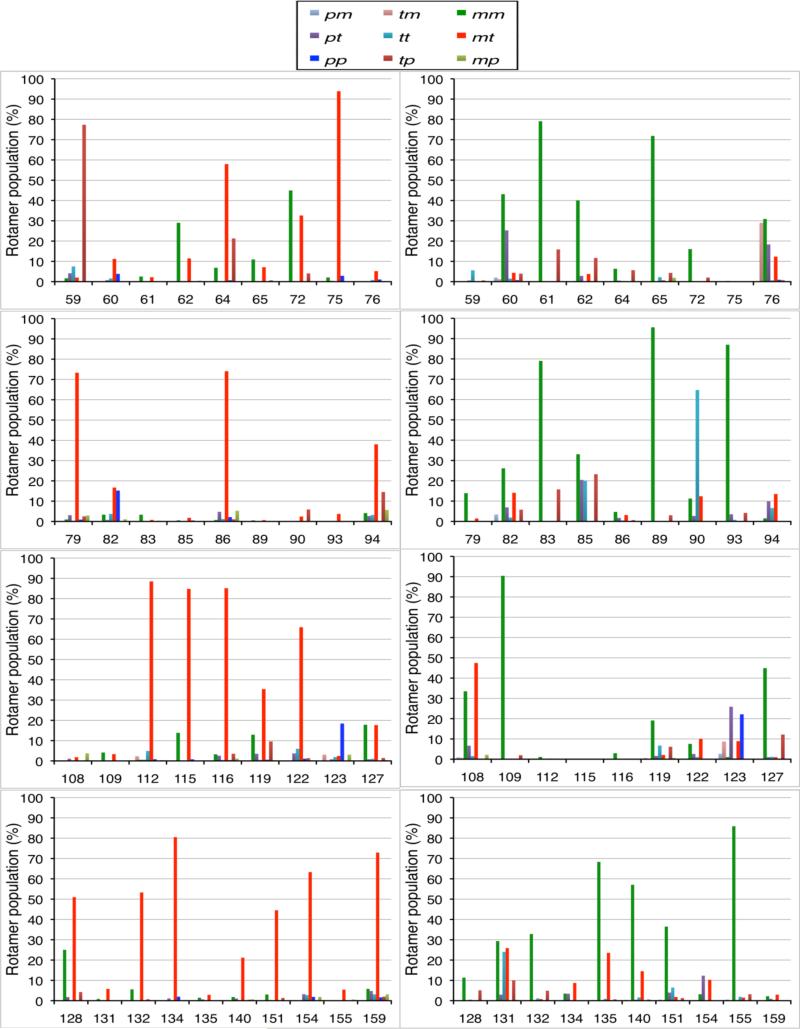
It is of interest to examine how the rotamer distribution at specific positions departs from the average trend. The results are summarized in Table 4. Due to its particular importance, it is helpful to first focus on the dihedral around the Sγ-Sδ bond, χ³. Isomerization of the Sγ-Sδ bond is opposed by a large energy barrier⁵ and is a relatively slow process on the timescale of ESR.²¹ Furthermore, the m:p equilibrium ratio was previously shown to be a critical determinant of the line shape of CW-ESR spectra.²¹ As observed in Table 4, χ³ shows a preference for either +90° (p) or -90° (m) in most cases. Spin-labels at positions 59, 64, 72, 75, 79, 86, 112, 115, 116, 122, 128, 134, 154 and 159 mainly prefer +90° (p) with population more than 70%, while spin-labels at positions 60, 61, 65, 76, 83, 85, 89, 90, 93, 108, 109, 123, 131, 135, 140 and 155 mainly prefer-90° (m).Only 7 spin-labels (positions62, 82, 94, 119, 127, 132 and 151) show significant occupancy of both rotamers. When χ³ is +90° (p), the preferred χ¹/χ² rotameric state is typically mt(Table 1 and Figure 6). This is observed at 16 positions along the α-helices, a number of them being near the C-terminus (79, 94, 112, 122, 132, 134, 154). When χ³ is -90° (m), the preferred χ¹/χ² rotameric state is typically mm. This is observed at 18 positions located along α-helices, a number of them being near the N-terminus (60, 61, 82, 83, 93, 108, 109, 127, 151). Few spin-labels (72, 108, 132, 151) also display both the mm and mt rotamers. The marked preference of χ¹/χ² for the mm and mt rotamers is consistent with the energy surface of the spin-label,¹⁹ suggesting that the surrounding residues do not lead to large effects. Returning to Table 1, it is clear that spin-labels inserted within α-helics largely prefer the χ¹/χ²/χ³ rotameric states mmm or mtp on average. The spin-labels that display a wider variability are either near the ends of an helix, in a loop, or buried. For example, spin-labels at positions 59, 90, and 123 are found to be in the unusual χ¹/χ²/χ³ rotameric state tpp ttm, and ppp, respectively. Position 59 is located in a loop while position 90 is buried within the solvent inaccessible protein core, and position 123 is the last residue of helix H5. Finally, regarding the χ⁴/χ⁵ rotameric state, the majority are either tp or tm. Only two positions are in the rotameric states mm(position 109) or tp (position 115) with a population greater than 50%. The predominance of these tp and tm rotamers is consistent with the initial parameterization of the spin-label.¹⁹ This suggests that these rotamers are predominant unless there are steric clashes with neighboring residues.

Table 4.

Total rotamer population (%) of χ¹ and χ² at χ³ ≈ 90° and 270° of the spin-label attached to the T4 Lysozyme obtained from restraint ensemble (RE) simulations.

Residue	p (+90°)	m (270°)	Residue	p (+90°)	m (270°)	Residue	p (+90°)	m (270°)
59	92.78	7.22	86	89.23	10.77	127	39.42	60.58
60	17.86	82.14	89	1.20	98.80	128	82.71	17.29
61	4.74	95.26	90	8.65	91.35	131	7.18	92.82
62	41.57	58.43	93	4.22	95.78	132	59.82	40.18
64	87.14	12.86	94	68.26	31.74	134	84.17	15.83
65	18.79	81.21	108	6.75	93.25	135	5.73	94.27
72	81.82	18.18	109	7.48	92.52	140	25.25	74.75
75	99.63	0.37	112	98.30	1.70	151	49.47	50.53
76	7.16	92.84	115	100.00	0.00	154	73.75	26.25
79	84.13	15.87	116	96.52	3.48	155	6.53	93.47
82	41.28	58.72	119	63.04	36.96	159	93.39	6.61
83	4.47	95.53	122	78.40	21.6
85	2.98	97.02	123	29.98	70.02

Figure 6.

Population of χ¹/χ² rotamers when χ³ is in the p state around +90° (left panel) or when χ³ is in the m state around -90° (right panel) for the 37 individual spin-labels attached to T4L obtained from RE simulations.

b) Comparison with available rotamer data from X-ray crystallography

Comparison with the available information from X-ray crystallographic structures of MTSSL spin-labels inserted into T4L^9-11 offers a powerful route to examine the validity of the rotamers populations extracted from the RE simulations. However, several X-ray structures, the electron density along the flexible side-chain Cα-Cβ-Sγ-Sδ-Cη-Cζ is missing beyond the Sδ atom, leaving the position and the orientation of the remaining chain and nitroxide ring undefined. In the small number of X-ray structures in which the Cη is resolved, it is observed that the dihedral angle χ³ of the Sγ-Sδ bond adopts either values of +90° or -90°. Transitions between these two well-identified states are opposed by a large energy barrier and occur infrequently according to computational analysis.^21,49 For this reason, comparison with X-ray data is mainly limited to χ¹/χ², corresponding to the region of the side-chain nearest to the backbone Cα-Cβ-Sγ-Sδ. The result of a comparison for spin-labels at nine positions (65, 72, 75, 76, 82, 115, 119, 131, 151) is given in Table 5.

Table 5.

Comparison of χ¹ and χ² rotamers of the spin-labels obtained from X-ray structures and RE simulations.

Residue	PDB ID	Exptl. Rotamer*	RE simulations*
65	3K2R	tp a,b,c	mm (83%)
72		(mm, tp)d	mm (64%), mt (32%)
75	-	mt a	mt (93%)
76	3K2R	tm c	tm; mm (30% each)
82	1ZYT	mm a,e	mm, mt (30% each)
115	2IGC, 2OU8	mm a,f	mt (84%), mm (15%)
	2OU8	tp a,f
119	3L2X	mm f	mm, mt (35% each)
131	2CUU(1), 3G3V(1)	mm a,e	mm, mt (30% each)
		(mm, tp, mt, tt)d	tt (25%), tp (10%)
	2CUU(2), 3G3V(2)	tp d,g
151	3G3X	mm e	mt (45%), mm (40%)

^aFleissner et al.¹³

^bLangen et al.¹⁵

^cToledo et al.¹⁴

^dSezer et at.²¹

^eFleissner et al.^11,12

^fGuo et al.¹⁰

^gGuo et al.⁹

The χ¹/χ² rotamers extracted from the RE simulations are broadly consistent with the information from the X-ray crystal structures for seven positions: a mm rotamer is observed at 72, 82, 115, 119, 131, and 151, a mt rotamer is observed at 75, and a tm rotamer is observed at 76. Analysis of the RE simulations suggests that the free energy difference between mm and mt is small. In the case of position 131, analysis of multifrequency ESR spectra using MD simulations concluded the rotamers mm, mt, tp, and tt were predominant.²¹ All four rotamers are observed in the RE simulations, and the first one is observed in the X-ray structure. In the case of position 72, there is no X-ray structure, but there is indirect information from analysis of multifrequency ESR spectra using MD simulations indicating that the mm and tp rotamers are the most stable,²¹ which is consistent with the results from RE simulations. The clearest disagreement concerns spin-label at position 65, as the rotamer is tp in the X-ray structure, whereas it is mm in the RE simulations. However, this position is problematic because the spin-label is involved in crystal contacts.¹⁵

For the dihedral angle χ¹, the most frequently observed rotamer in X-ray structures is m, although the t rotamer is also observed at a few positions. The m rotamer is also predicted to be the most stable energetically according to computational studies.^18,19 It has been argued that the m and t rotameric states of χ¹ might be stabilized by an interaction between the sulfur Sδ atom of the spin-label with the backbone nitrogen N and oxygen O atoms,¹⁸ though further analysis indicates that such interactions is very weak.¹⁹ For the dihedral angle χ², the predominant rotamer observed in X-ray structures is m, which is also frequently observed in the RE simulations but absent from the conventional MD or the LES simulations. Thus, there is closer agreement between the conformations from X-ray structures and those extracted from ESR/DEER experiments using RE simulations than with those obtained from unbiased MD or LES simulations. It is likely that these differences reflect the fact that the rate at which the experimental samples are frozen is slow on the molecular timescale, thereby leading to a partial annealing of some side-chains rotameric conformations to local minimum energy conformations. It is noteworthy that the nine sites (65, 72, 75, 76, 82, 115, 119, 131, 151), which are in the helix surface sites in T4L, either prefer the mm or mt rotamer for χ¹/χ².

c) Simplified representation of the spin-label for structural refinement

An important outcome of the present analysis of RE simulations is a detailed characterization of the rotamer population for MTSSL spin-labels bound to T4L based on ESR/DEER data. This information is critically important for the interpretation of ESR experiments, particularly given the general paucity of data about the conformation of spin-label. Nevertheless, these results were obtained by applying an extensive computational framework with RE simulations that may seem somewhat cumbersome if one's sole purpose is to utilize ESR/DEER data for structural refinement. This framework is not without some drawbacks. For instance, because the replicas of the spin-labels are represented with all atomic details, fairly long RE simulations may be required to allow for the conformational transitions of the five dihedrals χ¹ to χ⁵ in order to adequately sample all the accessible rotameric states. Furthermore, introducing multiple copies of the protein was necessary in the present application to avoid steric clashes between neighboring spin-labels.

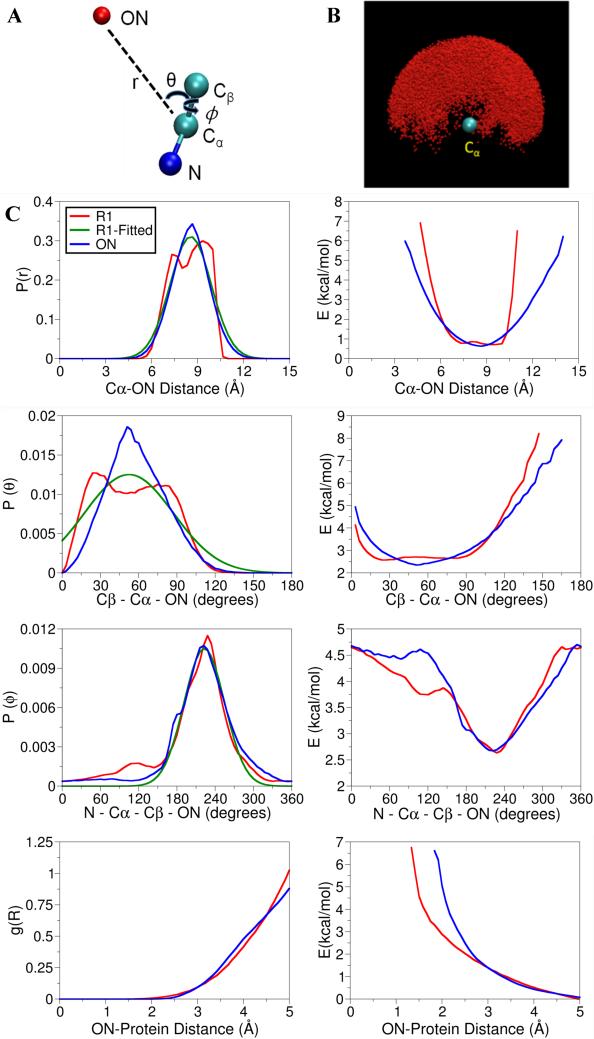
Although all these technical difficulties can be surmounted, it is tempting to try to find ways to further simplify the computational framework without compromising accuracy. A key observation guiding our efforts to design a simplified method is that structural refinement based on ESR/DEER data with RE simulations ought to be concerned only with translating the information from histograms of inter-atomic distances between the multiple copies of the oxygen of the nitroxide spin-labels into backbone constraints. In the context of structural refinement, the detailed population of accessible rotameric states represents an excess of information that is used only indirectly. In fact, the detailed molecular representation of the spin-labels is needed because it serves to accurately position the oxygen atom relative to the protein backbone. Therefore, one potential route towards a simplified framework is to take a shortcut and discard the rest of the spin-label and retain only the nitroxide oxygen as a dummy ON particle linked to the backbone. Such a simplified representation avoids the burdensome task of accounting for a large ensemble of Boltzmann-weighted spin-label rotamers. Yet, it is perfectly adequate for the purpose of translating the information from ESR/DEER data into the protein structure—as long as one has the ability to determine the position of the ON atom accurately relative to the backbone without modeling the molecular structure of the spin-label itself. The position of this dummy ON particle relative to the N, C_α, and C_β of the backbone can be parameterized via a few simple energy terms (bond, angle dihedral) to best-reproduce the statistical distribution of the spin-label side chains deduced from the all-atom RE simulations analysis (Figure 7A). As shown in Figure 7B, the configurations extracted from the RE simulations reveal that the oxygen atom of the nitroxide spin-label is distributed within a half-sphere around the C_α atom with respect to the N, C_α, and C_β atoms of the labeled residue. Interestingly, the distribution is almost uniform and does not seem to be strongly correlated with any given rotameric states.

Figure 7.

(A) Cartoon representation of the spin-label side chain, R1, is replaced with a single dummy nitroxide atom, which is attached to the C_α atom of the protein backbone. Three valuables, C_α – ON distance, C_β – C_α – ON angle and ON-C_β – C_α – N torsion are used to parameterize the dummy atom; (B) the dynamics of nitroxide oxygen of spin-labels around the C_α atom obtain from RE simulation; (C) Comparison of distribution and potential of mean force of the distance, angle, dihedral angle and nonbond interactions obtained from MD simulations with R1 and dummy nitroxide atoms.

The parameterization of the dummy nitroxide atom was carried out by determining the force constant for the Cα-ON bond (r), the C_β–C_α–ON angle (θ) and the N–C_α–C_β–ON dihedral angel (ϕ) (Figure 7A). The spatial distribution of the nitroxide oxygen atom is mapped in terms of the Cα-ON bond (r), the C_β–C_α–ON angle (θ) and the N–C_α–C_β–ON dihedral angel (ϕ), under the assumption that the values of three variables are uncorrelated (Figure S12). The distributions over r, θ and ϕ extracted from the RE simulation are shown in Figure 7C (red lines). The probability of finding the ON is maximum at a distance of about 8.0 Å from the C_α and the width of the distribution is about 5 Å. The distribution for θ is quite broad going from 0° to 110° and there appears to be two shallow humps at about 25° and 85°. There is one predominant rotameric state for the dihedral angle ϕ positioned around 180-280°, peaking around 240°. The probability distribution functions are then modeled on the basis of 3 simple energy terms, V_r = k_r(r – r₀)², V_θ = k^θ(θ – θ₀)² and V_ϕ = k_ϕ (1+cos(nϕ – ϕ₀)), where k_r, k_θ, and k_ϕ are the force constants for the distance, the angle and dihedral potentials and n represents the dihedral multiplicity. In addition, a Lennard-Jones 6-12 potential was used to account for the excluded-volume interactions between the ON particle and the rest of the protein. The radial distribution (R) of all nonbond interactions involving ON atom of the spin-label was calculated in a shell of 5Å radius and the distribution was converted to the corresponding Boltzmann energy. The result, shown in Figure 7C, indicates that the probability of finding an ON atom is almost zero between 0Å and 2.5Å from any protein atom, which is also evident from the large energy at this region, while the change in energy between 4Å and 5Å is very small (<0.5 kcal/mol). Optimized Lennard-Jones parameters are R_min = 4Å and E_min = -0.05 kcal/mol. Non-bonded interactions between the ON dummy atoms and the water molecules are switched off by using the keyword NBFIX in the parameter file, which can be read by both the NAMD⁴⁸ and CHARMM⁴⁷ program package. The optimal force constants for k_r, k_θ, k_ϕ are 0.5 (kcal/mol)/Ų, 1.0 (kcal/mol)/rad₂ and 1.9 (kcal/mol)/rad², respectively. A multiplicity of n=1 is used for the N–C_α–C_β–ON dihedral angle.

Having parameterized the ON dummy atom representation, we performed 5 ns MD simulation of T4L labeled with ON dummy atom at 37 sites. The calculated ON-ON distance distributions are slightly broader than the experimental ESR/DEER histograms, although the results are somewhat improved compared with the conventional MD simulations carried out with the detailed spin-label models with explicit solvent (Figures S6 and S13). The average distances obtained from MD simulation and experimental spin-spin distance distributions were compared using a linear regression analysis. The correlation between averaged measured and simulated distances is 0.91. These results were compared with those obtained from the Multiscale Modeling of Macromolecular systems (MMM) software package developed by Yevhen Polyhach and Gunnar Jeschke to analyze ESR/DEER data ²⁸. With MMM, the modeling is carried out on the basis of a pre-calculated library of ~200 rotamers which are then inserted at individual sites on a fixed T4L protein backbone. Configurations with clashes are discarded and a Boltzmann-weighted probability distribution is produced for each inserted spin-label, and finally an average pair distance is calculated for each pair of spin-labels. The correlation coefficient of the average distances obtained from MMM with ESR/DEER data is 0.85, which is slightly smaller to the correlation coefficient of 0.91 obtained from MD simulations with the simplified dummy ON spin-label described above.

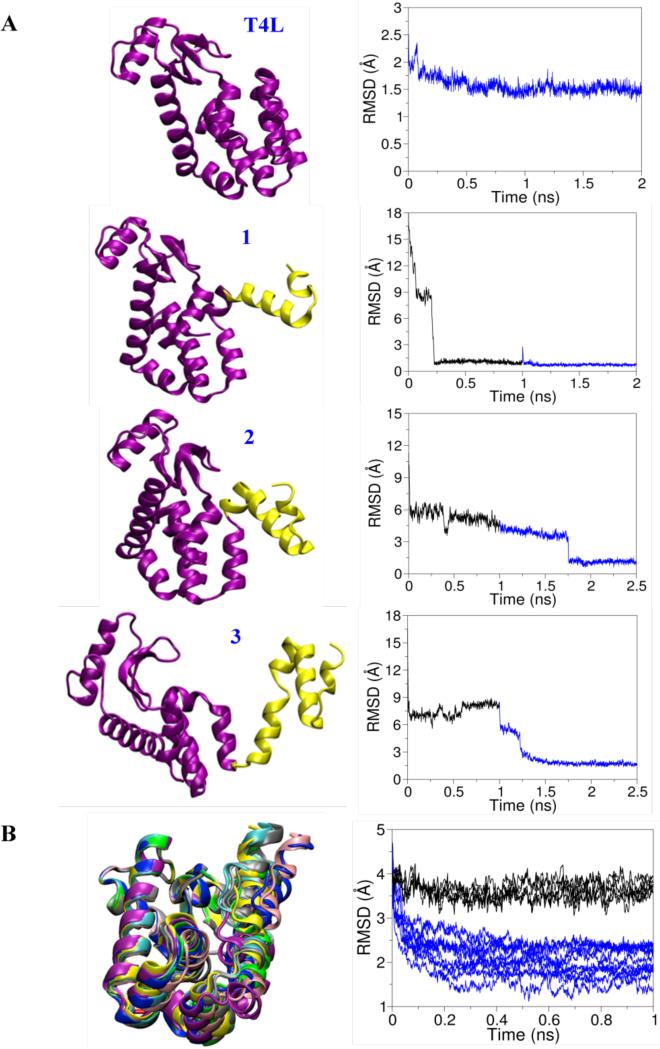
d) Illustrative structural refinement with artificially distorted conformations of T4L

The simplified dummy ON spin-label model, together with the RE simulation method, can be used to refine protein structures. As a first illustrative test, the T4L structure was refined with the RE simulation from its X-ray structure. Dummy ON atoms were attached to the 37 sites of the spin-labels in T4L and were replicated 25 times for the RE simulations. A 2ns RE simulation was performed starting from the X-ray crystal structure equilibrated from MD (in vacuum and with explicit solvent). The root mean square deviation (rmsd) over the trajectory calculated with respect to the original X-ray structure shows that the rmsd flattens out after 400ps and remains almost constant to a value of about 1.4Å (see Figure 8A). The inter-spin distance distributions are very similar to those obtained from experiment and with those obtained from RE simulation performed with the whole spin-labels (Figure S18). As a second test, the ability of the method to correct artificially distorted structures of T4L was examined. Figure 8 shows some of the distorted structures that were refined with the RE simulations. A total of 8 distorted structures were created by altering the dihedral angles in the turns or loops that are connecting pairs of helices, starting from the C-terminal helix of T4L (Figure 8). Some of the distorted models have a backbone atom rmsd of more than 15Å relative to the X-ray structure. In the refinement, an initial stage of MD simulation was first carried out using a flat-bottom harmonic distance restraints as commonly used in NMR refinement based on NOE relaxation data. The 51 average distances obtained from ESR/DEER data were used. After several ns of simulation, the rmsd of the backbone atoms of all distorted T4L with respect to the X-ray structure flattens out. The distorted structures of T4L improved for all the structures. However, the rmsd for seven distorted structures remained large, in the range of 5-17Å, from the X-ray structure. Only one distorted model reached a value of 1.7Å rmsd (Figure 8). To see if the models could be further improved, RE simulations were then performed starting from the final configuration obtained from the previous simulations. The rmsd of the backbone atoms of most of the models improved considerably, demonstrating that the RE method with the simplified dummy ON spin-label is able to further refine these structures (Figure 8). However, the backbone rmsd for some distorted models remained larger than 6Å (Figures S19 and S20). This mainly shows the limitation of a sampling algorithm that is based on straight MD simulations, even in the presence of the RE biasing. There are, however, alternative and more powerful computational strategies that have the ability to refine such highly distorted protein structures, and improve the overall rmsd down to ~4Å.^27,62 Therefore, as a final illustrative test, we sought to examine the ability of the RE method to refine 10 structures that are only moderately distorted to ~4Å rmsd (Figure 8B). In comparison, MD simulations were also performed with a NOE-like flat-bottom harmonic distance restraints. The average backbone atom rmsd, obtained from the last frame of the RE simulations, were found to be about 1.8Å with respect to the X-ray structure. In contrast, many of the models refined with the NOE-like distance restraint remained at 3.5Å rmsd (3 models refined to 2.0-3.5 Å rmsd). These results demonstrate the usefulness of RE simulation method with the simplified representation of the spin-label as a dummy ON particle for structural refinement.

Figure 8.

Cartoon representation of X-ray and distorted structures of T4L and the respective root mean square deviation of the distorted backbone atoms with respect to the X-ray structure obtained from NOE and RE simulations colored in black and blue, respectively. A. The x-ray structure is denoted by T4L and the distorted structures are denoted by 1, 2 and 3 depending on the number of distorted helices. The distorted and undistorted residues of the T4L structures are colored in yellow and purple, respective. B. Ten distorted T4L structures, with a backbone atom rmsd of about 4Å from the X-ray crystal structure, are refined using the NOE and RE simulations colored in black and blue, respectively. Each distorted structure is represented with a particular color scheme. Three black traces from NOE (black) going down to rmsd of 3.1Å, 2.8Å and 2.2Å, respectively, are not shown for the sake of clarity.

CONCLUSION

An extensive characterization of the rotamer population of the spin-labels attached to T4 lysozyme (T4L) has been carried out using a novel multiple-copy restrained-ensemble (RE) simulation method to incorporate ESR/DEER distance histogram data. In RE simulations, a global energy restraint forces the simulation spin pair distances collected from multiple copies of the system to match with the experimental distance histograms obtained from ESR/DEER. Here, 51 distance distributions for 37 nitroxide spin-labeled T4L were constrained to the experimental distributions. In contrast, results obtained from single-copy MD and unrestrained LES simulations deviate significantly from the experiments and therefore the conformational preferences of the spin-labels could be very different with these simulations when compared to experiment. In most cases, the rotamers along χ¹ and χ² at χ³ ≈ 90° and 270° are predominantly mt and mm, respectively. On the other hand, multiple rotameric states are found for χ⁴ and χ⁵ at χ³ ≈ 90° and 270°. Overall, these findings are in good agreement with the available information from X-ray crystallographic structures,^9-15,21 ESR lineshape analysis^6,21,63 and ab initio studies.^16,18 Few spin-label side chains prefer other rotameric states or multiple rotamers depending on their positions in T4L. Based on the rotameric preferences, we classified the spin-labels broadly into two groups: (1) sites in the helices will most likely prefer either mm or mt or both mm and mt rotamers and (2) sites on to the solvent-exposed loop structures, or sites completely buried in the solvent inaccessible hydrophobic cores will prefer variable rotameric states.

To develop an efficient strategy aimed at protein structural refinement based on ESR/DEER distance histograms, we designed and parameterized a simplified dummy nitroxide atom “ON” reproducing the statistical distribution of the spin-label side chains deduced from the all-atom RE simulations analysis. The 51 average spin pair distances calculated from these dummy ON spin-label are found in excellent agreement with those obtained from experiment, with a correlation coefficient of 0.91. This result demonstrates that the simplified ON dummy representation is an effective approach to accurately calculate distances between spin-labels at two sites on a protein. Artificially distorted structures of T4L were successfully refined with the final structures deviating from the X-ray structures by an rms deviation of only a few angstroms. The extent of distortion of the initial structure will dictate over the refinement process. Therefore, it is important to obtain an X-ray or NMR derived initial structure that is close to the target structure. In most cases, short several nanosecond RE simulations were sufficient to refine the distorted T4L structures. Current efforts with the RE simulation method are aimed at determining the various conformational states of ion channels and membrane transporters using ESR/DEER data.