Electron counting and beam-induced motion correction enable near atomic resolution single particle cryoEM

Abstract

In recent work with large high symmetry viruses, single particle electron cryomicroscopy (cryoEM) has reached the milestone of determining near atomic resolution structures by allowing direct fitting of atomic models into experimental density maps. However, achieving this goal with smaller particles of lower symmetry remains extraordinarily challenging. Using a newly developed single electron counting detector, we confirm that electron beam induced motion significantly degrades resolution and, importantly, show how the combination of rapid readout and nearly noiseless electron counting allow image blurring to be corrected to subpixel accuracy. Thus, intrinsic image information can be restored to high resolution (Thon rings visible to ~3 Å). Using this approach we determined a 3.3 Å resolution structure of a ~700 kDa protein with D7 symmetry showing clear side chain density. Our method greatly enhances image quality and data acquisition efficiency - key bottlenecks in applying near atomic resolution cryoEM to a broad range of protein samples.

INTRODUCTION

Recent advancements in single particle electron cryomicroscopy (cryoEM) have demonstrated its capability for determining near atomic resolution three-dimensional (3D) structures of large protein assemblies with high symmetry, such as non-enveloped viruses with^1–5 or, in one case, without⁶ icosahedral symmetry. This resolution is sufficient to allow the path of the polypeptide chain to be directly traced in the experimental density maps obviating the need for prior structural information. While in principle such resolutions should be obtainable for smaller macromolecular complexes or those without high symmetry⁷, in practice, obtainable resolutions have been in the 5 ~ 10 Å regime, sufficient for docking crystal structures but not for de novo structure determination.

Owing to the sensitivity of the sample to radiation damage, single particle cryoEM requires averaging a large number of low dose images of the same sample. Combining this data into a 3D reconstruction requires that microscope aberration parameters be determined for each micrograph as well as precise 3D orientation and translation for each individual particle image. While the quality of microscopes have been steadily improved, two key limiting factors have been the quality of the image-recording medium and image blurring caused by either instability of the sample stage or motion induced by the illuminating electron beam. Given the very low signal-to-noise ratio (SNR), image quality can significantly limit how accurately these parameters can be determined, hence the concern about the quality of the image detector. Of paramount importance is the efficiency of recording high-resolution information and reducing noise introduced by the detection process. The dominant electron image recording media are either photographic film or scintillator based charge-coupled device (CCD) cameras. However, neither satisfies the need for both high resolution (film being better) and high throughput image acquisition (only possible with electronic detectors).

The recent development of a new generation of complementary metal-oxide-semiconductor (CMOS) cameras can overcome both limiting factors. These new cameras directly detect incoming electrons in the silicon without the need for a scintillator, affording the advantages of a traditional CCD camera with greatly improved detective quantum efficiency (DQE) at high frequency, comparable to photographic film^8,9,10. A number of recent efforts have characterized the performance of the DE-12 camera from Direct Electron, LP (San Diego, CA)^11,12, and showed that the 3D reconstruction calculated from data recorded by this camera reached a level that is close to its Nyquist limit¹¹.

Image blurring resulting from the beam striking the sample is a major limiting factor to resolution when imaging frozen hydrated biological samples¹³. In practice, beam induced motion seems impossible to prevent^14,15, and deteriorates most images from “perfect” to marginal for high-resolution cryoEM¹⁶. The effect can be approximated as Gaussian blurring and quantified by analogy with the crystallographic temperature factor^17–19, predicting a greater than 5-fold decrease in signal at 3 Ź³. Thus beam-induced motion is a major limiting factor to routine high-resolution single particle cryoEM.

The high frame rate of new CMOS based direct cameras (10~40 frames/sec) provides a means to correct for such image blurring by recording a “movie” throughout the exposure. That is, a single exposure is fractionated into a number of subframes with sufficiently short duration that the motion is frozen to an acceptable level¹³. The drawback is that while the signal decreases with fractionation, camera readout noise on each subframe remains constant¹⁵. Even so, in the case of large objects such as viruses^20,21 or ribosomes²² particles, it has been possible to use the subframes as if they were independent images during the refinement resulting in an increase in resolution. However, for smaller objects the much lower SNR of each particle within a single subframe compromises the ability to accurately determine particle orientation. For this reason, we focused on a detector that minimizes both detection and readout noise as well as choosing to correct beam induced motion at the level of either the whole frame or large fractions of a frame.

While detection efficiency is significantly improved with direct detection, a statistically varying amount of energy is deposited for each electron event (Landau noise), adding noise to the otherwise high quality detection process. To surmount this problem, the K2 Summit direct electron detection camera from Gatan, Inc. was designed to allow practical detection of individual electron events, thereby eliminating the Landau noise problem^23,24. This requires very rapid frame rate and fast electron detection algorithm to minimize counting two electrons striking the same pixel in quick succession as a single event (coincidence loss). The K2 camera has a fixed internal frame rate of 400 frames/sec and the ability to centroid the electron peak (super-resolution mode) to determine its location to sub-pixel accuracy. Once detected, individual electron events are then digitally accumulated over time. By counting the primary electrons rather than simply integrating charge, as is done in traditional cameras, both the Landau noise and the readout noise of the detector can be effectively rejected, thereby dramatically improving the DQE.

Here, we demonstrate that the K2 operated in electron counting mode is superior to both photographic film and traditional CCD cameras for imaging frozen hydrated samples. Most importantly, the near noiseless readout allows for accurate registration of dose-fractionated subframes collected throughout the exposure to correct for beam-induced motion. To aid in the correction, we developed an algorithm that maximizes the self-consistency of the derived image shifts. Combining electron counting imaging and motion correction, we determined a ~3.3 Å resolution 3D reconstruction of the archaeal 20S proteasome (~700 kDa and D7 symmetry).

RESULTS

DQE and linearity of the K2 Summit

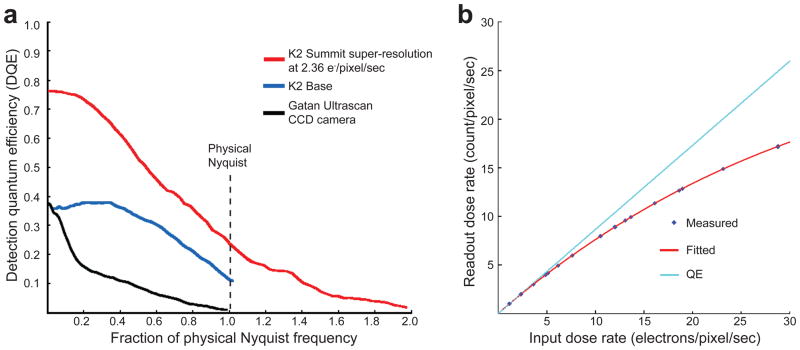
We determined the DQEs of the K2 Summit in both the conventional charge accumulation (linear) mode and the super-resolution counting mode (Fig. 1a). As expected, the DQE in K2 counting mode is significantly higher at all spatial frequencies than either the K2 in linear mode or a well-characterized scintillator based camera²⁵.

Figure 1. Detective Quantum Efficiency (DQE) and Detector Conversion Efficiency (DCE) of K2 Summit electron counting camera.

a. DQEs of K2 Summit were measured in both counting (red curve, taken at 2.36 e⁻/pixel/sec) and linear charge accumulation modes (blue curve), and are compared with the DQE of a typical scintillator-based CCD camera, the Gatan US4000 Ultrascan (black). b. The dose dependent DCEs of K2 Summit counting mode. Electron counts were measured as a function of incident electron dose rates and were fit to a polynomial curve. The straight line represents the ideal linear response with a slope of 0.87, corresponding to the quantum efficiency of the camera.

The finite internal readout rate limits the maximum electron dose rate that can be tolerated for successful counting. To investigate this, we measured the relationship between the input electron dose rate, e⁻/pixel/sec, and the camera readout rate, counts/pixel/sec (Fig. 1b). At a dose rate up to 5 e⁻/pixel/sec the response is very close to linear, with a slope approximating the very low dose quantum efficiency (measured as 87%). At higher dose rates undercounting becomes increasingly significant, with the additional coincidence loss of ~11% at 10 e⁻/pixel/sec to ~29% at 32 e⁻/pixel/sec. The measured data is well fit with a polynomial curve (Fig. 1b), which was used to determine the exact dose rate used for each image. We limited the dose rate used in our data acquisition to 8 ~ 10 e⁻/pixel/sec.

Motion correction with dose fractionated imaging

The optimal dose rate determined above requires a prolonged exposure time to record an image in order to achieve a targeted total dose, such as 20 ~ 30 e⁻/Ų, and image quality could be compromised by sample stage drift. To overcome this problem, we broke the total exposure into a stack of subframes and then mitigated image blurring by aligning all subframes within one exposure, an approach previously proposed but not fully tested¹³. As indicated above, accurate alignment is greatly facilitated by the nearly noiseless recording made possible by single electron detection and digital accumulation on the K2 camera. While our initial thought was to simply correct mechanical drift during the long exposures, it became apparent that beam-induced blurring was a major problem and could also be effectively compensated.

We developed a method to align all frames that exploits redundant information between non-adjacent subframes to obtain robust sub-pixel accuracy (see Online Methods). To explore how well induced motion could be corrected in images of frozen hydrated protein sample having low levels of contrast, we used recombinant archaeal 20S proteasome from Thermoplasma acidophilum (700 kDa and D7 symmetry) as our test specimen. Its crystal structure has been determined to 3.4 Å resolution (pdb code: 1PMA)²⁶, and our best previous 3D reconstruction of the same protein was at ~5.6 Å using photographic film²⁷.

Images were recorded from our Tecnai Polara (FEI) using the K2 in super-resolution counting mode at a magnification of 31kX, corresponding to a physical pixel size of 1.22 Å. The beam intensity was set to ~8 counts/physical-pixel/sec, corresponding to a dose rate of ~10.5 e⁻/physical-pixel/sec on camera. Images were recorded as stack of 24 subframes each of which was accumulated for 0.2 sec, resulting in an average of ~1.7 counts/physical-pixel in each subframe, and a total specimen dose of ~35 e⁻/Ų.

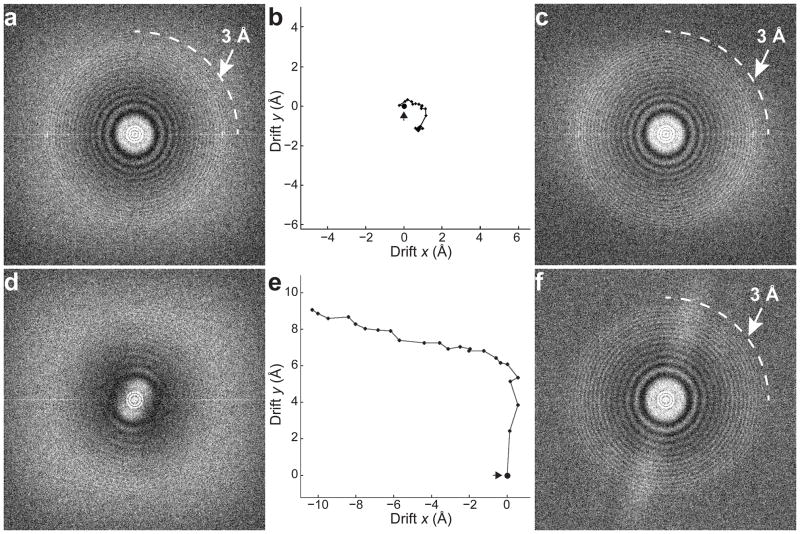
We collected 553 super-resolution image stacks and used 126,729 particles for the final 3D reconstruction. For each image stack, we generated an uncorrected image, which is the direct summation of all subframes without alignment, and a corrected image after alignment. Among the entire dataset, only a few images showed no obvious signs of motion induced image blurring or resolution loss (Fig. 2a). Even for such near perfect images, a small motion is apparent (Fig. 2b and Supplementary Fig. 1) and motion correction does slightly improve high-resolution information (Fig. 2c). At a defocus of ~1μm, this image has excellent contrast (Supplementary Fig. 1a).

Figure 2. Motion correction restores the lost high-resolution information.

a. Fourier transforms of an image of frozen hydrated archaeal 20S proteasomes. This is a near “perfect” image where Thon rings extend to near 3 Å. The cross correlation (CC) between image Thon rings at 10 ~ 5Å and simulated ideal Thon rings over the same resolution range is 0.192. b. The 24 individual subframes were cross correlated and relative positional shifts determined as described in the text and Supplementary Methods. Based on these calculations, the path of motion between the first subframe (large black dot) and last can be determined. c. Fourier transform of the same image after motion correction, where the Thon ring CC is now 0.233. d. Fourier transform of a worse image showing a predominantly unidirectional resolution cut-off at ~20Å. The Thon ring CC is only 0.092. e. The trace of motion between subframes. f. Fourier transform of the same image after motion correction showing that resolution has been isotropically restored, and the Thon ring CC improved to 0.238. The narrow white band was caused by residual fixed pattern noise in each frame, which was subsequently eliminated.

Unlike the rare superb images, the majority of uncorrected images show clear motion induced deterioration of high-resolution signal (Fig. 2d). The calculated frame-displacement trace shows that the motion was large and not unidirectional (Fig. 2e); this, the speed of the motion, and the fact that the Polara has a very stable stage, all suggest that the observed motion was mostly beam-induced rather than due to mechanical instability. Motion correction gives a very symmetrical Fourier transform in which Thon rings are seen to 3 Å resolution in all directions (Fig. 2f), demonstrating that the subframe alignments are sufficiently accurate to restore high-resolution information to a degree only previously possible in the very rare perfect images. In fact only 4 images out of a total of 553 images have a total accumulated motion of ~4 Å or less, whereas the majority have a total motion of more than 10 Å during the 5 second exposure (Supplementary Fig. 2). Additionally, using CTFFIND²⁸, it is evident that cross correlations between high-resolution Thon rings of images and simulations are significantly improved for all motion corrected images (Supplementary Fig. 3). Thus, motion correction allows a large portion of images that would otherwise be discarded to be rescued, essentially making every collected image count.

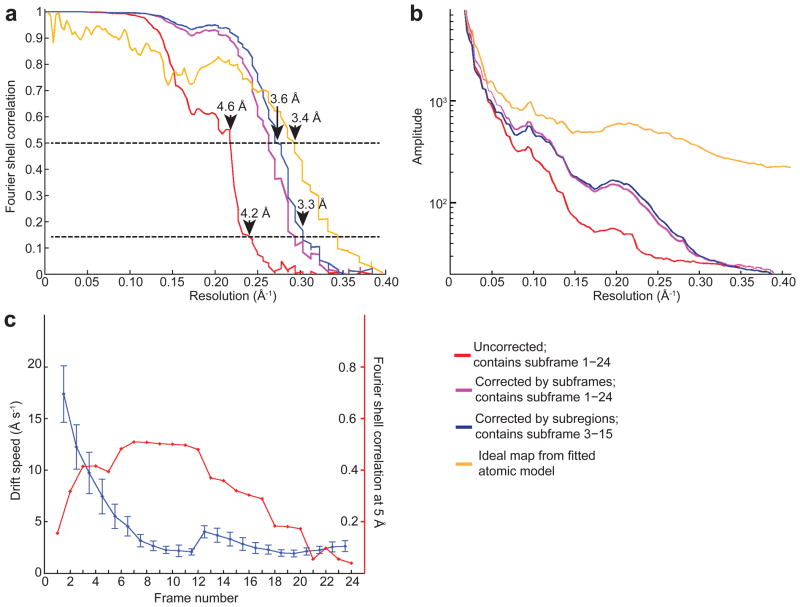
More important is the impact of motion correction on the actual 3D reconstruction (Fig. 3). We determined 3D reconstructions using both uncorrected and corrected images. Using the uncorrected data it was possible to obtain a map with a nominal resolution around 4.2 Å (Fig. 3a) which was a dramatic improvement over the best ever achieved for this sample on film (5.6 Å), demonstrating the very high quality of K2 images. Correcting the beam-induced motion for all subframes with a single shift produces another leap in resolution to 3.5 Å, and results in a 3D density map with better high-resolution features (Supplementary Fig. 4). Comparing the Fourier power spectrum calculated from these two 3D reconstructions also shows a significant improvement in Fourier amplitude, corresponding to a reduction in temperature factor of the 3D reconstruction (Fig. 3b)¹⁸.

Figure 3. Analysis of motion induced image blurring on resolution of the 3D reconstruction.

a. Comparison of Fourier Shell Correlation (FSC) curves from 3D reconstructions using images without motion correction (red), images corrected using the entire subframe and containing all subframes (purple), and images corrected by subregion and containing subframe 3 – 15 (blue). Horizontal dashed lines are shown for both the FSC = 0.5 and 0.143 criteria. The FSC curve between the final map and that calculated from the fitted atomic model is shown in gold. b. Comparison of rotational averages of Fourier power spectra of the different 3D reconstructions (the same colors as in a). c. The average speed of motion from the entire dataset of 553 images vs. subframe number is shown (blue). Error bars indicate standard deviations of each average. Note the roughly exponential decay of initial motion as the sample equilibrates in the electron beam. The quality of 3D reconstructions calculated using particle data taken from the indicated individual subframes are quantified by the FSC value at 5 Å resolution (red) derived from Supplementary Fig. 5a. The same particle parameters were used for all 24 3D reconstructions.

Beam-induced motion in the frozen hydrated specimen

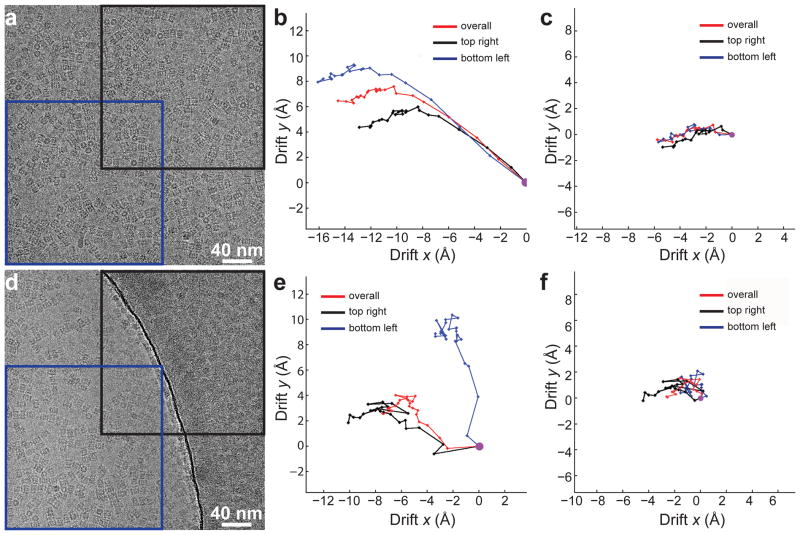
While assuming that the entire subframe responds equivalently allows the majority of the motion to be corrected, previous work²⁰ has demonstrated that the motion is non-uniform. To explore the ability to accurately correct more local motions, we further divided each subframe area into a number of regions and determined the motion of each (Fig. 4). For the sample and dataset used here, the smallest region for which the alignment could stably be determined was about 2,000×2,000 pixels. As expected, in many images, motions in different areas are significantly different (Fig. 4b and e). However, such differences typically became small after a few subframes (Fig. 4c and f). Indeed, analysis of the 553 images shows that motion is fast in the beginning of the exposure and slows down quickly (Fig. 3c). Thus, discarding the first 5 subframes would result in a significantly smaller average image motion of less than 1 Å in the 0.2 sec accumulation used here (Supplementary Fig. 2). A similar observation was described previously but the magnitude of motion in the first few subframes was significantly larger²¹.

Figure 4. Subregion motion correction.

a. An image of vitreous ice embedded 20S proteasomes taken completely within a single hole. Red and blue squares represent two different subregions of 2048 × 2048 pixels. b. Comparison of displacement traces determined from the two subregions (black and blue) with that determined using the entire subframe (red). Note that the trends of motions in the subregions are similar, although their speeds in the first few subframes are different. c. Subframe displacement traces from the same image after removing the first 5 frames. The difference between two regions is significantly less than that in b. d–f. Similar to a–c, but the image spans both the hole and the surrounding supporting carbon film. The displacement traces from subregions of carbon film and vitreous ice indicate that they behave very differently under the electron beam. After removal of the first 5 subframes, the remaining shifts are similarly reduced.

While beam induced motion is largest in the first few frames, beam induced sample damage is at a minimum. To ascertain the high-resolution information content across the entire exposure, we calculated 24 3D reconstructions using particle images from each single subframe out of the image stack and the same reconstruction parameters, which were based on refinement against the complete corrected images (Supplementary Fig. 5). The FSC curves (Supplementary Fig. 5a) show that the resolution initially increases, corresponding to the decreased speed of image motion, and after the15th subframe decreases due to accumulated radiation damage. The FSC values at 5 Å of each single frame 3D reconstruction correlate well with the average motion speed (Fig. 3c).

3D reconstructions of archaeal 20S proteasome

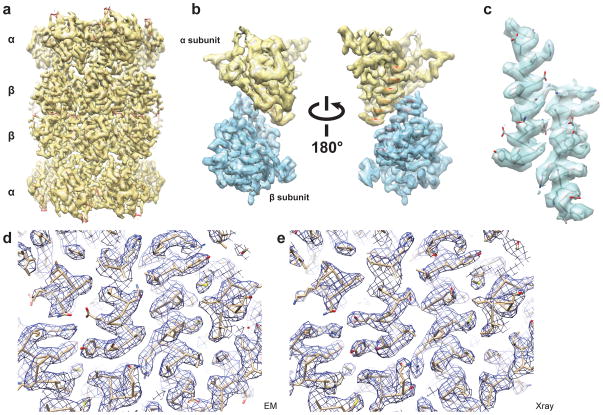
To obtain the best reconstruction, we corrected beam-induced motions using 3 × 3 subregions of 2048 × 2048 pixels and then refined the 3D reconstruction using a frequency-limited refinement procedure²⁹ (Supplementary Fig. 6a, Online Methods). We further excluded the first two subframes (deteriorated by fast motion) and last 10 subframes (deteriorated by radiation damage) from calculating the final 3D reconstruction. The final 3D reconstruction has a nominal resolution of 3.3 Å (Fig. 3a) and is based on a total dose of ~17.5 e⁻/Ų, although the full dose of 35 e⁻/Ų was used for particle refinement. This nominal resolution was confirmed by the gold standard FSC (Supplementary Fig. 6b)²⁹. This 3D reconstruction, its FSC curve and the rotational average of its Fourier power spectrum are noticeably better than that calculated from all subframes and using the entire subframe for motion correction (Fig. 3, and the density map in Supplementary Fig. 4c). While the difference in amplitude between the red and blue curves is not well represented by a single exponential fall-off (B factor), the equivalent B-factor improvement ranges from ~100 Ų at 10 Å to ~50 Ų at 5 Å. In the 3D density map (Fig. 5a–c), the C_α main chain can be traced unambiguously and most side chain densities are well resolved, validating the nominal resolution estimated from the FSC curve (Fig. 3). The atomic structure including most of side chains of T. acidophilum 20S proteasome fits well into the final 3D density map, except for a small reverse turn loop of 3 residues in the β-subunit (Met22, Glu23 and Asn24). These residues have much higher temperature factors in the 3.4 Å crystal structure, and can be remodeled to fit nicely into the density map (Supplementary Fig. 7). The overall quality of the cryoEM 3D density map is very similar to a 3.4 Å 2Fo-Fc map from the crystal structure (Fig. 5d and e). The nominal resolution as well as the overall quality of the density map is similar to several recently obtained reconstructions of much larger icosahedral viruses having much higher internal symmetry².

Figure 5.

Final 3D reconstruction of archaeal 20S proteasome reveals clear side chain detail

a. 3D density map of T. acidophilum 20S proteasome filtered to a resolution of 3.3 Å. b. Two different views of asymmetrical α- and β-subunit segmented from the 3D density map shown in a. The main chain can be traced throughout the entire map. c. Two α-helices segmented from the α-and β-subunits showing clear density for the majority of side chains. d. A portion of the cryoEM density map showing clear side chain densities. The docked atomic structure was refined to fit the density map by molecular dynamic flexible fitting procedure. e. The same portion of a 2Fo-Fc map of 3.4 Å crystal structure calculated using the atomic structure (pdb code: 1PMA).

Discussion

The potential of single particle cryoEM has been demonstrated by the recent near-atomic resolution structures of large icosahedral viruses. While all the methodologies enabling this capability can be applied to a broad range of proteins, those with smaller size and less symmetry pose additional challenges. Here we show that the combination of electron counting together with a new motion correction algorithm make such resolutions obtainable for smaller and lower symmetry samples. In fact, our 3.3 Å structure (Fig. 5c) is comparable in resolution and map quality to the crystal structure (3.4 Å, Fig. 5e), strongly indicating the power of single particle cryoEM for detailed structural biology.

Importantly, the electron counting camera is superior to both photographic film and linear types of digital cameras. Its benefits derive from improved DQE at high resolution (demonstrated by the ~3 Å Thon rings; Fig. 2) and excellent DQE at low resolution (allowing small proteins to be imaged at the relatively low defocuses favorable for high resolution). In this study, images of 20S proteasome showed excellent contrast even when recorded at a defocus of ~1 μm at 300 kV (Supplementary Fig. 1), which was impossible when using either photographic film²⁷ or a scintillator based CCD camera³⁰.

The other critical advantage of a counting camera is the combination of essentially noiseless imaging and a high output frame rate. Together, these enable optimal collection and alignment of dose fractionated data without the information loss inherent to any linearly accumulated camera. This not only provides a means for motion correction but also enables a better understanding and treatment of beam-induced motion, which is probably the most challenging physical problem in cryoEM^13–15. Without correction, the vast majority of images were deteriorated by beam-induced motions and only a very small fraction (~1%) could be characterized as close to “perfect”. Motion correction improved the quality of almost all images (Supplementary Fig. 3) and Thon rings from a large number of corrected images are seen at close to 3 Å (Fig. 2), which is comparable or better than images of icosahedral virus samples recorded on photographic film². Ideally, beam-induced motion should be corrected at the individual particle level during refinement of the 3D reconstruction as demonstrated recently²¹. However, even using electron counting, the SNR of a single 20S particle in a single subframe is much too low to permit accurate alignment. Instead, we used subregion motion correction and rejection of the first few frames as an alternative to improve local motion correction.

Potentially, the correction of beam-induced motion can be further improved. Our results indicate that the motion speed is very high in the first few frames and removing these frames resulted a better 3D reconstruction. However, the specimen is least damaged by electron beam radiation during the first fractions of an exposure³¹. A shorter subframe accumulation time would reduce motion blurring captured within each subframe, and thus might rescue the discarded first few subframes. We tested this with a small image set in which 5 sec exposure images were fractionated into 50 subframes that each had an average of ~0.8 counts/pixel. The beam-induced motions were correctable (Supplementary Fig. 8 and 9), but at the expense of significantly more computation and data storage space. It will be worth exploring combining our approach (using finer dose-fractionated subframes) with that described by ref. 21 (averaging adjacent subframes and estimating the motion trajectory).

The final 3D reconstruction presented here was calculated from ~120,000 particles having D7 symmetry, which is many more than theoretically predicted⁷. While high resolution can be achieved with many fewer particles (Supplementary Fig. 10), particle alignments were from the full dataset. It may be possible to mitigate this effect by recording images with more subframes and a much higher total electron dose to boost the low-resolution amplitudes for better alignment, while only using the early subframes for the reconstruction. With this and other improvements, it should be possible to get much closer to theoretical predictions.

In conclusion, by combining an electron counting camera with dose fractionation and correction of motion induced image blurring, we have achieved a near-atomic resolution reconstruction of a ~700 kDa protein with only D7 symmetry. The motion correction greatly enhanced high-resolution data acquisition efficiency, and should facilitate application of near-atomic resolution single particle cryoEM to a broad range of protein samples.

ONLINE METHODS

Motion correction based on redundant measurements

Algorithm

Assuming that a dose fractionated image stack contains n subframes, f₁, f2, …, f_n, the relative shift between two adjacent subframes, f_i and f_i+1, is r_i = [x, y]. The goal of any motion correction algorithm is to accurately determine all r_i (i = 1 to n-1). A commonly used algorithm is to determine r_i by locating the peak position in the cross correlation map between two adjacent subframes f_i and f_i+1, or between one fixed subframe and every other subframe. In these approaches, each r_i is determined only by a single measurement. While computationally efficient, this approach has potential disadvantages, i) it is difficult to estimate accuracy from a single measurement; ii) any residual fixed noise pattern from hot or dead pixels or otherwise imperfect dark current correction will generate a strong cross correlation peak in the center of correlation maps, which can over-shadow the real peak from image alignment, iii) this problem is compounded by low signal-to-noise ratios (SNR) that can broaden the cross correlation peak or iv) small amount of image shift between adjacent subframes that can bury the true peak in the side of a false origin peak. Thus, the accuracy of single measurement approach is limited by unpredictable errors caused by complicated shapes and features of cross correlation peak.

Instead, we use redundant measurements for a more accurate and self-consistent determination of image shifts. A relative shift, b_ij, between any two subframes, f_i and f_j where j > i, is the summation of shift vectors between all intervening adjacent subframes, r_i (Supplementary Fig. 11):

$${\mathit{r}}_i+{\mathit{r}}_{i+1}+\dots +{\mathit{r}}_{j-1}={\mathit{b}}_{ij}.$$ (1)

b_ij can be measured by locating the maximum value of the cross correlation map, often after applying a B-factor (see blow), between the subframes f_i and f_j. By determining all possible image shifts between any two subframes, we generate a set of linear equations which contains m = (n-1)n/2 equations like equation (1):

$$\{\begin{array}{lll}{\mathbf{r}}_1\hfill & =\hfill & {\mathbf{b}}_{12}\hfill \\ {\mathbf{r}}_1+{\mathbf{r}}_2\hfill & =\hfill & {\mathbf{b}}_{13}\hfill \\ \hfill & \dots \hfill & \hfill \\ {\mathbf{r}}_2+{\mathbf{r}}_3+{\mathbf{r}}_4\hfill & =\hfill & {\mathbf{b}}_{25}\hfill \\ {\mathbf{r}}_2+{\mathbf{r}}_3+{\mathbf{r}}_4+{\mathbf{r}}_5\hfill & =\hfill & {\mathbf{b}}_{26}\hfill \\ \hfill & \dots \hfill & \hfill \\ {\mathbf{r}}_i+\dots +{\mathbf{r}}_{j-1}\hfill & =\hfill & {\mathbf{b}}_{ij}\hfill \\ \hfill & \dots \hfill & \hfill \end{array}.$$ (2)

Because the number of equations is much greater than the number of unknowns r₁, …, r_n−1, equation (2) is an over-determined set of linear equations. It can be rewritten in a matrix form as:

$$A\mathit{r}=\mathit{b},$$ (3)

where A is an m×(n-1) coefficient matrix, r = [r₁, r₂, …, r_n-1]^T, b = [b₁₂, b₁₃, …, b_ij, …]^T (j > i), superscript T indicate transposition. A least-square solution of r can be calculated by the generalized inverse matrix method as following:

$${\mathit{r}}_{\text{s}}={(A^{T}A)}^{-1}{A}^{\text{T}}\mathit{b}.$$ (4)

The residual error of each measured shift b_ij can be calculated by

$$\mathrm{\Delta }b=\left|\right|A{\mathit{r}}_{\text{s}}-\mathit{b}\left|\right|.$$ (5)

Δb can be used to qualify the accuracy of xy-shift determination. In the current study, any equation with a residual error larger than a give criterion, such as 1 pixel, is removed from equation (2) and (3) unless removing it makes A become not full ranked. Afterwards, Eq. 4 is recalculated to get the final solution, r_s. Finally, all subframes are shifted to the same origin by changing the phase in their Fourier transform. Summation of all corrected subframes produces an image in which motion induced image blurring is corrected.

Centroid of cross correlation peak at sub-pixel precision

The peak position in the cross correlation map between two subframes can be directly determined to a precision much better than 1 pixel. In the cross correlation map, the peak position is first identified, then an area of 16 × 16 pixels around the peak is cropped out from the cross correlation map. The Fourier transform of the cropped area is then padded to a larger area of 512 × 512 pixels, followed by an inverse Fourier transform, allowing the position of the cross correlation peak to be determined by Fourier interpolation to precision of 1/32 pixel. This procedure is equivalent to but computationally more efficient than the direct interpolation in the cross correlation map by sinc function profile fitting.

Applying motion correction to images of frozen hydrated protein samples

While the method described above is applicable to motion correction of any multi-subframe image stack, applying it to dose fractionated image stacks of frozen hydrated protein samples recorded with the K2 Summit in electron counting mode benefits from additional considerations.

Fixed pattern noise

A critical factor that influences the accurate determination of small shifts is any residual fixed pattern noise, which usually results from imperfect gain normalization and dark reference subtraction or any uncorrected dead or hot pixels on the camera. This pattern is identical in each subframe and generates a strong and sharp peak in the origin of the cross correlation map. Under very low dose conditions, this peak is often stronger than the real cross correlation peak from image alignment. We took two strategies to avoid or to reduce the influence of fixed pattern noise.

Because these problems are generally caused by individual pixels, the contribution of fixed noise pattern to the Fourier transform is mostly beyond half Nyquist limit. Thus the severity of this problem can be minimized by applying a low pass filter such as a B-factor to all subframes:

$$e^{-\frac{1}{2}{BH}^2}$$ (6)

where B is the factor with unit of pixel², and H is the spatial frequency with the unit of pixel⁻¹. A B-factor of 100 ~ 200 pixel² is sufficient to reduce the intensity of the sharp correlation peak corresponding to the fixed noise pattern, but not to significantly influence the shape of the real cross correlation peak from image alignment. While applying a B-factor means that only low-resolution information is used for subframe alignment, motion correction does restore high-resolution information in the corrected image (Supplementary Fig. 12).

The second strategy is to set a minimal subframe interval between any two subframes that are used for determination of b_ij in equation (1) and (2). This is to avoid aligning a subframe with its immediate adjacent subframes, where the image shifts between which are relatively small and the cross correlation peak is very close to the peak from the fixed noise pattern.

Frame exposure time

Ideally, the subframe recording time should be kept as short as possible to minimize the uncorrectable image motion captured in each subframe. Motion within the subframe elongates the cross correlation peak and introduces a larger error in identifying the peak position. Furthermore, fractionating the total dose into more subframes produces more equations in (2), which have the potential to reduce statistical errors. However, a shorter subframe accumulation time also reduces the average counts per pixel, and thus reduces the SNR of each subframe, which in turn weakens and broadens the cross correlation peak. Thus, for a fixed total dose, there is of limit of how many subframes can be used while maintaining a satisfactory alignment accuracy. We have tested the algorithm described above and obtained satisfactory results from fractionating 10 subframes in 1 second. Under this condition, the average counts per pixel is ~0.8 (Supplementary Fig. 9 and 10). With this shorter exposure, the fast beam-induced motion in the first few frames can be better corrected.

We implemented the algorithm described here into a program that runs on graphic processing units (GPU) for fast processing. Correction of an image contains 24 subframes of 3840 × 3840 pixels takes ~10 seconds to complete on a single GTX580 GPU.

Materials and experimental procedures

Materials, instrumentation and data acquisition

The Thermoplasma acidophilum 20S proteasome was expressed and purified from Escherichia coli according to established protocols ^27,30. A drop of 2 μL of purified 20S proteasome at a concentration of ~0.9 μM was applied to glow-discharged Quantifoil holey carbon grids (Quantifoil, Micro Tools GmbH, Germany), and plunge-frozen by using a Vitrobot Mark III (FEI company, USA). Images of frozen hydrated T. acidophilum 20S proteasome were collected on a FEI TF30 Polara electron microscope (FEI Company, Hillsborough, OR) equipped with a field mission electron source and a Gatan K2 Summit camera (Gatan Inc., Pleasanton, CA). The microscope was operated at an accelerating voltage of 300 kV.

The K2 camera has 3840 × 3840 physical pixels. All counting images were recorded using super-resolution mode, resulting in 7680 × 7680 super-resolution pixels. Fresh hardware and software flat fielding gain and dark references were carefully prepared using the Gatan Microscopy Suite (GMS) for each dose rate used immediately before data acquisition. The pixel sizes at different magnifications were calibrated by using hexagonal ice lattice at −185°C. All images of frozen hydrated protein samples used here were recorded at a nominal magnification of 31 kX, corresponding to a physical pixel size of 1.22 Å at the specimen level. We used UCSFImage4 to control all data acquisition. All images were recorded with a defocus in the range of 0.8 ~ 1.9 μm. Grids of frozen hydrated samples were imaged at dose rate of ~8 counts/physical pixel/sec for 5 seconds with a total specimen dose of ~34 e⁻/Ų. Each image was fractionated into 25 subframes, with 0.2 seconds subframe accumulation time. The first subframe was discarded due to a slight delay in shutter opening, resulting in a partial exposure. After collecting 553 images, 20 more images were collected with a 5 second exposure, but fractionated into 50 subframes that each has 0.1 seconds subframe accumulation. These 20 images were not used for the 3D reconstruction but only for testing motion correction at a lower subframe dose (Supplementary Figs. 9 and 10). All images were saved as stacks of subframes in full resolution for later processing. An uncorrected dataset was generated by direct summation of all subframes within one image stack.

Determination of DQE

DQEs of the K2 Summit in both the linear and super-resolution counting mode were measured by knife-edge images recorded at an acceleration voltage of 300 kV. DQE was measured as described in ref. 32 and similar to the method described in ref. 33. The method relies on the conversion of the fundamental definition of DQE as SSNR_out/SSNR_in to the form MTF²/(NPS/dose) and on the use of an image of the shadow of a post-TEM-optics edge as a source of known frequency content for the MTF measurement. Since an edge image spans a range of signal levels, detector linearity has been a precondition for the use of this method. In the case of a detector which exhibits a gradual change in DCE due to changes in coincidence loss as dose is increased, dose levels need to be used at which dose dependence is small and all measurements need to be taken at the same dose rate to ensure consistent calibration. The dose chosen for data acquisition and the dose used for DQE measurement, 2.4 e⁻/physical pixel/s, was at a level where the deviation from linearity in the DCE curve (Fig. 1b) is very small. This means that the error in the edge-shadow DQE method will be small. Attempts to measure DQE at 10 e⁻/pixel/s and higher doses lead to overestimates caused by the non-linearity of coincidence loss.

Determination of DCE

A series of super-resolution images without specimens were recorded at incremental dose rates from 1 to 30 counts/pixel/sec by adjusting the beam intensity. Multiple measurements were taken for each data point. For each counting image, a corresponding image recorded with the K2 Summit operating in linear mode was also recorded at the same beam condition. During the image acquisition, the exposure time was also changed from 40 sec at 1 count/pixel/sec to 10 second at 30 counts/pixel/sec in order to maintain a total dose of at least 40 e⁻/pixel. The DCE curve shown in Figure 1b was obtained by plotting the averaged readout rate (counts/pixel/sec) from the counting image against the input dose rate (e⁻/pixel/sec), and a polynomial curve was fitted against all data points. The input dose rate was calculated from the counts of the corresponding linear image, which we calibrated at a high dose rate as one electron generates 30.0 ± 0.5 counts. The linear mode calibration was measured using the Gatan GIF drift tube and Keithley 6485 picammeter set to its slowest sampling rate. Once determined, the fitted polynomial curve was used to calculate actual input dose rate from the readout count rate on camera for subsequent experiments.

The slope of straight line in Figure 1b is 0.87, corresponding to the quantum efficiency (QE) determined as the slope of tangent line of the fitted polynomial curve at origin. Coincidence loss, which causes the camera readout to deviate from a linear relationship, was calculated as the differential between the observed cunts and those expected with a finite QE.

Image processing

All super-resolution subframes were 2 × 2 binned for further processing. The final image pixel size is 1.22 Å. All binning was calculated by using Fourier cropping, in which a Fourier transform from the original 7680 × 7680 pixel image was calculated, and a central 3840 × 3840 pixel area was cropped out followed by a reverse Fourier transform to produce an image of 3840 × 3840 pixels that is 2 × 2 binned from the original image. Initial defocus values of each image were determined by using CTFFIND3²⁸ on uncorrected and 4 × 4 binned datasets.

We corrected beam-induced motion in each image by using the algorithm described above. For 24 subframe image stacks, the minimum subframe interval was set to 7 to avoid alignment between very adjacent subframes, which could have very small shift and result in inaccurate subframe alignment. Thus, a total 138 comparison were carried out for a total 24 subframes. The corrected image stacks were evaluated by using CTFFIND3²⁸, setting the resolution range to 10 ~ 5 Å. The cross correlation value before and after motion correction was used to monitor the motion correction procedure.

Side view particles of 20S proteasome were picked automatically using FindEM³⁴. All picked particles were first subjected to standard procedures of multiple rounds of multi-reference alignment and classification implemented in SPIDER ³⁵. Particles within bad 2D classes were discarded. Remaining bad particles were removed by further manual inspection. The final dataset contains 129,008 particles. GeFREALIGN³⁶ was used to refine and determine the 3D reconstructions with D7 symmetry following a frequency-limited refinement procedure²⁹. A map calculated from the atomic structure of the archaeal 20S proteasome (pdb code: 1PMA) was used as initial model. The Euler angles and in-plane shift were first determined by global search followed by local refinement (mode 4 in GeFREALIGN). The resolution of search and refinement was limited to 15Å and the 3D reconstruction at each cycle was calculated to the Nyquist limit. We carried out a total of 5 cycles of global search, local refinement and 3D reconstruction. This was followed by an addition 25 cycles of local refinement (mode 1 in GeFREALIGN). The resolution for the refinement was gradually increased to 5 Å. At this stage the resolution of 3D reconstruction had reached 3.4Å. We continued refinement for another 10 cycles with the resolution of refinement gradually increased to 3.5 Å. A total of 126,729 particles were used in the final 3D reconstruction, after rejecting 2,279 particles based on a phase residual cut-off. The resolutions of 3D reconstructions were estimated by using Fourier Shell Correlation curves using FSC = 0.143 criteria¹⁸, but the resolutions corresponding to the FSC = 0.5 were also given. The final 3D reconstruction, which contains only subframes 3–15, has a resolution of 3.3 Å (Supplementary Fig. 6a).

In light of the recent development of using a “gold standard” FSC to estimate the resolution ²⁹, we repeated the entire data processing by splitting the data into two half datasets with even and odd numbered particles and processed them separately. The first initial model was the same as described above and the initial search and refinement was limited to 15 Å. The final FSC curve calculated between the two independently processed sets gave the gold standard FSC curve, which is very similar to the FSC curve obtained previously (Supplementary Fig. 6b), attesting to the high signal to noise ratio in the reconstruction. We also calculated an FSC curve between the gold standard map and the conventional map, which gave an FSC = 0.5 at 3.3 Å (red curve in Supplementary Fig. 6b). This excise confirms the resolution we had obtained by the frequency-limited refinement procedure. All figures were prepared from the map calculated from the frequency-limited refinement method. As pointed out previously over-fitting can be prevented by either frequency-limited refinement or gold standard procedures²⁹, it is not surprising that the two procedures gave the same resolution.

After particle picking, we carried out subregion motion correction. Each subframe was divided into 3 × 3 subregions of 2048 × 2048 pixels with overlap, which generated 9 subregions stacks. The motion correction was carried out on each subregion separately. All particles were assigned to the nearest subregion according to the distance to the centers of 9 subregions, and boxed out from the corrected image from the corresponding subregion. The final 3D reconstruction was calculated from the subregion motion corrected image stack, which yielded an improved FSC. To calculate the final 3D reconstruction, we further removed the first 2 and the last 10 subframes, using only subframes 3 to 15 of each subregion corrected image stack. The amplitude of the final 3D density map was scaled to the ideal density map from the atomic structure, and low-pass filtered to the estimated resolution.

Docking of atomic structure

The atomic structure of T. acidophilum 20S proteasome (pdb code: 1PMA) was first docked as a rigid body into the 3D density map by using the fit-in-map function from UCSF Chimera³⁷. The atomic structure, including both main chain and side chains, fits well into the final 3D density map, except for a small loop of 4 residues. The fitting was further refined by using the molecular dynamics flexible fitting (MDFF) procedure³⁸.